An auxetic structure with negative Poisson's ratio exhibits distinctive mechanical properties in contrast to conventional structures, garnering interest in various fields. However, current research has predominantly focused on the design and optimization of auxetic structures, with limited exploration of their practical applications. In this study, we utilized 3D printing technology to fabricate a soft auxetic structure with triangular shaped perforations, examining the mechanical properties based on geometric structure. Additionally, by inserting shape memory alloys into the fabricated soft auxetic structure, we achieved active two-dimensional deformations and confirmed its selective object permeability. This technology holds the potential to have far-reaching implications across a broad spectrum of industries.

음의 푸아송 비를 갖는 오그제틱 구조는 일반적인 구조와 상반된 거동 특성을 지니고 있어 에너지 흡수, 로봇 등의 다양한 분야에서 관심받고 있다. 하지만, 현재까지는 오그제틱 구조의 설계 및 최적화에 대한 연구가 중점적으로 진행되고 있으며 이를 활용하는 연구는 미비한 실정이다. 따라서, 본 연구에서는 3D 프린팅 기술을 활용하여 삼각형 형태의 천공을 가진 소프트 오그제틱 구조를 제작하여 기하학적 구조에 따른 기계적 물성을 확인하고, 푸아송 비의 변화를 계산하였다. 또한, 제작한 소프트 오그제틱 구조 내에 형상기억합금을 삽입함으로써 오그제틱 구조의 능동적 2차원 변형을 구현하고 이의 선택적 물체 투과성을 확인하였다. 이 기술은 소프트 로봇, 웨어러블 전자기기, 통기성이 제어되는 차세대 의류, 스마트 유연 센서 등 넓은 범위에 걸쳐 다양한 산업분야에 파급효과를 불러올 수 있을 것이다.

Keywords: 오그제틱 구조(Auxetic structure), 형상기억합금(Shape memory alloy), 형상 모핑(Shape morphing), 3D 프린팅(3D printing)

음의 푸아송 비를 갖는 오그제틱 구조는 일반적인 구조에 비해 우수한 압축저항, 높은 인성 및 전단 계수, 에너지 흡수 및 소산, 낮은 균열 전파 등의 구조적 특성을 가지고 있어 “기계적 메타물질”이라고 불리며 최근 스포츠, 모빌리티, 우주, 항공 등의 다양한 분야에서 관심을 받고 있다[1-6]. 특히, 오그제틱 구조는 재진입 구조, 카이랄 구조, 회전 유닛 구조, 무작위 연결 구조, 상호작용입자 등 다양한 형태가 존재하며 단위 셀의 선택에 따라 구조의 거동에 아주 큰 영향을 받기에 현재까지는 재료의 조성과 복합재 구성보다는 오그제틱 구조 자체의 설계 및 최적화에 따른 거동 제어 연구가 활발하게 진행되고 있다[7-12]. 그 중, Grima와 Evans가 제시한 회전 유닛 기반 오그제틱 구조는 다른 오그제틱 구조들과 비교하여 아주 높은 음의 푸아송 비를 갖는 장점이 있고, 다양한 회전 유닛 셀을 바탕으로 2D에서 3D로 형상 변화를 할 수 있는 가능성을 보여주었다[13].
따라서, 본 연구에서는 회전 삼각형 천공(triangular shaped perforations, TSP) 기반 소프트 오그제틱 구조를 제작하고, 기하학적 설계 요소에 따른 구조의 기계적 특성을 파악해보고자 한다. 아직까지 오그제틱 구조와 능동적 형상 변형 소재가 결합된 연구가 전무하기에, 추가적으로 소프트 삼각형 천공 구조 내에 형상기억합금(shape memory alloy, SMA)을 삽입하여 선택적 투과성을 갖는 능동형 액추에이터를 제작하고, 구조 내 SMA의 수에 따른 거동을 확인할 것이다. 삼각형 천공 구조는 형상 변화에 따라 중심부의 공간이 생기기 때문에 이를 활용한 선택적 물체 투과성을 시연하고자 한다.

2.1 재료 및 기기
본 연구에서는 PDMS (Sylgard 184 a/b, Dow corning), SMA (Nitinol, XUNSHI), PVA 필라멘트(DY PVA, 덕유항공)를 별도의 처리없이 그대로 사용하였다. 3D 프린터는 플래시포지 어드벤트4 프로를 사용하였으며, Arduino Uno 보드와 고출력 서보모터(MG995, 에듀이노)를 활용하여 성능 평가를 진행하였다. 3D 구조 설계와 이미지 분석에 각각 Inventor와 Image J 소프트웨어를 사용하였다.
2.2 PDMS 물성치 테스트
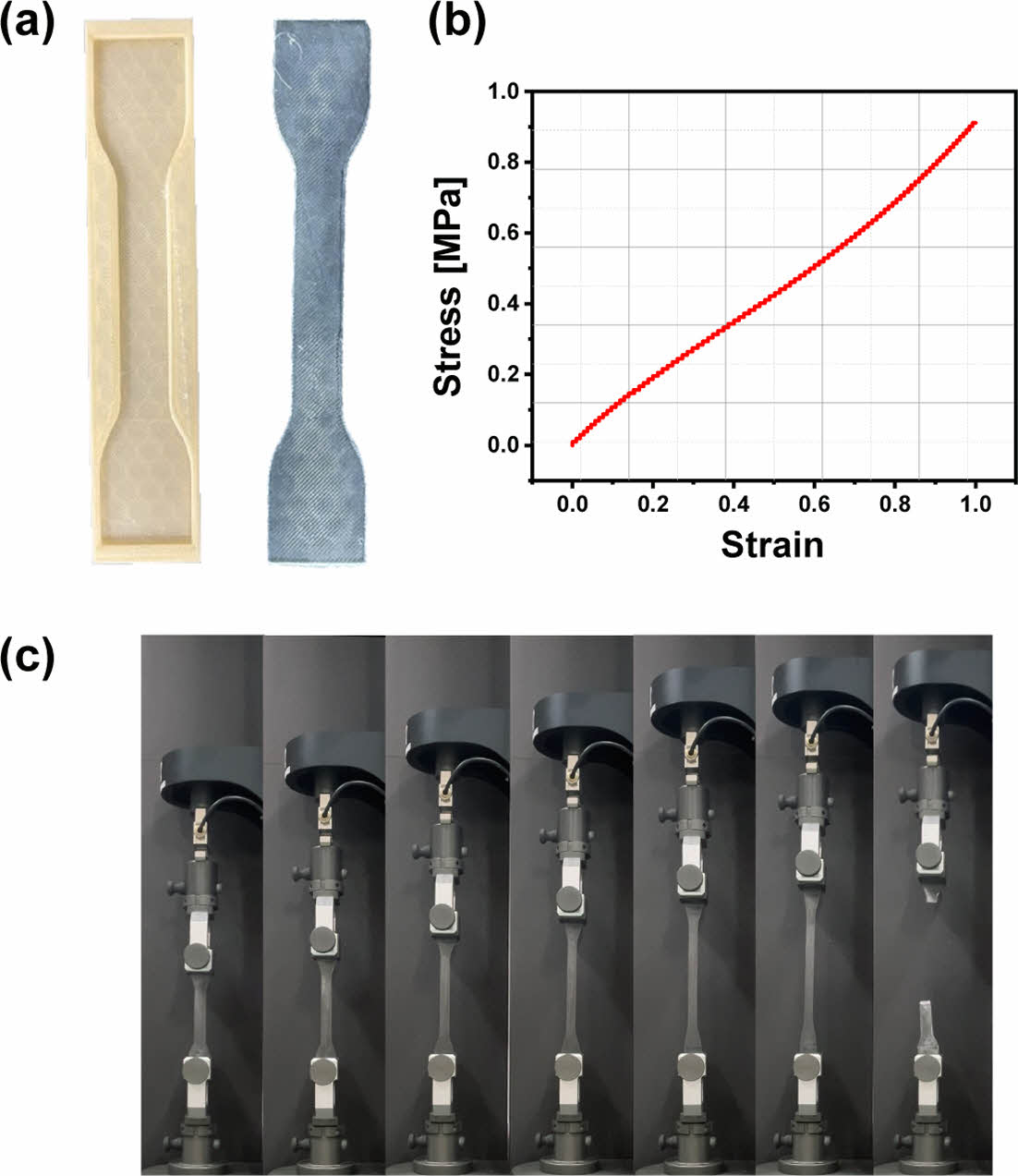
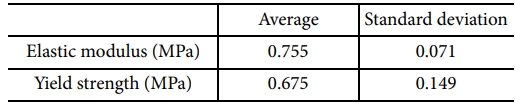
본 연구를 진행하기 앞서, 연구에 사용하는 PDMS의 물성치를 파악하기 위해 3D 프린터를 이용해 ASTM D412 형상의 몰드를 제작하고 이에 PDMS를 부어 시편을 제작하였다. 제작한 시편은 인장기(UNITEST M1, TEST ONE)를 사용하여 테스트하였다. 인장 속도는 20 mm/min으로 설정하고 실험을 수행하였으며, 그 결과는 Fig. 1에 나타나 있다. 주제와 경화제를 10:1로 섞은 PDMS의 탄성계수와 항복강도의 값은 Table 1에 나타나있다. 이는 시편 6개에 대한 평균과 표준편차이다. 탄성 계수의 기울기 범위는 응력-변형률 선도 내 선형적으로 변하는 구간에 대한 기울기 범위인 0.0098 MPa 부터 0.4903 MPa까지 지정하여 계산하였다. 계산된 값은 단면변화를 고려하지 않은 초기 단면을 기준으로 사용한 값이다.
2.3 소프트 삼각형 천공 구조의 제작
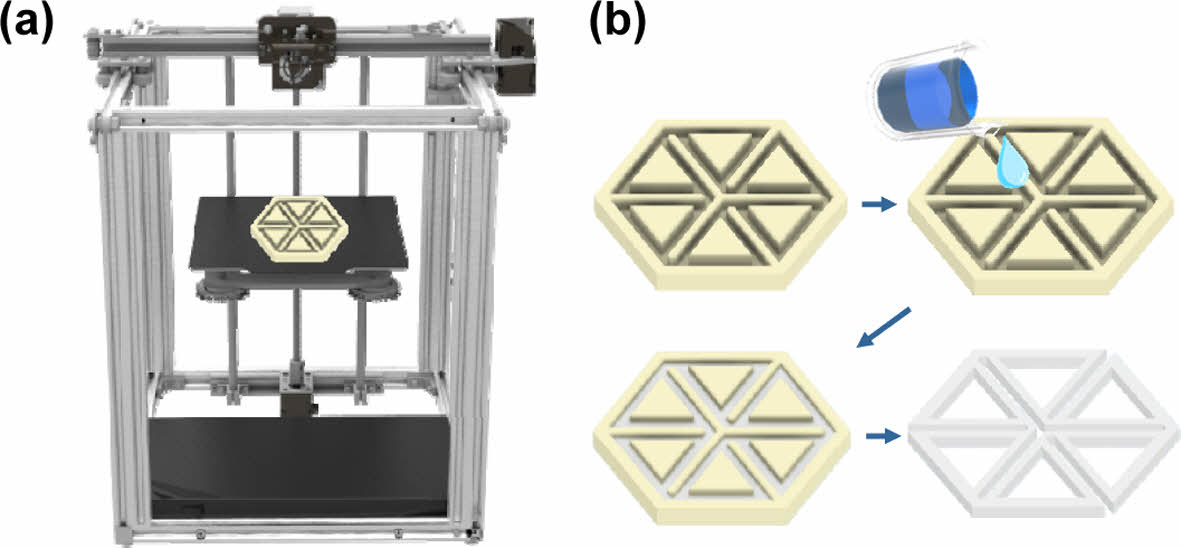
음의 푸아송비를 갖는 삼각형 천공 구조는 Fig. 2와 같은 거동을 보인다. 이 구조를 활용해 소프트한 삼각형 천공 구조를 제작하기 위하여, Inventor 프로그램을 통해 음각 형태의 몰드를 설계하였다. 먼저 3D 프린터로 음각 형태의 몰드를 제작하고 PDMS를 그 위에 부어 굳힘으로써 PDMS 기반 소프트 삼각형 천공 구조를 제작할 수 있도록 하였다. 그 제작 과정은 Fig. 3에 잘 나타나 있다.
소프트 구조를 제작할 때 가장 중요하게 고려해야 할 부분은 몰드와 구조의 안정적 박리이며, 이를 위하여 본 연구에서는 물에 녹는 수용성 필라멘트인 PVA를 몰드의 재료로 사용하였다. 3D프린터를 활용하여 PVA 몰드를 준비하는 동시에, PDMS의 주제와 경화제를 10:1 무게 비율로 교반하여 준비한다. 여기서 PDMS 주제는 30 g, 경화제는 3 g을 사용하였다. 이 후, 제작된 PVA 음각 몰드에 PDMS를 부어 상온에서 약 40시간 굳힌다. 일반적으로 온도를 높이며 경화하지만, 온도를 60도이상 높일 경우 PVA 몰드의 변형이 일어나는 경우가 있어 상온에서 경화시켰다. PDMS가 덮인 몰드를 물 속에 넣고 48시간 이상 녹인 후 필라멘트를 분리하면 소프트한 TSP 구조체를 쉽게 얻을 수 있다.
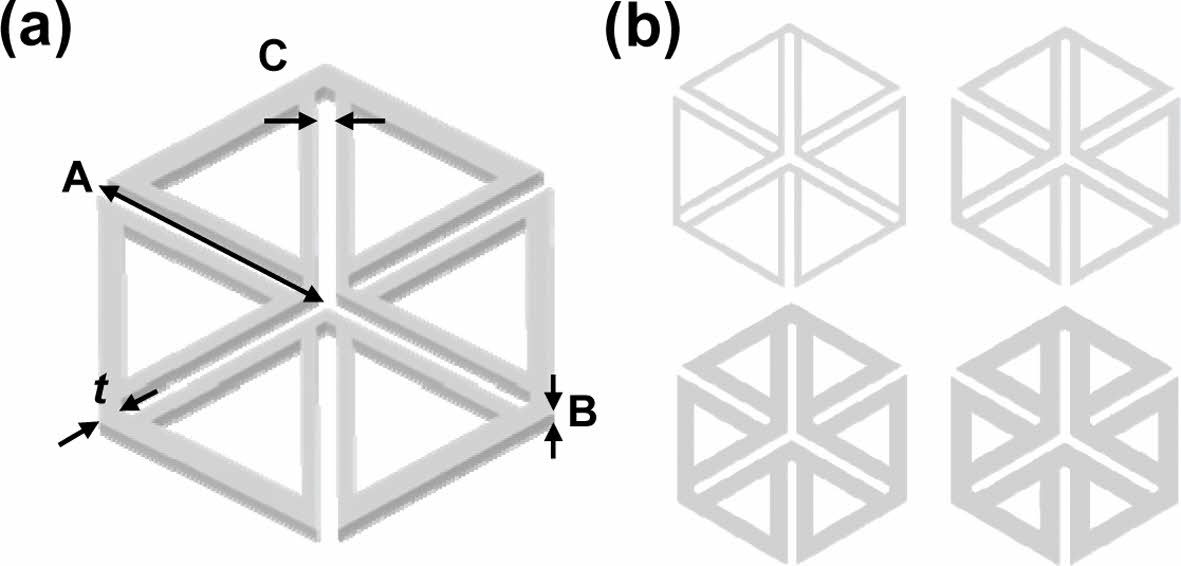
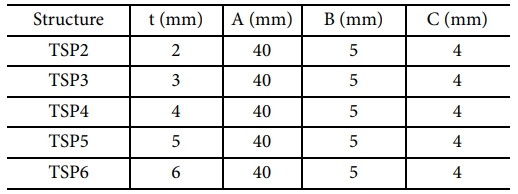
본 연구에서는 소프트 삼각형 천공 구조의 두께에 따른 기계적 거동 특성을 파악하고자 하였으며, 두께 및 설계 요소들은 Table 2에 나타나 있다. TSP 뒤에 붙은 숫자는 각 구조의 이음부 두께 t를 의미한다. Fig. 4(a)에 t, A, B, C가 나타내는 요소를 표현해주고 있으며, A는 구조의 삼각형 한 변의 길이, B는 구조체의 높이, C는 구조체 내부 공간 사이의 거리를 각각 의미한다. Fig. 4(b)는 소프트 삼각형 천공 구조의 두께 별 모식도를 나타낸다.
2.3 SMA 포함 소프트 삼각형 천공 구조 제작
Fig. 5는 SMA를 포함하는 소프트 삼각형 천공 구조를 제작하는 과정을 보여준다. Fig. 5(a)는 SMA 포함 소프트 삼각형 천공 구조의 모식도이며, Fig. 5(b)는 모식도에 상응하는 실제 구조의 사진이다. 구조의 중심부에 SMA가 들어가 전압 인가에 따라 구동 됨으로써, 삼각형 천공 구조가 펼쳐지는 형태가 될 수 있고, 시간이 지남에 따라 PDMS의 자체 강성 덕분에 초기 상태로 다시 돌아오게 되어 재사용이 가능하다.
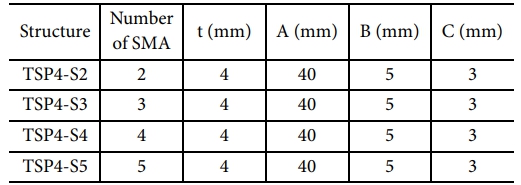
SMA를 포함하는 소프트 천공 구조를 제작하는 방법은 상기 단순 소프트 천공 구조를 제작하는 방법에서 PDMS를 붓기 전에 SMA를 삽입해주는 과정만 추가된다. 3D 프린터로 제작된 PVA 몰드에 SMA를 추가할 수 있는 구멍을 뚫고, SMA를 삽입한다. SMA는 별다른 형상을 기억시키지 않아, 열이 가해지면 직선 형태로 펼쳐지게 되어 있다. SMA가 삽입된 몰드에 동일하게 PDMS 주제 30 g과 경화제 3 g을 섞은 용액을 부어 실온에서 약 40시간 이상 굳힌다. 이후 물 속에서 수용성 필라멘트를 제거하여 SMA를 포함하는 소프트 천공 구조를 얻는다. 각 구조체는 Table 3과 같은 조건으로 제작하였다. 본 구조체는 앞선 실험에서 두께가 4 mm인 TSP4 구조를 활용하여 제작하였다. 이는 두께가 너무 얇을 경우, SMA의 개수를 목표치만큼 끼울 수 없고 너무 두꺼운 경우 구조체가 움직이기에 어려움이 있을 것으로 판단해 두께가 4 mm인 구조체를 선택해 제작하였다. Table 3에 나와 있듯이, TSP4-S의 뒤에 표기된 숫자는 구조에 삽입된 SMA의 개수를 의미한다.

3.1 소프트 삼각형 천공 구조의 기계적 특성
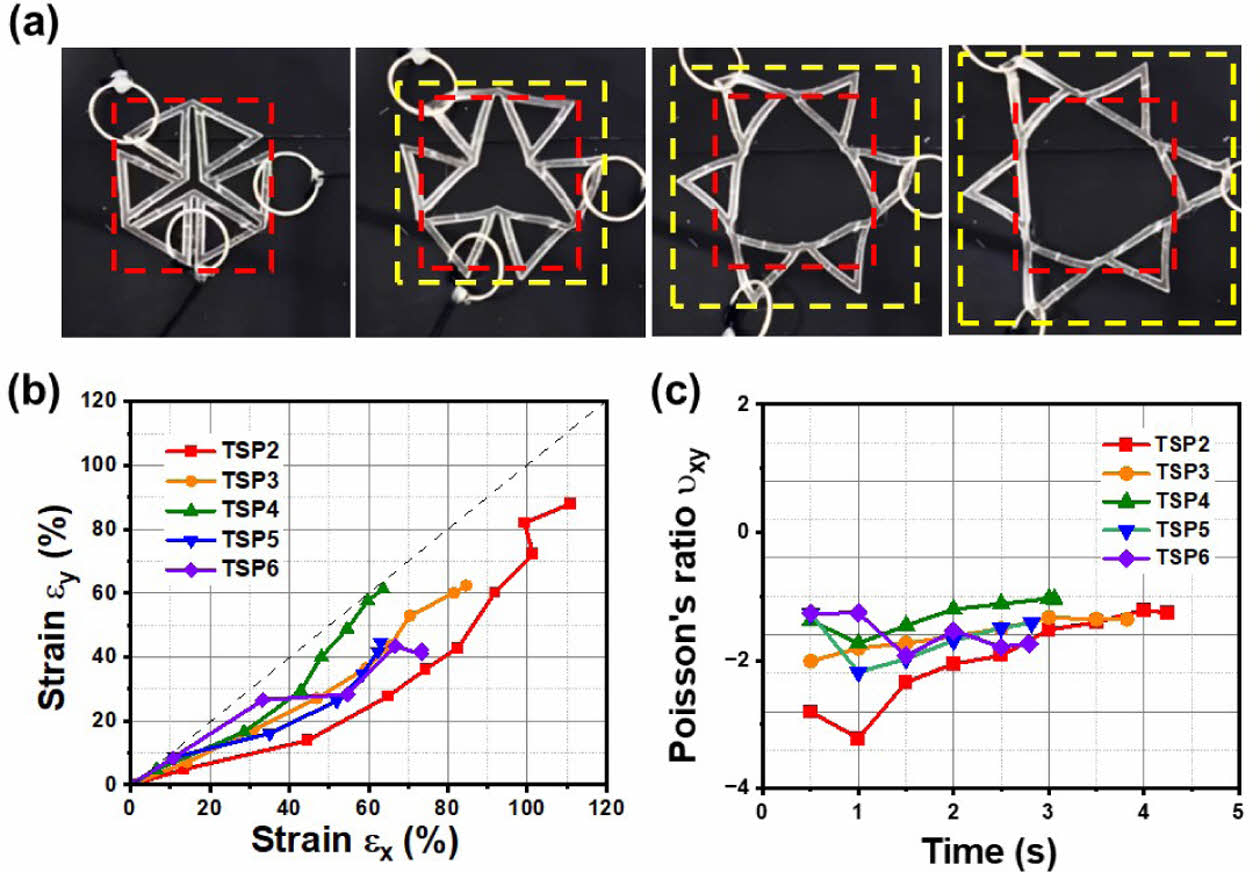
소프트 천공 구조의 정확한 수직 및 수평 방향 거동을 정확하게 실험하고 측정하기 위하여 구조를 세 방향으로 당겨주는 기구를 제작하였다. 세 개의 모터를 동일한 간격으로 배치하고, 거리 및 회전 속도 등의 조건을 동일하게 설정한다. 모터 축에는 실을 당겨줄 도르래를 설치하고, 도르래에는 줄을 연결한다. 연결한 줄 끝에는 링을 달아 구조체를 잡을 수 있도록 한다. 기구를 완성했다면, 완성된 기구의 링에 구조체를 걸어 연결한다. 이때, 링의 초기 위치는 모두 동일한 위치에서 시작한다. 본 실험에서의 초기 위치는 Fig. 6(a)에 나타나 있듯이 각 삼각형의 꼭지점이며, 모터를 작동하면 동시에 줄이 당겨지면서 오그제틱 구조의 음의 푸아송 비를 나타내는 구조 변형을 야기하게 된다. 모터는 구조체가 끊어질 때까지 작동시킨다. 이 후, 구조체의 변화를 0.5 s 간격으로 측정해 실험값을 얻는다. Fig. 6(a)의 사진들에 표기된 빨간색 박스는 실험 전 구조의 크기이고, 파란색 박스는 모터 구동 후 변화한 구조의 크기인데, 사진으로도 본 연구에서 제작한 소프트 삼각형 천공 구조가 음의 푸아송 비 특성이 나타나는 것을 확인할 수 있다.
본 실험에 따른 소프트 삼각형 천공 구조의 변형률 측정 값과 푸아송 비는 Fig. 6(b)와 Fig. 6(c)를 통해 확인할 수 있다. Fig. 6(b)는 각 구조 별 가로 변형률 값에 따른 세로 변형률 값을 나타낸 그래프이다. 그래프의 이상적인 형태는 점선으로 표기된 선형적인 값을 따라가는 게 맞지만, TSP2를 보면 두께가 얇을수록 소프트한 소재 기반 구조의 낮은 안정성 때문에 비선형적 거동을 보이는 것을 확인할 수 있다. 두께가 두꺼워지면서 점차 선형적인 거동을 보여주지만 TSP5와 TSP6는 너무 강한 구조 강성 때문에 가로 변형에 따라 세로 변형이 잘 일어나지 않는 모습을 보였다. 따라서 TSP4 구조가 가장 이상적인 선형 변형의 모습을 보여주는 것을 확인할 수 있다. TSP2 구조는 가로 및 세로변형률이 110.81%, 87.95%일 때 파단되었으며, TSP3, TSP4, TSP5, TSP6 구조는 각각 (84.57%, 62.35%), (63.64 %, 61.18%), (62.99%, 44.44%), (73.33%, 42.16%)일 때 파단되었다. 또한 Fig. 6(c)에 나타난 시간에 따른 푸아송 비의 변화를 보면, 두께가 얇을수록 변형이 많이 일어나 가장 높은 최고 푸아송 비를 보여주었으며 두께의 증가에 따라 점점 최고 푸아송 비가 감소함을 확인할 수 있다.
3.2 SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조의 구동 특성
다음으로, SMA의 개수에 따른 SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조의 가로 및 세로 변형률을 SMA에 전압을 인가하며 측정하였다.
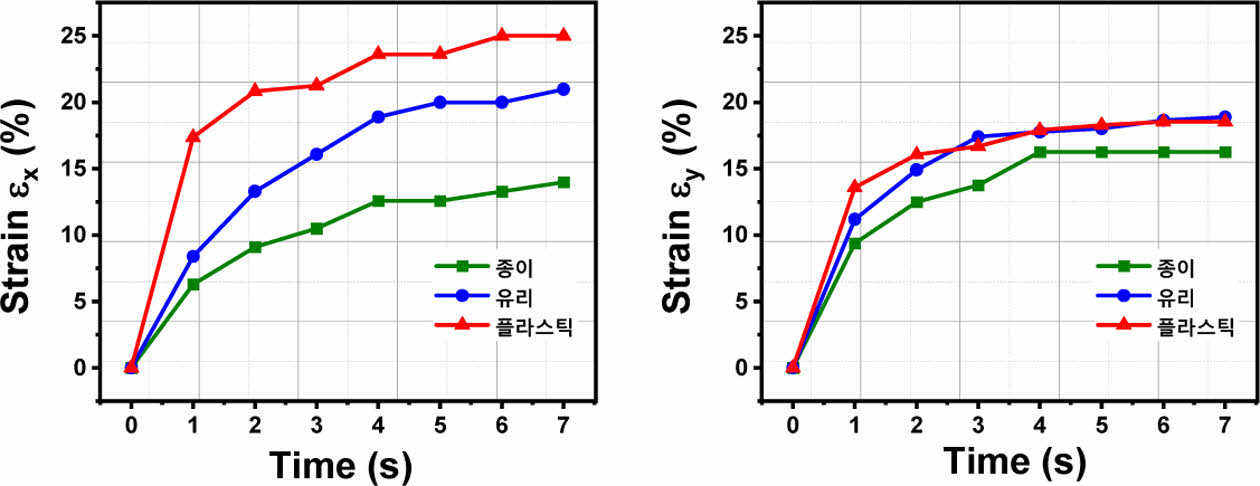
먼저 바닥 판의 마찰이 SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조의 거동에 미치는 영향을 파악하기 위한 실험을 진행하였다. 실험에 사용될 바닥 판은 종이, 유리, 플라스틱으로 선정하였다. 제작된 구조체를 종이, 유리, 플라스틱에 각각 올려 기준점을 표시하고, 파워 서플라이에 연결된 악어 집게 위치를 고정함으로써 외부로 노출되는 SMA 영향을 최소화하였다. 이후 SMA 끝 단에 파워 서플라이를 연결하고 3.5 A의 균일한 전원을 공급하여, 구조가 더 이상 변하지 않을 때까지 실험을 진행하였고, 실험 결과는 Fig. 7와 Fig. 8에 나타나 있다. Fig. 8의 결과를 보면, 플라스틱 바닥 위의 구조체가 다른 구조체보다 동일한 시간 대비 더 많은 변형을 보이는 것을 확인하였다. 이는 PDMS 자체가 끈적한 표면을 갖고 있어 종이와 유리보다는 표면이 코팅된 플라스틱에서 상대적으로 더 잘 움직이기 때문이다. 따라서 이후 모든 실험은 플라스틱 바닥 기반으로 진행되었다.
SMA 개수 별 구조체의 변화과정은 Fig. 9의 구조 변형 사진들을 통해 확인할 수 있다. SMA의 개수가 증가함에 따라 동일한 시간 동안 가로 및 세로 변형이 더 많이 되는 것을 확인할 수 있으며, 구조 변형 후 중심부의 공간도 더 커지는 것을 확인할 수 있다.
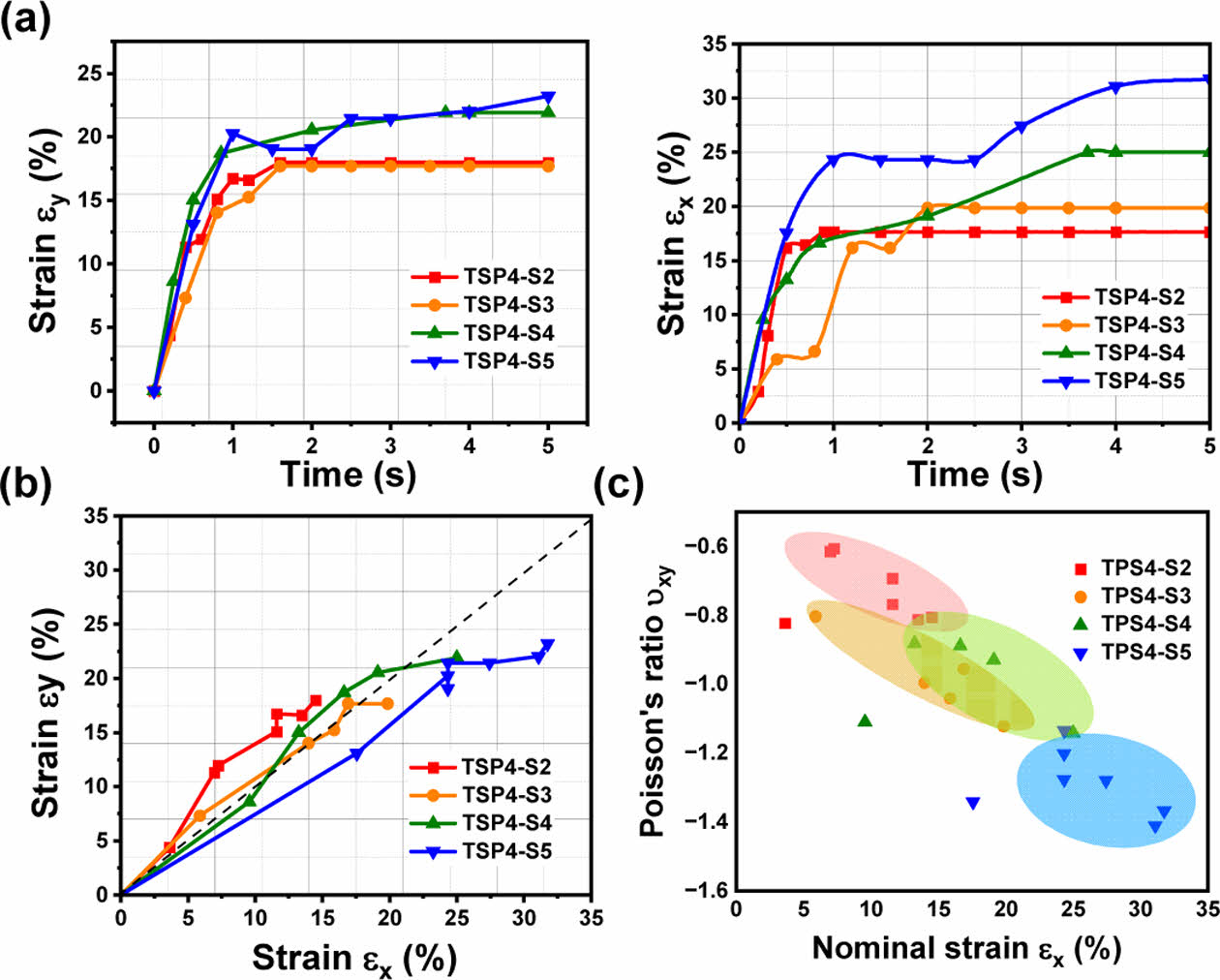
Fig. 10(a)는 SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조의 시간 별 가로 변형률과 세로 변형률을 각각 표기한 그래프이다. 내부 SMA의 온도가 균일하게 올라가지 않아 비선형적인 변형률 값이 나타나긴 했지만, SMA의 개수가 많아짐에 따라 변형률 값이 높아진다는 것을 확인할 수 있다. SMA를 구동시켰을 때, 개수가 많아지더라도 변형률 값이 지속적으로 증가하지는 않았으며, Fig. 6에 나타난 중심부 공간과 변형률 값을 비교해보면 내부 SMA의 구동에도 구조가 완전히 전개되지 못하여 변형량이 다소 작은 단점을 확인할 수 있었다. 반면, 비교적 가로와 세로 변형률이 선형 관계를 보이는 것을 Fig. 10(b)에서 확인할 수 있고 SMA의 개수가 증가함에 따라 가로와 세로 최대 변형률 값 모두 높다는 것을 한눈에 확인할 수 있다. TSP4-S5는 31.76%와 23.21%의 가로 및 세로 최대 변형률을 보여주었으며, 그에 반해 TSP-S2는 각각 14.49%, 17.98%의 가로 및 세로 최대 변형률을 보여주었다. Fig. 10(c)에서는 각 구조의 가로 변형률에 따른 푸아송 비 값을 확인할 수 있다. 이 실험을 통해, 모든 구조에서 음의 푸아송 비 특성이 확인됨과 동시에, SMA 개수가 많아질수록 오그제틱 구조의 음의 푸아송 비가 높아짐을 확인하였다.
삼각형 천공 구조의 중요한 특징 중 하나는 이 구조가 음의 푸아송 비 특성을 보이며 거동할 때, 중심부의 공간이 변형되며 물체의 선택적 투과가 가능하다는 것이다. 따라서 본 연구에서도 제작된 SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조의 중심부 크기를 제어함으로써 물체 선택적으로 통과시키는 실험을 간단하게 진행하였다. TSP4-S4를 선택하여 진행하기로 하였으며, 이는 Fig. 10(b)의 그래프에서 확인할 수 있듯이 SMA에 전압을 인가하였을 때 가장 선형적으로 거동하는 구조이기 때문이다. SMA에 전압을 인가하기 전에는 투과하지 못했던 물체가 전압을 인가함에 따라 중심부의 천공을 통해 투과하고, 전압을 인가하지 않을 때 되돌아오는 것을 Fig. 11에서 확인할 수 있다.

본 연구에서는 소프트 삼각형 천공 구조를 설계하고 제작하여 기계적 특성을 파악하였으며, 이에 형상기억합금을 추가적으로 넣어 구조가 능동적으로 형상 변형하도록 제작하였다. 소프트 삼각형 천공 구조의 이음부 두께가 얇을수록 가로 및 세로 변형이 더 많이 됨을 확인할 수 있었으나 소프트 소재의 특성 상 구조적 안정성이 떨어져 비선형적 거동을 보였다. 파단 될 때까지 가장 선형적인 구조는 TSP4였다. SMA-PDMS 복합재 기반 소프트 삼각형 천공 구조에서는 SMA의 개수가 증가할수록 변형률이 30%까지 높아졌으며, 물체의 선택적 투과까지 시연하였다. 다만, 소프트 소재 기반 오그제틱 구조의 연구가 많이 진행되고 있지 않아 다양한 응용에 활용되기 위해서는 더 많은 연구기 필요할 것으로 보인다.

이 연구는 금오공과대학교 대학 연구과제비로 지원되었음(2022).