In this paper, development of tape-springs made of composite materials was conducted for the deployment structures along with design, analysis, fabrication, and numerical and experimental investigation of mechanical behavior of the tape-springs. To this end, the tape-springs were manufactured according to three stacking patterns, and numerical and experimental investigation were conducted to determine whether or not they were damaged during bending with various selected composite materials. Finally, optimal stacking patterns that do not cause damage were selected during bending. With this information, the four-point bending test was conducted to obtain the moment-rotation curves. From results, it was confirmed that the nonlinear hysteresis phenomenon of the tape-springs was properly realized according to folding and unfolding. Therefore, it was confirmed that the composite material tape spring was properly developed

본 논문에서는 전개장치용 복합재료 테이프 스프링 개발을 위해 테이프 스프링의 설계, 해석, 제작 및 기계적 특성을 검토하였다. 이를 위해 다양한 복합재료 소재를 선정하고 3개의 적층 패턴에 따라 제작하여 굽힘 시 파손여부를 구조해석과 실험적으로 검토하였다. 이중 파손이 발생하지 않고 잘 굽혀지는 소재와 적층 패턴을 선정하였다. 이렇게 확보된 정보를 이용해 전개구조물용 테이프 스프링을 개발하고 4점 굽힘 시험을 통해 구조적인 특성을 검토하였다. 시험 결과로부터 굽힘과 펴짐에 따라 모멘트-회전 곡선에서 테이프 스프링 고유의 비선형 히스테리시스 현상이 적절히 구현됨을 확인하였다. 따라서 복합재료 테이프 스프링이 적절히 개발된 것을 확인하였다

Keywords: 테이프 스프링(Tape-spring hinge), 복합재료(Composite materials), 전개 장치(Deployable structure), 파손 기준(Failure criteria), 인공위성(Satellites)

인공위성에 접혀서 탑재된 태양전지판, 안테나 등 수납된 구조물이 임무수행을 위해 궤도 환경에서 전개되기 위해서는 다양한 전개 메커니즘을 사용한다. 이때 전개 메커니즘은 토크스프링과 모터를 이용한 구동장치가 널리 사용한다. 토크스프링은 접혔을 때 저장되는 굽힘 변형에너지로 구조물을 전개하는 가장 간단한 전개 메커니즘으로 모터를 사용하는 구동장치에 비해 가볍고 신뢰도가 높아 국내외 많은 위성사업에 태양전지판, SAR 안테나, 안테나 붐 전개에 널리 사용되어 왔다[1-3]. 토크스프링 중 유연한 테이프 스프링을 이용한 전개 메커니즘은 형상이 간단할 뿐만 아니라 고유의 비선형 히스테리시스에 의해 전개 충격이 감소되는 특징이 있어 국내 다목적실용위성에 장착되는 태양전지판 전개에 사용되었다.
테이프 스프링의 기계적 특성 관련 연구는 Wuest와 Mansfield에 의해 모멘트-회전 곡선을 분석한 방법이 처음 소개된 이후 꾸준하게 연구되고 있다[4-10]. 기존에 우리나라에서 개발되는 다목적실용위성 태양전지판에 사용되는 테이프 스프링은 상용 판매되는 스테인리스(Stainless Steel, STS) 재질의 줄자를 기본 소재로 제작하여 전개 모멘트와 전개 강성을 자유롭게 조절하는데 어려움이 있다. 물론, 금속으로 제작된 테이프 스프링을 자체 개발할 수도 있으나 소요되는 테이프 스프링이 소량이므로 개발비용 측면에서 적절하지 않다. 또한, 우주에서 다양한 온도 환경에 노출될 때 금속 재질의 열팽창으로 인해 길이가 급격히 변화하기 때문에 안테나 및 붐 등 고정밀도를 요구하는 우주 구조물에 적용되기 어렵다. 이러한 문제를 해결하기 위해 해외에서는 높은 비강성, 비강도 및 낮은 열팽창계수를 갖는 복합재료를 적용한 테이프 스프링을 연구하고 제작하여 항공 우주분야에 사용하고 있다[11-16].
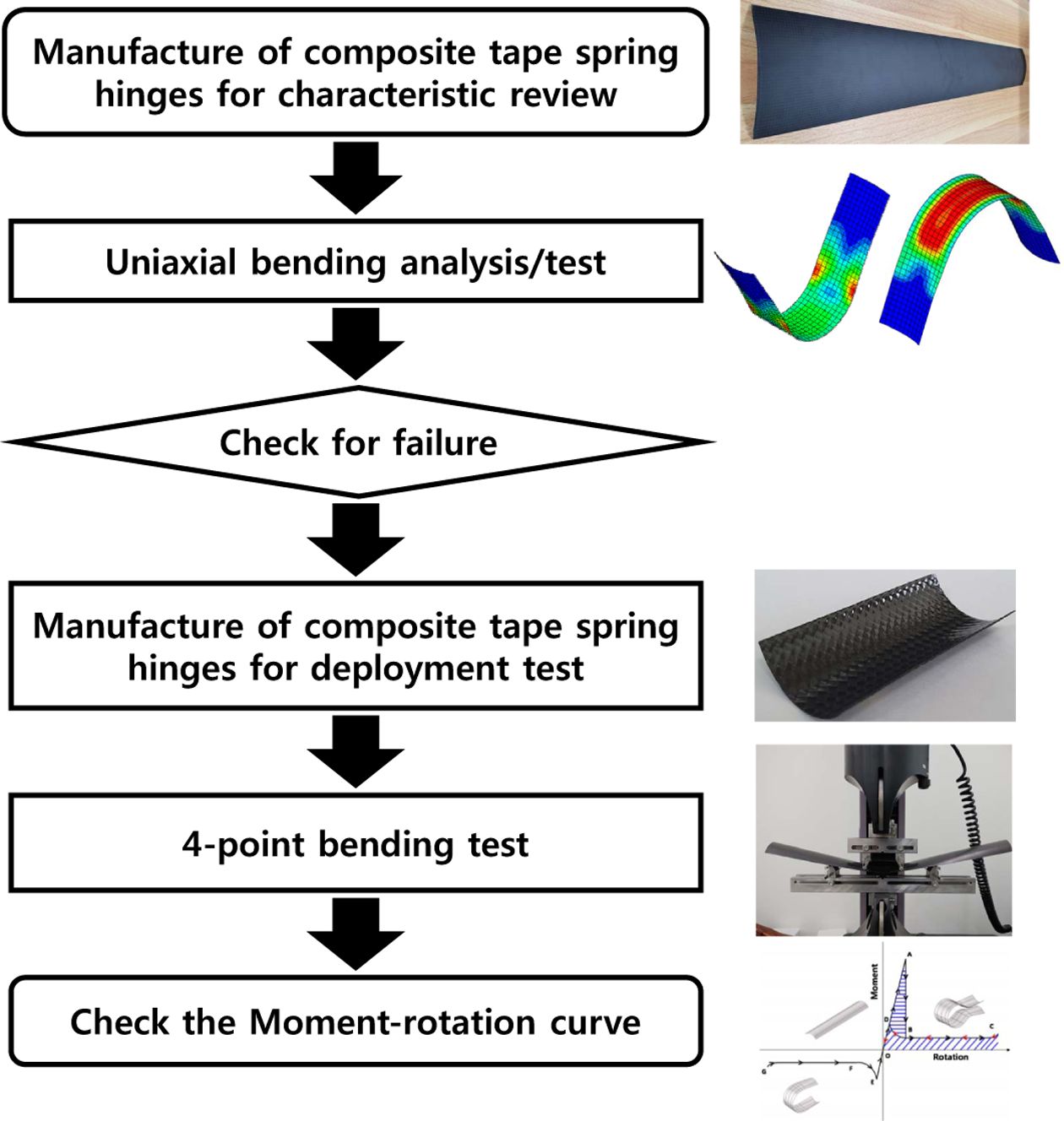
본 연구에서는 복합재료 테이프 스프링을 국내에서 시판되는 소재를 이용해서 개발하여 전개구조물로의 활용 가능성을 Fig. 1과 같이 검토하도록 한다. 이를 위해서 기본 특성검토용 테이프 스프링을 단방향 복합재료(UD, unidirectional composite), 직물 복합재료(Woven fabric composite)으로 여러 적층각을 고려해서 제작한다. 구조해석과 간단한 굽힘 시험을 통해 제작 가능성 여부를 검토하고 도출한 최적의 소재와 적층각을 찾는다. 3장에서는 2장에서 얻어진 소재와 적층각 정보를 이용해 시편을 제작하고 4점 굽힘 시험을 통해 모멘트-회전 특성커브 측정하여 확인한다. 모멘트-회전 특성커브에서 비선형성과 히스테리시스를 통해 테이프 스프링의 고유 특성을 보유하고 있는지 확인하고 개발 성공 여부를 판단한다.

2.1 테이프 스프링의 기계적 특성
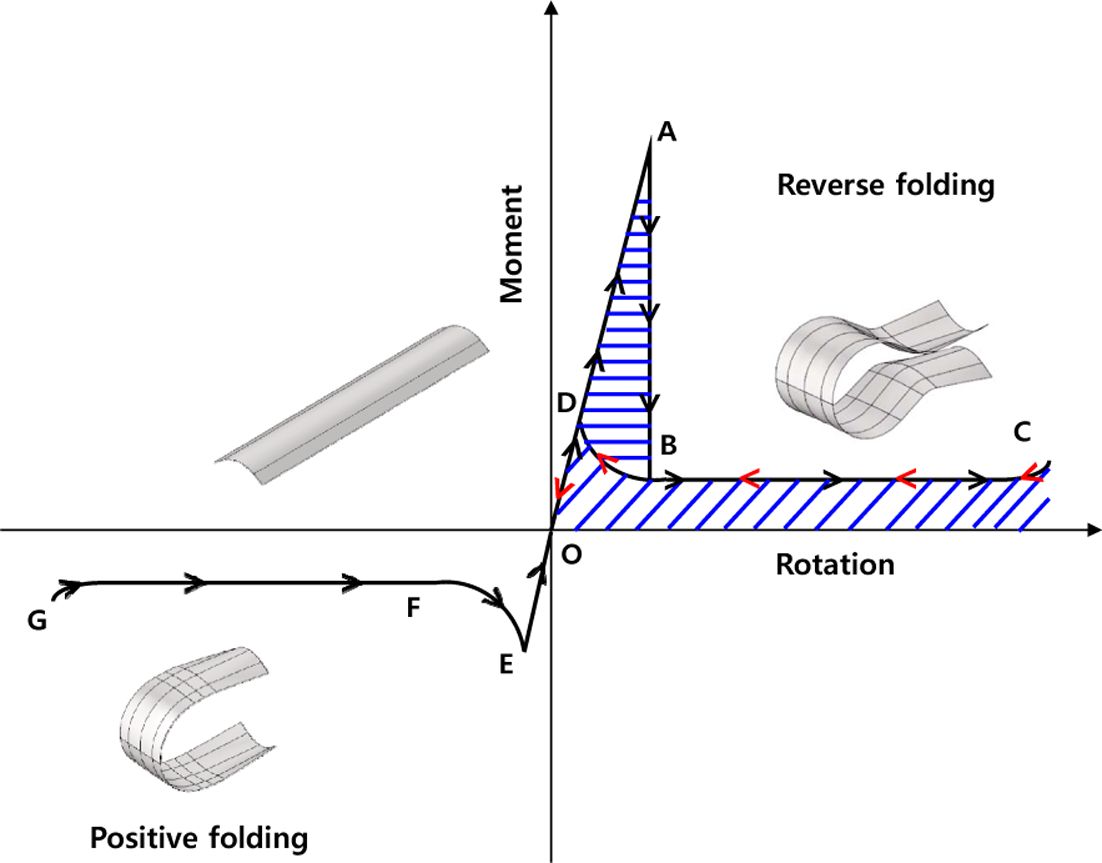
테이프 스프링은 앞서 언급하였듯이 굽힘모멘트에 의한 회전 거동에 관해서 비선형 히스테리시스 거동을 보여준다. Fig. 2는 테이프 스프링의 특성을 나타내는 굽힘모멘트-회전 프로파일로 역방향 굽힘(reverse folding)의 경우 굽혀질 때 O-D-A-B-C를 따라가지만 펴질 때는 C-B-D-0의 경로로 원상복구되며 이때 ABD로 둘러싸인 면적은 에너지 소산을 의미한다. 즉 굽힘모멘트의 경로가 작동 방향에 따라 변하며 고유의 비선형 히스테리시스 현상이 구현되는 것을 확인할 수 있다[3].

2.2 복합재료 테이프 스프링 설계
전개구조물에 적합한 복합재료 테이프 스프링 개발을 위해 복합재료 테이프 스프링의 전체 길이, 곡률 반경, 중심 내각, 두께와 같은 설계 변수를 이용해서 테이프 스프링을 설계하였다[17]. 여기서, 복합재료 테이프 스프링의 두께는 소재로 사용되는 복합재료의 종류와 적층수에 따라 결정된다.
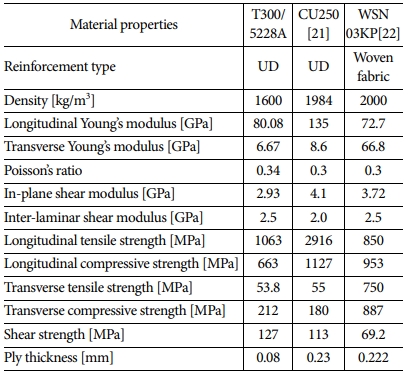
복합재료 테이프 스프링의 소재로 사용될 제조용 복합재료의 종류는 크게 단방향 복합재료, 직물 복합재료가 있다[18,19]. 본 연구에서는 국내에서 수급할 수 있고 복합재료 테이프 스프링 제작에 사용되었던 T300/5228A와 기계적 물성이 비슷한 복합재료를 Table 1과 같이 선정하였다[20-22]. 첫 번째 복합재료는 단방향 복합재료인 한국 카본의 CU250이고 두 번째는 직물 복합재료인 SK케미칼의 WSN 03KP이다.

2.3 복합재료 파손 이론
복합재료 테이프 스프링 굽힘 해석을 위해 복합재료 파손 이론을 검토하였다. 굽힘 해석 시 발생하는 응력 성분들은 재료파손에 영향을 미치며, 이를 고려하여 2차 항 이상을 복합재료 파손에 적용해야 한다. 따라서 가장 널리 사용되는 아래의 수식 (1), (2), (3)과 같은 Tsai-Hill, Tsai-Wu, 최대주응력 파손 이론을 파손 해석에 모두 사용하였다[23-25].




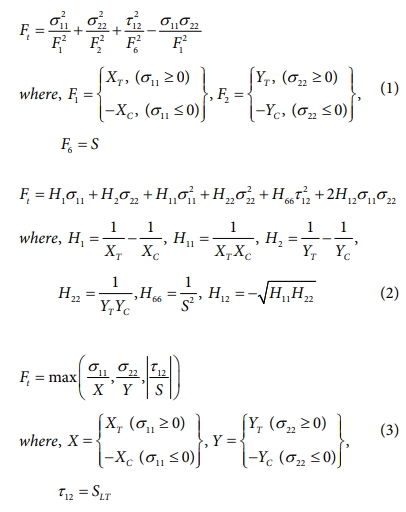
여기서 σ₁₁은 복합재료 테이프 스프링의 길이(Longitudinal) 방향 응력, σ₂₂은 가로(Transverse) 방향 응력, τ₁₂은 면내전단(In-plane Shear) 방향의 응력이다. 그리고 X_T와 X_C는 길이 방향, Y_T와 Y_C는 가로 방향에서 복합재료의 인장강도와 압축강도이고 S는 평면 내 전단강도이다. F_t는 파손지수(failure index)이며 1보다 큰 경우 파손을 의미한다.

2.4 복합재료 테이프 스프링 굽힘 해석
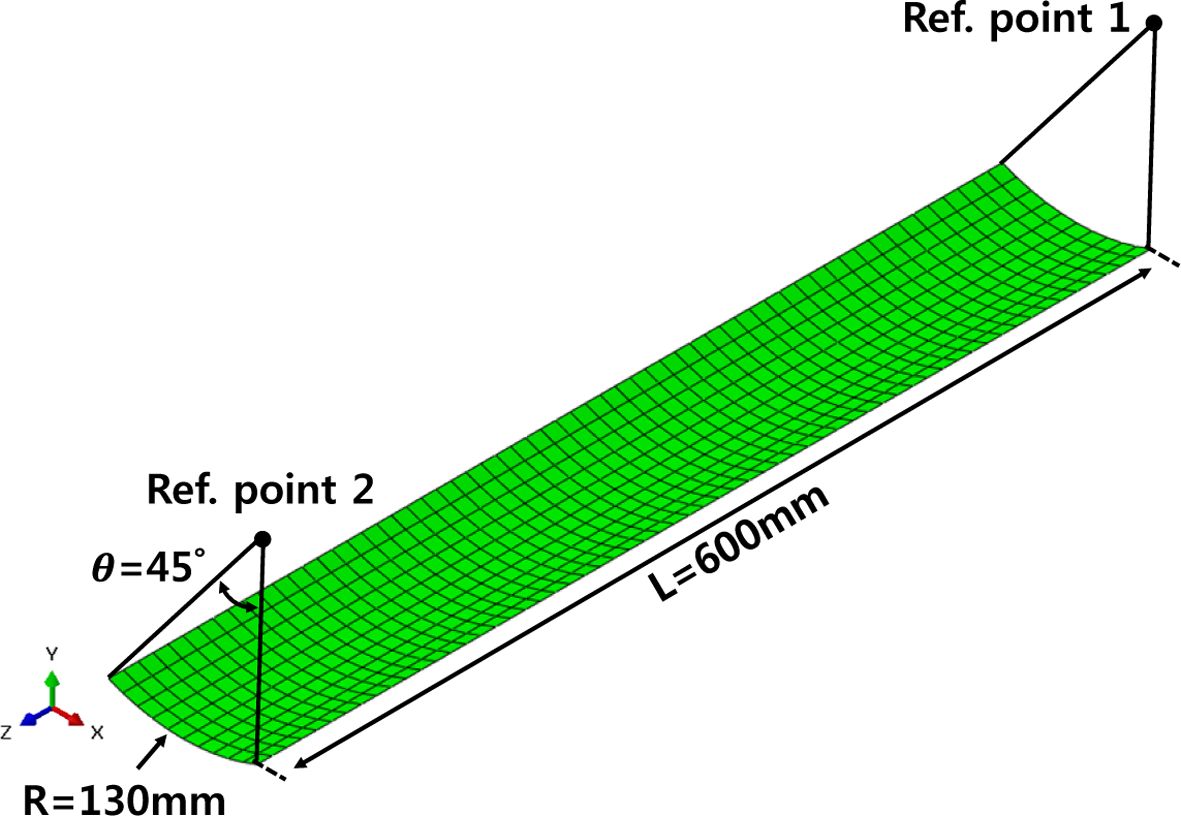
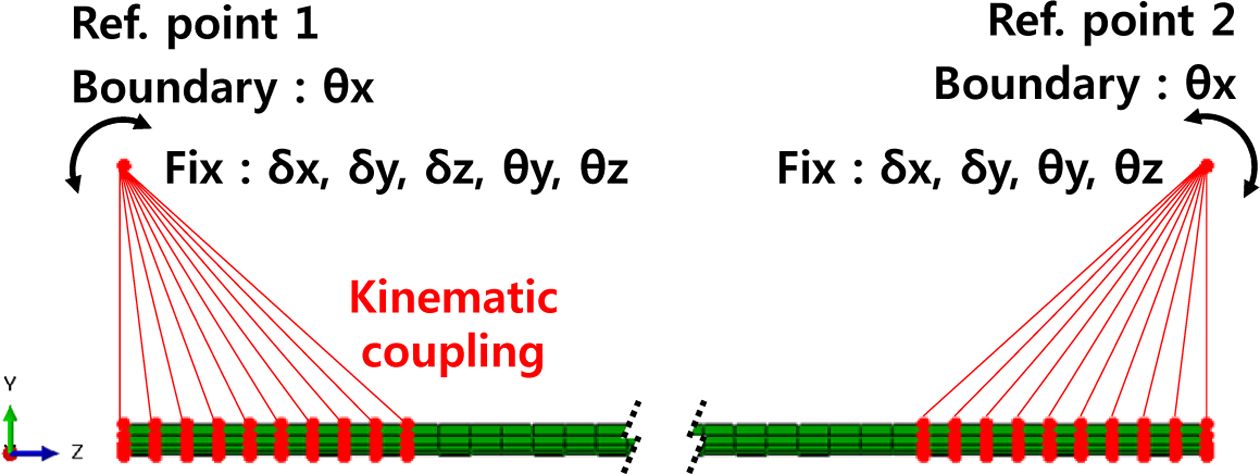
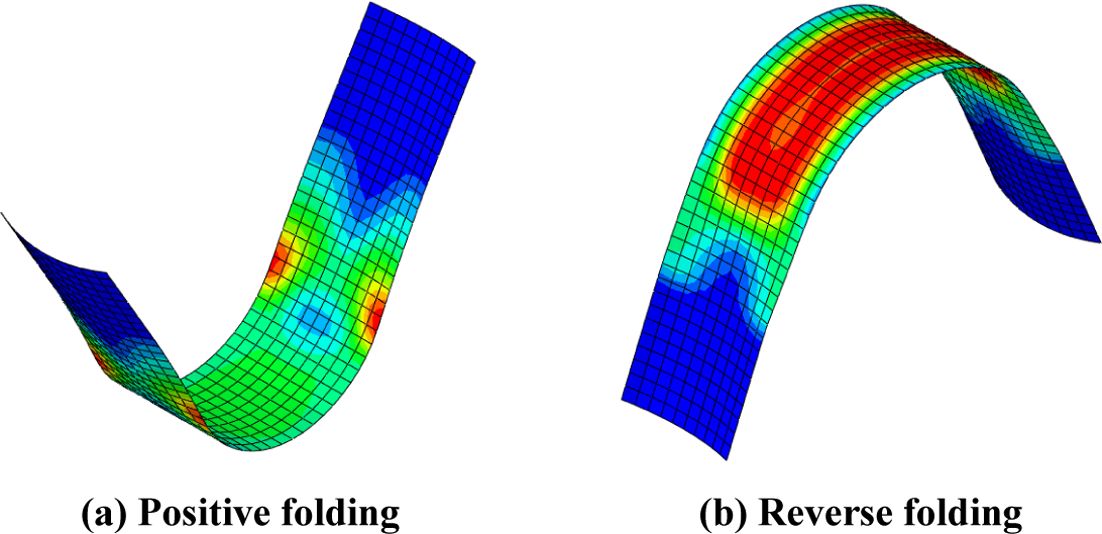
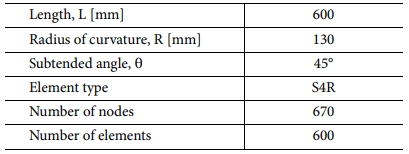
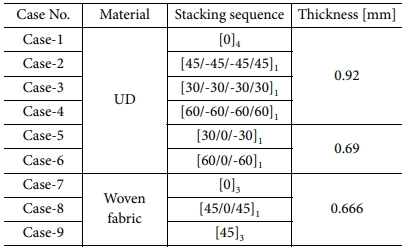
굽힘 하중에서의 복합재료 테이프 스프링의 파손 여부 및 특성을 검증하기 위해 1축 굽힘 해석을 수행하였다. 복합재료 테이프 스프링 모델의 정보는 Table 2 및 Fig. 3과 같다. 해석 케이스는 복합재료 종류와 적층 각도에 따라 Table 3과 같이 설정하였다. 1축 굽힘 해석은 ABAQUS/Explicit을 사용하여 Fig. 4와 같이 테이프 스프링 끝단의 절점을 각각 1번 기준점(Ref. point 1)과 2번 기준점(Ref. point 2)에 Kinematic coupling으로 연결한다. 그리고 기준점 1은 5개의 자유도(δ_x, δ_y, δ_z, θ_y, θ_z), 기준점 2는 4개(δ_x, δ_y, θ_y, θ_z)의 자유도를 구속하고 각 기준점의 x축 회전 자유도(θ_x)에 회전값을 적용하여 Fig. 5와 같이 정방향(Positive direction), 역방향(Reverse direction) 굽힘 해석을 수행하였다.
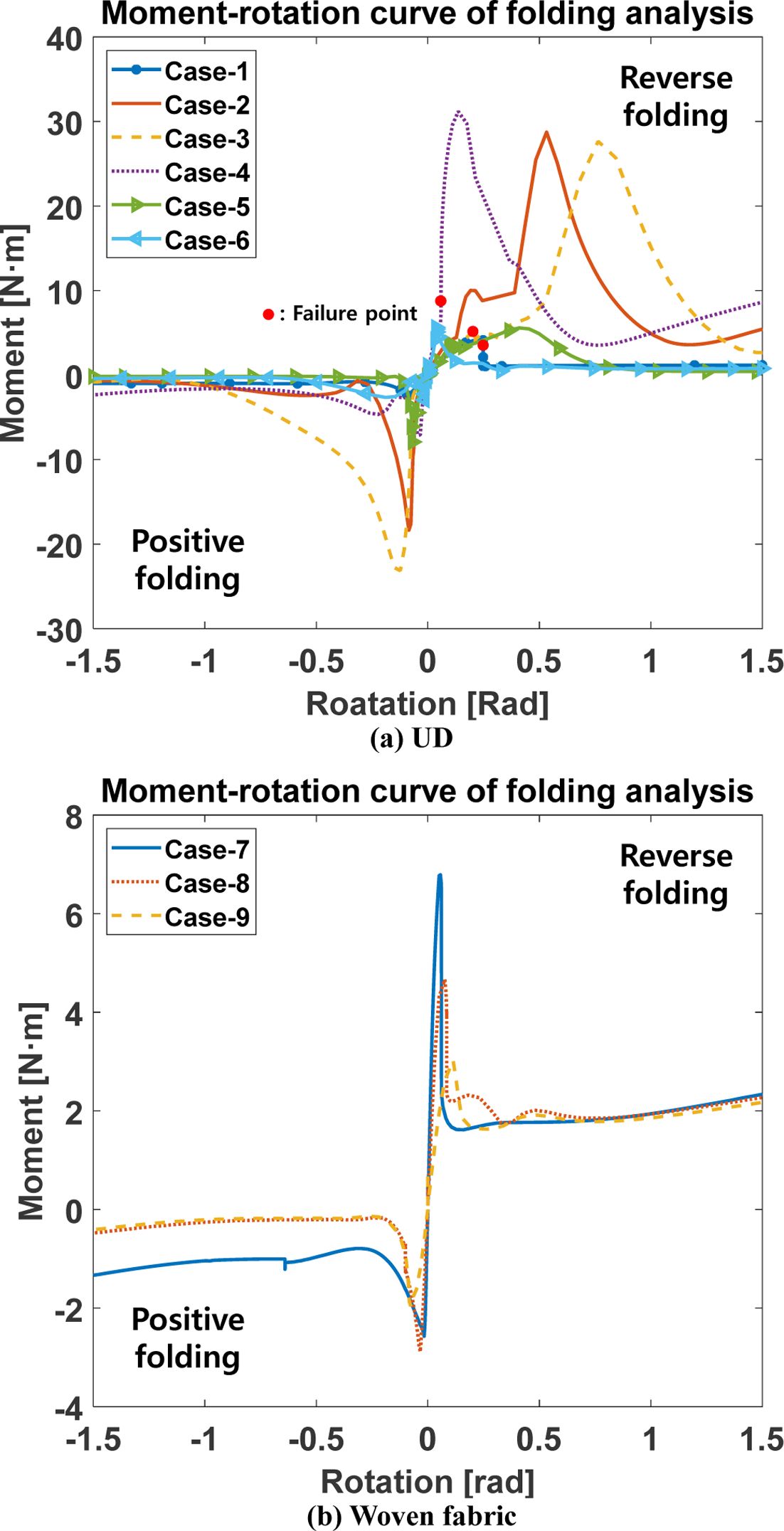
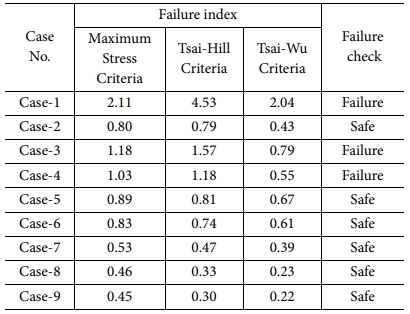
굽힘 해석에서 단방향 복합재료 모델의 해석 결과는 Fig. 6a와 같이 모멘트-회전 곡선에 snap-through 좌굴에 의한 첨점의 위치가 일정하게 발생하지 않고 나타났다. 반면에 직물 복합재료 모델의 해석 결과에서는 모멘트-회전 곡선의 첨점이 대략 일정하게 나타나는 특성을 확인하였다. 최대 응력이 발생하는 역방향 굽힘 해석에서 첨점에서 최대 응력을 산출하여 최대 응력 이론, Tsai-Hill, Tsai-Wu 파손 이론을 적용하여 Table 4와 같이 파손 여부를 판단하였다. 파손 이론을 적용한 결과, 직물 복합재료 해석 모델의 파손 지수가 모두 1보다 낮았다. 하지만 단방향 복합재료 해석 모델은 6개의 케이스 중 3개의 파손 지수가 1보다 높아 파손 가능성이 높음을 확인하였다.

2.5 복합재료 테이프 스프링 제작
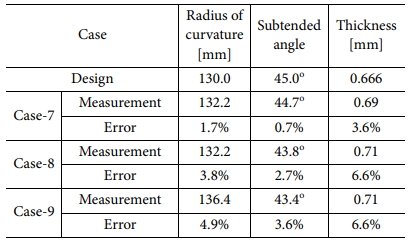
본 연구에서는 복합재료 테이프 스프링의 굽힘 거동 특성을 확인하기 위해 복합재료 테이프 스프링을 제작하였다. 우선 복합재료 테이프 스프링의 치수에 맞게 알루미늄 몰드를 제작하고 Fig. 7과 같은 과정을 통해 복합재료 테이프 스프링을 제작한다. 이때 경화 조건은 각 복합재료의 제조사에서 제공하는 온도, 압력으로 설정하였다[21,22]. Table 3에 나타난 모든 해석의 경우를 제작하였다. 제작 결과 단방향 복합재료로 제작한 경우 적층 각도가 0°인 Case-1은 Fig. 8a와 같이 설계 형상과 유사하게 제작되었지만, Case-2~Case-4의 경우 성형 과정에서 발생하는 적층 각도의 미세한 편차에 의해 Fig. 8b와 같이 뒤틀림이 발생하였다. 또한, Case-5와 Case-6은 적층된 복합재료가 상∙하부 적층 각도의 균형이 잡히지 않아 Fig. 8c와 같이 복합재료가 크게 뒤틀렸다. Case-1의 경우에도 굽힘 시험을 수행한 결과 Fig. 8d와 같이 중간이 갈라지면서 파손이 발생하였다. 반면 직물 복합재료는 준등방성 특성이 있어 Fig. 9 및 Table 5와 같이 모두 설계 치수와 큰 오차 없이 제작되었으며 굽힘 테스트를 수행하였을 때 굽힘 후 전개가 적절히 일어남을 확인하였다.

3.1 4점 굽힘 시험
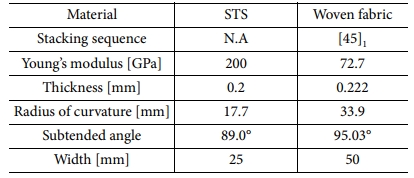
앞서 도출된 복합재료 테이프 스프링의 기계적 특성을 확인하기 위해 ASTM D6272의 규격에 맞춰 Fig. 10의 MTS사의 복합 시험기를 사용하여 Fig. 11과 같이 4점 굽힘 시험을 수행하였다. 4점 굽힘 시험 시편은 Table 6에 나타나듯이 전개 메커니즘으로 검증이 된 STS 테이프 스프링과 거의 같은 두께를 갖는 WSN 03KP[45]₁인 복합재료 테이프 스프링을 사용하였다. 그리고 곡률반지름과 굽힘모멘트의 관계를 나타내는 수식 (4)와 같이 같은 곡률반지름에서 STS 테이프 스프링과 유사한 굽힘모멘트를 갖는 복합재료 테이프 스프링을 설계하였다. 복합재료는 STS보다 탄성계수가 낮기 때문에 폭을 2배 늘려 관성모멘트를 증가시켰다. 4점 굽힘 시험은 정방향과 역방향으로 snap-through 좌굴이 발생할 때까지 하중과 변위를 측정하여 모멘트-회전 곡선으로 환산하였다.



여기서 ρ은 곡률반지름, M은 굽힘모멘트, E는 탄성계수, I는 관성모멘트를 나타낸다.

3.2 결과 분석
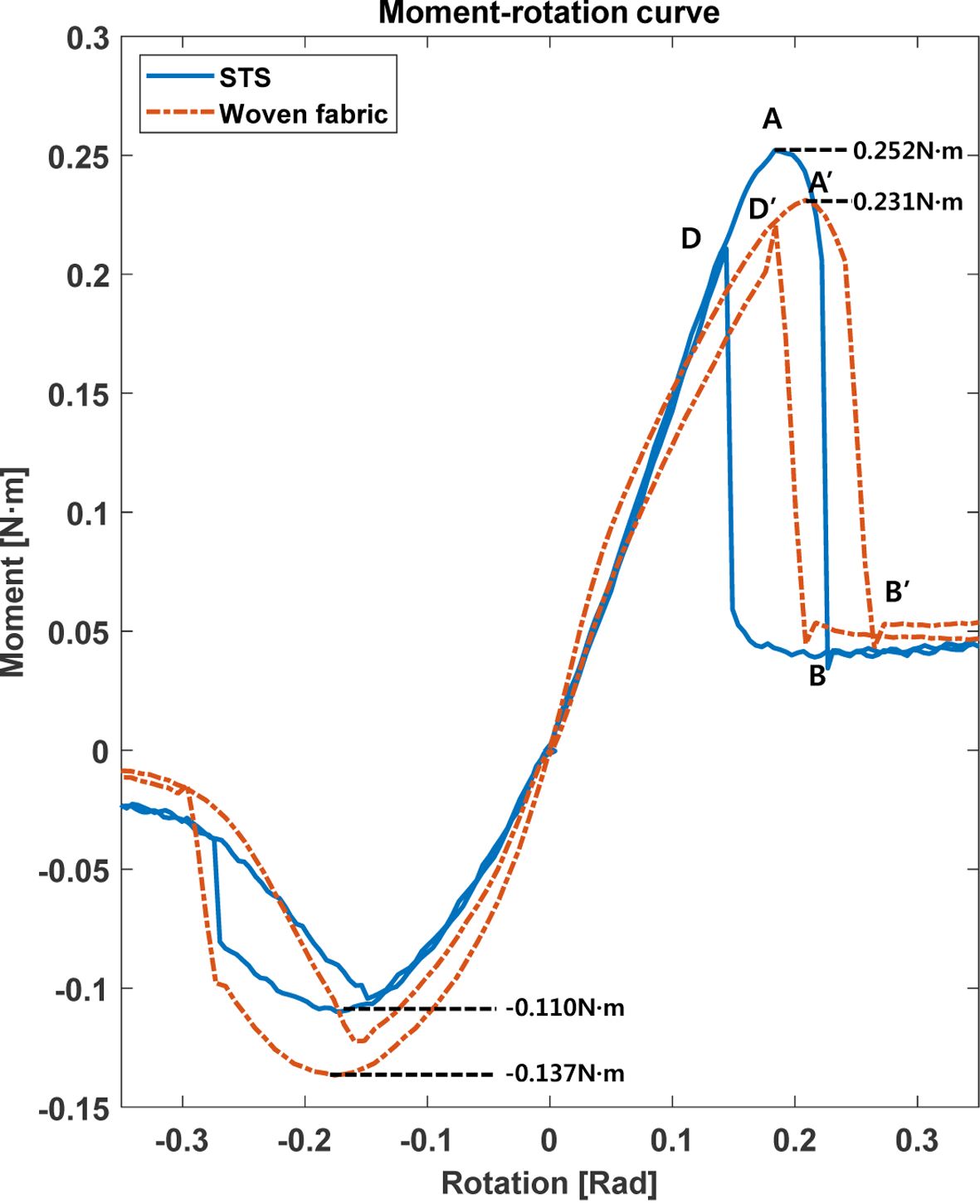
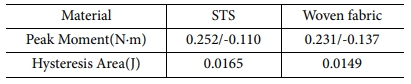
4점 굽힘 시험의 결과는 Table 7 및 Fig. 12와 같이 히스테리시스 특성과 모멘트-회전 곡선을 나타내었다. 역방향 굽힘의 경우 회전이 증가할 때 기울기가 선형으로 증가하다가 snap-through 좌굴이 발생할 때 두 시편 모두 급격하게 굽힘모멘트가 낮아짐을 확인하였다. 이때 복합재료 테이프 스프링의 최대 및 최소 굽힘모멘트는 각각 0.231 N∙m, -0.137 N∙m이며 STS 테이프 스프링의 최대 및 최소 굽힘모멘트는 각각 0.252 N∙m, -0.110 N∙m였다. 에너지 소산 능력을 의미하는 ABD, A’B’D’의 면적은 0.0165 J, 0.0149 J로 각각 유사하게 나타났다. 따라서 복합재료 테이프 스프링의 히스테리시스 특성을 확인하여 전개 시 충격에너지를 소산하는 테이프 스프링의 특성을 갖고 있음을 확인하였다.

본 연구에서는 국내에서 시판되는 복합재료를 이용해서 전개장치용 복합재료 테이프 스프링을 개발을 시도하였다. 이를 위해 단방향 복합재료(CU250)와 직물 복합재료(WSN 03KP)로 제작한 복합재료 테이프 스프링의 특성을 파악하기 위해 여러 적층 배열에 따라 정방향, 역방향 1축 굽힘 해석을 진행하여 모멘트-회전 곡선과 파손 여부를 확인하였다. 그 결과, 직물 복합재료로 설계한 모델은 치수대로 테이프 스프링이 제작되었고 굽힘 시험에서도 잘 굽혀진 후 전개되는 것을 확인하였다. 정밀한 분석을 위해 4점 굽힘 시험을 수행하였으며 복합재료 테이프 스프링이 STS 테이프 스프링과 마찬가지로 비대칭굽힘모멘트, 히스테리시스 능력을 보유함을 확인하였다. 이러한 연구 결과는 다양한 우주환경에서 사용되는 전개구조물에 최적화된 복합재료 테이프 스프링을 적용할 수 있을 것으로 기대된다. 추후 연구에서는 복합재료 테이프 스프링 힌지의 에너지 소산 능력을 높이기 위해서 강성과 강도가 높은 YSH 계열의 우주급 복합재료 소재를 사용하고, 복합재료의 적층수∙적층각의 따른 기계적 특성에 관한 연구가 수행될 예정이다.

본 연구는 2018년도 과학기술정보통신부의 재원으로 한국연구재단의 지원을 받아 수행된 것이며, 지원에 대해 진심으로 감사드립니다(NRF-2018M1A3A3A02065478).