SMC(Sheet molding compound) composite is mainly used for forming of vehicle’s body. Considering the car accident, it is essential to research the impact behavior and characteristics of materials. It is difficult to identify them because the impact process is completed in a short time. Therefore, the impact damage analysis using FE(finite element) model is required for the impact behavior. The impact damage analysis requires the parameters for the damage model of SMC composite. In this paper, ANN(artificial neural network) technique is applied to obtain the parameters for the damage model of SMC composite. The surrogate model by ANN was constructed with the result in LS-DYNA. By comparing the absorption energy in drop weight test with the result of ANN model, the optimized parameters were obtained. The acquired parameters were validated by comparing the results of the experiment, the FE model and the ANN model

복합재료 중에서 SMC(sheet molding compound) 복합재료는 자동차의 차체 성형에 주로 쓰이고 있다. 자동차 산업에서는 차량 사고를 고려하여야 하므로 재료의 충돌 거동 및 특성에 관한 연구는 필수적이다. 충돌은 짧은 시간에 일어나기 때문에 육안으로 확인이 어렵다. 따라서 충돌 거동을 확인하기 위해서는 유한요소 모델을 이용한 충돌 손상 해석이 필요하다. 충돌 손상 해석을 위해서는 SMC 복합재료의 손상 모델에 대한 파라메터가 요구된다. 본 연구에서는 SMC 복합재료의 손상 모델에 대한 파라메터를 획득하기 위해 인공신경망 기법을 적용하였다. LS-DYNA에서 파라메터에 따른 결과를 이용하여 대체 모델을 구성하였다. 자유 낙하 충돌 실험에서 얻은 흡수 에너지와 인공신경망 모델을 이용한 흡수 에너지를 비교하여 최적화된 파라메터를 획득하였다. 획득한 파라메터를 유한요소 모델에 적용해 결과를 비교하여 파라메터의 신뢰성을 검증하였다.

Keywords: SMC 복합재료(Sheet Molding Compound), 인공신경망(Artificial Neural Network), 손상 모델(Damage Model), 충돌 손상(Impact Damage), 파라메터(Parameter)

최근 환경규제 강화에 따른 탄소 배출 감소를 위해 전 세계적으로 노력하고 있다. 자동차 산업에서는 차체의 경량화를 통해 연비 향상, 탄소 배출의 감소와 동시에 안정성 유지 또는 향상을 이루기 위한 연구가 활발히 이루어지고 있으며 그 중 한 가지 대안으로 복합재료를 이용한 경량 소재 개발이 주목받고 있다[1]. 다양한 복합재료 중에서 SMC(sheet molding compound) 복합재료는 열경화성 수지, 유리섬유, 충전제 등을 혼합하여 함침시켜 제작된다. SMC 복합재료는 치수 안정성, 성형성, 내부식성 뿐만 아니라 비용도 저렴하며 자동차 산업에서 차체 성형에 많이 사용되고 있다[2,3].
자동차 산업에서 소재를 적용하기 위해서는 안전사고에 대비하여 차량 충돌 시 발생하는 부품 손상과 탑승자 및 보행자의 안전을 고려하여야 하므로 소재의 충돌 거동 및 특성이 중요하다. 복합재료를 사용할 경우에는 충돌 하중으로 인해 외부에는 손상이 없더라도 내부에 손상 여부가 존재할 수 있으며 충돌이 수십 ms 이내의 짧은 시간에 일어나서 육안으로 확인하기 어려운 점이 있다. 복합재료의 손상은 점진적으로 나타나서 구조물의 강도를 저하시키기 때문에 충돌에 대한 손상 거동을 확인하기 위한 유한요소 해석이 필요하다[4,5]. 그러나 충돌 손상 해석을 위해서는 손상 모델에 대한 파라메터인 인장강도, 압축강도, 전단강도 등의 파손 물성들이 요구되는데, 이는 실험으로 획득하기 어려운 점이 있다. 본 연구에서는 이를 해결하기 위한 방안으로 예측 모델을 이용하여 역추정 기법을 사용하였다. 예측 모델 기법 중 하나인 인공신경망(artificial neural network, ANN) 기법은 생물학적인 뇌의 구조에서 기인하여 하나 이상의 층(layer)과 층에 존재하는 다수의 노드(node)를 연결하는 신경망을 생성하여 비선형 공학 문제를 해결할 수 있는 예측 기법이다[6].
따라서 본 연구에서는 실험으로 획득하기 어려운 파손 강도를 인공신경망 기법을 적용한 대체 모델(surrogate model)을 이용하여 SMC 복합재료의 손상 모델에 대한 파라메터를 역추정하였다. 파라메터에 따른 유한요소 해석 결과를 이용하여 대체 모델을 구성하고, 자유 낙하 충돌 실험(drop weight test)으로 얻은 흡수 에너지(absorption energy)와 비교하여 최적화된 파라메터를 획득하였다. 획득한 파라메터로 유한요소 모델에 적용하여 결과를 비교함으로써 획득한 파라메터에 대한 신뢰성을 확보하였다.

2.1 실험 시편
SMC 복합재료는 불포화 폴리에스테르수지, 유리섬유, 충진제 등의 다양한 재료를 혼합하여 함침시켜 제조한다.
본 연구에서 사용한 SMC 복합재료는 한국ACM 사에서 제공받았으며, 유리섬유 부피분율이 약 26%이고 크기가 150 × 100 × 3 mm³, 밀도는 1,911 kg/m³이다.
2.2 충돌 실험
본 연구에서는 충돌체의 위치 에너지에 따른 흡수 에너지를 이용하여 SMC 복합재료의 파손 모델의 파라메터를 역추정하기 위해 자유 낙하 충돌 실험을 수행하였다. 실험 장비는 크게 충돌체와 고정 베이스로 구성되고, 충돌체의 무게와 높이를 조절하여 실험하고자 하는 위치 에너지(potential energy)를 가진 충돌체가 시편에 충돌하여 실험이 이루어진다. 본 연구에서 사용한 실험 장비는 Fig. 1과 같고, 시편은 Fig. 2와 같이 고정되고, 실험 조건은 충돌 전 충돌체의 위치 에너지이다. 모든 실험은 ASTM D7136/D7136M의 규격을 준수하여 수행하였다[7].
충돌체가 시편에 충돌하면 실험 장비 내부의 압전소자로 인해 가속도 변화를 측정하여 속도와 이동거리를 계산하고, 시편에 가해진 하중을 측정한다. 이때 시편의 흡수 에너지는 하중-변위 곡선의 적분 값이고[8], 식 (1)과 같다.



여기서 A.E 
는 흡수 에너지, F 는 시편에 가해지는 하중, l 은 가해진 하중에 의한 시편의 변위량이다.
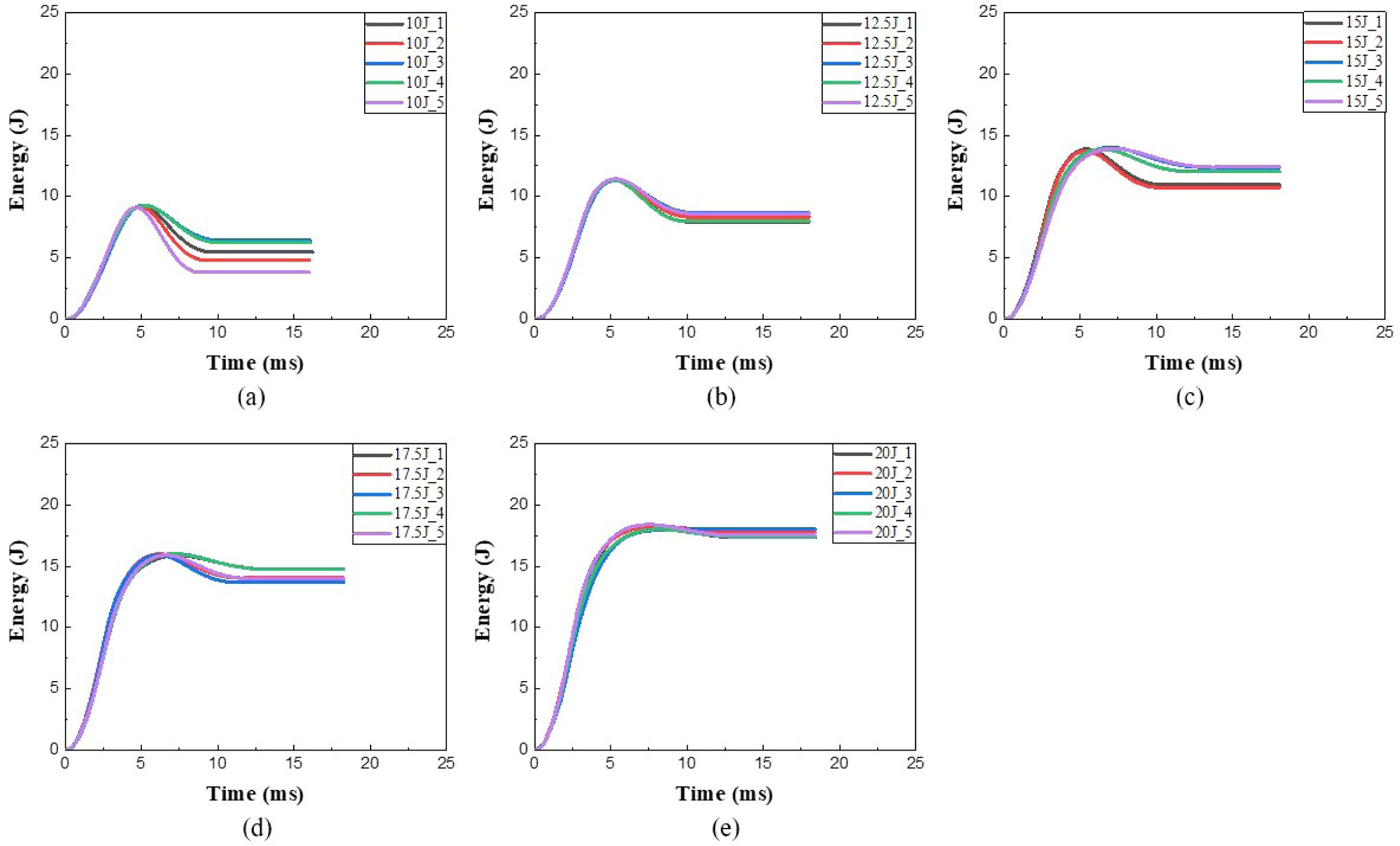
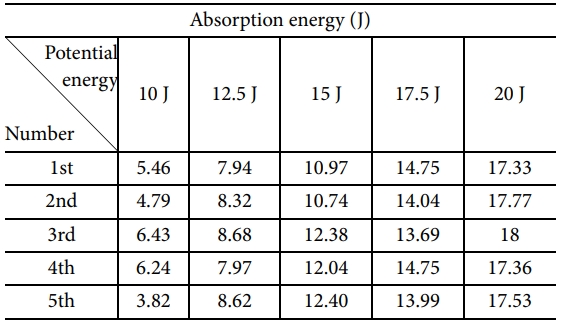
본 연구는 충돌체의 위치 에너지를 10 J부터 20 J까지 2.5 J 간격으로 실험을 수행하였다. 각 위치 에너지 조건에 따른 에너지 곡선은 Fig. 3에 나타내었고, 실험 후 시편 형상은 Table 1에 나타내었다. 에너지 곡선에서 최댓값은 충돌 에너지(impact energy)이며, 이는 시편이 최대 하중을 받을 때의 에너지이다. 에너지 곡선의 마지막에 일정하게 유지되는 값은 흡수 에너지이며, 충돌체가 시편에 충돌하는 동안 시편이 흡수한 총 에너지이다. 이러한 충돌 에너지와 흡수 에너지의 차이는 반발 에너지이며, 충돌체가 시편에 충돌한 후 탄성 충돌로 인해 시편에서 충돌체로 에너지가 다시 전달되는 에너지이다. Fig. 3을 통해 충돌체의 위치 에너지가 클수록 최대 하중 이후의 에너지 곡선이 완만해지는 것을 확인할 수 있으며, Table 1과 같이 시편이 많은 에너지를 흡수하면서 손상 영역이 확대되는 것을 볼 수 있다. 이는 위치 에너지가 클수록 시편에 큰 하중이 가해지기 때문이다. 자유 낙하 충돌 실험 결과에 대한 SMC 복합재료의 흡수 에너지는 Table 2와 같다. Fig. 3에서 볼 수 있듯이 12.5 J의 위치 에너지 조건에서의 실험 결과가 가장 안정적이고 에너지 곡선의 경향성이 일치하여 본 연구에서는 12.5 J의 위치 에너지 조건에 대해서 수행하였다.

3.1 인공신경망 기법
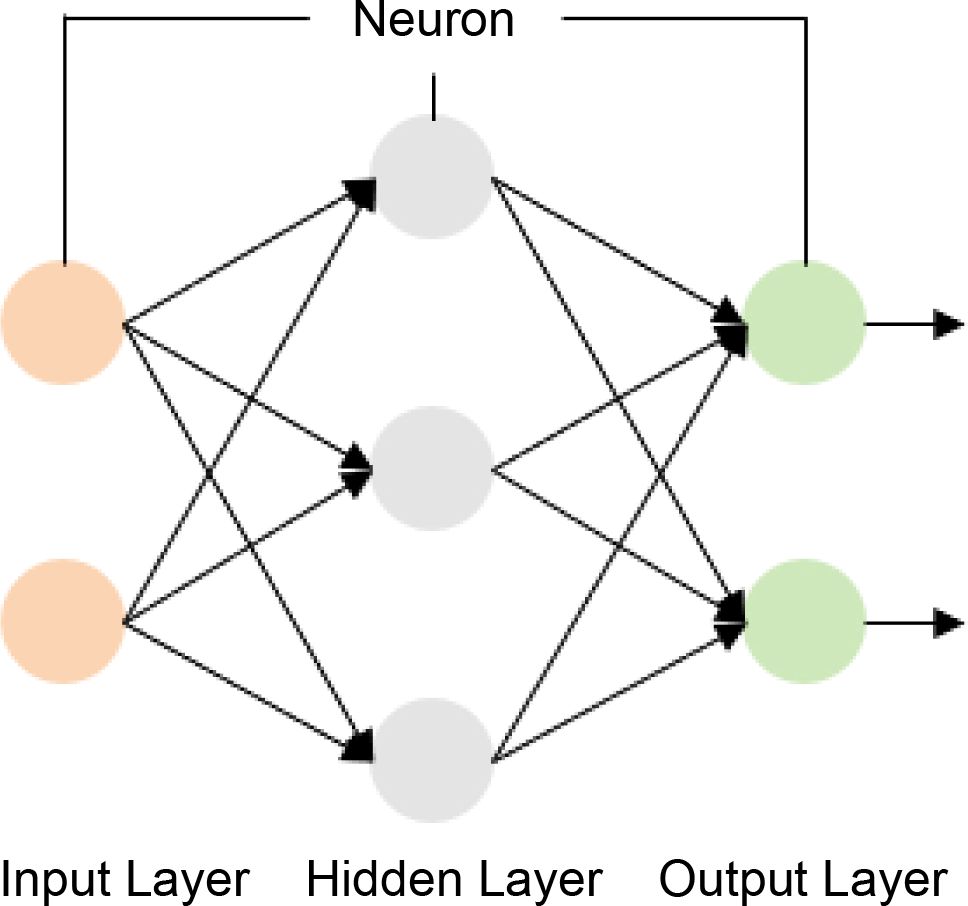
인공신경망은 인간이나 동물 두뇌의 신경망을 흉내내어 기계로 하나의 신경망을 구성하는 머신 러닝 기법 중 하나이다. 인간의 두뇌가 신경세포인 수많은 뉴런으로 하나의 망 형태로 되어있는 것에 착안된 인공신경망은 하나 이상의 층과 층 사이에 존재하는 다수의 뉴런을 이용하여 비선형 공학 문제를 예측할 수 있다.
인공신경망 모델은 Fig. 4와 같이 일반적으로 1개의 입력층(input layer)과 출력층(output layer), 다수의 은닉층(hidden layer)로 구성된다. 각 층에는 다수의 노드가 존재하는데, 이는 생물학적으로 뉴런이 된다. 여기서 입력층과 출력층의 노드의 개수는 각각 입력 데이터와 출력 데이터의 개수가 된다. 노드는 입력(x_i
)을 받으면 가중치 함수(weight function, w_ij)를 이용해 계산하고, 활성함수(active function, j
)에 입력하여 외부로 출력(y_j)하며 식 (2)와 같이 표현된다[9]. Fig. 5



여기서 b 는 바이어스(bias) 값이다. 활성함수는 노드에서 입력 받은 데이터를 다음 층으로 출력할지를 결정하는 역할을 하는데, 비선형 함수로 이루어져있다. 대게 활성함수는 계단 함수(step function), 시그모이드 함수(sigmoid function) 등이 있다[9].
3.2 유한요소 모델링
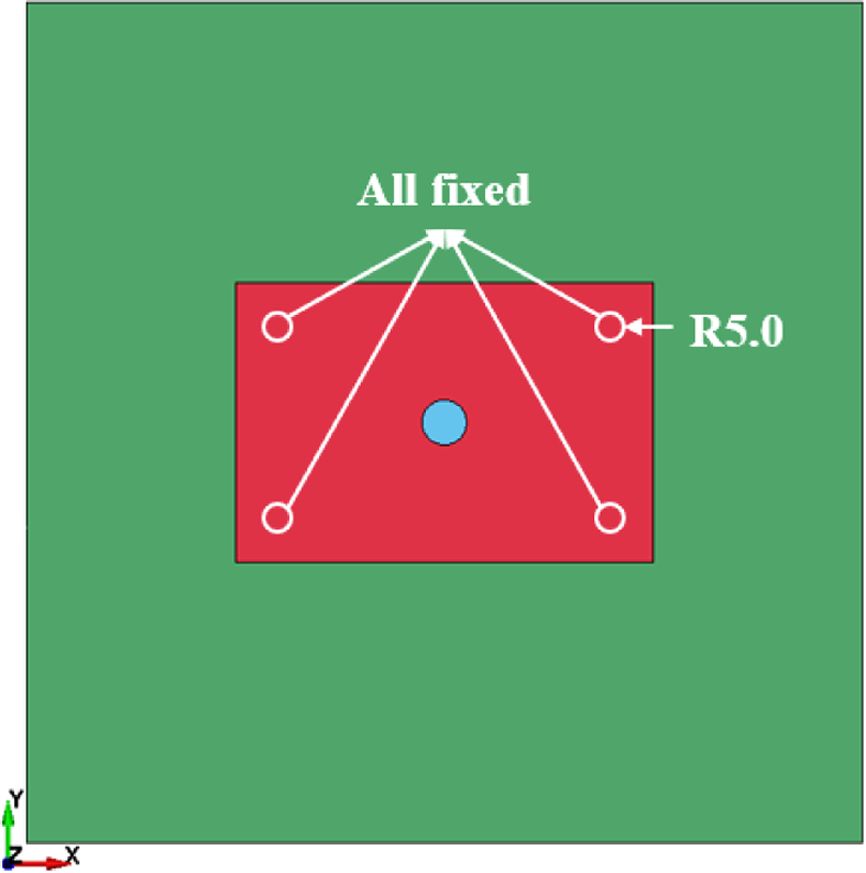
본 연구는 인공신경망 기법을 적용한 대체 모델을 구성하기 위해 유한요소 해석 프로그램인 LS-DYNA를 이용하였다. 해석 모델로는 고정 베이스, 시편, 충돌체 세 모델로 구성하였다. 충돌체는 시편과 충돌하는 부분만 고려하여 실험 장비에 장착된 충돌체 끝부분의 반경과 동일한 반구로 모델링하였다. 실험에서의 충돌체 무게와 동일하도록 밀도를 부여하였고, 이를 고정 베이스와 함께 강체로 가정하였다. 시편의 두께 방향으로 충돌 실험이 진행되었으므로 두께 방향 응력을 고려하는 것은 필수적이다. 본 연구에서는 shell 요소를 이용하여 하나의 shell 요소층에 다수의 적분점(integration points)을 부여함으로써 두께 방향의 응력을 고려하도록 하였다.
실험에서는 고정 베이스에 시편을 올리고 시편이 움직이지 못하도록 클램프로 고정한다. 해석 상에서는 클램프의 크기를 고려하여 모든 방향의 구속 조건을 부여하였다. SMC 복합재료는 적층된 복합재료와는 달리 재료들을 섞어 함침시켜 만들어져서 섬유가 랜덤 배향(random orientation)이기 때문에 재료의 방향을 정의하기 어렵고 섬유가 무작위로 분포되어 있다. 따라서 본 연구에서는 SMC 복합재료를 등방성이라 가정하였다.
3.3 복합재료 손상 모델
LS-DYNA에서 복합재료 손상 모델로는 크게 층내 분리(intralaminar)와 층간 분리(interlaminar)에 대한 해석 모델이 있다[10]. SMC 복합재료는 다른 복합재료와는 달리 적층한 복합재료가 아니므로 층간 분리는 제외하였다. 그 외 복합재료 손상 모델로는 MAT22(COMPOSITE_DAMAGE) 모델과 MAT55(ENHANCED_COMPOSITE_DAMAGE) 모델 등이 있는데, MAT55는 MAT22의 상위 버전으로 본 연구에서는 MAT55 모델을 사용하였다. MAT55는 점진적 파손 모델(progressive failure model)로서 시편이 파손된 이후에 최대 응력이 잔류 응력으로 점진적으로 감소되도록 하고, 삭제된 요소와 붙어있는 요소의 재료 강도 저하를 유발한다. MAT55는 섬유 방향 인장, 압축 손상 모드는 Chang/Chang 모델로 식 (3)과 (4), 기지 방향 인장, 압축 손상 모드는 Tsay/Wu 모델로 식 (5)를 이용한다[11].

- Tensile fiber mode


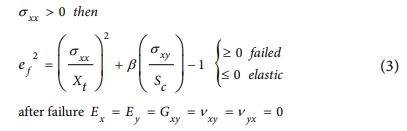
- Compressive fiber mode


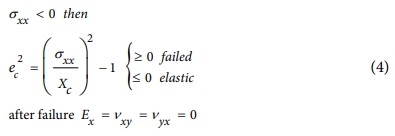
- Tensile and compressive matrix mode



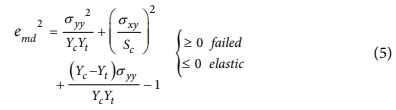
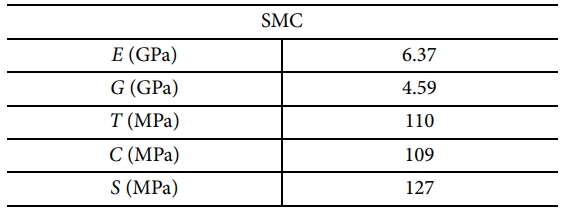
여기서 σ_xx, σ_yy, σ_xy는 각각 시편이 받는 x, y, xy방향 응력(stress)이고, X_t, X_c, Y_t, Y_c, S_c는 각각 x 방향 인장강도와 압축강도, y 방향 인장강도와 압축강도, 전단강도이고, E_x, E_y, G_xy, n_xy는 각각 x 방향 탄성계수, y 방향 탄성계수, xy 방향 전단계수, xy 방향 푸아송 비(Poisson’s ratio)이고, β는 전단 항에 대한 상수이다. MAT55을 적용하여 손상 해석을 수행하기 위해서는 탄성계수(E), 전단계수(G), 인장강도(T), 압축강도(C), 전단강도(S)를 입력하여야 한다. 이 파라메터들은 실험으로 얻기 어려우므로 대체 모델을 이용하여 획득하려는 값들이다.
3.4 대체 모델 구축
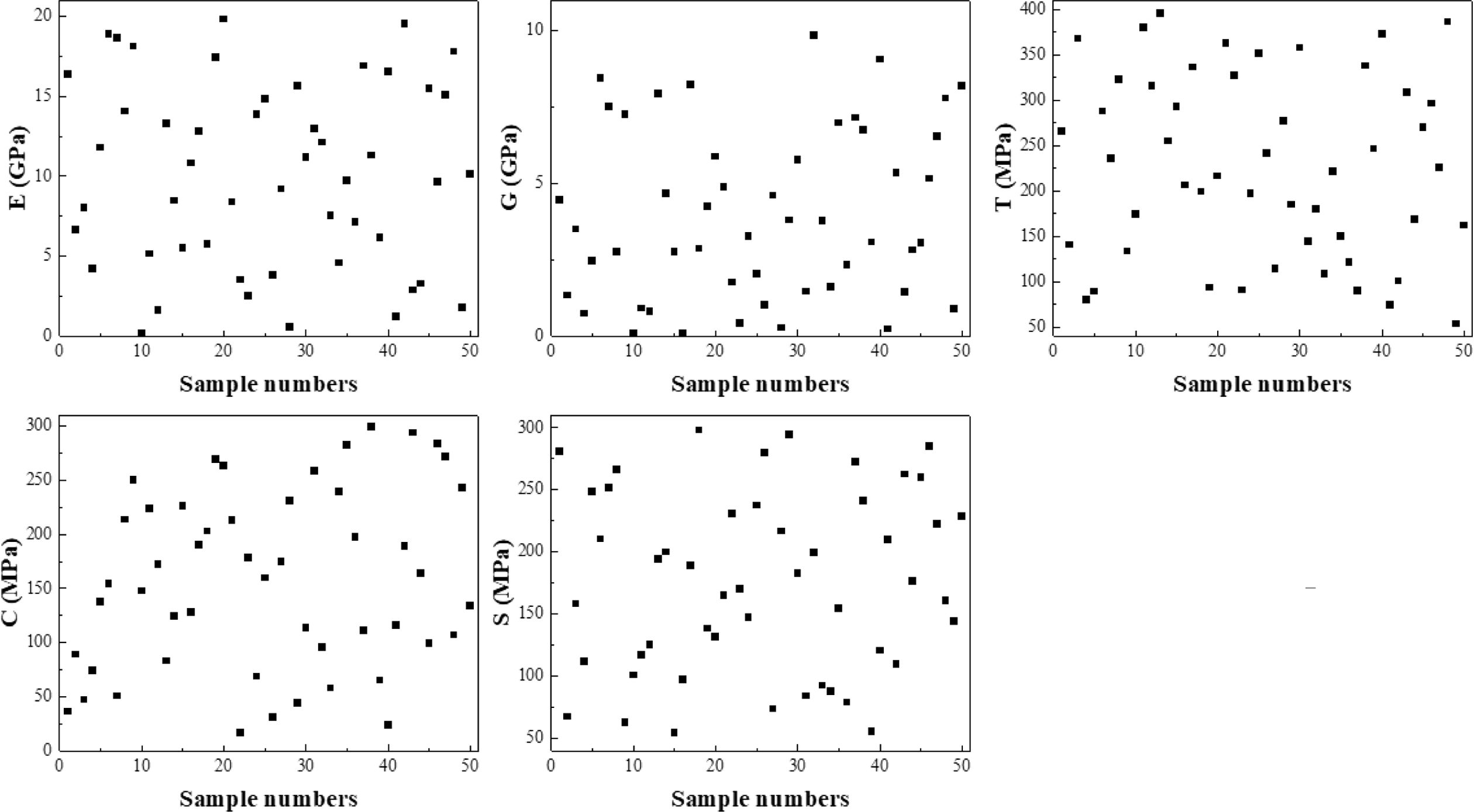
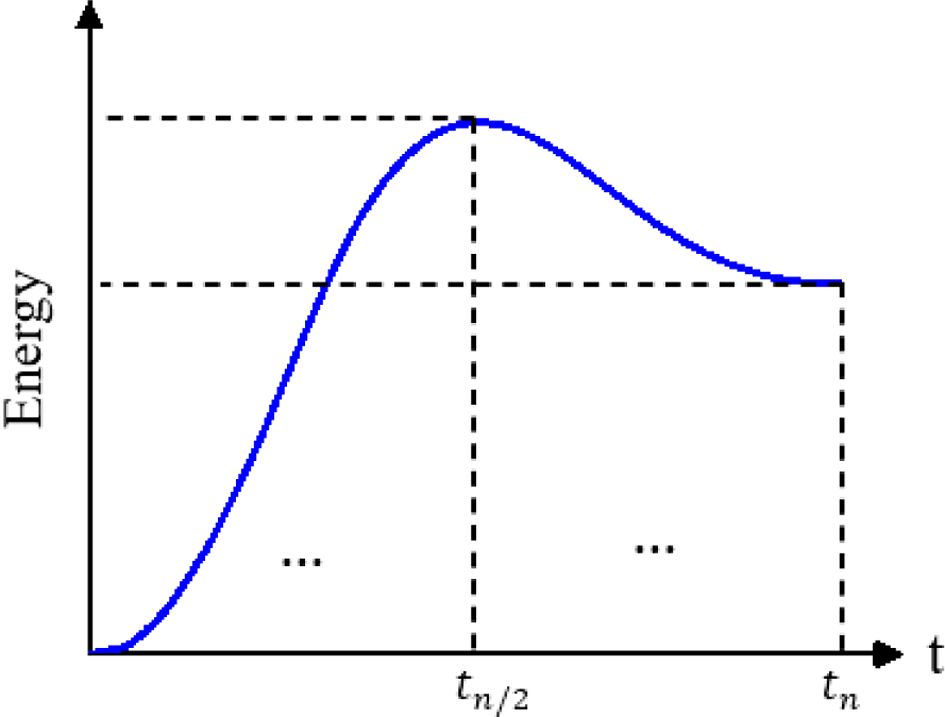
본 연구에서는 MATLAB 프로그램을 이용하여 각각 100개의 노드를 가진 은닉층 2개로 이루어진 인공신경망 기반 대체 모델을 구성하였다. 대체 모델을 구성하기 위해 훈련 데이터(training samples)를 LHS(Latin hypercube sampling) 기법을 이용해 각각 50개씩 추출하여 Fig. 6에 나타내었다. 충돌 해석과 같은 동적 해석에서는 시간의 영향을 크게 받기 때문에 시간을 고려하여야 한다. 따라서, 입력 데이터는 획득해야 하는 파라메터, 출력 데이터는 Fig. 7과 같이 충돌되는 시간과 그에 해당하는 에너지 값으로 선정하였다. 대체 모델을 훈련하기 위해서 훈련 데이터의 훈련(training), 검증(validation), 시험(test) 비율을 각각 70%, 15%, 15%로 설정하였다. 대체 모델을 훈련할 훈련 알고리즘으로는 베이즈 정규화 역전파(Bayesian regularization backpropagation)를 이용하였다. 이 알고리즘은 각 층을 통과할 때마다 가중치와 바이어스를 업데이트하여 제곱 오차와 가중치의 결합을 최소화하여 일반화가 잘 되는 신경망을 생성한다. 활성함수로는 쌍곡탄젠트(hyperbolic tangent) 시그모이드 함수를 이용하였다.



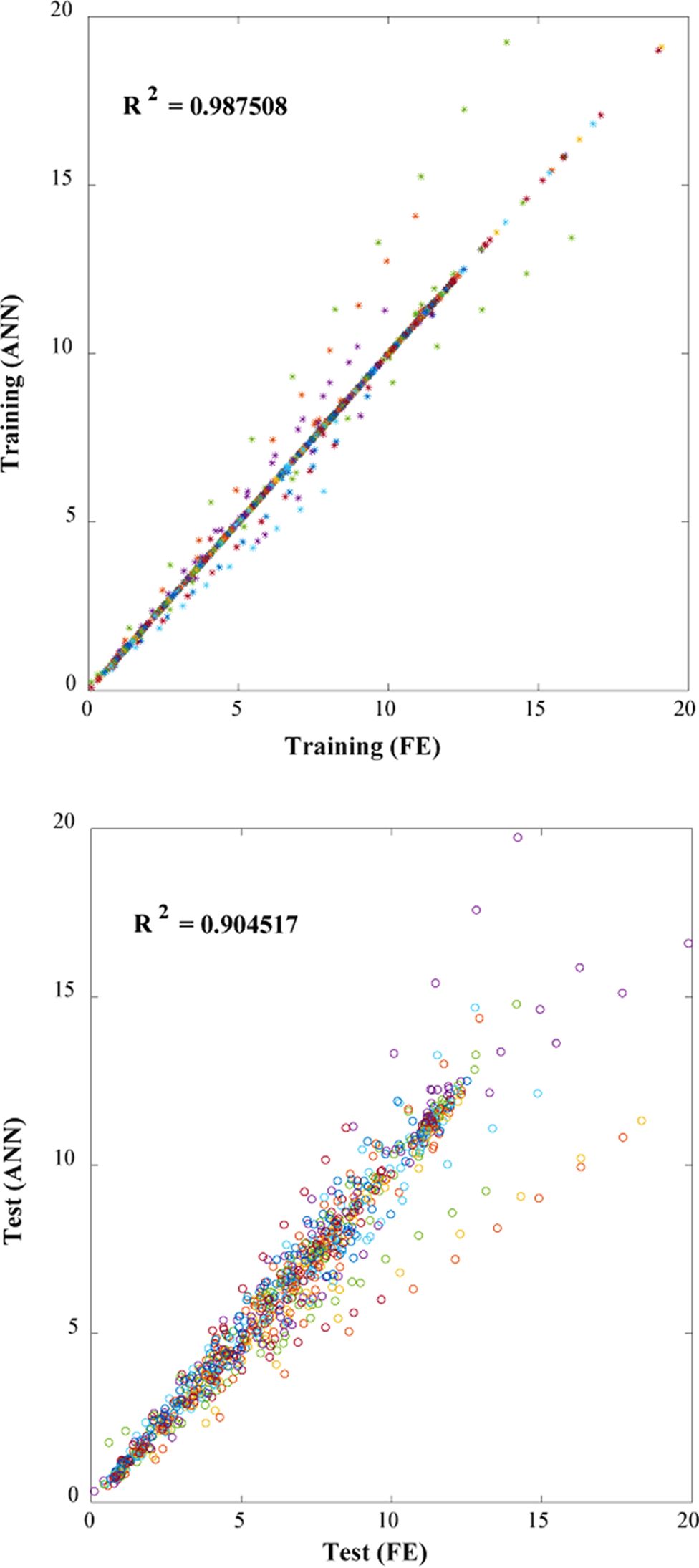
이렇게 구성된 대체 모델은 훈련 데이터를 기반으로 만들어졌기 때문에 이외의 데이터를 이용하여 검증할 필요성이 있다. 그에 따라 시험 데이터를 random sampling으로 50개를 추출하여 신뢰성 검증을 위해 결정계수(coefficient of determination, R²)를 계산하여 Fig. 8에 나타내었다.



여기서 y_i 는 유한요소 해석 결과, 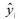는 대체 모델의 결과, 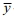는 y_i 의 평균이다. 결정계수는 1에 가까울수록 높은 신뢰성을 가지는데, 0.9 이상일 때 신뢰성이 있다고 판단한다[12]. Fig. 8을 보면 시험 데이터를 이용한 대체 모델의 결정계수가 0.9이므로 신뢰성을 가진 인공신경망 기반 대체 모델을 구성하였다고 판단할 수 있다.
3.5 손상 모델에 대한 파라메터 획득
신뢰성을 가진 인공신경망 모델을 이용하여 실험 결과와의 오차를 최소화하는 파라메터를 찾기 위해 최적화 함수를 도입하였다. GA(genetic algorithm)는 문제에 대한 결과를 무작위로 생성한 후 해답 집단을 진화시켜서 좋은 해답을 얻게 하는 집단 기반 최적화 기법이다. 최적의 파라메터를 얻기 위해 평균 제곱근 오차(root mean square error, RMSE)를 이용하였고, GA를 통해 평균 제곱근 오차가 최솟값을 가지는 파라메터를 얻었다.




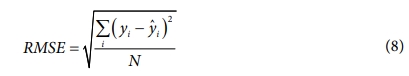
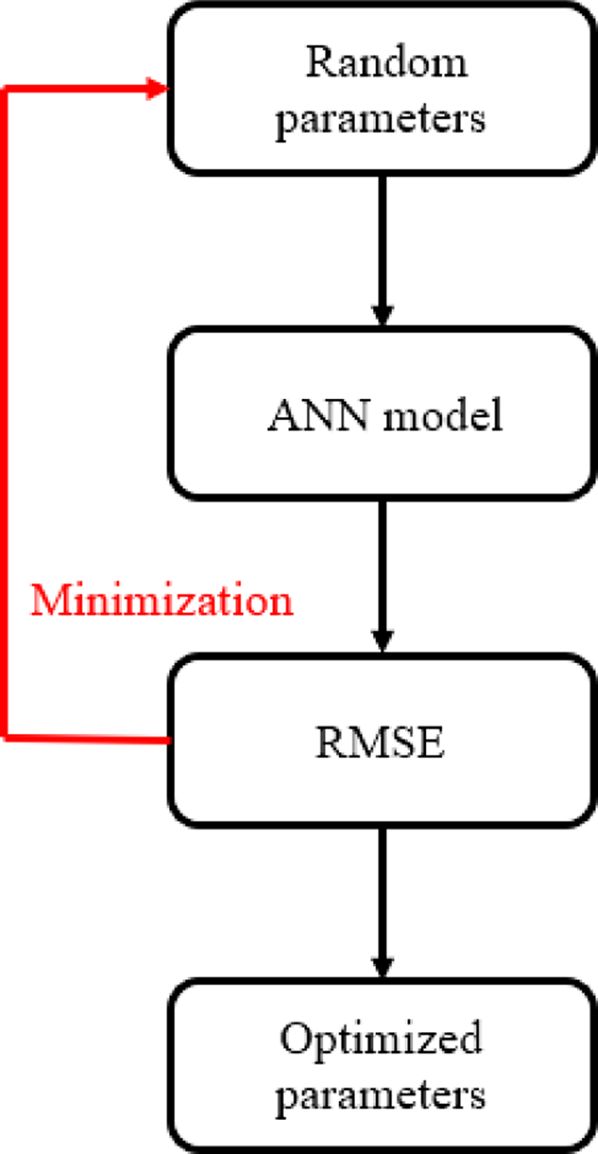
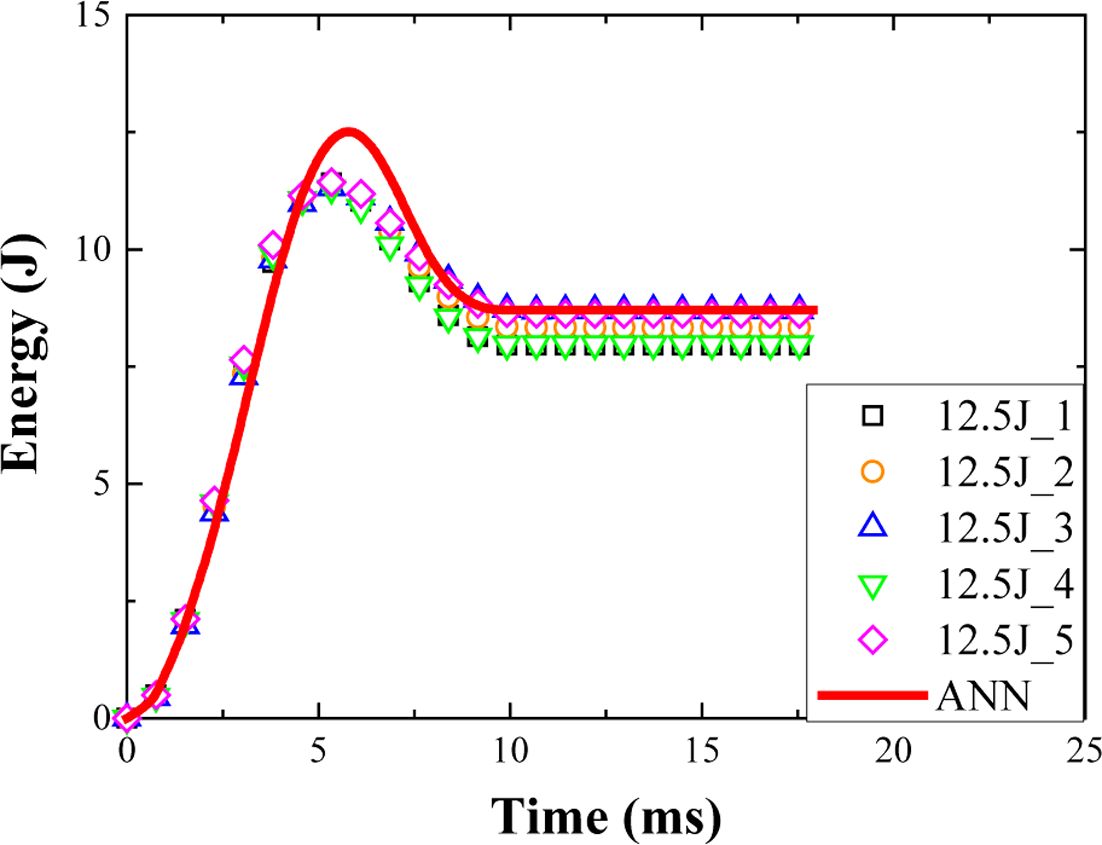
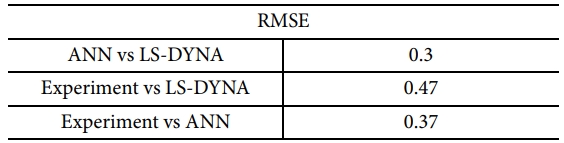
여기서 y_i 는 실험값, 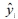는 인공신경망 모델을 이용한 결과, N 은 데이터 개수이다. 평균 제곱근 오차는 0에 가까울수록 높은 신뢰성을 가지고, 대체로 1.0 이하일 때 신뢰성이 있다고 판단한다[12]. Fig. 9는 GA 함수를 통한 파라메터 최적화의 흐름도를 나타낸 것이다. GA로부터 정해진 범위 내의 임의의 수가 인공신경망 모델에 입력되어 결과를 얻는다. 그 결과를 이용하여 평균 제곱근 오차를 계산하는데, 이를 반복 계산하여 평균 제곱근 오차가 최솟값을 가지는 파라메터를 도출한다. 이렇게 최적화된 파라메터는 Table 3에 나타내었다. 획득한 파라메터가 신뢰성을 가지는지 검증하기 위해 유한요소 해석을 수행하여 실험과 해석 결과의 에너지 곡선을 비교하여 Fig. 10에 나타내었고, 해석 결과, 인공신경망 모델의 결과, 실험 결과의 평균 제곱근 오차에 대한 결과를 Table 4에 나타내었다. 실험 결과와 LS-DYNA의 결과의 평균 제곱근 오차가 0.47이고, Fig. 10에서 볼 수 있듯이 에너지 곡선의 경향성이 동일하므로 획득한 파라메터가 신뢰성을 갖추었다고 판단할 수 있다.
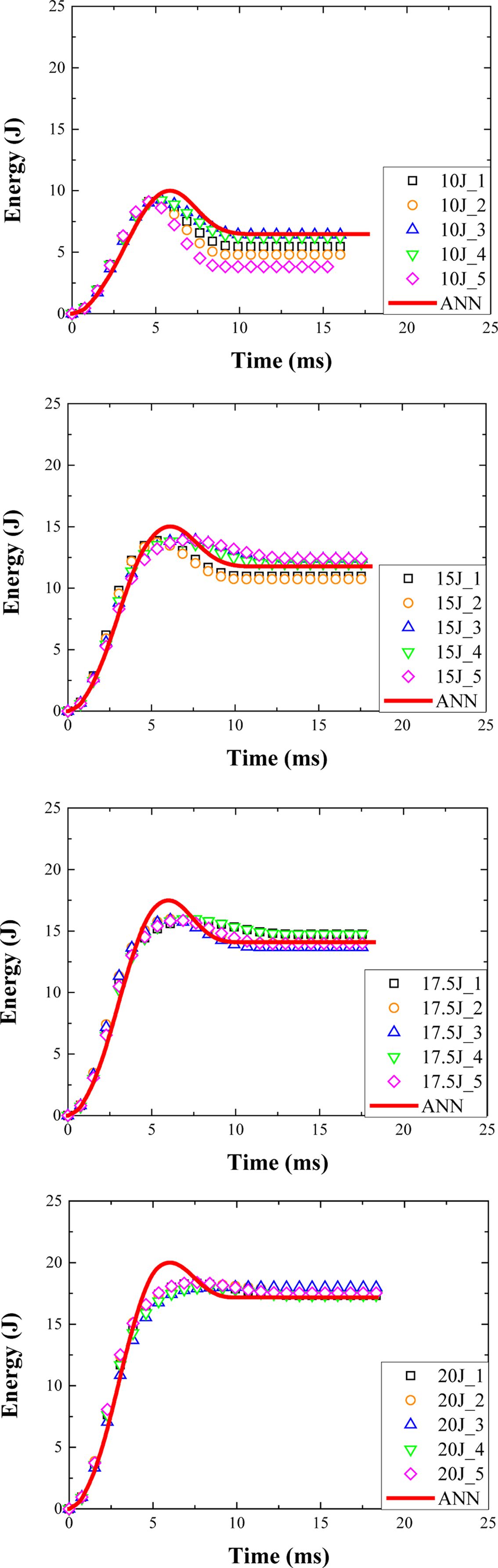
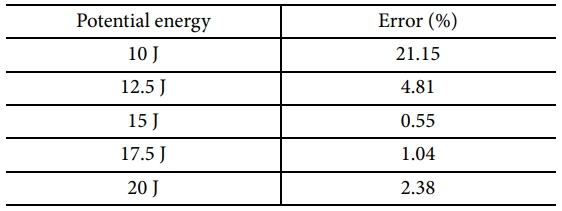
본 연구는 SMC 복합재료의 충돌 손상 해석에서의 손상 모델인 MAT55의 파라메터를 획득하는 것이기 때문에 획득한 파라메터를 다른 위치 에너지 조건(10 J, 15 J, 17.5 J, 20 J)에 대해서도 실험 결과와 해석 결과를 비교하여 Fig. 11에 나타내었다. 또한, 해석 결과의 흡수 에너지와 실험 결과의 평균값과의 오차를 Table 5에 정리하였다.
본 연구는 12.5 J의 위치 에너지에 대해서 인공신경망 기법을 적용한 대체 모델을 구성하여 최적화된 파라메터를 획득하였다. 획득한 파라메터를 이용하여 다른 위치 에너지 조건에 대해서도 비교해 본 결과, 흡수 에너지의 오차가 대체로 5% 이내에 존재하고 흡수 에너지 곡선 또한 동일한 경향성을 지니기 때문에 인공신경망 기법을 이용하여 획득한 파라메터가 신뢰성을 가진다고 판단된다.

본 연구에서는 SMC 복합재료의 손상 모델에 대한 파손 물성을 획득하기 위해 인공신경망 기법을 적용하여 역추정하였다. 인공신경망을 적용한 대체 모델을 구성하기 위하여 자유 낙하 충돌 실험으로부터 얻은 12.5 J의 위치 에너지에서의 흡수 에너지를 이용하였다. 복합재료 손상 모델로는 MAT55 모델을 이용하였으며, MAT55의 파라메터인 탄성계수, 전단계수, 인장강도, 압축강도, 전단강도를 예측하고 신뢰성을 검증하였다. 본 연구 결과를 요약하면 다음과 같다.
(1) 단순화된 유한요소 모델을 만들었고, 손상 모델의 파라메터에 대해서 훈련 데이터와 시험 데이터를 추출한 후 그에 따른 결과를 이용하여 각각 노드 100개를 지닌 2개의 은닉층으로 이루어진 인공신경망 기반 대체 모델을 구성하였다. 구성된 인공신경망 모델은 결정계수가 0.9의 값을 보이므로 신뢰성을 갖춘 모델이다.
(2) 구성된 대체 모델로부터 최적화 함수를 이용하여 최적화된 파라메터를 획득하였다. 획득한 파라메터를 이용하여 실험과 해석 결과를 비교함으로써 흡수 에너지의 오차율과 에너지 곡선의 경향성이 동일함을 보여 획득한 파라메터의 신뢰성을 검증하였다.

이 논문은 부산대학교 기본 연구지원사업(2년)에 의하여 연구되었음. 이에 관계자 여러분께 감사드립니다.