This study developed a machine learning model to predict the cross-sectional properties of pultruded hybrid composite structures. The model aims to optimize the mechanical performance of these structures, which depends on factors such as material properties, layer thickness, fiber volume fraction, and cross-sectional shape. The machine learning model takes 5 cross-sectional variables and 8 material property variables as inputs to predict 4 cross-sectional property variables. To generate the training data for the model, a finite element-based 2D cross-sectional analysis model was employed. The accuracy of the 2D model was validated against a 3D finite element analysis, showing a maximum error of 0.56%. With 50,000 training samples, the trained feed-forward neural networks achieved an average error of 1.6%. This model is expected to be valuable during the design phase of beam-shaped components using various materials, even without any analysis software.

본 연구는 인발 공정으로 제작된 하이브리드 복합재 보 구조물의 단면 물성을 예측하는 기계학습모델을 개발하였다. 보 구조물의 기계적 성능은 소재의 물성, 층별 두께, 섬유 분율, 단면의 형상 등 구성 요소의 조합에 따라 결정된다. 기계학습모델은 하이브리드 보 구조물의 기계적 성능을 최적화하는 조합을 탐색하는데 활용될 수 있다. 기계학습모델은 단면 변수 5개, 소재 물성 변수 8개를 입력받고, 단면 물성 변수 4개를 예측한다. 기계학습에 필요한 학습 데이터는 유한 요소 기반의 2차원 단면 해석 모델로부터 생성되었다. 2차원 단면 해석 모델은 3차원 유한 요소해석 모델과 비교하였을 때 최대 0.56% 오차를 가진다. 학습 데이터는 50,000개 생성되었으며, 학습된 순방향 신경망들은 평균 1.6% 오차를 보였다. 기계학습모델은 입력값에 따라 단면 물성을 즉시 제공하며, 별도의 해석 소프트웨어가 없어도 작동할 수 있다. 향후 다양한 소재가 함께 사용되는 보 형태의 부품 설계 단계에서 유용하게 사용될 것으로 기대된다.

Keywords: 기계학습(Machine learning), 단면 물성(Cross-sectional property), 인발(Pultrusion), 유한요소해석(Finite element analysis), 하이브리드 복합재료(Hybrid composite)

최근 자동차 산업에서는 연비 및 전비 개선을 위해 차체 경량화 수요가 증가하고 있다. 차체 경량화에 적합한 후보 소재 중 하나로 섬유 강화 복합소재가 주목받고 있다[1,2]. 섬유 강화 복합소재는 루프 패널[3], 리어 빔[4], 언더커버[5], 서브 프레임[6], 도어 임팩트 빔[7]에 적용된 사례가 있다. 그러나 복합재 부품은 금속 재료 대비 원소재가 비싸고 성형 시간이 길어서 제조 원가가 비싸다. 따라서 기존 복합재 성형 방법들은 복합재 부품을 대규모 양산하기에는 한계가 있다[8].
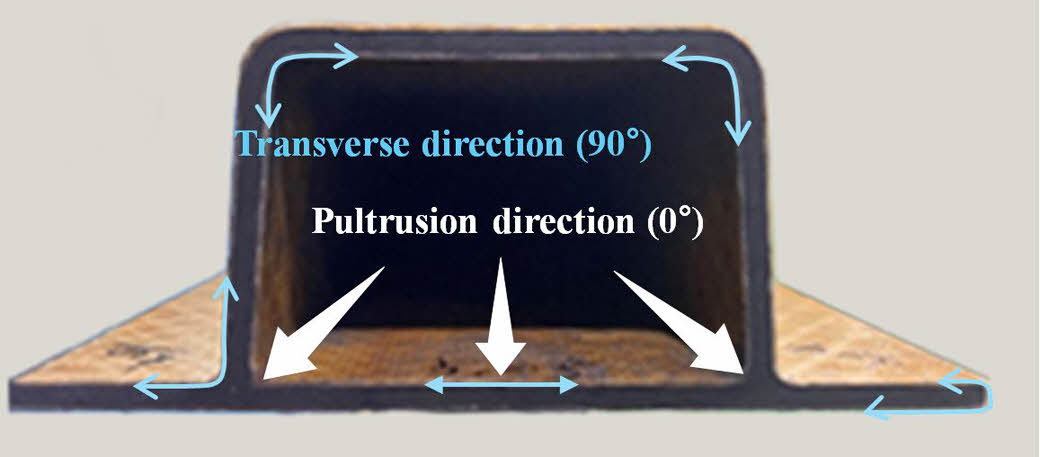
이러한 문제점을 해결하기 위해 복합재 구조물을 인발 공법으로 양산하려는 연구가 수행되어 왔다[9-11]. 인발 공정은 보강 섬유를 열경화성 수지에 함침시킨 후 기계적 힘으로 당기면서 가열 금형을 통해 원하는 단면 형상대로 경화시킨다. 이러한 연속 제조 공정은 단면이 일정하고 길이가 긴 복합재 부품을 대규모 생산하는데 유리하다. 게다가, 인발 복합재는 높은 섬유 함유율과 균일하고 일관된 물성을 가진다. 또한, 인발 공정은 소재 손실을 최소화하고 높은 생산 수율을 보장하여 원가 절감에 유리하다. 하지만 인발 공정은 단면의 형상 자유도가 낮은 한계가 있다. 또한, 인발 복합재를 구성하는 섬유들은 연신 방향으로 정렬되어 있어 90° 특성이 취약하다. Fig. 1은 인발 공정으로 제작된 하이브리드 복합재 구조물을 보여준다. 하이브리드 인발 복합재는 90° 방향의 보강 섬유를 포함하는 다축 직조 직물(Multiaxial fabrics)을 단일 방향(Unidirectional) 섬유와 함께 성형한 것이다[12]. 단일 방향 섬유를 둘러싼 직물 복합재가 90° 특성을 보강한다.
단면이 일정한 인발 구조물은 단면의 형상, 소재의 물성, 소재 간 비율에 따라서 구조물의 기계적 성능이 결정된다. 2개 이상의 비등방성 재료가 혼합된 복합재는 단면 설계 자유도가 많다. 따라서 최적의 성능을 가진 하이브리드 인발 복합재를 설계하기 위해서는 단면 설계 변수에 따른 기계적 성능을 잘 예측하는 것이 중요하다. 비등방성 소재로 제작된 구조물의 2차원 단면 해석 프로그램들이 개발되어왔다[13-16]. 주로 3차원 로터와 풍력 블레이드의 1차원 빔 공탄성 해석을 위해 사용되었다. 그러나 프로그램 별로 사용법이 각기 다를 뿐만 아니라 설계 변수를 변경하면 전, 후처리 과정을 다시 반복해야 한다.
본 연구에서는 기계학습 기반의 단면 해석 모델을 개발하였다. 이 모델은 해석 프로그램에 접근할 수 없거나 익숙하지 않은 설계 엔지니어들이 쉽게 사용할 수 있다. 이 모델은 단면 형상이나 소재 물성 정보를 입력받으면 별도의 전, 후처리 없이 즉시 단면의 기계적 성능을 예측한다. 기계학습에 필요한 데이터는 상용 유한 요소해석 프로그램을 통해 생성되었다. 생성된 학습 데이터는 순방향 신경망을 학습하는 데 사용되었다. 학습된 기계학습모델은 다양한 소재와 단면 형상을 가진 하이브리드 인발 복합재의 단면 강성을 평균 1.6% 오차로 예측한다.

2.1 단면 물성
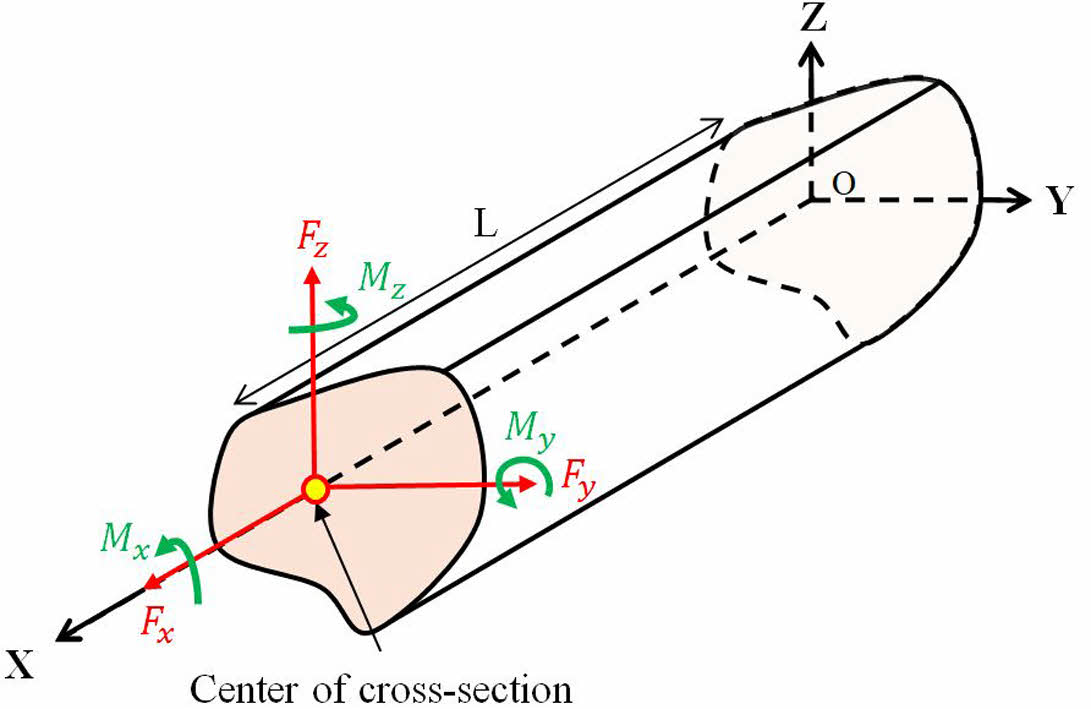
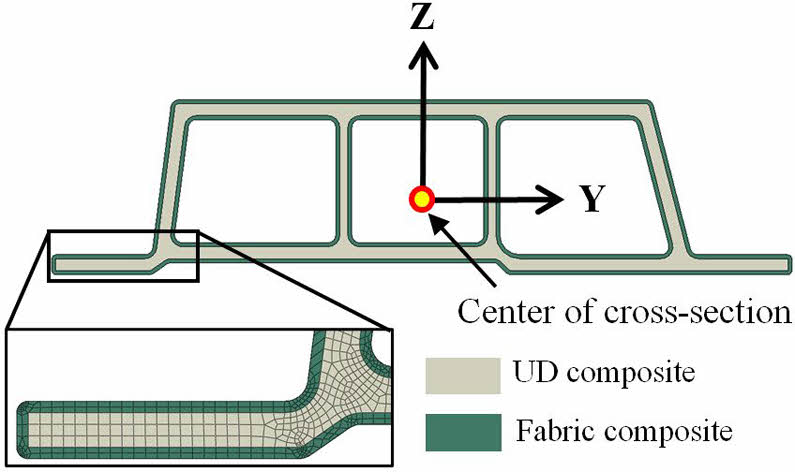
Fig. 2와 같이 임의의 단면 형상과 재료 분포를 갖는 구조물은 수식 (1)과 같은 단면 강성 행렬(K)을 가진다. 단면 강성 행렬의 성분으로부터 단면 물성을 계산할 수 있다. 이때, 단면 중심에 따라 단면 물성이 달라지기 때문에 단면 중심 설정에 주의해야 한다. 단면 물성은 단면 특성과 단면 강성을 포함한다. 단면 특성은 인장 중심(또는 도심), 전단 중심, 주 굽힘축 경사도를 포함한다. 인장 중심은 인장과 굽힘이 연계되지 않는 단면 상의 위치이고, 전단 중심은 전단과 비틀림이 연계되지 않는 단면 상의 위치이다. 주 굽힘축 경사도는 인장 중심을 기준으로 Y 방향과 Z 방향 굽힘이 서로 연계되지 않기 위해 필요한 축 회전 각도를 의미한다. 단면 강성은 축 강성(EA), 비틀림 강성(GJ), 그리고 굽힘 강성 (EI_y, EI_z)을 포함한다. 계산 과정은 문헌[17]에 자세히 서술되어 있다.



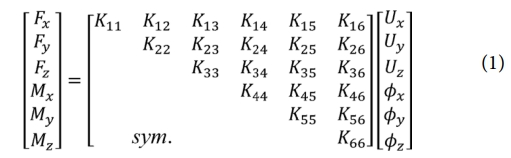
2.2 단면 물성 해석 모델
단면 물성은 상용 유한 요소해석 프로그램 ABAQUS가 지원하는 BEAM SECTION GENERATE 모델[18]을 활용하여 계산되었다. 2차원 단면 모델은 비등방성 탄성 재료 및 다중 재료로 구성된 하이브리드 복합재 단면의 물성을 계산할 수 있다. 또한, 비대칭 개단면 (Open section)의 물성을 계산할 수 있으며, 계산된 단면 물성은 1차원 빔 해석에 직접 연계될 수 있다. 게다가, 이 모델은 기계학습 데이터를 효율적으로 생성할 수 있기 때문에 채택되었다. 사용자는 Python script 기반으로 단면의 형상과 소재의 물성을 변경할 수 있고, 별도의 텍스트 파일에 출력된 단면 물성 덕분에 후처리 과정을 생략할 수 있다.
Fig. 3은 임의의 비대칭 개단면을 가진 하이브리드 인발 복합재의 2차원 유한 요소 모델을 보여준다. 심재(Core)는 UD 섬유 강화 복합소재이며, 면재(Skin)는 직물 섬유 강화 복합소재이다. 심재의 경우, 인발 방향인 X 방향이 섬유 물성 방향이다. 면재는 심재의 모서리를 따라 둘러싸고 있다. 면재의 1 방향은 인발 방향과 일치하고, 면재의 2 방향은 심재의 모서리를 따르는 이산(Discrete) 벡터로 설정되었다. 이 모델은 3차원 뒤틀림(Warping) 효과를 고려하는 약 40,000개의 WARPF2D3와 WARPF2D4 요소로 구성되었다. 별도의 경계 조건 설정은 필요하지 않다.
일반적으로 비등방성 복합재 단면의 경우 임의의 중심축에서 구한 강성 행렬은 식 (1)과 같이 행렬의 모든 성분이 0이 아닐 수 있다[19]. 특히 비대각 성분이 0이 아닌 경우, 인장 시 굽힘이나 비틀림과 같은 연계(coupling) 현상이 발생하는 것은 잘 알려져 있다. 본 연구에서는[19]에서 보여준 바와 같이 특정 하중 조건에서 연계 현상을 분리시키는 단면 중심을 찾는다. 예를 들어, 단면 해석 모델로 구한 Fig. 3 단면의 인장 중심에 축을 위치시켜 구한 강성 행렬은 아래와 같다.



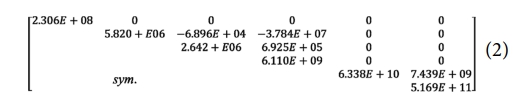
이 때 UD composite의 물성은 E₁ = 140 GPa, E₂ = 7 GPa, v₁₂ = 0.3, v₂₃ = 0.3, G₁₂ = 5 GPa, G₂₃ = 3.3 GPa을 사용하였으며, Fabric composite의 물성은 E₁ = 60 GPa, E₂ = 60 GPa, v₁₂ = 0.05, v₂₃ = 0.05, G₁₂ = 3.3 GPa, G₂₃ = 2 GPa을 사용하였다. UD와 Fabric 모두 1 방향이 X 방향과 일치되게 적층되었다.
식 (2)의 강성 행렬은 축을 인장 중심에 위치시켜 구했기 때문에, 첫번째 행에서 K₁₁을 제외한 모든 비대각 성분이 0으로 나타났다. 즉, 인장 중심의 정의대로 X 방향 인장이 굽힘이나 비틀림과 분리(decouple)되었으며, K₁₁이 곧 인장 강성 EA임을 쉽게 알 수 있다. 하지만, 식 (2)에서 비대각 성분인 K₅₆은 0이 아니다. 이는 Y축 굽힘 M_y에 의해서는 Z 방향 굽힘 Φ_z이 연계되어 발생할 것을 알 수 있다. 즉 각각의 단면 물성은 각각의 단면 물성 정의에 따른 단면 중심에서 구해야 한다. 본 연구에서는 EA 외에 YZ 단면에서 구할 수 있는 GJ, EI_y, EI_z를 다룬다. 단면 해석 모델을 통해 전단 중심을 기준으로 GJ를, 주 굽힘축 경사도를 기준으로 EI_y와 EI_z를 구하였다. 각 경우에 대한 강성 행렬 및 대각/비대각 성분에 대한 조사는 식 (2)의 예와 크게 다르지 않아 추가로 다루지 않았다.
2.3 단면 물성 검증 결과
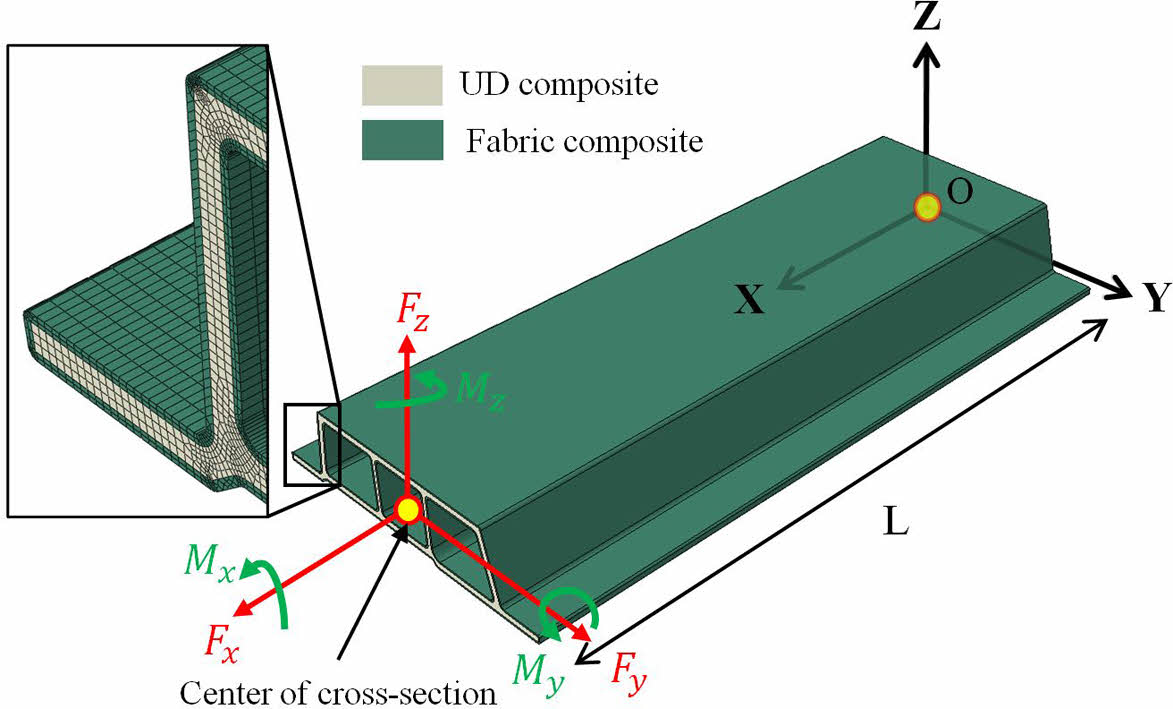
2차원 단면 해석 모델로 구한 Fig. 3 단면의 단면 물성은 3차원 유한요소 해석 모델로 검증하였다. Fig. 4에서 보는 것과 같이 3차원 유한 요소해석 모델은 2차원 모델과 동일한 단면 형상 및 재료가 설정되었다. 이 모델은 약 870,000개의 C3D8R 요소로 구성되었다. 하중면의 단면 중심과 고정면의 단면 중심에 기준점(Reference point)을 각각 정의하였다. 단면 중심은 2차원 단면 해석으로부터 계산된 인장 중심 또는 전단 중심의 좌표가 적용되었다. 기준점의 자유도와 단면에 위치한 절점의 자유도는 ABAQUS가 지원하는 kinematic coupling 기능을 통해 3 자유도(U_x, U_y, U_z)에 대하여 종속 관계를 가진다. 하중면의 기준점에 하중 조건이 적용되었으며, 고정면의 기준점은 U_x=U_y=U_z=0으로 설정되었다. 비틀림 해석의 경우에는, 면외 방향 뒤틀림을 반영하기 위해서 U_z 자유도는 기준점에 종속되지 않았다. 단면 물성 계산에 필요한 변위 데이터는 하중면의 기준점에서 출력되었다. 3차원 모델의 해석 시간은 약 600초이다.
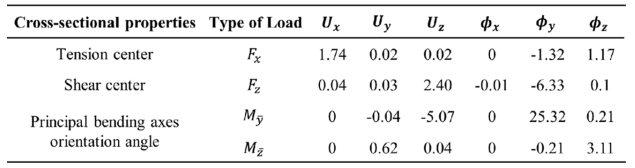
Table 1은 2차원 모델로 계산한 단면 특성 값을 3차원 모델에 적용한 후, 하중을 가했을 때 변형량을 보여준다. 인장 중심에 X 방향 인장 하중을 가한 경우, U_y와 U_z가 거의 0에 가깝다. 이는 인장과 굽힘이 디커플링 된 것을 의미한다. 다시 말해서, 2차원 모델이 계산한 인장 중심은 정확하다. 전단 중심에 Z 방향 전단 하중을 가한 경우, Φ_x가 0에 가깝다. 이는 전단과 비틀림이 연계되지 않는다는 것을 의미한다. 따라서, 2차원 모델이 계산한 전단 중심은 정확하다고 말할 수 있다. 2차원 단면 해석을 통해 계산한 주 굽힘축 경사도를 3차원 모델에 반영하였다. 인장 중심을 기준으로 회전된 단면에 Y축 모멘트를 가한 경우, Z축 회전 변형은 매우 작다. 또한, Z축 모멘트를 가한 경우에는 Y축 회전 번형이 매우 작다. 이는 두 굽힘 변형이 서로 독립적으로 발생한다는 것을 의미한다. 따라서 2차원 모델이 제공하는 주 굽힘축 경사도가 정확하다는 것이 정성적으로 검증되었다.
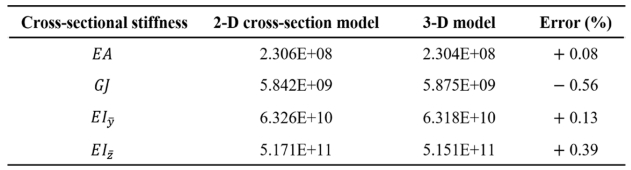
Table 2는 2차원 단면 해석 모델과 3차원 모델을 통해 계산된 단면 강성 값들을 보여준다. 3차원 모델의 단면 강성은 하중면의 기준점으로부터 획득한 변위 데이터와 수식 (3)~(6)을 통해 계산되었다. 굽힘 강성은 주 굽힘축 경사도를 반영한 단면으로부터 비교되었다. 2차원 단면 해석 모델은 최대 0.56%의 오차를 가진다. 결론적으로, 2차원 단면 해석 모델은 임의의 형상을 가진 하이브리드 인발 복합재의 기계적 성능을 정확하고 효율적으로 계산할 수 있다.

3.1 학습 데이터
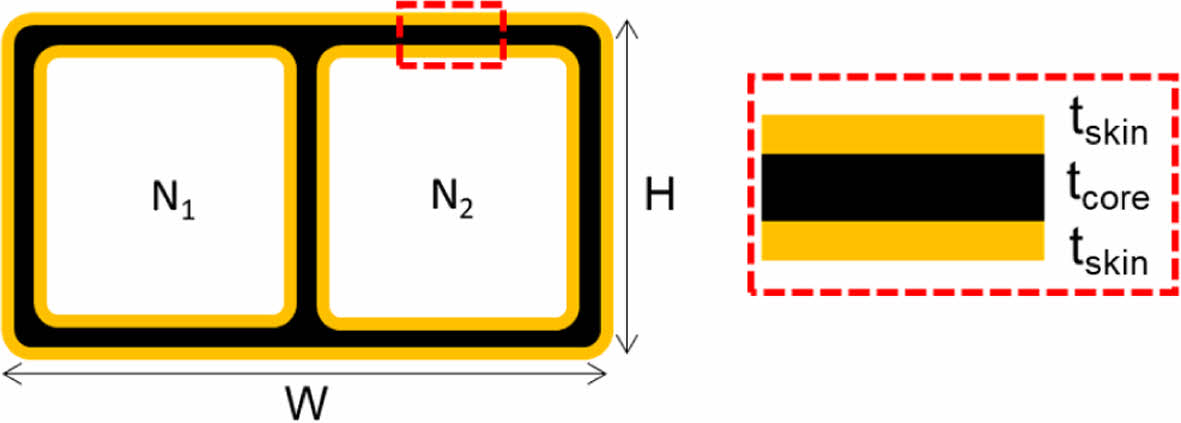
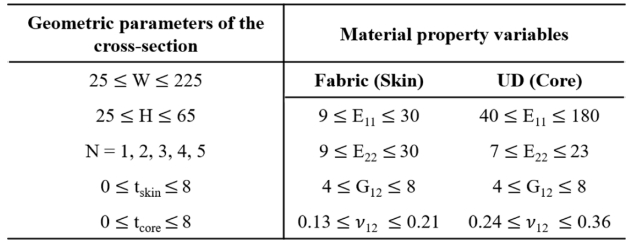
학습 데이터는 임의의 단면 형상과 소재 물성에 대한 변수 13개와 단면 강성 변수 4개로 구성된다. Fig. 5와 Table 3은 단면 형상 변수 5개와 소재 물성 변수 8개의 범위를 보여준다. 단면은 중공을 가진 사각형 하이브리드 복합재이다. 심재의 내부와 외부는 면재로 둘러싸여 있으며, 전체 두께는 최대 8 mm이다. 면재의 물성 범위는 다축 직조 직물 복합재 4종을 고려한다. 심재는 단일 방향 섬유 강화 복합재 2종을 고려한다. 단면 해석 모델에 입력이 필요한 나머지 물성 값들은 문헌[20,21]을 참고하여 상수(Constant) 또는 지정된 값의 비율로 가정되었다. 단면 강성 변수는 단면 해석 결과로부터 얻은 EA, GJ, EI_y, EI_z이다.
학습 데이터를 생성하는 과정은 다음과 같다. 먼저, ABAQUS의 단면 해석 파일을 생성하는 Python script를 만들었다. Python script는 단면 형상과 소재 물성을 입력받으면 완전한 단면 해석 파일을 생성한다. 이후 13개의 입력 변수가 지정된 범위 내에서 무작위로 선택되었다. 무작위 입력 변수들을 반영한 Python script는 단면 해석 파일을 작성하였다. 단면 해석 파일은 ABAQUS 서버에 제출되고, 단면 강성이 작성된 파일이 출력된다. 이 모든 과정은 MATLAB을 활용하여 처리되었으며, 전체 50,000쌍의 학습 데이터가 구축되었다. 이 중에서 90%는 학습에 사용되었고, 5%는 학습 검증에 사용되었다. 나머지 5%는 테스트에 사용되었다. 위 비율은 경험적으로 결정되었으며, 최대한 많은 데이터가 학습에 참여하도록 학습 데이터 비율을 90%로 결정하였다. 검증과 테스트에는 비율로는 5%지만, 각각 2,500 쌍의 충분히 많은 자료가 사용되었다.
3.2 인공 신경망
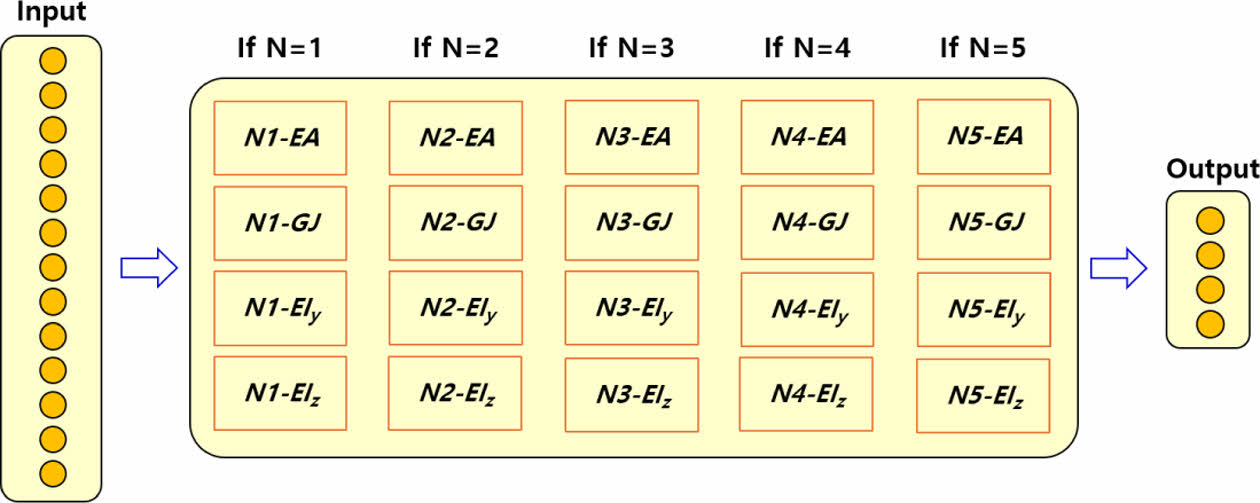
Fig. 6에서 보는 것과 같이 기계학습모델은 20개의 순방향 신경망(Feed-forward neural network)으로 구성된다. 각각의 신경망은 중공 개수와 단면 강성 종류에 따라서 별도로 학습되었다. 그 이유는 학습 데이터가 값 차이가 큰 변수를 동시에 포함하는 경우, 손실(Loss) 값에 편향을 야기하여 최적점을 찾는 것을 어렵게 만들기 때문이다. 중공 개수에 따라 출력 변숫값 차이가 크고, 단면 강성 사이의 값 차이가 크다.
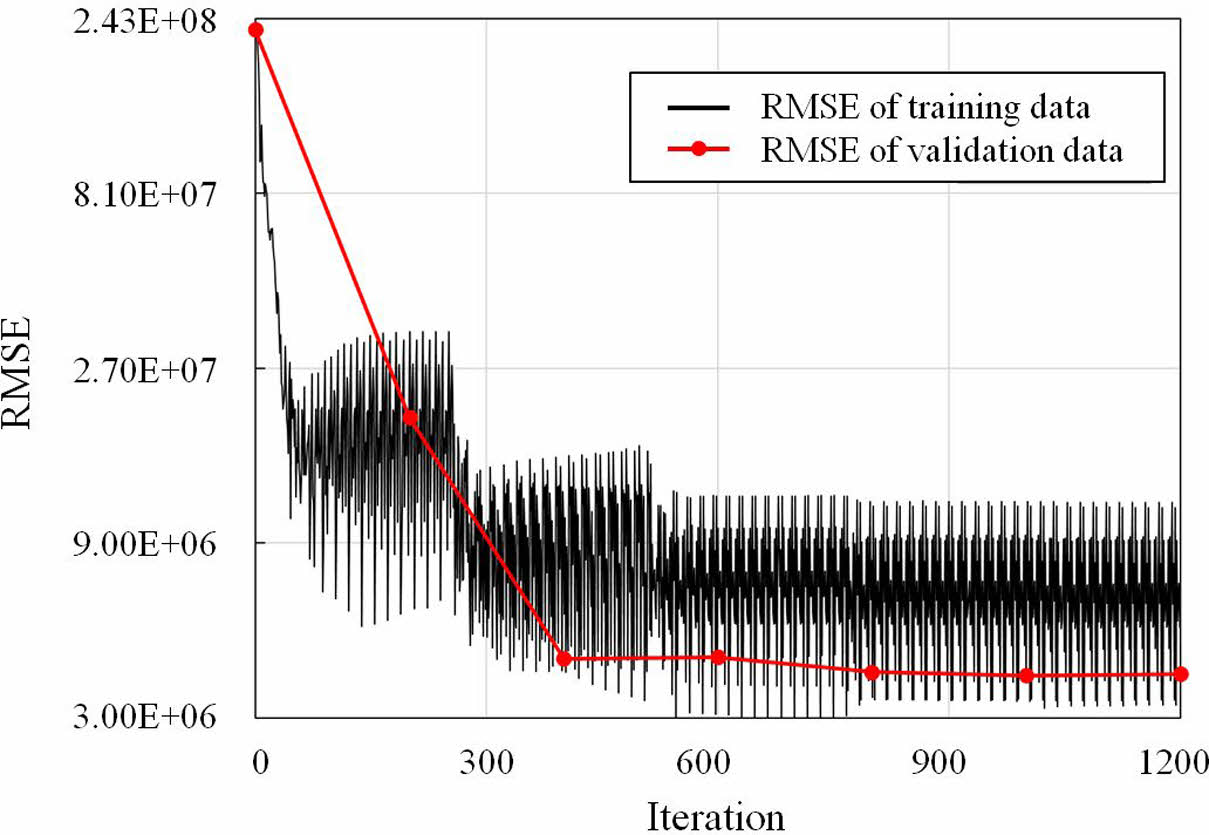
하나의 순방향 신경망의 구조는 12-[256-128-64-32-32]-1이다. 중공 개수를 제외한 12개의 변수를 입력받고 단면 강성 1가지를 출력한다.[256-128-64-32-32]는 5개의 은닉층 (Hidden layer)을 구성하는 노드 개수를 의미한다. 노드 개수는 경험적으로 탐색되었다. 모든 은닉층 뒤에는 정규화층과 ReLU 활성화 함수층을 배치하였다. RMSE (Root mean square error) 손실 함수와 아담 최적화 알고리즘을 통해 신경망이 학습되었다. 미니 배치 사이즈는 256쌍으로 설정되었다. Fig. 7은 중공 1개를 가진 하이브리드 복합재의 축 강성을 예측하는 신경망의 학습 반복수에 따른 RMSE를 보여준다. 10에폭부터 RMSE가 수렴하였으며, 학습에는 약 3분이 소요되었다. 기계학습모델은 평균 2.6%의 오차율을 보였다.
3.3 하위 구간 오차율 개선
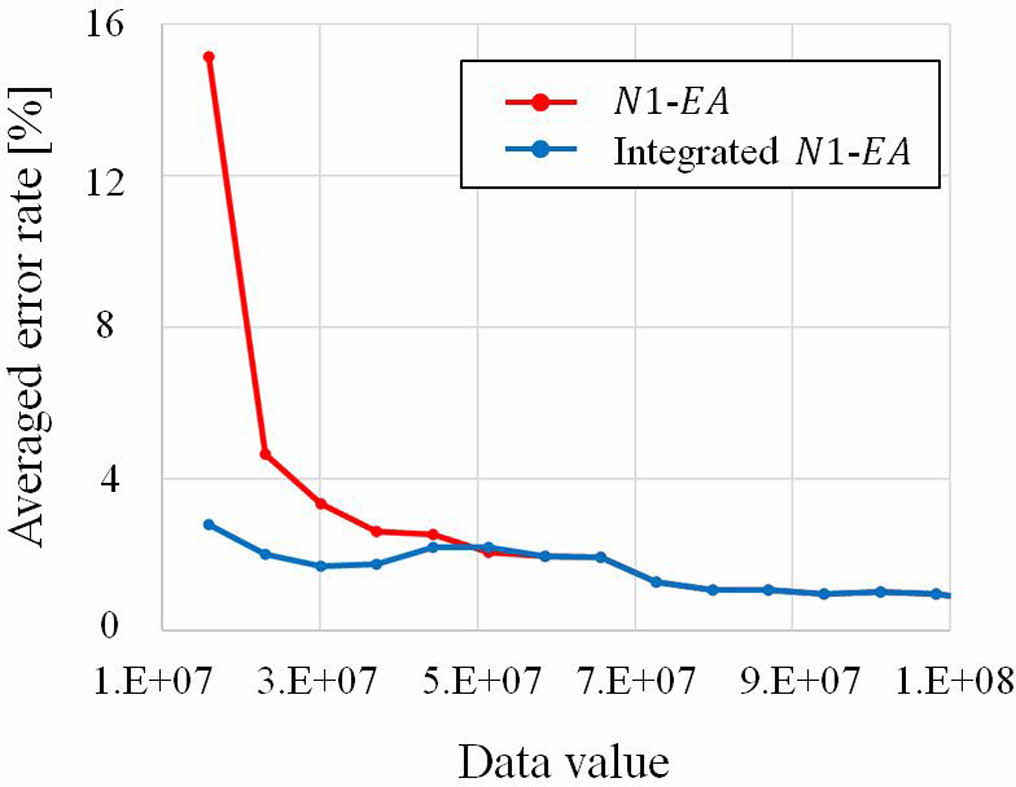
RMSE 손실 함수를 사용하는 경우, 예측 데이터의 값이 전체 데이터 중에서 작은 구간일 때, 오차율이 커지는 문제가 있다. 예를 들어, 100을 102로 예측한 것과 10을 12로 예측한 것은 둘 다 2의 오차를 가진다. 하지만 전자는 2%의 오차율을 가지고 후자는 20%의 오차율을 가진다. Fig. 8의 빨간색 선도는 N1-EA 신경망이 작은 크기의 데이터 값에 대해서 높은 오차율을 가지는 것을 보여준다. 특히 데이터 값의 크기가 하위 0~3% 구간에서 높은 오차율을 보인다. 이를 극복하기 위해서 하위 구간의 데이터로만 학습된 별도의 신경망이 추가되었다. 별도의 신경망은 하위 0~5% 구간의 데이터들로 학습시켰다. 하위 3% 구간의 데이터로만 학습시키면 학습 데이터가 제한적이어 3% 이상 구간에 대해서는 외삽 예측하여 기존 신경망과 매우 큰 차이를 발생시킬 수 있기 때문이다. 학습된 별도의 신경망은 기존 신경망과 통합되었다. 개선된 오차율은 Fig. 8의 파란색 선도와 같다. 이러한 전략을 모든 신경망에 적용하였다. 하위 구간 오차율이 개선된 기계학습모델은 평균 오차율 1.6%을 보였다.

본 연구에서는 단면 구조 및 복합재 적층 양상에 따라 하이브리드 인발 복합재의 구조적 성능을 예측할 수 있는 모델을 개발하였다. 학습 데이터 생성에는 2차원 단면 해석 모델이 활용되었다. 2차원 단면 해석 모델은 3차원 유한 요소 모델 대비 최대 0.56%의 오차를 가진다. 단면 해석 모델을 Python script로 매개변수화함으로써 50,000개 데이터를 효율적으로 생성하였다. 기계학습모델은 20개의 신경망 조합이며, 하위 구간 오차율 개선을 위해 별도로 학습된 신경망이 통합되었다. 그 결과, 기계학습모델은 평균 1.6% 오차율을 가졌다. 향후 CNN 신경망을 활용하여 복잡한 단면 형상을 가진 구조물의 성능을 예측하는 기계학습모델로 확장될 수 있다. 동시에 선행 설계 시간과 비용을 절감할 수 있을 것으로 기대된다.

본 연구는 현대자동차그룹으로부터 연구비를 지원받아 수행되었음.