- Design of Anisotropic Piezoelectric Actuators Using Smooth Topology Optimization
Seyyed Ali Latifi Rostami*, Hyoung Jun Lim**†
* Aerospace Systems Research Center, Gyeongsang National University
** School of Mechanical and Aerospace Engineering, Gyeongsang National University- 매끄러운 위상 최적화 기법을 활용한 이방성 압전 액추에이터 설계
Seyyed Ali Latifi Rostami* · 임형준**†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This study investigates the optimization of piezoelectric actuators by integrating anisotropic material properties with topology optimization (TO) techniques to enhance performance and manufacturability. The finite element method was employed to analyze the behavior and performance of piezoelectric actuators, revealing that anisotropic materials exhibit superior design potential compared to isotropic and moderately anisotropic materials. Optimized designs demonstrate complex polarization and deformation patterns, significantly improving actuator efficiency. However, anisotropy introduces challenges, such as stress concentrations and potential structural weaknesses, requiring careful design considerations. Building upon existing studies, this research not only addresses these challenges but also presents a novel approach by combining anisotropic material properties and smooth TO techniques, optimizing both structural performance and manufacturing feasibility. This integrated method provides practical advancements for additive manufacturing and expands the potential of piezoelectric actuators in high-performance aerospace and industrial applications.
본 연구는 이방성 재료의 특성과 위상 최적화(Topology Optimizaiton, TO) 기법을 결합하여 압전 액추에이터의 성능과 제조 가능성을 최적화하는 방안을 탐구하였다. 유한요소법을 이용하여 압전 액추에이터의 동작과 성능을 분석하였으며, 이방성 재료는 등방성 및 준등방성 재료에 비해 우수한 설계 가능성을 보이는 것으로 나타났다. 최적화된 설계는 복잡한 분극 및 변형 패턴을 나타내어 액추에이터의 효율성을 향상시킨다. 그러나 이방성 재료는 응력 집중과 구조적 약점과 같은 설계 상의 과제를 초래하며, 신중한 설계 고려가 요구된다. 본 연구는 기존 연구를 기반으로 이러한 문제를 해결하는 동시에, 이방성 재료 특성과 매끄러운 위상 최적화 기법을 결합한 새로운 접근법을 제시하여 구조적 성능과 제조 가능성을 동시에 최적화하였다. 이러한 통합적 방법은 적층 제조(Additive Manufacturing)에서 실질적인 발전을 제공하며, 고성능 항공우주 및 산업 응용 분야에서 압전 액추에이터의 활용 가능성을 확장한다.
Keywords: 위상최적화(Topology Optimization), 이방성 재료(Anisotropic Materials), 압전 액추에이터(Piezoelectric Actuators), 매끄러운 경계(Smooth Boundary), 유한요소법(Finite Element Method)
압전 소자는 정밀성, 경량 설계, 그리고 전기 신호를 기계적 운동으로 효율적으로 변환하는 능력 덕분에 에너지 및 정밀 기계 기술 발전에 필수적인 요소로 자리 잡고 있다[1]. 압전 액추에이터는 진동 제어, 가변 형상 구조(morphing structures), 적응형 광학(adaptive optics) 등 다양한 응용 분야에서 성능을 향상시키는 데 기여하며, 효율적인 에너지 변환과 소형화된 설계가 요구되는 기술에서 중요한 역할을 한다. 또한, 극한 환경에서도 높은 신뢰성을 보여 센서 및 에너지 하베스팅 장치와 같은 정밀 응용 분야에도 널리 활용된다[2-4].
최근 스마트 구조(smart structures) 연구는 기존 적층 방식이나 증폭 메커니즘과 같은 전통적 접근법으로 인한 제한된 변위 성능을 극복하려는 방향으로 발전하고 있다[5, 6]. 기존 방식은 효과적이지만 부피가 크고 확장성이 낮은 설계를 초래할 수 있다[7]. 이에 따라, 위상 최적화(Topology Optimization, TO)는 효율적이고 확장 가능한 설계를 가능하게 하는 강력한 도구로 주목받고 있으며, 특정 제약 조건 하에서 소자의 재료 배치를 최적화하여 강성 극대화[8], 열 전도[9], 스마트 소자 개발[10] 등의 과제를 해결하는 데 성공적으로 적용되고 있다.
압전 액추에이터 설계에 위상최적화를 적용한 기존 연구는 액추에이터 성능 향상에 있어 중요한 기여를 했지만, 몇 가지 한계가 존재한다. 예를 들어, Silva 등[7]은 균질화 이론을 사용하여 미세 구조를 최적화하였으나, 고유 진동수(Eigen-frequency)에만 초점을 맞추고 역압전 효과를 간과하였다. 이후 Kang 등[8]은 소자의 재료 배치와 작동 전압을 동시에 최적화하는 연구를 통해 이를 개선하였으며, Wang 등[9]은 레벨셋(level set) 함수를 사용하여 형상과 위치를 정의하고 최적화를 수행하였다. Schlinquer 등[10]과 Fang 등[11]은 각각 실험적 검증 및 이동 가능한 공극(Moving Morphable Void, MMV) 기법을 통해 압전 소자의 재료 분포를 최적화하는 데 기여하였다. 그러나 이 연구들은 대부분 제조 가능성이나 매끄러운 경계 표현과 같은 실제 적용 가능성에 대한 고려가 부족했다.
최근 적층 제조(Additive Manufacturing, AM)와 위상최적화의 통합은 고성능 설계를 위한 새로운 가능성을 열고 있지만, 소자의 이방성이 초래하는 설계 및 제조 상의 도전 과제는 여전히 해결해야 할 과제로 남아 있다[13]. AM에서는 적층 방식의 특성상 방향 차이가 발생하며[14], 이는 성능 저하 요인으로 작용하거나, 의도적으로 활용될 경우 설계 효율을 향상시키는 기회가 될 수 있다.
본 연구는 압전소자의 이방성 특성을 통합하고 매끄러운 위상최적화 기법을 적용하여 압전 액추에이터 설계의 성능과 제조 가능성을 최적화하는 새로운 접근법을 제안한다. 기존 연구들이 종종 제조 가능성과 재료 방향성의 상호작용을 간과했던 것과 달리, 본 연구는 성능과 제조 가능성 간의 상충 관계를 체계적으로 분석하고, 매끄러운 경계 표현을 통해 적층 제조와 같은 실제 제조 환경에서 실용적인 설계를 구현하고자 한다. 이를 통해 항공우주 및 정밀 공학과 같은 고급 응용 분야에 적합한 고성능, 고신뢰성 압전 소자 설계를 위한 새로운 방향성을 제시한다.
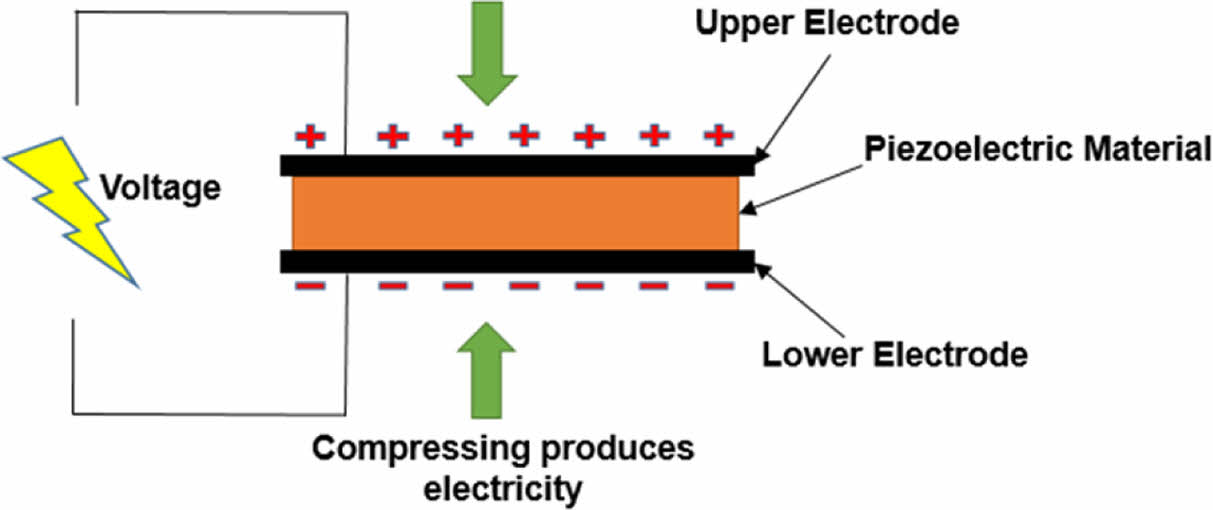
압전 플레이트는 압전 효과를 활용하여 기계적 하중이 가해질 때 전하를 생성(직접 압전 효과)하거나 전기장이 가해질 때 변형(역압전 효과)하는 얇고 평평한 구조물이다. 이러한 특성은 센서, 액추에이터, 소형 에너지 하베스팅 장치 등 다양한 공학적 응용 분야에서 유용하게 활용된다[12-14]. 예를 들어, 압전 액추에이터는 전기장을 통해 정밀한 기계적 변위를 생성하여 초점 조정 메커니즘, 미세 위치 제어 등 정교한 조정이 필요한 작업에 중요한 역할을 한다. 대표적인 사례로는 나노포지셔너(nanopositioner)와 같은 미세 조작이 요구되는 장치에서의 활용이 있다.
본 연구에서는 Fig. 1에 나타난 바와 같이 압전 플레이트를 대상으로 한다. 두께 대 길이 비율이 작은 것으로 가정하며, 압전 플레이트의 움직임은 면내(in-plane)로 제한되어 모델이 2차원 문제로 단순화된다. 얇은 플레이트의 양면에 전극이 부착되어 수직 분극이 형성되지만, 전극의 두께가 매우 얇아 플레이트의 탄성에 유의미한 영향을 미치지 않는다고 가정한다.
더 나아가, z-방향으로 분극을 적용함으로써 전기장은 z축을 따라 0이 아닌 값을 가지게 된다.
2.1 선형 압전 분석
전기탄성(electroelastic) 구성 조건에 대해, 일반화된 해밀턴 원리는 식 (1)로 표현될 수 있다[15]. 이 식에서는 자기 효과(magnetic effects)가 무시되었음을 명시한다.
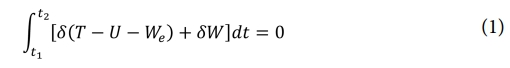
여기서 총 운동 에너지 T, 총 포텐셜 에너지 U, 그리고 전기 에너지 We는 아래 식과 같이 정의된다.

여기서 u, S, T는 각각 기계적 변위 벡터, 기계적 변형률 성분 벡터, 그리고 기계적 응력 성분 벡터를 나타낸다. 전기 변위 벡터는 성분 D로 표현되며, E는 전기장 성분 벡터를, V는 부피를, t는 행렬의 전치를 나타낸다.
2.2 압전 플레이트의 구성방정식
열 결합(thermal coupling)을 무시하고 압전 구성 모델에서 평면 응력(plane stress)을 가정하면, 이러한 상호 작용을 지배하는 일반적인 구성 방정식은 식 (3)으로 표현할 수 있다[16].

여기서 cE는 탄성 강성 행렬(elastic stiffness matrix)을 나타내며, e는 압전 행렬(piezoelectric matrix), eS는 유전율 행렬(permittivity matrix)을 의미한다. 압전 층에 대한 평면 응력(plane-stress) 구성 방정식은 다음과 같다.
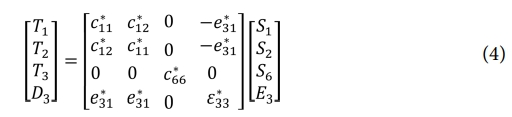
이는 식 (3)의 축소된 2차원(2-D) 형태를 나타낸다. 식 (4)에서의 탄성, 압전, 그리고 유전 성분은 Voigt 표기법을 따르며, 여기서 1, 2, 3은 각각 x, y, z방향을 나타낸다.
2.3 압전 액추에어이터의 이방성
이방성은 재료 물성이 방향에 따라 달라지는 특성을 의미하며, 이는 압전 재료에서 중요한 요소로 작용한다. 등방성 재료와 달리, 이방성 재료는 강성, 압전 계수, 유전 특성이 방향에 따라 변화를 나타낸다. 이러한 방향 의존적 특성은 변위를 극대화하거나 작동 효율을 향상시키는 등, 응용 분야별 요구에 맞춰 재료 특성을 정렬함으로써 압전 액추에이터의 성능을 향상시킨다.
본 연구에서는 평면 응력 구성 방정식을 사용하여 압전 재료의 이방성 거동을 모델링하였다. 일반적으로, 일반적으로, 식 (4)에 나타난 압전 구조의 평면 응력 성분은 3차원 구성요소로부터 다음과 같이 유도될 수 있다:
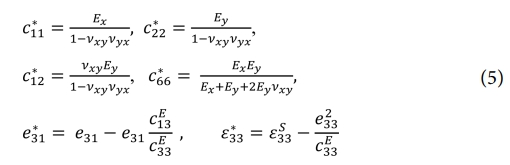
식 (4) 및 (5)는 방향 의존적 재료 특성이 응력, 변형률, 전기 변위를 어떻게 변화시키는지 보여주며, 이방성 재료와 등방성 재료의 차이를 명확히 한다. 강성 및 결합 행렬은 이러한 방향 의존성을 반영하도록 수정되며, 이는 최적화 과정과 결과로 나타나는 액추에이터 성능에 직접적인 영향을 미친다.
2.4 유한요소 정식화
변형률-변위 행렬(Bu)과 요소 기울기 행렬(Bf)의 값을 사용하여, 전기장과 변형률은 다음과 같이 표현될 수 있다.

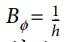 이며, u, Φ, h는 각각 기계적 변위 벡터, 전기 포텐셜의 스칼라 값, 그리고 압전 플레이트의 두께를 나타낸다. 표준 갤러킨 방법(Galerkin’s method)을 사용하고 감쇠를 무시하면 요소 선형 미분 방정식은 다음과 같이 얻을 수 있다.
이며, u, Φ, h는 각각 기계적 변위 벡터, 전기 포텐셜의 스칼라 값, 그리고 압전 플레이트의 두께를 나타낸다. 표준 갤러킨 방법(Galerkin’s method)을 사용하고 감쇠를 무시하면 요소 선형 미분 방정식은 다음과 같이 얻을 수 있다.
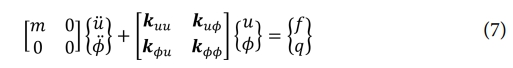
kuu는 기계적 강성 행렬(mechanical stiffness matrix), kuf는 압전 결합 행렬(piezoelectric coupling matrix), kff는 유전 강성 행렬(dielectric stiffness matrix)을 나타낸다. f는 외부 기계적 힘(external mechanical force)을, q는 전하(charge)를 의미한다. 본 연구에서는 정적 작동(static actuation)에 초점을 맞추므로 동적 효과는 고려하지 않는다. 따라서, 작동을 위한 전역 유한요소(FEM) 방정식은 다음과 같이 표현될 수 있다.

이 방정식은 가해진 전기 포텐셜에 의해 발생하는 기계적 변위를 계산하는 데 사용된다. 식 (8)의 성분들은 식 (9)를 이용하여 다시 정리할 수 있으며, 보다 자세한 유한요소 정식화는 선행연구를[11] 통해 참고할 수 있다.
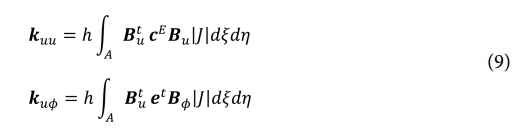
|
Fig. 1 Piezoelectric plate situated between two electrodes |
3.1 재료 보간 기법
본 연구는 밀도 기반 접근법인 solid isotropic material with penalization (SIMP) 방법을 활용하며, 이는 특히 압전 액추에이터와 에너지 하베스터 설계에 널리 적용되고 있다[35]. 본 연구에서는 PEMAP 모델을 확장하여 압전 재료 분포와 분극(양 또는 음)을 최적화하기 위해 설계 변수 p를 도입하여 압전 소자의 분극을 포함하였다. 최적화 과정에 분극을 포함함으로써 액추에이터 설계 품질이 향상되며, 이를 통해 PEMAP-P 모델[11,17]이 다음과 같이 적용되었다.
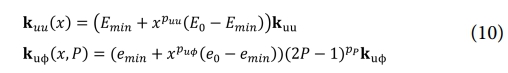
여기서 x는 요소별 재료 밀도를 나타내며, 값은 0에서 1까지 범위를 가진다. E0와 e0는 최대 밀도(x=1)에 해당하는 재료 특성을 나타내며, Emin과 emin과 같은 작은 값은 각각 강성 행렬(stiffness matrix)과 결합 행렬(coupling matrix)에서 시스템의 비정상적 상태(ill-conditioning)를 방지하기 위해 도입된다. 본 논문에서는 이러한 최소 값을 emin=Emin=10-9 [7,11]로 설정하였다. P는 분극 변수(polarization variable)로 값이 0과 1 사이에 있으며, 분극 방향을 결정한다. puf , puf , pp는 각각 강성, 결합 행렬, 그리고 분극 값에 대한 페널티 계수(penalization coefficient)를 나타낸다.
3.2 결정론적 위상 최적화 문제 정의
압전 액추에이터 설계를 위한 최적화 문제 정의는 식 (11)로 표현된다. 기존 접근법[16]에 기반하여, 평면 압전 액추에이터의 최적화 과정은 목적 함수 Jact를 최소화함으로써 구조의 특정 위치에서 최대 변위를 달성하는 것을 목표로 한다.
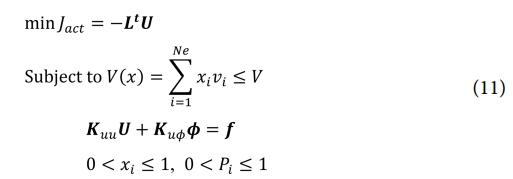
여기서 벡터 L은 시스템의 변위 벡터 U로부터 출력 변위를 추출하는 항목이며, 재료 부피에 대한 부등식 제약은 재료 부피 vi의 합으로 계산된다. 여기서 아래 첨자 i는 요소의 인덱스를 나타내며, 1부터 영역 내 요소 개수 Ne까지의 범위를 갖는다. 앞서 언급된 바와 같이, 요소별 재료 밀도 xi와 극성 Pi는 값이 0과 1사이를 가지는 설계 변수이다. 본 연구에서는 목적 함수 Jact에 대한 민감도 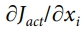 를 계산하기 위해 표준 수반 방법(adjoint method)을 사용하였다. 이를 정의하기 위해 확장된 라그랑지안 P는 식 (12)로 정의할 수 있다.
를 계산하기 위해 표준 수반 방법(adjoint method)을 사용하였다. 이를 정의하기 위해 확장된 라그랑지안 P는 식 (12)로 정의할 수 있다.
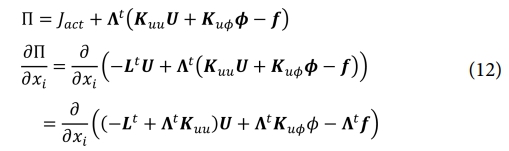
여기서 L는 유한요소 형태에서 선형 운동량 보존의 지배 방정식을 고려하는 라그랑지 승수(Lagrange multiplier)를 의미하며, 수반 방정식(adjoint equation)은 식 (13)으로 유도된다.

식 (13)에서 제시된 수반 방정식(adjoint equations)은 자기수반(self-adjoint)하지 않으며, 각 반복(iteration)마다 해를 구해야 한다. 그러나 LU 분해 및 Cholesky 분해와 같은 표준 분해 방법을 사용할 수 있으므로 이 과정에서 계산 효율성에는 큰 영향을 미치지 않는다. 따라서, 목적 함수의 민감도는 다음과 같이 계산된다.
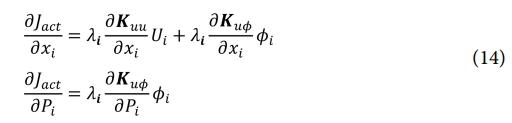
여기서 λi는 전역 수반 벡터 Λ의 요소 형식(elemental format)을 나타낸다. 설계 변수에 대한 압전 강성 행렬(piezoelectric stiffness matrix) 및 결합 행렬(coupling matrix)의 미분은 식 (10)을 사용해야 하며, 그 결과는 다음과 같이 표현된다.
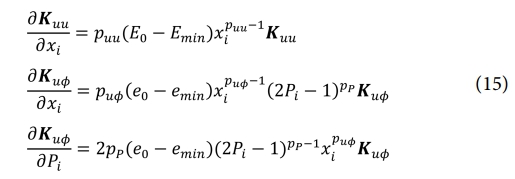
민감도 해석이 수행되고 제약 조건이 정의된 후, 설계 변수의 최적화는 이후 섹션에서 논의된 최적화 알고리즘을 사용하여 수행된다. 결정론적 위상 최적화(Deterministic Topology Optimization, DTO)에서 사용된 매개변수와 상수의 값은 Schlinquer[10]의 연구를 기반으로 설정되었다.
3.3 매끄러운 위상 최적화 표현
이번 섹션에서는 매끄러운 경계를 가지는 최적화 구조를 얻기 위해, 요소 기반 설계 변수 θk를 매끄럽게 표현하기 위해 연속변수로 전환한다. 이상적으로 설계는 고체 또는 공극 상태로 구성되며, 이때 θik는 {0,1} 값을 갖는다. 매끄러운 경계를 가진 최적화된 위상을 나타내기 위해, 요소 밀도 θik는 전체 설계 영역에서 보간되어 θk(x, y)를 형성한다. 이후, 투영 함수(projection function) φk(x, y)=θk(x, y)-th가 정의되며, 이 함수를 통해 최적화된 위상이 해당 함수의 제로 컨투어(zero contour)로 표현된다[18].
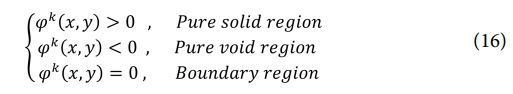
투영 함수에 의해 생성된 매끄러운 경계 설계는 이미지 처리 기법(image processing techniques)에 기반한다. 이 매끄러운 설계와 이산 요소 기반 구성 간의 차이를 정량화하기 위해, 매끄러운 설계를 메쉬 도메인으로 다시 매핑하고 각 요소의 부피분율(volume fraction)을 계산한다. 이는 vk = {v1k v2k ....., vNk}로 표현할 수 있다. 부유 임계값(floating threshold)은 각 반복(iteration)마다 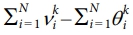 의 차이에 기반하여 갱신된다[19]. θk와 vk간의 정렬 정도는 평균 제곱 오차(mean square error)를 통해 평가되며, 이는 매끄러운 설계가 원래의 요소 기반 레이아웃에 얼마나 충실한지를 나타내는 지표로 작용한다.
의 차이에 기반하여 갱신된다[19]. θk와 vk간의 정렬 정도는 평균 제곱 오차(mean square error)를 통해 평가되며, 이는 매끄러운 설계가 원래의 요소 기반 레이아웃에 얼마나 충실한지를 나타내는 지표로 작용한다.

요소 기반 설계와 매끄러운 설계 간의 결과가 t ¡Ì 0.001일 때 근사하게 일치함을 확인할 수 있다 [20].
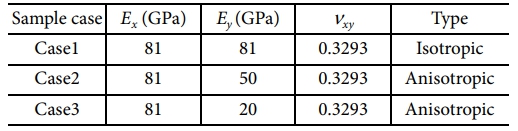
본 연구에서는 최근 연구를 참고하여, 위상 최적화 구조의 유효성을 실험을 통해 입증한 두 가지 압전 액추에이터 구성, 즉 푸셔(pusher)와 그리퍼(gripper)를 수치 예제로 고려하였다[7,11]. 재료의 불확실성을 반영하기 위해 영률(E0)과 압전 계수(e0)는 한계적으로 균일한 2차원 랜덤 필드로 표현하였다. 유한요소 해석에서는 사각형 유한요소(bilinear quadrilateral element)를 사용하며, 변위와 극성 변수는 모두 노드에서 평가된다. 수치 해석은 Intel(R) Core(TM) i7-13700 2.10 GHz 시스템에서 수행되었다. 수치 예제에 사용된 재료 특성은 Table 1에 나와 있다. 본 논문에서는 최종 경계의 이방성과 매끄러움의 중요성을 보여주기 위해 3가지 샘플 사례를 사용하였다.
4.1 푸셔(Pusher)
첫 번째 예제는 간단한 푸셔(pusher) 메커니즘을 다루며, 이는 Fig. 1에 정리되어 있다. Fig. 2
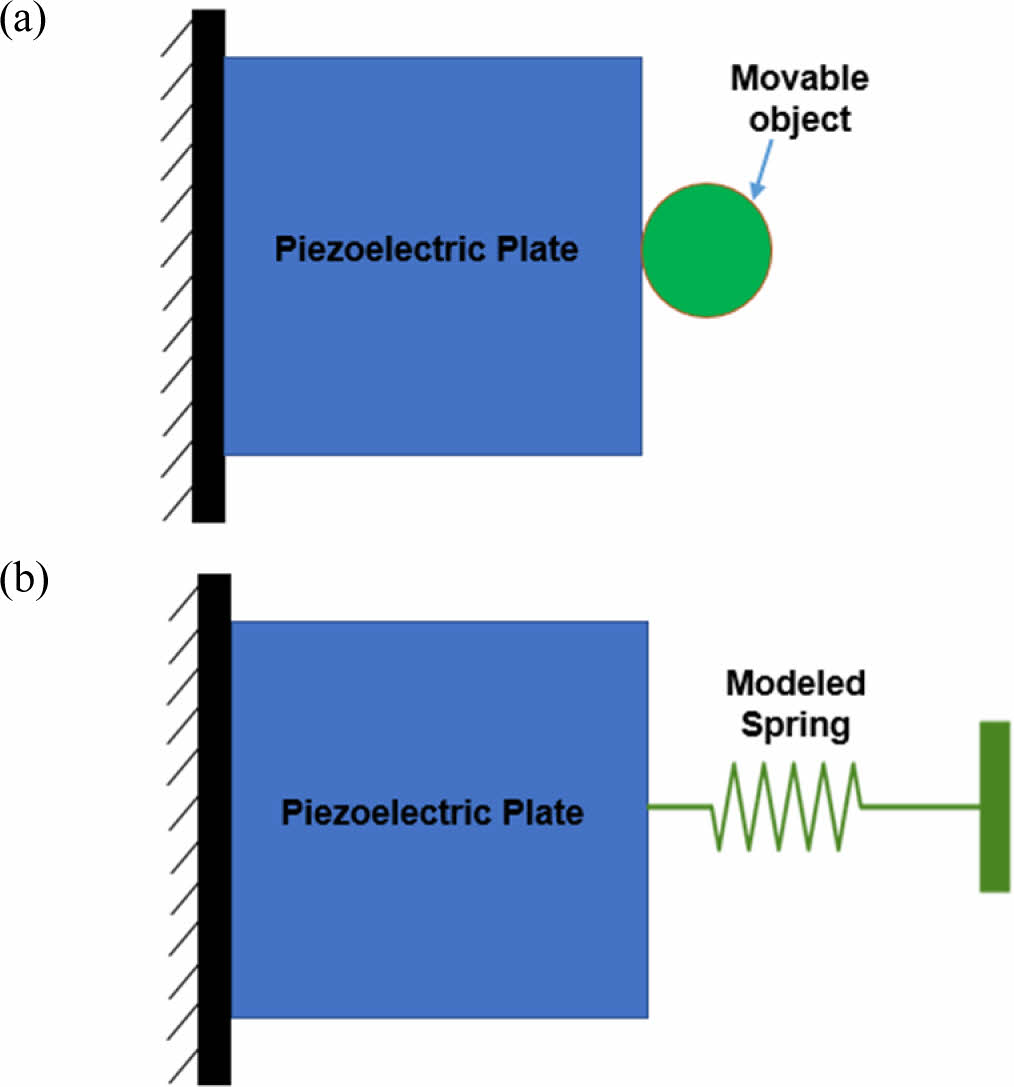
길이마다 100개의 요소로 구성된 정사각형 영역이 고려되었으며, 대칭성을 이용하여 구조물의 상단 절반만을 최적화 대상으로 설정하였다. 오른쪽 끝에 위치한 이동 가능한 물체는 가상 스프링 기법(fictitious spring method)을 통해 구현되었다. 스프링 상수는 0.005로 설정되었으며, 이는 작은 값이지만 물체 근처에서의 재료 제거를 효과적으로 방지하기 위해 선택되었다[7].
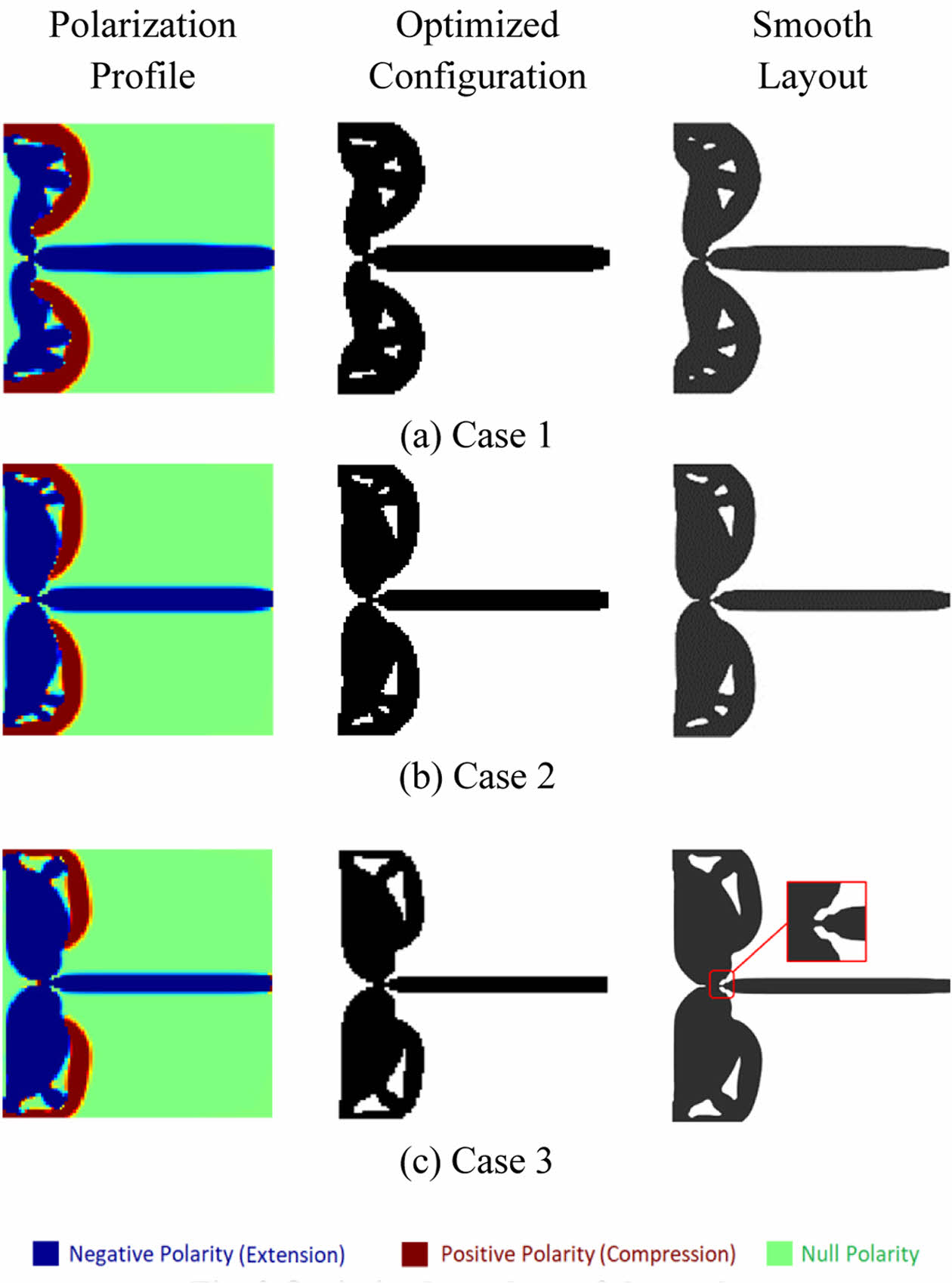
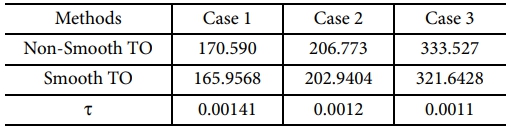
모든 수치 예제에서 페널티 계수 Puu와 Puf는 각각 3과 4로 설정되었으며, 이는 선행연구 결과를 바탕으로 선정되었다[11]. 목표 재료 부피는 0.3으로 설정되었으며, 위상 최적화 결과는 Table 2에 요약되어 있다. 또한, Fig. 3은 위상최적화의 결과로 도출된 분극 프로파일, 재료 밀도, 및 매끄러운 경계 레이아웃을 보여준다.
Table 2와 Fig. 3의 결과를 바탕으로, Case 1(등방성 재료)의 경우 성능 지표(출력 변위)가 세 가지 사례 중 가장 낮은 값을 보였다. 이는 등방성 재료가 변위를 증대시키는 데 덜 효과적임을 나타낸다. 반면, Case 3(이방성 재료)은 x방향에서의 탄성계수가 y방향보다 훨씬 높은 강한 이방성을 보이며, 이는 출력 변위 증대에 기여하지만 동시에 응력 집중과 단일 노드 연결 문제를 초래한다. 이는 Fig. 3(c)에 빨간색 테두리로 표시된 응력 집중 및 단일 노드 연결과 같은 문제로 이어진다. x방향에서 높은 강성으로 인해 변형에 강하게 저항하지만, y방향에서는 저항이 약해 과도한 변형이 발생한다. 결과적으로, Fig. 3(a), (b), (c)는 각각 이방성 정도에 따라 Case 1(등방성), Case 2(중간 이방성), Case 3(강한 이방성)의 최적화 결과를 나타낸다.
또한, Table 2에 제시된 t 값은 매끄러운 위상 최적화와 매끄럽지 않은 위상 최적화 간의 설계 충실도를 평가하는 중요한 지표로 활용된다. t 값은 Case 1에서 0.00141, Case 2에서 0.0012, 그리고 Case 3에서 0.0011로 점차 감소하는 경향을 보인다. 이는 이방성이 강할수록 매끄러운 설계와의 차이가 줄어들며, 매끄러운 설계가 이방성 재료의 특성을 효과적으로 반영하고 있음을 시사한다. 특히, t 값이 낮을수록 매끄러운 설계가 요소 기반 설계와 더 높은 충실도를 가진다는 점에서, Case 3에서의 낮은 t 값은 강한 이방성 조건에서도 설계의 정밀도가 유지됨을 보여준다.
Fig. 3내 첫번째 열은 분극 프로파일을 나타낸다. 파란색, 빨간색, 초록색은 각각 음의 분극(negative polarization), 양의 분극(positive polarization), 그리고 분극이 없는 영역을 나타낸다. 두번째 열의 결과는 주어진 조건에서의 최종 구조이며, 마지막 열의 경과는 매끄러운 경계를 얻기 위한 처리를 진행한 결과이다. 여기서, 매끄럽지 않은 위상 최적화(Non-smooth TO)는 제조 가능성 제약이 없기 때문에 매끄러운 위상 최적화(Smooth TO)와 비교했을 때 성능 지표에서 더 나은 결과를 보인다.
푸셔의 결과는 압전 액추에이터 설계에서 재료의 이방성을 고려하는 것이 중요함을 강조한다. 이방성 재료는 방향에 따른 컴플라이언스(compliance)를 활용하여 변위를 증대시키며, 특히 하중을 미는(push) 응용 분야에서 효과적이다. 매끄러운 위상 최적화(smooth TO)는 경계의 정규성(boundary regularity)이 중요한 현대 기술, 특히 3D 프린팅과 같은 적층 제조(additive manufacturing) 공정에서 제작 가능성 측면에서 더 실용적이다. Case3에서 관찰된 성능 향상은 높은 정밀도와 큰 변위를 요구하는 응용 분야에서 이방성 재료를 활용할 잠재력을 시사한다.
4.2 그리퍼(Gripper)
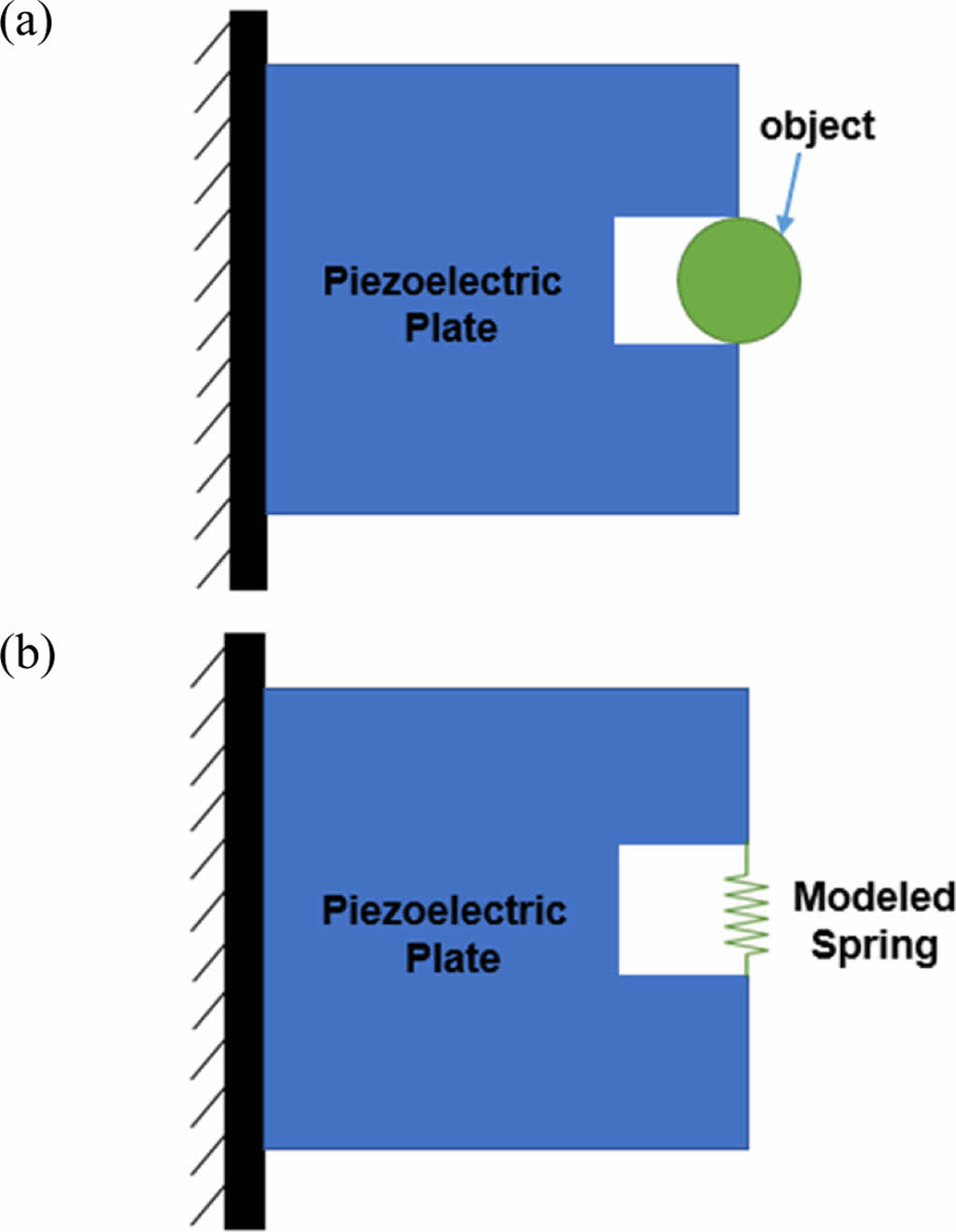
두 번째 예제의 그리퍼(gripper)는 Fig. 4에 나타난 바와 같이 물체를 잡을 수 있도록 설계 및 최적화되었다. 설계 영역은 왼쪽이 고정된 직사각형 플레이트로 구성된다. Fig. 4(b)는 기계적 모델을 나타내며, 설계 영역, 고정 경계 조건(clamped boundary condition), 그리고 오른쪽에 위치한 가상 스프링(fictitious spring)을 보여준다. 이 가상 스프링의 계수는 푸셔와 같은 이유로 0.003으로 설정되어 그리퍼의 턱(jaws)을 모델링한다[9].
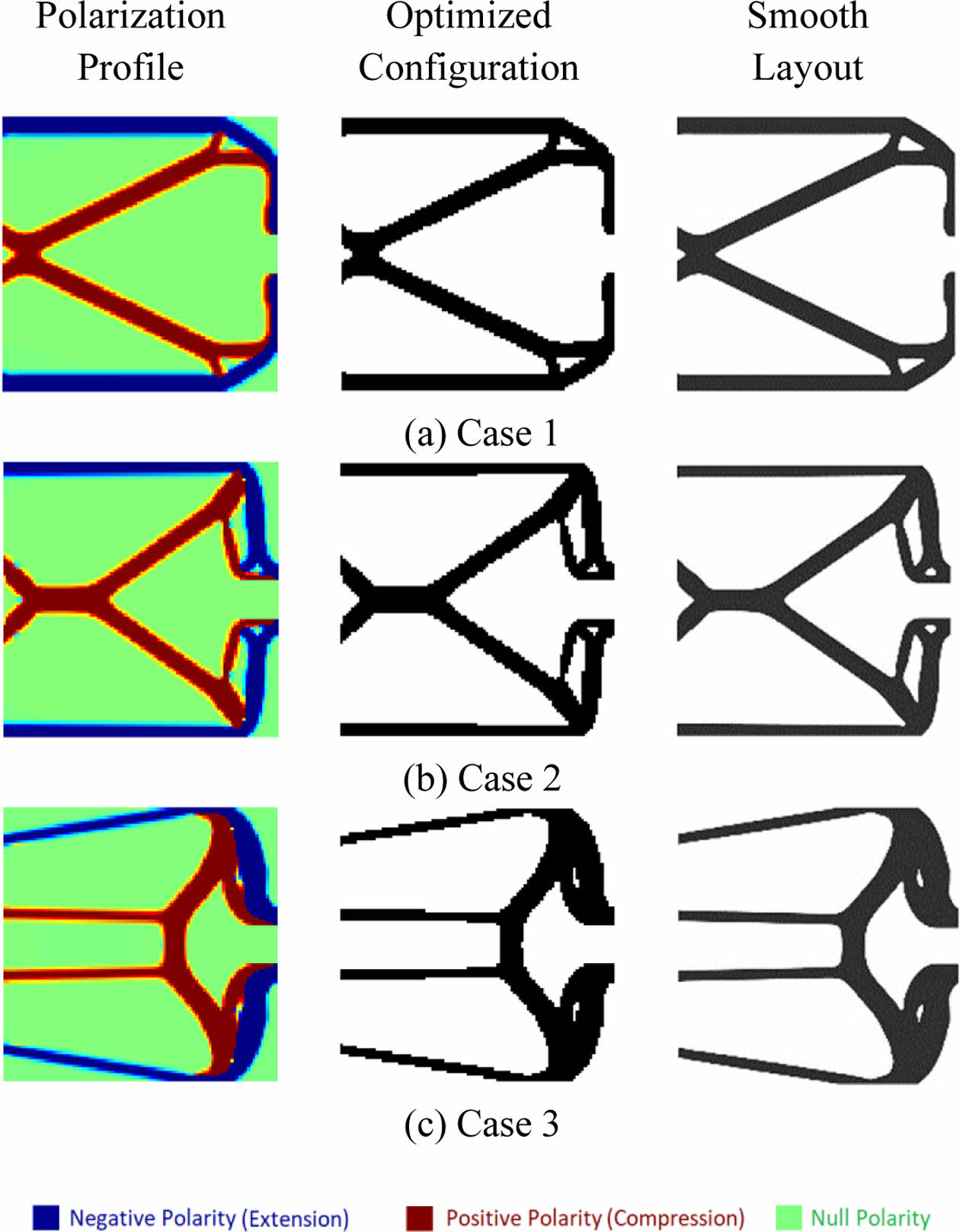
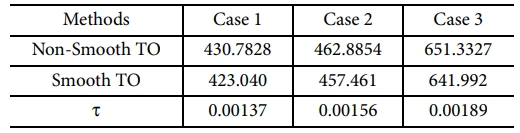
Fig. 5에는 다양한 레이아웃에 대한 위상 최적화 결과가 제시되어 있다. 또한, 각 사례의 최적화된 값은 Table 3에 나열되었다. 본 예제에서 최종 부피 분율(volume fraction)은 0.3으로 설정되었다.
푸셔(pusher)와 유사하게 등방성 재료는 가장 낮은 성능을 보이며, 이는 효과적인 그립(grip) 힘을 생성하는 능력이 제한적임을 나타낸다. 반면, Case 3은 이방성 특성이 더 큰 변형과 그립 힘 생성을 가능하게 하여 가장 높은 성능을 나타낸다. 매끄러운 위상 최적화의 결과도 푸셔에서의 결과와 같은 경향을 가지며, 이는 액추에이터 최적화에서 재료 이방성의 가치를 강조한다. 매끄러운 위상최적화는 성능이 다소 저하될 수 있지만, 정밀한 그립이 요구되거나 제조 제약 조건을 고려할 때 실용적인 설계에 더 적합하다.
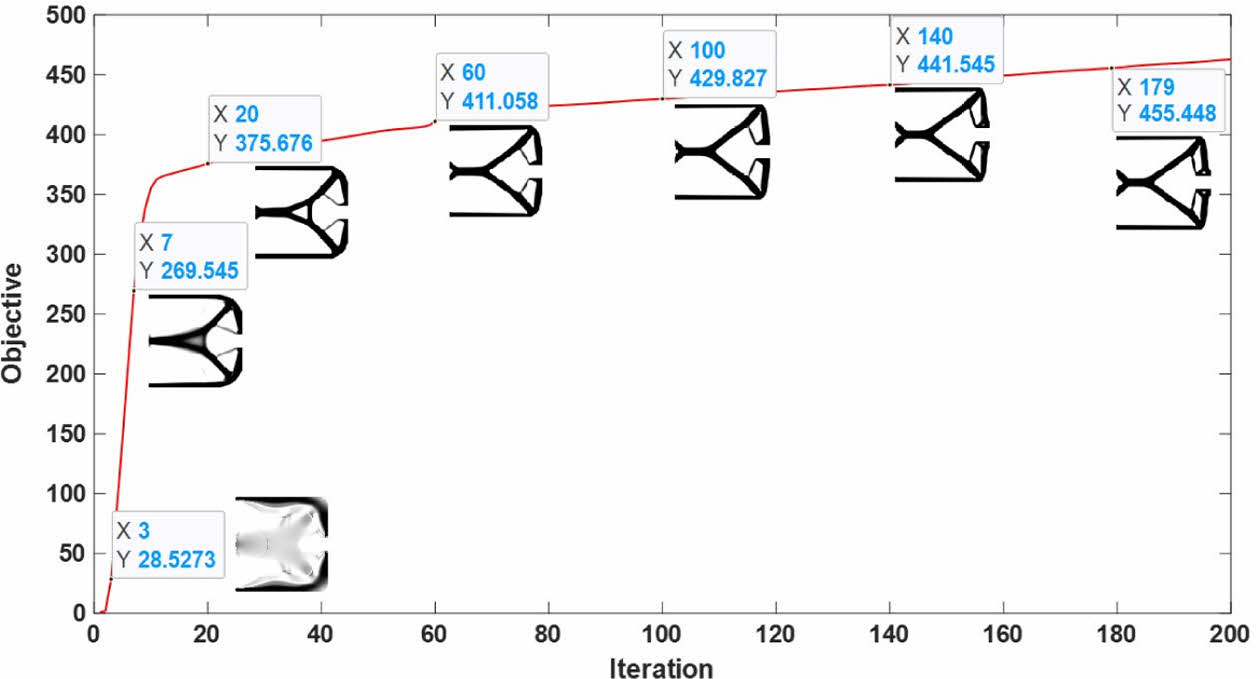
마지막으로, 반복 해석을 통한 최적화 결과는 Fig. 6을 통해 수렴성을 확인할 수 있다.
|
Fig. 2 Design configuration of the pusher: (a) illustration of the pusher and movable object, and (b) corresponding boundary condition |
|
Fig. 3 Optimized topology of the pusher |
|
Fig. 4 Piezoelectric actuator (gripper): (a) specifications for practical use and (b) finite element software implementation |
|
Fig. 5 Optimized topology of the gripper |
|
Fig. 6 Evolution of optimized structure |
본 연구는 고성능 압전 액추에이터 설계에서 이방성과 위상 최적화(Topology Optimization, TO) 접근법의 중요성을 강조하였다. 특히 방향성 차이가 큰 이방성 재료(Case 3)는 항상 등방성 및 준등방성 재료에 비해 높은 활용성을 가지며, 첨단 응용 분야에서의 가능성을 보여준다. 이방성 사례의 최적화된 위상은 복잡한 분극 및 변형 패턴을 나타내며, 재료 방향성이 설계 성능에 미치는 영향을 입증한다. 그러나 이방성은 응력 집중 증가 및 단일 노드 연결과 같은 설계상의 문제를 야기할 수 있으며, 설계 과정에서 응력 분포를 신중히 고려해야 한계를 수반하고 있다. 위상최적화 기법을 활용하면 이러한 문제를 완화하고 액추에이터의 신뢰성과 효율성을 향상시킬 수 있다.
일반적인 위상최적화는 더 높은 구조적 성능을 달성하지만, 들쭉날쭉한 경계로 인해 제작 및 응력 해석이 복잡해저 후처리가 필수적이다. 하지만, 매끄러운 위상최적화는 산업적 요구에 더 부합하며, 견고하고 제조 가능한 압전 액추에이터 설계를 위한 균형 잡힌 솔루션을 제공한다. 이러한 연구 결과는 재료 특성과 제조 제약을 모두 고려하여 고성능 및 신뢰성을 갖춘 기기를 개발하기 위한 핵심기술요소로 앞으로의 활용성을 기대할 수 있다.
본 연구는 과학기술정보통신부가 지원하는 연구과제(RS-2024-00397400)와 경상국립대학교 글로컬대학 30 사업의 지원을 받아 수행된 것이며, 지원에 대해 진심으로 감사드립니다.
- 1. Chaillet, N., and Régnier S., Microrobotics for Micromanipulation, John Wiley & Sons, 2013.
-

- 2. Zou, J., and Xia, X., “Topology Optimization for Additive Manufacturing with Strength Constraints Considering Anisotropy,” Journal of Computational Design and Engineering, Vol. 10, 2023, pp. 892-904.
-

- 3. Park, J., Kim, S.-R., Kim, K.-S., Kim, G., Kim, S.-H., Lee, B.-J., Jeong, A., An, J., Kim, S.J., and Lee, S.-M., “Effects of PZT Powder on Vibration and Compression Properties of Ti Powder/Polymer Concrete Composites,” Composites Research, Vol. 35, 2022, pp. 134-138.
-

- 4. Zhou, Y., Nomura, T., Zhao, E., and Saitou, K., “Large-Scale Three-Dimensional Anisotropic Topology Optimization of Variable-Axial Lightweight Composite Structures,” Journal of Mechanical Design, Vol. 144, 2021.
-

- 5. Liu, B., and Cui, Y.J., “Topology Optimization of Multi-material Structures Considering Anisotropic Yield Strengths,” Computer Methods in Applied Mechanics and Engineering, Vol. 418, 2024, 116520.
-

- 6. Anurangi, J., Herath, M., Galhena, D.T., and Epaarachchi, J.J., “Electrochemical and Structural Performances of Carbon and Glass Fiber-reinforced Structural Supercapacitor Composite at Elevated Temperatures,” Functional Composites and Structures, Vol. 6, 2024, 035004.
-

- 7. Silva, E.C.N., Fonseca, J.S.O., and Kikuchi, N.J., “Optimal Design of Piezoelectric Microstructures,” Computational Mechanics, Vol. 19, 1997, pp. 397-410.
-

- 8. Kang, Z., Wang, R., and Tong, L.J., “Combined Optimization of Bi-material Structural Layout and Voltage Distribution for In-plane Piezoelectric Actuation,” Computer Methods in Applied Mechanics and Engineering, Vol. 200, 2011, pp. 1467-1478.
-

- 9. Wang, S., Rong, W., Wang, L., Xie, H., Sun, L., and Mills, J.K.J., “A Survey of Piezoelectric Actuators with Long Working Stroke in Recent Years: Classifications, Principles, Connections and Distinctions,” Mechanical Systems and Signal Processing, Vol. 123, 2019, pp. 591-605.
-

- 10. Schlinquer, T., Homayouni-Amlashi, A., Rakotondrabe, M., and Ousaid, A.M.J., “Design of Piezoelectric Actuators By Optimizing the Electrodes Topology,” IEEE Robotics and Automation Letters, Vol. 6, 2021, pp. 72-79.
-

- 11. Fang, L., Meng, Z., Zhou, H., Wang, X., and Guo, X.J., “Topology Optimization of Piezoelectric Actuators Using Moving Morphable Void Method,” Structural and Multidisciplinary Optimization, Vol. 66, 2023, pp. 32.
-

- 12. Latifi Rostami, S.A., Kolahdooz, A., Chung, H., Shi, M., and Zhang, J.J., “Robust Topology Optimization of Continuum Structures with Smooth Boundaries Using Moving Morphable Components,” Structural and Multidisciplinary Optimization, Vol. 66, 2023, pp. 121.
-

- 13. Li, S., Yuan, S., Zhu, J., Wang, C., Li, J., and Zhang, W., “Additive Manufacturing-driven Design Optimization: Building Direction and Structural Topology,” Additive Manufacturing, Vol. 36, 2020, 101406.
-

- 14. Ooms, T., Vantyghem, G., Thienpont, T., Van Coile, R., and De Corte, W., “Compliance-based Topology Optimization of Structural Components Subjected to Thermo-mechanical Loading,” Structural and Multidisciplinary Optimization, Vol. 66, 2023, pp. 126.
-

- 15. So, S., and Kim, D., “Topology Optimization of a Lightweight Multi-material Cowl Cross Member Using Matrix Input with the Craig Bampton Nodal Method,” Composites Research, Vol. 32, 2019, pp. 243-248.
-

- 16. McClintock, H., Temel, F.Z., Doshi, N., Koh, J.-S., and Wood, R.J., “The milliDelta: A High-bandwidth, High-precision, Millimeter-scale Delta Robot,” Science Robotics, Vol. 3, 2018, pp. eaar3018.
-

- 17. Homayouni-Amlashi, A., Schlinquer, T., Mohand-Ousaid, A., and Rakotondrabe, M., “2D Topology Optimization MATLAB Codes for Piezoelectric Actuators and Energy Harvesters,” Structural and Multidisciplinary Optimization, Vol. 63, 2021, pp. 983-1014.
-

- 18. Wang, Y., Luo, Z., Zhang, X., and Kang, Z., “Topological Design of Compliant Smart Structures with Embedded Movable Actuators,” Smart Materials and Structures, Vol. 23, 2014, 045024.
-

- 19. Porn, S., Nasser, H., Coelho, R.F., Belouettar, S., and Deraemaeker, A., “Level Set Based Structural Optimization of Distributed Piezoelectric Modal Sensors for Plate Structures,” International Journal of Solids and Structures, Vol. 80, 2016, pp. 348-358.
-

- 20. Zhang, X., and Kang, Z., “Dynamic Topology Optimization of Piezoelectric Structures with Active Control for Reducing Transient Response,” Computer Methods in Applied Mechanics and Engineering, Vol. 281, 2014, pp. 200-19.
-

 This Article
This Article
-
2025; 38(1): 42-49
Published on Feb 28, 2025
- 10.7234/composres.2025.38.1.042
- Received on Nov 29, 2024
- Revised on Jan 23, 2025
- Accepted on Feb 3, 2025
 Services
Services
Shared
 Correspondence to
Correspondence to
- Hyoung Jun Lim
-
School of Mechanical and Aerospace Engineering, Gyeongsang National University
- E-mail: hj.lim@gnu.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.