- A Study on the Optimal Design of UAM Composite Boom Structures through RVE-Based Structural Analysis
Ji-Hun Seok*, Seonghun Park*†, Sung-Youl Bae**†
* School of Mechanical Engineering, Pusan National University, Busan, Korea Korea
** Institute of Ceramic Engineering and Technology, Aerospace Convergence Materials Center, Korea- 대표체적요소 기반 해석을 활용한 UAM 복합재 붐 구조 최적설계 연구
석지훈* · 박성훈*† · 배성열**†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
This study aimed to evaluate the feasibility of optimal design for composite aircraft structures by calculating material properties for structural design based on a Representative Volume Element (RVE) approach. Traditional composite structure design for aircraft typically requires conservative safety factors due to limited consideration of factors like manufacturing parameters, degradation effects, curing temperature, and post-curing, which restricts lightweight design and optimization. Additionally, calculating the design properties of traditional composite structures required repeated lamina-level experiments that reflect the actual materials and processes used in manufacturing, with further experiments needed for changes in base material, fiber content, and additives. In this study, RVE-based analysis was used to calculate design properties that incorporate composite microstructural characteristics (such as porosity and fiber content), and these results were compared with those from conventional analysis to assess the potential for optimal design. The analysis showed that traditional methods had a 30% deviation from experimental values, while the RVE-based approach achieved a deviation within 4%, demonstrating higher accuracy. Applying this approach to the design of Urban Air Mobility (UAM) boom structures resulted in over 40% weight reduction compared to traditional aluminum alloys while maintaining adequate structural stability. This study suggests that RVE-based analysis is an effective method for predicting properties in the early design stage, contributing to performance optimization and weight reduction. Thus, RVE-based analysis shows potential for broad application in lightweight structure design for aircraft and UAM systems.
본 연구는 복합재 항공기 구조물의 설계과정에서 대표체적요소(RVE) 기반의 설계 물성치 산정방법을 통한 구조 최적화 설계 가능성을 확인하기 위한 목적으로 수행되었다. 기존의 항공기 등 복합재 구조 설계에서는 제조 인자, 열화 영향, 경화 온도, 후 경화 여부 등의 복합재 구조설계 부분 안전계수를 반영하여 보수적 안전계수를 적용함으로써 경량 설계 및 최적화에 한계가 있었다. 또한, 기존 복합재 구조물 설계 물성치를 산정하기 위해서는 실제 복합재 구조물 제조에 적용되는 소재 및 공정을 반영한 라미나 단위의 반복 실험이 요구되며, 원소재, 섬유함유율, 첨가제 등 구성변화에 따라 추가적인 실험이 필요하였다. 본 연구에서는 RVE 기반 해석을 통해 복합재 미시구조 특성(기공률, 섬유함유율)을 반영한 설계 물성치를 산정하여 기존의 해석법과 비교함으로써 최적 설계 가능성을 검토하였다. 해석결과, 기존 해석법은 실제 실험값 대비 10%의 차이를 나타냈지만, RVE 기반 해석은 실험값 대비 4% 이내의 차이를 보여 높은 정확성을 확인할 수 있었다. 이를 도심항공모빌리티(UAM) 붐 구조 설계에 적용한 결과, 기존 알루미늄 합금 대비 40% 이상 경량화가 가능하였고, 충분한 구조적 안정성을 확보할 수 있었다. 본 연구는 복합재 구조 설계에서 RVE 기반 해석이 개념설계 단계에서 정확한 물성 예측을 가능하게 하는 효과적인 기법임을 시사하며, 복합재 구조물의 성능 최적화와 경량화에 기여할 수 있는 방법임을 보여준다. 이를 통해 RVE 기반 해석은 항공기 및 UAM과 같은 경량 구조물 설계에 폭넓게 응용될 가능성을 제시한다.
Keywords: 도심항공모빌리티(Urban Air Mobility, UAM), 대표체적요소 기반 구조해석(Representative Volume Element-based Analysis), 붐 구조(Boom structure), 최적설계(Optimal Design), 섬유강화복합재(Fiber Reinforced Plastics, FRP)
급격한 도시화와 인구 증가로 인해 대도시에서는 교통 혼잡, 에너지 소비 증가, 대기 오염 문제가 심화되고 있으며, 이는 환경과 삶의 질에 악영향을 미치고 있다. 이러한 문제를 해결하기 위해 전기 추진방식의 UAM (Urban Air Mobility, 도심항공모빌리티)이 도심 내에서 승객과 화물을 신속하게 운송하여 교통 체증 완화, 에너지 소비 절감, 탄소 배출 감소 등의 이점을 제공할 수 있는 차세대 교통수단으로 주목받고 있다[1-5].
UAM의 붐 구조는 회전익과 동체를 지지하는 필수적인 대형 구조물로, 경량화와 고강도가 동시에 요구된다. 이러한 요구를 충족하기 위해 섬유강화복합재(Fiber Reinforced Plastic, FRP)는 핵심적인 소재로써 고려되고 있다. FRP는 뛰어난 비강도, 비강성, 내부식성을 제공하며, 다양한 산업 분야에서 활용되고 있다. 항공기, 자동차 산업분야 적용을 위한 FRP에 대한 연구가 지속적으로 이루어지고 있으며, 그 적용 범위 또한 확장되고 있다.
FRP의 제조 과정에서는 기공, 불규칙한 섬유 분포, 섬유 정렬 불량 등의 제조 결함이 발생할 가능성이 있으며, 이는 FRP의 기계적 성능에 악영향을 미친다. 이러한 결함은 복합재의 강도와 탄성률을 저하시켜 전체적인 구조적 성능에 부정적인 영향을 미칠 수 있기에 이를 해결하기 위해서는 미세 결함을 정확하게 분석하고, 이를 고려한 신뢰성 있는 설계법을 제시하는 것이 요구된다[6-11].
본 연구는 복합재의 원소재, 섬유 형태, 섬유함유율, 기공률 등이 고려되어 설계된 RVE(Representative Volume Element, 대표체적요소) 모델을 바탕으로 소재 단위 미시구조 해석을 수행하여 FRP의 물성을 산정하였고, 이를 UAM 붐 구조의 경량화 및 구조적 안전성 확보를 위한 구조 해석에 적용하는 것을 목표로 한다. 또한, 최근 항공기 내·외장재로 주목받고 있는 탄소섬유강화복합재와 유리섬유강화복합재의 붐 구조에 대한 적용 가능성을 평가하였다. 이를 통해 UAM 붐 구조의 소재로써 신뢰성과 재현성이 우수한 재료와 최적의 설계 방안을 도출하고자 하였다[12-15]. UAM 붐 구조의 설계 절차는 아래와 같이 요약할 수 있다.
① 기초 물성 분석 – 원소재와 복합재의 기계적 특성 및 미시구조 특성(기공률, 섬유함유율)을 실험을 통해 도출
② 미시구조 해석 및 물성치 산정 – ①을 통해 도출된 데이터를 기반으로 소재단위 미시 구조 해석 모델을 설계하고, 미시구조를 고려한 물성치를 산정
③ UAM 붐 구조 설계 및 해석 – ②를 통해 도출된 구조설계 물성치를 활용하여 UAM 붐 구조해석에 적용하여 구조해석 결과 도출
④ 기존 금속 소재 UAM 붐 구조와 최적 설계된 붐 구조의 경량화, 안전계수 비교를 통한 설계 평가 및 성능 분석
2.1 대표체적요소
RVE는 복합재료의 거시적 물성을 예측하기 위해 선택된 최소 단위 체적이며, 복합재의 미시구조 특성을 반영하여 물성치를 산정하는 데 사용된다. RVE는 섬유와 매트릭스 같은 이질적인 구성 요소들이 주기적으로 배열된 모델로 구성되며, 이를 통해 복합재 내부의 불균일성과 미시적 특성을 효과적으로 반영할 수 있다. RVE 기반 해석은 복합재의 미시구조가 실제 실험값에 근접하는 높은 정확도의 물성치를 제공하므로, 초기 설계 단계에서 설계 최적화를 가능하게 한다. 이는 전통적인 해석법과 비교할 때 더 정밀하고 신뢰할 수 있는 물성 예측을 가능하게 한다. RVE 기반 해석에서는 주기적 경계 조건이 적용되어 RVE 경계에서 일관된 응력 및 변형률 상태가 유지된다. 이러한 조건은 해석 결과의 일관성과 정확성을 보장하며, RVE 내의 응력 및 변형률 분포를 수치적으로 해석하여 매크로 스케일에서 평균 물성치를 산정하는 데 활용된다. 이는 다음과 같은 수식을 통해 정의된다:
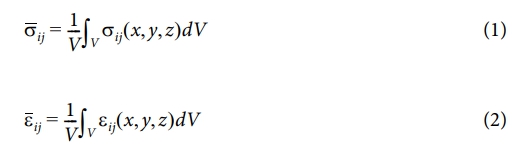
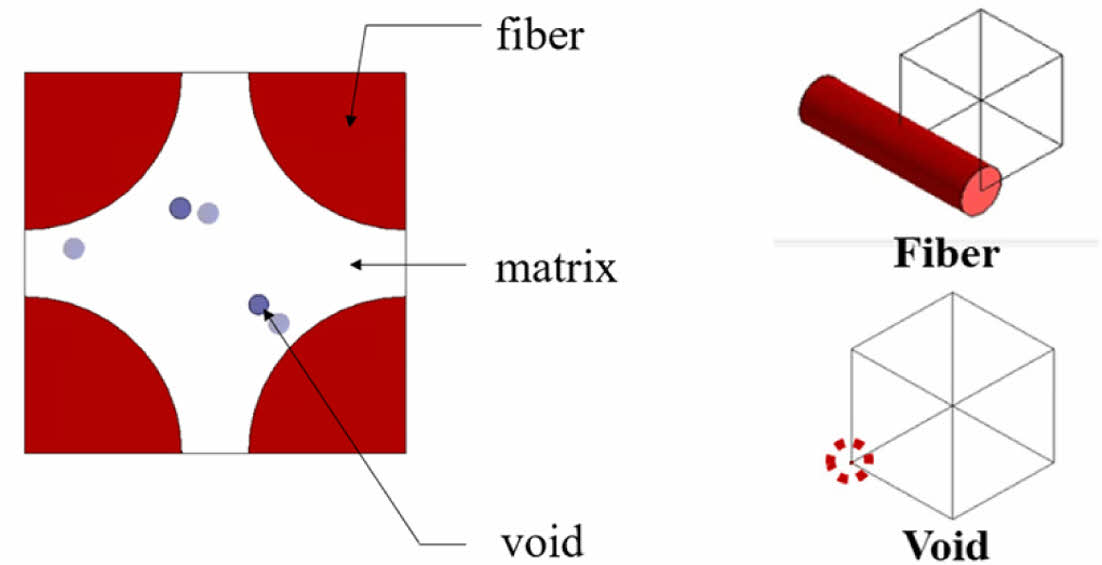
이 수식은 RVE의 부피 내에서 응력과 변형률의 평균 값을 나타내며, 이를 통해 거시적 관점에서 복합재의 물성을 산정할 수 있다. 전통적인 해석법은 복합재의 특성을 보수적으로 예측하는 경향이 있는 반면, RVE 기반 해석은 섬유함유율, 기공률, 섬유 형태 등 다양한 미시구조 변수를 반영하여 보다 정밀한 물성 예측이 가능하다. Fig. 1은 RVE 모델을 통해 복합재 내 섬유, 수지(매트릭스), 기공의 분포를 나타내었다. 본 연구에서는 RVE 기반 해석을 통해 산정된 물성치를 UAM 붐 구조 설계에 적용함으로써 경량화와 구조적 안정성을 입증하였다.
|
Fig. 1 RVE model illustrating the distribution of fiber, matrix and voids |
3.1 대표체적요소 기반 구조 설계
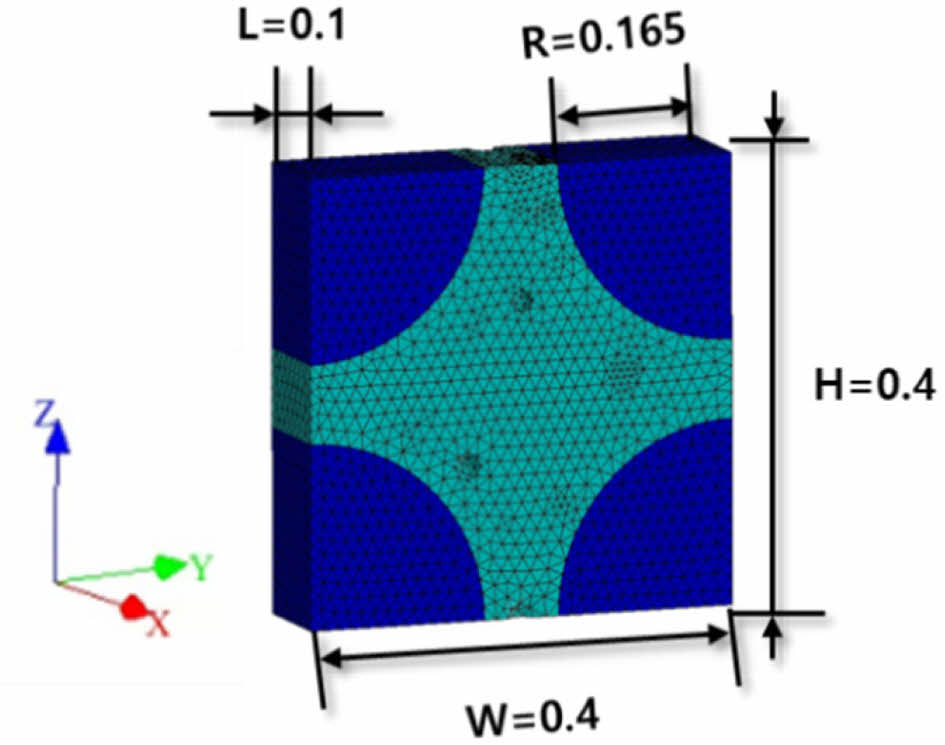
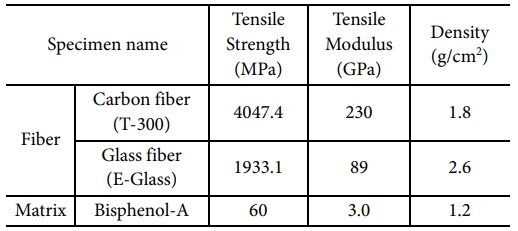
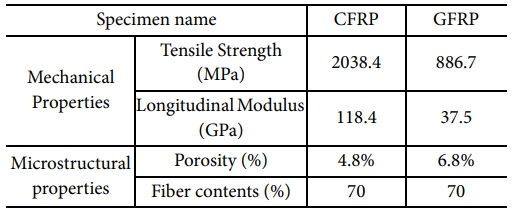
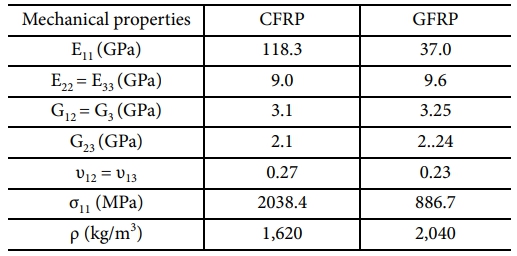
도심항공모빌리티 붐 구조에 적용할 2종의 FRP에 대한 물성을 도출하기 위해 상용 프로그램인 DIGIMAT을 사용하여 RVE 모델을 설계하였다. RVE구조는 Fig. 2에서 나타낸 바와 같이 L(Length):W(Width):H(Height) = 0.1:0.4:0.4의 비율로 설계되었고, 절점은 7,938개, 요소는 38,120개로 구성하였다. 구조의 물성은 Table 1과 Table 2에 나타내었다. 탄소섬유는 T-300, 유리섬유는 E-glass를 사용하였고, 수지는 에폭시 비스페놀 A를 적용하였다. 기공의 형태는 Ellipsoid 형태로 설계되었고, 기공률은 CFRP의 경우, 4.8%, GFRP의 경우, 6.8%로 설계되었다.
3.2 경계 조건
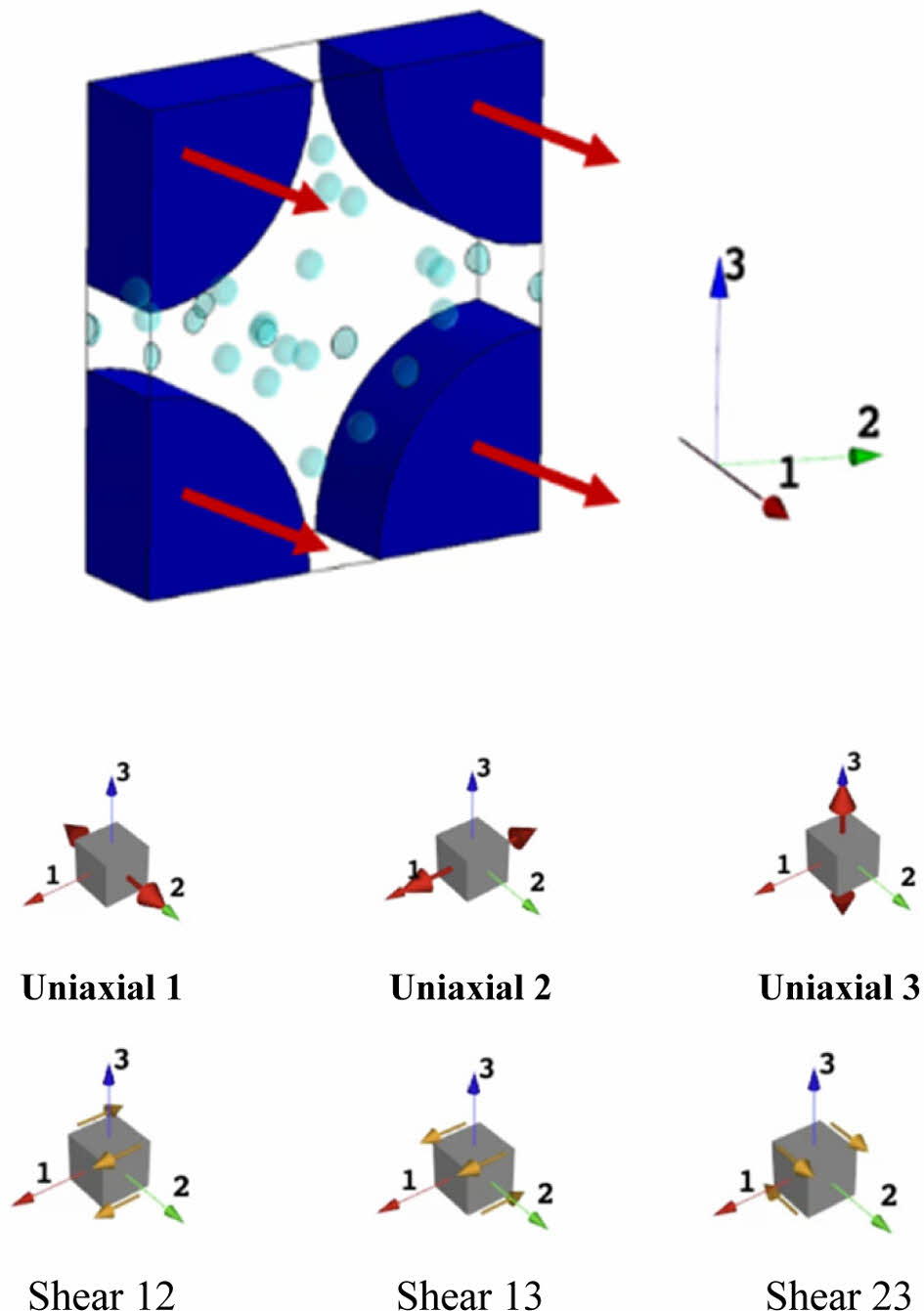
Fig. 3에서와 같이 각 방향의 경계 조건을 설정하여 1, 2, 3 방향에 대한 축방향(uniaxial)과 전단(shear) 강성을 도출하였다. 경계 조건은 RVE 모델의 각 면에 대해 적절히 적용되었으며, 이는 각 방향에서 발생하는 응력과 변형률 반응을 체계적으로 분석하기 위한 것이다. 축방향 하중은 각 방향(1, 2, 3)에 대해 독립적으로 적용되어, 각 축에 대한 강성을 평가하고 복합재의 축방향 물성을 파악하였다. 전단 하중은 12, 13, 23 방향으로 설정되어 각 면에서 발생하는 복합적인 전단 반응을 측정하고 해석하였다. 이러한 경계 조건의 설정은 RVE 해석 시 복합재의 기계적 성질을 더욱 정확히 평가할 수 있도록 하며, 다양한 하중 조건 하에서 복합재의 응답 특성을 반영할 수 있도록 설계되었다. 이를 통해 기공, 섬유 배향 등 미시 구조 요소가 각 방향의 강성에 미치는 영향을 세부적으로 분석할 수 있었다.
3.3 RVE 기반 미시구조해석 결과
본 연구에서는 복합재의 기계적 물성을 예측하기 위해 혼합법칙(이론), 상용 소프트웨어인 Ansys ACP, 그리고 Digimat 기반의 RVE 해석을 사용하여 각 해석 방법의 정확성을 비교하였다. 기존 해석으로는 Ansys ACP에서 제공하는 적층 구조 해석 기능을 통해 CFRP와 GFRP의 물성을 계산하였으며, 개선된 해석으로는 Digimat을 통해 기공과 섬유 직경을 반영한 RVE 기반 모델을 구축하여 정밀한 물성 예측을 수행하였다. 모든 해석 결과는 실험값과 비교하여, 예측 정확성을 평가하였다. 혼합법칙을 적용한 경우, 복합재의 탄성계수는 다음 식에 의해 계산된다:
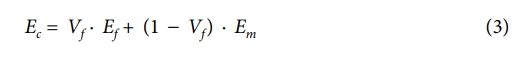
여기서 Ec는 복합재의 탄성계수, Vf는 섬유의 부피분율, Ef는 섬유의 탄성계수, Em은 매트릭스의 탄성계수이다. 혼합법칙을 통해 이론적으로 계산한 CFRP와 GFRP의 탄성계수는 각각 실험값 대비 36%, 45%의 오차를 보였다. Ansys ACP로 얻은 물성치는 혼합법칙과 유사한 결과를 보였으며, 실험값과 각각 4%, 10%의 차이를 나타냈다. 반면, Digimat을 활용한 RVE 해석에서는 기공 및 섬유 직경과 같은 미세구조를 반영한 결과, CFRP와 GFRP의 탄성계수가 실험값과 각각 1%, 3%의 오차율을 보였다. 이는 실험값에 가장 근접한 결과로, 미시구조 해석이 복합재 물성 예측에 있어 높은 신뢰성을 가지는 방법임을 확인할 수 있었다. 이러한 결과는 Fig. 3과 Table 3에 제시되어 있으며, 다양한 해석 방법에 따른 복합재 물성의 차이를 확인할 수 있다.
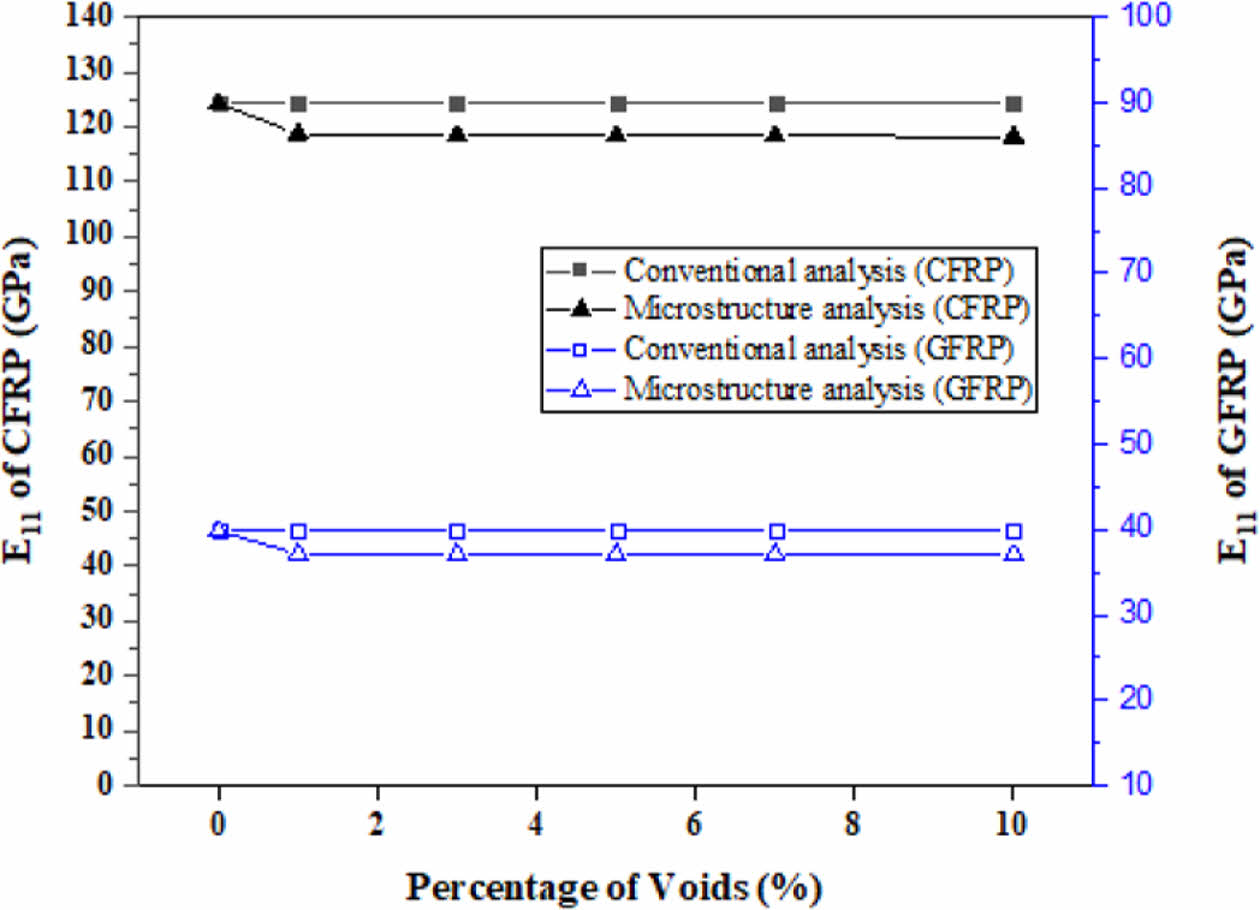
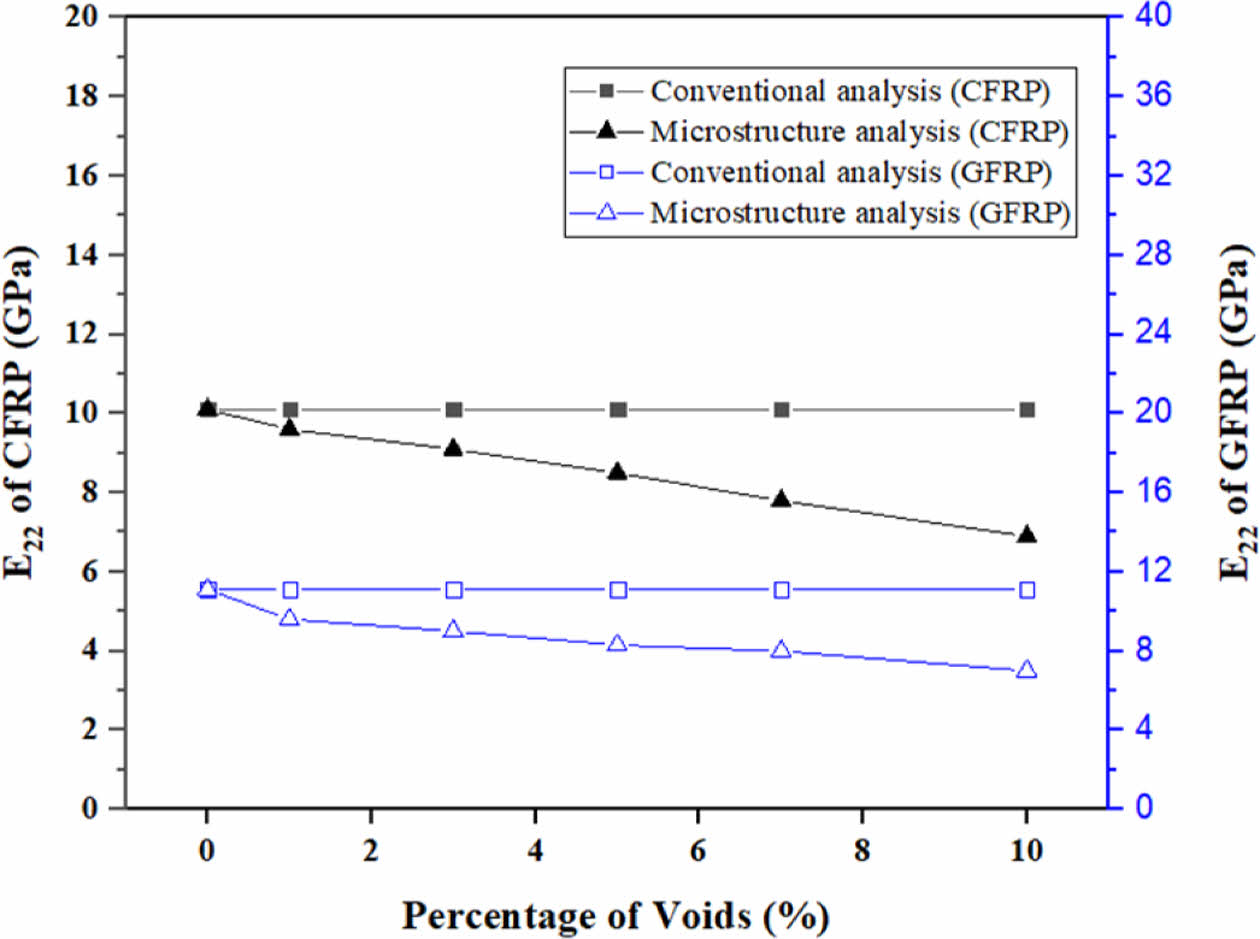
Fig. 4와 Fig. 5는 기공률 증가에 따른 CFRP 및 GFRP의 Longitudinal Modulus와 Transverse Modulus 감소 경향을 보여준다. 기존 해석법은 기공률 증가에 따른 변화를 충분히 반영하지 못하는 반면, RVE 기반 해석은 이러한 기공의 영향을 반영한 결과값을 확인할 수 있었다. Longitudinal Modulus의 경우, CFRP는 기존 해석에서 약 124.2 GPa로 나타났으나, 기공률이 10% 증가했을 때 RVE 기반 해석에서는 118.21 GPa로 감소하였다. GFRP의 경우 기존 해석에서는 39.8 GPa였으나, RVE 기반 해석에서 기공률 10% 시 37.02 GPa로 저하되었다. Transverse Modulus의 경우, GFRP는 기존 해석에서 약 11.1 GPa였지만, RVE 기반 해석에서는 기공률 10% 증가 시 7 GPa까지 감소하였다. CFRP의 Transverse Modulus 역시 기존 해석에서 약 10.1 GPa였으나, RVE 기반 해석에서는 기공률 10%에서 6.9 GPa로 감소하였다. 이는 Longitudinal Modulus보다 Transverse Modulus가 기공의 영향에 더 민감하게 반응함을 시사하며, RVE 기반 해석이 미시구조적 요소의 영향을 더 정확히 반영할 수 있음을 보여준다.
3.4 물성치 산정
RVE 해석을 바탕으로 CFRP 및 GFRP의 기계적 물성치를 도출하였다. 산정된 탄성계수, 인장강도 등의 값은 실제 실험값과의 비교를 통해 실제 실험값과 5% 이내의 신뢰성 있는 물성치가 도출되었다. 도출된 물성치는 Table 4에 정리되었으며, 기존 이론값들과 비교해 높은 정확도를 나타냈다.
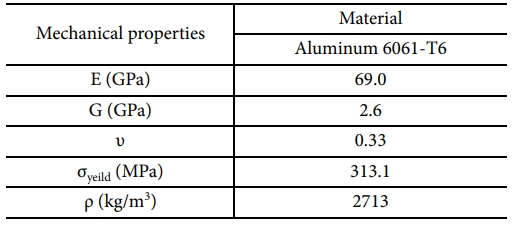
비교 기준으로 사용된 Aluminum 6061-T6의 기계적 물성치는 Table 5에 제시되어 있다. 이 합금은 복합재료와의 성능 비교를 위한 기준으로 사용되었으며, 실험값에 대한 참조로 활용되었다. 미시구조 해석을 통해 얻어진 결과는 기존의 해석 방법들보다 훨씬 정밀한 예측을 제공하였다. 특히, 미세 결함을 반영한 분석을 통해 기존 해석 방법에서 발생할 수 있는 실제 값과의 차이를 최소화하였다. 이러한 결과는 미시구조 해석이 복합재의 물성 예측에 있어 신뢰성 있는 방법임을 확인시켜 주었다.
|
Fig. 2 Geometric dimensions and meshing of three-unit cells in a fiber bundle |
|
Fig. 3 Material orientation of fibers and boundary conditions for loading types in the RVE model |
|
Fig. 4 Longitudinal modulus comparison of CFRP and GFRP with void content (Conventional vs. Microstructure analysis) |
|
Fig. 5 Transverse modulus comparison of CFRP and GFRP with void content (Conventional vs. Microstructure analysis) |
|
Table 3 Comparison of mechanical properties predicted by different analysis methods |
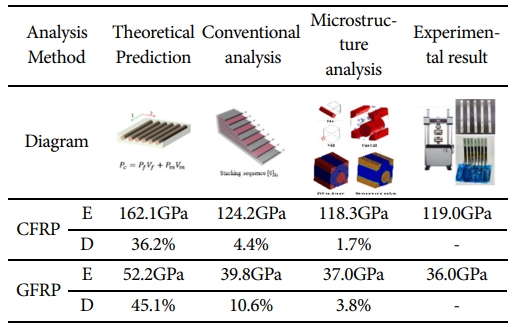
*E: Longitudinal Modulus, D: Difference |
4.1 도심항공모빌리티 붐 구조 설계
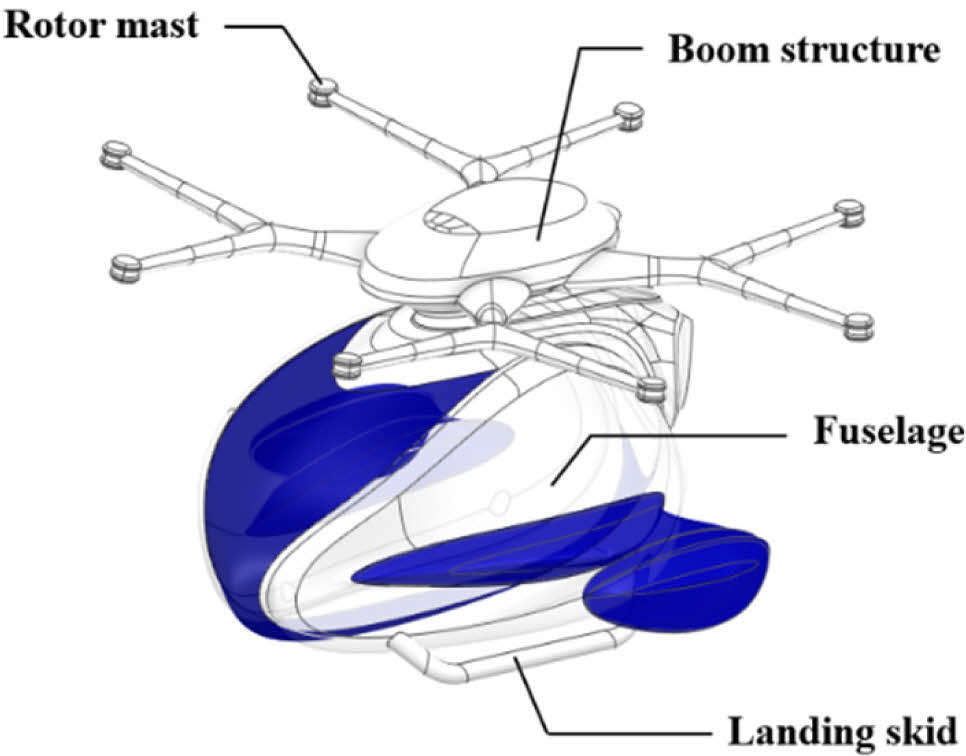
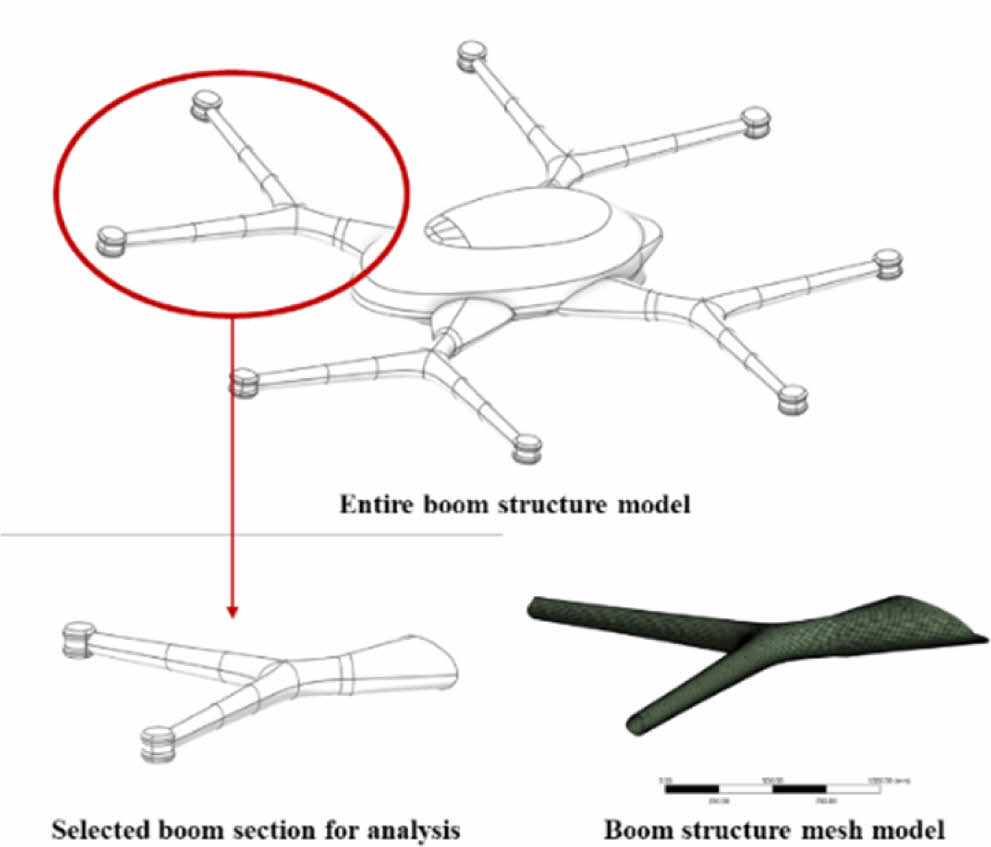
도심항공모빌리티의 붐 구조의 최적설계를 위하여 상용 프로그램인 Ansys의 Spaceclaim을 이용하여 4개의 붐 구조에 대해 길이 1900 mm, 두께 4 mm로 붐 구조를 설계하였다. UAM의 구조는 로터 마스트, 붐 구조, 동체, 랜딩 스키드로 나누어 나타내었고, Fig. 6을 통해 설계된 UAM 구조를 나타내었다. 붐 구조 설계의 경우, ACP(pre)를 통해 0.2 mm 두께로 20 ply, 4 mm로 복합재를 적층 설계하였고, 모델은 CFRP, GFRP, Aluminum 6061-T6 재료 물성을 적용한 3가지 붐 구조를 설계하였다. 모델의 단순화를 위하여 Fig. 7과 같이 붐 구조의 모델을 단순화하여 유한요소모델을 생성하였다.
4.2 도심항공모빌리티 붐 구조의 경계조건
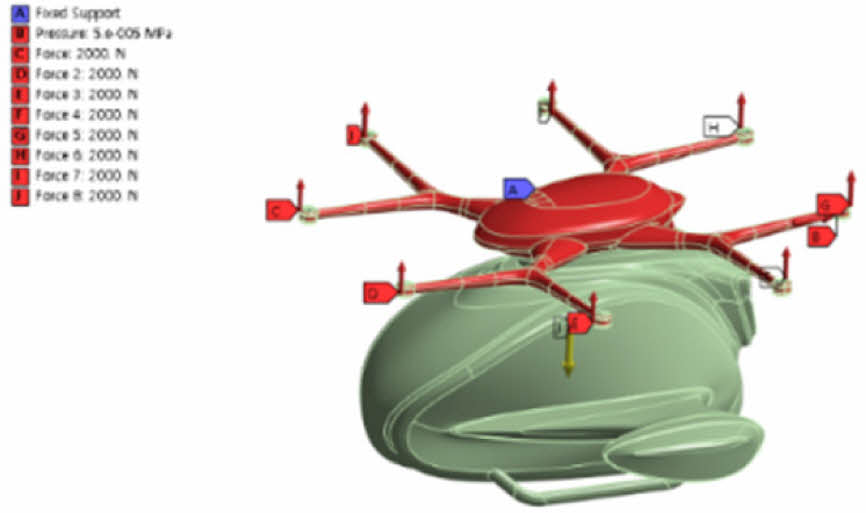
도심항공모빌리티 붐 구조의 최적 설계를 위해 주요 하중인 추력 하중, 자중 하중, 및 공기 저항력을 고려하여 정적 하중 해석을 수행하였다. 각 하중은 다음과 같이 정의된다.
1. 추력 하중(Thrust Force)
추력 하중은 항공기의 비행을 위해 회전익에서 발생하는 힘으로, 총 추력은 아래와 같은 식으로 정의된다.

여기서 T는 회전익에서 발생하는 총 추력이다. 본 연구에서는 항공기의 회전익 8개에서 발생하는 총 추력을 16,000 N으로 설정하였으며, 각 회전익은 2,000 N의 추력을 발생시킨다. 이 추력은 붐 구조의 회전익부를 통해 전달되어 전체 구조에 작용한다.
2. 자중 하중(Weight Force)
비행체의 총 자중은 항공기 제조사에서 제시한 150 kg으로 설정되었으며, 중력가속도 g는 9.81 m/s2를 적용하여 자중 하중을 계산하였다. 이 하중은 붐 구조 전체에 균일하게 분포된 하중으로 설정되었다.

3. 공기 저항력(Drag Force)
비행 속도 9 m/s에서 발생하는 공기 저항력은 고도 300 m에서 공기 밀도 ρ = 1.225 kg/m3를 적용하여 계산되었다. 붐 구조의 단면적과 공기 속 항력 계수는 각각 1.5066 m² 및 0.8로 설정되어 공기 저항력을 계산하였다.

4. 구속 조건(Boundary Conditions)
붐 구조의 고정된 끝단은 변위와 회전이 제한된 고정 경계 조건을 적용하여 회전익이 동체와 연결된 지점에서 변위와 회전이 발생하지 않도록 설정하였다.
붐 구조에 대한 해석 평가를 위해 하중 및 경계 조건을 Fig. 8에 나타내었으며, 정적 하중을 적용하여 해석을 수행하였다. 이를 바탕으로 붐 구조에 발생하는 응력과 변형을 평가하였다.
4.3 해석 결과
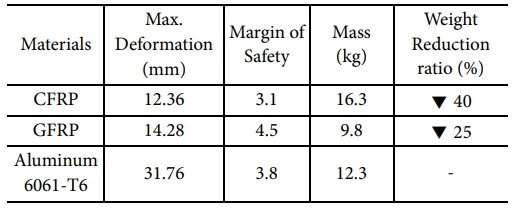
ANSYS 시뮬레이션을 통해 UAM 붐 구조에 Aluminum 6061-T6, CFRP, GFRP 재료를 적용하여 하중 해석을 수행하였다. 세 가지 재료를 적용한 붐 구조의 무게, 최대 변형량, 그리고 안전계수를 산출하였으며, 그 결과는 Table 6에 제시되어 있다. CFRP를 사용한 경우 알루미늄 합금에 비해 40% 이상의 무게 절감이 가능하였고, GFRP는 25%의 무게 절감을 기대할 수 있었다. 또한, 복합재의 경우 Puck 파손이론을 적용하였고, 금속의 경우 항복응력 기반 안전계수를 적용하여 각 재료의 안전성을 평가하였다. CFRP와 GFRP를 사용하여 설계된 붐 구조의 안전계수와 최대 변형량을 기존 알루미늄 합금과 비교한 결과, 세 재료 모두 유사한 안전성을 나타냈다. 특히, FRP 재료는 경량화 효과를 고려했을 때, 기존 금속 재료 대비 재료적인 이점을 제공하였다. 이러한 분석을 통해 FRP 재료는 UAM 붐 구조 설계에 있어 기존 재료를 대체할 수 있는 가능성이 크다는 결론을 도출할 수 있었다.
|
Fig. 6 3D model of the UAM structure |
|
Fig. 7 Design model and finite element model of the UAM boom structure |
|
Fig. 8 Loading and boundary conditions |
본 연구에서는 대표체적요소 기반의 미시구조 해석을 통해 실제 물성과 유사한 정밀 물성을 산출하고, 기존 해석과의 비교를 통해 복합재 물성 예측의 정확성을 평가하였다. 또한, 상용 구조해석 프로그램을 활용한 설계 및 구조해석을 통해 UAM 붐 구조의 재료로써 FRP 재료의 적용 가능성을 검토하였다.
(1) 본 연구에서 RVE 기반 미시구조 해석은 CFRP와 GFRP의 물성을 실험값과 각각 1%, 3% 이내의 오차로 예측하며, 기존 해석 방법과 비교해 가장 높은 정확성을 보였다. 이는 RVE 해석이 기공과 섬유 직경과 같은 미시구조적 요소를 반영하여 복합재 물성 예측의 신뢰성을 향상시킬 수 있음을 확인하였다.
(2) CFRP와 GFRP의 transverse modulus는 기공률 증가에 따라 각각 약 32%와 37% 감소하는 경향을 보였으며, longitudinal modulus는 CFRP의 경우 약 5%, GFRP의 경우 약 7% 감소하는 패턴을 확인할 수 있었다. 특히, transverse 방향의 강성이 기공률에 더 민감하게 반응함을 보여주며, RVE 해석이 기존 방법에서 고려되지 않았던 기공률의 영향을 정밀하게 분석할 수 있음을 입증한다.
(3) UAM 붐 구조에 CFRP와 GFRP를 적용한 결과, 알루미늄 합금 대비 각각 40%와 25%의 무게 절감 효과가 확인되었다. 또한, 두 복합재는 알루미늄 합금보다 높은 안전계수를 유지하며 충분한 구조적 안정성을 제공하여 FRP가 경량화와 고강도를 동시에 충족할 수 있음을 입증하였다. 이러한 결과는 경량화와 고강도가 동시에 요구되는 UAM 설계에서 FRP 재료가 더 나은 운송 효율을 제공할 수 있음을 나타낸다. 특히, 전기 추진 시스템에서의 경량화는 에너지 효율을 극대화하는 데 기여할 것으로 판단된다.
(4) 본 연구를 통해 RVE 기반 해석이 기공과 같은 미시구조 요소를 반영함으로써 복합재 물성 예측에서 높은 신뢰성과 효율성을 제공할 수 있음을 확인하였다. 앞으로는 이 해석 방법을 다양한 조건에 적용하고 실제 구조물의 실험 결과와 비교 검증하여, RVE 해석의 실용성과 정확성을 보다 강화할 계획이다. 이는 복합재 설계와 적용 시 정밀한 물성 예측에 기여할 수 있을 것이다.
- 1. Nayak, N.V., “Composite Materials in Aerospace Applications”, International Journal of Scientific and Research Publications, Vol. 4, No. 9, 2014, pp. 1-10.
- 2. Mrazova, M., “Advanced Composite Materials of the Future in Aerospace Industry,” Incas Bulletin Vol. 5, No. 3, 2013, pp. 139-150.
- 3. Hardmana, A., Crispoa, L., Sirolaa, T., and Jalayera, S., “Structural Design Optimization for CFRP in a Personal Aerial Vehicle Propulsor Boom,” Canadian Aeronautics and Space Institute AERO, 2021.
-

- 4. Littell, J., Putnam, J., and Hardy, R., The Evaluation of Composite Energy Absorbers for use in UAM eVTOL Vehicle Impact Attenuation, 2019.
- 5. Wang, Z., Wang, X., Zhang, J., Liang, W., and Zhou, L., “Automatic Generation of Random Distribution of Fibers in Long-fiber-reinforced Composites and Mesomechanical Simulation,” Materials & Design, Vol. 32, No. 2, 2011, pp. 885-891.
-

- 6. Huang, T., and Gong, Y., “A Multiscale Analysis for Predicting the Elastic Properties of 3D Woven Composites Containing Void Defects,” Composite Structures, Vol. 185, No. 1, 2018, pp. 401-410.
-

- 7. Dong, C., “Effects of Process-induced Voids on the Properties of Fibre Reinforced Composites,” Journal of Materials Science & Technology, Vol. 32, No. 7, 2016, pp. 597-604.
-

- 8. Heinrich, C., Aldridge, M., Wineman, A.S., Kieffer, J., Waas, A.M., and Shahwan, K., “The Influence of the Representative Volume Element (RVE) Size on the Homogenized Response of Cured Fiber Composites,” Modelling and Simulation in Materials Science and Engineering, Vol. 20, No. 7, 2012, pp. 25.
-

- 9. Gao, X., Yuan, L., Fu, Y., Yao, X., and Yang, H., “Prediction of Mechanical Properties on 3D Braided Composites with Void Defects,” Composites Part B: Engineering, Vol. 197, No. 15, 2020.
-

- 10. Jiang, H., Jiang, H., Ren, Y., Liu, Z., and Zhang, S., “Microscale Finite Element Analysis for Predicting Effects of Air Voids on Mechanical Properties of Single Fiber Bundle in Composites,” Journal of Materials Science, Vol. 54, 2019, pp. 1363-1381.
-

- 11. Bae, S.Y., Kim, B.S., Lee, S.L., Kim, W.J., and Kim, Y.H., “Structural Design of Multi-Megawatt Wind Turbine Blade by Classical Lamination Theory,” Journal of Ocean Engineering and Technology, Vol. 28, No. 2, 2014, pp. 147-151.
-

- 12. Kim, Y.H., Bae, S.Y., Jo, Y.D., and Moon, K.M., “Structural Design and Analysis of Autonomous Underwater Vehicle by Fiber Reinforced Plastics,” Journal of the Korean Society of Mechanical Engineers, Vol. 32, No. 11, 2008, pp. 937-942.
-

- 13. Bae, S.Y., Bae, K.M., and Kim, Y.H., “Evaluation of Mechanical and Vibration Characteristics of Aluminum Bonded Damping Panels for Automotive Parts,” Composites Research, Vol. 32, No. 2, 2019, pp. 113-119.
- 14. Seok, J.H., Kim, Y.H., and Bae, S.Y., “A Study on the Optimal Design of UAM Seats,” Modern Physics Letters B, Vol. 39, 2024, 2441012.
-

- 15. Choi, J.W., “Effect of Triphenylphosphine Addition for the Fast Curing Epoxy-anhydride CFRP System,” Modern Physics Letters B, Vol. 39, 2024, 2441009.
-

 This Article
This Article
-
2024; 37(6): 466-472
Published on Dec 31, 2024
- 10.7234/composres.2024.37.6.466
- Received on Nov 6, 2024
- Revised on Nov 29, 2024
- Accepted on Nov 30, 2024
 Services
Services
Shared
 Correspondence to
Correspondence to
- Seonghun Park*, Sung-Youl Bae**
-
* School of Mechanical Engineering, Pusan National University, Busan, Korea Korea
** Institute of Ceramic Engineering and Technology, Aerospace Convergence Materials Center, Korea - E-mail: paks@pusan.ac.kr, bsy@kicet.re.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.