Tire friction tests depend on various environmental and testing conditions such as road conditions, temperature, vehicle weight, and driving conditions. These variables limit the fundamental understanding of the correlation between tire characteristics and friction behaviors. Therefore, a theoretical approach to friction between tread compounds and road surfaces is required as a first step in understanding tire friction mechanisms. The test methods for tread compounds typically include sliding and rolling friction tests. However, rolling friction tests face difficulties in characterizing high-speed friction behaviors and are significantly affected by heat and wear during testing, making it challenging to apply friction theories for detailed analysis. Despite these difficulties, rolling friction tests are crucial for analyzing tire rolling resistance and braking performances. This paper employs the Klüppel & Heinrich friction theory to sliding friction and investigates the correlation between sliding and rolling friction. Through the friction theory, quantitative contributions of adhesion and hysteresis friction mechanisms are identified across a wide slip velocity range. As a result, the correlation between sliding and rolling friction showed a high coefficient of determination, above 0.876. These findings confirm that rolling friction behaviors in high-speed regions can be predicted through sliding friction master curves, as well as the contributions of adhesion and hysteresis friction, which are significant on rough and dry surfaces. This study has the potential to impact tread compound design for tunable tire friction behaviors.

타이어 마찰은 온도, 환경적 요소 등 여러 요인이 복합적으로 작용하기에 실차평가하는 것은 한계가 있으므로 마찰시험과 이론을 기반으로 한 연구가 중요해지고 있다. 일반적으로 타이어 마찰을 시험하는 방법은 미끄럼 및 구름마찰 두 가지 방식이 있다. 그 중 구름마찰시험은 타이어 회전저항 및 제동 성능을 분석하는데 활용되는 주요 마찰시험이다. 하지만 높은 온도와 마모 발생으로 인해 마찰 특성이 변화하고, 마찰이론을 적용하기 어려운 한계가 있다. 따라서 마찰이론을 기반하여 고속에서의 구름마찰 특성을 예측할 수 있는 분석방법이 필요하다. 본 논문은 Klüppel & Heinrich 마찰이론을 적용하여 광범위한 속도영역에서 점착 및 히스테리시스 마찰의 영향으로 세부적인 마찰특성을 분석할 수 있는 미끄럼마찰과 구름마찰 간의 상관관계를 연구하여 실험으로 측정하기 어려운 영역의 구름마찰 특성을 예측하는 방법을 연구하였다. 분석범위는 Anti-lock Brake System (ABS) 분석에 주로 활용되는 구름마찰 커브의 최대값 영역으로 선정하였다. 결과적으로 분석범위 내의 두 마찰 간의 상관관계가 0.876 이상의 높은 결정계수를 나타내었다. 이러한 결과로부터 고속영역의 구름마찰 특성을 미끄럼마찰로 예측할 수 있음을 확인하였다. 또한, 일반적인 거칠고 마른 노면에서는 점착 및 히스테리시스 마찰이 가장 큰 영향을 미치는 것으로 나타났으며, 나타났으며, 이러한 마찰의 영향도를 분석함으로써 타이어 설계 및 성능평가에 지대한 영향을 미칠 수 있을 것으로 기대된다.

Keywords: 구름마찰(Rolling friction), 미끄럼마찰(Linear friction), 마찰 마스터커브(Friction master curve), 마찰이론(Friction theory), 타이어 트레드 컴파운드(Tire Tread Compound)

타이어 마찰이란 타이어의 트레드와 노면 간의 접촉 상태에서 차랑 주행 시 발생하는 저항력을 의미한다. 타이어 마찰특성 분석을 통해 차량과 타이어에 요구되는 성능인 핸들링, 내마모성, 제동, 연비 등을 분석할 수 있다[1]. 하지만 타이어 마찰은 온도, 트레드 컴파운드 물성, 트레드 패턴, 주행 및 슬립 속도, 환경적 요소 등과 같이 여러 요인이 복합적으로 작용하기 때문에[2] 타이어 마찰에 대한 실차시험의 재현성이 떨어지는 한계가 있다. 따라서 트레드 컴파운드의 마찰특성을 평가하고 이를 고무 마찰이론에 적용하여 타이어 마찰특성에 영향을 미치는 인자의 정량적 기여도를 파악하는 이론적 분석이 중요해지고 있다[3].
일반적인 마찰시험 방법은 미끄럼마찰 시험과 구름마찰 시험이 있다. 미끄럼마찰 시험은 컴파운드가 특정 속도로 노면에 미끄러질 때 발생하는 마찰력을 측정하는 시험방법이다[4]. 구름마찰 시험은 타이어 회전속도와 주행속도의 차이를 변화시킴에 따라 발생하는 마찰력을 측정하는 시험방법이다[5].
하지만 구름마찰 시험을 통해 타이어 마찰특성을 분석하는 데에는 몇 가지 한계가 있다. 먼저 구름마찰 시험은 고속영역에 대한 마찰특성 분석의 어려움이 있다. Lundberg 등[6]은 타이어와 노면 간의 상호작용을 분석하기 위한 구름마찰 시험장비를 구축하였지만 60 km/h 이상의 마찰특성을 분석하기에는 어려움이 있었다. Shinone 등[7]은 타이어 트레드 패턴에 따른 마찰특성을 97.6 mm/s의 저속에서 수행한 바 있다. 하지만 고속도로와 같은 주행조건에서의 타이어 마찰특성을 이해하기 위해서는 트레드 컴파운드의 고속영역에서의 마찰특성 분석이 필요하다.
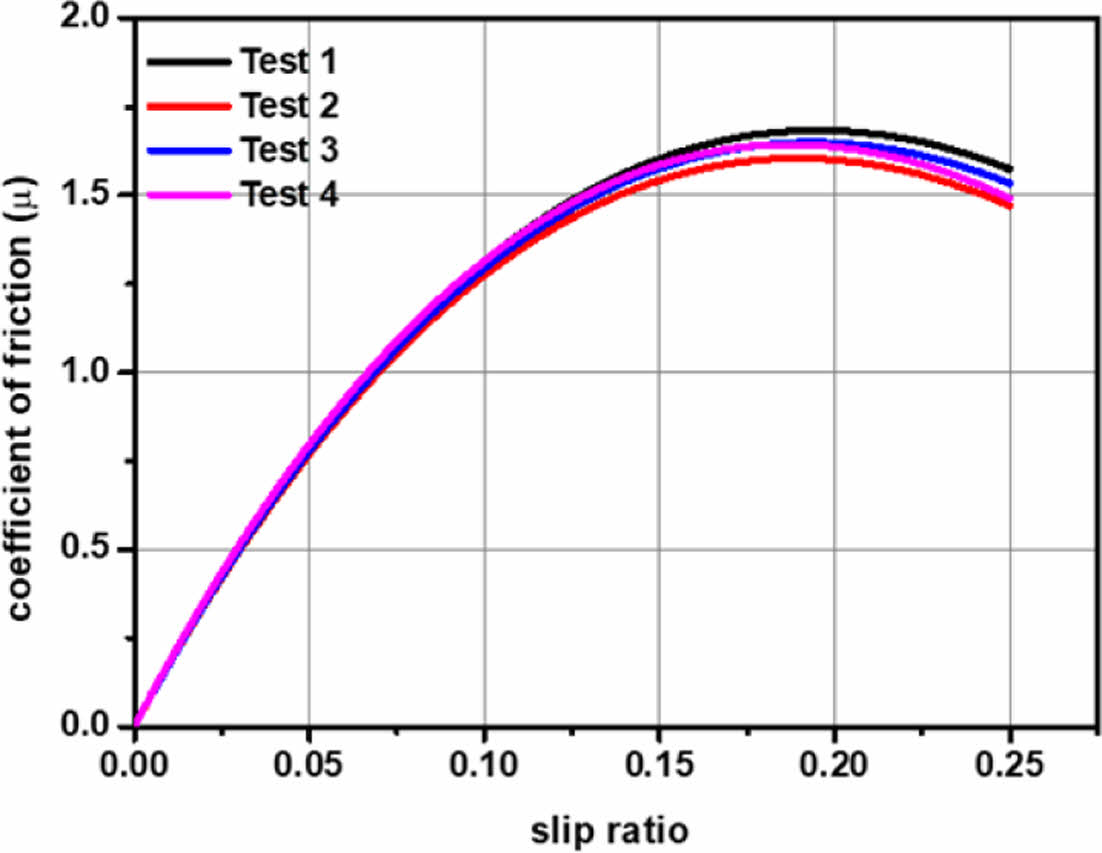
더욱이 구름마찰 시험은 미끄럼마찰보다 상당히 고속에서 평가하기 때문에 노면과 컴파운드 간의 마찰온도가 최대 70^oC까지 상승하며 마찰에 의해 발생하는 마모량도 많다[8]. 그리고 다양한 요인이 복합적으로 작용하면서 시험을 진행할 때마다 발생하는 마모량과 마찰온도가 상이하다. 이로 인해 Fig. 1과 같이 동일한 시험조건에도 시험결과의 편차가 상당히 발생하므로 고무와 노면 사이의 접촉을 통해 발생하는 마찰거동을 세부적으로 분석하는데 어려움이 있다. Klüppel & Heinrich 마찰이론[3]에 따르면 아스팔트와 같이 거칠고 마른 노면에서 발생하는 마찰은 열과 마모 영향보다 점착(Adhesion) 및 히스테리시스(Hysteresis) 마찰이 지배적인 영향을 미칠 것으로 분석한다. 따라서 마모와 열의 영향이 포함된 구름마찰 시험결과에 마찰이론을 적용하여 분석하는 것은 한계가 있다.
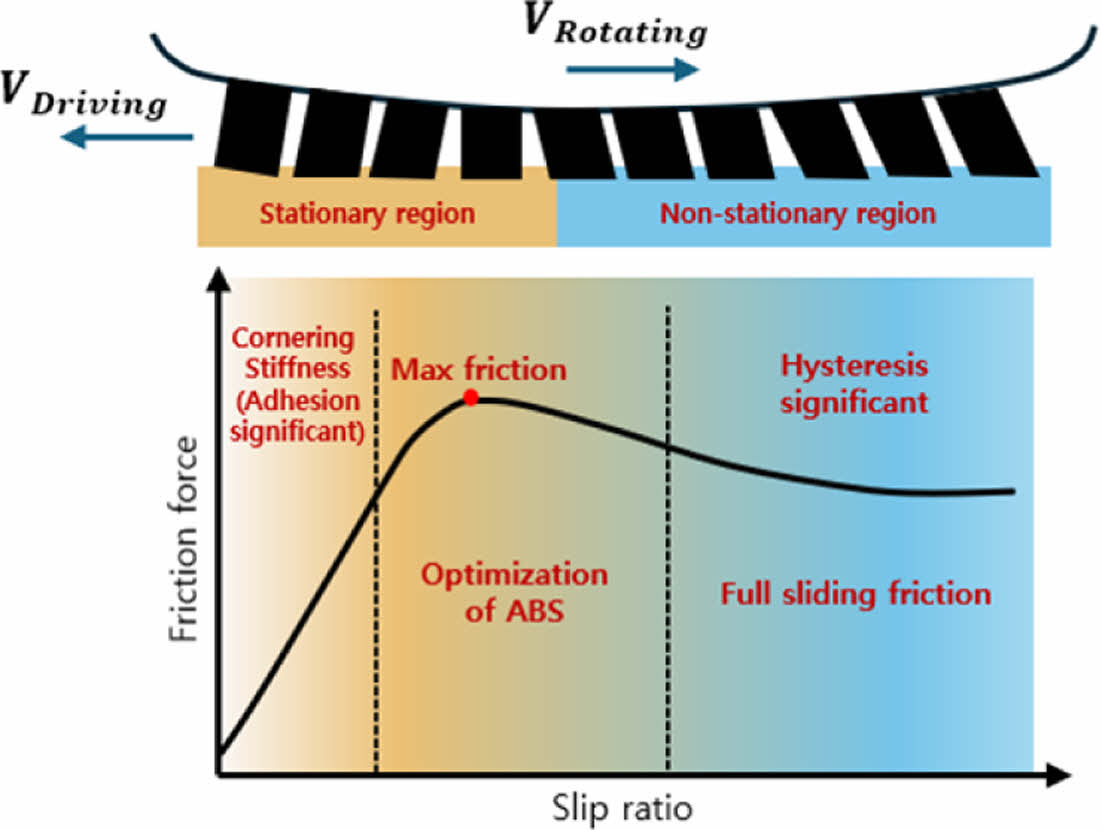
그럼에도 불구하고 구름마찰 시험은 미끄럼마찰 시험과 달리 1회 평가를 통해 Fig. 2와 같이 타이어 마찰에서 중요한 Anti-lock Brake System (ABS) 영역[9,10]의 슬립율(Slip Ratio)까지의 마찰특성을 확보할 수 있기 때문에 산업계에서 널리 사용되고 있다. 따라서 구름마찰 시험의 장점을 활용하여 보다 정확한 타이어 마찰 분석을 위해서 고속에서의 구름마찰특성을 예측할 수 있는 방법 및 마찰시험 결과를 마찰이론에 따라 세부적으로 분석하는 방법이 필요하다.
Klüppel & Heinrich[11]는 고분자 분야에서 주로 사용하는 시간-온도 중첩의 원리를 미끄럼마찰 시험을 통해 확보한 마찰특성에 적용하여 광범위한 슬립속도에서의 마찰특성을 예측하는 마찰 마스터커브를 구축하였고, 이를 통해 슬립속도에 따라 달라지는 고무마찰 메커니즘의 기여도를 정략적으로 분석할 수 있는 마찰이론을 정립하였다.
본 연구는 미끄럼마찰 시험을 통해 확보한 마찰 마스터커브에 Klüppel & Heinrich 마찰이론을 적용하여 점착과 히스테리시스에 의한 마찰 기여도를 분석하였고, 미끄럼마찰과 구름마찰 간의 상관관계를 분석하여 마찰이론을 통해 구름마찰특성을 예측하는 연구를 수행하였다.
기존 구름마찰 관련 연구를 살펴보면 Giuseppe Carbone 등[12]은 고무재료에 대한 구름마찰 시험결과를 예측할 수 있는 이론적 모델링을 구축하였다. 이론적 모델링을 통해 마찰시험 결과를 높은 정확도로 예측할 수 있는 방법을 구축하였지만 고무마찰 메커니즘에 따른 마찰특성을 세부적으로 분석하는데 한계가 있다.
따라서 Klüppel & Heinrich 마찰이론을 통해 구름마찰 특성을 예측할 수 있다면 광범위한 슬립속도 및 고무마찰 메커니즘에 따른 정량적인 마찰특성 분석이 가능하기 때문에 트레드 컴파운드의 구름마찰 시험을 통해 타이어 회전저항 및 제동성능을 분석하는데 더욱 높은 신뢰성과 효과적인 컴파운드 설계 방안 도출이 가능할 것으로 예상된다.

2.1 고무마찰 메커니즘
Klüppel & Heinrich 마찰이론은 타이어 마찰의 많은 연구분야에 적용되고 있으며 시험을 통해 측정하기 힘든 속도에 대한 마찰특성을 고무마찰 메커니즘에 따라 세부적으로 분석할 수 있다[11,13,14].
고무마찰 메커니즘은 고무와 노면 간의 발생하는 마찰을 식 (1)과 같이 점착(Adhesion) 마찰, 히스테리시스(Hysteresis) 마찰, 응착(Cohesion) 마찰, 점성(Viscous) 마찰의 4가지 요소로 구분한다.



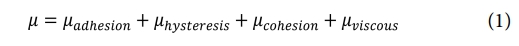
여기서 μ는 마찰계수(Coefficient of friction)을 나타낸다. 그리고 일반적인 거칠고 마른 노면에서는 점착마찰과 히스테리시스 마찰이 지배적으로 작용하기에 응착 마찰과 점성 마찰의 영향은 무시할 수 있다고 가정한다.
2.1.1 점착 마찰
점착마찰은 고무와 노면 간의 접촉을 통해 분자간 인력으로 형성되며 식 (2)와 같이 정의된다.



여기서 τ_s는 실계면전단강도, σ₀는 겉보기수직응력 그리고 A_c와 A₀는 각각 실접촉면적과 겉보기접촉면적을 나타낸다[15].
2.1.2 히스테리시스 마찰
히스테리시스 마찰은 고무가 노면에 접촉 후 떨어질 때 발생하는 변형에 의한 마찰로 식 (3)과 같이 정의된다.



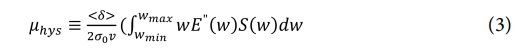
여기서 <δ>는 노면 돌기에 의해 가진된 고무 층의 두께, E”및 S은 각각 주파수에 따른 고무의 손실에너지와 노면의 거칠기를 푸리에 변환(Fourier-transform)을 통해 주파수 스케일로 나타낸 Power Spectrum Density (PSD)를 나타낸다[16].
해당 점착 및 히스테리시스 마찰 모델은 고무 컴파운드의 점탄성과 표면에너지, 노면의 표면 거칠기와 표면에너지를 통해 속도에 따른 마찰특성을 예측할 수 있음을 제시한다[17].
2.2 마찰 마스터커브
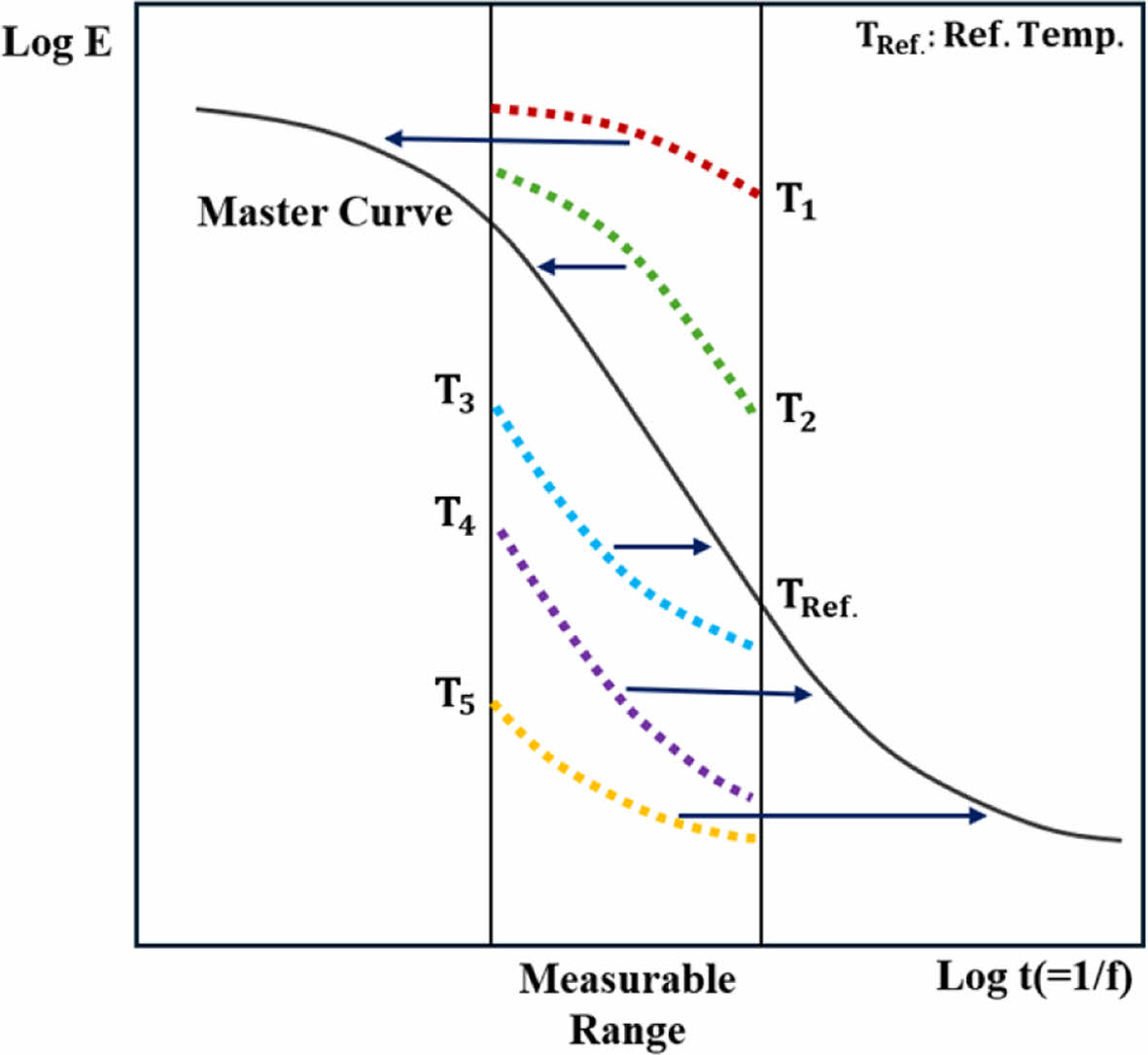
마찰 마스터커브는 고무재료 물성인 점탄성과 미끄럼마찰거동 간의 관계를 통해 구축되는 마스터커브이다. 이는 고분자 재료의 물성을 해석하기 위해 일반적으로 사용하는 시간-온도 중첩의 원리를 마찰에 적용한 개념이다. 시간-온도 중첩의 원리는 Fig. 3과 같이 점탄성 재료의 온도변화를 기반으로 주파수에 따른 기계적 거동을 예측하는 방법이다[18]. 여기서 E는 점탄성 모듈러스, T_n은 온도, T_Ref.는 기준온도(Reference temperature), t는 시간, f는 주파수를 나타낸다.
따라서 이 원리를 마찰속도에 적용하여 넓은 속도 범위에서의 마찰특성을 분석할 수 있는 마찰 마스터커브를 구축할 수 있다.

본 연구에서 사용한 재료는 무작위로 선택된 3 종류의 일반적인 승용차 타이어의 트레드 컴파운드로, 각기 다른 성분으로 구성되어 있다.
3.1 마찰 시험
3.1.1 미끄럼마찰 시험
미끄럼마찰 시험은 마찰계수 시험기(Neoplus, Korea)를 이용하여 측정하였다. 시험조건은 0.1~5 mm/s의 속도로 시험을 진행하였고 온도별 마찰특성을 분석하기 위해 5~40 ^oC에서 동일한 속도조건으로 시험을 진행하였다. 노면은 사포 (P120)를 적용하여 시험을 진행하였다. 사포노면은 포장도로 표면에서 마찰평가한 결과와 동일한 마찰경향을 보이며[19] 타이어 마찰평가 시 주로 사용되는 노면 중 하나이다.
3.1.2 구름마찰 시험
구름마찰 시험은 Rotational Traction Measuring System, RTMS (Ueshima, Japan)를 이용하여 마른 노면에서 컴파운드의 구름마찰 특성을 측정하였다. 시험조건은 30 km/h 주행속도를 기준으로 0~25%로 슬립율을 변화시켜 마찰시험을 진행하였으며 노면은 미끄럼마찰 시험과 동일한 사포를 사용하였다.
3.2 시간-온도 스윕(Time-Temperature Sweep) 시험
마찰 마스터커브를 구축하기 위해 필요한 점탄성 데이터는 점탄성 마스터커브이며 이는 시간-온도 스윕 시험데이터를 기반으로 구축된다[17]. 시간-온도 스윕 시험은 다양한 온도조건에서 시간에 따른 재료 거동의 변화를 측정하는 시험이다. 따라서 각 컴파운드의 온도별 점탄성 거동을 측정하기 위해 DMA850 (TA Instruments, USA) 장비를 사용하여 2% strain level에서 시간-온도 스윕 시험을 실시하였다.
3.3 접촉각 시험
점착마찰을 정의할 때 필요한 실계면전단강도는 접착 일 (Work of adhesion, ∆γ)을 통해 계산된다[18]. ∆γ는 식 (4)와 같이 두 고체가 접촉할 때 단위 면적당 계면 자유 에너지의 변화이다. 여기서 γ_S, γ_R는 각각 사포노면과 트레드 컴파운드의 표면에너지를 나타낸다. 따라서 DSA-25(KRUSS, Germany) 장비를 활용하여 트레드 컴파운드와 사포노면의 접촉각 측정을 통해 표면 에너지를 계산하였고 두 표면 간의 발생하는 접착 일을 계산하였다.



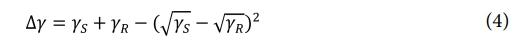
접촉각 시험에서 사용한 표면에너지 측정방법은 Owen, Wendt, Rable and Kaeble (OWRK) method를 사용하였다.
3.4 표면 거칠기 시험
고무마찰 메커니즘을 정의하는데 필요한 노면의 표면 거칠기를 측정하기 위해 SJ-411 (Mitutoyo, Japan)장비를 활용하여 ISO 1997 표준에 따른 사포의 표면 거칠기를 측정하였다. 측정방법은 접촉식 방식을 적용하였고 실제적인 노면의 표면 특성을 고무마찰 메커니즘에 적용하기 위해 P-profile을 적용하였다. 측정 조건은 포괄적인 사포노면의 표면 특성을 계산하기 위해 여러 위치에서 거칠기를 반복 측정하였다.

4.1 마찰 마스터커브
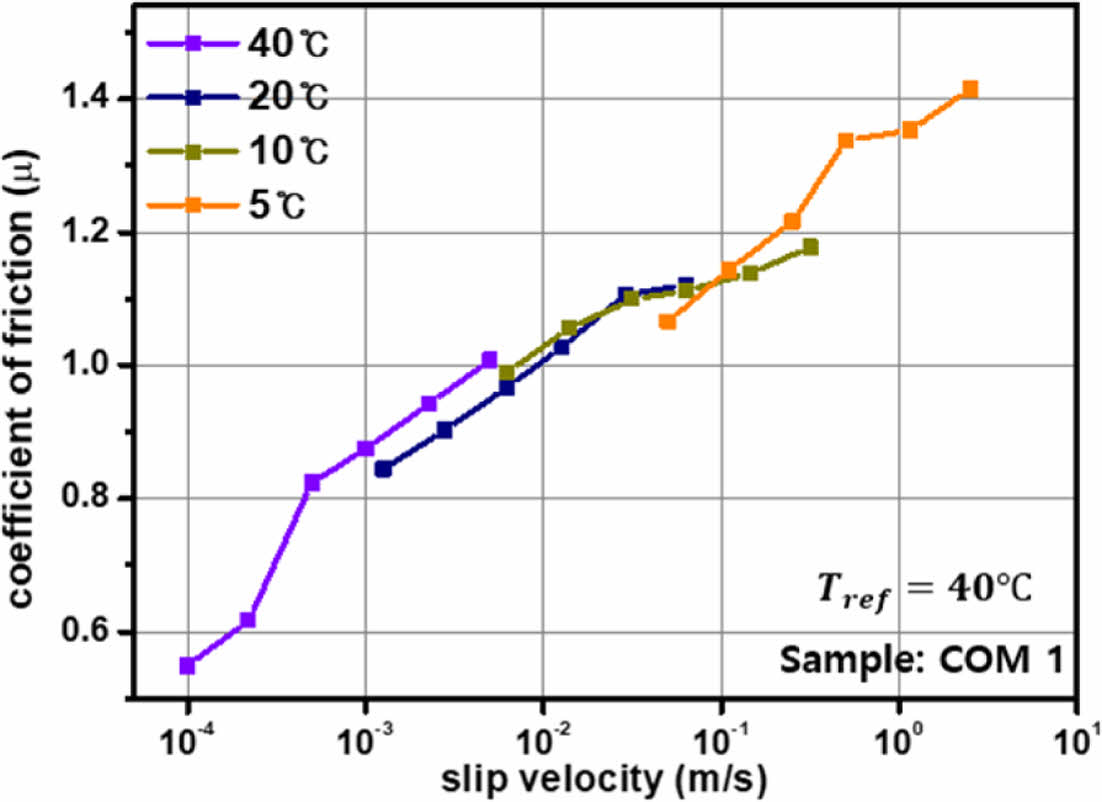
미끄럼 마찰결과와 시간-온도 중첩의 원리를 통해 구축한 점탄성 마스터커브를 통해 3 종류의 트레드 컴파운드의 마찰 마스터커브를 Fig. 4와 같이 구축하였다.
마찰 마스터커브를 구축하기 위한 기준온도(T_ref)는 구름마찰 커브의 최대값에 해당하는 마찰온도인 40^oC로 선정하였고 기준온도를 중심으로 수평이동하여 0.1~5 mm/s의 속도범위를 0.1~25 mm/s로 확장할 수 있었다.
결과적으로 Fig. 4와 같이 실험적으로 얻은 마찰 마스터커브에서 2.5 m/s의 속도까지 각 트레드 컴파운드의 마찰특성을 확인할 수 있었고 마찰이 선형적으로 증가하는 모습을 확인할 수 있었다.
4.2 마찰이론 모델링(Linear Friction Modeling)
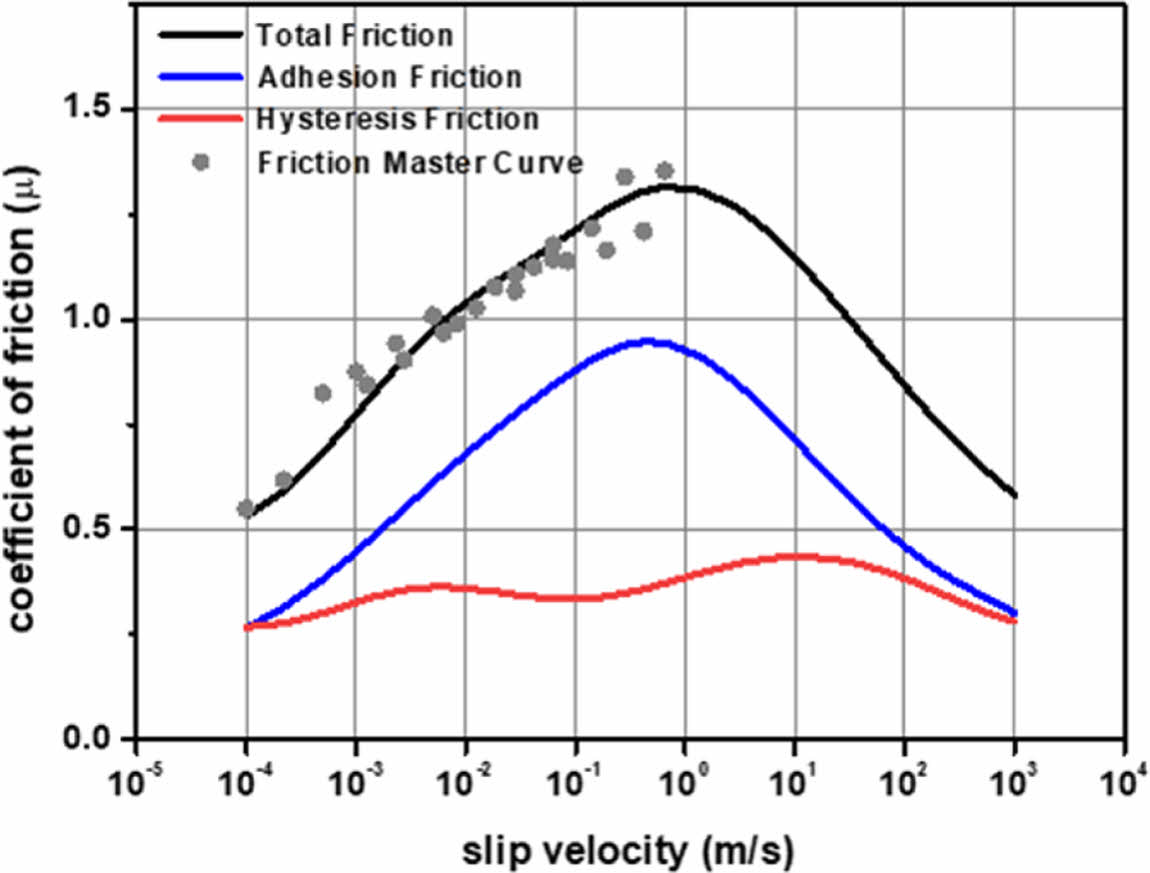
실험적 마찰 마스터커브에서 확인할 수 있는 속도범위보다 넓은 속도에 대한 마찰특성을 파악하기 위해 마찰 마스터커브에 Klüppel & Heinrich 마찰이론을 적용하여 Fig. 5와 같이 마찰이론 모델링을 구축하였다.
점착 마찰은 실접촉면적과 실계면전단강도를 고려하여 계산하였다. 먼저 노면의 거칠기와 트레드 컴파운드의 점탄성을 통해 트레드 컴파운드와 노면이 접촉했을 때의 실접촉면적을 계산하였다. 그리고 트레드 컴파운드의 점탄성 및 노면 간의 접착일을 통해 노면이 접촉한 후 떨어질 때 필요한 실계면전단강도를 계산하였다. 이를 식 (2)에 적용하여 각 트레드 컴파운드가 노면에 마찰 시 발생하는 점착마찰을 계산하였다.
히스테리시스 마찰은 마찰로 인해 고무표면의 미세 돌기가 변형하여 발생하는 손실에너지와 노면의 거칠기를 식(3)에 적용하여 계산하였다.
Fig. 5에 따르면 본 연구에 적용한 트레드 컴파운드는 점착마찰이 모든 속도영역의 마찰거동에 큰 영향을 끼침을 확인할 수 있었다. 그러나 5^oC의 마찰 마스터커브 결과는 마찰 이론 모델링 결과와 일부 차이를 보였다. 이러한 차이는 마찰계수 시험기 내부와 외부의 온도 차이로 발생한 습도가 영향을 미친 것으로 사료된다.
4.3 미끄럼마찰과 구름마찰 간의 상관관계
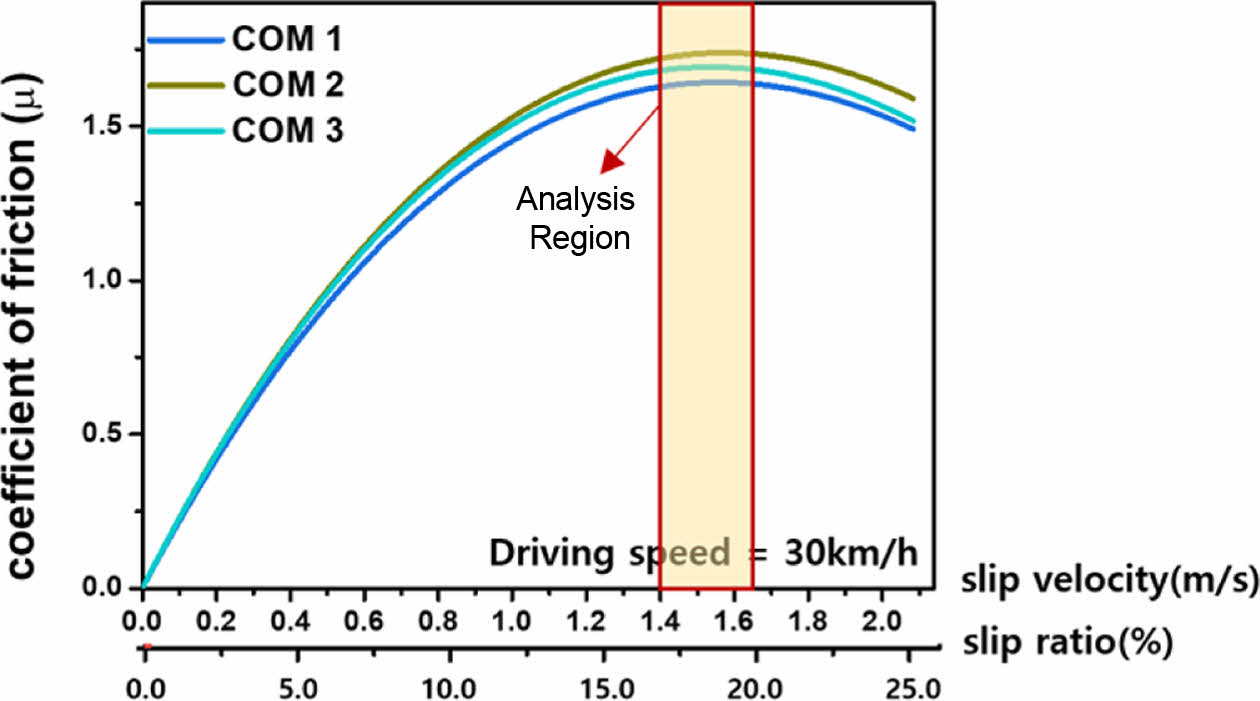
마찰이론 모델링 결과와 구름마찰 시험결과를 통해 두 마찰 간의 상관관계를 분석하였다. 상관관계 분석범위는 Fig. 6와 같이 타이어 제동성능 분석에 가장 큰 영향을 미치는 구름마찰 시험결과의 최대값 영역을 선정하였다. 이는 차량의 ABS 성능을 분석하는데 주로 활용되는 영역이다.
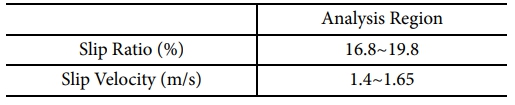
본 연구에 적용된 3 종류의 트레드 컴파운드 최대값 영역은 Table 1과 같이 16.8~19.8%에서 형성되었다. 이를 마찰이론 모델링 결과와 비교하기 위해 주행속도 30 km/h에 각 해당 슬립율을 곱하여 슬립속도로 변환하였고, 분석범위 내의 미끄럼 및 구름마찰의 상관관계를 분석하였다. 분석기준은 선형 회귀 모델을 적용하여 상관관계식을 도출하고 그에 따른 결정계수를 통해 상관관계를 분석하였다.
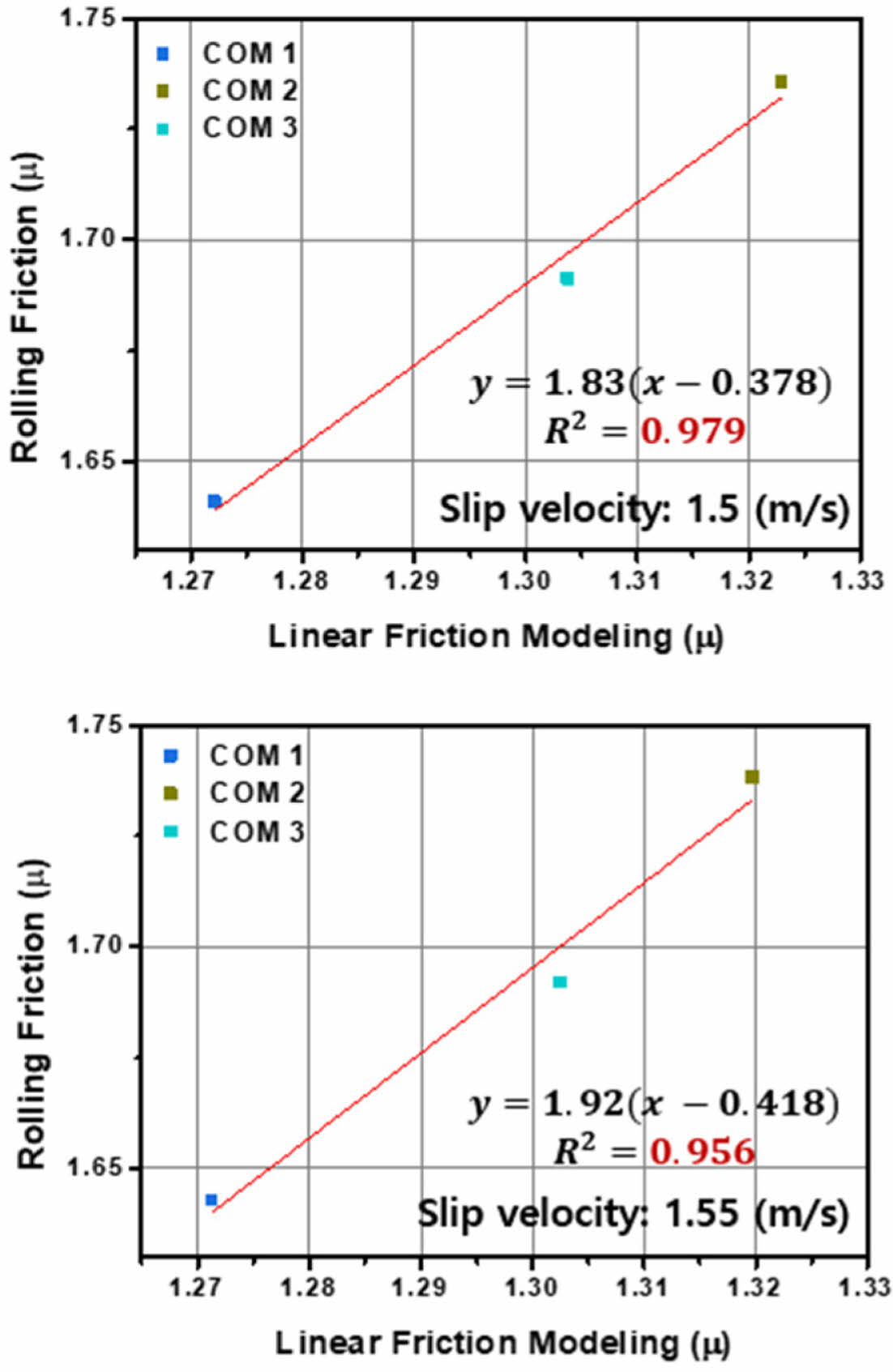
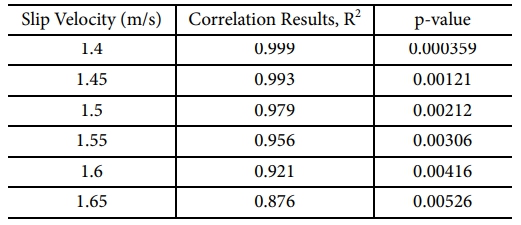
동일한 슬립속도에서 미끄럼 및 구름마찰 결과를 비교했을 때, Fig. 7과 같이 3 종류의 트레드 컴파운드에 대한 두 마찰 경향이 일치하는 결과를 나타내었다. 이를 전체 분석범위로 비교해보면 Table 2와 같이 전체 슬립속도에 대한 두 마찰의 상관관계가 0.876 이상의 결정계수를 형성하였다. 공학적 통계학 기준[20]에 따르면 결정계수가 0.8 이상의 값을 가질 때, 두 비교대상이 강한 선형관계를 가지는 것으로 분석하기에 전체 슬립속도에 대한 두 마찰결과는 높은 상관관계를 이룬다고 분석할 수 있다. 이는 미끄럼마찰 결과를 통해 80% 이상의 구름마찰 거동을 예측할 수 있음을 시사한다.
추가적으로 상관관계 결과에 대한 신뢰성을 높이기 위해 F-통계량에 따른 p-value를 분석하였다. F-통계량은 선형 회귀 모델의 통계적 유의성을 검정하는 데 사용되는 지표이며, 이에 따른 p-value를 통해 유의성을 분석한다. 일반적으로 p-value가 0.05 이하인 경우 높은 통계적 유의성을 가진다고 판단하는데, 본 연구에서는 분석범위 내 슬립속도에서 상관관계식의 p-value가 0.01이하로 매우 높은 통계적 유의성을 가지고 있음을 확인할 수 있다.
이를 통해 실험적으로 분석하기 어려운 고속에서의 구름마찰특성도 동일하게 미끄럼마찰특성으로 예측할 수 있는 근간이 될 것으로 분석한다.

구름마찰의 특성을 미끄럼마찰로 분석하기 위해 Klüppel & Heinrich 마찰이론을 적용한 마찰이론 모델링과 30 km/h에서 측정한 구름마찰 간의 상관관계를 도출하였다. 구름마찰 시험결과의 최대값 영역을 분석범위로 설정하여 비교한 결과, 각 슬립속도에 대한 미끄럼마찰과 구름마찰 간의 상관관계를 선형관계식으로 도출하였으며, 이는 0.876 이상의 높은 결정계수를 나타내었다.
결과적으로 본 연구는 재료의 점탄성 물성과 마찰 마스터커브를 활용하여 실험을 통해 알 수 있는 속도영역뿐만 아니라 그 이상의 속도영역에서도 사포 노면에서의 구름마찰특성을 미끄럼마찰특성으로 예측할 수 있음을 보여주었다. 이는 구름마찰의 특성을 점착 마찰과 히스테리시스 마찰의 영향으로 분석할 수 있는 주요 연구 결과로, 향후 타이어 설계나 회전저항 및 제동성능 평가에 중요한 영향을 끼칠 수 있을 것으로 판단된다.
더하여 본 연구는 사포노면 및 30 km/h라는 특정 시험 조건에서 상관관계를 도출하였다. 향후 다양한 노면 및 다른 속도조건에서도 일정한 상관관계를 확립함으로써, 시험 측정이 어려운 60 km/h 이상 고속영역의 구름마찰 특성을 마찰이론 모델링으로 예측하는 연구의 신뢰성을 높일 계획이다.

This work has supported by the Technology Innovation Program (20013794, Center for Composite Materials and Concurrent Design) and has funded by Hyundai Motor Company.