This study proposes a hybrid composite where a thin copper film (Cu film) is embedded in carbon fiber reinforced plastic (CFRP), and quantum annealing is applied to derive the combination of Cu film placement that maximizes the through-thickness thermal conductivity. The correlation between each ply of CFRP and the Cu film is analyzed through finite element analysis, and based on the results, a combination optimization problem is formulated. A formalization process is conducted to embed the defined problem into quantum annealing, resulting in the formulation of objective functions and constraints regarding the quantity of Cu films that can be inserted into each ply of CFRP. The formulated equations are programmed using Ocean SDK (Software Development Kit) and Leap to be embedded into D-Wave quantum annealer. Through the quantum annealing process, the optimal arrangement of Cu films that satisfies the maximum through-thickness thermal conductivity is determined. The resulting arrangements exhibit simpler patterns as the quantity of insertable Cu films decreases, while more intricate arrangements are observed as the quantity increases. The optimal combinations generated according to the quantity of Cu film placement illustrate the inherent thermal conductivity pathways in the thickness direction, indicating that the transverse placement freedom of the Cu film can significantly affect the results of through-thickness thermal conductivity.

본 연구에서는 탄소섬유 강화 플라스틱(CFRP)에 얇은 구리 필름(Cu film)이 배치된 hybrid composite이 제안되었으며, 두께 방향 열전도도가 최대가 될 수 있는 Cu film 배치 조합을 도출하는데 양자 어닐링(Quantum Annealing)이 적용되었다. CFRP의 각 ply와 Cu film간의 상관관계 분석이 유한요소 해석을 통해 수행되었으며, 수행된 결과를 바탕으로 조합 최적화 문제가 정의되었다. 정의된 문제를 양자 어닐링에 임베딩하기 위한 공식화 과정이 진행되었으며 이를 통해 CFRP의 각 ply에 투입될 수 있는 Cu film 수량에 관한 목적함수와 제약조건이 수식으로 구현되었다. 공식화된 수식은 D-Wave 양자 어닐러에 임베딩되기 위해 Ocean SDK(software development kit)와 Leap을 통해 프로그래밍 되었으며, 양자 어닐링 과정을 통해 두께 방향 열전도도가 최대를 만족하는 최적의 Cu film 배치 조합이 도출되었다. 도출된 배치 조합은 투입될 수 있는 Cu film의 수량이 적어질수록 단순한 배치 형태를 나타내었으며, 수량이 많아질수록 세밀한 배치를 보였다. Cu film의 배치 수량에 따라 생성된 최적 조합들은 두께 방향으로의 고유 열전도 경로를 나타내었으며, Cu film의 횡방향 배치 자유도가 두께 방향 열전도도 결과에 민감하게 나타날 수 있음을 보였다.

Keywords: 탄소섬유 강화 플라스틱(CFRP), 하이브리드 복합재(Hybrid composite), 열전도도(Thermal conductivity), 양자 어닐링(Quantum annealing), 조합 최적화(Combination optimization)

탄소섬유 강화 플라스틱(Carbon-Fiber Reinforcement Plastics, CFRP)은 높은 비강도와 비강성 그리고 우수한 내식성을 나타내는 복합재이다. 또한 CFRP는 내열성이 높아 고온에서도 안정적인 기계적 특성 유지가 가능하다[1]. 이러한 장점들로 인해 항공 우주 및 우주 응용 분야에서는 지속적으로 광범위하게 CFRP가 적용되고 있다[2-4]. 특히 기술이 발전함에 따라 CFRP로 구성된 고성능 장치들은 효과적인 방열 성능이 요구되어진다. 열전도도에 있어서 CFRP는 섬유가 지배적으로 더 나은 면내 방향(In-plane)의 열전도도를 나타내지만[14] 기지의 절연특성으로 인해[5-7] 두께 방향의 열전도도는 매우 낮은 값을 나타내게 된다. 따라서 기지와 섬유의 서로 다른 열적 특성으로 인해 CFRP는 고유의 열적 이방성을 나타내게 된다. 이러한 고르지 못한 열전도 특성은 효과적이지 못한 방열 성능으로 이어지게 될 수 있다[8]. 이러한 문제는 나노 필러 형태의 탄소 나노 튜브[9,10], 그래핀[11], 금속 나노 입자[12] 등을 첨가한 hybrid composite 형태로 개선되어질 수 있지만 대다수의 접근 방식들은 실제 실험이 주를 이루기에 시간과 비용이 많이 소요되는 단점이 존재한다. 이러한 현실적 제약을 극복하고자 Kim 등[13]은 meta-heuristic algorithm 중 하나인 유전 알고리즘(Genetic Algorithm)을 이용하여 복합재의 열전도도 향상을 위한 최적 구조 설계를 수행한 바 있다. 최근에는 AI와 머신러닝의 학습을 통한 접근 방식[14]으로 앞선 단점들의 극복과 실패에 대한 리스크의 최소화를 구현할 수 있지만 실제 해결하고자 하는 문제의 대다수는 그 복잡성에 의한 여러 로컬 최소값과 안장점의 존재로 인해 기존 알고리즘을 통한 효율적인 최적값 수렴이 어렵다[15]. 특히 변수가 다양 해질수록 경우의 수는 기하급수적으로 증가하게 되는데, 해당 대규모 전역 영역에서의 최적값 도출에 있어 양자 컴퓨터는 앞서 제시된 제약을 극복하기 좋은 전략이 될 수 있다[15-17]. 현재 양자 컴퓨터는 양자 논리 게이트(Quantum logical gate)와 양자 어닐링(Quantum Annealing, QA)으로 분류되며 조합 최적화에 특화되어 있는 양자 어닐러가 가장 빠르게 상용화되어 있는 상태이다[18]. 이러한 양자 어닐러를 통한 QA를 수행하기 위해서는 먼저 조합 최적화에 해당하는 문제가 정의되어야 하며, 양자 어닐러에 임베딩하기 위해서는 정의된 문제의 목적함수를 Quadratic Unconstrained Binary Optimization (QUBO) 형태나 Ising model 형태 중 하나로 공식화되어야 한다[19,20]. 따라서 공식화 과정이 QA의 핵심이라 할 수 있다. Imanaka 등[21]은 방열판 복합재의 혼합비에 따른 높은 방열성, 부착성, 경량화를 만족하는 조합 최적화를 수행하였다. 이를 위해 열전도도, 열팽창계수 및 비중을 QUBO형태로 공식화하였다. 공식화된 목적 함수는 QA와 호환이 가능하지만 해당 연구에서는 Fujitsu Digital Annealer(DA)를 통해 최적화가 수행되었다. 조합 후보로 선정된 10개 재료에 대한 총 변수 1024개의 조합 최적화는 10초 이내에 빠른 최적값 도출을 나타내었으며 도출된 조합은 혼합물 법칙을 통해 해당 복합재료의 특성 검증이 이루어졌다.
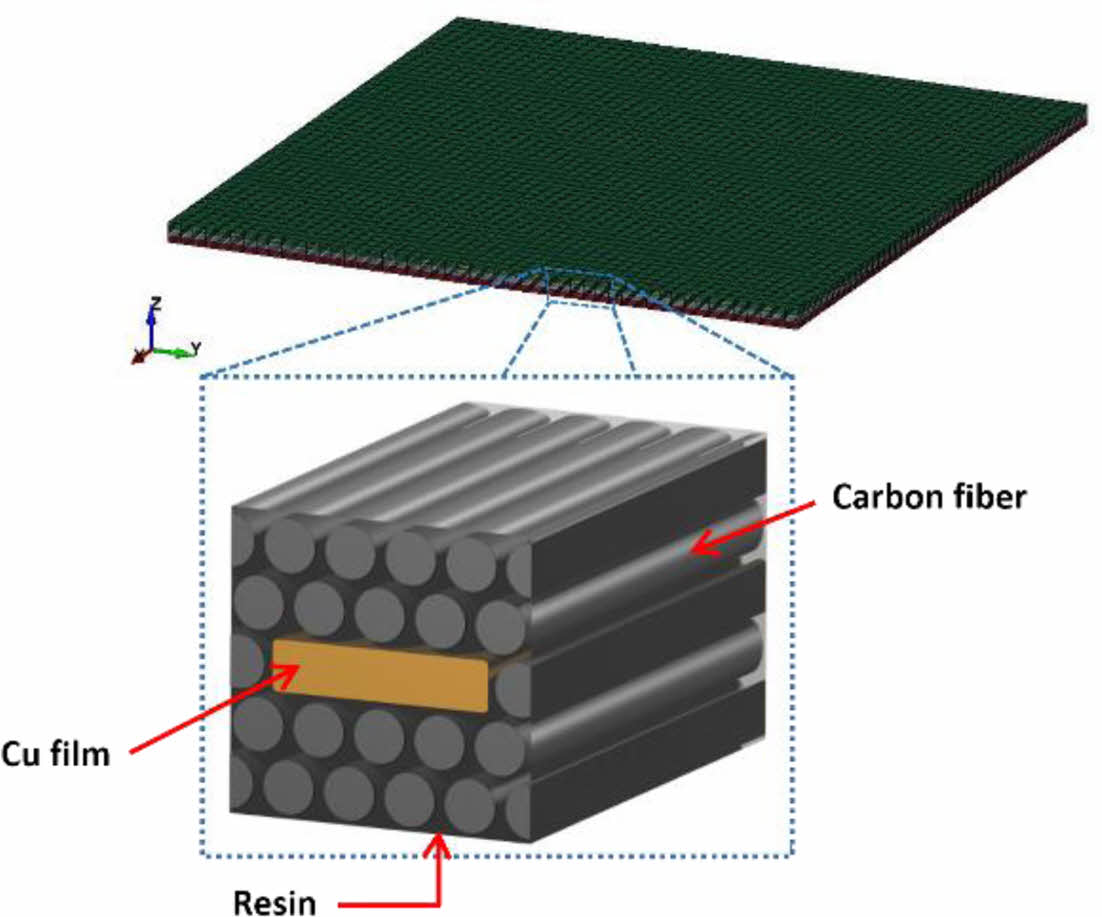
본 연구에서는 Fig. 1에서와 같이 제한된 개수의 얇은 구리 필름(Cu film)이 배치된 CFRP 기반 hybrid composite(Cu film CFRP)이 제안되었으며 이를 통해 최적의 두께 방향 열전도도를 나타낼 수 있는 Cu film의 배치를 QA를 통해 효율적으로 도출하고자 한다. 먼저 열전도도의 도출을 위해 Laser Flash Analysis(LFA) 방식이 유한요소해석(Finite Element Analysis, FEA)으로 구축 및 적용되었으며 QA를 위한 문제 정의를 위해 Cu film 배치 조건과 투입될 각 ply의 적층 순서간 상관관계 분석 이루어졌다. 해당 상관관계 결과를 바탕으로 조합 최적화 문제 정의가 수행되었으며 Cu film CFRP의 과도한 무게 증가를 제한하기 위한 Cu film 배치 제약이 적용된 목적함수가 공식화되었다. 이렇게 공식화된 목적함수는 양자 컴퓨터에 임베딩됨으로써 QA를 통한 조합 최적화가 이루어졌으며 도출된 Cu film의 최적배치 조합은 FEA를 통해 pure CFRP 대비 향상된 두께 방향 열전도도의 비교 분석으로 진행되었다.

2.1 두께 방향 열전도도 도출을 위한 FEA
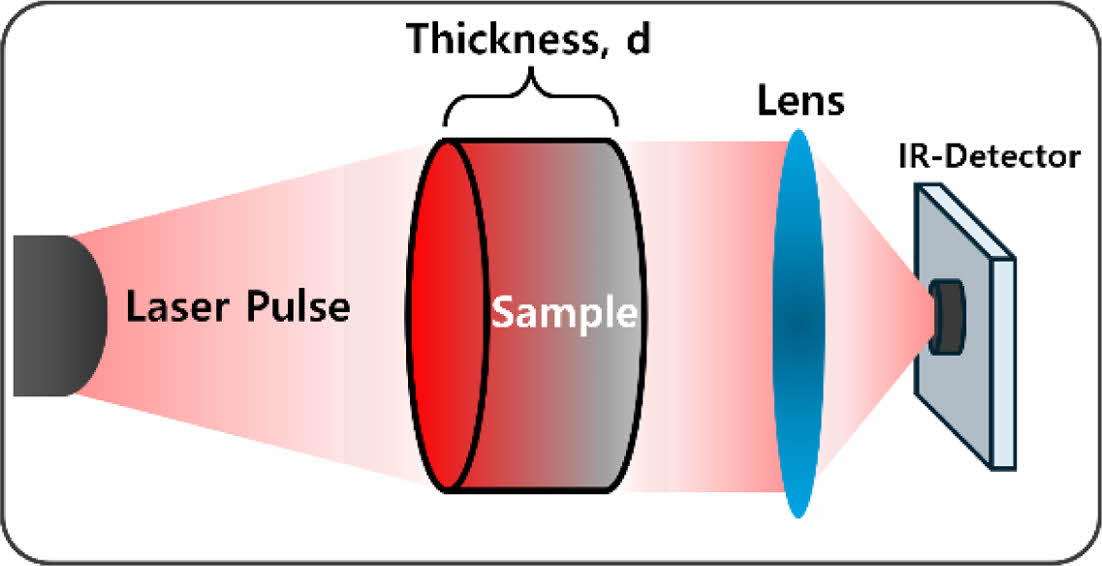
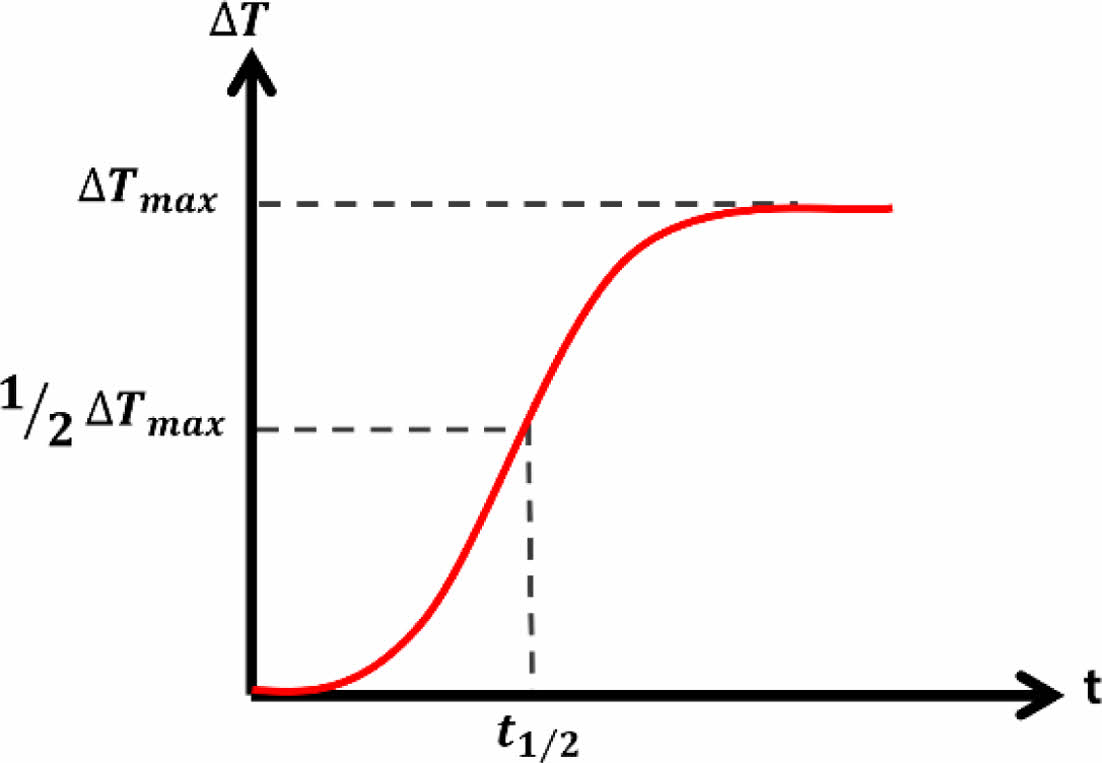
Cu film CFRP의 두께 방향 열전도도 도출을 위한 방식으로 Transient method 중 하나인 LFA 방식이 적용되었다. 측정 과정은 ASTM-E1461[22]에 따라 Fig. 2에서와 같이 시편에 laser pulse를 가하여 반대편의 온도 변화(∆T) 검출이 이뤄지게 된다. 측정된 ∆T는 Fig. 3과 같은 시간에 따른 온도변화 그래프로 나타나며 시편 두께에 따른 열확산도 계산을 거쳐 열전도도가 도출되는 방식이다. 이상적인 단열의 경우 열확산도는 식 (1)에 의해 계산된다[23].



여기서 α는 열확산도, 0.1388은 heating zone과 detector의 최대 온도차의 50%(1/2∆T_max)에 해당하는 상수, d는 시편의 두께, t_1/2은 1/2∆T_max까지의 도달 시간을 나타낸다.
도출된 열확산도는 최종 식 (2)를 통해 열전도도로 계산되어진다.



여기서 λ는 열전도도, ρ는 시편의 밀도, C_p는 시편의 비열을 나타낸다.
이러한 LFA 방식은 시편 가열 시간이 짧고 시편의 크기가 다른 열전도도 측정법에 비해 상대적으로 작다는 장점이 존재한다[24]. 이는 해석 시간 단축에 용이하게 작용될 수 있다.
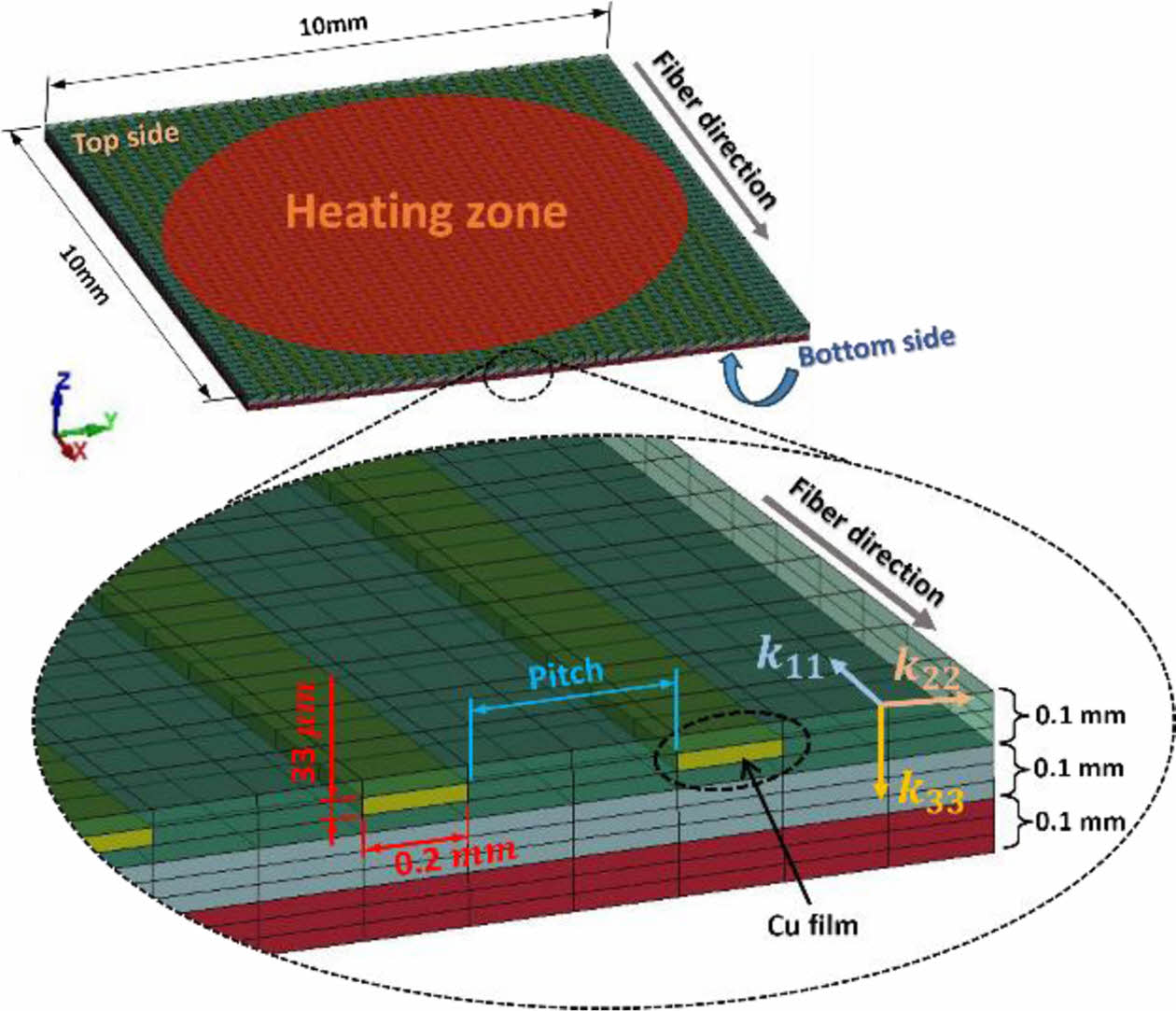
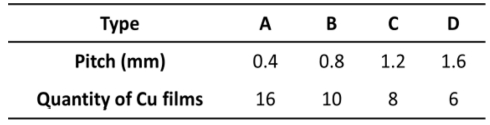
LFA를 구현한 FEA 모델은 LS-DYNA를 통해 구축되었으며 Fig. 4과 같다. 시편의 형상은 가로, 세로 10 mm의 정사각형이며 요소의 총 개수는 7,500개이다. CFRP의 각 ply 두께는 0.1 mm이고 Uni-direction(UD) type에 [0]_3T의 조건으로 구현되었으며 Bottom side에서 Top side 방향으로 1,2,3순의 ply 번호가 할당되게 된다. CFRP의 열적 이방성은 In-plane에서의 열전도도인 섬유방향 k₁₁과 섬유의 횡방향 k₂₂ 그리고 두께방향 k₃₃으로 정의될 수 있으며, MAT-021_ ORTHOTROPIC_THERMAL을 통해 구현되었다. Cu film의 형상은 폭 0.2 mm, 두께 33 mm이며 길이는 CFRP와 동일한 10 mm이다. Cu film은 구리로 구성되어 있으므로 T01-THERMAL_ISOTROPIC을 통해 열적 등방성이 구현되었다. Cu film의 경우 배치되는 개수가 사이 간격을 나타내는 Pitch를 통해 결정되며 배치는 Fig. 4에서와 같이 ply 두께의 1/2 위치에 적용되게 된다. 또한 Cu film은 CFRP의 섬유 방향과 일치하도록 배치되게 된다. 배치되는 경우는 Table 1에서와 같이 총 4가지 type에 한해서 배치되어질 수 있다. Laser pulse에 의한 heating zone은 Top side 면적의 70%에 10 ms동안 20 mW/mm²의 heat flux가 투입되며 반대편인 Bottom side에서 Fig. 3에서와 같은 시간에 따른 온도변화 그래프가 도출되게 된다. 그 외 측면은 모두 단열로 설정되었으며 Top side와 Bottom side의 경우 대류와 복사에 의한 열전달은 고려되지 않는다.
2.2 Thermal properties
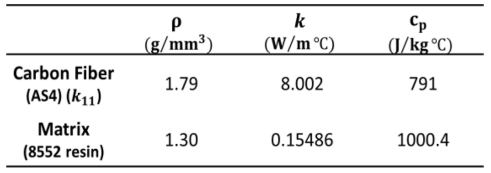
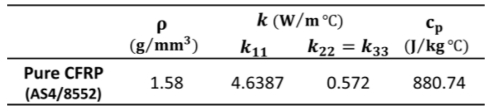
CFRP는 섬유 부피분율에 따라 그 열전도도가 다르게 나타난다. 따라서 FE 모델에 적용될 CFRP의 열적 특성은 혼합물 법칙을 통해 섬유와 기지 각각의 고유 열적 특성이 적용되어 도출되었다. 섬유와 기지는 각각 AS4와 8552 resin의 열적 특성이 적용되었으며 그 특성은 Table 2와 같다[25]. CFRP의 전체 밀도(ρc)는 식 (3)을 통해 계산되게 된다.



여기서 ρ_f 와 ρ_m은 각각 섬유와 기지의 밀도를 의미하고 u_f 와 u_m은 섬유와 기지의 부피분율을 나타내며 u_f = 0.514이고 u_m = (1 - u_f )에 의해 0.4286으로 적용되었다. Fig. 4에서 정의된 CFRP의 열전도도 k₁₁, k₂₂, k₃₃은 D.J Radcliffe 등[26]의 이론적 수식인 식 (4)와 식 (5)를 통해 도출될 수 있으며 k₁₁의 경우 식 (4)를 통해 계산되어진다.



여기서 k_f와 k_m은 각각 섬유와 기지의 열전도도를 의미한다. k₂₂와 k₃₃의 경우 UD 형태의 CFRP에서 각 열전도도는 서로 동일하다고 가정할 수 있으며[27] 이를 식 (5)와 같이 나타낼 수 있다.



여기서 ε은 경험적 비례 계수이며 본 연구에서는 AS4/8552의 두께 방향 열전도도인 k₃₃의 실제 측정 결과[25]에 근거하여 그 평균 오차율 0.132%를 만족하는 e인 8.109가 적용되었다.
비열(c_p)의 경우 식 (6)을 통해 나타낼 수 있게 된다[28].



여기서 c_f 와 c_m은 각각 섬유와 기지의 비열을 나타낸다. 따라서 위 혼합물 법칙 수식들을 통해 도출된 pure CFRP의 열적 특성은 Table 3과 같다.
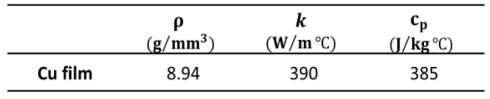
Cu film의 경우 열적 등방성을 만족하므로 Table 4와 같은 열적 특성이 적용되었다[29].
2.3 Ply별 Cu film 배치에 따른 상관관계 분석
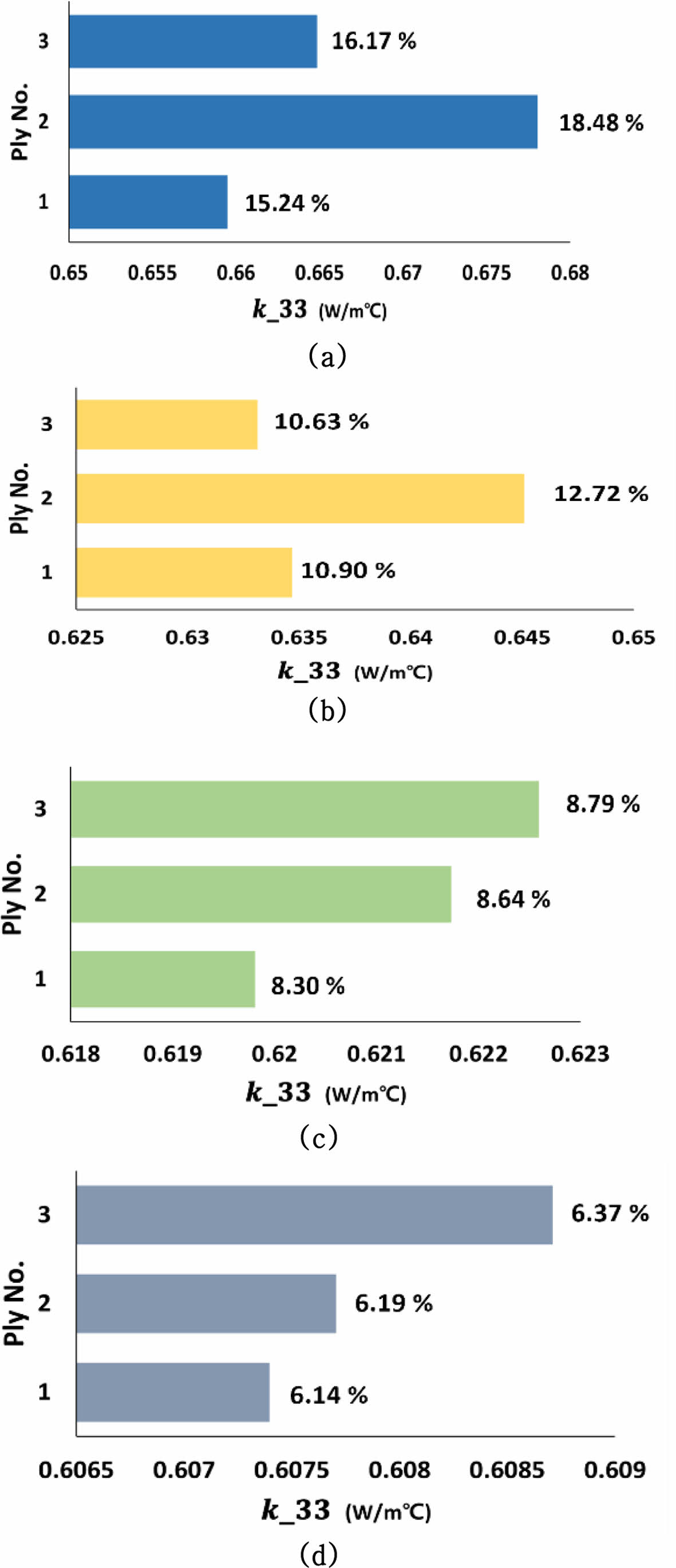
QA 적용을 위한 문제 정의와 공식화 수행을 위해 Cu film이 배치된 ply의 적층 순서에 따른 k₃₃간 상관관계 분석이 선행되었다. 적용된 Cu film은 Table 1의 총 4가지 type이 각각 적용되었고 Cu film이 배치된 각각의 Cu film CFRP는 pure CFRP(k₃₃=0.572 W/m^oC)와의 비교를 통해 k₃₃의 증가율로 나타내었다. Fig. 5(a)는 1에서 3번 ply에 Type-A가 각각 배치되었을 때의 결과를 나타내며 2번 ply에서 18.48% (0.659 W/m^oC), 3번 ply에서 16.17% (0.665 W/m^oC), 1번 ply에서 15.24% (0.659 W/m^oC)로 도출되었다. Type-A는 Cu film의 투입량이 가장 많으며 배치 간격이 매우 조밀하다. 이는 열 확산에 있어 매우 유리하며 곧 열전도도의 증가로 나타나게 된다. 따라서 heating zone인 3번 ply와 1번 ply 사이에서 효율적으로 열전달이 가능한 2번 ply에서의 k₃₃가 최대로 나타나게 된 것으로 사료되어진다. Fig. 5(b)는 Type-B에 해당하며 2번 ply에서 12.72% (0.645 W/m^oC), 1번 ply에서 10.90% (0.635 W/m^oC), 3번 ply에서 10.63% (0.633 W/m^oC) 순으로 증가율이 도출되었다. Type-B 역시 Type-A와 같이 2번 ply에서의 k₃₃ 증가율이 가장 크게 나타났으며 오히려 1번 ply에서의 k₃₃가 그 다음으로 크게 도출되었다. Fig. 5(c)의 경우 Type-C에 해당하며 3번 ply에서 8.79% (0.622 W/m^oC), 2번 ply에서 8.64% (0.621 W/m\degc), 1번 ply에서 8.30% (0.619 W/m^oC)의 증가 경향을 보였다. Fig. 5(d)의 Type-D 역시 3번 ply에서 6.37% (0.609 W/m^oC), 2번 ply에서 6.19% (0.608 W/m^oC), 1번 ply에서 6.14% (0.607 W/m^oC)로 Type-C와 유사한 증가 추세를 나타내었다. Type-C와 Type-D의 경우 Cu film의 배치 간격이 Type-A와 B에 비해 크며 투입량 역시 적다. 이로 인해 ply의 층간 열확산이 느리게 작용한 결과로 보이며 Type-A와 B에 비해 열에 민감한 반응을 나타내지 못한 것으로 이해할 수 있다. 따라서 heating zone에 가까워질수록 k₃₃가 점점 증가하는 추세를 나타낸 것으로 사료되어진다.

3.1 조합 최적화 문제 정의
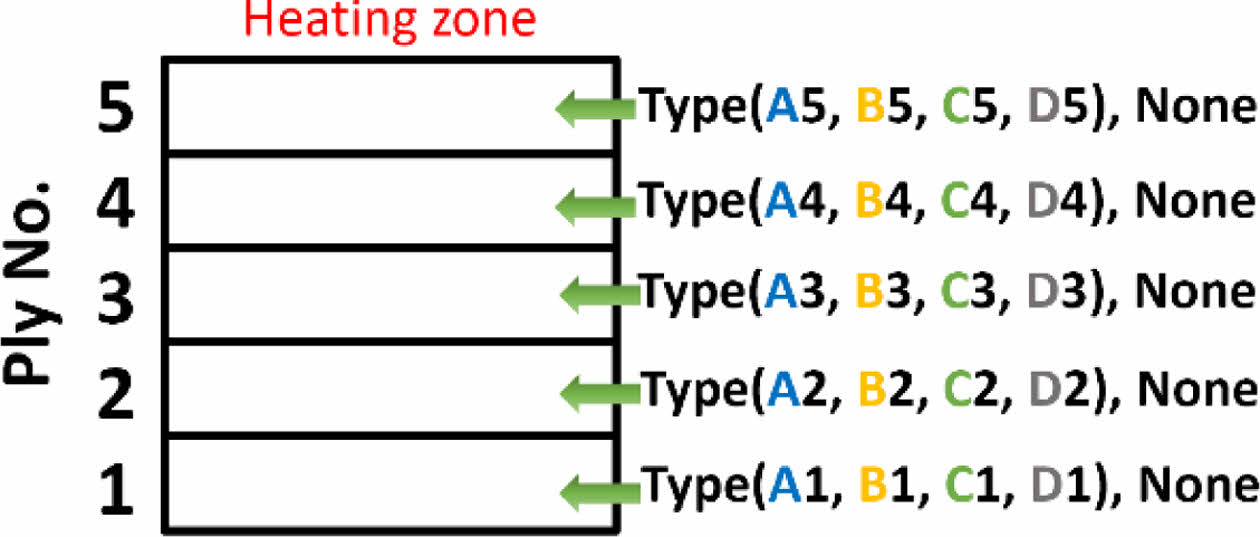
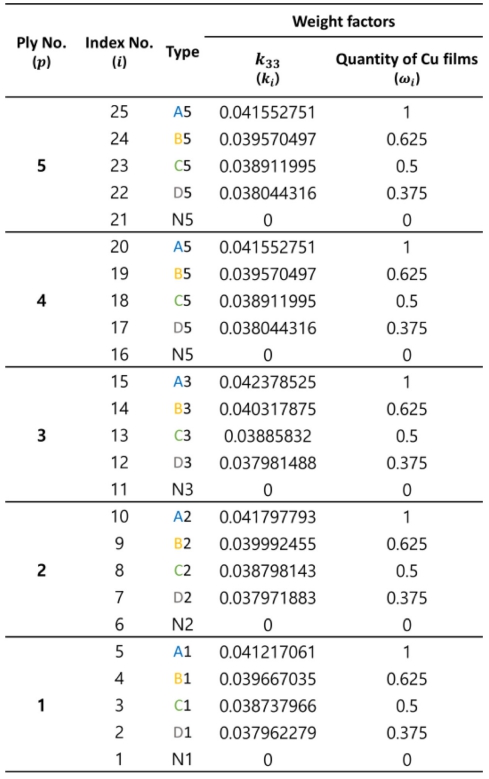
본 조합 최적화 문제는 Cu film CFRP의 ply수 확장([0]_3T→[0]_5T)을 통해 해결하고자 하는 조합 최적화 문제의 복잡성을 증가시켜 정의되었다. 총 5개의 ply에 개별적으로 적용되어질 수 있는 조합 후보들은 Cu film의 Type-A부터 Type-D와 아무것도 투입이 안된 상태인 None을 포함하여 총 5가지이고 Fig. 6와 같이 총 25가지의 조합 후보들로 구성되었으며 전체 가용 조합의 수는 5⁵=3,125이다. ply 수가 확장됨에 따라 각 Type별 Cu film의 각기 다른 k₃₃ 증가율 표현은 Fig. 5의 결과를 바탕으로 각 ply 사이 k₃₃를 선형보간 하여 유도되었으며, 조합 후보간 각 ply에서의 k₃₃ 우세함을 나타낼 수 있는 가중치(k_i)로 적용되게 된다. 각 ply에서의 k₃₃와 Cu film 배치 수량 간 데이터 일관성을 위한 정규화(Normalization)가 수행되었으며 전체 조합 후보들은 Table 5와 같이 나타낼 수 있다. 이러한 조합 후보들을 갖는 최적화 문제에는 전체 배치 가능한 Cu film의 무게제한을 두는 제약 조건이 부여되게 되며 이를 위해 Type별 Cu film의 배치 수량이 제약조건의 가중치(w_i)로 적용되게 된다. 또한 각 ply에서는 해당 ply 번호에 해당하는 Cu film이 중복으로 선정될 수 없도록 하는 제약조건이 추가로 적용되게 된다.
3.2 정의된 문제 공식화
QA는 목적함수로 시스템의 전체 에너지 함수(E(x))를 양자의 물리적 현상(superposition, entanglement, tunneling)을 이용해 최소값을 도출하는 과정이다. 이러한 에너지 함수는 Ising model과 QUBO로 표현될 수 있으며, Ising model의 경우 -1, 1인 spin 형태의 변수가 적용되고 QUBO의 경우 binary 형태인 0, 1의 변수가 적용된다. 위 문제 정의에서 각 ply에 할당될 Cu film 배치 조건은 배치가 안되었을 경우 0, 배치되었을 경우 1인 binary 형태로 표현될 수 있다. 따라서 binary 변수를 사용하는 QUBO 형태로 목적함수를 공식화할 수 있으며 식 (7)과 같다[30].



여기서 x_i와 x_j는 xi, xj ∈ {0,1}를 만족하는 binary 변수를 나타낸다. a_i는 linear coefficient를 의미하며 앞서 선정한 가중치가 해당 항에 적용되게 된다. b_ij는 quadratic coefficient를 의미하는데, 본 연구에서는 Cu film의 배치 유무를 나타내는 binary 변수항만 적용되기에 x_i만 사용된다. 이로 인해 QUBO형식이 선형계획법(linear programming)형식으로 정의될 수 있게 된다. 따라서 x_i항만이 사용되기에 b_ij항은 적용되지 않게 된다.
앞서 정의된 문제에 대한 목적함(E_k(k))는 아래 식 (8)과 같이 나타낼 수 있다.



여기서 i는 i∈{1,2,...,25}를 만족하며 Table 5의 Index No.를 의미한다. k_i는 i에 해당하는 k₃₃가 k로 적용되게 된다. 각 ply에 적용될 Cu film의 배치 조합은 최대가 되어야 하지만 QA에서는 에너지 함수가 최저인 바닥상태가 최적 솔루션으로 도출되므로 전체 수식에 -부호를 부여하여 최대값 도출이 이뤄지도록 적용되었다.
Cu film 무게 제한을 나타내는 제약조건은 식 (9)와 같이 나타낼 수 있다.



여기서 ω_i는 Table 5의 정규화 된 Cu film 투입 수량을 의미하며 W는 Cu film CFRP에 투입될 수 있는 전체 Cu film의 수량을 나타낸다.
각 ply에서 선정될 수 있는 Cu film 후보들은 총 5개를 만족해야 하며 각 ply에서의 binary 변수의 합이 1이 되는 것으로 표현될 수 있다. 따라서 해당 제약조건은 식 (10)과 같이 나타낼 수 있다.



여기서 p는 Table 5에서와 같이 각 ply의 번호를 의미하며 P∈{1,2,...,25}를 만족한다.
3.3 QA를 통한 조합 최적화 수행
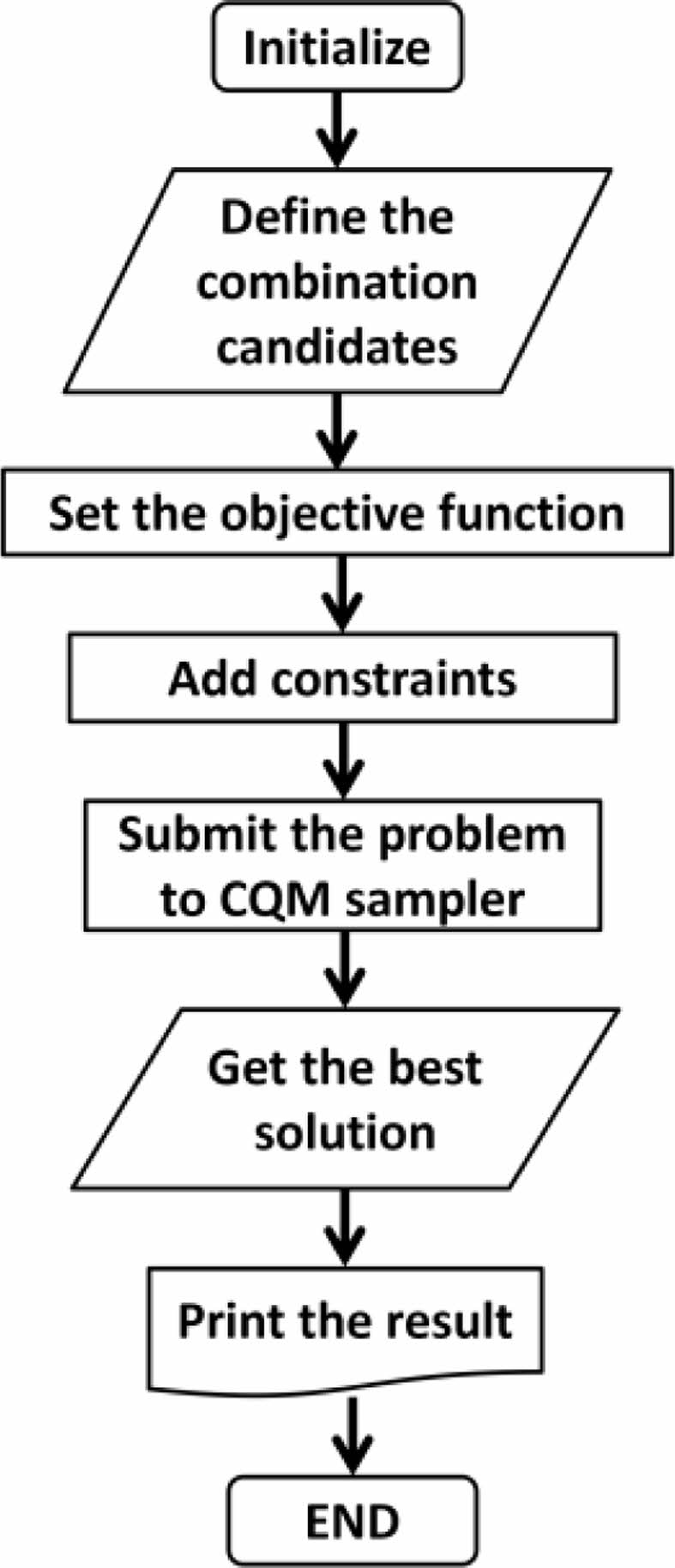
정의된 조합 최적화 문제로부터 공식화된 수식은 D-Wave에서 제공하는 python 기반 SDK(software development kit)인 Ocean의 dimod API(Application Programming Interface)를 통한 프로그래밍과 D-Wave Leap 양자 클라우드 서비스를 통한 양자 컴퓨터로의 임베딩 과정이 Fig. 7의 순서로 수행되었다. 정의된 문제는 제약조건이 포함되어 있으므로 초기 Initialize에서 CQM(constrained quadratic model) 선언을 통해 D-wave에서 제공하는 CQM sampler가 적용되었다. 조합 후보의 정의는 dictionary 형태로 입력되게 되며 각각의 dictionary 요소들은 binary항으로 표현되게 된다. 따라서 식(8)의 목적함수는 binary항으로 표현된 모든 조합후보와 k_i간 곱의 합으로 프로그래밍 되며, 식 (9)의 경우 목적함수와 동일하게 표현되나 배치가능한 Cu film의 최대 설정 개수 이하를 만족하도록 제약조건이 적용되게 된다. 본 연구에서는 6가지 경우(Cu film의 최대 배치 제한 개수: 24, 32, 40, 48, 56, 64)에 대해서만 수행되었다. 식 (10)의 경우는 정해진 index No.안에서 모든 binary항의 합이 1이 되도록 작성되었다. LeapHybridCQMSampler의 선언을 통해 sampler를 정의하고 작성된 목적함수와 제약조건들은 양자컴퓨터에 임베딩되어 최적화가 수행되게 되며 각 경우마다 5번씩 반복 수행되었다.

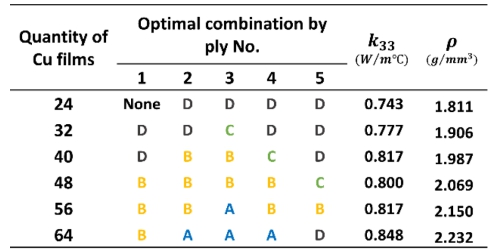
Cu film의 최대 배치 제한 개수로 선정된 6가지 경우에 대한 QA 결과를 통해 도출된 최적의 Cu film 배치 순서는 Table 6과 같이 도출되었다. 각 Quantity of Cu films는 제약조건으로 지정된 가용 배치 수량을 의미하며 도출된 최적 배치 조합은 ply 번호 순으로 나열되었다. 각 최적 조합들은 LFA 방식의 FEA를 통해 k₃₃가 계산되었으며, 밀도(r)는 각 최적 조합이 적용된 Cu film CFRP의 전체 밀도를 나타낸다. 도출된 각각의 최적 조합을 보면 배치될 수 있는 Cu film 수량이 많아질수록 배치 간격이 조밀한 Type 위주로 조합이 형성된 것을 볼 수 있으며, 반대로 수량이 적어질수록 조합이 단조롭게 구성되는 양상을 볼 수 있다. 이는 Cu film 수량 제한이 제약조건으로써 우세하게 작용한 결과로 사료되어진다.
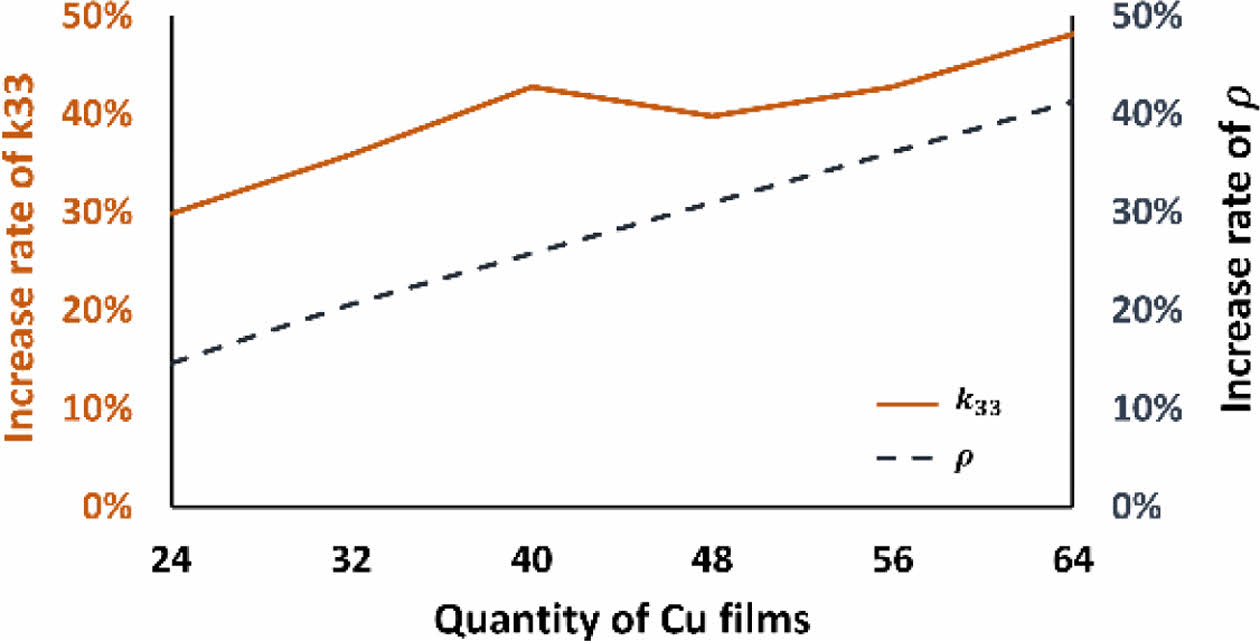
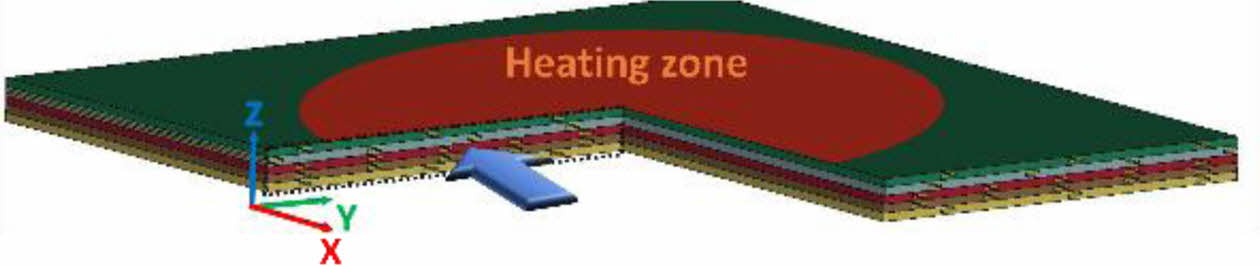
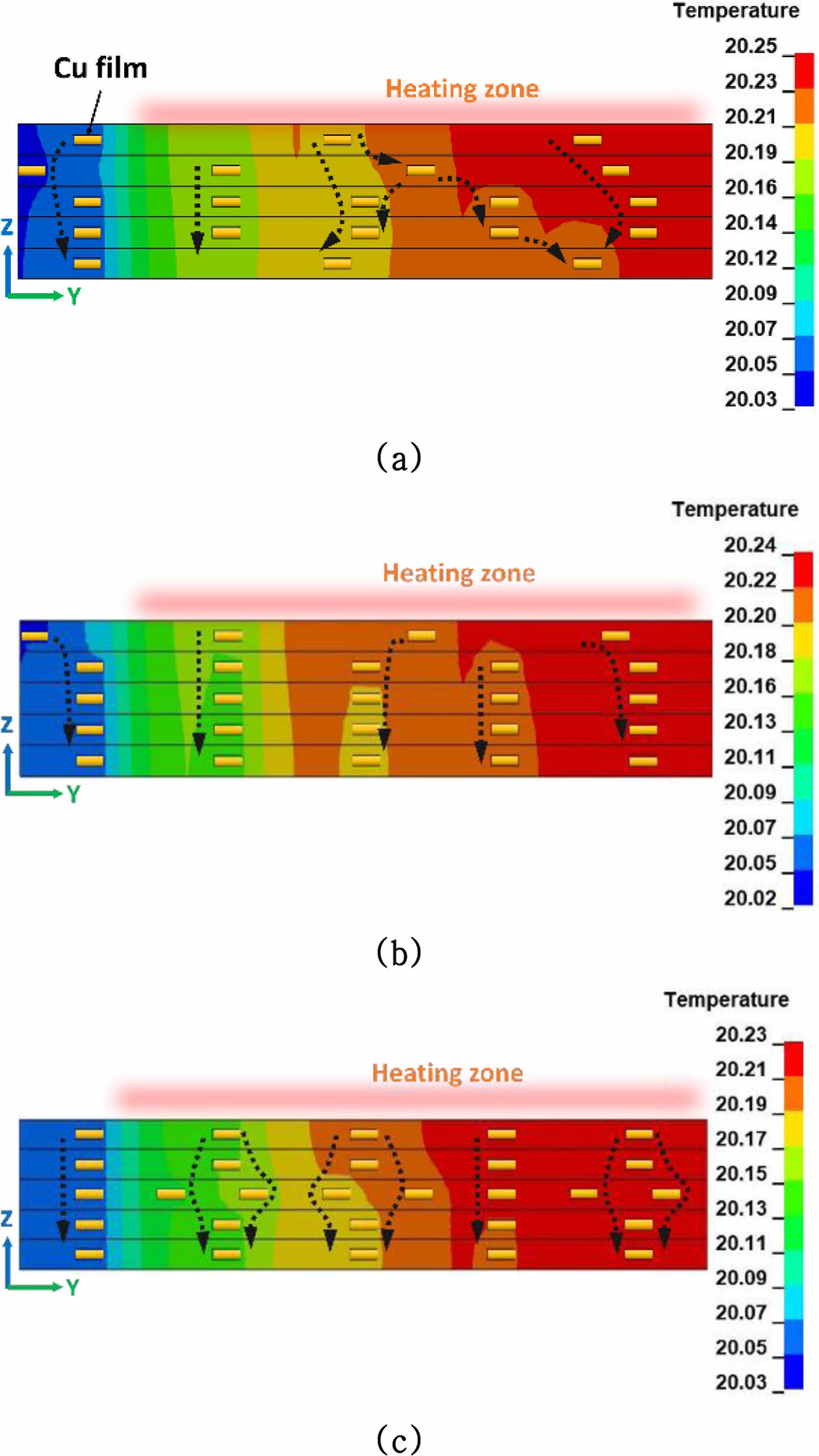
Fig. 8은 Table 6의 결과를 바탕으로 Cu film 배치 수량에 따른 pure CFRP 대비 k₃₃와 밀도의 증가율을 나타낸다. Cu film 수량이 증가함에 따라 Cu film CFRP의 밀도 역시 선형적으로 증가하는 것을 볼 수 있다. 하지만 k₃₃증가율의 경우 40개 다음으로 48개(0.800 W/m^oC)에서 감소되었다가 56개(0.817 W/m^oC)에서 다시 증가하는 결과를 보였다. 해당 수량(40, 48, 56개)에서의 두께 방향 열전달 상태를 나타내기 위해 Fig. 9에서 가리키는 단면 영역에서의 온도 분포 결과가 Fig. 10과 같이 도출되었다. 해당 결과는 Cu film CFRP의 Top과 Bottom side에서의 최대 온도차(DT_max)에 도달하였을 때의 온도 분포 결과이다. 각 온도 분포 결과는 특정 조합으로 형성된 Cu film 배치 패턴의 영향을 나타내며 곧 두께 방향으로의 열전도 경로(Heat conductive pathway)가 형성되었음을 보여준다. 여기서 Fig. 10(b)에서의 Cu film 배치는 Fig. 10(a)와 Fig. 10(c)에 비해 상대적으로 Y축 방향으로의 배치 자유도가 낮음을 알 수 있다. Cu film은 CFRP 대비 빠른 열전도가 가능하기에 서로 인접하게 배치될 수록 연쇄적인 열전도 과정이 유도될 수 있지만 Fig. 10(c)와 같은 경우 열전도 경로가 국부적으로 형성되어 Fig. 10(a)와 Fig. 10(b)에 비해 상대적으로 감소한 k₃₃ 증가율이 도출된 것으로 사료되어진다.

본 연구에서는 CFRP(UD, [0]_3T)의 k₃₃ 향상을 위해 제한된 개수의 얇은 Cu film이 배치된 Cu film CFRP가 제안되었으며, 한정된 배치 수량에 따른 최적의 Cu film 배치 조합 도출이 QA를 통해 수행되었다.
조합 최적화 문제 정의를 위해 CFRP의 ply 순서와 각 ply에 배치될 Cu film 개수간 상관관계 분석이 진행되었고 이러한 분석은 FEA를 통해 k₃₃를 도출함으로써 수행되었다. 이를 통해 [0]_5T로 확장된 CFRP에서의 k₃₃가 최대가 되는 Cu film 배치에 대한 조합 최적화 문제가 정의되었다. QA 적용을 위해 정의된 문제의 목적함수와 제약조건에 대한 공식화가 수행되었으며, 양자 컴퓨터에 공식화된 문제를 임베딩함으로써 QA를 통한 6가지 경우의 Cu film 배치에 대한 최적 조합이 도출되었다. 주요 결론은 다음과 같다.
Cu film의 배치 조건과 적층 순서에 따른 k₃₃의 증가량은 Cu film의 배치 간격이 좁을 수록 중간 ply에서 높게 나오며, 배치 간격이 넓을 수록 상부 ply에서 높게 도출되게 된다. 중간 ply의 Cu film 배치 간격이 좁은 경우 상부 ply에서 하부 ply로의 층간 열확산에 있어 효율적으로 작용될 수 있기에 k₃₃가 높게 도출된 것으로 사료된다. 반면 Cu film 배치 간격이 넓은 경우에는 간격 사이에 열전도도가 낮은 CFRP로 인해 중간과 하부 ply에서의 열확산이 더디게 발생하게 된다. 따라서 heating zone의 열을 바로 전도할 수 있는 상부 ply에서의 k₃₃가 높게 도출된 것으로 사료된다.
각 Cu film 최적 배치 조합은 Cu film 배치 수량이 많아질수록 배치간격이 조밀한 Type 위주로 형성되었으며, 수량이 적을수록 단조로운 구성의 조합이 형성되었다. 이는 Cu film의 수량 제한이 제약 조건으로 강하게 작용한 결과에 의한 것으로 사료된다.
Cu film의 조합을 통해 형성된 각 배치 패턴은 두께 방향으로의 고유 열전도 경로를 나타내었다. 이러한 열전도 경로의 형성은 Cu film의 횡방향 배치 자유도에 따라 다르게 나타나며 배치 자유도가 높을 수록 더욱 개선된 k₃₃가 도출될 수 있을 것으로 판단된다.
향후 연구에서는 섬유의 배향 조건까지 고려한다면 더욱 다양한 조합에 의한 개선된 k₃₃ 결과를 도출할 수 있을 것으로 사료되며 이러한 연구 결과는 향후 hybrid composite의 열 관리 성능을 개선하는데 기여할 수 있을 것으로 기대된다.

본 논문은 한국 정부(MSIT)의 재원으로 국가과학기술연구회(NST)의 지원을 받아 수행되었습니다(CRC23011-210). 또한 이 논문은 2023년도 정부(과학기술정보통신부)의 재원으로 한국연구재단 양자정보과학 연구개발생태계 조성사업의 지원을 받아 수행된 연구임(2020M3H3A1110365).