In this study, a molecular dynamics simulation study was performed to investigate the size-dependent electroelastic properties of single-walled boron nitride nanotubes(BNNT). To describe the elasticity and polarization of BNNT under mechanical loading, the Tersoff potential model and rigid ion approximation were adopted. For the prediction of piezoelectric constants and Young’s modulus of BNNTs, piezoelectric constitutive equations based on the Maxwell's equation were used to calculate the strain-electric displacement and strain-stress relationships. It was found that the piezoelectric constants of BNNTs gradually decreases as the radius of the tubes increases showing a non-negligible size effect. On the other hand, the elastic constants of the BNNTs showed opposites trends according to the equivalent geometrical assumption of the tubular structures. To establish the structure-property relationships, localized configurational change of the primarily bonded B-N bonded topology was investigated in detail to elucidate the BNNT curvature dependent elasticity

본 연구에서는 분자동역학 전산모사를 통해 육방정계 단일벽 질화붕소 나노튜브(BNNT)의 반경 변화에 따른 압전탄성 변화를 규명하였다. 질화붕소의 거동을 비교적 잘 모사하는 Tersoff 포텐셜과 기계적 하중인가에 따른 질소 및 붕소원자의 상대변위로 인한 분극의 정량화를 위해 강체 이온 근사를 채택하였다. 선형 압전탄성 구성방정식을 기반으로 각각의 질화붕소에 변형률을 인가하고 이에 따른 전기적 변위와 응력을 산출하여 압전상수와 영률을 각각 예측하였다. 그 결과, BNNT의 압전상수는 반경이 증가함에 따라 점진적으로 감소하는 양상을 보였다. 반면 탄성계수의 경우 불연속적 구조를 가지는 질화붕소를 등가의 연속체 구조로 등가시키는 방법에 따라 증가 또는 감소하는 경향을 보였다. BNNT의 곡률변화에 따른 물성변화를 가상실험에 기반한 경험적 모델로 근사하기 위해 BNNT의 튜브반경-압전탄성물성 간 상관관계식을 제안하였다. 또한 BNNT의 반경변화에 따른 물성을 곡률의 관점에서 설명하기 위해, BNNT와 질화붕소 나노시트(BNNS)의 결합에너지와 탄성변형에 따른 원자간 결합길이 변화가 각각의 구조의 변형에너지 증가에 기여하는 정도를 상호 비교하였다

Keywords: 압전(Piezoelectric), 나노전자(Nanoelectronics), 질화붕소 나노튜브(Boron Nitride Nanotube), 분자동역학 전산모사(Molecular dynamics simulation)

21세기를 기점으로 비약적으로 발달한 소재경량화 기술과 저차원 나노물질 설계기술은 고분자 기반 소재의 적용을 통한 전자기기들의 경박단소화를 가속화시키고 있다. 최근 착용 가능한(Wearable) 기기를 넘어 신체에 부착하거나(Attatchable) 신체 내부에 직접 삽입이 가능한(Implantible) 기기에 관한 연구가 활발히 진행됨에 따라, 다양한 요구조건을 동시에 만족시킬 수 있는 저차원 나노재료 기반 다기능성 나노복합재에 대한 수요가 크게 증가하고 있다[1,2]. 1994년 이론적으로 먼저 설계된 이후 1995년 실험적으로 합성된 바 있는 질화붕소 나노튜브(BNNT)는 이러한 다기능성재료 분야에서 주목받고 있는 저차원 구조체로서, 탄소나노튜브(CNT)와 유사한 구조를 가져 뛰어난 기계적 물성을 지님과 동시에[3] 질소와 붕소 원자들의 비중심대칭(Non-centrosymmetric) 구조에 따른 분극현상을 통해 압전성을 띄게된다[4]. 뿐만 아니라 CNT보다 뛰어난 열적/화학적 안정성[5]과 높은 열전도 특성[6], 낮은 신체 유독성[7] 및 뛰어난 중성자 차폐능[8]은 BNNT가 다기능성 나노필러로서의 무궁무진한 가능성을 제시하고 있다. 특히 고분자 기지내에 분산된 나노복합재로 응용될 경우, 박막, 직물, 적층 구조 등의 유연한 나노 구조 설계에 있어 기존 3차원 세라믹 압전재료의 유연성한계를 극복할 수 있는 대안으로 자리매김할 것으로 전망된다[9,10].
그러나 고순도 BNNT 생산의 기술적 어려움을 비롯하여 수지 내 분산문제, 생산단가, 물성측정기술의 한계 등 이상적인 다기능성 나노복합재 제조에 있어 여전히 극복해야할 기술적 한계가 존재하기 때문에[11], BNNT 상용화를 위한 선결과제인 구조-물성-환경-성능 상관관계의 정립을 위해서는 인실리코 해석을 통한 재료물성 예측 연구가 필수적으로 뒷받침되어야 한다. 인실리코 해석을 통한 재료의 전기기계적 물성 예측은 주로 밀도범함수 이론을 통해 진행되어왔다. 밀도범함수 이론 계산은 제일원리 계산이기 때문에 실험적 측정이 어려운 극한스케일 거동에 대한 정확한 값을 제공할 수 있으나, 전자구조의 최적화와 이에 따른 원자 간 상호작용을 일일히 계산해야 하기 때문에 고려할 수 있는 시스템의 크기에 있어 여전히 많은 제약이 따른다. 이러한 문제를 돌파하기 위해 최근에는 분자동역학 전산모사를 적용하여 BNNT와 같은 나노구조체 및 고분자복합재의 압전상수와 유전상수를 예측한 사례들이 보고되고 있으며[12], 해석 모델과의 연계를 통해 다중 스케일에서의 이론적 계산과 연계하는 멀티스케일 모델링 또한 다양하게 시도되고 있다[13-16].
BNNT의 압전탄성에 대한 분자동역학 전산모사 연구는 다수의 문헌이 보고되어 왔으나[12-14], 아직까지 압전탄성 거동 모사를 위한 최적화 된 포텐셜 파라메터의 제시나 나노구조-압전물성 간 상관관계에 대한 충분한 이해는 여전히 부족한 상태이다[12]. 특히 나노재료의 경우 열/기계/전기 및 이들이 연성화 된 상사거동문제에 있어 나노구조체의 크기에 따른 물성변화가 나타나게 된다[21]. 따라서 본 연구에서는 질화붕소 나노튜브(BNNT)와 나노시트(BNNS)의 압전탄성 물성을 분자동역학 전산모사를 통해 예측하기위한 최적의 포텐셜 파라메터 셋을 도출하고, 나노튜브의 대표적인 구조적 특성인 키랄성(chirality)이 압전탄성 물성에 미치는 영향을 규명하였다. 또한 곡률에 따른 BNNT 압전탄성변화를 반경에 대한 근사식으로 제시하였으며, 이러한 크기효과를 튜브형상에 따른 곡률과 연계하여 이해하기 위해 하중인가에 따른 원자간 결합길이와 결합각 변화가 BNNT와 BNNS의 내부응력 변화에 기여하는 정도를 정량적으로 비교하였다.

2.1 분자 모델링 및 포텐셜 파라메터
BNNT의 분자모델링은 상용 분자동역학 해석 프로그램인 Material Studio 2018을 사용하였으며[22], 에너지 최소화 과정과 열탄성거동 예측을 위한 앙상블 전산모사는 Sandia National Lab에서 배포하는 비상용 소프트웨어 프로그램인 Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS)를 이용하여 진행하였다[23]. BNNT의 크기변화에 따른 압전물성 예측을 위해 나노튜브의 키랄 벡터의 간격을 (5,0)에서부터 (80,0)까지 다양화하였으며, 키랄 벡터에 따른 BNNT의 반경은 Table 1에 요약되어 있다. BNNT의 압전성은 지그재그 구조에서만 나타난다고 알려져 있으며, 이에 따라 의자형구조에 해당하는 키랄 벡터는 고려되지 않았다[4]. BNNT의 길이효과를 배제하기 위해 튜브의 길이방향으로는 주기경계조건을 적용하였으며, 튜브의 원주방향으로는 하중인가에 따른 자유로운 포아송수축 및 팽창이 가능하도록 자유표면 조건을 적용하였다. 비교군으로 사용된 질화붕소 나노시트(BNNS)는 10 nm × 10 nm 크기로 모델링하였으며, 주기경계조건을 면내 방향으로만 적용하여 자유단효과가 완전히 배제된 단일층 나노시트의 거동이 모사되도록 하였다.
원자간 포텐셜은 질화붕소의 거동을 묘사하기 위해 가장 많이 적용되어 온 Tersoff 포텐셜을 채택하였다[18]. Tersoff 포텐셜은 질화붕소의 다양한 구조에 대해 기계적 물성, 열전도계수 등에 대해 다양하게 변형되어 왔지만, 질화붕소의 압전탄성적 거동을 묘사하기 위한 가장 최적화 된 파라메터 조합에 대해서는 여전히 경험적인 결과들만이 발표된 상태이다. 따라서 본 연구에서는 질화붕소 나노구조체에의 거동묘사를 위해 적용되어 온 Tersoff 포텐셜 파라메터 중 가장 대표적인 다섯 개의 파라메터 셋을 이용하여 압전 상수와 영률을 도출한 이후 이를 제일원리 계산과 비교하는 과정을 통해 가장 최적의 파라메터 셋을 도출하는 작업을 우선적으로 수행하였다. 그 결과 Ju 등에 의해 제시된 파라메터 셋이 BNNT와 BNNS의 압전 상수와 영률을 상대적으로 정확히 예측하는 것을 확인하였다. 이에 대한 보다 자세한 내용은 참고문헌[12]의 첨부자료와 본문의 내용을 통해 확인할 수 있다.
2.2 Maxwell 방정식 기반 정압전 구성방정식
BNNT의 압전상수와 영률을 예측하기 위한 정압전 전산모사의 경계조건은 Maxwell 방정식을 기반으로 유도되는 선형 압전 구성 방정식과 훅의 법칙(Hook’s law)의 연성을 통해 모사할 수 있으며, 다음과 같다[12].



여기서 σ_ij, C_ijkl, 그리고 e_kl는 각각 응력텐서, 강성행렬 텐서, 그리고 변형률 텐서이다. 또한 E_l와 D_i는 각각 BNNT에 가해지는 외부 전기장과 전기적 변위이며, e_lij와 k_ij는 각각 BNNT의 압전상수와 유전율을 의미한다. 해당 수식을 변형률-응력, 변형률-분극 관계식으로 정리하면 아래의 수식 (2), (3)과 같으며,



여기서 하첨자 E는 외부 전기장을 제한한 조건을 의미한다. 본 연구에서는 수식 (2)와 (3)을 기반으로 하여 BNNT의 길이방향에 대한 기계적 변형률 인가에 따른 튜브 내부 응력변화와 분극 변화 변화를 통해 BNNT의 영률과 압전상수를 계산하는 정압전법을 적용하였다.
정압전 구성방정식을 기반으로 BNNT의 압전상수와 탄성계수를 분자동역학 전산모사를 통해 예측하기에 앞서, Table 1에 제시된 모든 BNNT 구조에 대해 켤레구배법(Conjugate gradient)을 활용한 에너지 최소화를 진행하였다. 이후 Nosé-Hoover의 확장된 해밀토니안 법을 이용한 등온등압(NPT) 앙상블 전산모사를 통해 상온/대기압 조건에서의 구조 평형화(equilibrium)를 수행하였다. 또한 압전탄성 거동에 미치는 온도의 영향을 최소화하기 위해 1K 조건에서 정준(NVT) 앙상블 전산모사를 3 나노초(ns) 동안 진행하였다.
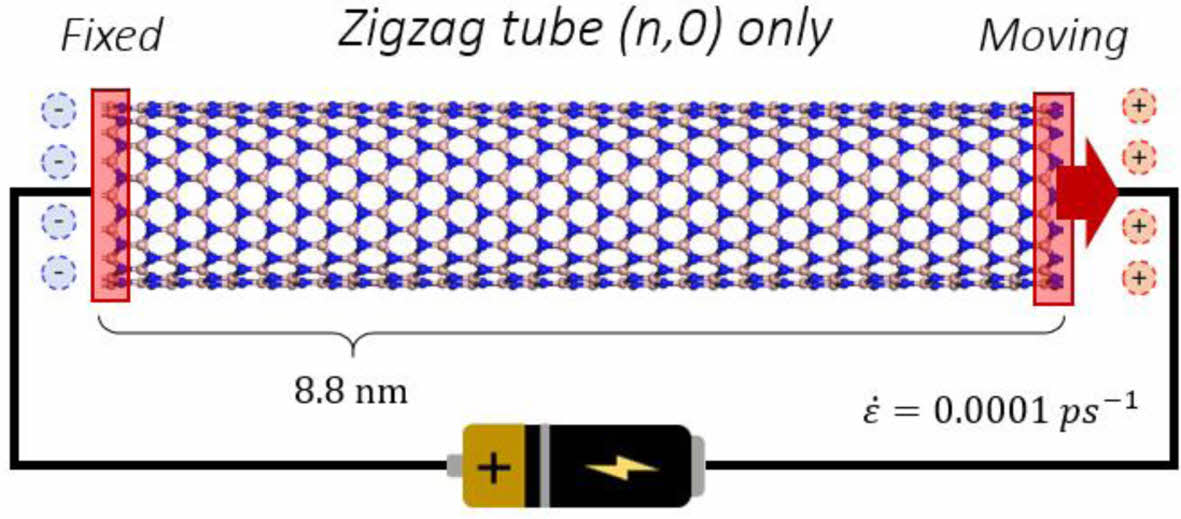
구조 평형화를 진행한 이후, BNNT에 1축인장을 부과하기 위해 Fig. 1과 같이 변위경계조건을 설정하여 정압전 전산모사를 진행하였다. 1축인장 전산모사는 0.0001/psec 의 진변형율 속도(true strain rate)로 진행하였으며, 진변형률이 2%에 이를때까지의 응력과 분극 값을 산출하여 BNNT의 영률과 압전상수를 계산하였다. 각각의 변형률 단계의 응력은 비리얼(virial)이론[19]을 바탕으로 도출하였으며, 분극은 전자-코어에 의한 분극 항을 제외하고 이온 분극 항만을 고려하여 다음과 같은 수식을 통해 계산하였다[12].



여기서 x₃ ⁱ, q_i, V는 각각 원자의 좌표와 전하량, 그리고 BNNT의 부피를 의미한다. 본 연구에서는 강체 이온 근사(rigid ion approximation)를 사용하였으며, 하중 인가 시 붕소와 질소 원자의 변위에 의해 발생하는 유효 분극을 묘사하기 위해 제일원리 계산으로 산출된 Born 유효 전하량(Born effective charge)을 사용하였다[20]. Born 유효 전하량의 경우 나노튜브의 키랄 벡터에 따라 변화하는 것으로 선행연구에서 보고된 바 있으며[20], 이에 따라 본 연구에서는 기존에 제시된 Born 유효전하를 BNNT의 반경에 대한 함수로 최소자승 근사하여 분극계산에 적용하였다. Born 유효전하 근사한 모델의 잔여값(residual) R²는 0.9953로 산출되었으며, 최소자승법에 Born 유효전하의 근사결과는 Fig. 2와 Table 1에 제시하였다.

3.1 BNNT의 크기변화에 따른 압전탄성계수
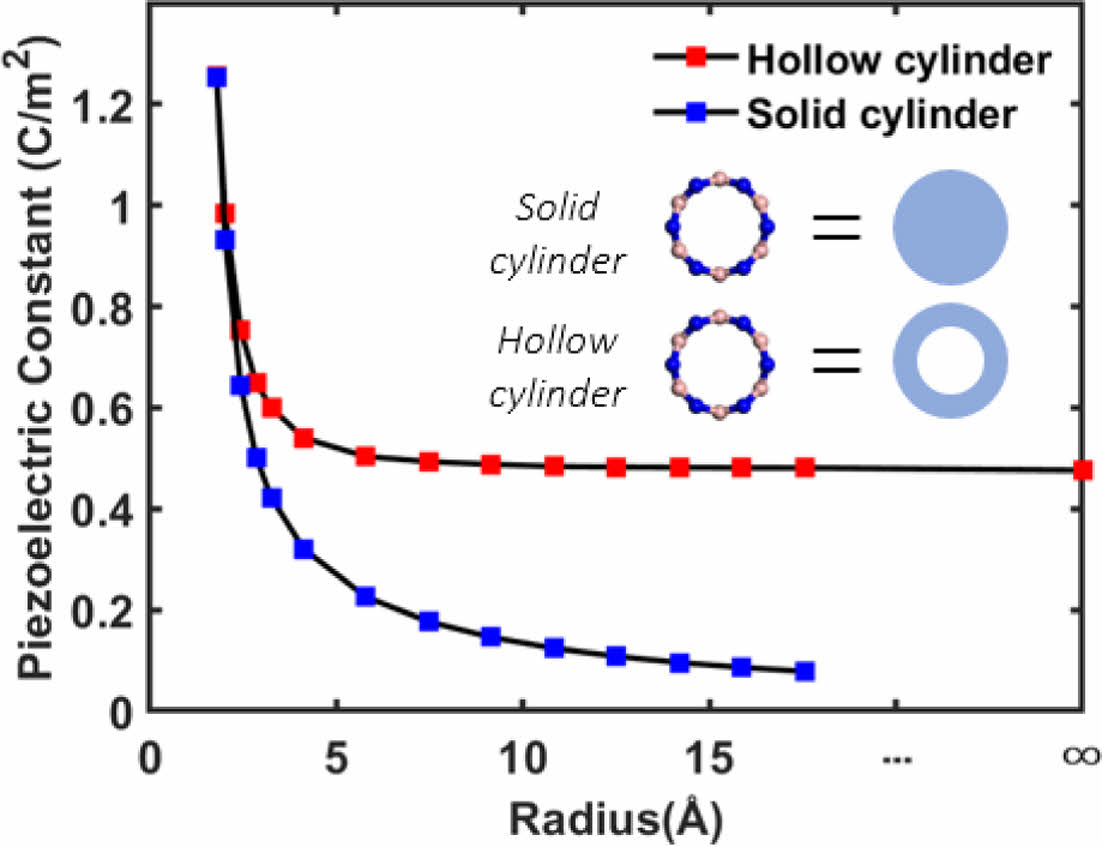
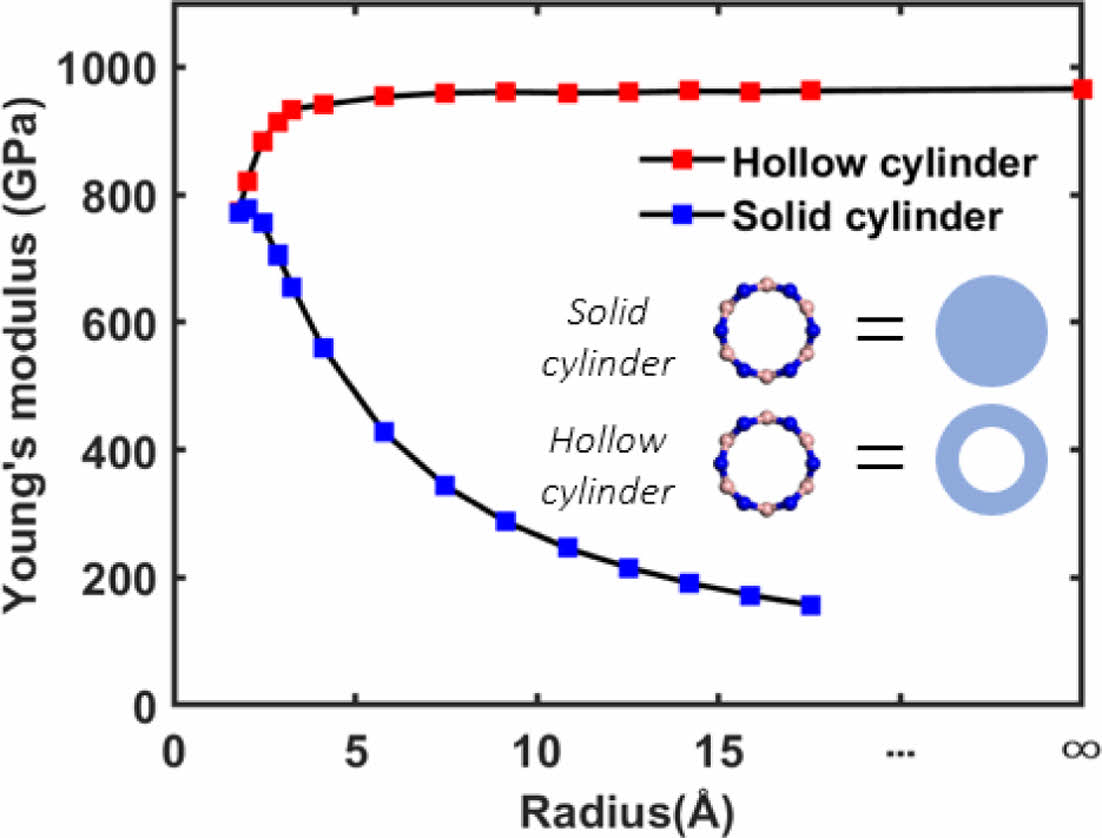
BNNT의 키랄 벡터 변화(반경 크기 변화)에 따른 압전 상수와 영률 변화는 Fig. 3과 Fig. 4에 각각 제시하였다. BNNT를 포함한 나노튜브의 물성을 인실리코해석을 통해 예측하는 경우, 구성방정식에서 정의되는 강성적 물리량인 영률, 압전상수 그리고 유전상수를 계산하기 위해서는 등가의 체적을 정의해야 한다. 본 연구에서는 나노튜브의 곡률이 무한한 경우에 해당하는 나노시트의 체적정의 까지를 고려하여, 나노튜브를 속이 꽉 찬 중실형의 Solid cylinder로 근사하는 방법과 더불어 튜브 내부를 빈 공간으로 가정한 중공형 Hollow cylinder 로 가정한 두 가지 케이스를 모두 반영하였다[12].
중공형 실린더로 가정한 경우, BNNT의 압전상수는 키랄 벡터가 증가함에 따라(튜브 반경 증가) 점진적으로 감소하는 경향을 보이는 반면, 영률의 경우에는 점진적으로 증가하는 것으로 나타났다. 또한 두 물성 모두 BNNT의 반경이 증가할수록 BNNS의 물성에 수렴하게 된다. 반면 중실형 실린더로 가정할 경우, BNNT의 압전 상수와 영률은 키랄 벡터가 증가함에 따라 모두 감소하는 경향을 보였다. 이러한 상반된 경향성은 탄소나노튜브의 탄성계수를 계산한 기존 문헌에서도 이미 보고된 바가 있다. BNNT는 튜브의 표면에만 원자들이 분포하기 때문에, 표면효과 측면에서는 가장 이상적인 구조를 가지고 있게 된다. 따라서 BNNT의 등가연속체 모델을 중실형 구조로 가정할 경우 단위체적당 변형에너지와 식 (4)에 정의된 분극은 튜브의 반경이 감소할수록 증가하게 되며, 이에 따라 BNNT의 영률과 압전상수는 반경감소에 따라 증가하게 된다.
3.2 BNNT 구조-물성 상관관계 수식화
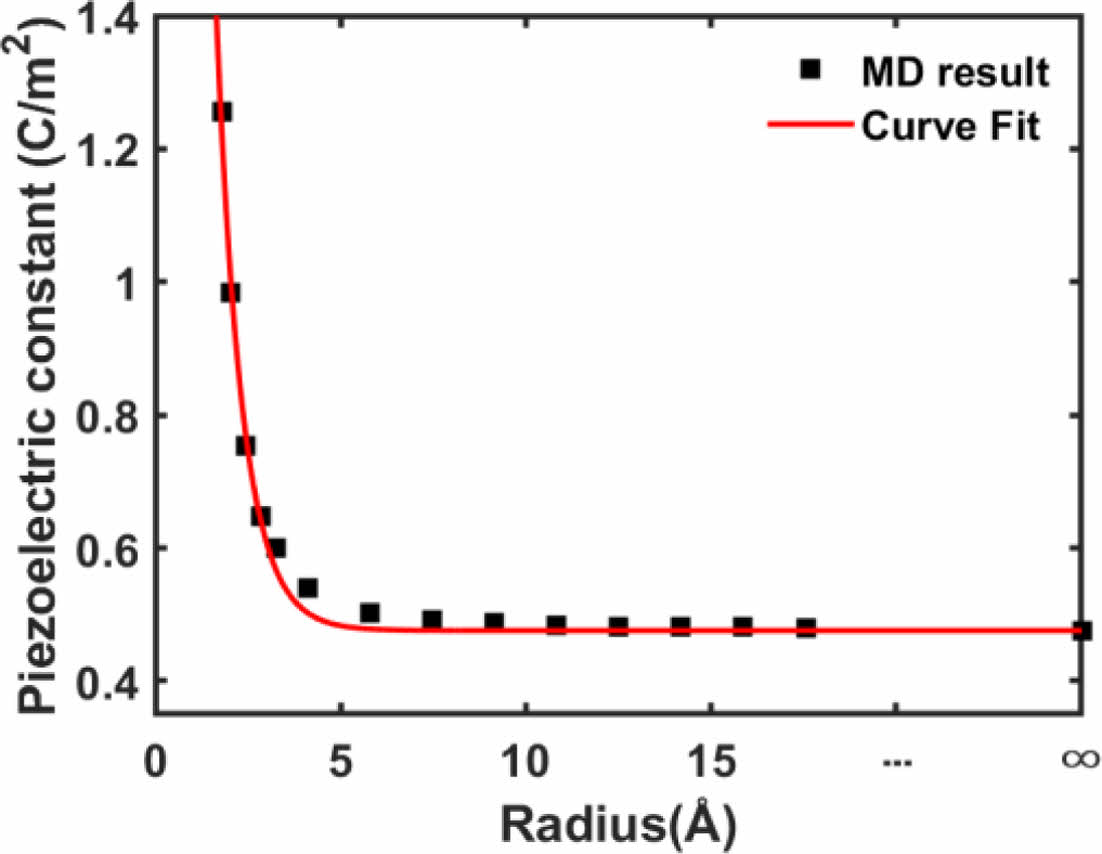
3.1절에서 확인한 BNNT의 구조-물성 상관관계는 지수함수의 형태로 근사할 수 있으며, 본 연구에서는 BNNT를 중공형 튜브로 간주한 경우에 대한 압전상수와 영률변화를 각각 식 (6)과 (7)의 형태를 따르는 것으로 가정하였다. 여기서 r은 BNNT의 반경을 의미하며, 계수 A, B, C, D는 최소자승법을 통해 도출되는 상수이다. 또한 Fig. 3과 4에서 관찰된 것처럼 BNNT의 압전상수와 영률은 반경이 증가할 경우 BNNS의 물성에 수렴하게 되므로, 최소자승 근사 시 BNNT의 압전상수와 영률은 BNNS의 물성에 수렴하는 것으로 가정하였다.



BNNT의 압전상수와 영률의 최소자승 근사 시 잔여값 R²는 0.9915, 0.9898로 계산되었으며, 나노튜브의 반경변화에 따른 압전탄성물성 변화를 근사한 결과는 Fig. 5와 6에 제시되어 있다. 식 (6)과 (7)에 제시된 근사모델은 BNNT의 크기변화에 따른 압전특성을 비교적 정확하게 반영하고 있다. 특히 BNNT의 반경이 가장 작은 (5,0) 튜브의 경우, BNNS에 비해 약 3배정도 높은 압전상수값을 보이고 있다. 또한 BNNS의 압전상수는 약 0.48C/m² 수준이며, 이 값은 기존의 제일원리계산 결과와 비교할 때 매우 유사한 수준이라 할 수 있다[17]. 따라서 Tersoff 포텐셜을 적용한 분자동역학 전산모사기법은 BNNT의 압전특성 예측에 있어 비교적 정확한 계산결과를 제공한다고 결론지을 수 있다. 특히 제일원리 계산은 온도변화에 따른 압전상수를 예측할 수 없으나, 앙상블 전산모사를 적용하는 분자동역학 전산모사는 이러한 온도효과를 반영할 수 있다는 점에 있어 BNNT를 에너지수확형 복합재로 적용하기 위한 나노복합재 설계에 있어 매우 유용한 가상실험 도구로 활용될 수 있다.
3.3 BNNT의 곡률효과
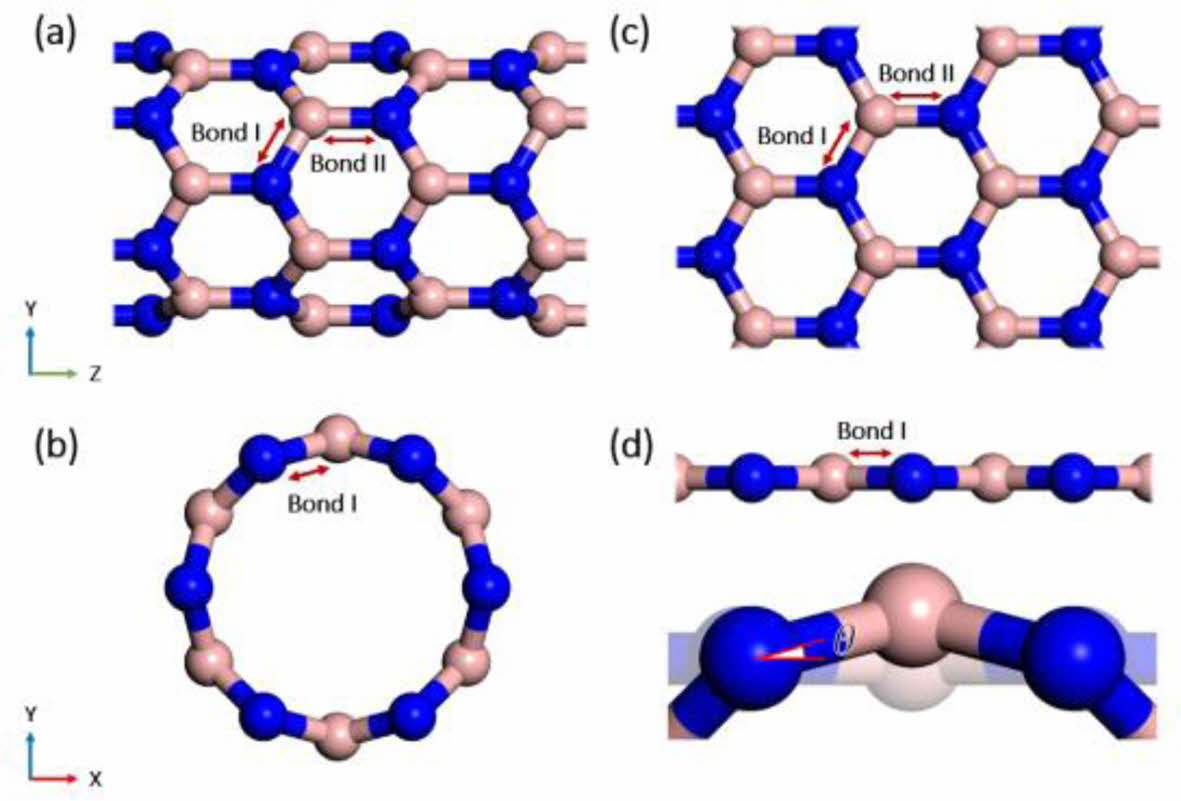
BNNT의 키랄성에 따른 구조-물성 상관관계를 분석하기 위해 Fig. 7과 같이 육방정계 질화붕소 구조를 유한한 곡률을 가지고 있는 BNNT (5,0)와 평면형을 유지하고 있는 BNNS에 대해 구조안정화를 진행한 이후 질소-붕소 간 결합상태를 상호비교하였다. 질화붕소의 육방정구조를 고려하여, Fig. 7(a)와 (c)에서 처럼 길이방향(Bond I)과 원환방향(Bond II)으로 배열된 2개의 질소-붕소 결합을 고려하였으며, 안정화된 구조에서의 결합길이와 결합에너지를 Table 2에 제시하였다. 그 결과 원환방향으로 배열된 Bond I의 경우 (5,0) BNNT 내에서의 결합길이가 BNNS에서의 경우보다 더 길며, 결합에너지의 크기는 더 작은 것으로 확인되었다. 이는 평면을 유지하는 시트구조에서 유한한 곡률을 가진 튜브형태로 변형되는 과정에서 Bond I의 결합강도가 약해짐을 의미한다. 또한 길이방향으로 배열된 Bond II의 결합길이 역시 Bond I에 비해서는 차이가 적지만 동일한 경향을 보이고 있으며, 이로 부터 BNNT의 반경이 감소(곡률이 증가)함에 따라 길이방향 영률이 영향을 받게됨을 알 수 있다.
안정화 상태에서의 결합길이 분석과 더불어 BNNT의 키랄성에 따른 압전상수 변화를 분석하기 위해 정압전 전산모사 과정에서 Bond I과 II의 결합길이 변화를 상호비교하였다. BNNT와 BNNS는 2%의 변형률에 이를 때까지 일축인장 변형을 하도록 했으며, Bond I과 Bond II의 결합길이 변화가 분극과 압전상수에 미치는 영향을 원자들의 상대변위와 연관지어 분석하였다. 해당 결과는 Fig. 8과 9에 각각 제시하였다. 먼저 BNNT와 BNNS의 변형률에 따른 Bond I의 길이변화의 경우 Fig. 8에 제시된 것과 같이 BNNT 구조에서 BNNS 보다 빠른 결합길이 변화가 관찰되었다. 그러나 Bond II의 경우 반대로 BNNS 구조에서 BNNT에 비해 보다 빠른 결합길이 변화가 관찰되었다. 질소와 붕소의 전하는 서로 반대의 부호를 가지고 있기 때문에 이러한 질소-붕소 간 결합길이 변화는 변형에 따른 분극변화량의 차이로 이어져 키랄성에 따른 압전상수 변화로 이어지게 된다. 질소-붕소 간 상대변위 변화와 이에 다른 분극변화는 Fig. 10과 같이 요약될 수 있다. Bond I의 변형량 증가는 표면전하 방향으로 배열된 질소-붕소 원자쌍에서의 상대변위를 변화에 따른 쌍극자모멘트 증가를 일으키게되며, 이에 따라 질화붕소의 일축인장 시 분극 증가로 이어지게 된다. 반면, Bond II의 변형량 증가는 쌍극자모멘트의 방향으로 인해 분극의 감소를 일으키게 되는데, BNNT의 경우 BNNS에 비해 변형량 증가폭이 더 작기 때문에 하중 인가에 따른 분극감소 또한 적게 된다. 이에 따라 동일한 변형률 조건에서도 BNNT에서의 분극증가가 BNNS에서의 분극증가보다 크게되어 보다 큰 압전효과를 나타낼 수 있게 된다.

본 연구에서는 분자동역학 전산모사를 이용하여 BNNT의 키랄 벡터 변화에 따른 압전탄성 물성의 변화를 예측하였다. BNNT의 압전탄성 물성을 가장 잘 예측할 수 있는 Tersoff 포텐셜 파라메터 셋을 선별하여 적용하였으며, BNNT의 키랄 벡터에 따른 질소와 붕소원자의 Born 유효 전하량을 튜브의 반경에 대한 근사식으로 보간하여 하중인가에 따른 분극계산에 반영하였다. 선형 압전 탄성 구성방정식을 사용하여 외부전기장이 제한된 일축인장 경계조건하에서 BNNT의 비리얼응력과 분극 변화량을 산출하여 반경에 따른 영률과 압전상수를 계산하였다. 그 결과 BNNT를 중실형 튜브구조로 간주할 경우 키랄 벡터가 증가함에 따라(반경이 증가함에 따라) 압전 상수는 감소하고 영률은 증가하여 2차원 질화붕소구조체인 질화붕소 나노시트(BNNS)의 물성에 수렴하는 것으로 나타났다. 이러한 크기효과를 단순한 경험적 모델로 제시하기 위해 BNNT의 영률과 압전상수를 반경에 대한 지수함수형태로 최소자승 근사하였다. 또한 이러한 크기효과의 원인을 BNNT의 곡률과 연계하여 이해하기 위해 안정화된 구조의 결합에너지 차이와 하중인가에 따른 원자간 결합길이 변화를 나노튜브의 곡률에 따라 정량적으로 비교하였다. 본 연구에서 정립된 방법론과 결과는 추후 다중벽 BNNT 및 적층형 BNNS의 압전탄성물성 예측과 이를 압전 복합재 설계에 적용하기 위한 멀티스케일 모델링 등에 유용하게 활용될 예정이다.

본 논문은 한국수력원자력(주)에서 재원을 부담하여 수행한 연구결과입니다(No. 23-Tech-04).