Due to the structural characteristic of a double roller, the double roller can have various deformation behaviors depending on a gap block design, even if dimensions and loading conditions for the double roller are the same. Based on this feature, we propose a strategy for designing the gap block of the carbon-fiber reinforced plastic (CFRP) double roller to minimize defects (e.g., sagging and wrinkling), which can be raised during the product conveying process, with the pursue of the lightweight design. In the suggested strategy, analysis cases are first selected by considering main design parameters and engineering tolerances of the gap block, and then deformation behaviors of these selected cases are extracted using the finite element method (FEM). Here, to obtain the optimal gap block parameters that satisfy the purpose of this study, deformation deviations in the contact area are calculated and compared using the extracted deformation behaviors. Note that the contact area in this work is located between the product and the roller. As a result, through the design method of the gap block proposed in this work, it is possible to construct the CFRP double roller that can significantly decrease the defects without changing the overall sizes of the roller. A detailed method is suggested herein, and the results are evaluated in a numerical way.

이중 롤러는 Gap block 설계에 따라 동일한 크기와 하중 조건에서도 다양한 변형 양상을 가질 수 있다. 이러한 특성을 활용하여, 본 연구에서는 제품 이송 과정에서 발생되는 주름과 같은 결함을 최소화하기 위한 Carbon-fiber reinforced plastic (CFRP) 이중 롤러의 Gap block 설계 방법을 제안한다. 가장 먼저, Gap block에 대한 주요 설계 변수와 공정 정밀도를 고려한 분석 case들을 선정하고, 유한 요소 해석을 활용하여 CFRP 이중 롤러의 변형 양상을 추출한다. 여기서, 본 연구의 목적을 만족하는 최적의 Gap block 설계를 수행하기 위해, 제품과 롤러가 접촉하는 지점들 간의 변형 편차에 기반하여 CFRP 이중 롤러의 변형 양상들을 비교 분석한다. 그 결과, 본 연구에서 제안한 Gap block 설계 방법을 통해, 롤러의 직경 또는 길이와 같은 전체적인 크기 변화없이 제품 이송 시 결함을 크게 감소시킬 수 있는 최적화된 CFRP 이중 롤러를 구축할 수 있었다.

Keywords: 이중 롤러(Double roller), 갭 블록(Gap block), 탄소섬유강화플라스틱(CFRP), 롤러 컨베이어 시스템(Roller conveyor system)

최근 디스플레이를 비롯한 다양한 산업 분야에서, 고도화된 제품의 높은 생산 수율 달성을 위한 신뢰성 높은 제조 라인의 구축이 요구되고 있다[1,2]. 이러한 요구를 만족하기 위해서는 작업 기계의 성능 향상과 같은 제조 공정의 개선뿐만 아니라 이송 과정 중 발생하는 결함을 최소화할 수 있는 정밀한 제품 이송 시스템의 구축이 필요하다[3,4].
제조 라인에서 제품을 이송하는 데 가장 많이 사용되는 시스템 중 하나인 롤러 컨베이어 시스템의 경우, 제품을 롤러 위에 직접 올려 놓고 이송하기 때문에 롤러 자체의 변형이 제품 결함에 영향을 주게 된다. 이 때, 롤러 자체의 하중과 제품 하중에 의한 다양한 변형 양상이 나타나며, 제품과 롤러의 접촉부에 발생되는 변형 양상 및 변형 편차로 인해 제품의 허용 범위 이상의 처짐 또는 주름이 발생할 수 있다. 특히 디스플레이와 같은 제품은 이러한 결함에 치명적일 수 있어, 제품과 롤러가 접촉하는 지점들 간의 변형 편차를 최소화하는 것이 정밀한 롤러 컨베이어 시스템을 구성하는 데 필수적이다[5-7].
직경과 같은 롤러의 크기를 직접적으로 변화시키는 것을 통해 접촉부의 변형 편차를 최소화할 경우, 단순 롤러 교체가 아닌, 전반적인 롤러 컨베이어 시스템의 재설계가 필요할 수 있기 때문에 롤러의 크기를 변경하는 것은 지양해야 한다. 롤러의 크기 변경없이 변형 편차를 최소화하는 데 가장 간편한 방법 중 하나는 롤러의 소재를 변경하여 강성을 높이는 것이다[8,9]. 특히, 무게 대비 강성이 뛰어난 탄소 섬유 강화 플라스틱(Carbon-fiber reinforced plastic, CFRP)을 활용할 경우, 롤러의 크기 변경으로 인한 다양한 문제를 회피함과 동시에 경량화된 고성능 제품 이송 시스템을 구성할 수 있다[10-12].
이러한 장점에도 불구하고, 롤러 컨베이어 시스템의 롤러 소재로 CFRP를 활용하는 것에는 여전히 해결해야 할 문제가 남아 있다. 특히, CFRP는 기타 다른 소재에 비해 높은 제조 단가를 갖는다는 단점이 있어 롤러 내부 구조에 많은 양의 CFRP가 사용되는 것은 피해야 한다[13]. 따라서, CFRP 소재를 효율적으로 활용함과 동시에 롤러의 크기 변화없이 변형 편차를 최소화하기 위해서는 롤러의 기하학적 구조 변경이 필요하다.
내부 파이프와 외부 파이프 사이에 gap block이 위치하는 구조를 갖는 이중 롤러의 경우, 기존 단일 롤러와 동일한 크기, 소재, 그리고 하중 조건이라 하더라도 gap block 설계 변수에 따라 다양한 변형 양상을 가질 수 있다[14]. 따라서, 이중 롤러 구조에 CFRP 소재를 적용한 CFRP 이중 롤러의 gap block 설계를 통해, 경량화된 고성능 제품 이송 시스템을 구축할 수 있다.
이러한 동기를 바탕으로, 본 연구에서는 제품 이송 과정에서의 결함을 최소화하기 위한 CFRP 이중 롤러의 gap block 설계 방법을 제안한다. 가장 먼저, gap block 주요 설계 변수인 폭과 배치 간격에 대해 공정 정밀도를 고려하여 분석 case들을 선정한다. 그런 다음 유한 요소 해석을 활용하여, 선정된 각 case별 CFRP 이중 롤러의 변형 양상을 추출한다. 이러한 변형 양상을 판단하는 기준으로써 접촉부의 변형 편차에 기반한 근거를 제시하여, 최적의 gap block 설계를 수행한다. 추가적으로, 이중 롤러의 구조적 특성 활용에 대한 유효성을 판단하기 위해 이중 롤러와 동일한 크기, 소재, 하중 조건에서 단일 롤러의 변형 양상을 추출하고, 최적 case와의 비교 평가를 수행한다.
본 논문의 구성은 다음과 같다. 먼저, Section 2에서는 CFRP 이중 롤러의 특성을 소개한 후 gap block 설계 변수 및 분석 case들을 선정하며, 이에 대한 해석 조건들을 설명한다. Section 3에서는 Section 2에서의 선정 case들에 대한 해석 결과를 바탕으로 최적의 gap block 설계 변수를 결정하며, 추가적으로 최적 gap block 설계 변수가 적용된 CFRP 이중 롤러의 효용성을 판단하기 위해, 기존 CFRP 단일 롤러와 비교 분석을 수행한다. 본 연구의 결론은 Section 4에 제시된다.

이번 Section에서는 본 연구에서 활용된 CFRP 이중 롤러의 기하학적 구조, 소재, 그리고 물성을 소개한다. 그 다음으로, 본 연구의 목적을 만족하는 CFRP 이중 롤러의 gap block 설계 변수를 정의하고, 이에 대한 분석 case들을 선정한다. 마지막으로, 정의된 gap block 설계와 분석 case들에 대한 해석 조건들을 설명한다.
2.1 Geometrical conditions and material properties of the CFRP double roller
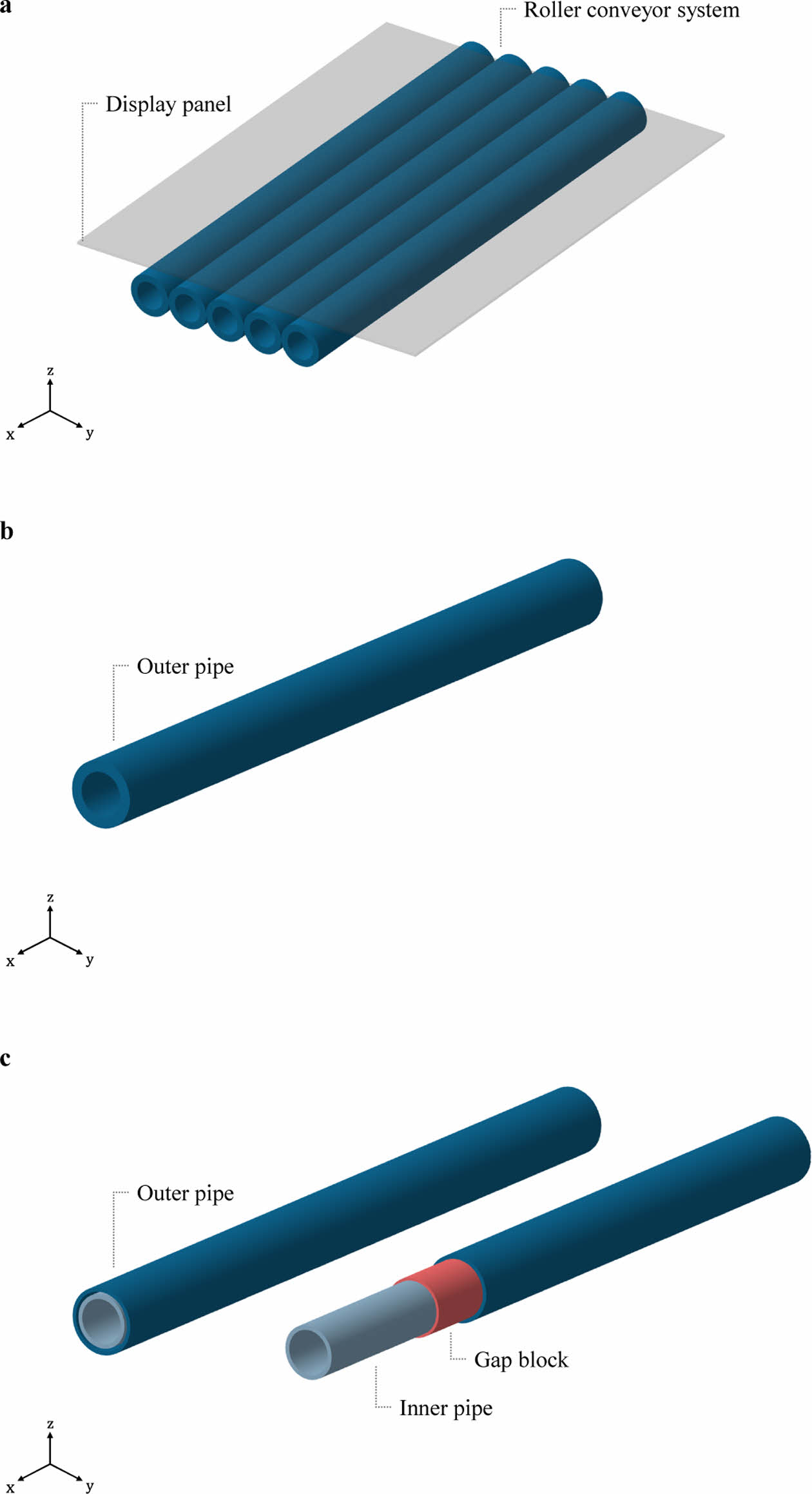
본 연구의 롤러 기반 제품 이송 시스템을 표현하는 모식도를 Fig. 1에 나타내었다. 롤러 컨베이어 시스템은 Fig. 1(a)에 나타낸 것과 같이 롤러 위에 제품을 직접 올려놓고 운반하는 시스템이며, 이번 연구에서는 Fig. 1(b)의 단일 롤러가 아닌, Fig. 1(c)에 나타낸 이중 롤러를 활용하였다.
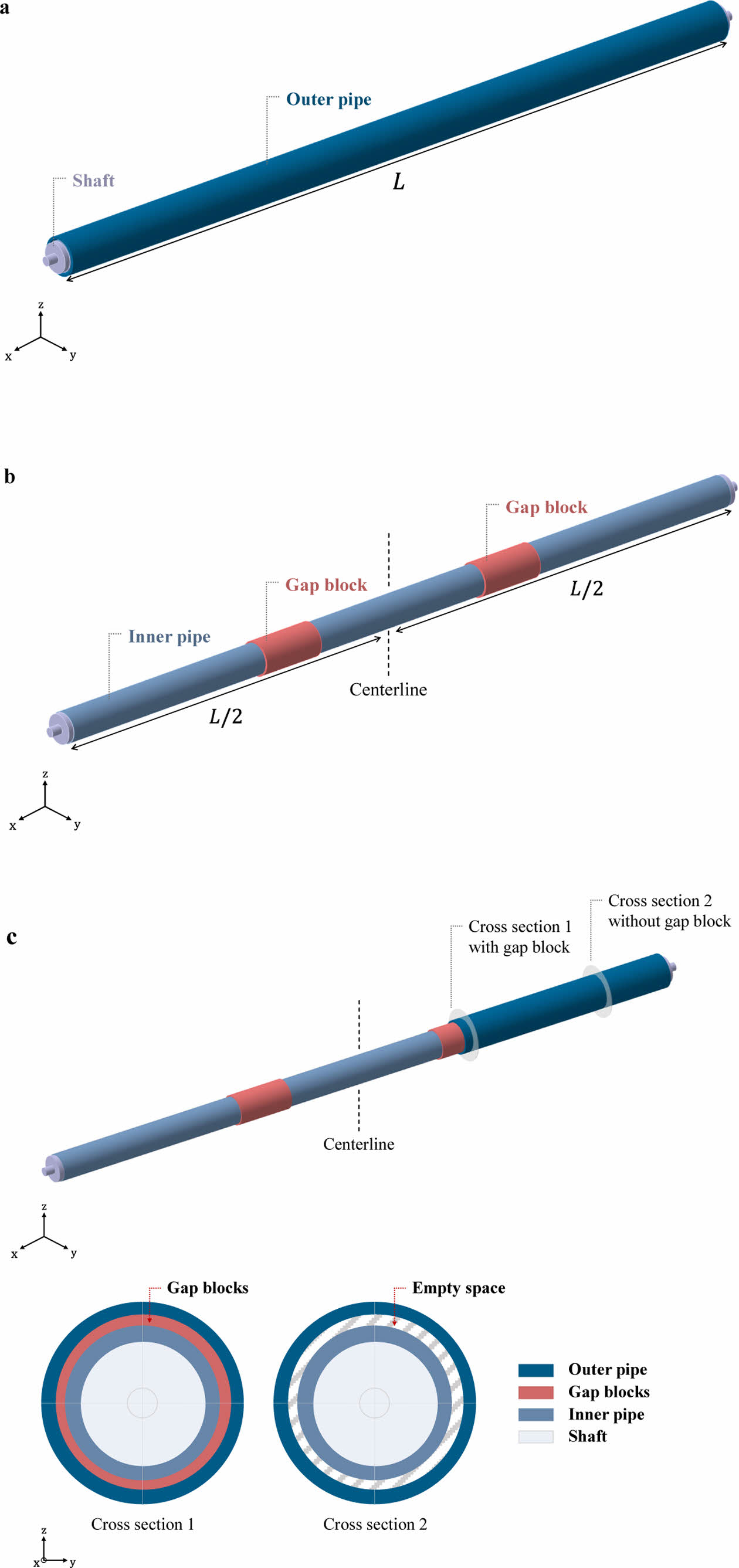
여기서, 본 연구에서 활용된 CFRP 이중 롤러에 대한 구체적인 기하학적 형상 및 구조는 Fig. 2에 나타내었다.
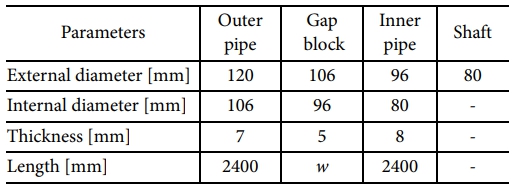
CFRP 이중 롤러는 내부 파이프와 외부 파이프, 그리고 2개의 gap block으로 구성되며 pipe-in-pipe 시스템과 유사한 구조를 갖는다[14,15]. 구체적으로, 내부 파이프와 외부 파이프는 x축 방향으로 동일한 길이를 가지며, 내부 파이프와 외부 파이프 사이에 위치하는 2개의 gap block은 CFRP 이중 롤러 전체 길이 L의 절반이 되는 중심선(centerline)을 기준으로 좌우 대칭이 되도록 배치된다. 여기서, gap block은 각각 내부 파이프 및 외부 파이프와 접촉하며, gap block이 존재하지 않는 부분에서는 내부 파이프와 외부 파이프 사이에 gap block 두께만큼의 빈 공간이 형성된다. Fig. 2에 표현된 CFRP 이중 롤러의 구체적인 크기 및 길이 정보는 Table 1에 표기되어 있다.
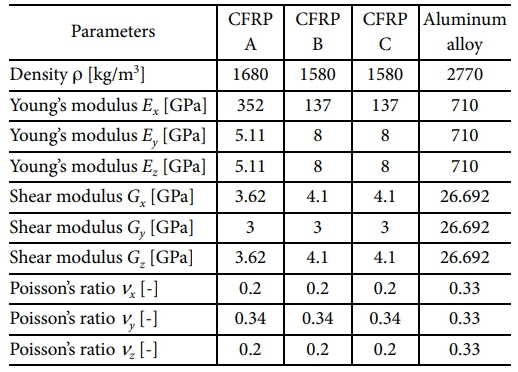
다음으로, 본 연구에서 사용된 CFRP 이중 롤러의 소재 및 물성을 소개한다. CFRP 이중 롤러의 내부 파이프와 외부 파이프에는 단방향 CFRP laminate를 적용하였으며, 이를 제외한 gap block과 shaft의 재료는 알루미늄 합금을 활용하였다[16,17]. CFRP 이중 롤러의 소재 종류는 Table 2에, 재료별 물성은 Table 3에 표기하였다.
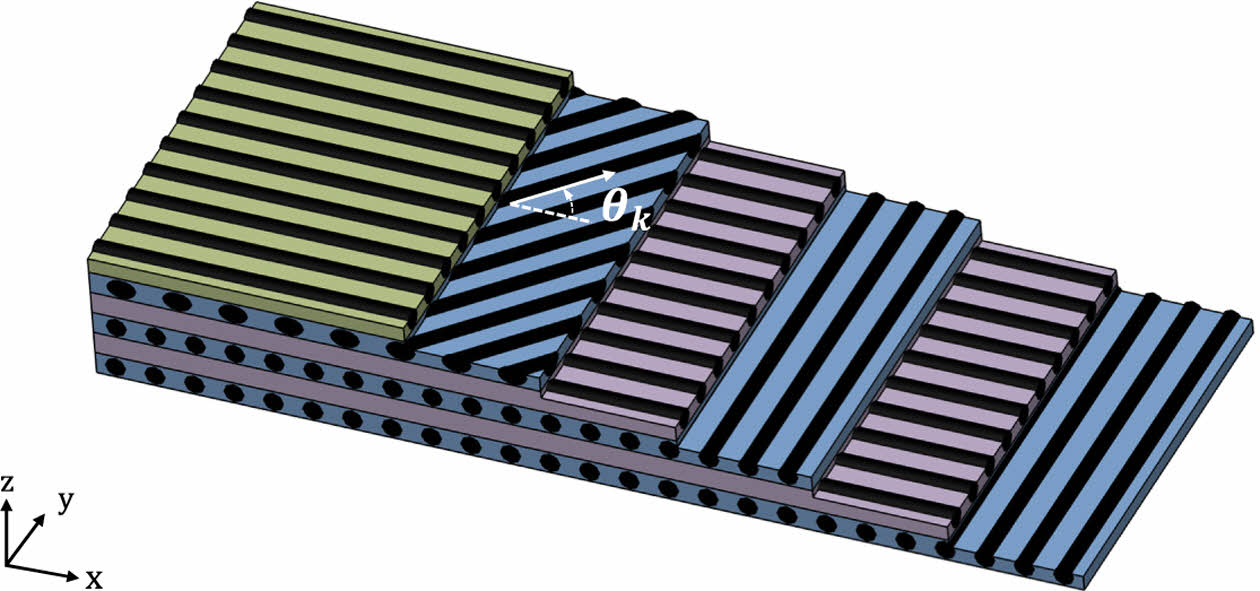
또한, CFRP 이중 롤러의 내부 파이프와 외부 파이프에 활용한 단방향 CFRP laminate 적층 구조는 Fig. 3에 나타내었다.
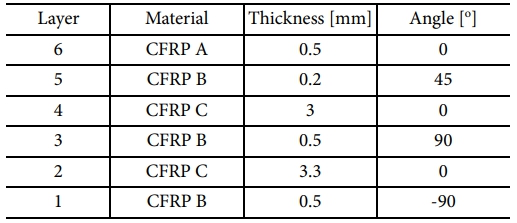
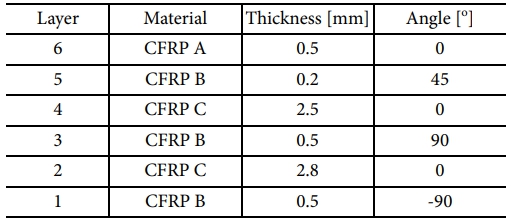
Fig. 3에 표현된 단방향 CFRP laminate의 경우, laminae의 섬유 방향에 따라 높은 강도 및 강성을 갖는 방향이 상이하기 때문에 다양한 섬유 방향을 갖는 laminae를 구성하여 제품을 설계하는 것이 중요하다[18-20]. 따라서, 본 연구에서는 내부 파이프와 외부 파이프에 각각 8 mm, 7 mm 두께의 6개의 층으로 적층된 CFRP laminate를 다양한 섬유 방향을 갖는 laminae로 구성하였다. 구체적인 단방향 CFRP laminae의 물성과 적층 두께 및 섬유 방향은 내부 파이프와 외부 파이프에 대하여 각각 Table 4와 Table 5에 표기하였으며, 섬유 방향은 Fig. 3에 나타낸 것과 같이 x 축과 섬유가 이루는 각도 θ_k로 정의한다(k = 1, ..., 6)[21].
Section 2.2에서는 CFRP 이중 롤러와 제품의 접촉부에 발생되는 변형 편차를 최소화하기 위한 gap block 설계 변수를 정의하며, gap block 설계 변수에 대한 공정 정밀도를 바탕으로 분석 case들을 선정한다.
2.2 Design gap block parameters in the CFRP double roller
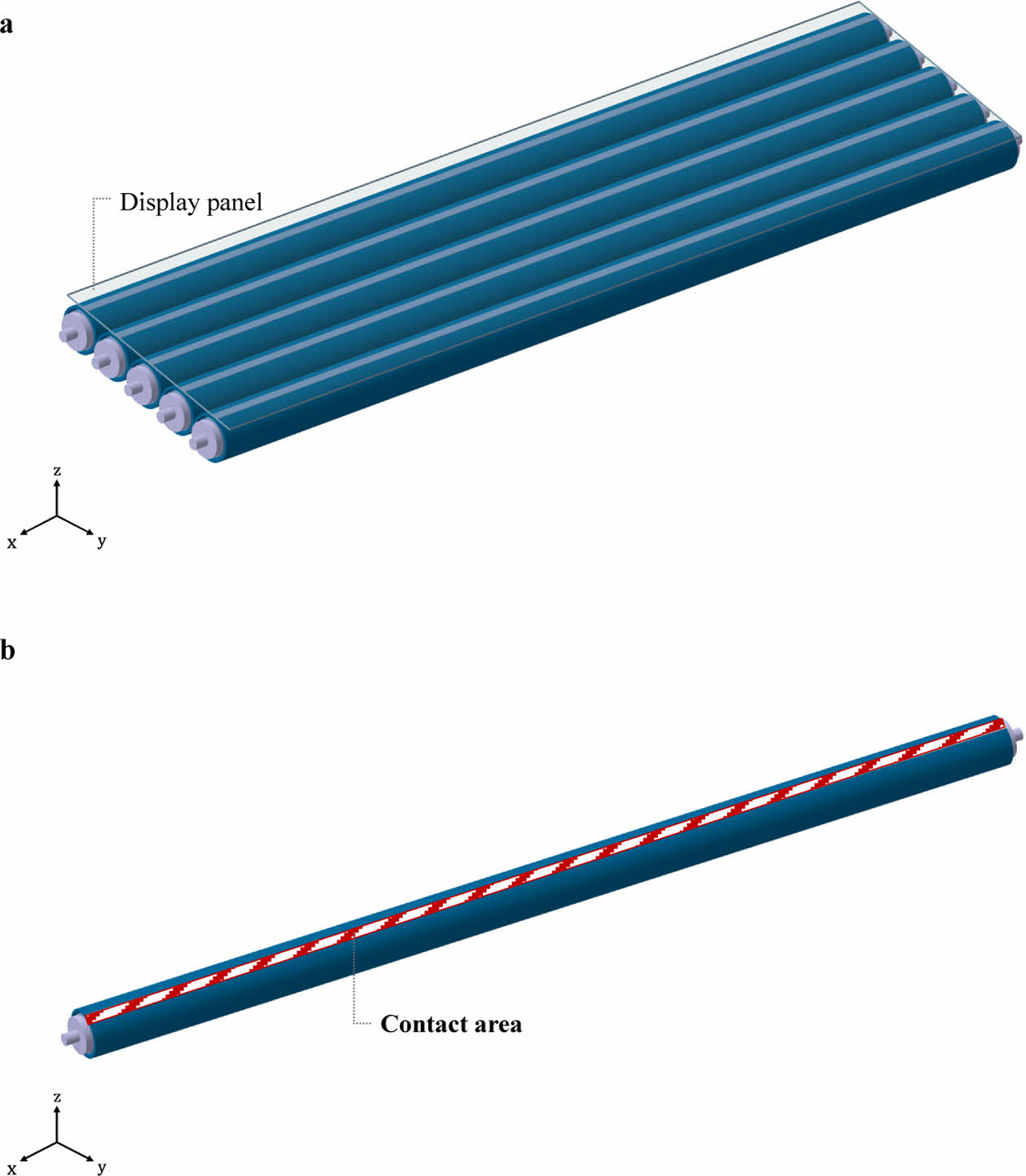
제품 이송 과정에서 발생되는 결함을 최소화하기 위해서는 CFRP 이중 롤러와 제품이 접촉하는 부위에서의 변형 편차를 최소화하는 것이 중요하다[5-7]. 본 연구에서 고려한 CFRP 이중 롤러와 제품의 접촉 부위(contact area)는 Fig. 4에 나타내었다.
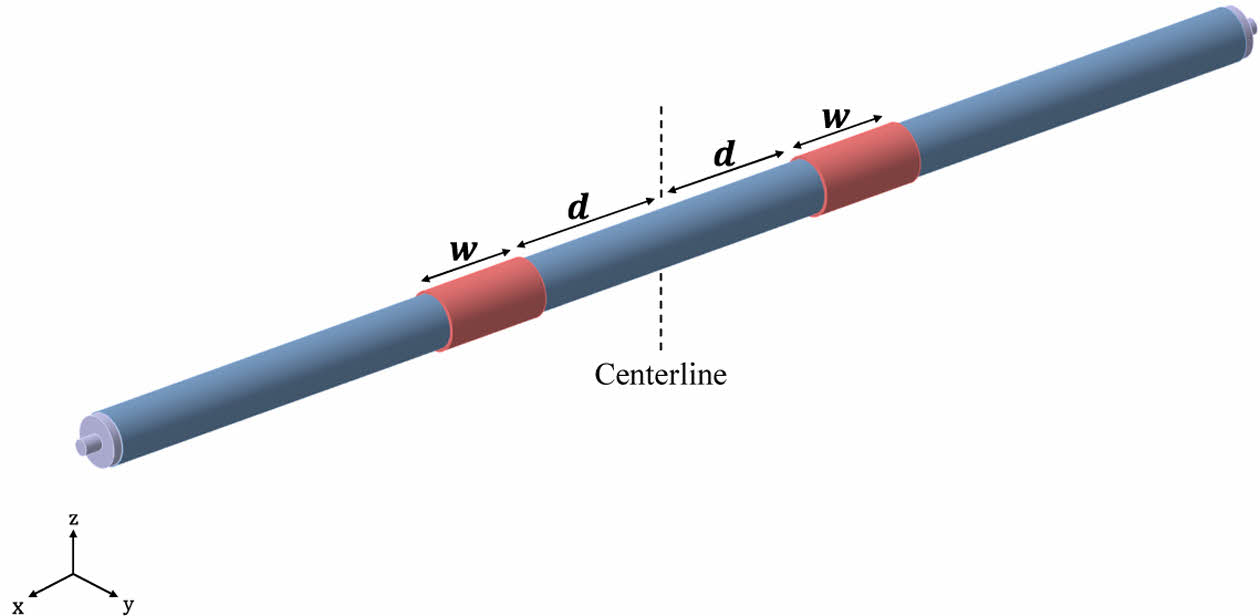
CFRP 이중 롤러의 구조적 특징으로 인해, gap block 설계에 따라 Fig. 4의 contact area에 다양한 변형 양상이 나타나게 된다[14]. 여기서, gap block의 주요 설계 변수 중 변형 양상에 직접적인 영향을 주는 x 축 방향 길이인 폭 w과 배치 간격 d, 두가지를 고려하며, Fig. 5에 두가지 변수를 나타내었다.
구체적으로, gap block 설계 변수 중 폭 w은 제작 정밀도를 고려함과 동시에 CFRP 이중 롤러 전체 길이 L의 10% 이내가 되도록 100 mm 및 200 mm인 경우로 구분한다. 또다른 gap block 설계 변수인 배치 간격 d은 조립 정밀도를 고려하여 중심선(centerline)을 기준으로 100 mm씩 늘어나도록 설정한다. 여기서, d = 0 mm인 경우는 두 개의 gap block이 중심선(centerline)에서 맞닿아 있음을 의미하기 때문에, 두 개의 gap block은 배치 간격 d = 0 mm에서부터 200 mm씩 멀어지게 된다. 본 연구에서, CFRP 이중 롤러의 전체 길이 L는 고정되기 때문에, gap block의 폭 w, 배치 간격 d, 그리고 CFRP 이중 롤러의 전체 길이 L는 다음과 같은 제약 조건 하에 놓인다.



식 (1)에 의해, w = 100 mm인 경우에는 배치 간격 d = 0 mm부터, 1,100 mm까지 12개의 case가, w = 200 mm인 경우에는 배치 간격 d = 0 mm부터, 1,000 mm까지 11개의 case가 산출되어, 총 23개의 분석 case들이 선정된다.
Section 2.3에서는 Section 2.1 및 2.2에서 정의한 CFRP 이중 롤러와 분석 case에 적용되는 해석 조건들을 설명한다.
2.3 Boundary conditions of the CFRP double roller
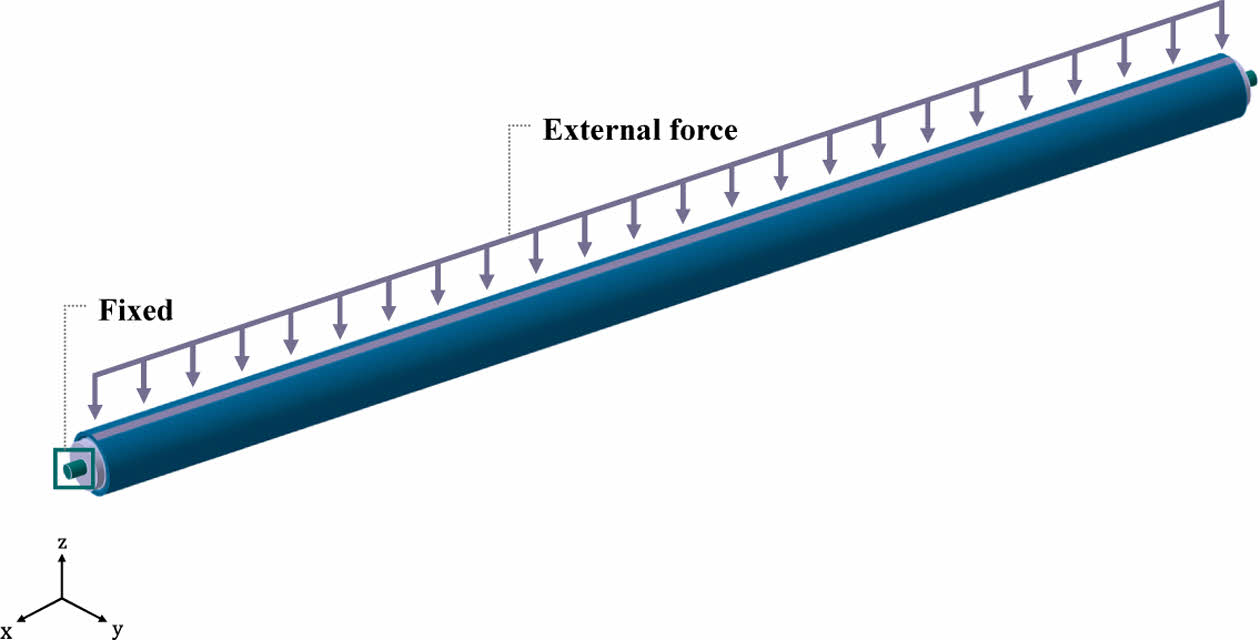
Section 2.1에서 정의한 CFRP 이중 롤러에 적용되는 경계 조건 및 하중 조건은 Fig. 6에 나타내었다.
구체적으로, CFRP 이중 롤러의 양 끝 shaft에는 fixed 경계 조건이 적용되며, 하중 조건으로는 -z 방향의 자중과, Fig. 6에 표현된 것과 같이 Fig. 4의 contact area에 10 kN의 분포 하중이 적용된다. 주어진 경계 조건 및 하중 조건을 바탕으로 Fig. 4의 contact area에서의 변형 편차를 계산하기 위해 활용한 소프트웨어는 ANSYS Workbench 2022 R2이다. 여기서, 막대한 계산 비용없이 효율적인 계산을 위해, 최대 mesh size는 10 mm를 초과하지 않도록 선정하였다[22]. 그 결과로 CFRP 이중 롤러의 해석 모델은 총 31,108개의 노드와 24,322개의 요소로 구성된다. 이번 Section에서 설명한 경계 조건 및 하중 조건은 Section 2.2에서 선정된 23개의 분석 case들에 대해 모두 동일하게 적용된다.
다음 Section에서는 도출된 해석 결과들을 비교 분석하고, 그 내용을 바탕으로 Fig. 4의 contact area에 발생되는 변형 편차를 최소화할 수 있는 최적의 gap block 설계 방법을 도출한다.

이번 Section에서는 Section 2에서 정의한 CFRP 이중 롤러의 gap block 설계 변수 폭 w과 배치 간격 d에 따라 나타나는 CFRP 이중 롤러의 변형 양상을 분석하고, Fig. 4의 contact area에 발생되는 변형 편차를 최소화할 수 있는 최적의 gap block 변수를 결정한다. 추가적으로, CFRP 이중 롤러와 동일한 크기 및 소재, 그리고 하중 조건을 가지는 CFRP 단일 롤러와의 비교 분석을 통해, 본 연구에서 수행한 CFRP 이중 롤러의 gap block 설계에 대한 유효성을 판단하고자 한다.
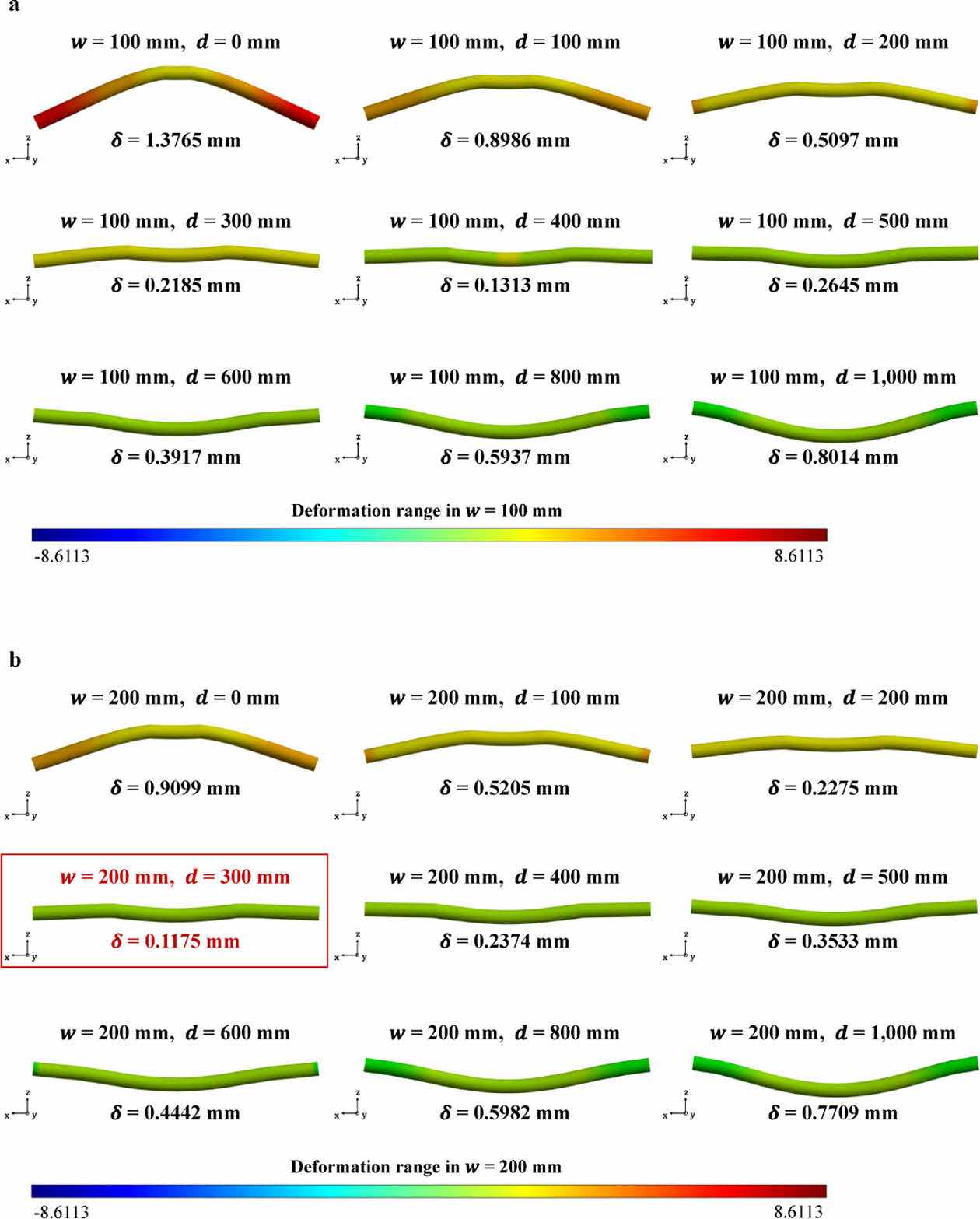
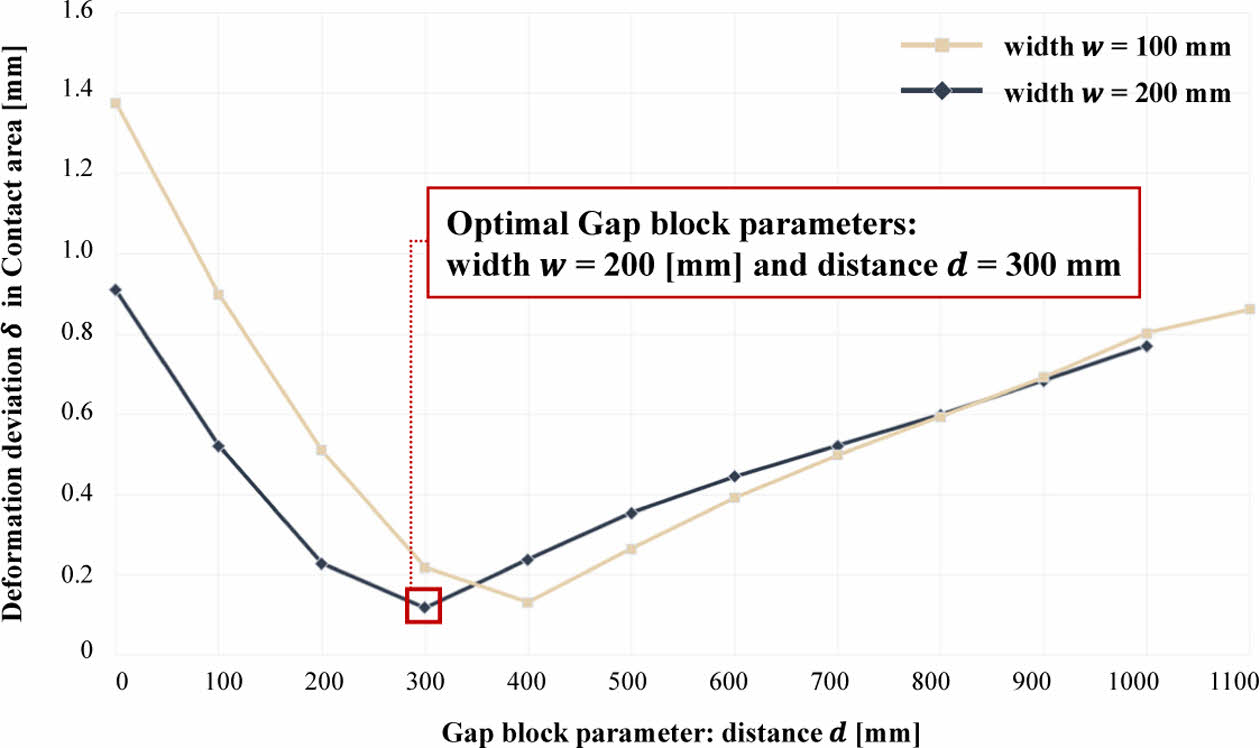
먼저, Section 2에서 선정한 gap block 설계 변수에 의한 CFRP 이중 롤러의 전체적인 변형 양상들 중 일부를 Fig. 7에 나타내었으며, Fig. 8에는 Section 2에서 선정된 전체 23개의 gap block 변수에 따른 변형 편차 d를 나타내었다. 여기서, 변형 편차 δ는 Fig. 4의 contact area에서 z 축 방향으로 발생된 변형 값들에 대한 편차 계산을 통해 도출된다.
Figs. 7 및 8을 통해 확인할 수 있는 것처럼, Fig. 4 내 contact area에서의 변형 편차 δ는 배치 간격 d에 따라 단조 증가/감소하는 것이 아니라, 특정 배치 간격까지는 감소하다가 그 이상부터 점차 증가함을 파악할 수 있다. 구체적으로, 특정 배치 간격(w = 100 mm일 때는 d = 400 mm, w = 200 mm일 때는 d = 300 mm)까지 배치 간격 d이 증가하면, CFRP 이중 롤러의 양 끝단에서의 변형이 점차 감소하기 때문에 변형 편차 δ가 감소하게 된다. 그 이후, 특정 값 이상으로 배치 간격 d이 증가 시, CFRP 이중 롤러의 중심부에 하중에 의한 변형이 크게 발생됨에 따라 다시 변형 편차 d가 증가하게 된다. 결과적으로, 본 연구에서 선정한 23개의 분석 case들 중, gap block의 폭 w = 200 mm 및 배치 간격 δ = 300 mm인 경우에서 가장 작은 변형 편차 d = 0.1175 mm를 가짐을 확인할 수 있다.
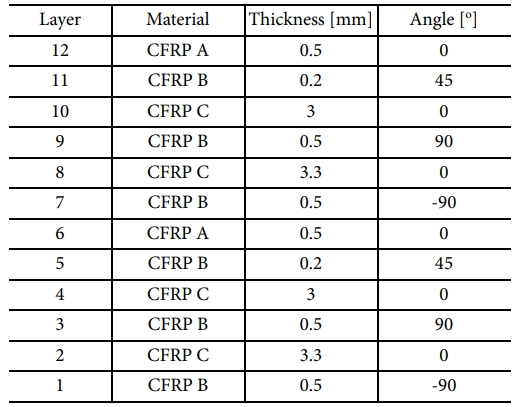
다음으로, CFRP 이중 롤러 구조를 활용한 본 연구의 gap block 설계 유효성을 판단하기 위해 CFRP 단일 롤러에 대한 추가 분석을 수행한다. CFRP 단일 롤러의 경우, CFRP 이중 롤러와 달리 내부 파이프 및 gap block 없이 외부 파이프와 shaft만으로 구성된다. 여기서, CFRP 단일 롤러의 외부 직경 및 x 축 방향 전체 길이는 CFRP 이중 롤러와 동일하다. 또한, CFRP 이중 롤러와 동일한 물성을 갖도록 하기 위해, CFRP 이중 롤러의 내부 파이프와 외부 파이프에 적용되었던 재료, 적층 두께 및 섬유 방향을 동일하게 활용하여 CFRP 단일 롤러의 외부 파이프를 구성하였다. 결과적으로, 비교 대상인 CFRP 단일 롤러의 외부 파이프는 12개의 층을 가지며, 총 두께는 15 mm가 된다. 구체적인 CFRP 단일 롤러에 대한 재료, 적층 두께 및 섬유 방향은 Table 6에 표기하였다. 그 외의, CFRP 단일 롤러에 적용되는 경계 조건 및 하중 조건, 그리고 변형 편차 d를 계산하는 contact area 모두 Section 2에서 소개한 CFRP 이중 롤러의 경우와 동일하다.
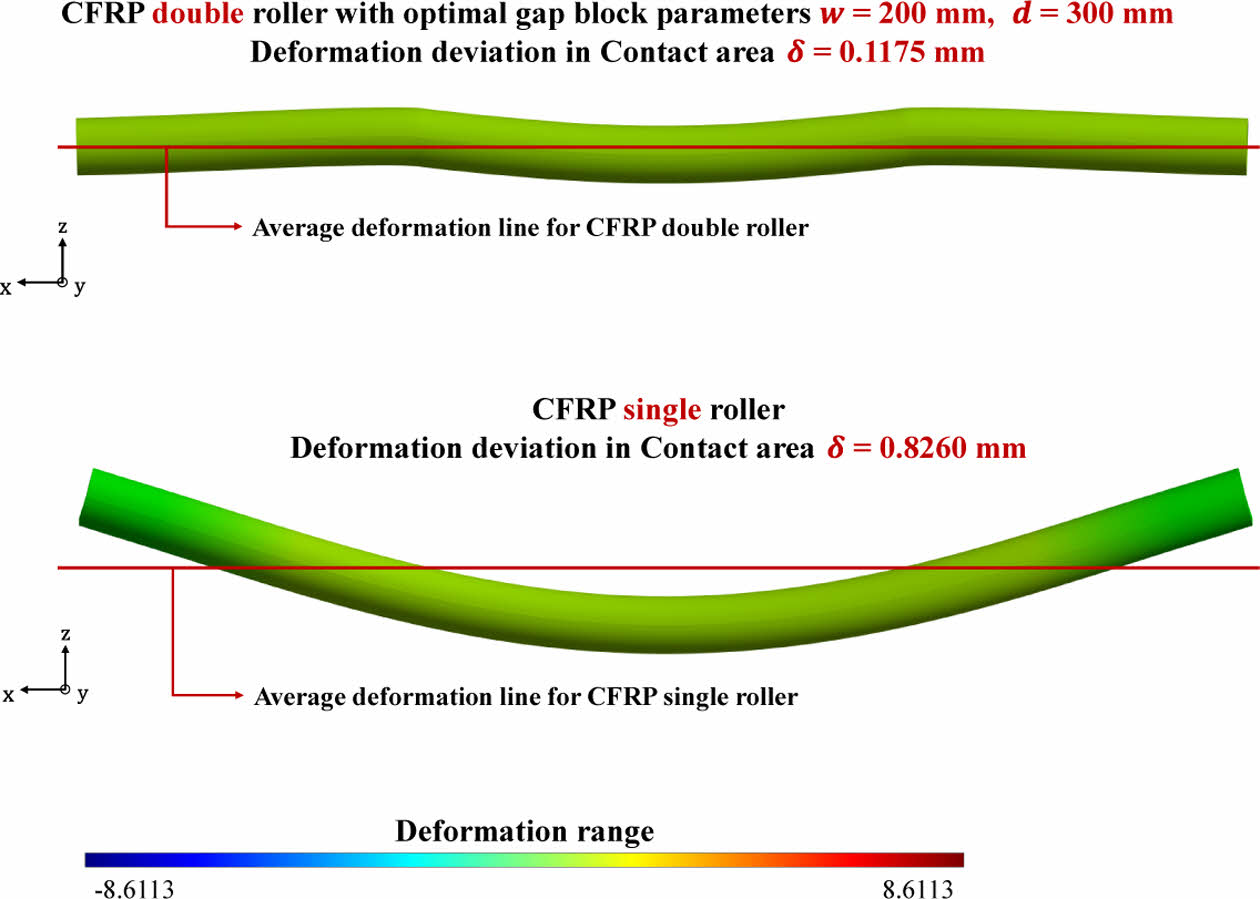
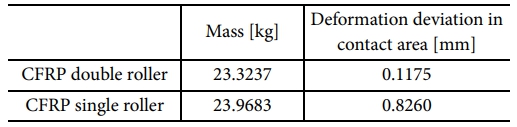
추가적으로 수행한 CFRP 단일 롤러의 해석 결과를 바탕으로, 이번 Section에서 얻은 최적의 gap block 설계 변수 값 (gap block의 폭 w = 200 mm 및 배치 간격 d = 300 mm)에 대한 CFRP 이중 롤러의 변형 양상과 CFRP 단일 롤러의 변형 양상을 비교한 결과를 Fig. 9에 나타내었다. 또한, Table 7에는 CFRP 이중 롤러와 CFRP 단일 롤러의 질량 및 Fig. 4의 contact area에서 계산된 변형 편차 d 값을 표기하였다.
Table 7에서, CFRP 이중 롤러와 CFRP 단일 롤러의 질량 차이는 약 0.6 kg으로 매우 유사함을 알 수 있다. 그러나, Figs. 7 및 9을 통해 파악할 수 있는 것처럼, CFRP 단일 롤러의 경우, CFRP 이중 롤러의 gap block 배치 간격 d이 특정 값 이상인 경우와 유사하게, 분포 하중에 대한 변형이 CFRP 단일 롤러 중심부에 집중되는 단일 양상만을 갖는다. 반면, gap block이 최적화된 CFRP 이중 롤러의 구조에서는 분포 하중에 대한 변형이 분산되게 된다. 따라서, CFRP 단일 롤러와 CFRP 이중 롤러의 질량이 매우 유사함에도 불구하고, CFRP 이중 롤러에서 약 86% 정도 작은 변형 편차 d를 가짐을 확인할 수 있다. 결과적으로, CFRP 이중 롤러 구조의 활용 및 gap block 설계를 통해, 유사한 조건을 가지는 CFRP 단일 롤러의 경우보다 변형 편차 d를 효과적으로 감소시킬 수 있음을 확인할 수 있다.

본 연구에서 우리는, 제품 이송 과정에서 롤러의 변형 편차에 의해 발생되는 제품 결함을 최소화하기 위하여, CFRP가 적용된 이중 롤러의 구조적 특성을 활용하고, 이에 대한 gap block 설계를 수행하였다.
구체적으로, CFRP 이중 롤러의 변형 양상에 직접적인 영향을 주는 gap block 설계 변수 폭 w과 배치 간격 d을 정의하였으며, 공정 정밀도와 CFRP 이중 롤러의 전체 길이 L를 고려하여 23개의 분석 case들을 선정하였다. 그런 다음, 유한 요소 해석을 활용하여 contact area에서의 변형 편차 d를 분석함으로써 선정 case들에 대한 최적의 gap block 폭 w과 배치 간격 d을 도출하였다. 추가적으로, 본 연구의 효용성을 검증하기 위해, CFRP 단일 롤러의 contact area에서의 변형 편차 d를 gap block 변수가 최적화된 CFRP 이중 롤러의 경우와 비교 분석하였다.
그 결과, gap block의 폭 w과 배치 간격 d 설계를 통해 CFRP 이중 롤러의 contact area에서의 변형 편차 d를 최대 11배 이상 감소시킬 수 있었다. 또한, 본 연구에서 활용한 CFRP 이중 롤러와 동일한 직경, 크기 및 물성 등을 갖는 CFRP 단일 롤러와 비교하였을 때, contact area에서의 변형 편차 d를 7배 이상 감소시킬 수 있음을 확인하였다. 다시 말해, 전체 직경 및 크기 변화 없이, 제품과의 접촉 지점에서의 변형 편차를 효과적으로 감소시킬 수 있기 때문에, 본 연구에서 제안한 방법을 통해 경량화된 고신뢰성 제품 이송 시스템을 구현하는데 효과적으로 기여할 수 있다고 판단된다.
본 연구에서는, 제품 이송 시스템에서 롤러의 변형 양상에 의해 발생될 수 있는 결함을 최소화하기 위해, contact area에서의 변형 편차를 최소화하는 CFRP 이중 롤러의 gap block 설계만을 수행하였으나, CFRP 이중 롤러의 구조적 특성 상 gap block 설계에 따라 여러 변형 양상을 가질 수 있기 때문에, 본 연구에서 제안된 방법이 다양한 목적의 산업 분야에 확장 및 적용될 수 있을 것으로 기대된다.
이번 연구에서 정의된 gap block 설계 변수는 이산화된 값이었지만, 추후 연구에서는 보다 정밀한 설계를 위해 연속된 gap block 설계 변수에 대한 고려가 필요하다. 또한, 단방향 CFRP laminate는 적층 수, laminae의 두께, 그리고 섬유 방향 등에 따라 물성이 크게 변화할 수 있기 때문에, 이러한 부분들에 대한 최적화가 고성능 CFRP 이중 롤러의 구현을 위해 반드시 필요할 것으로 판단된다[23-26]. 추가적으로, 이번 연구에서는 수치해석을 기반으로 CFRP 이중 롤러의 gap block 설계를 수행하고 그 효용성을 확인하였으나, 실제 섬유의 Grade 및 기지재를 활용하여 CFRP 이중 롤러의 효용성을 실험적으로 확인하는 것 역시 필요하다. 앞서 언급한 한계점을 해결하기 위한 CFRP 이중 롤러 연구는 추후에 진행될 것이다.