In this paper, a Progressive Damage and Failure Analysis (PDFA) modeling method was developed using ABAQUS/EXPLICIT to predict in-plane damage and delamination for Open-Hole Compression (OHC) testing. The proposed PDFA model was constructed based on Hashin criteria and cohesive behavior. The strength and stiffness of OHC specimens with three types of stacking sequences [(45/-45/0₂)₃]_s, [(45/0/-45/90)₃]_s and [45/-45/0/45/-45/90/(45/-45)₂]_s were compared to comprehensively evaluate the validity of the Finite Element(FE) model of PDFA. The strength and stiffness of the OHC specimens were predicted relatively well, with less than a percentage error 10.0 %. For the numerical simulation case for each layup, the damage initiation/evolution of OHC specimens were evaluated for delamination and tension/compression matrix damage before and after failure

본 논문에서는 압축 하중을 받는 오픈 홀(open-hole compression) 탄소섬유 복합재(carbon fiber reinforced plastic, CFRP) 시편의 평면 내 손상(in-plane damage) 및 층간 분리(delamination)를 예측하기 위한 모델링 방법을 제안하고 유한요소해석(finite element analysis)을 수행하였다. 유한요소모델은 오픈 홀 복합재 시편의 점진적 손상 및 파손 분석(progressive damage and failure analysis)을 위해 Hashin 파손 기준(hashin failure criteria)과 표면 기반 응집 거동(cohesive behavior) 모델을 기반으로 구성되었으며 ABAQUS/EXPLICIT Solver를 활용하여 해석을 수행하였다. 유한요소해석의 타당성을 종합적으로 평가하기 위해 세 가지 유형의 적층 패턴(stacking sequences)을 가지는 오픈 홀 압축 복합재 시편에 대한 시험 결과와 비교하였다. 오픈 홀 압축 시편의 강도와 강성은 백분율 오차(percentage error) 10.0 % 미만으로 비교적 잘 예측하였으며 오픈 홀 복합재 적층판의 인장/압축 매트릭스 손상 상태 및 원공(hole) 근처의 복합재 계면 층간 분리에 대한 손상 상태를 추출하여 평가하고 분석하였다

Keywords: 복합재료(Composite materials), 오픈 홀 압축(Open-Hole compression), 유한요소해석(Finite element method), 점진적 손상 및 파손 분석(Progressive damage and failure analysis), 층간 분리(Delamination)

복합 재료는 기존 금속 재료에 비해 중량 감소 및 기계적 특성 측면에서 상당한 장점을 가지며 최근에는 다양한 산업 응용 분야에서 기존의 금속 재료를 복합 재료로 대체하고 있다. 항공우주 산업에서는 볼트 및 리벳으로 체결되는 다수의 원공이 있는 복합 구조물에 허용 설계치(design allowable values)를 반영하기 위한 목적으로 원공을 가진 복합재 적층판의 인장 및 압축 시험을 활용하기도 한다[1-3]. 그러나 복합재료는 시편 내 섬유 손상(fiber damage), 매트릭스 균열(matrix crack) 및 층간 분리(delamination) 등의 복잡한 파손 네트워크가 발생하며 파손 예측의 불확실성으로 인해 신뢰성 있는 설계를 달성하기 어렵다[4,5]. 따라서, 오픈 홀 복합재의 강도 뿐만 아니라 점진적인 손상(progressive damage) 및 파손(failure)을 정확하게 분석하고 예측하기 위해 다양한 유한요소해석 모델이 개발되고 있다.
오픈 홀 복합재 적층판의 강도를 예측하기 위해 가장 널리 사용되는 방법 중 하나는 Whitney와 Nuismer이 제안한 점 응력(point stress) 또는 평균 응력 모델(average stress model)이다[6]. 제안된 모델은 응력 집중이 발생하는 복합재료 내에서 발생된 응력의 정도가 파괴를 결정한다고 가정하고 응력이 발생한 영역의 크기를 반영하는 재료상수로서 특성 길이의 개념을 도입하였다. Lee 등[7]은 다양한 재료 상수 및 형상(원공 대 폭의 비)을 가진 원공이 있는 복합재 적층판의 파손 하중을 근사적으로 예측할 수 있는 방법을 제안하였다. Soutis 등은 응집 영역 모델(cohesive zone model)을 활용하여 압축을 받는 노치 복합 적층판의 미세 좌굴 손상 영역을 나타내어 해당 적층판의 압축 강도를 예측하였다[8]. Chang 등은 Yamada-Sun과 Hashin의 파손 기준을 통합하여 손상 축적과 개방형 복합 적층판의 강도를 예측하기 위한 2차원 점진적 손상 모델을 개발하였다[9]. 최근 압축 하중을 받는 오픈 홀 섬유 강화 복합재의 점진적인 손상을 모델링하기 위한 다양한 유한요소해석모델이 개발되었음에도 불구하고 불안정성으로 인한 해석의 수렴 문제, 메시 종속성, 층간 분리 및 국부 좌굴 변형을 평가하기 위한 모델링 등 강도와 손상을 예측하는 것은 여전히 어려운 작업이다.
따라서 본 연구에서는 오픈 홀 압축 시험 유한요소해석에 여러가지 손상 및 파손 모델을 적용함으로써 발생하는 해석의 수렴 문제를 해결하기 위해 ABAQUS/EXPLICIT Solver를 활용하였으며 세 종류의 다른 적층 패턴을 가지는 오픈 홀 복합재 압축 시편의 점진적 손상 및 층간 분리를 모사하기 위해 Hashin 파손 기준 및 표면 기반 응집 거동 모델을 기반으로 하는 유한요소모델을 제안하였다. 시험 결과의 강도, 초기 강성을 유한요소해석 결과와 비교하여 유한요소모델의 타당성을 검증하였으며 오픈 홀 탄소섬유 복합재 시편의 점진적 손상에 대한 평가는 인장/압축 수지(matrix) 손상의 시작/진전(initiation/evolution) 및 층간 분리에 대해 평가하였다.

2.1 복합재 손상 및 파손 기준
Hashin 파손 기준은 복합재의 파손 거동을 예측하는 데 사용되며 손상되지 않은 재료가 선형 탄성 거동(linear elastic behavior)을 따른다고 가정하며, 소성 변형(plastic deformation) 없이 복합 재료의 손상의 시작(initiation)과 진전(evolution)을 예측하는 것을 목표로 한다. Hashin의 강도 기준은 손상의 시작을 예측하는 데 사용되며, 손상의 진전은 손상 과정 중 소실된 에너지와 선형 재료의 연화(softening)에 의해 결정된다. 이 파손 기준은 섬유 및 수지의 손상을 포함한 다양한 파손 모드를 고려하며 복합 적층판의 강도 및 강성을 정량화 하기 위한 프레임워크(framework)를 제공한다. Hashin 파손 이론의 손상 시작 기준의 일반적인 형태는 다음 식과 같다[10,11]:

섬유 인장 파손 모드 (δ₁₁≥0):



섬유 압축 파손 모드 (δ₁₁<0):



수지 인장 파손 모드 (δ₂₂≥0):



수지 압축 파손 모드 (δ₁₂≥0):



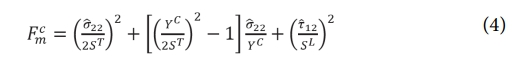
Hashin 파손 기준의 손상 진전 기능은 손상이 재료 강성의 점진적인 저하를 특징으로 하여 재료 파손으로 이어진다고 가정한다. 손상 시작 후 특정 모드에 대한 손상 변수(damage variable)는 식 (5)로 나타내어진다.



여기서 δ⁰_eq는 해당 모드의 손상 시작 기준이 충족된 초기 등가 변위이고, δ^f_eq는 각 파손 모드에서 재료가 완전히 손상된 변위이다. 손상 변수 d에서 d = 0은 손상이 없음을, 0 < d< 1은 부분적인 손상을, d = 1은 완전한 손상을 나타낸다.
2.2 계면 손상 모델
응집 거동 모델은 주로 두께가 무시할 수 있을 정도로 작은 계면에 적용하기 위한 것이며 복합재의 층간 분리 현상을 모사하기 위해 사용된다. 이 모델은 이중 선형 견인-분리 법칙(bi-linear traction separation law)을 사용하여 정의되는 응집 영역 모델과 매우 유사한 기능을 가진다. 손상 시작은 공칭 응력의 비율을 포함하는 이차 상호 작용 함수가 1의 값에 도달할 때 발생하는 것으로 가정한다. 이 기준은 다음과 같이 표현할 수 있다.



혼합 모드 파손에서에서는 Benzeggagh-Kenane (B-K) 파손 기준이 활용된다. 이 기준은 다음 식과 같이 표현할 수 있다[12]:



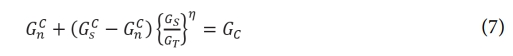
여기서 G_S = G_s + G_t이며 G_T = G_n + G_s + G_t과 같다. G_n^C, G_s^C는 각각 하중이 적용되는 면의 수직 방향과 전단 방향의 임계 파단 에너지이며 η는 B-K 혼합 모드 지수이다.

3.1 유한요소해석 모델링 및 경계조건
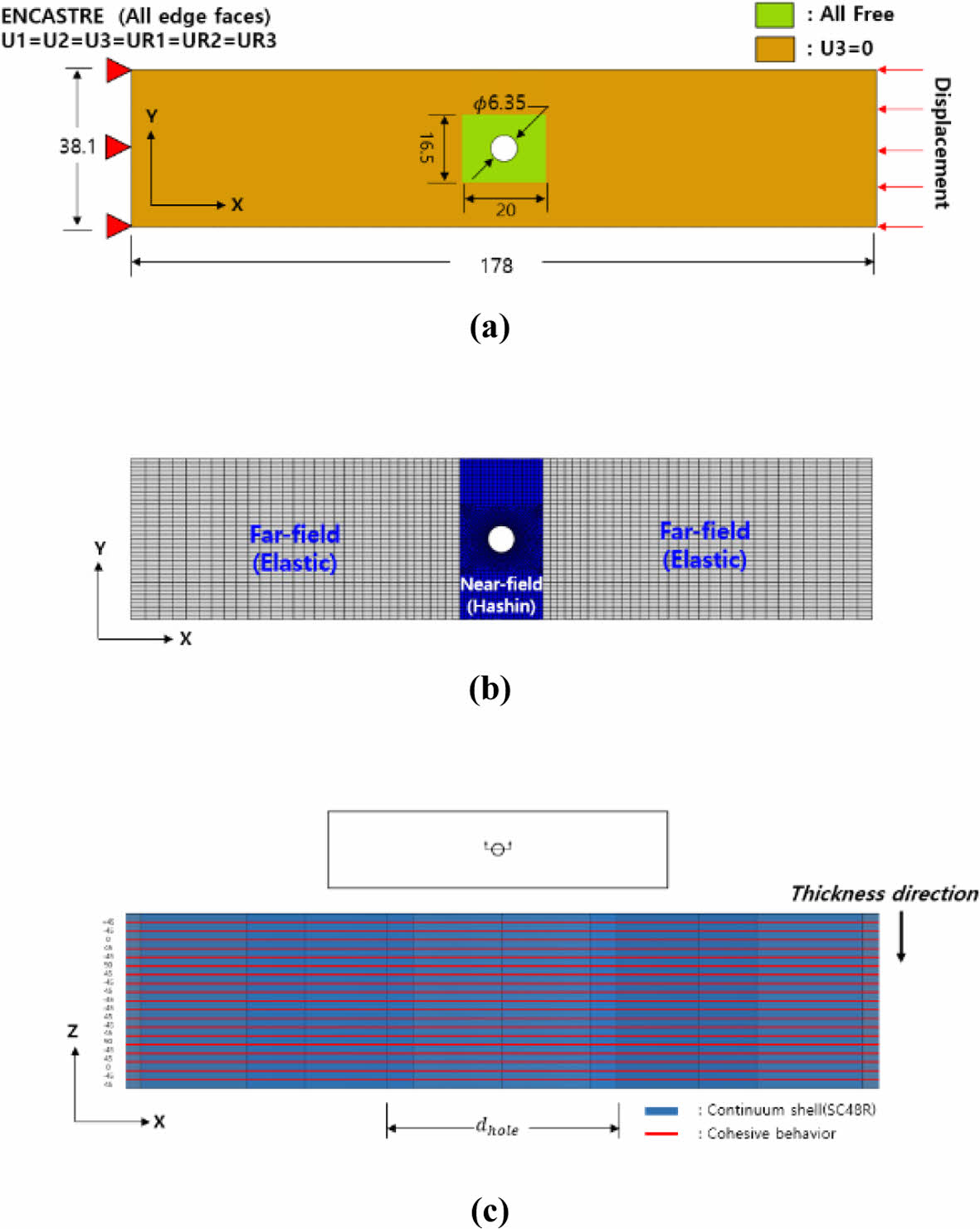
압축 하중을 받는 오픈 홀 탄소섬유 복합재 시편 대한 유한요소 모델은 Fig. 1(a)에 표시된 바와 같이 ASTM D6484 절차 A[13]에 의거하여 실험에 사용된 것과 동일한 형상으로 경계 조건을 적용하였으며 시편의 그립(grip) 영역을 생략하여 전체 모델 길이를 줄였다. 경계 조건은 압축 방향으로 하중을 적용하고 다른 쪽 끝은 모든 방향으로 고정하였다. 녹색으로 표시된 원공 주변 영역(20 mm × 16.5 mm)을 제외하고 나머지 원거리 영역(노란색)은 두께 방향으로 구속 조건을 적용하여 오픈 홀 압축 시험 치구(test fixture)를 모사하였다. 재료 물성 모델은 원거리 영역(흰색)으로 표시된 나머지 영역은 시뮬레이션에서 선형 탄성 영역으로, 원공 주변 파란색 영역은 Hashin 파손 기준에 해당되는 재료 모델로 정의하였다(Fig. 1(b)). 각 라미네이트의 평면 외 변형(out of-plane deformation)과 국부 좌굴(local buckling)을 모사하기 위해 원공 주위는 0.5 mm 메시 크기의 8-노드 3D 연속체 쉘 요소(SC8R)로 모델을 구성하였다. 층간 분리를 모사하기 위한 응집 거동 모델은 Fig. 1(c)와 같이 복합재 층간 사이의 계면에 적용하여 모델링하였다.
3.2 재료 물성 모델
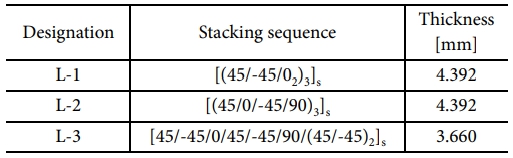
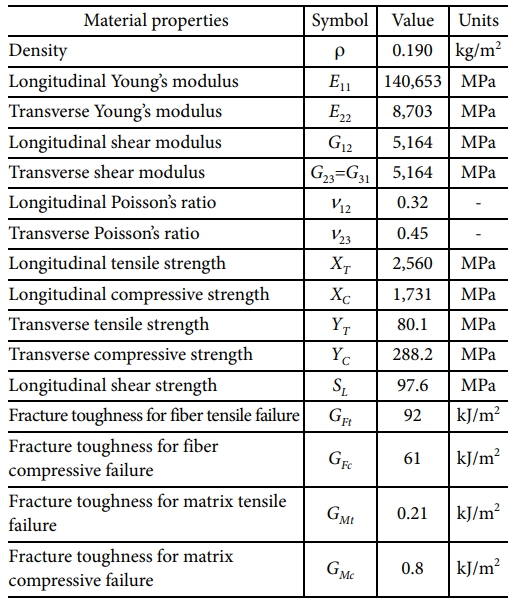
압축 하중을 받는 복합재 적층판의 손상은 적층 패턴에 매우 민감하기 때문에 세 가지 다른 적층 패턴을 적용하였다[14]. Table 1은 오픈 홀 탄소섬유 복합재 시편의 적층 패턴 종류에 따른 두께 정보를 나타낸다. 다수의 0^o 방향의 24겹의 플라이 수를 가지는 복합재 적층판이 L-1, 준등방성을 가지는 24겹 복합재 적층판이 L-2, 다수의 45^o 방향의 적층각이 포함된 20겹의 복합재 적층판이 L-3로 명명되었다. 경화된 복합소재의 공칭두께가 0.183 mm인 일방향 탄소섬유 프리프레그(unidirectional carbon-fiber prepreg) 소재 IM7/8552의 재료 특성은 Table 2에 제시된 대로 오픈 홀 복합재 시편의 유한요소모델에 적용되었다[15,16]. 각 복합재 적층판 계면의 응집 거동에 대한 기계적 특성 및 해석 물성은 Table 3에 나타내었다[16].

4.1 응력-변형률 선도 비교
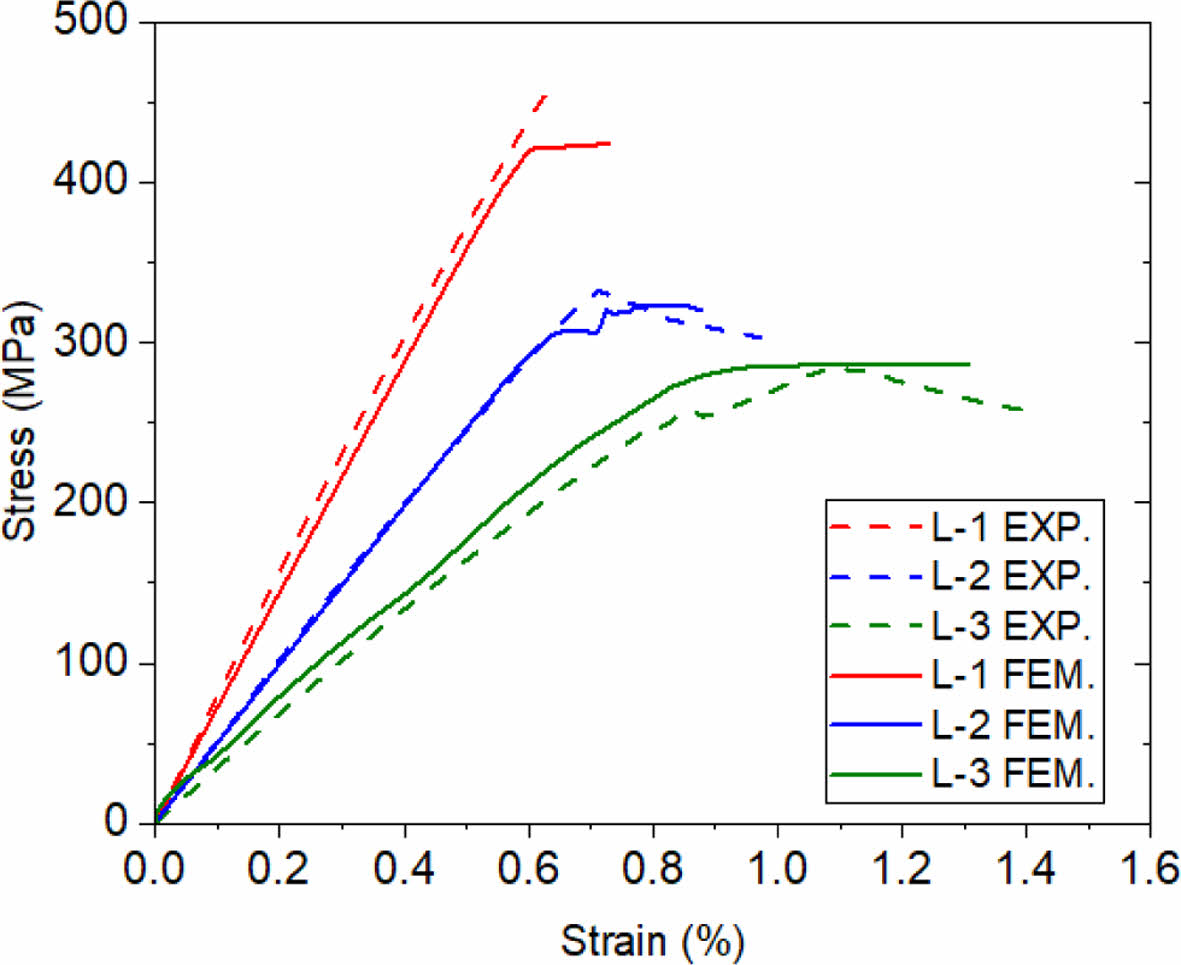
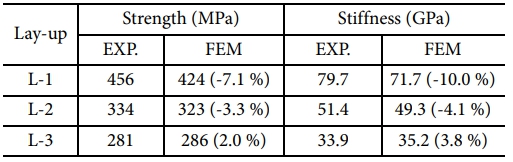
유한요소해석 결과와 오픈 홀 압축 시험에 대한 비교 연구는 문헌에서 수행된 시험 결과를 사용하여 수행되었다[17]. Fig. 2는 시편의 응력-변형률 선도를 보여 주며 점선은 시험 결과를 나타내고 실선은 해석에서의 예측 결과를 나타낸다. 손상된 요소의 과도한 왜곡(distortion)으로 발생하는 수치 오류로 인해 해석이 종료되며 유한요소해석에서의 응력-변형률 선도 예측 결과는 최대 파손 하중에 도달 한 지점까지 그래프에 표시된다. 유한요소해석 결과에서 L-1 및 L-2 적층 패턴을 가지는 오픈 홀 복합재 시편의 응력-변형률 응답은 초기부터 최대 하중 직전까지 선형적인 응답을 보이는 반면, L-3 시편의 응답은 약 0.45 % 변형률에서 파괴 변형률까지 비선형적인 응답을 보인다. Table 4는 각 오픈 홀 압축 시험에 대해 최대 하중에서의 강도 및 초기 강성의 실험값과 유한요소 해석결과를 비교하였다. 백분율 오차는 실험값을 기준값으로 사용하여 계산되었다. 유한요소해석결과는 강도와 강성에 대해 전반적으로 비교적 잘 일치하였다. L-1 시편의 초기 강성은 약 10.0 % 과소평가된 반면, L-2, L-3 시편의 강성은 4.1 % 오차범위 내에서 일치하는 것으로 나타났다.
4.2 층간 분리 및 복합재 라미네이트 변형
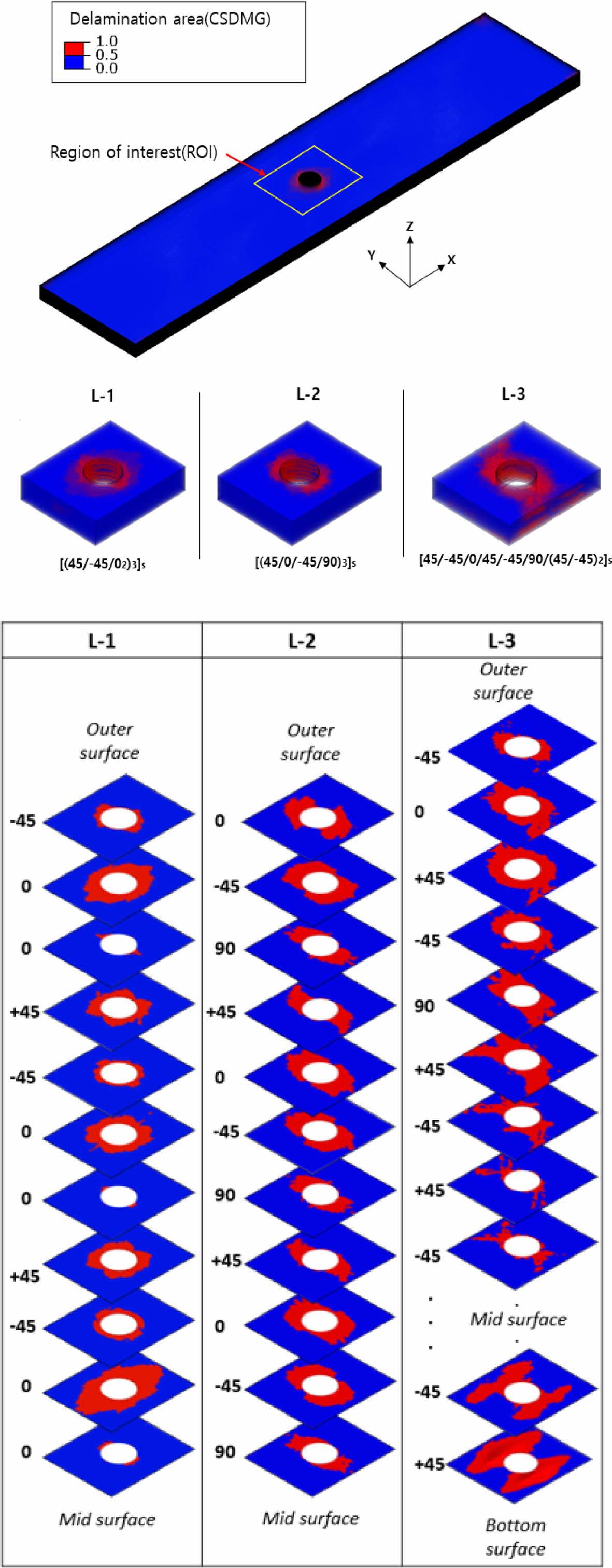
층간 분리에 대한 해석 결과는 Fig. 3과 같이 시험 파손 하중 직전에 복합재 원공 근처에 발생하는 손상으로 평가하였다. 붉은색으로 나타나는 영역이 계면이 손상된 영역이며 층간 분리는 원공 주변에서 시작하며 층간 분리 영역은 각 적층 패턴 마다 다르다. 시편 L-1의 경우 층간 분리 영역은 주로 하중 방향으로 분포하며 L-2의 경우 하중의 횡 방향, L-3의 경우 각 층의 라미네이트에 따라 불규칙하게 분포되어 있다. 세 개의 모든 적층 패턴 중 다른 계면에 비해 0^o 라미네이트와 적층 각도가 변화하는 인접한 라미네이트에서 층간 분리 영역이 더 큰 것을 알 수 있다.
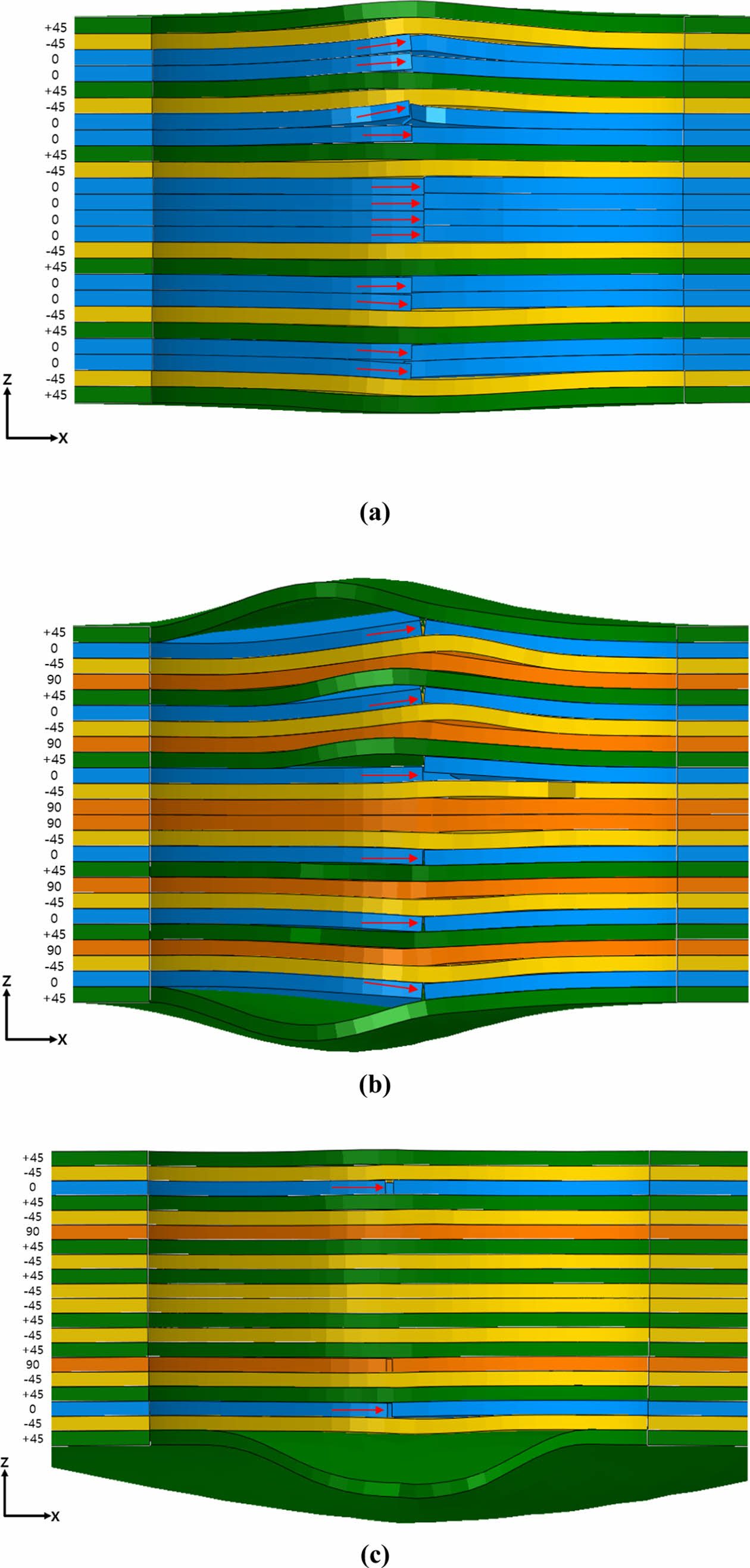
Fig. 4는 복합재 시편의 파손 직전에 발생한 원공 근처에서의 변형된 복합재 라미네이트 단면을 보여준다. 섬유 압축 파손이 발생한 부분은 붉은색 화살표로 표시되어 있다. Fig. 4(a)에서, 두 겹의 0^o 라미네이트 내에서 섬유 압축 파손으로 삭제된 요소(elements)로 인해 라미네이트가 적층 된 평면을 벗어나 두께방향으로 변형이 발생한다. 이 변형은 인접한 라미네이트의 층간 분리를 일으키는 주요 원인으로 볼 수 있다. 이와 대조적으로, 복합재 적층판 중앙에 있는 0^o 라미네이트는 두께 방향으로 큰 변형없이 파단 된다. Fig. 4(b)에서 0^o 라미네이트 층에 인접한 ±45^o 층은 두께 방향으로 과도한 변형이 발생하며 Fig. 4(C)에서는 최 외각에 있는 라미네이트 한 층이 국부적인 좌굴이 나타나면서 ±45^o 라미네이트에서 큰 변형이 발생했음을 보여준다. 이 변형은 최외각층에서 넓은 영역에 걸쳐 층간 분리를 유발한다. 압축 하중을 받는 오픈 홀 압축 복합재 시편에서 층간 분리는 라미네이트 하부 좌굴(sub-laminate buckling) 또는 섬유 압축 파손(fiber compressive failure)를 유발하며 라미네이트의 두께방향으로 발생되는 변형은 하중 지지 능력 감소(load-carrying capability)의 주요 원인임을 알 수 있다.
4.3 복합재 매트릭스 손상 시작 및 진전
유한요소해석 결과에서는 세 가지 종류의 적층 패턴을 가지는 오픈 홀 압축 시편들의 파손이 발생하는 시점의 전후에 대한 수지 손상의 시작 및 진전을 보여준다. 손상 변수는 각 손상 시작 기준(섬유 인장, 섬유 압축, 수지 인장, 수지 압축)에 도달하여 손상 변수가 1.0 이상이면 손상 기준이 충족된다.
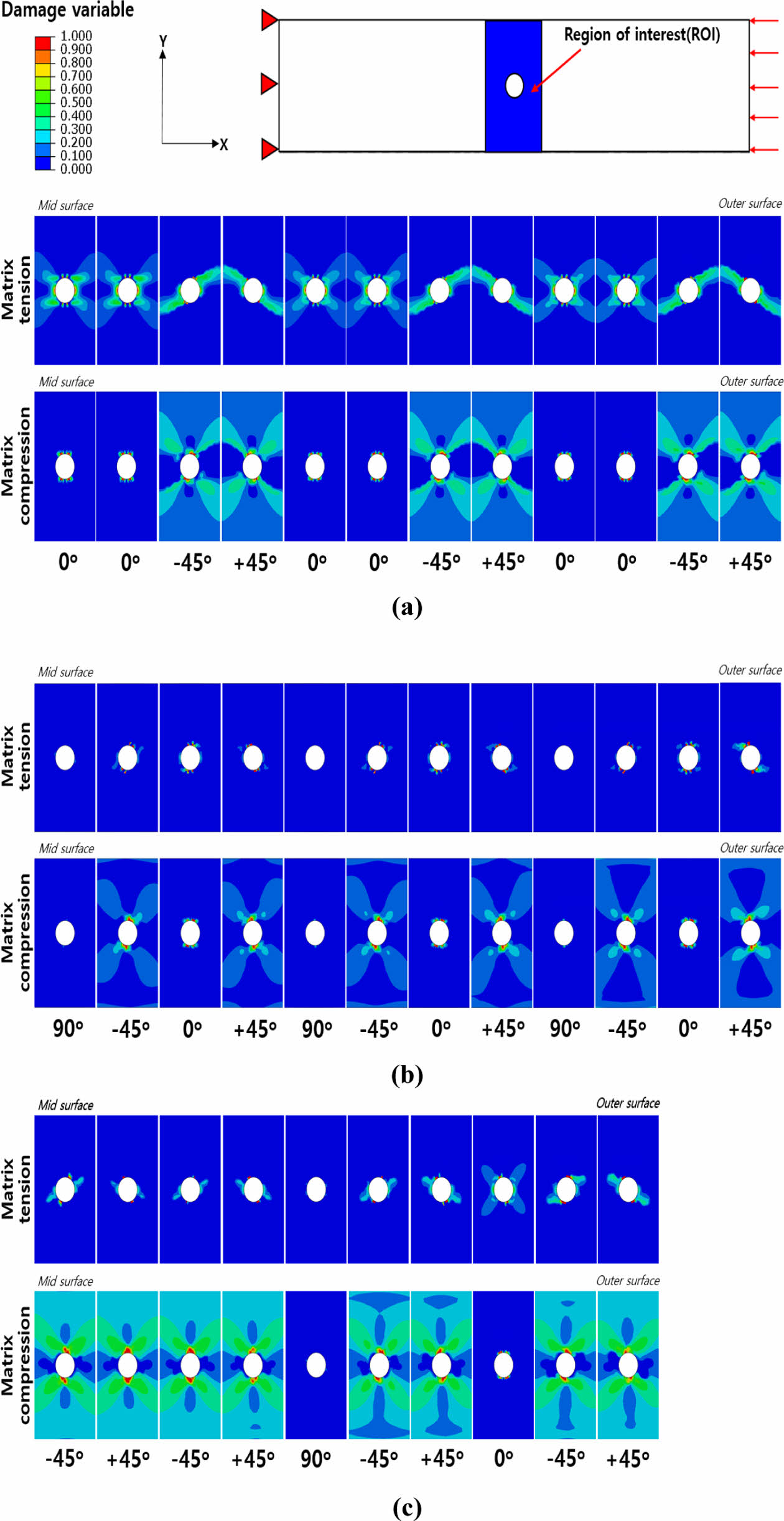
Fig. 5는 세 가지 다른 적층 패턴의 오픈 홀 압축 시편에 대해 파손 하중의 91 % 수준에서의 수지 압축 손상 시작 상태를 보여준다. 세 종류의 시편 모두 원공 근처에서 매트릭스 손상이 시작되며, 압축으로 인한 매트릭스의 손상 시작은 하중 방향의 횡 방향으로 분포되어 있는 것을 확인할 수 있다. 오픈 홀 압축 복합재 시편의 라미네이트 중 ±45^o 라미네이트의 수지 손상이 0^o 및 90^o 라미네이트에 비해 더 두드러지게 나타나는 것을 볼 수 있다. L-1 시편의 경우, 원공 중앙 위 부분에서 0^o 인장으로 인한 국부적인 손상 시작이 발생하며 ±45^o 라미네이트에서는 하중 방향의 횡 방향으로 손상이 시작된다. L-2 및 L-3 시편에서의 수지 인장 손상 시작은 ±45^o 라미네이트에서 국부적으로 발생하며 수지 압축 손상이 횡 방향으로 손상 시작이 발생되는 것을 확인 할 수 있다. 90^o 라미네이트에서는 대체적으로 손상이 미미한 것을 볼 수 있다.
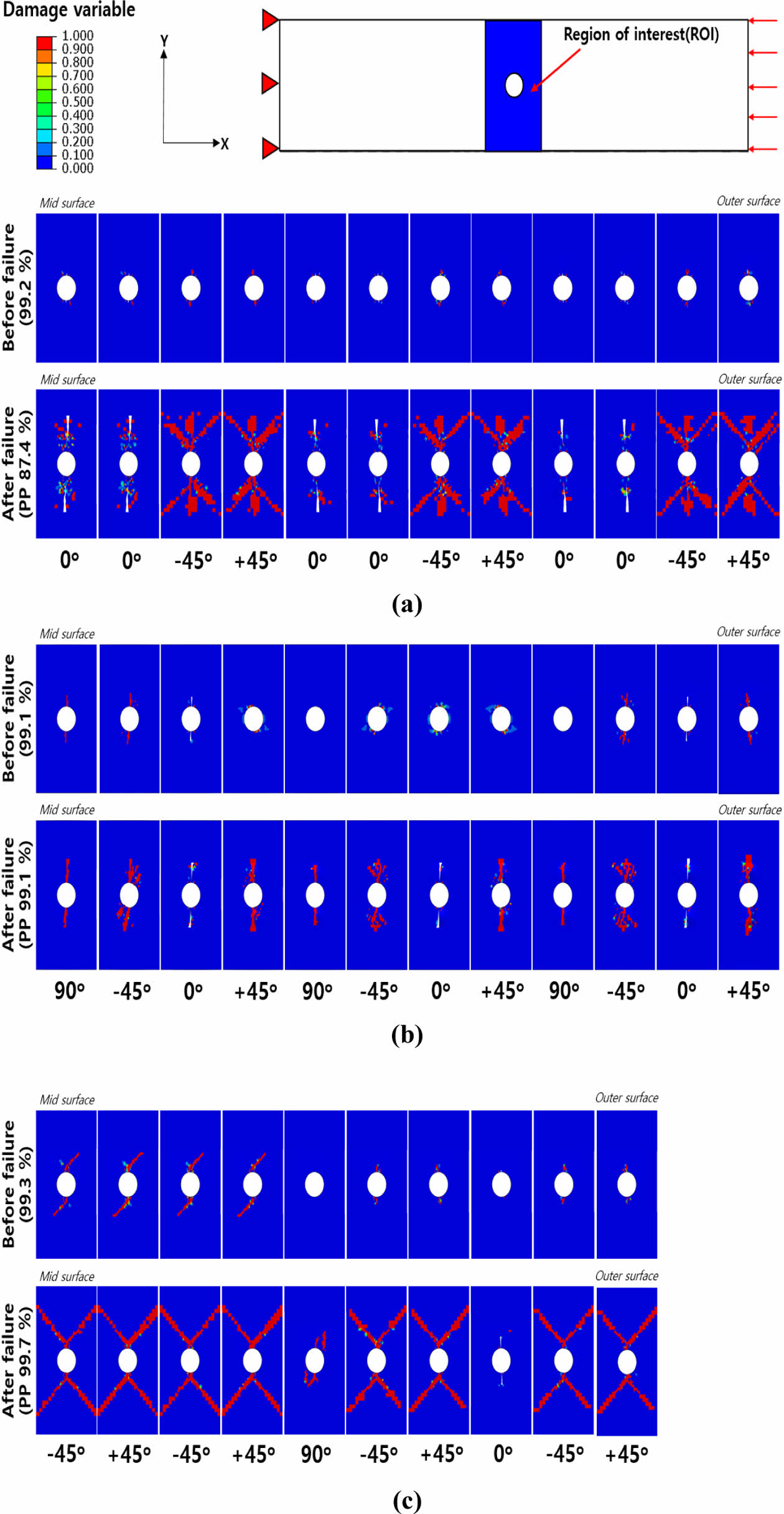
본 Fig. 6은 세 가지 다른 적층 패턴의 오픈 홀 압축 시편에 대한 파손 직전 및 파손 이후의 수지 압축 손상의 진전 상태를 보여준다. 하중 수준은 최대 파손 하중에 대한 백분율로 표시되며 PP(post-peak)는 파손 이후를 나타낸다. 모든 L-1, L-2, L-3 복합재 시편의 파손 전에는 원공주위에서 작은 영역에 걸쳐 하중 방향의 횡 방향으로 수지 손상이 발생하는 것을 확인할 수 있으며 파손 이후에서는 시편 내의 0^o 방향의 라미네이트에서 섬유 압축 파손으로 인해 요소가 삭제되는 것을 확인할 수 있었다. 전반적으로 ±45^o 라미네이트에서 압축으로 인한 수지의 손상 영역이 가장 넓은 것을 확인할 수 있었다.

본 연구에서는 ABAQUS/EXPLICIT를 이용하여 압축 하중을 받는 오픈 홀 복합재 시편의 점진적 손상 및 파손 거동을 예측하기 위해 hashin 파손 기준과 표면 기반 응집 거동 모델 기반으로 유한요소모델을 생성하고 유한요소해석을 수행하였다. ASTM 시험 기준과 기존 문헌들을 통해 재료 특성과 경계조건을 적용하여 오픈 홀 압축 복합재 시편의 유한요소모델을 구성하였다. 유한요소해석에서의 예측 결과는 강도와 강성 측면에서 백분율 오차 10.0 % 이내로 비교적 잘 일치하였다. 층간 분리는 원공의 가장자리에서 시작되며 발생하는 영역은 적층 패턴에 따라 다른 것을 확인할 수 있었다. 수지 압축 손상 또한 원공 근처에서 시작되며 ±45^o 라미네이트에서 손상 영역이 두드러졌다. 본 연구에서 제시한 유한요소해석 모델링 방법을 활용하여 항공 및 자동차 복합재 구조물의 패스너가 적용되는 구조물에서의 점진적 손상 및 파손 분석을 하기 위한 목적으로 활용할 수 있을 것으로 판단된다.

본 논문은 한국재료연구원 기초연구프로그램 (탄소 장섬유 열가소성 복합재를 응용한 충돌흡수 일체형 구조 기술 개발, PNK9060)과 산업통상자원부 소재부품기술개발사업으로 지원된 연구결과입니다(멀티셀 구조 인발 부품 및 재활용 탄소섬유 열가소성 중간재 적층 부품 기반 차체 센터 모듈 제조 기술 개발, 20017479). 지원에 대해 진심으로 감사드립니다.