The sandwich structure, consisting of a core and a face sheet, is used for lightweight structural application. Generally, cellular structures like honeycomb, foam, and lattice structures are utilized for the core. Among these, lattice structures have several advantages over other types of structures. In other studies, curved lattice structures were reported to have higher mechanical properties than straight structures by converting shear stresses acting on the structure into compressive stresses. Moreover, the addition of vertical struts can have a positive effect on the mechanical properties of the lattice structure. For the purpose, two lattice structures with Circle Arch (CC) and Circular Arch with a vertical column (CC_C) were studied, which were fabricated by using selective laser sintering was conducted. The result showed that CC_C has dramatic performance improvements in specific strength, modulus, and strain energy density compared to CC, confirming that vertical struts played a significant role in the lattice core. Finite element analysis was employed to determine the cause of the stress behavior of CC and CC_C. This study is expected to help design structurally superior lattice cores and sandwich structures

Keywords: Sandwich structure, Lattice core, Additive manufacturing, Selective laser sintering, Arch structure

A sandwich structure consists of outer face sheets and an inner core located in between, and this type of structure finds applications in various fields like aerospace, automotive, and electronics, as it effectively reduces the overall weight of the structure [1]. The face sheet supports the bending and in-plane loads acting on the structure. It typically consisted of very thin materials with high strength and stiffness. The core supports the compressive and shear loads acting on the structure and utilizes materials that are relatively lightweight and have low strength and stiffness compared to the face sheet. Typical structures utilized for the core include honeycomb, foam, and lattice. These are referred to as cellular structures, each of which is a repeating arrangement of hexagonal hollow spaces, gas pockets, lines, or faces [2-5]. Among these structures, the lattice structure offers superior stiffness and strength when compared to the foam structure, and provides high heat dissipation and greater freedom of shape compared to the honeycomb structure [3,6].
The lattice structure has a difficulty in fabrication than other cellular structures, but this has been addressed with the development of additive manufacturing (AM), one of the next-generation manufacturing processes. AM, also known as 3D printing, refers to the process of involves building products by adding materials layer by layer rather than the traditional process of removing materials. AM processes have a high degree of fabrication and design freedom, allowing for the creation of complex lattice structures utilizing a wide variety of materials [3].
Powder bed fusion (PBF) is a process in which a powdered material is melted or sintered to create a product. Compared to other 3D printing processes, PBF provides high mechanical properties and durability, and has the advantage that the powder used in the process acts as a support, so no support is required while printing. Among them, selective laser sintering (SLS), in which polymers are sintered by laser, is one of the processes suitable for lattice structure fabrication [7,8].
Lattice structures can be categorized into the surface-based lattice and strut-based lattice structures. The surface-based lattice structures have a repeated pattern of curved surfaces, such as gyroid and diamond structures [9,10]. On the other hand, strut-based lattice structures consist of nodes and struts. Nodes refer to the points where two or more struts intersect, while struts are the structural elements that connect the nodes. These lattices can be categorized according to the placement of nodes and the shape of struts [11]. Representative shapes of strut-based lattices based on the arrangement of nodes include Tetrahedral [12], Pyramidal [13-15], and 3D-kagome [16,17]. Typical strut geometries include straight lines and curved lines [18-21]. Methods to improve the mechanical properties of strut-based lattices include node optimization, changing strut geometry and dimensions, and placing additional struts [8,16,20]. Research by Long B. has shown that curved struts can convert shear stresses acting on the structure into compressive stresses, and thus higher strength and toughness can be expected compared to straight struts [22]. According to the study by Y. Shen, the addition of vertical struts can be expected to improve structural performance [19].
In this study, quasi-static compression tests were conducted utilizing a circular arch lattice fabricated using the SLS process. The stiffness, strength, and strain energy density of the designed lattice were analyzed to determine the effect of additional vertical struts in the circular arch lattice.

2.1 Lattice Core Design
The designed lattice structure consists of three distinct components: flanges for connecting with the face sheet, shear struts to support shear and compressive stresses, and vertical struts to support mainly compressive stresses. The shear strut and the vertical strut have the same diameter of 1 mm. The unit cell is composed of eight arched-shaped shear struts with a volume of 8×8×13.4 mm³ and optionally includes a compression strut in the center. Fig. 1(a) shows Circular Arch (CC) is made of arched shear struts only, and Fig. 2(b) illustrates a Circular Arch with column (CC_C) made of vertical struts added to the CC structure.
The compression specimens for the experiments were composed of a total of nine-unit cells by arranging in 3∙3∙1 depicted in Fig. 2. Each specimen has a relative density (ρ_rel) of 5.31% (CC) and 5.9% (CC_C), which is calculated using the Eq. (1).



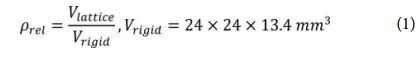
2.2 Fabrication
Fig. 3 is a photograph of the actual fabricated specimen. The specimens were produced using a 3D SYSTEMS ProX SLS 6100 machine and Duraform ProX PA material. The process conditions and properties of the equipment and materials employed for the specimens are shown in Tables 1 and 2.

Quasi-static compression tests were performed at a rate of 0.5 mm/min, up to a compression distance of 3 mm. The test was operated under the guidelines of ASTM C365. A total of six specimens were employed, with three specimens for each design (CC, CC_C). Fig. 4 shows a universal testing machine (Ametek Inc., USA) and CP-156-St (Compression plate) that were utilized for the experiments. The apparent stresses (σ_a) in the z-direction as shown in Fig. 2 were calculated based on the plane area of 24×24 mm². Additionally, the strains (ε_h) in the core height were calculated using the specimen's height of 13.4 mm, excluding the flange.
Fig. 5 shows the stress-strain curves of the lattice structure obtained from the compression test. The curves represent each lattice structure specimen and distinguished by color, with black representing CC_C and red representing CC. Both design exhibit a stable elastoplastic behavior, with a clear elastic region entering the plastic region after reaching the yield stress. In the case of CC, a plateau stress behavior was observed in the plastic zone, where the stress remained at a constant level, consistent with the behavior typically observed in most cellular structures. On the other hand, CC_C exhibited a strain-softening behavior in which the stress decreased in the plastic zone. The key distinction between these two specimens is the presence or absence of vertical struts. Therefore, this variation in stress behavior can be attributed to the existence of the vertical strut in the lattice structure.
The analysis of the experimental video was conducted to further understand the behavior of the specimen during the experiments at a constant strain rate. Fig. 6 provides a summary of the observed specimen behavior. In the case of the arched shear struts, as the strain increases, they tend to stretch horizontally while maintaining the shape of an arch. In the case of the vertical strut, buckling occurred at a strain of 0.1. As the strain further increased, the buckling deformation become more pronounced, leading to the failure of some vertical struts.
Therefore, it was confirmed that the arched shear struts that maintain their shape during compression cause a stable stress-strain curve in the plastic zone in Fig 5. In contrast, the vertical struts, which underwent buckling and subsequent failure after a certain strain, displayed stress-softening behavior.
Fig. 7 shows the results of the specific strength, specific modulus, and specific strain energy density of CC and CC_C calculated by dividing each measurement of strength, modulus, and strain energy density by the relative density. For the relative density, the density of the material (Durafoam ProX PA) is multiplied by the density of the lattice structure.
For strain energy density, the area under the stress-strain curve up to a strain of 0.224 was calculated and used. The maximum specific strength, specific modulus, and specific strain energy density were 180.2 (±3.5) kPa, 2.61 (±1.2) MPa, and 33.0 (±0.8) kPa for CC, and 446.1 (±31.2) kPa, 12.5 (±6.9) MPa, and 63.2 (±10.3) kPa for CC_C, respectively.
It is noteworthy that CC_C displayed significantly higher values compared to CC. Specifically, CC_C demonstrated 123.0%, 332.4%, and 72.2% higher maximum specific strength, specific modulus, and specific strain energy density compared to CC. It should be mentioned that CC_C had an 11.1% higher relative density than CC due to the addition of vertical struts. Despite this relative density increase, the property improvements in CC_C were substantial. This confirms that the vertical strut parallel to the direction of stress applied for a very important role in the compressive stress acting on the specimen.
In addition, CC_C showed a higher standard deviation compared to CC. This is analyzed as a defect in some vertical struts of the CC_C specimen. Since the vertical struts play a large role in compression, it is predicted that the defects here contribute significantly to lowering the overall mechanical properties.

4.1 Finite Element Analysis Modeling
The commercial program ABAQUS/2020 was used for the analysis. The material property modeling for the analysis was based on the results of the horizontally printed property evaluation of Duraform ProX in a study by Anders Lindberg [23]. The experimentally measured properties correspond to the nominal properties, while for the finite element analysis it is necessary to utilize the true property values and not the nominal properties. The nominal properties can be converted to true properties using the following equations (Eq. (2)-(3)). Fig. 8 shows the nominal and true stress-strain lines of the properties used in the analysis.
Dynamic/Explicit Step was used for the analysis. Material properties were modeled using ‘Elastic’ for elastic behavior, ‘Plastic’ for plastic behavior, and ‘Ductile damage’ for damage behavior. A 10-node modified quadratic tetrahedron (C3D10M) was used as the element for the analysis. For the loading and boundary conditions, a rigid plate was modeled to describe the actual compression test behavior, and contact conditions were imposed on the flange surface. One surface of the plate was fully constrained, while the opposite surface was given a final deformation of 3 mm.



subscripts: T: true, n: nominal
4.2 FE Analysis Results and Discussion
Fig. 9 is the analysis result of the same strain as the experimental video analysis in Fig. 6. Both CC and CC_C showed high stress distribution at the flange, arched shear strut, and the nodes between the struts. Also, the specimen deformation shape showed the same trend as the experimental results.
The arched shear struts deformed horizontally while maintaining the arch shape, while the vertical struts buckled. These results support the fact that CC and CC_C have different stress behavior. Fig. 10 shows the stress-strain curves of the simulation and experiment. The analytical results show the same elastoplastic deformation behavior as the experimental results, with a plateau stress behavior in the case of CC and a strain-softening behavior in the case of CC_C. However, the analytical results showed higher stiffness and strength than the experimental results, which was analyzed through literature survey. In a study by I. Maskery, who evaluated the properties of Nylon 12-based EOS polyamide PA 2200, it was confirmed that the tensile and compressive properties are anisotropic [9], and in a study by A. Lindberg, whose properties are referenced in this study, it was confirmed that the mechanical properties vary depending on the printing direction of the SLS method [23]. In addition, in a study by J. Kozak, it was concluded that variables affecting the product properties such as powder size and re-used powder percentage, production environment, and output conditions affect the actual results [24].
Consequently, the utilization of material properties in the literature and the lack of consideration of variables affecting product properties are the main reasons for the discrepancies in the analytical results. Nevertheless, it was found that the FE analysis provides a good description of the experimental trends in compression behavior.

In this study, experimental and analytical studies were conducted on circular arch lattice cores utilizing the selective laser sintering (SLS) process. The quasi-static compression test results showed that both types of specimens, CC and CC_C, exhibited typical elastoplastic deformation behavior with a clear elastic region and entered the plastic region after reaching the yield stress. The video analysis showed that the arched shear struts stretched horizontally, while the vertical struts buckled as the strain increased.
When comparing the mechanical properties of lattice structures with the presence or absence of vertical struts, CC_C with vertical struts showed superior results in specific strength, specific modulus, and specific strain energy density compared to CC. This result confirms that vertical struts play a major role in withstanding compressive stresses. The finite element analysis using the material properties from the references confirmed the deformation behavior of the shear and vertical struts similar to that of the experiment, supporting the results of the specimen behavior analysis. In conclusion, this study is expected to contribute to the design of lattice cores with improved structural performance.

This research was conducted by the Original Technology Development Project “Design and Fabrication of Multifunctional Electromagnetic Structures for Unmanned Vehicle” (2020M3C1C1A01084756) funded by the Ministry of Science and ICT, and by the Field-Linked Future Leading Talent Development Project (2022H1D8A3037396) funded by the National Research Foundation of Korea, and we sincerely thank them for their support.