This paper proposes a new finite element formulation based on enhanced first-order shear deformation theory including the transverse normal strain effect via the mixed formulation (EFSDTM-TN) for the effective thermo-mechanical analysis of laminated composite structures. The main objective of the EFSDTM-TN is to provide an accurate and efficient solution in describing the thermo-mechanical behavior of laminated composite structures by systematically establishing the relationship between two independent fields (displacement and transverse stress fields) via the mixed formulation. Another key feature is to consider the thermal strain effect without additional unknown variables by introducing a refined transverse displacement field. In the finite element formulation, an eight-node isoparametric plate element is newly developed to implement the advantage of the EFSDTM-TN. Numerical solutions for the thermo-mechanical behavior of laminated composite structures are compared with those available in the open literature to demonstrate the numerical performance of the proposed finite element model.

본 논문에서는 복합소재 적층 구조물의 열-기계적 거동을 효과적으로 예측할 수 있는 8절점 판 요소 기반 전산해석 기법을 제안하고자 한다. 횡방향 수직 변형이 고려된 개선된 일차전단변형이론을 바탕으로 유한요소 정식화를 수행하였으며, 독립적으로 가정되는 변위장 및 응력장 사이의 타당한 수학적 관계식을 도출함으로써 해석 결과의 정확도와 계산 과정의 효율성을 동시에 향상시키고자 하였다. 또한, 횡 방향 변위장의 개선을 통해 횡방향 수직 변형을 효과적으로 고려함으로써, 복합소재 적층 구조물의 열적 거동 예측 과정에서의 신뢰성을 확보하고자 하였다. 수치 예제로써 열-기계 하중을 받는 2차원 복합소재 적층평판을 고려하였으며, 3차원 탄성해 및 참고문헌에서 활용 가능한 해석 결과와의 비교, 검토를 통해 제안된 유한요소 해석 기법의 성능을 검증하였다

Keywords: 복합소재 적층평판(Laminated composite plates), 유한요소해석(Finite element analysis), 열-기계적 거동(Thermo-mechanical behavior), 횡방향 수직 변형(Transverse normal strain)

최근 들어 주목받고 있는 다양한 환경 이슈들과 맞물려 에너지 효율 향상을 위한 고강도 경량 구조물의 활용도가 지속적으로 증가하고 있다. 이러한 측면에서 설계 요구 사항에 따라 강화섬유 및 수지 등과 같은 두 가지 이상의 상반된 특성을 갖는 재료들을 조합함으로써 최적화된 무게 당 강성비를 제공할 수 있는 섬유강화 복합소재가 그 대안으로써 각광받고 있으며, 특히 연속섬유 복합소재 적층 구조물의 경우 고강도 경량 특성을 극대화할 수 있기 때문에 항공기체 산업 등과 같은 고부가가치 산업 분야에 지속적으로 적용되고 있는 실정이다. 상기 언급된 연속섬유 복합소재 구조물은 타 소재 대비 우수한 기계적 특성을 구현할 수 있다는 장점이 있지만, 횡방향 응력 성분들로 인해 층간 미끄러짐, 층간 분리 등과 같은 적층 구조물이 태생적으로 갖는 기계적 결함이 유발될 수 있기 때문에 구조물 설계 과정에서 횡방향 응력 분포에 대한 정확한 예측이 필요한 상황이다[1-12].
이에 따라 복합소재 적층 구조물의 횡방향 응력 성분들을 정확하게 예측하기 위한 해석 기법들이 지속적으로 개발되어 왔다. 일차전단변형이론(FSDT: First-order Shear Deformation Theory) 및 고차전단변형이론(HSDT: Higher-order Shear Deformation Theory) 등이 순차적으로 개발되었으며[1,2], 나아가 층간 경계면에서 불연속적으로 변하는 지그재그 변위장을 정의함으로써 복합소재 적층 구조물의 횡방향 응력 성분들을 보다 정확하게 예측할 수 있는 효율적 고차이론(EHOPT: Efficient Higher Order Plate Theory)이 Cho와 Parmerter에 의해 개발되었다[3]. 효율적 고차이론은 적층 구조물의 거동 예측 과정에서 보다 정확한 솔루션을 제공하지만, ANSYS 및 ABAQUS 등과 같은 기존 상용 S/W들과 직접 호환이 어려운 유한요소 정식화 과정이 요구되는 문제점이 있다. 상기 문제에 대한 해결 방안으로써 혼합변분이론을 바탕으로 변위장과 응력장을 독립적으로 가정하되, 변위장 및 응력장 사이의 타당한 수학적 관계식 도출을 통해 해석 결과의 정확도와 계산 과정의 효율성을 동시에 향상시킬 수 있는 개선된 일차전단변형이론(EFSDTM: Enhanced First-order Shear Deformation Theory via Mixed formulation)이 Kim과 Cho에 의해 제안되었다[4]. 개선된 일차전단변형이론은 상용 S/W 해석 과정에서 활용되고 있는 일차전단변형이론과 동일한 계산 과정을 수행하기 때문에 범용성의 측면에서 명확한 장점을 가진다.
한편, 복합소재 구조물에 대한 적용 산업 분야가 지속적으로 확장됨에 따라 설계 과정에서 보다 다양한 외부 환경에서 구동되는 복합소재 구조물의 다물리적 거동 예측이 필요한 상황이다. 특히 고온/다습 등과 같은 외부 환경에서는 복합소재 구조물의 성능 저하를 유발하는 열 변형이 발생될 수 있기 때문에 복합재료 적층 구조물의 열적 거동을 정확하게 예측하기 위한 해석 기법들이 개발되어 왔다. 고차전단변형이론을 바탕으로 복합소재 적층 구조물의 열적 거동 예측을 위한 연구가 Rohwer 등에 의해 수행되었으며[5], Lo 등은 포물선 형태의 횡방향 변위장을 가정함으로써 복합소재 구조물의 열 변형 예측 과정에서 중요한 요소인 횡방향 수직 변형을 효과적으로 고려하고자 하였다[6]. Cho와 Oh는 효율적 고차이론을 바탕으로 복합소재 구조물의 열-기계-전기적 특성 등과 같은 효과적인 다물리적 거동 예측을 위한 연구를 수행하였으며[7], 고차 지그재그 면내 변위장과 열팽창 계수를 포함하는 횡방향 변위장을 가정함으로써 복합소재 적층 구조물의 열적 거동을 효율적으로 예측하기 위한 연구가 Kapuria와 Achary에 의해 수행되었다[8]. 상기 언급된 복합소재 적층 구조물의 열적 거동 예측을 위한 해석 기법들은 모두 고차 이론을 기반으로 개발되었으며, 고차 이론들이 가지는 계산 효율성의 한계점을 보완하기 위한 방안으로써 Han 등은 혼합변분이론을 바탕으로 횡방향 수직 변형이 고려된 개선된 일차전단변형이론(EFSDTM-TN: Enhanced First-order Shear Deformation Theory including the Transverse Normal strain effect via Mixed formulation)을 개발하였다[9]. 횡방향 수직 변형이 고려된 개선된 일차전단변형이론은 열 하중 성분들을 횡방향 변위장에 도입해줌으로써 추가적인 변수 도입이 없는 기존 변수만으로 복합소재 적층 구조물의 열적 거동을 효과적으로 예측할 수 있으며, 이에 따라 열적 거동 예측을 위한 유한요소 정식화 과정에서 상용 S/W들과 연계가 가능하다는 장점을 가진다.
상기 연구 배경에 따라 본 연구에서는 횡방향 수직 변형이 고려된 개선된 일차전단변형이론의 범용성 확보를 위한 유한요소 정식화 검증을 수행하였다. 유한요소 정식화 과정에서 8절점 판 요소를 고려하였으며, 해당 유한요소 정식화 과정은 MATLAB(MATLAB R2020b, Mathworks, USA)를 통해 구현되었다. 제안된 유한요소 해석 기법은 독립적으로 가정되는 변위장과 응력장 사이의 타당한 수학적 관계식을 도출해줌으로써 해석 결과의 정확도와 계산 과정의 효율성을 동시에 만족시킬 수 있으며, 동시에 횡방향 변위장의 개선을 통해 복합소재 적층 구조물의 열적 거동을 보다 효과적으로 예측하고자 하였다. 수치 예제로써 2차원 복합소재 적층 구조물에 대한 열-기계적 거동 예측을 수행하였으며, 계산된 결과를 3차원 탄성해 및 참고문헌에서 활용 가능한 해석 결과들과 비교, 검토함으로써 제안된 유한요소 해석 기법의 성능을 검증하고자 하였다[1,9,13].

2.1 혼합변분이론
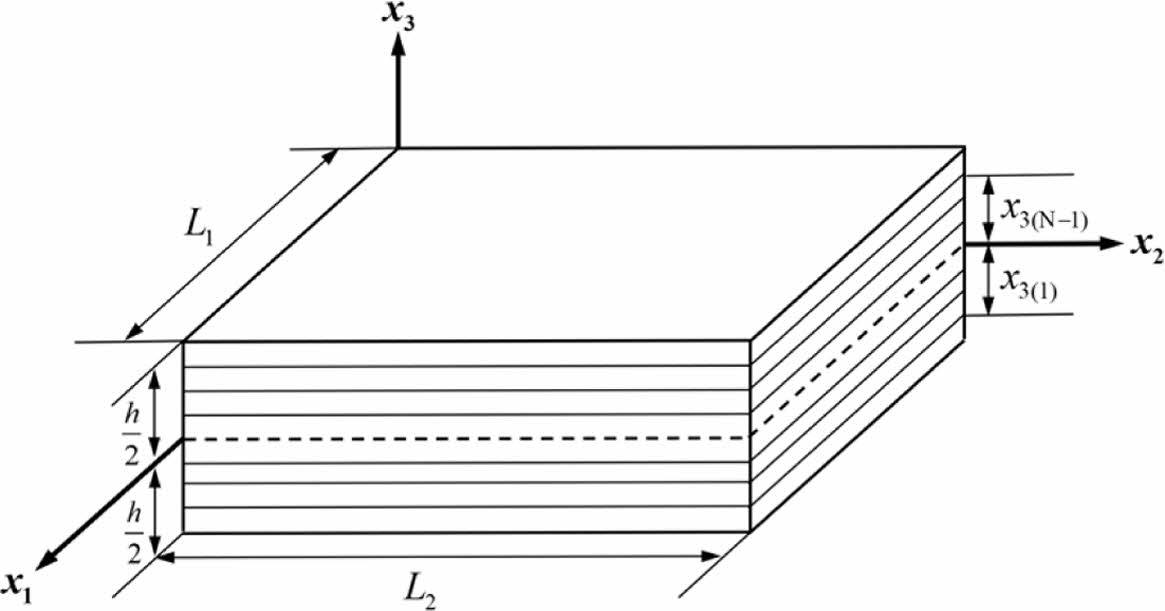
본 연구에서는 단사정 물성치(monoclinic material property)를 가지는 2차원 복합소재 적층 평판을 고려하였으며, Fig. 1은 복합소재 적층 평판에 대한 기하학적 형상 및 기준 좌표축을 나타낸다. Fig. 1에서 L₁, L₂는 복합소재 적층 평판에 대한 면내 방향 길이를 나타내며, h는 적층 평판의 두께를 나타낸다. 두께 방향 위치를 나타내는 x₃은 h/2와 -h/2 사이의 값을 가진다.
또한, 평면응력 상태를 만족하는 2차원 Hellinger-Reissner 범함수는 다음과 같이 주어진다[9].



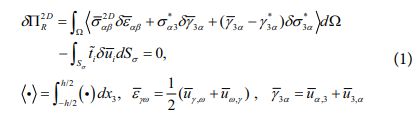
식 (1)과 같이 주어지는 범함수에서 변위장과 응력장이 독립적으로 가정된다. 여기서 상첨자 (●̅),(●)는 변위장 및 응력장으로부터 정의되는 텐서를 의미하며, 본 연구에서는 횡방향 응력장을 독립적으로 가정하였다. 또한, t͞͞,S_σ는 외부 하중 및 응력 경계면을 나타낸다.

2.2 횡방향 변위장의 개선
복합소재 적층 구조물의 열적 거동을 정확하게 예측하기 위해서는 두께 방향으로의 변형인 횡방향 수직 변형이 반드시 고려되어야 한다. 기존에 제안된 대부분의 해석 기법들은 포물선 형태의 횡방향 변위장을 가정함으로써 횡방향 수직 변형을 효과적으로 고려할 수 있지만, 이에 따라 해석 과정에서 미지 변수가 증가하기 때문에 계산 효율성이 저하된다는 문제점이 있다. 상기 문제에 대한 대안으로써 본 연구에서는 아래와 같은 개선된 형태의 횡방향 변위장을 도입하였다[9].



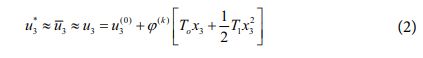
식 (2)에서 T₀,T₁는 열 하중 성분들을 나타내며, φ^(k)는 층별로 평면 응력 조건을 만족시키기 위한 상수이다. 식 (2)와 같이 주어지는 개선된 형태의 횡방향 변위장을 가정함으로써 평면 응력 상태에서 추가적인 변수 도입이 없이 복합소재 적층 구조물의 열적 거동을 효과적으로 예측할 수 있게 된다.

2.3 횡방향 응력장
복합소재 적층 구조물의 열-기계적 거동을 보다 정확하게 예측하기 위해 Hellinger-Reissner 범함수의 횡방향 응력장으로써 효율적 고차이론을 가정하였으며, 초기 변위장은 아래와 같이 주어진다[9].



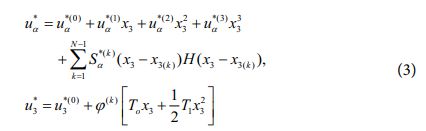
식 (3)에서는 개선된 형태의 횡방향 변위장을 가정하였으며, N은 복합소재 적층 수, S^(k)*_α는 횡방향 전단 응력 조건들을 만족시키기 위해 층간 경계면에서 지그재그 형태로 변화하는 변위의 기울기를 나타낸다. 식 (3)과 같이 주어지는 초기 변위장을 바탕으로 표면 전단 무응력 조건을 부과함으로써 아래와 같은 관계식을 정의할 수 있다.



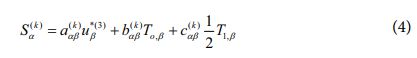
또한, 층간 경계면에서의 전단응력 연속 조건을 부과하면 초기 변위장은 아래와 같이 개선된 형태로 표현이 가능해진다[9].



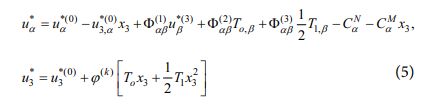
식 (5)에서 새롭게 정의되는 C^N_α,C^M_α은 면내 보정 계수로써 아래와 같이 표현된다[9].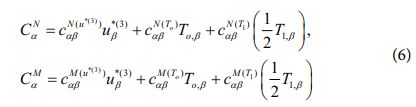



식 (6)과 같은 면내 보정 계수는 독립적으로 가정되는 변위장과 응력장 사이의 타당한 수학적 관계를 도출하는 과정에서 Saint-Venant의 원리를 바탕으로 새롭게 정의되는 계수이며[9], 이러한 면내 보정 계수의 도입을 바탕으로 복합소재 적층 구조물에 대한 열-기계적 거동 예측 과정에서 신뢰도 높은 해석 결과를 제공할 수 있게 된다. 또한, φ⁽¹⁾_αβ,φ⁽²⁾_αβ,φ⁽³⁾_αβ 는 아래와 같이 정의된다.



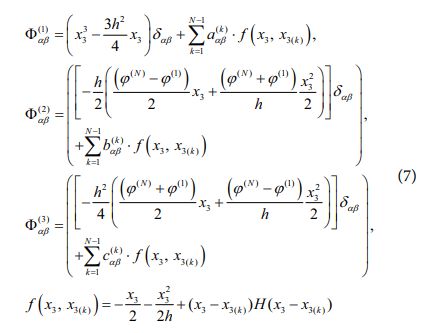
여기서 δ_αβ는 Kronecker delta 함수를 나타내며, 식 (5)-(7)로 정의되는 변위장을 바탕으로 Hellinger-Reissner 범함수에서 정의되는 횡방향 응력 성분들을 아래와 같이 정의할 수 있게 된다.

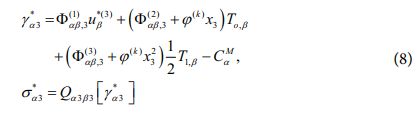
2.4 변위장
복합소재 적층 구조물의 열-기계적 거동 예측 과정에서 계산 과정의 효율성을 향상시키기 위해 Hellinger-Reissner 범함수의 변위장으로써 아래와 같이 주어지는 개선된 형태의 횡방향 변위장을 갖는 일차전단변형이론을 가정하였다[9].



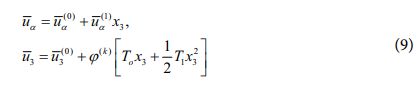
또한, 식 (9)로부터 변형률 및 면내 응력 성분들을 아래와 같이 정의할 수 있다.



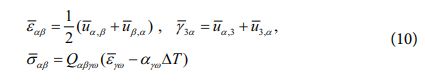
2.5 독립된 두 이론 사이의 관계식
횡방향 응력장과 변위장 사이의 타당한 수학적 관계식은 아래와 같이 주어지는 Hellinger-Reissner 범함수의 혼합항을 바탕으로 정의할 수 있다.



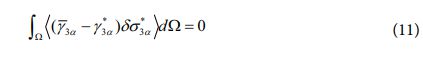
또한, 횡방향 응력장으로부터 도출되는 전단력은 아래와 같이 주어진다.



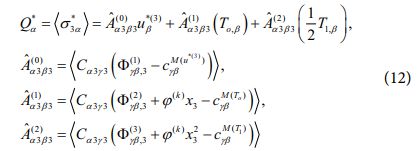
여기서 식 (11)과 식 (12)에 의해 횡방향 응력장 및 변위장 사이의 관계식을 아래와 같이 정의할 수 있다[9].



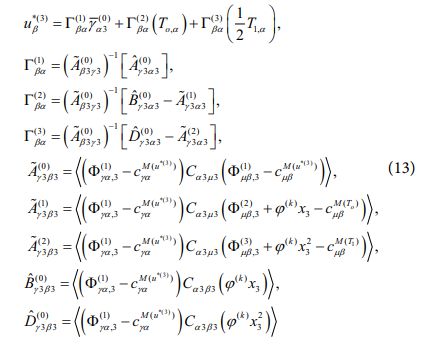
또한, 식 (13)을 통해 아래와 같이 전단력 Q*_α를 변위장의 변수들로 표현할 수 있게 된다.



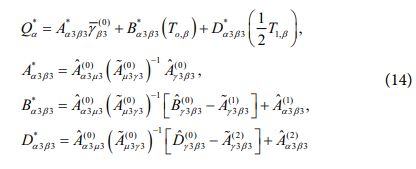
2.6 지배방정식 및 후처리 과정
상기 정의된 횡방향 응력장과 변위장 사이의 타당한 수학적 관계식을 바탕으로 아래와 같이 변위장 성분만을 활용한 지배방정식을 정의할 수 있게 된다[9].



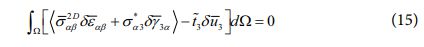
또한, 식 (15)로부터 정의되는 평형방정식은 아래와 같이 주어진다.



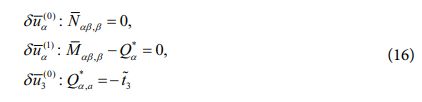
여기서 Q*_α는 횡방향 응력장으로부터 정의되는 전단력을 의미하며, 이를 통해 복합소재 적층 구조물에 대한 거동 예측 과정에서 보다 정확한 전단력을 고려할 수 있게 된다. 동시에 식 (13)에 근거한 후처리 과정을 통해 효율적 고차이론의 변위장을 복원해줌으로써, 보다 정확한 변위 및 응력 분포 예측이 가능해진다. 최소 자승 오차법을 통해 아래와 같은 평균 변위 관계식이 주어진다[9].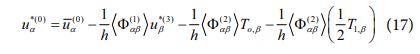



식 (17)과 같이 u^*(0)_α에 대한 관계식이 정의됨에 따라, 효율적 고차이론의 변위장 u^*_α은 아래와 같이 도출된다.



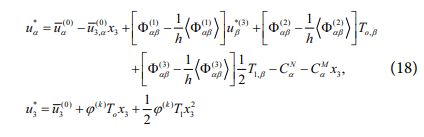
식 (18)에서 u^*(0)_β은 식 (13)에 의해 변위장 성분들로 표현 가능하기 때문에, 효율적 고차이론의 변위장을 수학적으로 타당하게 복원할 수 있게 된다. 또한, 아래와 같은 평형방정식을 통해 보다 정확한 횡방향 전단 응력 성분을 도출하고자 하였다.

본 절에서는 횡방향 수직 변형이 고려된 개선된 일차전단변형이론을 바탕으로 유한요소 정식화를 수행하였다. 후처리 과정에 근거한 변위 및 응력 복원 과정을 고려하여 유한요소 정식화 과정에서 8절점 등매개변수 판 요소를 고려하였으며, 개선된 일차전단변형이론의 계산 과정에서 활용되는 변위장 성분들에 대한 이산화 과정은 아래와 같이 주어진다.



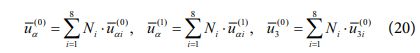
식 (20)에서 N_i는 8절점 등매개변수 판 요소에서 i-번째 절점에 대한 형상 함수를 나타낸다.

3.1 요소 강성 행렬
요소 강성 행렬은 변형에너지에 대한 최소 포텐셜 에너지의 원리를 통해 정의할 수 있으며, 8절점 판 요소에 대한 미지 변위 성분들은 아래와 같은 벡터 형태로 표현이 가능하다.



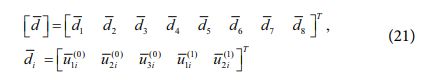
또한, 식 (20) 및 (21)을 바탕으로 변형률 성분들을 아래와 같이 정의할 수 있다.



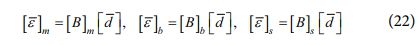
여기서 B 행렬은 아래와 같이 주어진다.



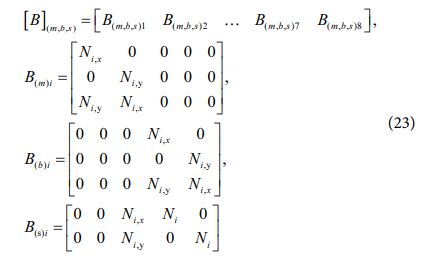
상기 변형률을 바탕으로 아래와 같이 요소 강성 행렬을 정의할 수 있다.



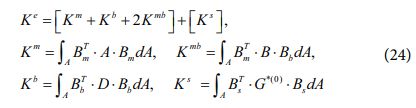
여기서 A, B, D 및 G^*(1) 행렬들은 아래와 같다.



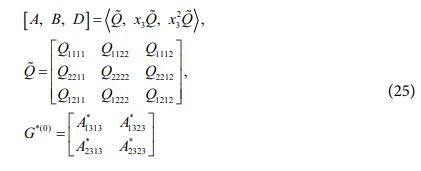
3.2 기계 및 열 하중
본 유한요소 정식화 과정에서는 기계 및 열 하중이 외부 하중으로써 고려되며, 기계 하중에 따른 외력 벡터는 아래와 같이 정의된다.



또한, 열 하중은 식 (8)과 식 (10)에 의해 다음과 같이 주어진다.



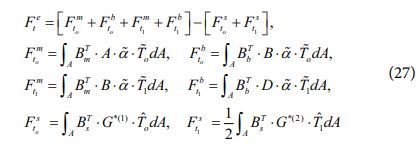
여기서 α̂,T̂_αT̂₁T̂_αT̂₁는 열팽창 계수 및 열 하중 성분들로 구성되는 행렬을 나타내며, G^*(1), G^*(2)는 식 (14)를 통해 정의되는 개선된 전단 강성 행렬을 나타낸다.



상기 개선된 일차전단변형이론을 바탕으로 유한요소 정식화 과정을 수행함으로써, 보다 다양한 형상 및 하중/경계 조건을 갖는 복합소재 적층 구조물에 대한 열-기계적 거동 예측 과정에서 해석 결과의 정확도와 계산 과정의 효율성을 동시에 향상시킬 수 있게 된다.

4.1 수치 예제 모델
본 연구를 통해 제안된 유한요소 해석 기법에 대한 효율성 및 정확도를 검증하기 위해 2차원 사각 평판 형태의 복합소재 적층 구조물에 대한 열-기계적 거동 해석을 수행하였다. 수치 예제로써 고려된 복합소재 적층 구조물에 대한 물성치를 아래와 같이 가정하였다.

- 복합소재 (1):


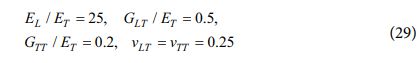
- 복합소재 (2):


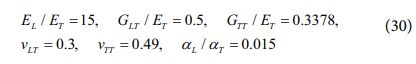
본 연구에서는 복합소재 (1)을 기계적 거동 예측을 위한 물성으로 고려하였으며, 복합소재 (2)를 열적 거동 예측을 위한 물성으로 고려하였다. 또한, (●)_L 및 (●)_T는 각각 강화섬유와 평행 및 수직한 방향에 대한 물성을 나타낸다. 동시에, 복합소재 구조물의 거동 예측을 위한 외력 성분들인 기계 및 열 하중을 아래와 같이 가정하였다.



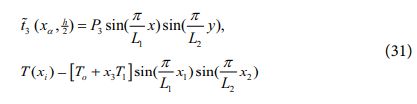
계산된 결과에 대한 비교/분석을 위해 무차원화를 수행하였으며, 3차원 탄성해 및 일차전단변형이론의 결과와 비교 분석을 수행하였다[1,9,13].

4.2 처짐 수렴도
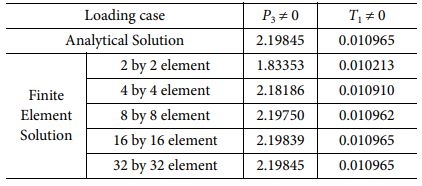
유한요소 정식화 과정에서 발생될 수 있는 수치적 오차를 분석하기 위해 도출된 유한요소 해석 결과를 해석해와 비교 분석을 수행하였다. 복합소재 적층 구조물의 열-기계적 거동에 대한 무차원화 처짐 결과를 Table 1을 통해 비교하였으며. 균일 분포 열 하중의 경우 처짐이 없기 때문에 비교 대상에서 제외하였다. Table 1을 통해 요소의 개수가 증가할수록 처짐 값이 수렴하며, 또한 사각 평판 구조물을 16 × 16 요소 이상으로 이산화한 경우 해석해와 비교하여 신뢰도 높은 처짐 결과를 제공한다는 사실을 확인하였다. 특히, 32 × 32
요소 조건에서 유한요소 해석 결과가 해석해와 일치하는 처짐 결과를 제공하며, 결과적으로 본 연구를 통해 수행된 유한요소 정식화 과정이 타당함을 확인할 수 있다.

4.3 변위 및 응력 분포
상기 처짐 분석 결과를 통해 32 × 32 요소 조건을 바탕으로 열-기계적 거동에 대한 변위 및 응력 분포 결과를 도출하고자 하였다.
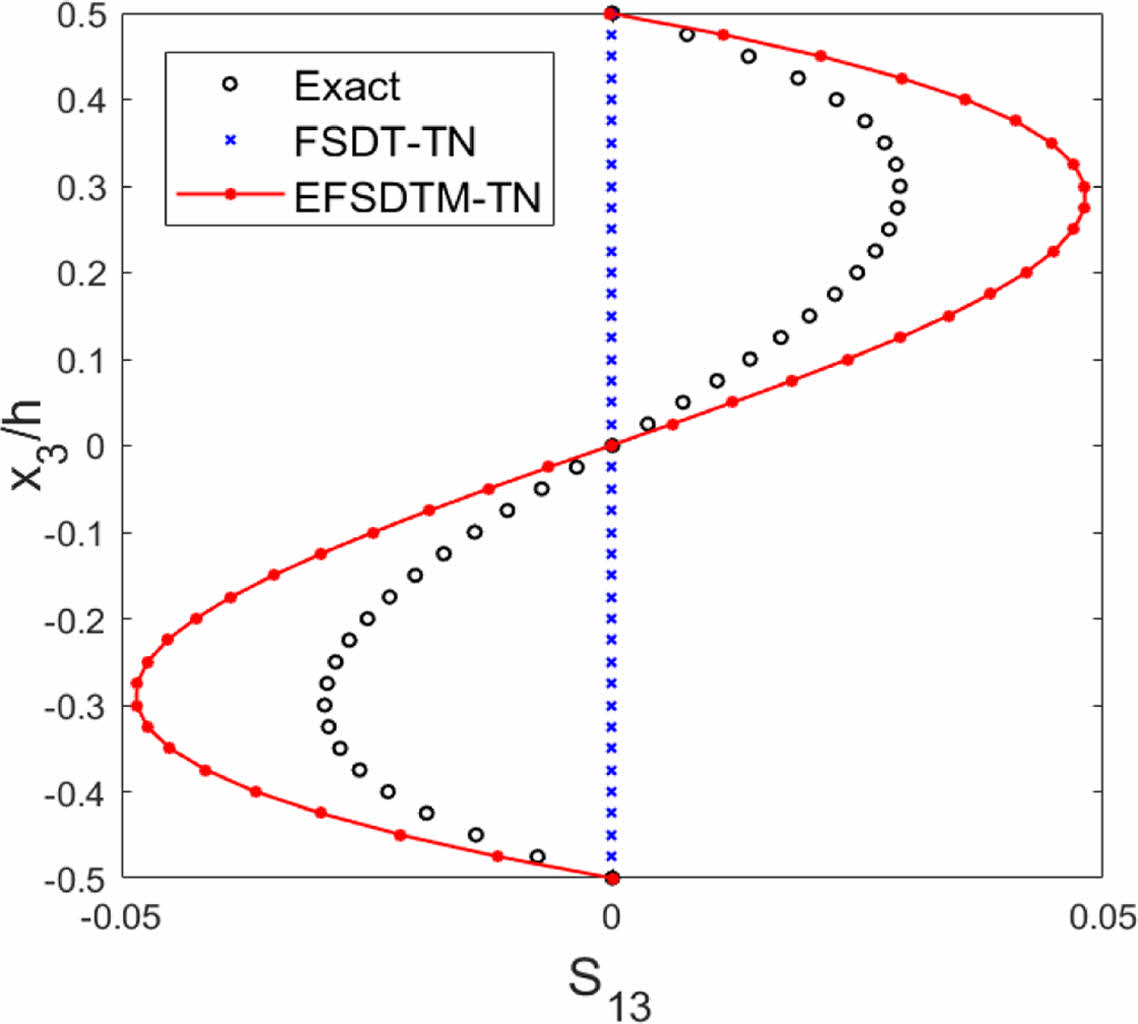
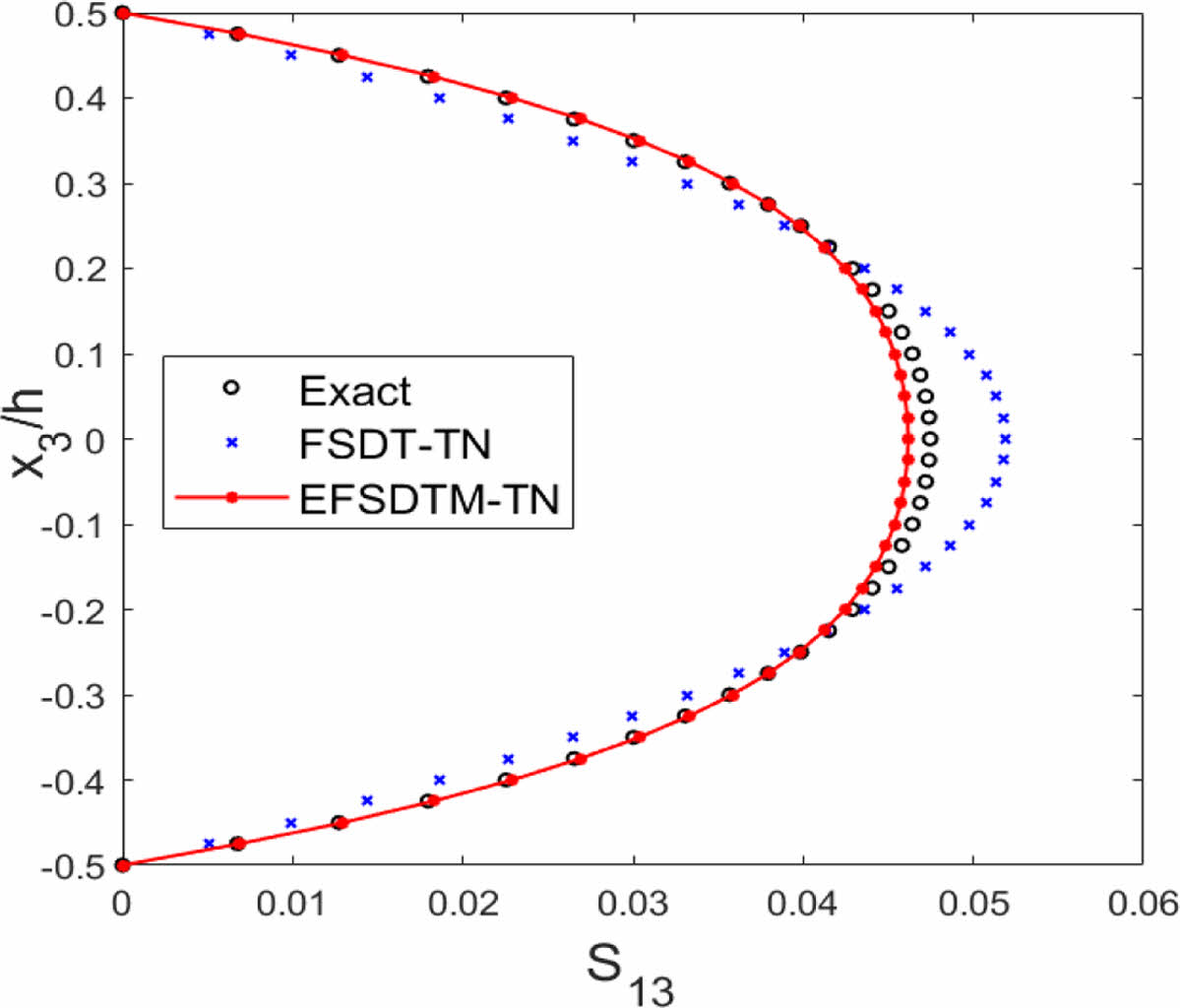
Figs. 2-3은 균일 및 선형 온도 분포를 받는 단일 층(Single layer) 복합소재 구조물에 대한 횡 방향 전단 응력 분포를 나타낸다. 균일 온도 분포를 받는 단일 층 복합소재 구조물의 경우(Fig. 2) FSDT-TN는 횡 방향 전단 응력 성분 예측 과정에서 무의미한 결과를 제공하는 반면, EFSDTM-TN는 3차 곡선 형태로 주어지는 횡 방향 전단 응력 분포를 비교적 정확하게 예측할 수 있다는 사실을 확인하였다. 또한, Fig. 3을 통해 EFSDTM-TN 및 FSDT-TN은 선형 온도 분포를 받는 단일 층 복합소재 구조물의 횡 방향 전단 응력 분포를 효과적으로 예측할 수 있으며, EFSDTM-TN의 경우 FSDT-TN과 비교하여 보다 정확한 솔루션을 제공함을 확인할 수 있었다.
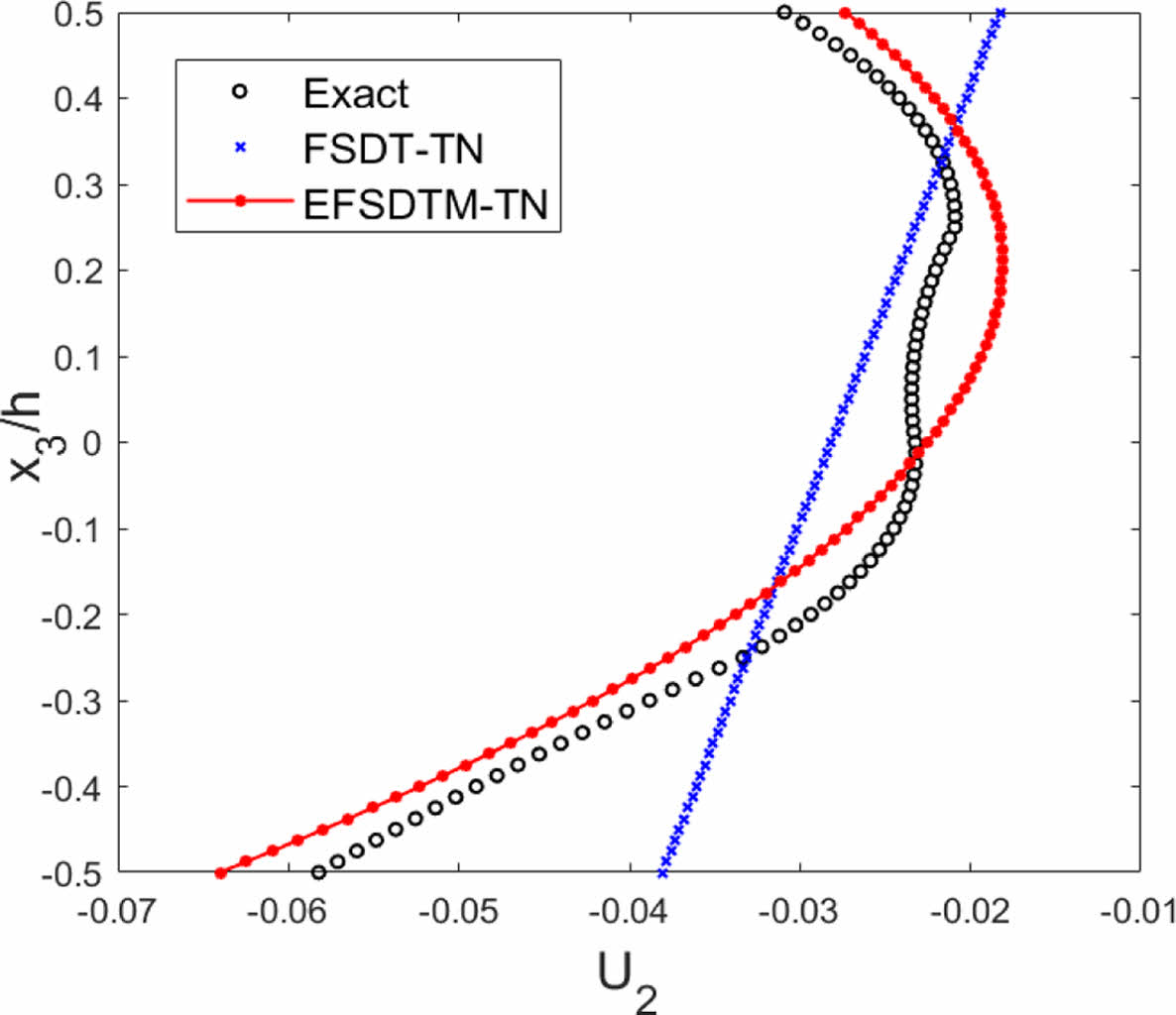
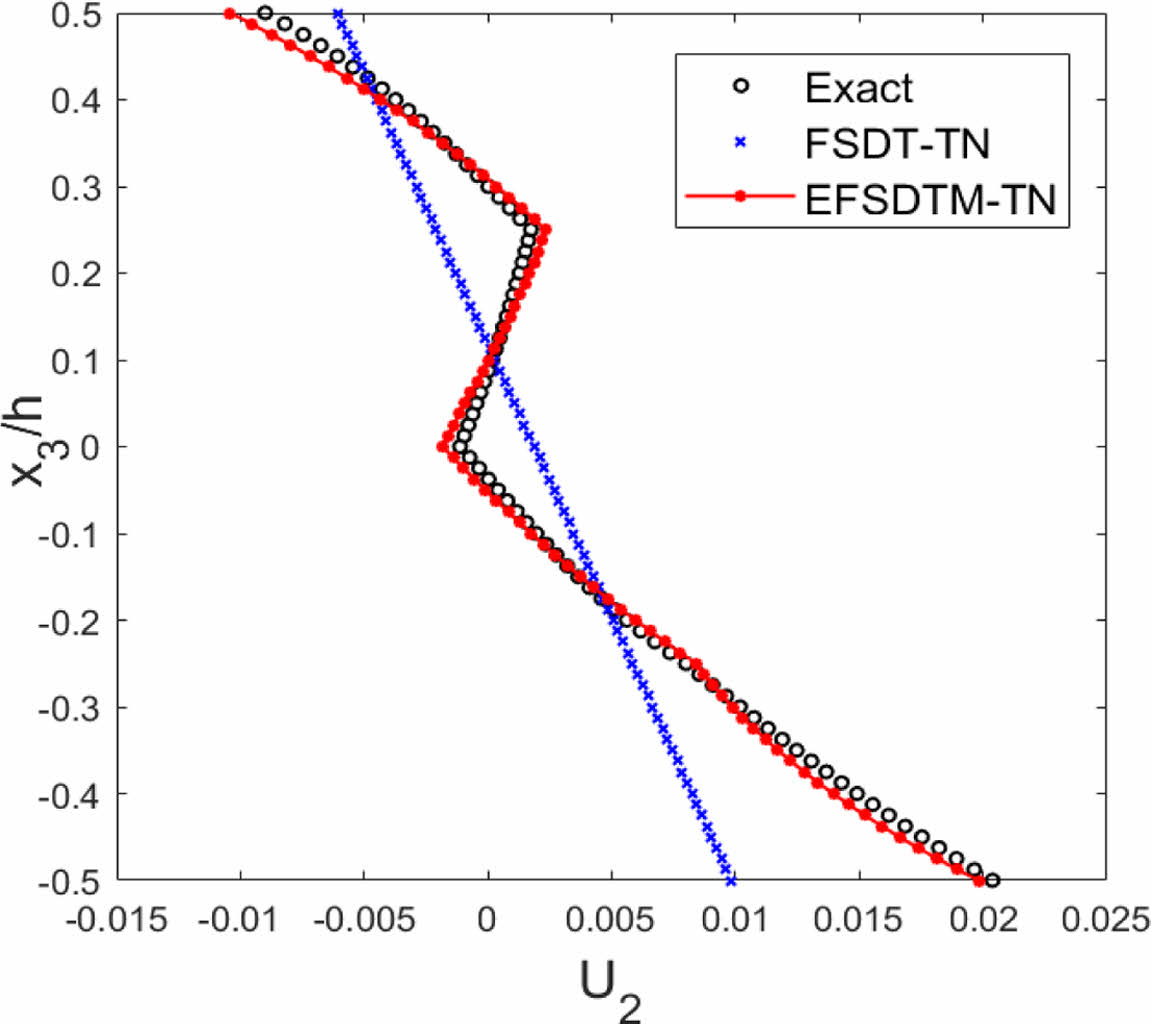
Figs. 4-5은 균일 온도 분포 및 기계 하중을 받는 비대칭 직교([90/0/90/0]) 복합소재 적층 구조물의 면내 변위 분포 결과를 나타낸다. Figs. 4-5을 통해 제안된 해석 기법인 EFSDTM-TN은 FSDT-TN와 동일한 계산 과정을 수행하지만, 복합소재 적층 구조물의 포물선 형태의 열 변위 및 zigzag 형태로 변화하는 기계적 변위를 보다 효과적으로 예측할 수 있다는 사실을 확인하였다.
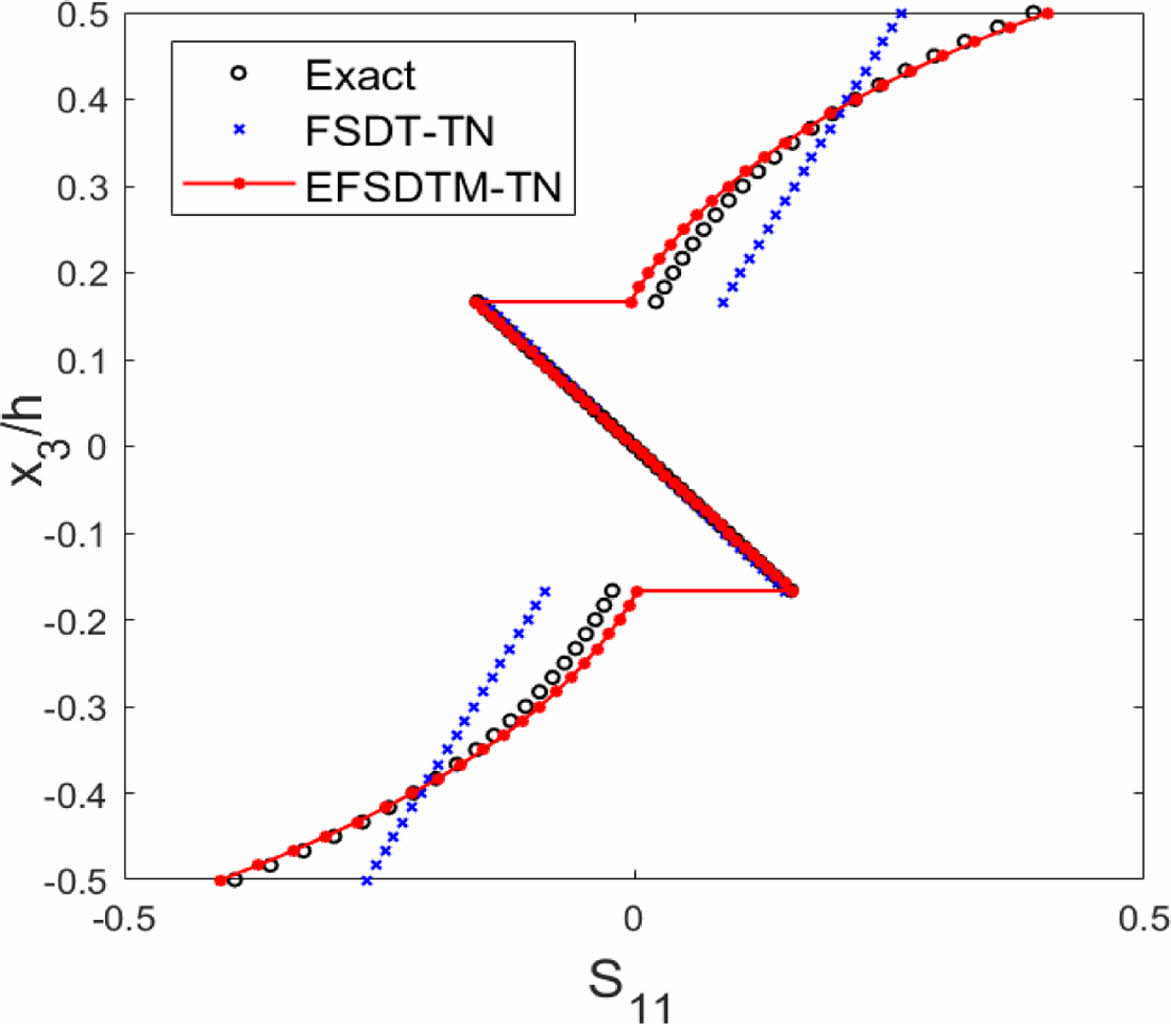
Fig. 6는 선형 온도 분포를 받는 대칭 직교([0/90/0]) 복합소재 적층 구조물의 면내 응력 분포 결과를 나타낸다. 복합소재 적층 구조물의 경우 적층 각도에 따라 층별 물성이 달라지며, 이에 따라 층간 경계면에서 불연속적인 면내 응력 분포 결과를 나타낸다. Fig. 6를 통해 EFSDTM-TN의 경우 이러한 면내 응력의 불연속적인 국소 분포를 정확하게 예측할 수 있음을 확인할 수 있었다.
반면, FSDT-TN는 전역 거동에 대한 예측은 가능하지만, 국소적 응력 분포 예측 과정에서 다소 부정확한 결과를 제공함을 확인하였다.
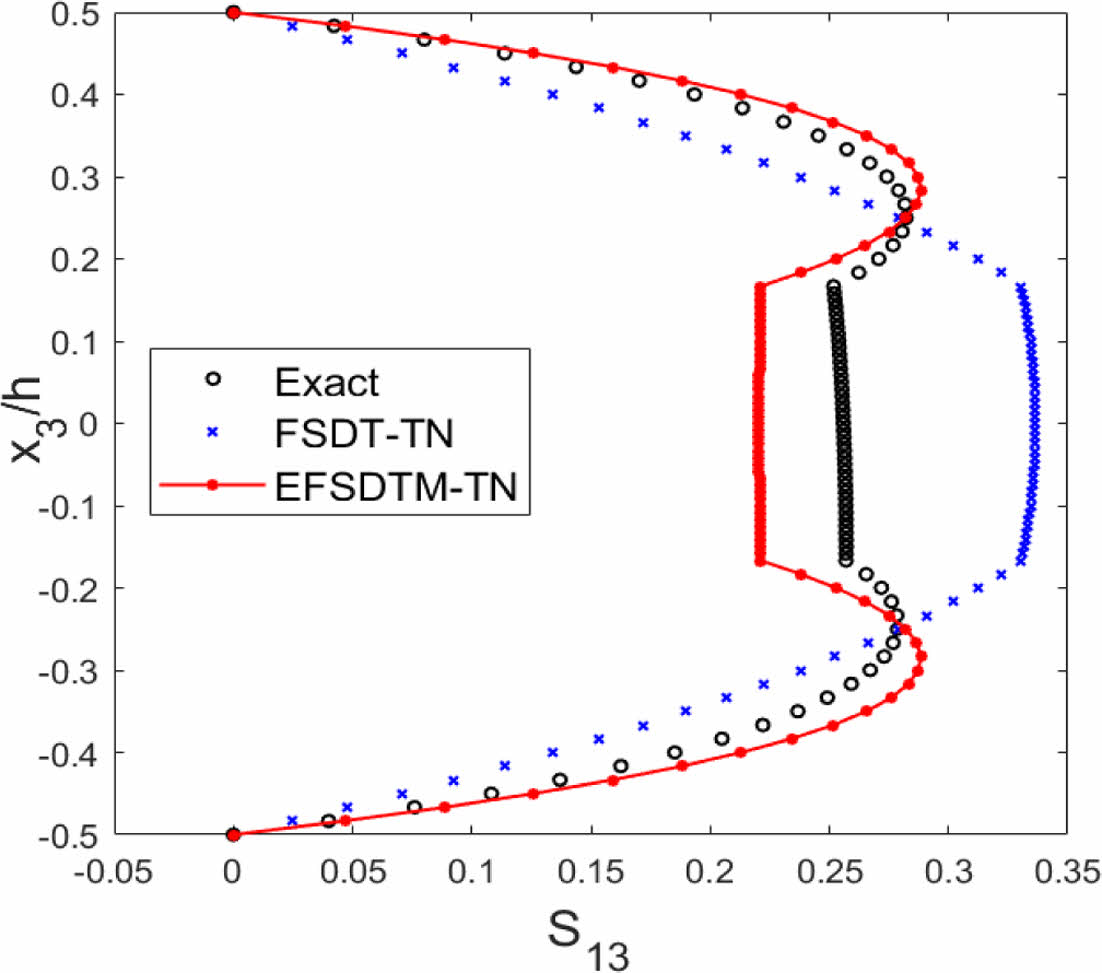
Fig. 7는 기계 하중을 받는 대칭 직교([0/90/0]) 복합소재 적층 구조물의 횡방향 전단 응력 분포 결과를 나타낸다. EFSDTM-TN의 경우 kink 형태의 횡방향 전단 응력 분포를 비교적 정확하게 표현할 수 있으며, 결과적으로 복합소재 적층 구조물 설계 과정에서 중요한 고려 사항인 횡방향 응력 분포 예측 과정에서 보다 정확한 솔루션을 제공한다는 사실을 확인하였다.

본 연구에서는 개선된 일차전단변형이론을 바탕으로 8절점 판 요소 기반 유한요소 해석 기법을 제안하였다. 제안된 유한요소 해석 모델에서는 혼합변분이론에서 독립적으로 가정되는 변위장과 응력장 사이의 타당한 수학적 관계식을 도출함으로써, 복합소재 적층 구조물의 열-기계적 거동 예측 과정에서 해석 결과의 정확도와 계산 과정의 효율성을 동시에 향상시키고자 하였다. 또한, 개선된 형태의 횡방향 변위장을 도입함으로써 복합소재 적층 구조물의 열적 거동 예측 과정에서 중요한 요소인 횡방향 수직 변형을 효과적으로 고려하고자 하였다.
수치 예제 해석 결과에 대한 비교/분석을 통해 제안된 유한요소 해석 기법의 정확도 및 효율성을 검증하였으며, 이를 통해 개선된 일차전단변형이론에 기반한 8절점 판 유한요소 해석 기법의 신뢰성을 확인하였다. 해당 연구 결과를 바탕으로 향후 다양한 형상 및 하중/경계 조건을 갖는 복합소재 적층 구조물의 열-기계적 거동 예측 과정에서 제안된 유한요소 해석 기법을 활용할 수 있을 것으로 사료된다.

본 연구는 금오공과대학교 학술연구비로 지원되었음(202003720001).