Original Article
  • The Effect of Fiber Volume Fraction Non-uniformity through Thickness Direction on the Torsional Buckling Load of Cylindrical Composite Lattice Structure

  • Min-Hyeok Jeon*, Hyun-Jun Cho*, Yeon-Ju Kim*, Mi-Yeon Lee*, In-Gul Kim*†

  • * Department of Aerospace Engineering, Chungnam National University 

  • 두께방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 비틀림 좌굴 하중에 미치는 영향

  • 전민혁* ·조현준*· 김연주* · 이미연*· 김인걸*†

  • This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

Abstract

A cylindrical composite lattice structure is manufactured by filament winding. The distribution of non-uniform fiber volume fraction induced by the manufacturing process can be observed. The stiffness and buckling characteristics can be influenced by non-uniform fiber volume fraction. In this paper, the effect of non-uniform fiber volume fraction through thickness direction on the torsional buckling load of the cylindrical composite lattice structure was examined. The stiffness variation induced by the non-uniform fiber volume fraction was applied to the finite element model, and buckling analysis was performed. The variations of buckling load with variations of fiber volume fraction were compared. The non-uniform fiber volume fraction reduced the torsional buckling load of the composite lattice structure


원통형 복합재 격자 구조는 필라멘트 와인딩 공법으로 제작되며 제작 공정에서 두께방향 섬유체적비 불균일이 발생할 수 있다. 섬유체적비 불균일은 구조의 강성에 영향을 미칠 수 있으며 강성 및 좌굴 특성이 변화할 수 있다. 본 연구에서는 두께방향 섬유체적비 불균일이 복합재 격자 구조의 비틀림 좌굴 하중에 미치는 영향에 대하여 분석하였다. 섬유체적비 변화에 의한 강성 변화를 유한요소 모델에 적용하였고 비틀림 하중을 가한 뒤 좌굴 해석을 수행하였다. 두께방향 섬유체적비 편차에 따른 좌굴 하중을 비교하였다. 섬유체적비 불균일에 의해 비틀림 좌굴 하중이 저하될 수 있음을 확인하였다


Keywords: 복합재 격자 구조(Composite lattice structure), 섬유체적비(Fiber volume fraction), 좌굴 하중(Buckling load), 비틀림 하중(Torsional load)

1. 서 론

복합재 격자 구조는 일방향 섬유의 높은 강성 및 강도를 이용하여 외부 하중을 감당할 수 있는 효율적인 구조이다[1,2]. 발사체의 인터스테이지, 위성 및 항공기의 동체, 안테나용 붐 형태와 같이 경량화가 요구되는 항공우주용 구조에 주로 사용된다[3-6]. 다양한 구조에 활용될 수 있으며 면내 인장, 압축, 굽힘 및 비틀림 등 다양한 하중을 감당하는 구조로 사용될 수 있다. 육각 격자 형태를 갖는 원통형 복합재 격자 구조는 필라멘트 와인딩 공법으로 제작되며 나선 방향의 헬리컬 리브(Helical rib), 원주 방향의 후프 리브(Hoop rib), 그리고 섬유가 교차하는 섬유교차부(Knot)가 존재한다. 압축, 전단, 굽힘 및 비틀림 하중을 받는 복합재 격자 구조의 좌굴 특성에 대한 연구들이 다수 수행되었다.
Vasiliev 등[1,7]은 복합재 격자 구조는 리브가 균일하게 배치된 구조이므로 등가의 강성을 갖는 적층판으로 가정하여 축방향 압축 좌굴 하중을 예측하였다. Totaro 등[8]은 복합재 격자 판재의 면내 국부 좌굴 하중을 예측할 수 있는 해석 모델을 제시하였고 시험 결과와 비교하여 검증하였다. Buragohain 등[9]은 원통형 복합재 격자 구조의 좌굴 시험을 수행하였고 유한요소 모델을 이용하여 시험 시편의 좌굴 하중을 예측하였다. 다양한 하중을 받는 복합재 격자 구조의 좌굴 하중에 대한 연구들이 수행되었다. Morozov 등[10]은 압축, 굽힘, 비틀림 하중을 받는 원통형 복합재 격자 구조의 좌굴 하중을 계산하였고 좌굴 성능을 향상시킬 수 있는 형상을 제시하였다. Totaro 등[11]은 압축, 굽힘, 비틀림 하중을 받는 콘형 복합재 격자 구조의 강성을 예측할 수 있는 해석적 등가 모델을 제시하였고 유한요소해석으로 검증하였다. Kang 등[12]은 복합재 격자 구조의 헬리컬 리브에서 수지응집층을, 후프 리브에서 섬유체적비 불균일을 관찰하였다. 두께방향 섬유체적비 불균일은 시험 및 해석 결과를 비교하여 검증되었다[12,13]. 이러한 단면 특성은 구조의 강성 및 좌굴 하중에 영향을 미칠 수 있다. Kong 등[14]은 두께방향 섬유체적비 불균일은 압축 좌굴 하중 저하에 영향이 있음을 확인하였다. 좌굴 하중 예측에 대한 많은 연구가 수행되었지만 두께방향 섬유체적비 불균일이 비틀림 좌굴 하중에 미치는 영향에 대한 연구도 필요하다.
본 연구에서는 후프 리브와 헬리컬 리브에서 관찰된 두께방향 섬유체적비 불균일을 적용하여 복합재 격자 구조의 유한요소 모델을 생성하였다. 모델에 축방향 비틀림 하중을 가하여 좌굴 해석을 수행하였다. 두께방향 섬유체적비 불균일이 비틀림 좌굴 하중에 미치는 영향에 대하여 분석하였다.

2. 유한요소해석

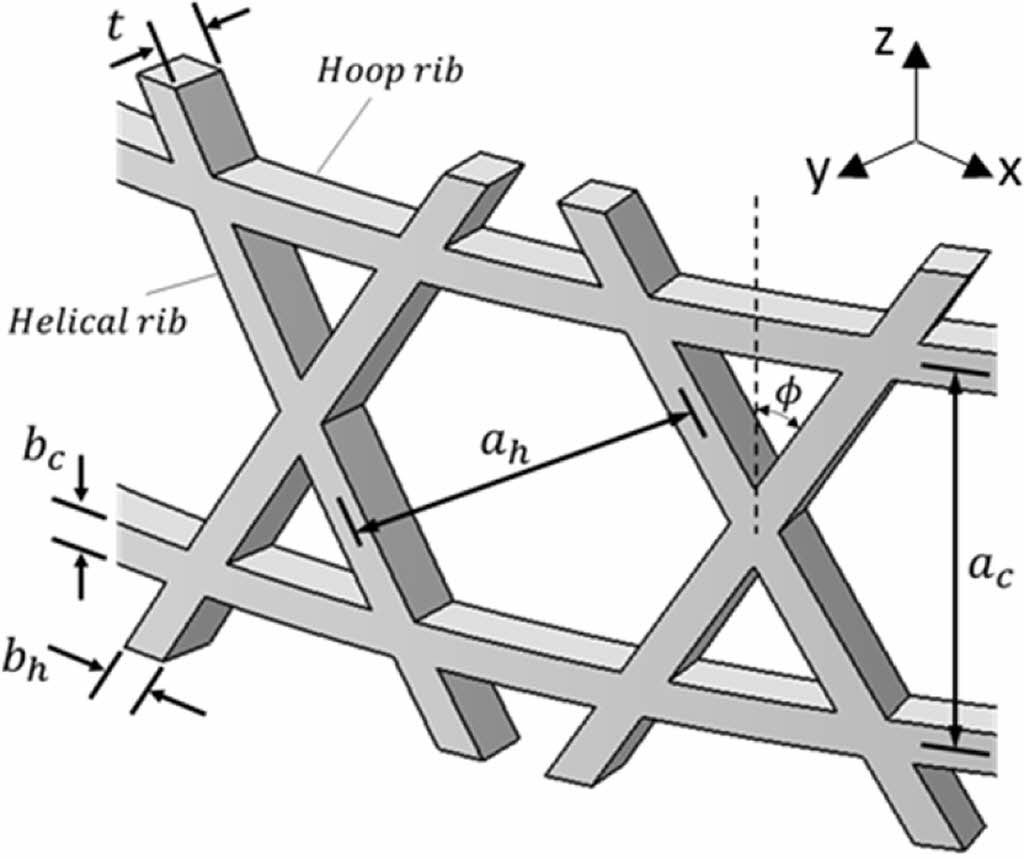
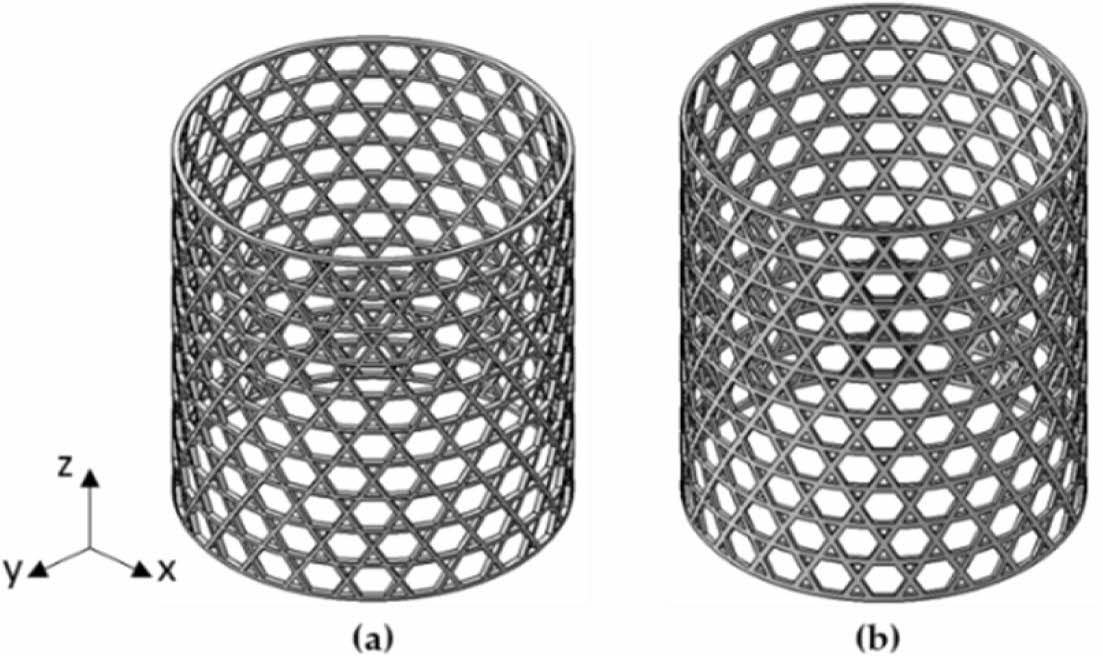
복합재 격자 구조의 형태는 Fig. 1과 같으며 헬리컬 리브 및 후프 리브로 구성된다. 다양한 격자 형태로 제작할 수 있으며 좌굴 성능이 우수하고 제작이 간편한 육각 및 삼각 격자 형태를 갖는 비등방격자(Anisogrid) 구조를 주로 사용한다. 본 연구에서는 Fig. 2와 같은 형상을 가지며 Table 1의 제원으로 설계된 원통형 복합재 비등방격자 구조를 이용하여 비틀림 좌굴 해석을 수행하였다.
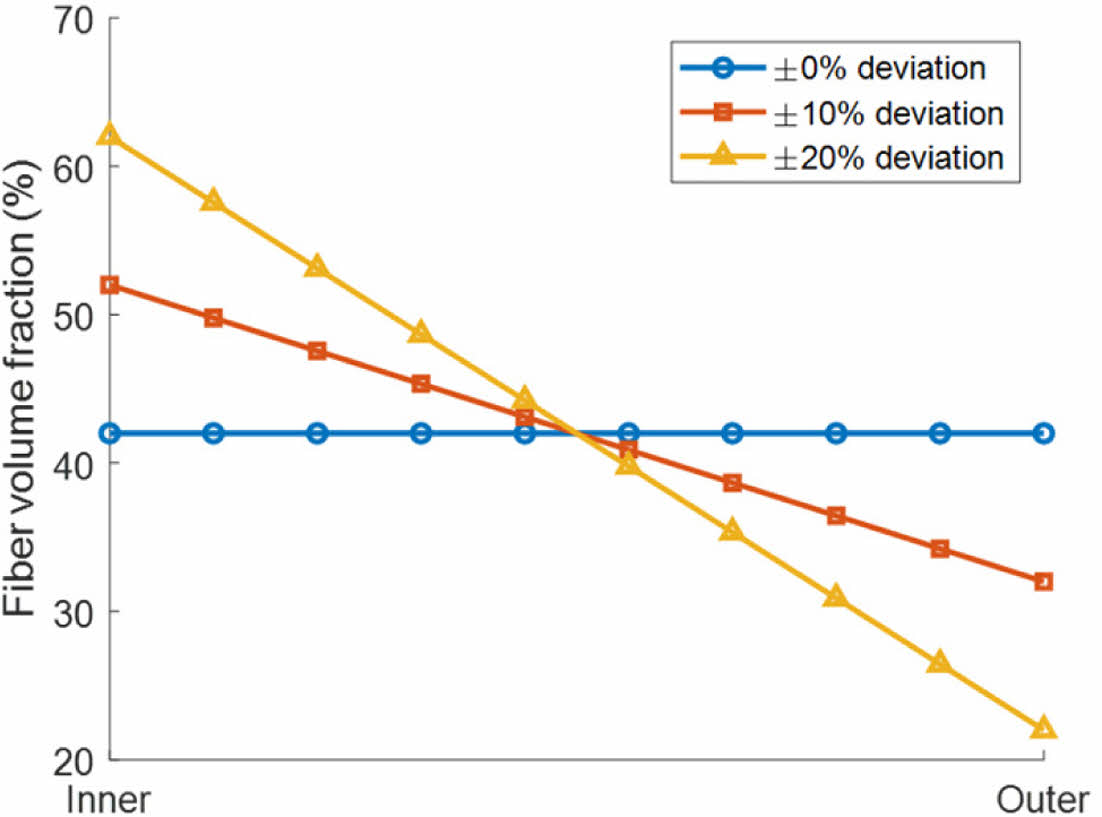
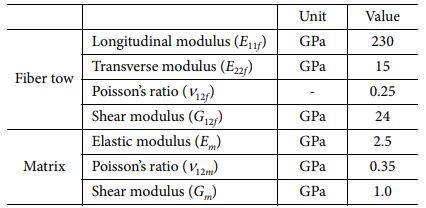
Kang 등[12]이 수행한 연구에서 측정된 복합재 격자 구조의 섬유체적비는 리브(t= 10 mm)에서 평균 42%이며 후프 리브에서의 섬유체적비는 두께방향으로 ±10%의 편차를 가지며 선형적으로 변화함이 관찰되었다. 본 연구에서는 후프 리브의 섬유체적비에 평균 42%와 측정된 수치 기준으로 ±10, 20%의 편차를 가지는 분포를 적용하였다. 항공기 동체와 같은 원통 구조는 비틀림 하중을 받으면 주로 외피 구조에서 전단 응력을 감당한다. 복합재 격자 구조에서는 헬리컬 리브가 이러한 외피의 역할을 할 수 있다. 섬유체적비 불균일이 헬리컬 리브에 존재하면 좌굴 하중에 더 큰 영향이 있을 수 있다. 추가 비교를 위하여 후프 리브 및 헬리컬 리브 전체에 두께방향 섬유체적비 편차를 ±20%로 적용한 모델을 이용하여 좌굴 하중 변화를 비교분석하였다. 섬유체적비 변화에 따른 강성 변화를 적용하기 위해 식 (1)-(4)의 Chamis micromechanical model[15]을 이용하여 강성을 계산하였고 섬유 및 수지의 물성은 Table 2에 정리된 T700/Epoxy의 값을 이용하였다[16].



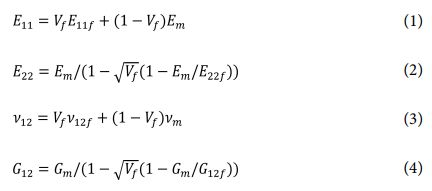
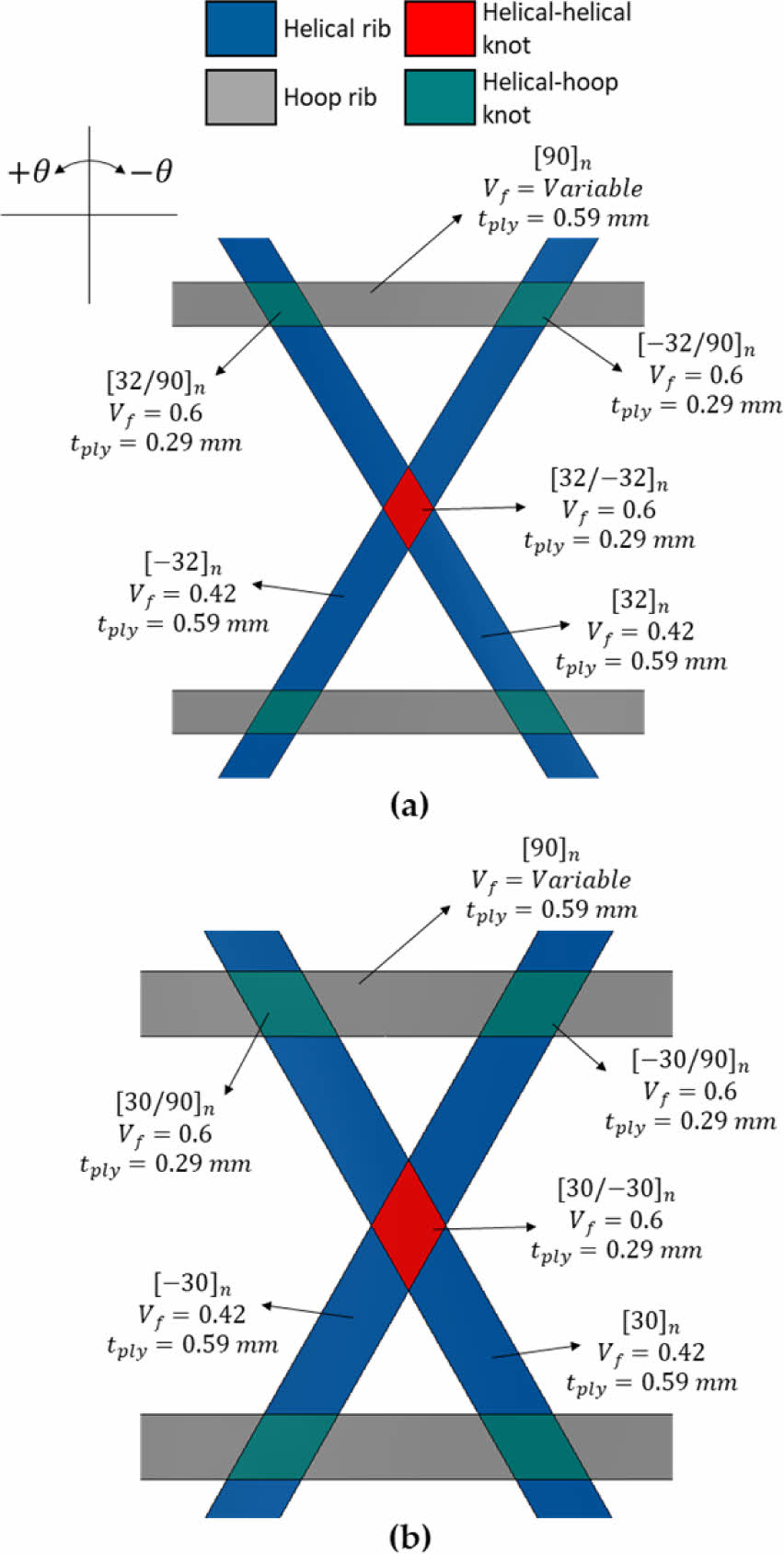
유한요소모델의 적층 조건은 Fig. 4와 같다. 모델링은 MSC.PATRAN을 이용하였고 두께방향으로 변화하는 강성을 적용하기 위해 2차원 Shell 요소(CQUAD4)를 사용하였다. 모델의 두께에 따라 적층수를 입력하였고 원통형 좌표계에 따른 적층각을 적용하였다. 두께방향 섬유체적비 불균일을 후프 리브에만 적용한 모델과 후프 리브, 헬리컬 리브에 적용한 모델을 이용하여 좌굴 해석을 수행하였고 결과를 비교하였다.
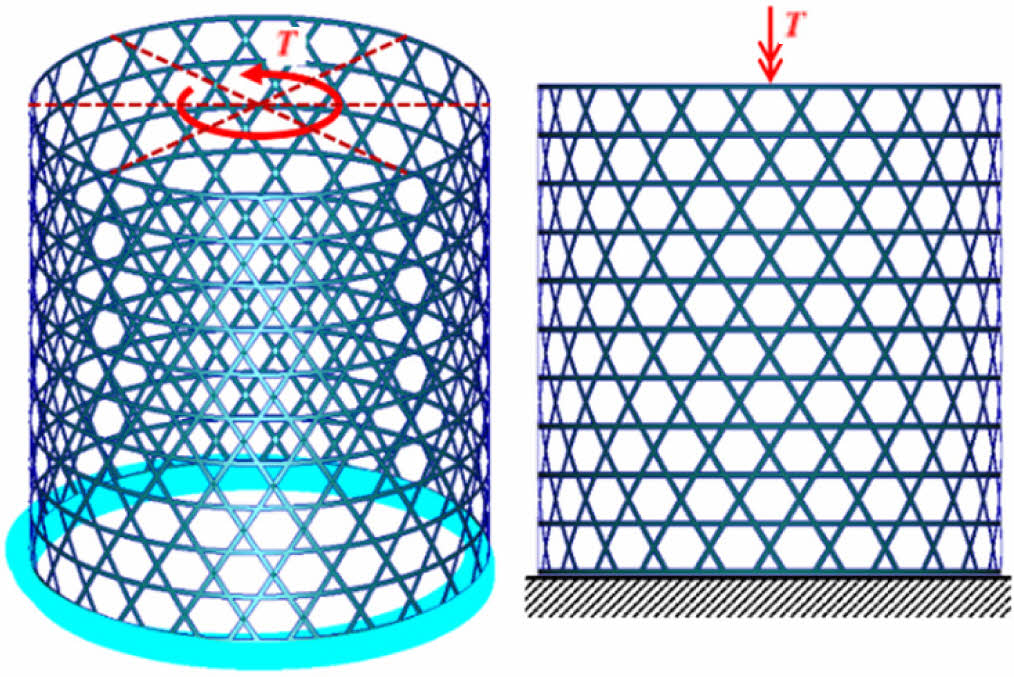
비틀림 하중을 받는 원통형 복합재 격자 구조의 좌굴 해석을 위한 조건은 Fig. 5와 같다. 원통 모델의 하단을 6자유도 구속하였다. 상단의 요소들은 강체 요소(RBE2)로 연결하였다. 강체 요소에는 별도의 구속 조건 없이 반시계방향으로 축방향 비틀림 하중을 적용하였다.

Fig. 1

Geometric parameters of composite lattice structure
Fig. 2

Composite lattice structures; (a) Structure 1 and (b) Structure 2
Fig. 4

Finite element model; (a) Structure 1 and (b) Structure 2
Fig. 5

Load and boundary conditions of FE model
Table 1

Dimensions of composite lattice structures
Table 2

Material properties of fiber and matrix
3. 결과 및 고찰

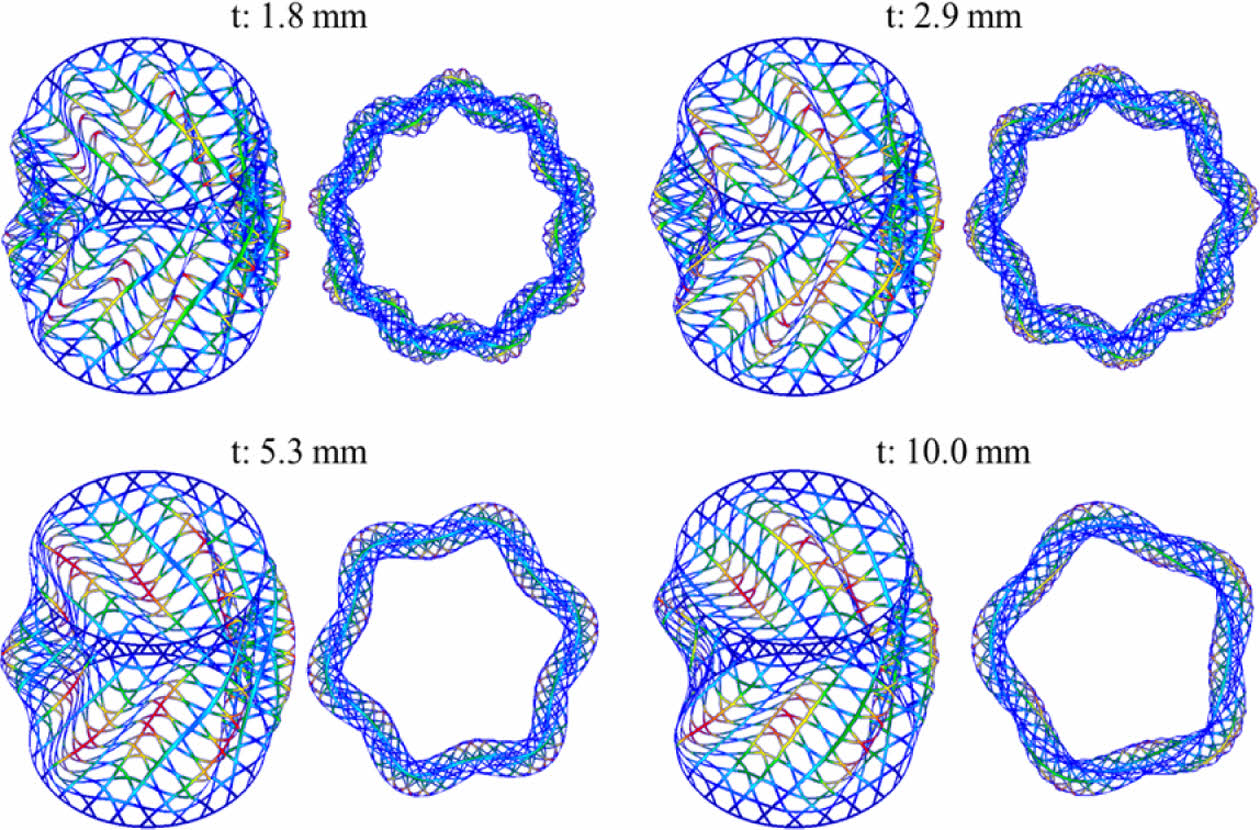
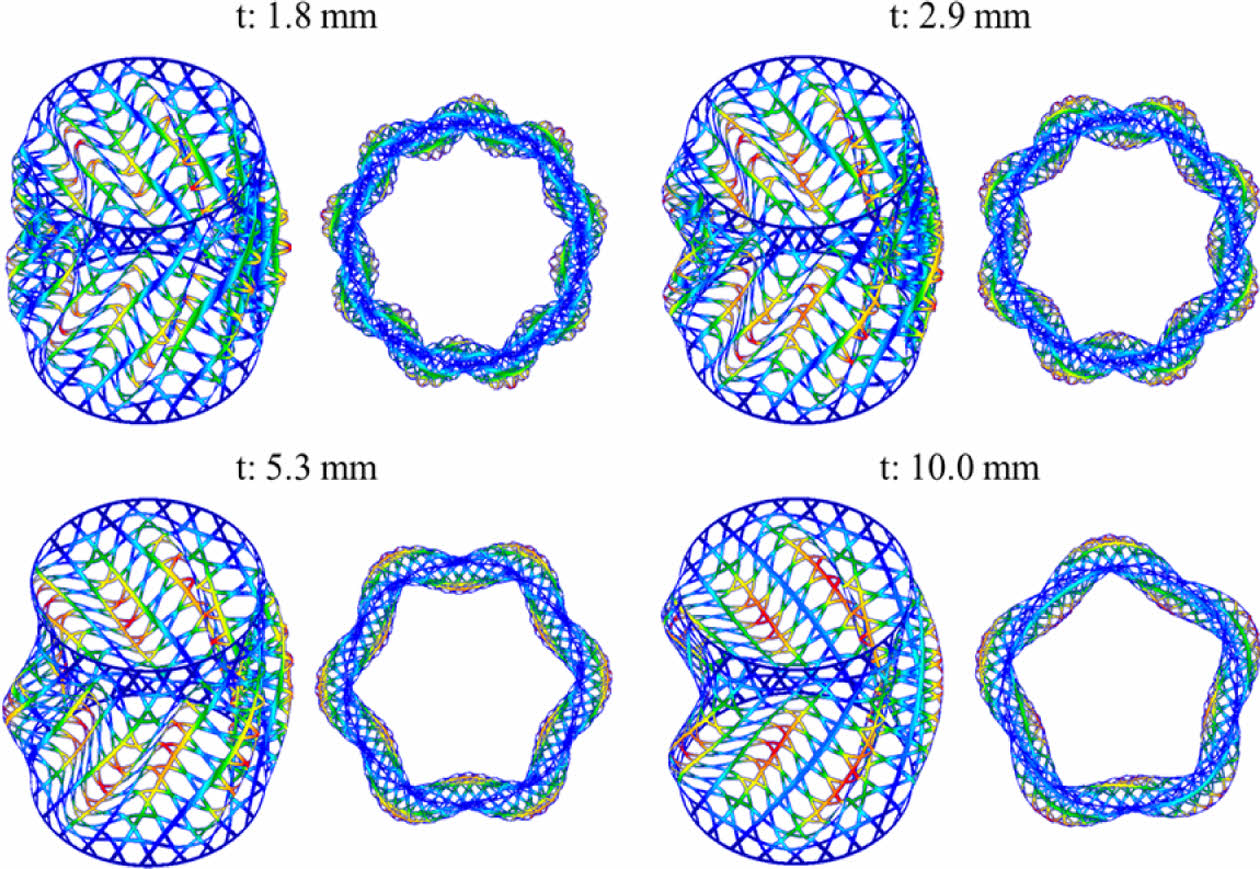
비틀림 하중을 받는 원통형 복합재 격자 구조의 좌굴형상은 Fig. 6, 7과 같다. 비틀림 하중이 가해진 방향으로 주로 나선 형태 및 원주 방향으로의 좌굴 파형이 관찰되었다. 두께가 두꺼워질수록 파장의 개수가 감소하고 파장의 길이가 증가하였다. 섬유체적비 편차에 관계없이 좌굴 형상은 동일하게 관찰되었다. 본 연구에서 적용한 섬유체적비 편차는 좌굴 형상에 큰 영향이 없음을 확인하였다.
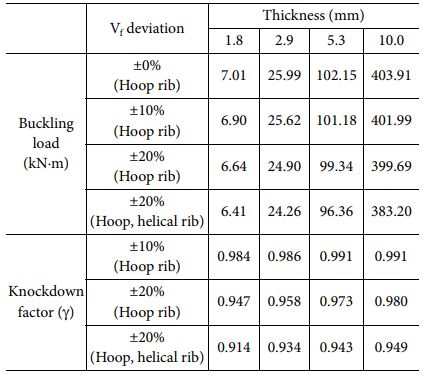
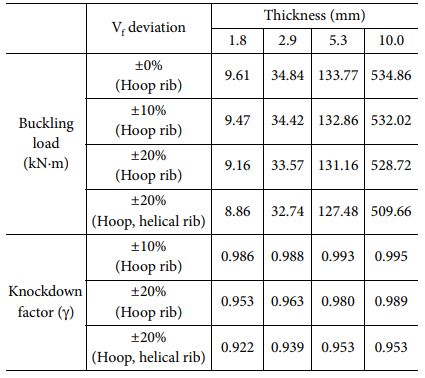
결함에 의해 저하되는 좌굴 성능은 식 (5)의 Knockdown factor(g)로 표현할 수 있다. 여기서 (Pcr)Perfect는 결함이 존재하지 않는 완벽한 구조의 좌굴 하중을 의미하며 (Pcr)Imperfect는 결함에 의해 저하된 좌굴 하중을 의미한다. 본 연구에서는 섬유체적비 불균일을 결함으로 간주하였고 섬유체적비 편차가 없는 모델의 좌굴 하중을 (Pcr)Perfect, 섬유체적비 편차에 의해 저하된 좌굴 하중을 (Pcr)Imperfect로 정의한 뒤 계산 결과를 비교하였다.



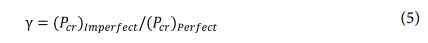
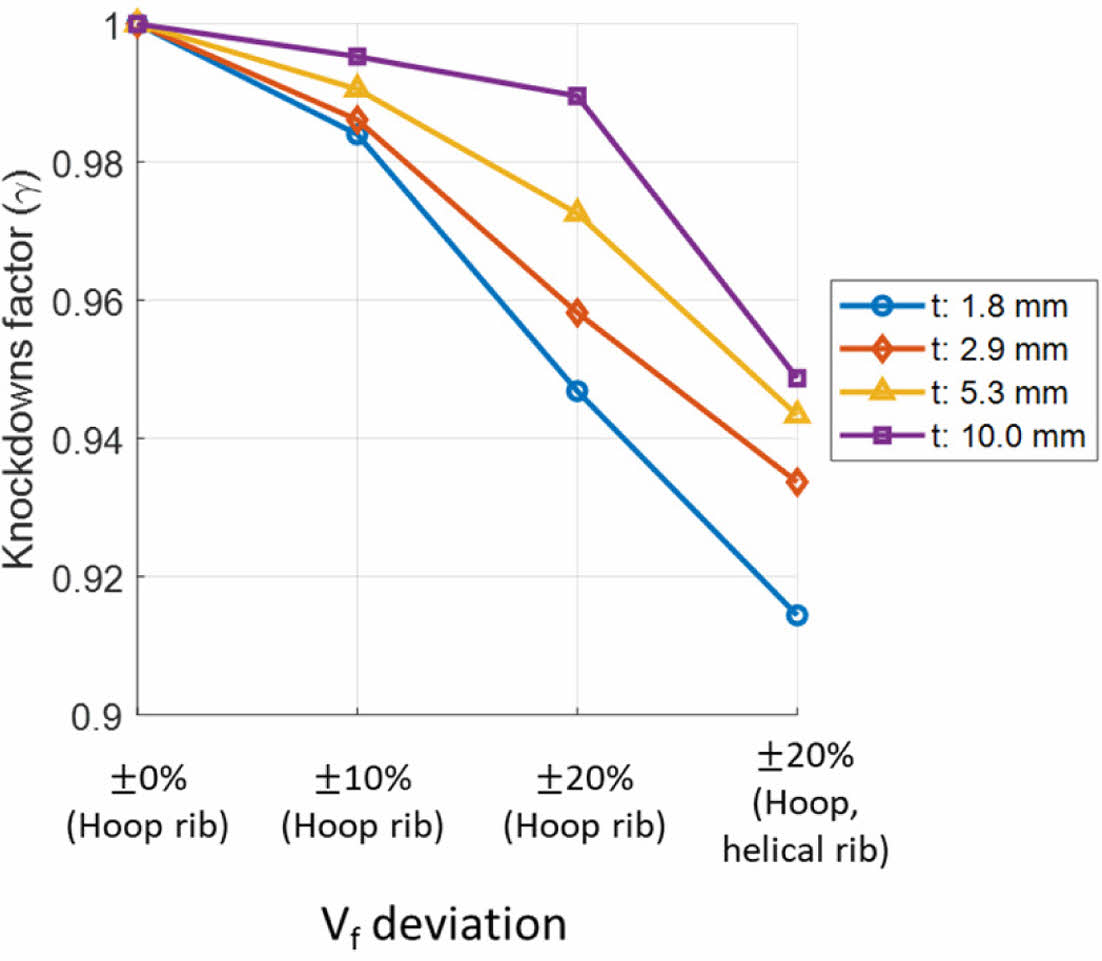
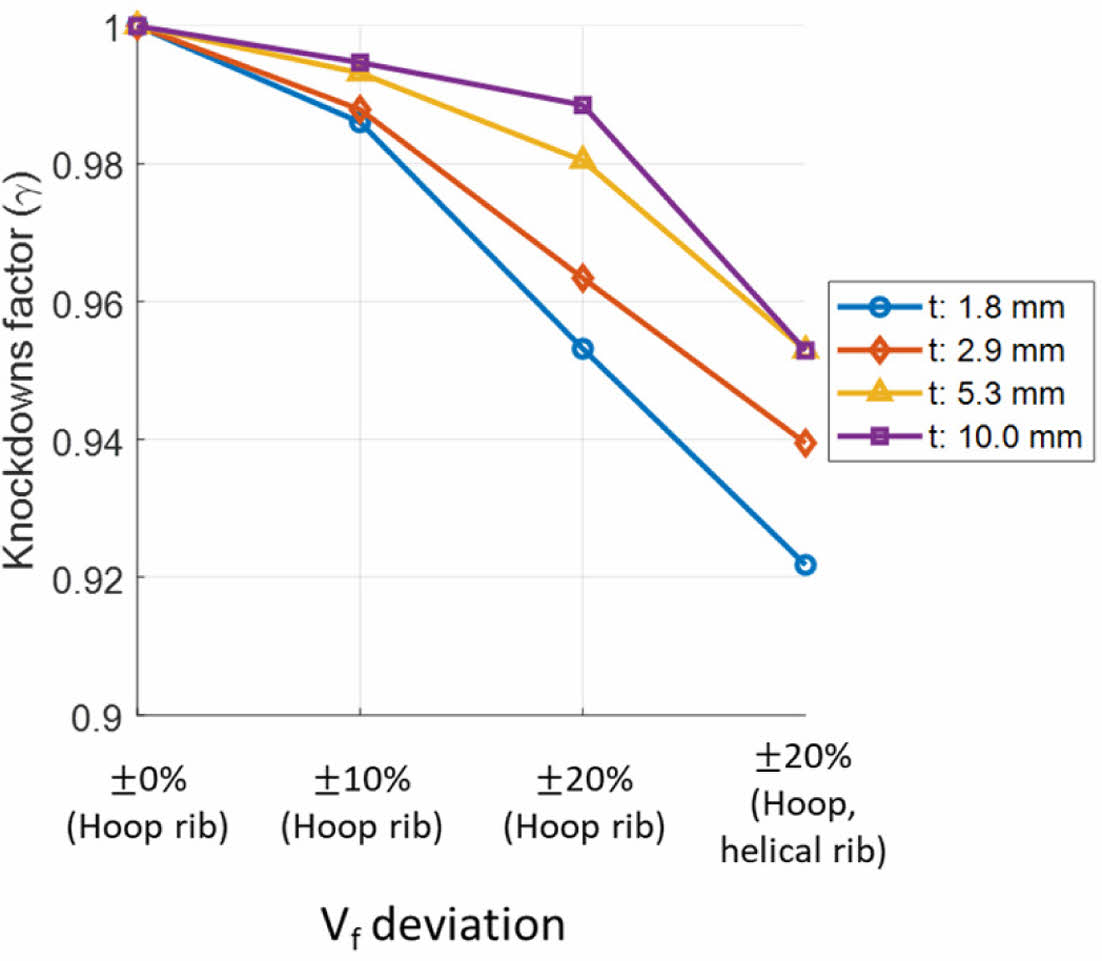
Table 3, 4에서 모델의 두께 및 섬유체적비 편차에 의한 좌굴 하중과 Knockdown factor를 비교하였고 Fig. 8, 9에서 Knockdown factor를 그래프로 비교하였다. 두께방향 섬유체적비 불균일에 의해 좌굴 하중이 저하됨을 볼 수 있다. 섬유체적비 불균일은 후프 리브에만 적용했을 때 두께가 10 mm인 두꺼운 모델에서는 좌굴 하중이 큰 차이가 없음을 확인하였다. 섬유체적비 편차가 커질수록 좌굴 하중이 크게 저하됨을 확인하였다. 같은 직경에서 두께가 얇은 모델일수록 낮은 Knockdown factor가 계산되었다. Structure 2에 비하여 리브 폭이 좁은 Structure 1에서 더 낮은 Knockdown factor가 계산되었다. 후프 및 헬리컬 리브 전체에 두께방향 섬유체적비 편차가 20% 존재하는 모델의 비틀림 좌굴 하중을 볼 수 있으며 섬유체적비 불균일이 헬리컬 리브에도 적용되면 비틀림 좌굴 하중이 약 8.6% 저하될 수 있음을 확인하였다. 제조 공정, 기술 등의 한계로 인한 섬유체적비 불균일에 의해 원통형 복합재 격자 구조의 비틀림 좌굴 하중이 감소할 수 있다. 그러므로 비틀림 좌굴이 발생할 수 있는 원통형 복합재 격자 구조 설계/최적화 단계에서 좌굴 성능을 만족시키기 위한 Knockdown factor를 고려한 설계가 필요하다. 섬유체적비가 불균일함에 따라 강성이 변화한다. 두께방향으로 중심축 기준으로 내경에서는 높은 강성이, 외경에서는 낮은 강성이 배치되면 복합재 적층판의 인장 강성도(Extensional stiffness)는 큰 변화가 없으나 굽힘 강성도(Bending stiffness) 및 연계 강성도(Coupling stiffness)가 변화한다. 비틀림 하중을 받을 경우 각각의 헬리컬 리브(±f)는 인장 하중과 압축 하중을 번갈아받으며 특히 압축 하중을 받는 헬리컬 리브는 인장 하중을 받는 헬리컬 리브에 비하여 섬유체적비에 따른 굽힘 강성의 변화에 민감하다. 후프 리브는 인장, 압축 하중을 번갈아 받는 헬리컬 리브로부터 전달되는 인장, 압축 및 굽힘 하중에 대하여 굽힘 모멘트 형태로 원형 형상을 유지하려는 구성요소이므로 섬유체적비에 따른 굽힘 강성의 변화에 영향을 받을 수 있다. 균일한 섬유체적비가 분포하는 모델과 비교하면 섬유체적비 변화에 따른 굽힘 강성의 변화가 비틀림 좌굴 하중을 저하시킬 수 있다.

Fig. 6

Buckling mode of Structure 1
Fig. 7

Buckling mode of Structure 2
Fig. 8

Knockdown factor of Structure 1
Fig. 9

Knockdown factor of Structure 2
Table 3

Buckling load and knockdown factor of Structure 1
Table 4

Buckling load and knockdown factor of Structure 2
4. 결 론

원통형 복합재 격자 구조에 존재하는 섬유체적비 불균일이 비틀림 좌굴 하중에 미치는 영향에 대한 수치적 연구를 수행하였다. 두께방향으로 불균일한 섬유체적비 분포를 적용하였고 섬유체적비 변화에 따른 강성을 유한요소 모델에 적용하였다. 유한요소 모델에 비틀림 하중을 가하여 좌굴 해석을 수행하였고 같은 직경에서 모델의 두께 변화에 의한 좌굴 형상을 비교하였다. 두께방향 섬유체적비 편차에 의한 좌굴 하중 저하를 분석하였다. 섬유체적비 편차가 커질수록 좌굴 하중이 큰 폭으로 감소하였다. 리브 두께가 얇을수록, 리브 폭이 좁을수록 좌굴 하중이 크게 감소하였다. 구조가 두꺼워질수록 섬유체적비 편차는 더 커질 수 있으므로 서로 다른 두께를 가진 구조의 단면검사 후 섬유체적비 분포를 관찰하여 모델에 적용할 계획이다. 항공기 동체나 유도무기, 발사체 동체와 같은 비틀림 하중을 받는 구조에 복합재 격자 구조를 사용할 경우 섬유체적비 불균일에 따른 Knockdown factor를 고려한 안전 계수를 적용해야 한다. 본 연구에서는 두께 방향 섬유체적비 불균일의 비틀림 좌굴 하중에 대한 영향을 분석하였고 향후 횡방향 하중 및 굽힘 모멘트에 의한 좌굴 하중 분석도 필요하다.

후기

본 연구는 민군협력진흥원(ICMTC)의 지원을 받아 수행한 연구입니다(15-CM-MA-12).

References
  • 1. Vasiliev, V.V., Barynin, V.A., and Rasin, A.F., “Anisogrid Lattice Structures-Survey of Development and Application,” Composite Structures, Vol. 54, No. 2-3, 2001, pp. 361-370.
  •  
  • 2. Vasiliev, V.V., Barynin, V.A., and Razin, A.F., “Anisogrid Composite Lattice Structures-Development and Aerospace Applications,” Composite Structures, Vol. 94, No. 3, 2012, pp. 1117-1127.
  •  
  • 3. Totaro, G., and De Nicola, F., “Recent Advance on Design and Manufacturing of Composite Anisogrid Structures for Space Launchers,” Acta Astronautica, Vol. 81, No. 2, 2012, pp. 570-577.
  •  
  • 4. Giusto, G., Totaro, G., Spena, P., De Nicola, F., Di Caprio, F., Zallo, A., Grilli, A., Mancini, V., Kiryenko, S., Das, S., and Mespoulet, S., “Composite Grid Structure Technology for Space Applications,” Materials Today: Proceedings, Vol. 34, 2021, pp. 332-340.
  •  
  • 5. Totaro, G., Spena, P, Giusto, G., De Nicola, F., Kiryenko, S., and Das, S., “Highly Efficient CFRP Anisogrid Lattice Structures for Central Tubes of Medium-class Satellites: Design, Manufacturing, and Performance,” Composite Structures, Vol. 258, 2021, 113368.
  •  
  • 6. Morozov, E.V., Lopatin, A.V., and Khakhlenkova, A.A., “Finite-element Modelling, Analysis and Design of Anisogrid Composite Lattice Spoke of an Umbrella-type Deployable Reflector of Space Antenna,” Composite Structures, Vol. 286, 2022, 115323.
  •  
  • 7. Vasiliev, V.V., Jones, R.M., and Man, L.I., Mechanics of Composite Structures, CRC Press, 2017.
  •  
  • 8. Totaro, G., De Nicola, F., and Caramuta, P., “Local Buckling Modelling of Anisogrid Lattice Structures with Hexagonal Cells: An Experimental Verification,” Composite Structures, Vol. 106, 2013, pp. 734-741.
  •  
  • 9. Buragohain, M. and Velmurugan, R., “Study of Filament Wound Grid-stiffened Composite Cylindrical Structures,” Composite Structures, Vol. 93, No. 2, 2011, pp. 1031-1038.
  •  
  • 10. Morozov, E.V., Lopatin, A.V., and Nesterov, V.A., “Finite-element Modelling and Buckling Anlysis of Anisogrid Composite Lattice Cylindrical Shells,” Composite Structures, Vol. 93, No. 2, 2011, pp. 308-323.
  •  
  • 11. Totaro, G., “Flexural, Torsional, and Axial Global Stiffness Properties of Anisogrid Lattice Conical Shells in Composite Material,” Composite Structures, Vol. 153, 2016, pp. 738-745.
  •  
  • 12. Kang, M.-S., Jeon, M.-H., Kim, I.-G., Kim, M.-G., Go, E.-S., and Lee, S.-W., “The Effect of the Fiber Volume Fraction Non-uniformity and Resin Rich Layer on the Rib Stiffness Behavior of Composite Lattice Structure,” Composites Research, Vol. 31, No. 4, 2018, pp. 161-170.
  •  
  • 13. Jeon, M.-H., Kong, S.-T., No, H.-R., Kim, I.-G., and Lee, S.-W., “Compression Test of Subelement and Tension Test of Hoop Rib for Stiffness Evaluation of Conical Composite Lattice Structures,” Composites Research, Vol. 33, No. 3, 2020, pp. 169-175.
  •  
  • 14. Kong, S.-T., Jeon, M.-H., Kim, I.-G., and Lee, S.-W., “The Effect of Fiber Volume Fraction Non-uniformity in Thickness Direction on the Buckling Load of Cylindrical Composite Lattice Structures,” Composites Research, Vol. 34, No. 2, 2021, pp. 129-135.
  •  
  • 15. Chamis, C.C., Simplified Composite Micromechanics Equations for Hygral, Thermal, and Mechanical Properties, NASA Technical Memorandum, 83320, 1983.
  •  
  • 16. Zhao, Z., Liu, P., Chen, C., Zhang, C., and Li, Y., “Modeling the Transverse Tensile and Compressive Failure Behavior of Triaxially Baided Composites,” Composite Science and Technology, Vol. 172, 2019, pp. 96-107.
  •  

This Article

Correspondence to

  • In-Gul Kim

  • Department of Aerospace Engineering, Chungnam National University

  • E-mail: igkim@cnu.ac.kr