The PIC design method is assigning different stacking sequences for each shell element through the preliminary FE analysis. In previous study, machine learning was applied to the PIC design method in order to assign the region efficiently, and the training data is labeled by dividing each region into tension, compression, and shear through the preliminary FE analysis results value. However, since buckling is not considered, when buckling occurs, it can’t be divided into appropriate loading type. In the present study, it was proposed PIC-NTL (PIC design using novel technique for analyzing load type) which is method for applying a novel technique for analyzing load type considering buckling to the conventional PIC design. The stress triaxiality for each ply were analyzed for buckling analysis, and the representative loading type was designated through the determined loading type within decision area divided into two regions of the same size in the thickness direction of the elements. The input value of the training data and label consisted in coordination of element and representative loading type of each decision area, respectively. A machine learning model was trained through the training data, and the hyperparameters that affect the performance of the machine learning model were tuned to optimal values through Bayesian algorithm. Among the tuned machine learning models, the SVM model showed the highest performance. Most effective stacking sequence were mapped into PIC tube based on trained SVM model. FE analysis results show the design method proposed in this study has superior external loading resistance and energy absorption compared to previous study

PIC 설계 방법은 선행 유한요소해석을 통해 하중 유형을 나누어, 각 구간마다 하중 유형에 강한 복합재료의 적층 각도 순서를 배치하는 방법이다. 기존 연구에서는 효율적으로 구간을 나누기 위하여 PIC 설계 방법에 머신 러닝이 적용되었으며, 학습 데이터는 선행 유한요소해석 결과 값을 통해 전체 요소의 일부인 참조 요소에서의 인장, 압축 그리고 전단과 같은 하중 유형으로 나누어 라벨링 되었다. 하지만 좌굴에 대해 고려되지 않아서 좌굴 발생 시, 적절한 하중 유형으로 나눌 수 없기 때문에 이를 해결하기 위한 방법이 필요하다. 본 연구에서는 좌굴이 고려되기 위한 새로운 하중 유형 분석 방법을 기존의 PIC 설계에 적용하는 기법(PIC-NTL)이 제안되었다. 좌굴의 하중 분석은 각 플라이(Ply)별 응력 3축 특성을 통해 진행되었으며, 요소의 두께 방향으로 동일한 크기의 두 영역으로 나누어진 판단 영역 내에서 결정된 하중 유형을 통해 대표 하중 유형이 지정되었다. 학습 데이터의 특성 값은 참조 요소의 좌표, 라벨(Label)은 각 판단 영역의 대표 하중 유형으로 구성되었으며, 이 데이터를 통해 머신 러닝 모델이 학습되었다. 머신 러닝 모델의 성능에 영향을 미치는 하이퍼파라미터는 베이지안 알고리즘을 통하여 최적 값으로 튜닝되었다. 튜닝 된 머신 러닝 모델의 중 SVM 모델이 가장 높은 예측률과 ROC-AUC로 나타났으며, 해당 모델을 통해 예측된 데이터가 유한요소 모델에 매핑되었다. 기존에 제안된 PIC 설계 방법과 비교하기 위하여 사각관 형태의 모델을 압축시키는 유한요소해석이 진행되었으며, 본 연구에서 제안된 설계 방법이 강도와 에너지 흡수율에서 더 우수함이 검증되었다

Keywords: 머신 러닝(Machine Learning), 복합재료(Composite Materials), PIC (Piecewise Integrated Composite)

최근 전세계적으로 이산화탄소 배출 규제의 강화 및 에너지 사용 제고와 관련되어 자동차 경량화 연구에 대한 필요성이 커지고 있다[1]. 그로 인하여 자동차 업계에서는 연비 향상, 전기 차량의 모터 시스템 그리고 부품 경량화 및 강도 향상 등에 대한 연구가 많이 진행되고 있다[2]. 경량화 소재로는 비철금속, 열가소성 플라스틱, 복합재료가 대표적으로 여겨지고 있으며, 특히 복합재료는 기존 재료보다 비강도, 비강성이 우수하여 광범위한 응용분야에 적용되고 있다. 특히, 자동차의 여러 부품에 복합재료를 적용하기 위한 연구가 활발하게 진행되고 있다. Cheon 등[3]은 승용차를 위한 새로운 유형의 하이브리드 복합재 범퍼 빔을 제안하고 유한요소해석을 수행하였으며, Belingardi 등[4]은 펄트루전(Pultrusion)으로 제조된 복합재료 범퍼 빔에 대해 수치해석으로 최적화된 단면 형상을 제안하였다. Kim 등[5]은 최적화된 자동차 하이브리드 복합재 범퍼 빔에 관한 연구를 진행하였다. 이처럼 복합재료 범퍼 빔에 대한 연구가 다양하게 시도되고 있으나, 범퍼 빔 전 영역에 단일 적층 각도 순서를 적용하는 것이 일반적이었다. Jeong 등[6]은 범퍼 빔을 5개의 균등한 영역으로 나누어 인장, 압축, 전단의 하중 유형을 분석하고 하중 유형에 따라 복합재료의 적층 순서를 나누어 배열하여 구간조합 복합재료 범퍼 빔을 제안하였다. 또 유한요소해석을 진행하여 하중 유형에 따라 적층 각도 순서 영역이 나누어진 범퍼 빔이 단일 적층 각도 순서를 적용한 범퍼 빔보다 최대 지지 하중 및 에너지 흡수율이 증가하는 것을 입증하였다. 하지만 임의로 5개의 균등한 구간을 나누어 하중 분석을 하였기 때문에 이에 대한 구간 최적화가 필요하여 Ham 등[7]은 머신 러닝(Machine Learning)을 적용하여 하중 유형에 따라 구간을 나누어 적층 각도 순서를 배치하는 PIC (Piecewise Integrated Composite)를 제안하였다. 전체 유한요소 중 일부 요소(참조 요소, Reference Element)에서 응력 3축 특성(Stress Triaxiality)의 평균값을 통해 하중 유형을 판단하여 머신 러닝 모델의 학습 데이터가 생성되었다. 하지만, 좌굴 발생 시, 적절한 하중 유형으로 나눌 수 없기 때문에 좌굴을 고려하여 인장, 압축 그리고 전단 외의 하중 유형으로 나눌 필요가 있다고 생각된다.
본 연구에서는 기존의 PIC 설계 기법에 좌굴 하중이 고려된 하중 유형 분석 방법을 적용한 설계 방법인 PIC-NTL(PIC Design Using Novel Technique for Analyzing Load Type)이 제안되었다. 하중 유형 분석 방법은 PIC 설계 기법에 머신 러닝이 적용되기 위한 학습 데이터 전처리 과정으로 제안된 하중 유형 분석 방법은 적층된 플라이(Ply)들을 동일한 두께의 두 영역으로 나누어 하중 유형이 판단되었다. 해당 영역들은 하중 유형 판단 영역이라 정의되었으며, 각 영역에서의 ply 마다 응력 3축 특성을 통해 하중 유형 분석이 진행되었으며, 해당 영역에서 가장 많이 나타난 하중 유형이 대표 하중 유형으로 결정되었다. 결정된 대표 하중 유형과 참조 요소에서의 좌표 값을 통해 학습 데이터가 구성되었으며 학습 데이터를 통해 머신 러닝 모델이 학습되었다. 머신 러닝 모델의 성능에 영향을 미치는 하이퍼파라미터는 베이지안 알고리즘(Bayesian Algorithm)을 통해 최적의 값으로 튜닝 되었으며, 최적의 성능을 가지는 모델을 통해 모든 요소의 하중 유형이 예측되었다. 예측된 데이터를 통해 유한요소 모델로 매핑(Mapping) 되었으며, 본 연구에서 제안된 설계 기법의 검증을 위하여 기존에 제안된 PIC 기법과 유한요소 해석을 통해 비교 검증되었다.

2.1 학습 데이터 생성 및 하중 유형 분석
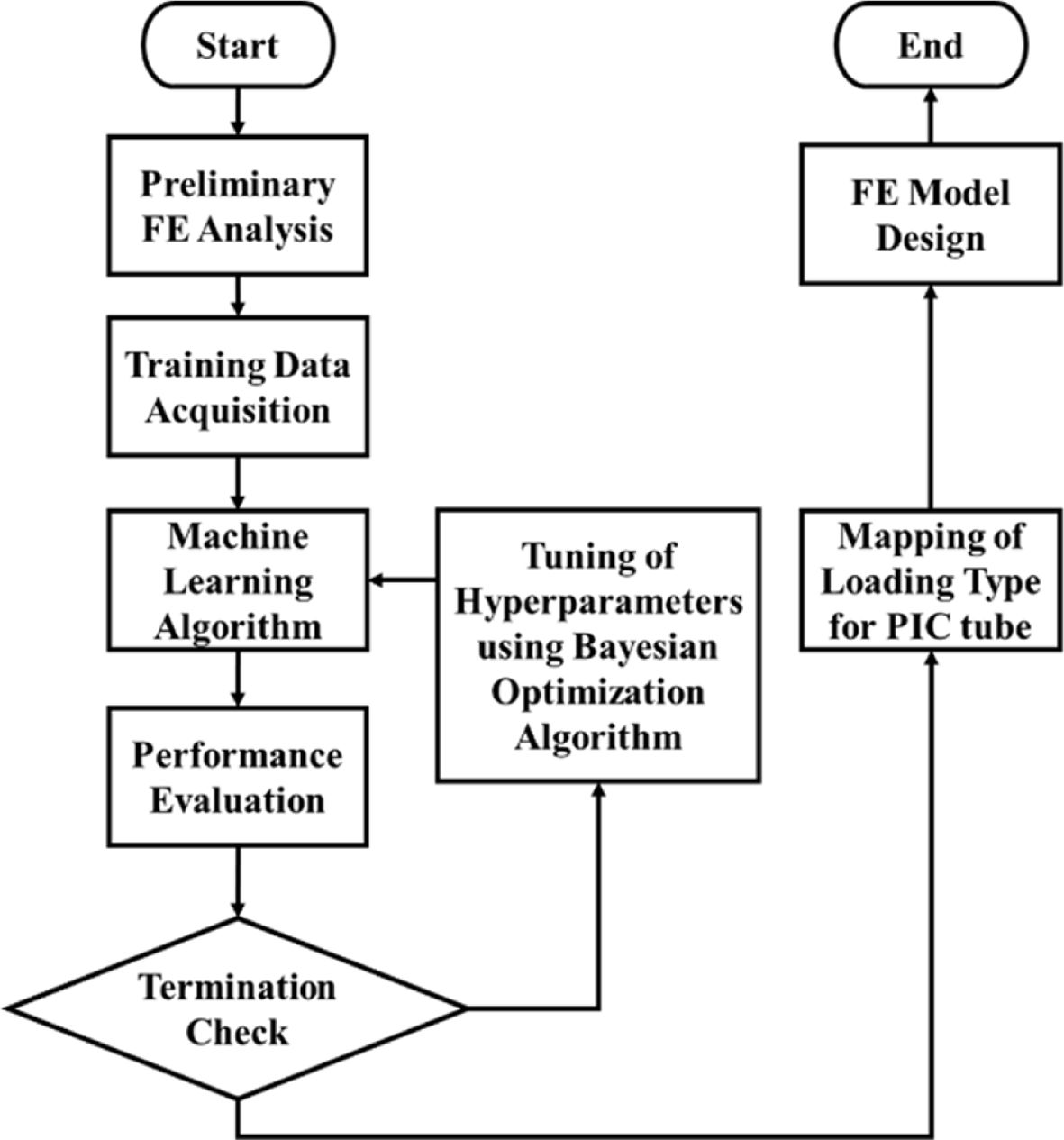
PIC (Piecewise Integrated Composite)는 선행 유한요소해석을 통해 하중 유형 분석이 진행되어, 이를 기반으로 FE 모델의 구간을 나눈 후, 각 하중 유형에 강한 적층 각도 순서를 배치하는 설계 방법이다. 구간을 효율적으로 나누기 위하여 머신 러닝 모델 중 분류(Classification) 기법이 사용되었다. 분류 기법은 주어진 데이터를 라벨(Label)별로 구별해내는 과정으로 다양한 분류 알고리즘을 통해 데이터와 데이터 라벨 값을 학습시키고 모델을 생성시키는 방법이며, 머신 러닝을 적용하기 위한 플로우 차트는 Fig. 1과 같다[8].
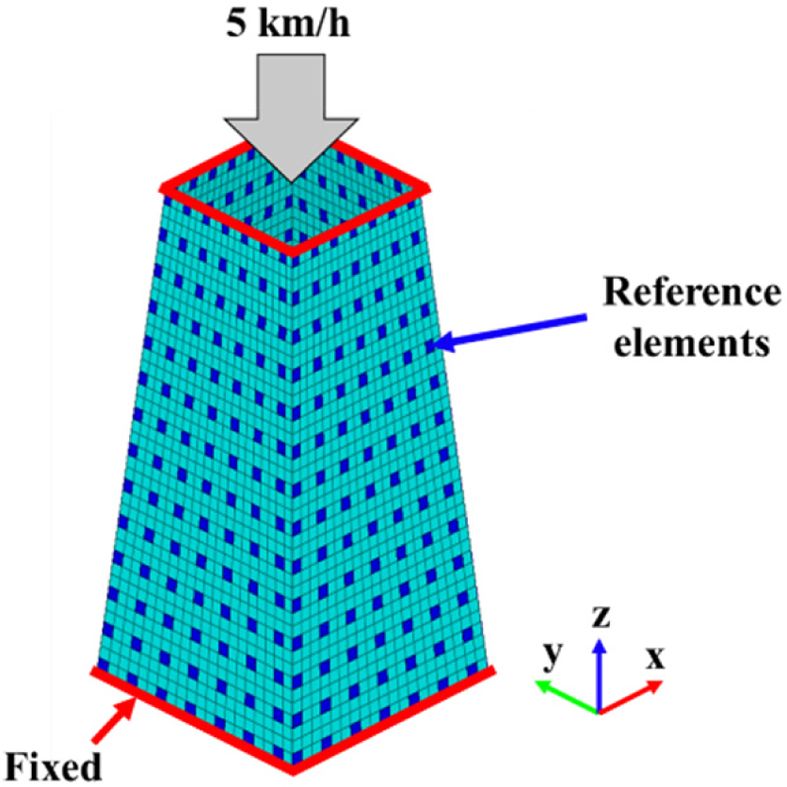
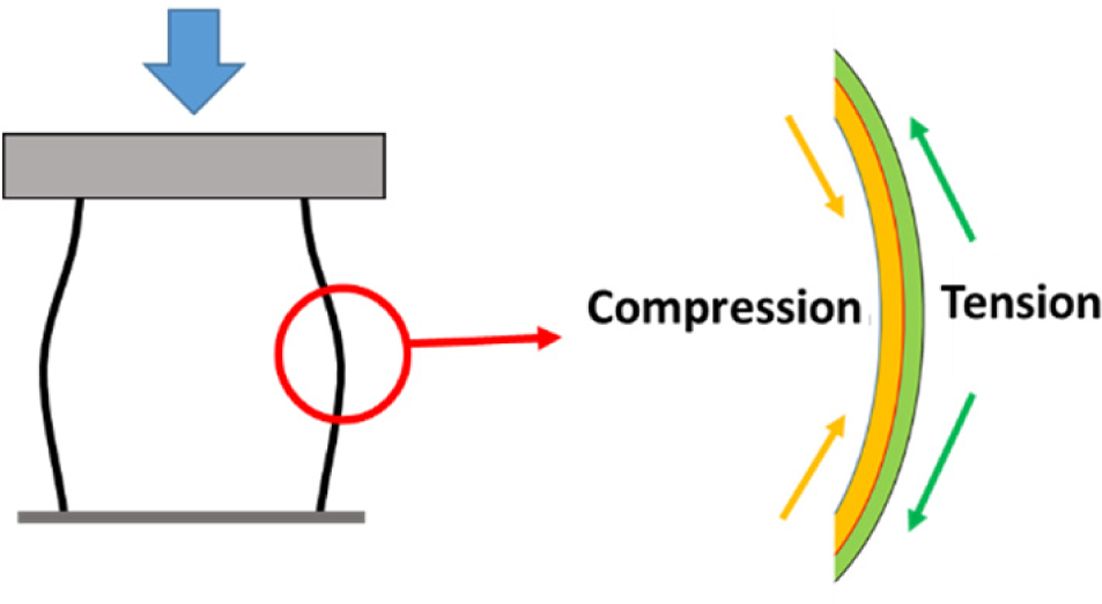
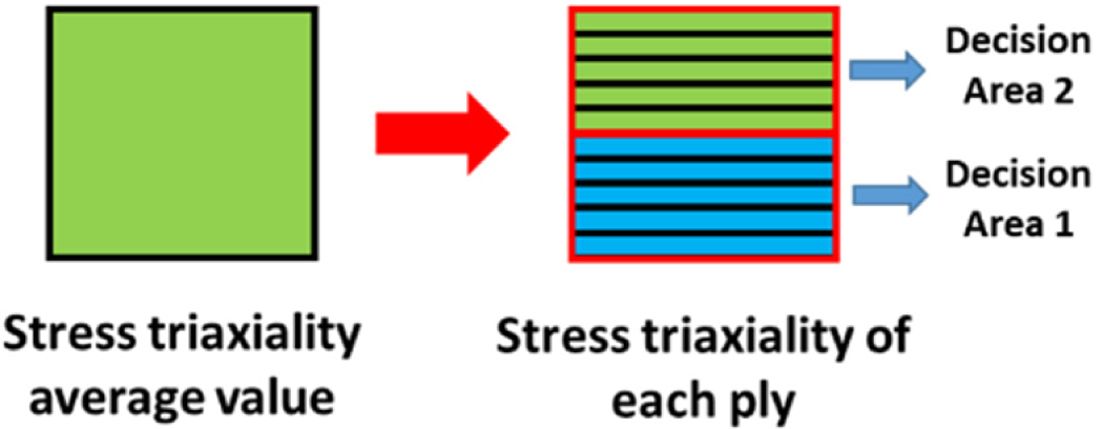
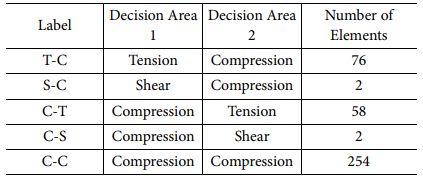
머신 러닝 기법이 PIC 설계 방법에 적용되기 위하여 우선적으로 학습 데이터가 생성되어야 한다. 학습 데이터를 생성하기 위하여 선행 유한요소해석을 통해 참조 요소에서의 응력 3축 특성 값 데이터를 얻었으며, Fig. 2와 같이 좌굴을 유도하기 위하여 사각관 형태의 유한요소 모델을 압축시키는 경계 조건으로 유한요소해석이 진행되었다. 상단부에서 변위가 제어되었으며, 변위 제어 속도는 5 km/h이다. 적층 된 플라이의 수는 30장이며, 요소의 개수는 3,200개이며, 참조 요소의 개수는 전체 요소의 약 12%인 392개이며, 배치는 규칙적으로 이루어졌다. 학습 데이터 특성 값은 참조 요소의 좌표로, 라벨은 하중 유형 판별 데이터로 이루어진다. 기존에 제안된 PIC 설계 기법에서의 하중 유형 판별 방법은 하나의 요소에서 각 플라이의 응력 3축 특성의 평균값을 통해 판별되었다[9]. 하지만 좌굴이 발생하였을 경우, Fig. 3에 나타난 것과 같이 윗부분 플라이에는 압축 하중, 아랫부분 플라이에는 인장 하중이 지배적인 것으로 나타나게 된다. 이러한 좌굴을 고려하기 위하여 본 연구에서는 Fig. 4에 나타난 것과 같이 두 개의 동일한 크기의 판단 영역을 설정하여 판단 영역 1, 2에서 가장 많은 하중 유형으로 나타난 것이 대표 하중 유형 1, 2라 정의되었다. 라벨은 각 판단 영역(Decision Area) 1, 2 순서대로 표기되었으며, 그 결과는 Table 1과 같다. 하중 유형 중 압축 유형이 지배적인 것으로 나타났으며 전단 유형은 다른 하중 유형보다 적게 나타난 것으로 나타났다.
2.2 머신 러닝 모델 및 하이퍼파라미터 최적화
머신 러닝 알고리즘을 앞서 생성된 학습 데이터를 통해 훈련시키게 되면 머신 러닝 모델이 생성된다. 본 연구에서는 결정 트리, SVM (Support Vector Machine), k-NN (k-Nearest Neighbors) 분류 알고리즘이 사용되었다. 각 알고리즘들은 고유의 하이퍼파라미터(Hyperparameter)를 가지고 있으며, 하이퍼파라미터에 의해 성능이 결정된다고 알려져 있다[10].
결정 트리는 분류 규칙으로 노드(Node)가 분기되는 과정을 통해 데이터를 분류하는 모델이고, 하이퍼파라미터는 Maximum Number of Splits과 Splits Criterion이 있다[11]. SVM은 초평면(Hyperplane)을 통해 경계를 결정하여 데이터를 분류하는 모델이며, 하이퍼파라미터로는 kernel function, kernel scale, box constraint level, 그리고 multiclass method가 있다[12]. k-NN 분류 알고리즘은 새로운 데이터를 입력 받았을 때, 해당 데이터와 가장 가까이 있는 k개의 학습 데이터를 통해 분류하는 모델이다. 하이퍼파라미터는 number of neighbors, distance metric, 그리고 distance weight가 있다[13].
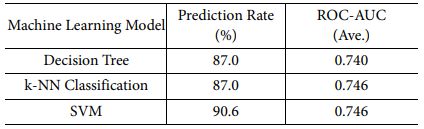
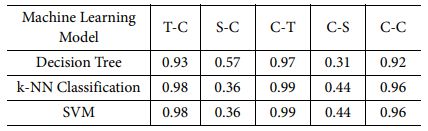
각 모델들은 하이퍼파라미터 튜닝을 통하여 최적의 성능을 이끌어 낼 수 있다. 본 연구에서는 베이지안 최적화 알고리즘을 통해 하이퍼파라미터 튜닝이 이루어졌다. 베이지안 최적화 알고리즘은 미분 불가능하고, 불연속이고, 계산에 시간이 걸리는 함수를 최적화하는 데 사용된다. 획득 함수(Acquisition Function)는 예상 개선값-비용 가중-플러스가(Expected-Improvement-Per-Second-Plus)가 사용되었으며 반복 횟수는 1,000회이다[14]. 하이퍼파라미터 튜닝을 통해 최적의 성능을 갖게 된 머신 러닝 모델의 성능 지표는 예측률과 ROC(Receiver Operation Characteristic)의 AUC(Area Under the Curve)의 평균값을 통해 비교되었다. ROC-AUC는 머신 러닝 모델의 성능을 라벨별로 나타내는 방법이다. 특히, 학습 데이터의 라벨들의 수가 불균형 할 때, 머신 러닝 모델을 평가하기 적합한 방법이다. ROC-AUC 값은 0부터 1까지의 값을 가지며, 1에 가까울수록 성능이 좋은 모델이다[15]. Table 2와 같이, SVM 모델이 예측률과 ROC의 AUC가 각각 90.6, 0.746으로 다른 모델보다 우수한 성능으로 나타났다. Table 3은 하중 유형에 따른 ROC의 AUC 값이며, 참조 요소의 수가 상대적으로 적었던 S-C와 C-S에서 낮은 성능이 도출되었다.
2.3 머신 러닝 적용 결과
우수한 성능으로 나타난 학습된 SVM 모델을 통해 선행 유한요소 모델의 요소 좌표에 대하여 하중 유형이 예측되었으며, 예측된 데이터는 유한요소 모델에 매핑(mapping)되었다.
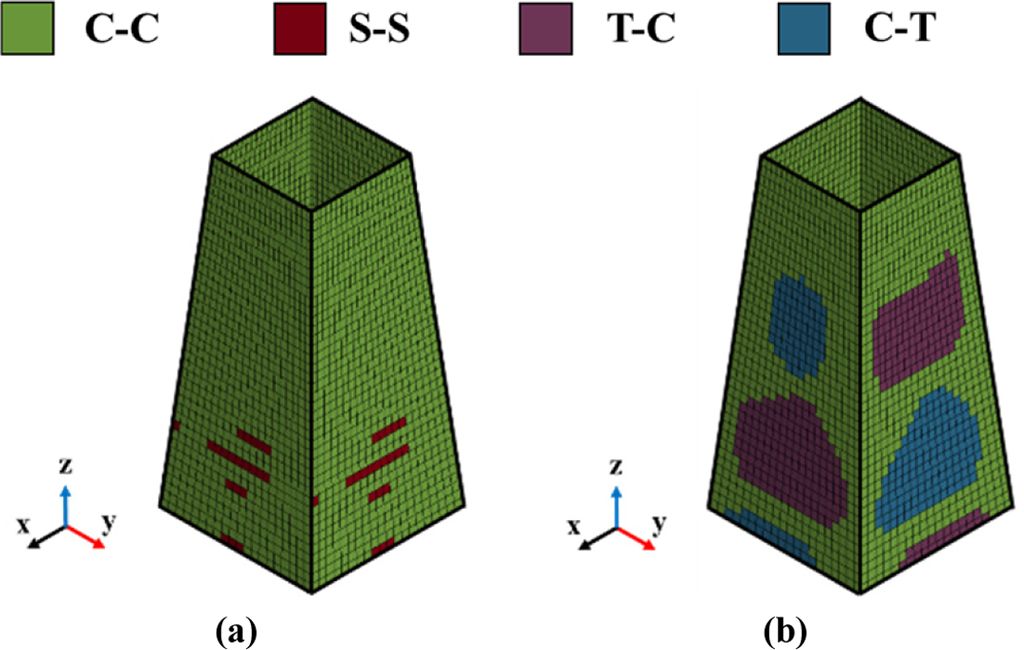
Fig. 5(a)는 기존에 제안된 PIC 기법을 통하여 예측된 데이터가 매핑 된 유한요소 모델이며, Fig. 5(b)는 본 연구에서 제안된 PIC 설계 기법을 통하여 예측된 데이터가 매핑 된 유한요소 모델이다. 기존의 방법에서는 하중 유형이 압축 유형이 지배적으로 나타났으며, 이는 각 요소에서의 응력 3축 특성을 평균 값으로 하중 유형이 판단되었기 때문으로 사료된다. 반면 제안된 PIC 기법은 좌굴에 의해 변형된 부분에서 하중 유형 T-C와 C-T로 예측되었으며, 그 외의 부분에서는 C-C로 예측되었다. 하지만, 참조 요소의 수가 상대적으로 적었던 S-C 및 C-S에 대하여 머신 러닝 모델이 예측하지 못한 것으로 나타났다.

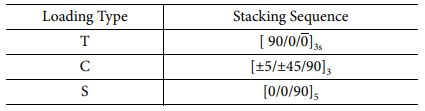
머신 러닝 기법이 적용된 사각관의 강도 향상을 검증하기 위하여 선행 유한요소해석과 동일한 조건의 해석이 진행되었으며, 본 연구에서 제안된 PIC-NTL과 기존에 제안된 PIC 기법이 적용된 설계 기법으로 만들어진 사각관이 비교되었다. 해당 모델에 적용된 재료는 T700 Carbon fibre/2510이다[16]. 각 하중 유형에 적용된 적층 각도 순서는 Table 4에 나타나져 있다[9].
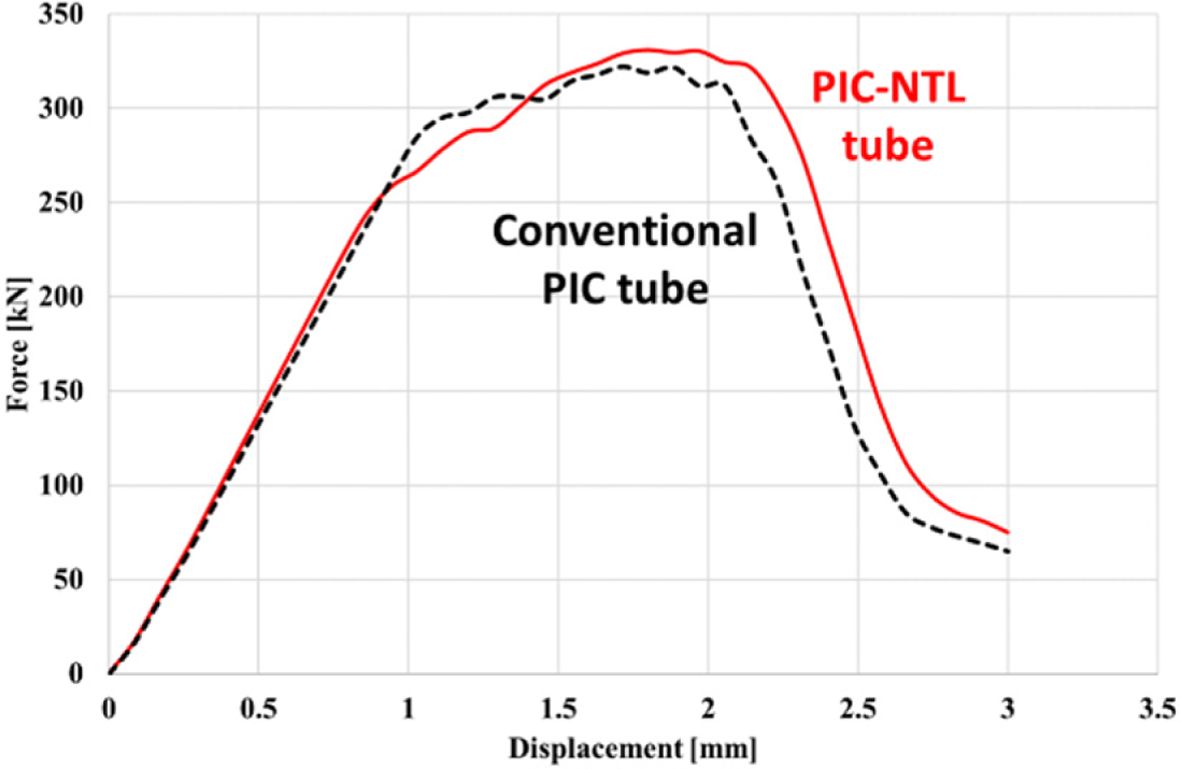
해석 결과는 Fig. 6과 같이 Force-Displacement 선도로 나타냈으며, PIC-NTL 기법으로 설계된 사각관의 최대 지지 하중은 약 322.2 kN으로 나타났고 기존의 설계 기법보다 약 2.7% 높게 나타났으며, 흡수 에너지는 약 526.1 J로 약 4.0% 높게 나타났다.
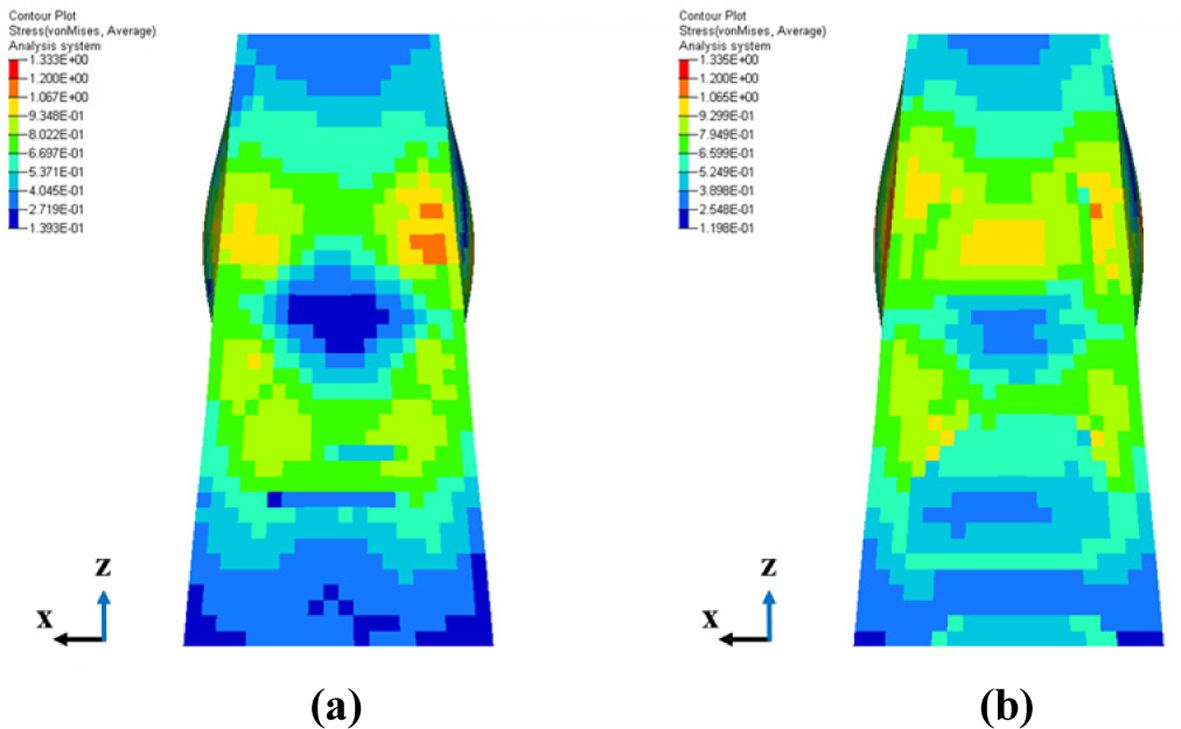
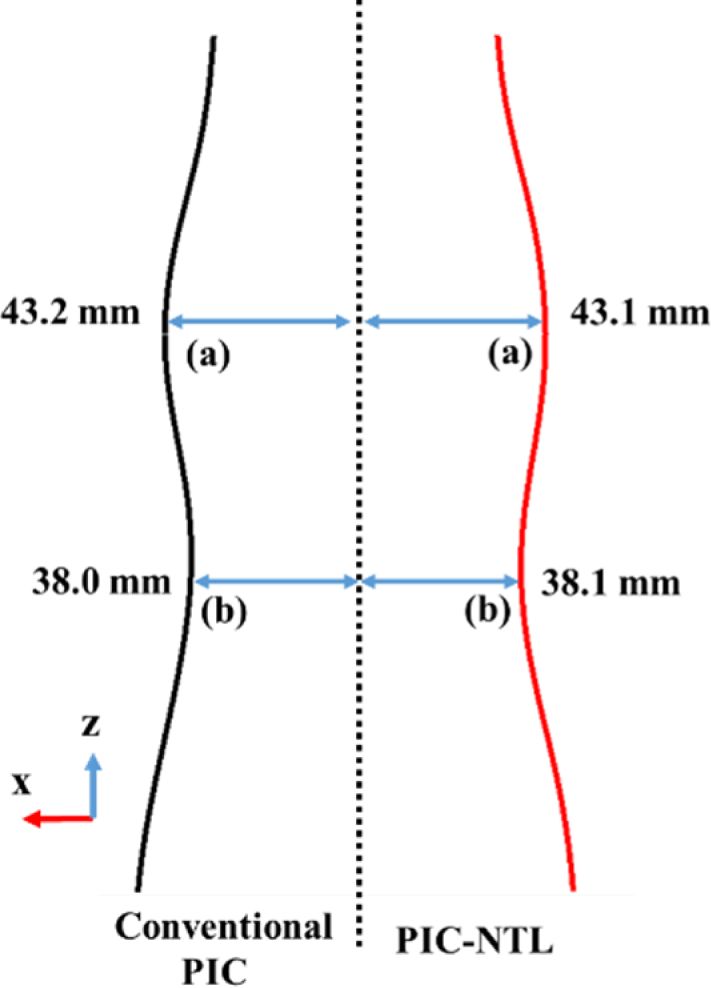
Effective stress contours는 Fig. 7과 같이 나타났으며, 기존에 제안된 PIC 설계 방법으로 모델링 된 사각관에서 더 많은 응력을 받는 것으로 나타났을 뿐만 아니라 국소 영역에서 응력이 집중되는 것으로 나타났다. 이는 해당 국소 영역에서 파단이 쉽게 일어날 것으로 보인다. 그리고 Fig. 8에 나타난 것과 같이 기존에 제안된 PIC 대비 PIC-NTL로 설계된 사각관의 좌굴에 인한 변형량 차이는 각각 (a), (b)에서 약 0.3%, 0.2%로 유사하게 나타났다. 이를 통해 기존의 적층 각도 순서 배치가 사각관의 변형량에 미치는 영향이 낮은 것으로 사료된다.

본 연구에서는 기존에 제안된 머신 러닝을 적용한 PIC 설계 기법에서 고려되지 않은 좌굴 분석을 위해 새로운 하중 유형 분석 방법이 제안되었다. 제안된 하중 유형 분석 방법은 참조 요소의 두께 방향으로 동일한 크기의 두 영역으로 나누어진 판단 영역에서 하중 유형을 분석하고, 각 판단 영역에서 가장 많은 하중 유형이 대표 하중 유형으로 지정하는 것이다. 학습 데이터의 라벨은 지정된 대표 하중으로 구성되었으며 판단 영역 1의 대표 하중 유형-판단 영역 2의 대표 하중 유형으로 표기되었다. 하중 유형 분석 결과, 압축 유형이 지배적인 것으로 나타났으며, 전단 유형은 상대적으로 다른 하중 유형보다 적게 나타났다. 학습 데이터를 통해 머신 러닝 모델이 학습되었으며, 머신 러닝 모델의 성능에 영향을 미치는 하이퍼파라미터는 베이지안 알고리즘을 통하여 최적값으로 튜닝되었다.
머신 러닝 모델 중 SVM 모델이 가장 높은 예측률로 나타났으며, ROC-AUC의 각 라벨의 평균값도 가장 높게 나타났다. 각 모델의 ROC-AUC 중, S-C와 C-S에서 상대적으로 낮은 값으로 나타났는데, 이는 참조 요소의 수가 상대적으로 적었기 때문이라 사료된다.
기존에 제안된 PIC 설계 기법과 비교하기 위하여 선행 유한요소해석과 동일한 경계조건으로 유한요소해석이 진행되었으며, 본 연구에서 제안된 PIC-NTL 기법으로 설계된 tube의 지지하중은 기존에 제안된 PIC 기법보다 약 2.7% 향상되었으며, 에너지 흡수율은 4.0% 향상된 것으로 나타났다. 이를 통해 본 연구에서 제안된 PIC-NTL 기법이 기존에 제안된 PIC 기법보다 더 우수함이 검증되었다.
참조 요소 수가 적은 하중 유형에 대하여 머신 러닝 모델이 더 잘 예측할 수 있도록 참조 요소 수에 대한 가중치 알고리즘에 대한 연구가 필요할 것이라 사료된다.
또한, 적층 각도 순서 배치가 유한요소 모델의 거동에 미치는 영향이 미미하므로 유한요소 모델의 기하학적 변수를 고려하여 계산 횟수(Iteration)를 줄일 수 있는 알고리즘 역시 필요할 것이라 사료된다.

본 연구는 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임. (NRF-2018R1D1A1B07051169).