In this study, an optimal structural design of composite helicopter blades is performed using the genetic algorithm-based optimizer PSGA (Particle Swarm assisted Genetic Algorithm). The blade sections consist of the skin, spar, form, and balancing weight. The sectional geometries are generated using the B-spline curves while an open-source code Gmsh is used to discretize each material domain which is then analyzed by a finite element sectional analysis program Ksec2d. The HART II blade formed based on either C- or D-spar configuration is exploited to verify the cross-sectional design framework. A numerical simulation shows that each spar model reduces the blade mass by 7.39% and 6.65%, respectively, as compared with the baseline HART II blade case, while the shear center locations being remain close (within 5% chord) to the quarter chord line for both cases. The effectiveness of the present optimal structural design framework is demonstrated, which can readily be applied for the structural design of composite helicopter blades

본 연구에서는 복합재료 블레이드에 대한 최적 구조설계 프레임워크를 구성하고, 이를 헬리콥터 블레이드에 적용하여 최적 구조설계를 수행하였다. 단면 형상의 경우 C형 및 D형 스파를 선택할 수 있게 구성하였으며, 최적설계 프레임워크는 유전자 알고리즘과 입자 군집 최적화 알고리즘을 결합한 PSGA를 활용하였다. 단면의 기하학적 모델링은 B-spline을 이용하여 구현하였고, 유한요소 모델 생성 프로그램 Gmsh를 통해 단면 유한요소모델을 만든 뒤 단면 해석 프로그램인 Ksec2D를 사용하여 구조해석 결과를 도출하였다. 본 최적설계 프레임워크를 HART II 블레이드에 적용하여 최적 구조설계를 수행한 결과, C형 스파 모델은 기준 형상 대비 무게 7.39%, D형 스파 모델은 6.65% 감소하였으며, 이때 전단중심은 모두 공력중심과 인접한(5% 이내) 결과를 도출하였다. 본 연구를 통해 일반적인 헬리콥터 블레이드의 단면에 적용할 수 있는 최적 구조설계 프레임워크의 유효성을 확인하였다

Keywords: 로터 블레이드(Rotor blade), 구조 최적화(Structural optimization), 유전자알고리즘(Genetic algorithm), 단면해석(Cross-section analysis)

헬리콥터 블레이드는 헬리콥터의 양력과 추력을 발생시키는데 가장 중요한 역할을 수행하는 핵심 요소이다. 구조동역학적 관점에서 헬리콥터 블레이드는 양력뿐만 아니라 회전에 따른 원심력 및 주기적인 피치운동에 따른 관성과 탄성력 등이 동시에 작용한다. 이와 같이 복합적으로 작용하는 하중을 견디기 위해 헬리콥터 블레이드는 높은 강성을 가지면서 동시에 가벼운 무게를 갖도록 설계되며, 이러한 조건을 충족하기 위해 보통은 복합재료를 이용하여 설계된다.
헬리콥터 블레이드는 단면의 크기에 비해 길이가 매우 긴 기하학적 형태를 갖는다. 이러한 특징으로 반복적인 계산이 많이 요구되는 최적 구조설계 단계에서는 단면과 1차원 보 형태로 단순화하여 계산하는 것이 효율적이다[1]. 따라서 최적 구조설계에서는 구조 형상, 재료 및 기타 물리적 특성이 다른 블레이드 여러 지점에서 단면해석을 수행하여 강성치과 관성치를 계산한 후 이를 블레이드 1차원 모델에 대입하여 구조동역학 해석을 수행한다. 이러한 해석 과정은 초기 설계 조건을 만족할 때까지 반복 수행한다.
블레이드 단면해석은 크게 유한요소기반 단면해석법[1-3]과 중심선기반 단면해석법[4-6]로 구분할 수 있다. 중심선기반 단면해석법은 속이 빈 박벽의 단면에 적용할 수 있는 방법으로, 각 단면의 벽을 1차원 곡선으로 근사화하고 이들을 선적분을 통해 블레이드 단면 물성을 계산하는 방법이다. 선행연구[7-9]에서 헬리콥터 블레이드의 최적설계를 중심선기반 단면해석법을 통해 수행한 바 있다.
유한요소기반 단면해석법은 2차원 유한요소를 사용하여 이산화하고, 각 요소들을 적분하여 단면 물성을 계산하는 방법이다. 이 방법의 경우 단면의 형태나 두께에 별다른 제한 없이 사용할 수 있으며, 많은 연구에서 이 방법을 사용하고 있다[4-6]. 그러나 블레이드 단면 최적설계 과정에서 단면 내부의 형상을 변경시키기 위해서는 단면의 기하학적 모델링을 변경하고, 이에 따라 해당 모델에 맞는 유한요소를 생성해야 한다. 따라서 단면 형상 변화에 제약이 많고 그만큼 정교하고 복잡한 알고리즘 구현이 요구된다. 선행연구[1-3,10,11]에서는 단면 내부 형상(스킨, 스파 등)의 두께, 너비 등을 변경시키는 방법의 최적설계를 제안한 바 있다. 하지만 이러한 방법들은 필요에 따라 내부 형상 자체를 변화시키는 것에 대해서는 어려움이 있다[6].
본 연구에서는 이러한 한계를 보완하고자 내부 형상을 선택적으로 사용하여 단면을 모델링하고, 각각의 설계 변수에 따라 최적설계하는 방법을 제안하였다. 개발된 방법은 선행연구 Ahn 등[10,11]의 최적설계 프레임워크에서 C스파 형상만을 다루었던 것을 개선하여, D형 스파를 추가하였다. D형 스파는 C형 스파와 다르게 웹(web)이 존재하여 전단중심의 위치가 C형 스파 대비 상대적으로 뒷전 쪽에 놓이게 된다. 헬리콥터 블레이드는 공력중심과 전단중심의 상대 거리에 따라 모멘트가 발생하게 되는데, 스파 형식에 따라서 헬리콥터 블레이드 설계 시 이러한 모멘트의 발생 정도를 조절할 수 있게 된다.

2.1 블레이드 단면 유한요소 모델링
본 연구에서 헬리콥터 블레이드의 단면 모델링은 단면의 기하학적 모델링을 수행하고, 2D 유한요소모델을 제작하는 순서로 진행된다.
기하학적 모델링은 먼저 블레이드 단면의 최 외곽 점들을 익형 종류에 따라 모델링 한 후, 해당 점들을 식 (1)과 같은 벡터 연산을 활용하여 내부 구조물을 구성하는 점들을 각 위치에 맞게 배치한다.



여기서 P(x₀, y₀) 는 임의의 점 좌표를 나타내고, t는 두께, r꙼̈ 는 방향벡터를 나타낸다. 이 연산을 통해 두께 t만큼 떨어진 점 P(x, y)를 구할 수 있다.
이렇게 구성된 점들은 근사곡선의 일종인 B-spline[12]을 활용하여 선 단위의 곡선 형태의 모델링을 수행한다. B-spline은 de Boor Cox 점화식으로 대표되는 기저함수와 제어점들 사이의 함수로 구성되는 근사곡선[13]으로써, 유선형의 기하를 갖는 헬리콥터 블레이드를 설계하는데 효율적이다[14]. 생성된 선 모델을 바탕으로 면(Surface)를 생성하고 이렇게 생성된 면 모델을 평면 유한요소로 분할하여 유한요소모델을 생성한다. 이러한 일련의 과정들은 유한요소 생성 프로그램인 Gmsh[15]를 이용하여 수행된다. Fig. 1은 HART II 외곽선을 따라 점, 선 단위의 모델링을 나타냈고, Fig. 2는 Gmsh를 통해 생성된 유한요소모델을 나타냈다.
이러한 모델링 과정을 통해 다양한 형상의 단면을 유한요소모델로 생성하는 것이 가능하며 본 연구에서는 해당 과정을 파이썬(Python)을 이용한 프로그래밍을 통해 자동화하여 다양한 설계 변수에 대응하는 모델링을 수행할 수 있도록 구현하였다.

2.2 최적 구조설계 프레임워크
본 연구에서 제안한 최적설계 기법의 타당성을 확인하기 위해 HART II 블레이드[16-18]를 대상으로 최적설계를 수행하였다. HART II 블레이드는 BO-105 기체 로터의 40% 축소형 로터로써 Jung 등[17]이 수행한 구조해석 결과를 검증 대상으로 선정하였다.
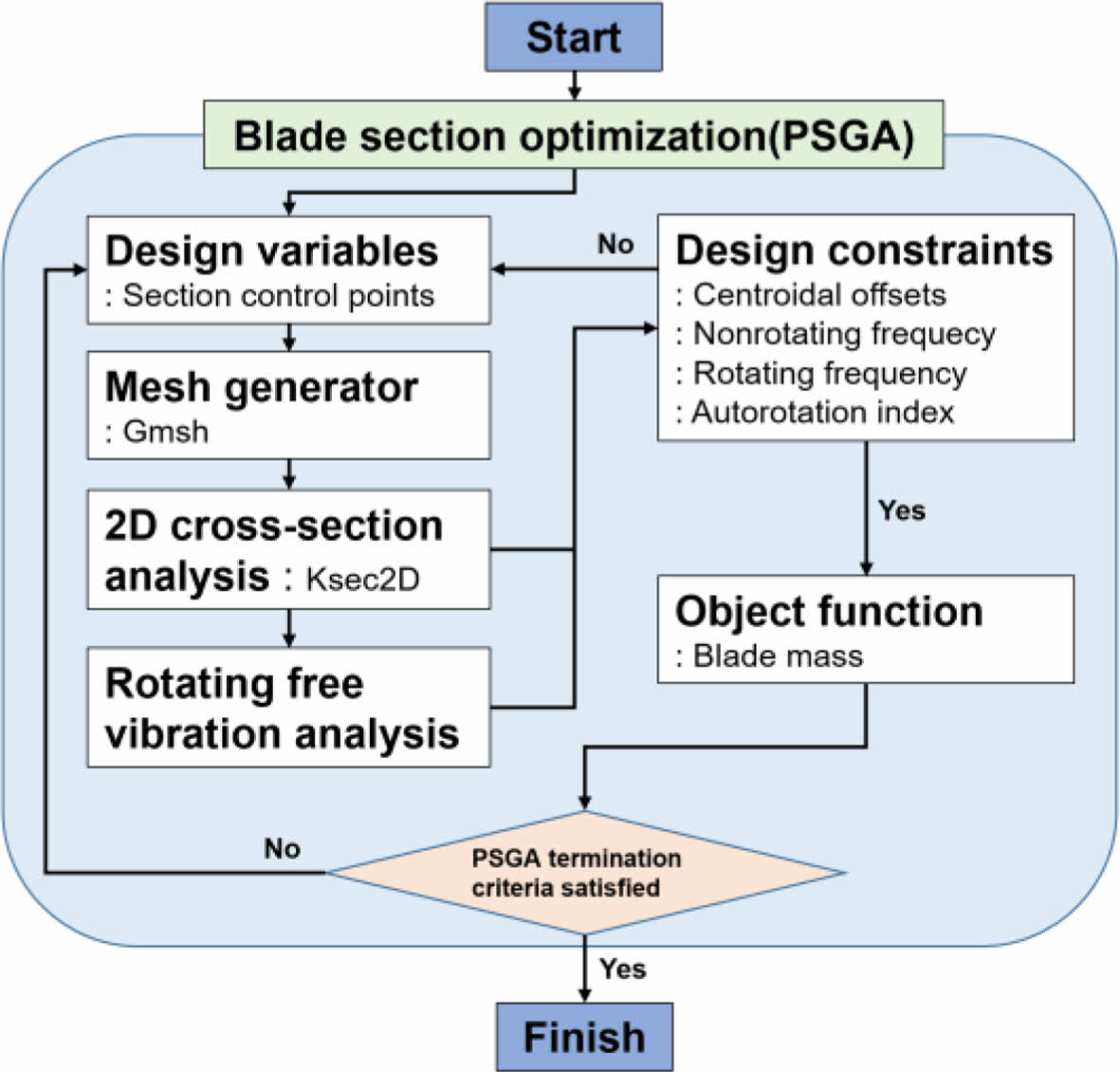
최적 구조설계를 위한 프레임워크는 Fig. 3과 같이 구성하였으며, 여기에는 크게 설계변수들을 설정하는 최적화 알고리즘 부분과 구조해석을 수행하는 부분으로 구분할 수 있다. 최적화 알고리즘은 Dhadwal 등[19]이 제안한 전역탐색 알고리즘인 PSGA 알고리즘(Particle Swarm assisted Genetic Algorithm)을 사용하였다. 기존의 유전자 알고리즘은 선택, 교차, 변이의 세 가지 방법을 이용하여 최적화를 수행한다. 이 경우 빠른 속도로 전역에 대한 최적해를 구할 수 있다는 장점이 있지만, 변수들의 분배 과정에서 값들이 편중될 수 있다. 이러한 문제점을 입자 군집 최적화는 전역에 흩뿌려진 변수들을 여러 방향으로 퍼트림으로써 개선했다[19]. PSGA는 앞의 두 기법의 장점을 차용한 기법으로, 본 연구에서는 설계 변수 전역에 대한 전역적인 최적해를 얻기 위해 PSGA를 사용하였다.
PSGA를 통해 설정된 설계변수들은 앞서 설명한 모델링 과정을 통해 Gmsh를 이용하여 유한요소모델을 생성하고, 단면해석 프로그램인 Ksec2D[20]를 통해 단면해석을 수행한다. Ksec2D로부터 단면요소에 대한 질량 및 강성행렬 결과를 얻게 되고, 회전 고유진동해석[21]을 통해 운용 rpm에서의 회전 고유진동수를 계산한다. 최종적으로 PSGA를 통해 해당 과정을 반복하여 최적 구조설계 결과를 도출하게 된다.
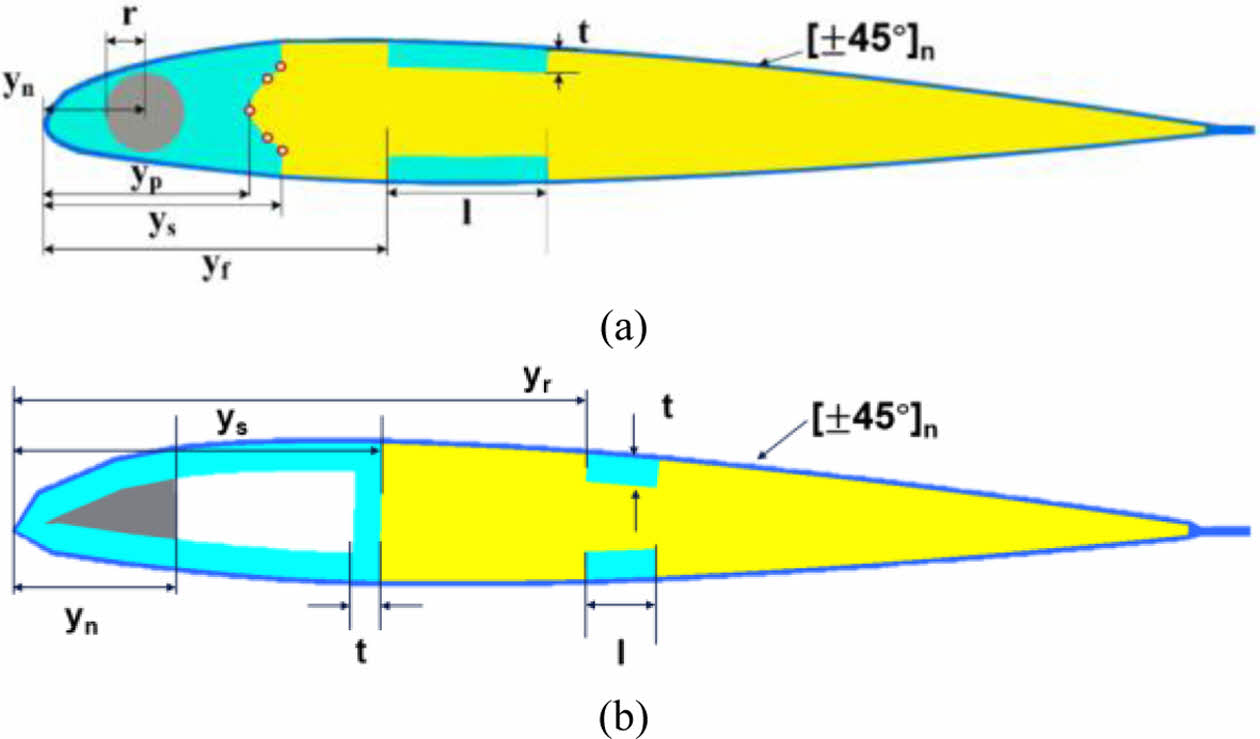
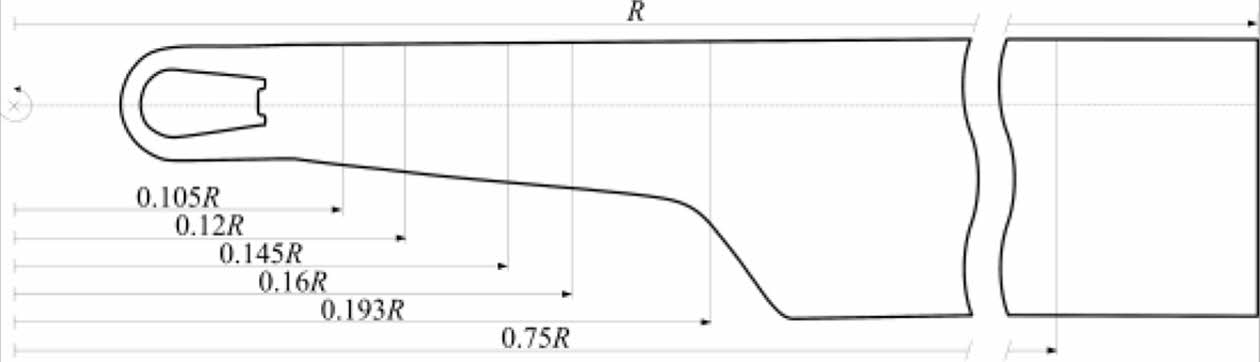
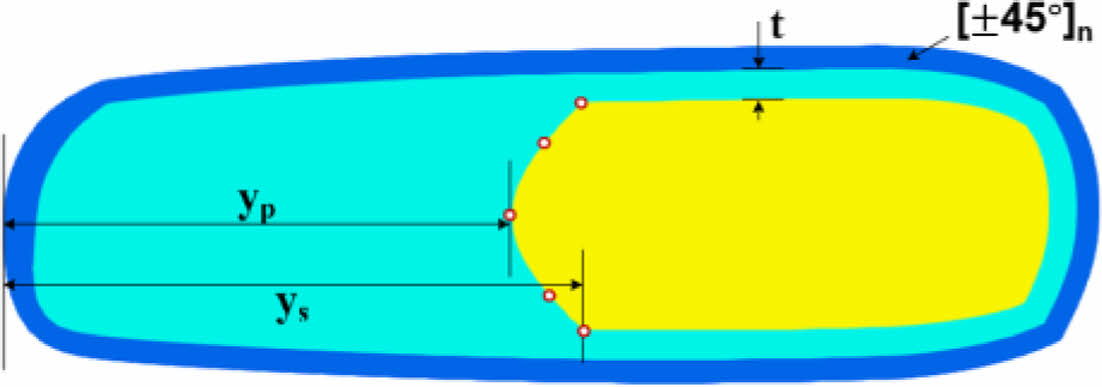
Fig. 4는 기준 단면 형상과 각각의 스파 형상에 따른 설계변수를 나타낸다. 이 때, n은 단면의 스킨 부분의 복합재료 적층 수이며, y_p와 y_s는 각각 C형 및 D형 스파 모델의 스파 길이, l은 후방 스파의 플랜지의 길이, t는 스파와 플렌지의 두께이다. 또한, y_n은 C형 스파 모델에서는 무게추의 위치를 D형 스파 모델에서는 앞전으로부터 떨어진 길이를 의미한다. r은 C형 스파를 갖는 단면에서의 무게추의 반지름이다. Fig. 5는 HART II 블레이드 단면에서 익형 부분과 루트 부분의 단면 위치를 나타냈고, 본 블레이드 최적설계를 위해서는 루트 영역에서 5개 익형 영역에서 1개를 선정했다. Fig. 6는 루트 영역 한 가지에 대한 단면의 형상과 설계변수를 나타낸 것이다.
본 연구에서의 최적화 문제는 다음과 같이 정의하였다.



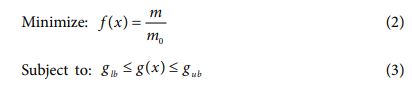
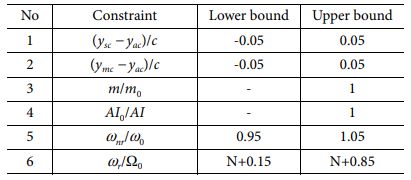
최적화 목적함수는 식 (2)와 같이 무게를 줄이는 것으로 설정하였다. 이 때 m은 무게를 나타내고, 하첨자 0은 기준이 되는 HART II 블레이드의 데이터를 의미한다. 구속조건은 식 (3)에 제시한 바와 같으며, g_ub와 g_lb는 각각 구속조건의 하한값 및 상한값을 나타낸다. 설계 세부 구속조건은 Table 1에 보였다. 이 때, Table 1의 1, 2번 구속조건은 익형 영역을 대표하는 단면인 로터 반지름의 75% (0.75R) 지점에서 단면의 전단 중심과 무게중심 이동에 대한 구속조건이다. y_sc, y_mc, y_ac은 각각 단면의 전단중심, 무게중심 및 공력중심의 위치를 나타낸다. 세 번째 구속조건은 블레이드 질량이 기준 대비 감소하도록 설정한 것이다. 다음은 자동회전 관성지수(AI)로써 무게 감소에 따라 자동회전 관성지수가 기준 대비 저하되는 것을 방지하고자 구속조건을 부가하였다. 5번 구속조건은 비회전(non-rotating) 고유진동수에 대한 조건으로 w_nr는 기준 형상의 1차 플랩(flap), 1차 래그(lag), 1차 비틀림(torsion)모드의 고유진동수를 의미하고, 이들이 최대 ±5% 이상 벗어나지 않도록 설정하였다. 마지막 구속조건에서 w_r는 회전고유진동수를 나타내며, W₀는 HART II 블레이드의 운용 회전수(1,041 rpm)이다. 해당 구속조건은 운용 환경에서 공진 현상을 회피하기 위하여 각 회전 고유진동수에서 ±0.15/rev만큼 이격하도록 설정하였다.

3.1 단면 유한요소 모델링 결과 검증
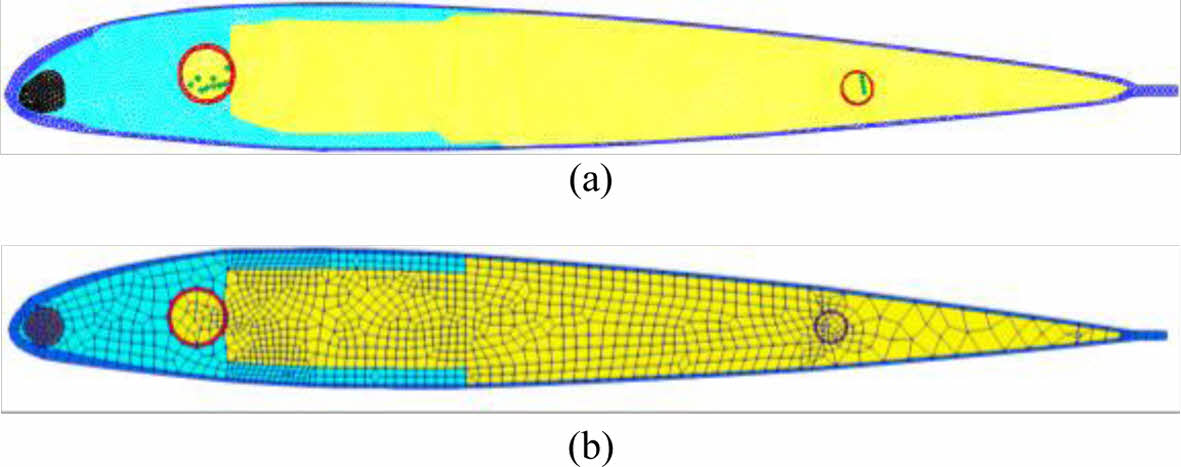
제안한 블레이드 단면 모델링 과정의 신뢰성을 검증하기 위해 HART II 블레이드 0.75R 지점의 단면과 비교하여 검증하였다. 먼저 해당 단면의 단면 정보를 얻기 위해 HART II 블레이드 CT 이미지[17]를 참고하였고, 해당 이미지를 바탕으로 앞에서 제시한 블레이드 단면 모델링 과정을 통해 유한요소모델을 재생성 하였다. Fig. 7(a)는 Jung 등[17]에서 보인 유한요소모델이고, Fig. 7(b)는 본 연구에서 재생성한 유한요소모델로 총 1,345개의 요소, 1,409개의 절점으로 구성된다.
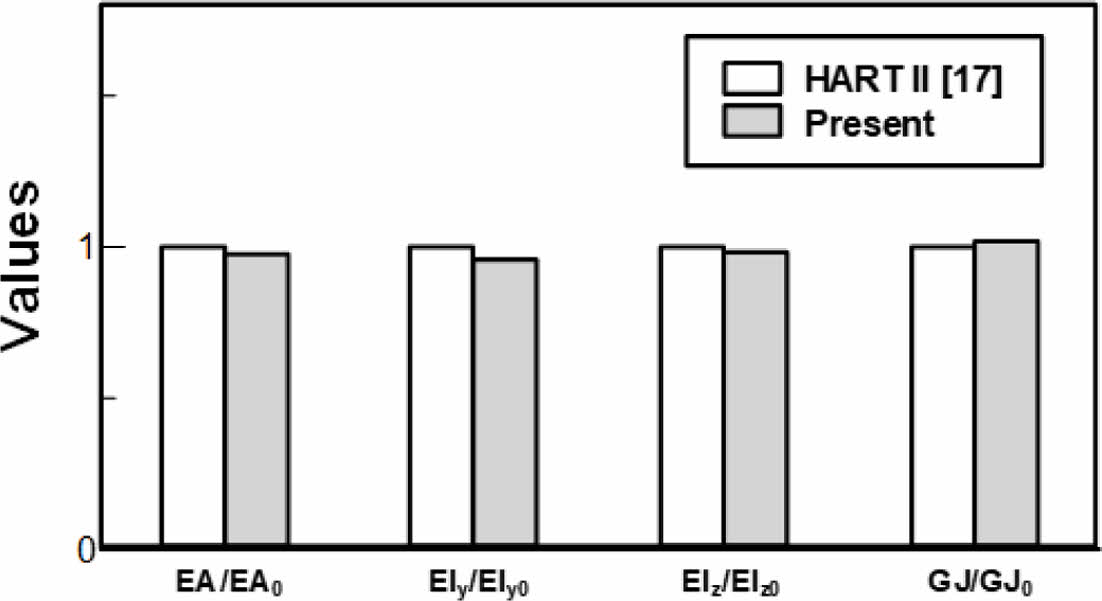
재생성 된 유한요소모델을 Ksec2D를 이용하여 단면해석을 수행하고, 이전 단면해석 결과와 비교하였다. Fig. 8은 재생성 된 모델의 강성도에 대한 단면해석 결과와 HART II 블레이드의 단면해석 결과를 기존 HART II 블레이드 단면해석 결과로 무차원화 시켜 비교한 그래프이다. 각 결과에서 알 수 있듯이 블레이드 강성치는 최대 6.4% 오차 이내로 나타냈다. 또한 전단중심과 무게중심의 위치는 기준형상 대비 2.1%의 오차를 보였다. 도출된 단면 형상에 대한 수치 비교를 통해 본 연구에서 제시한 단면 모델링 기법이 어느 정도 유효함을 확인하였다.

3.2 블레이드 구조 최적설계
본 연구에서 구성한 최적 구조설계 프레임워크를 통해 D형 스파 형상을 갖는 단면에 대해 최적 구조설계를 수행하였으며, 기존 C형 스파 형상을 갖는 단면[11]과 비교하였다. 블레이드 루트 영역은 스파 형상의 영향이 적은 구간으로 D형 스파의 최적 구조설계 과정에서는 C형 스파 모델의 최적 구조설계 결과로 나온 루트 영역의 단면을 그대로 사용하였다.
블레이드 최적 구조설계를 위해 최적탐색기(PSGA) 설정은, 계산 정밀도 및 수렴성을 확보하기 위해 한 세대의 인구수는 60으로 설정하였고, 최대 인구수는 50,000, 그리고 목적함수 최대 계산 횟수는 100,000으로 설정하였다. 또한 목적함수의 값의 오차가 10^-5이내가 되거나 30세대 이상 같은 값이 반복될 경우 수렴한 것으로 판단하여, 계산이 종료되도록 구성하였다.
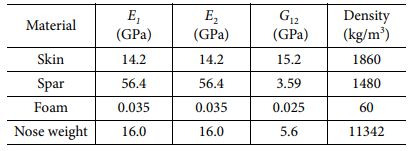
Table 2는 본 연구에서 사용한 재료와 그 물성 값을 나타낸 것이다. 단면의 스킨에 사용된 재료는 유리섬유(GFRP)로 ‘한국화이바’의 ‘GU150NS’[21]를 사용하였고, [±45^o]의 복합재료 적층각을 갖도록 구성하였다. 단면의 스파에 사용된 재료는 직조형 탄소섬유(CFRP woven)으로 ‘SK chemical’의 ‘WSN-3K’[22]를 사용하였다. 나머지 폼과 무게 추의 경우 기존 Jung 등[18]의 HART II 블레이드에 사용된 재료와 동일한 재료를 사용하였다.
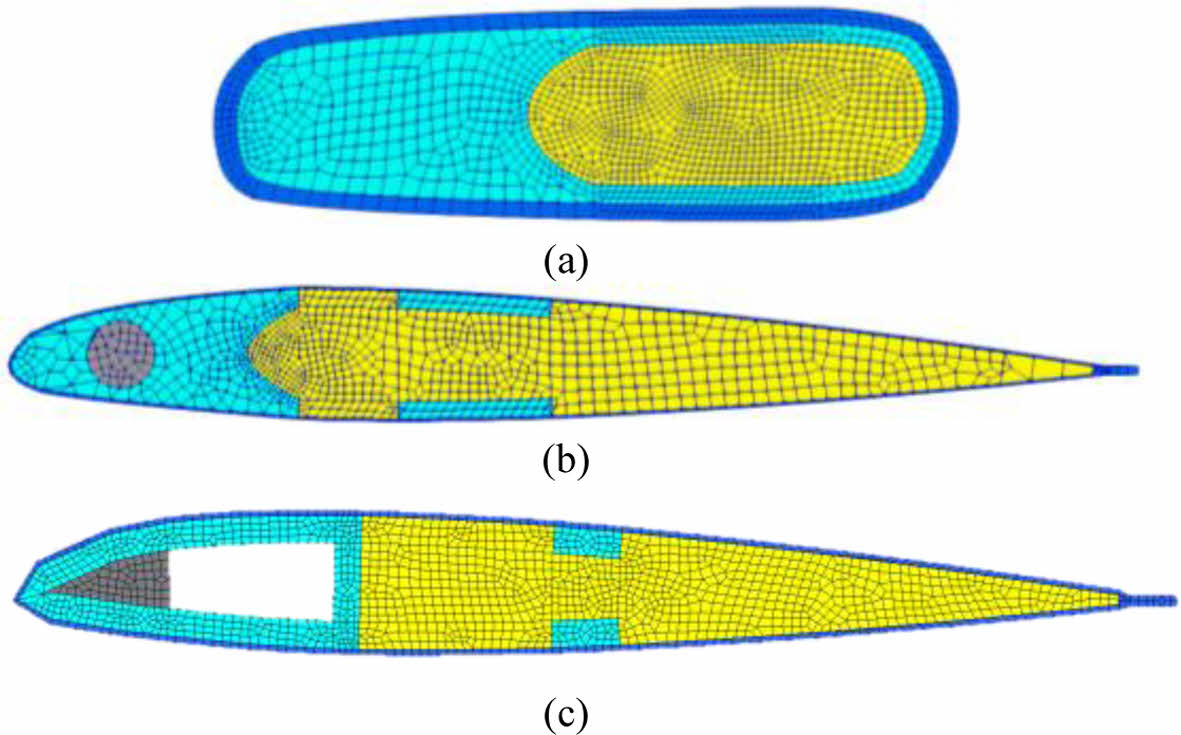
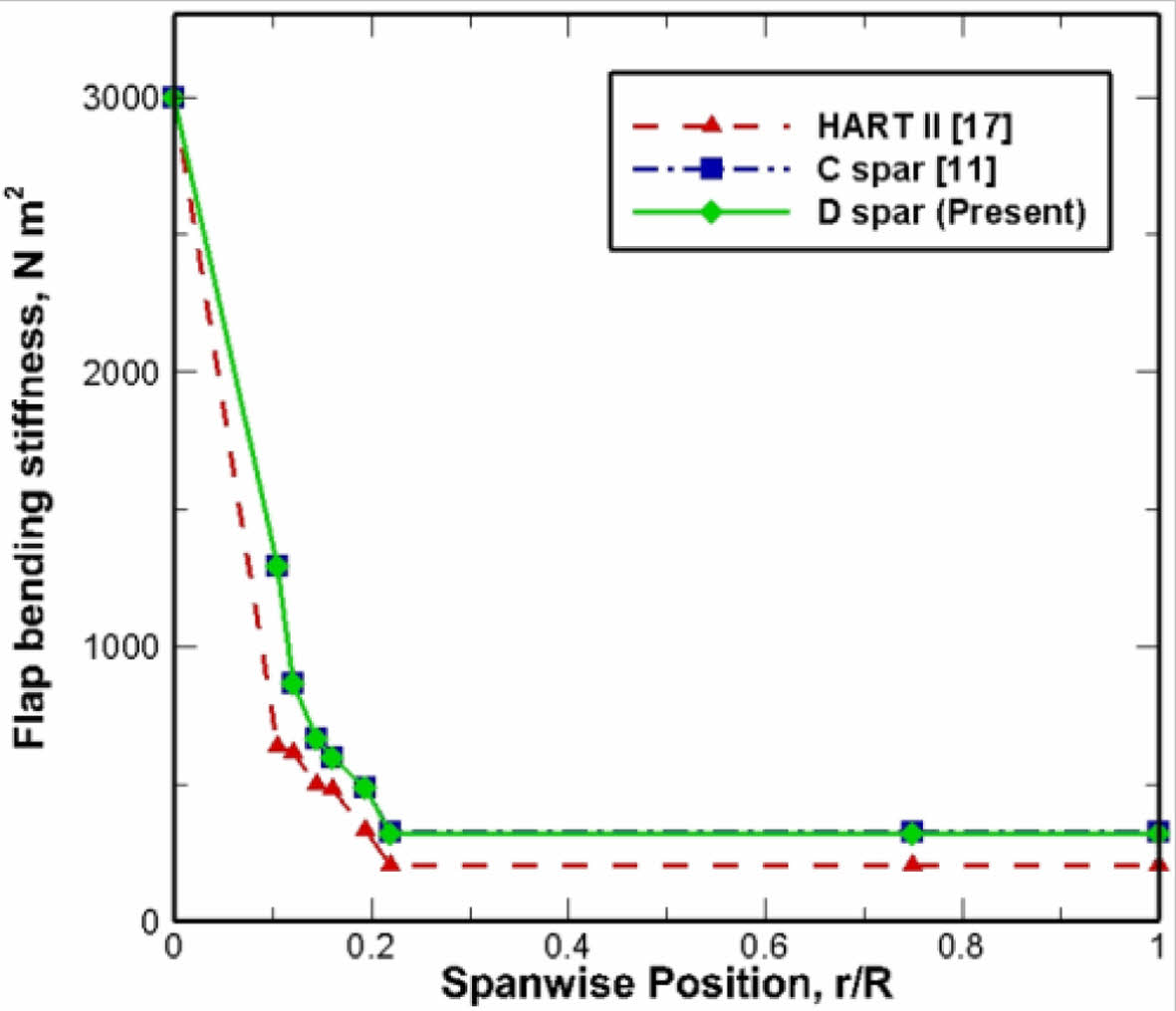
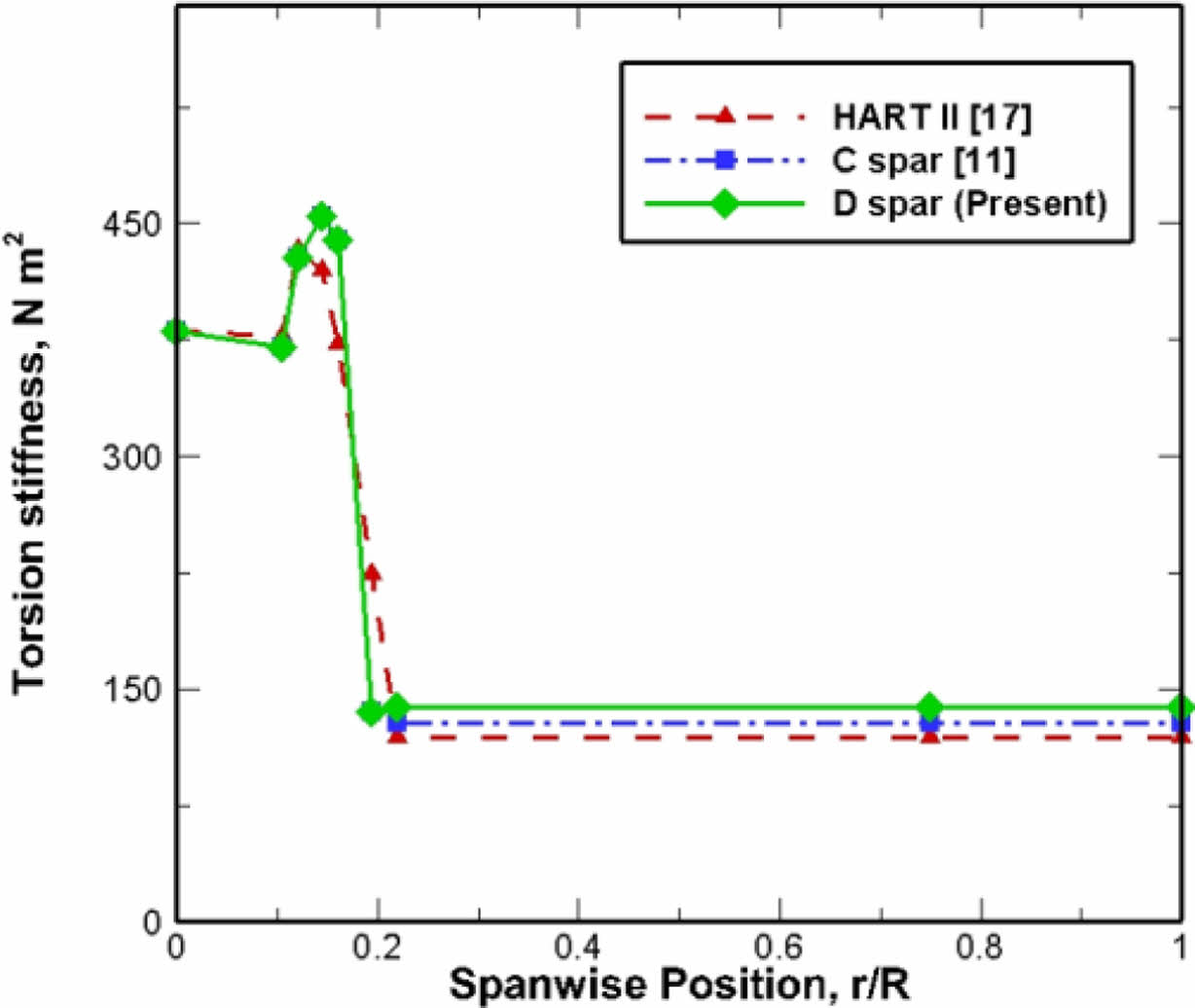
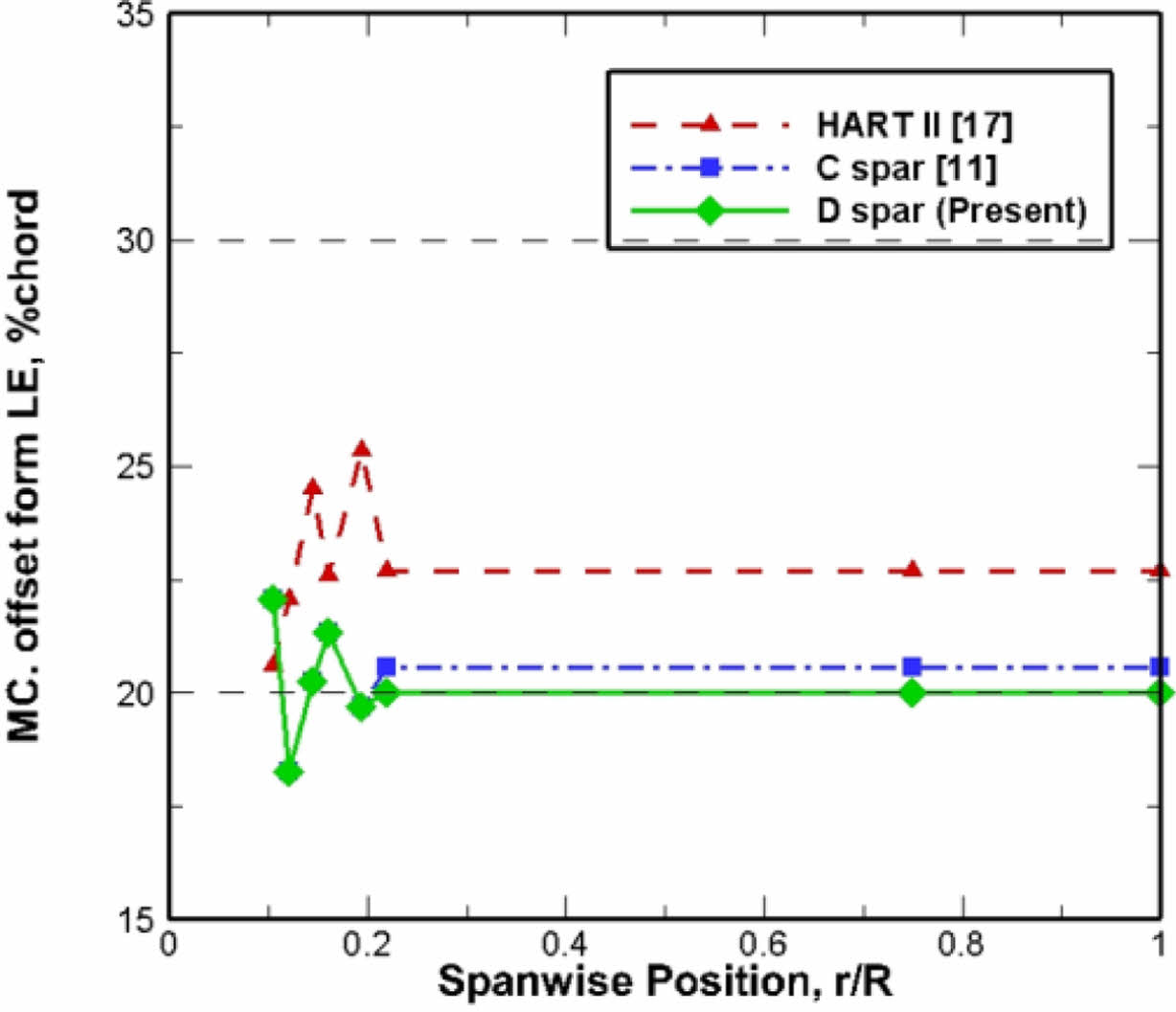
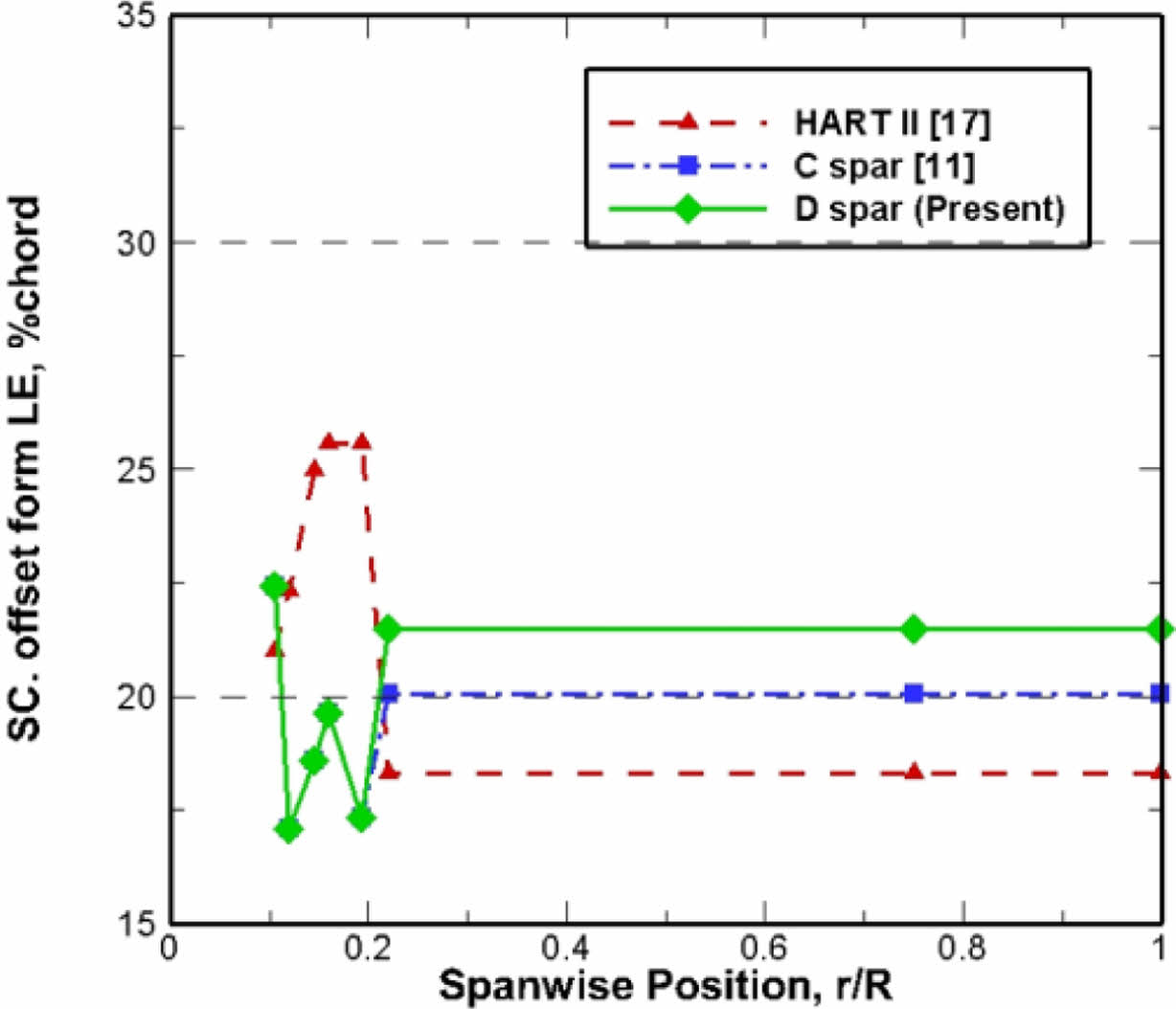
최적화 결과 총 136세대의 계산이 진행되었고, 총 8,539회의 계산이 수행되었다. Fig. 9은 최적 구조설계에 따른 0.16R 지점의 루트 단면에 대한 최적설계 결과와 C형 및 D형 스파 모델의 최종 형상을 나타냈다. 블레이드 질량의 경우 기준 재료[18]에 비해 비강성이 큰 재료를 스파에 사용하는 관계로, 루트 영역의 질량이 감소된다. 이에 반해 익형 영역의 질량은 기준 대비 증가하는 바, 이는 루트 영역의 무게 감소로 자동회전 관성지수가 기준치 이하로 떨어지지 않도록, Fig. 9(b), (c)의 최종 형상처럼 무게추 면적이 증가하여, HART II 블레이드 대비 증가하였다. 전체 질량은 감소되는 결과로 나타났다. 기준 대비 C형 스파 모델은 7.39% 감소된 1.91 kg, D형 스파 모델은 6.65% 감소된 1.93 kg으로 계산되었다. Fig. 10과 Fig. 11는 굽힘 강성과 비틀림 강성의 분포를 HART II 블레이드의 구조해석 결과[17]와 비교하여 나타냈다. 무게중심(MC)과 전단중심(SC)의 위치는 Fig. 12 및 Fig. 13에 보이는 바와 같이, D형 스파 모델은 웹의 영향으로 전단중심의 위치가 C형 스파에 비해 뒷전으로 이동하여 약 1.5%의 차이를 보였다.
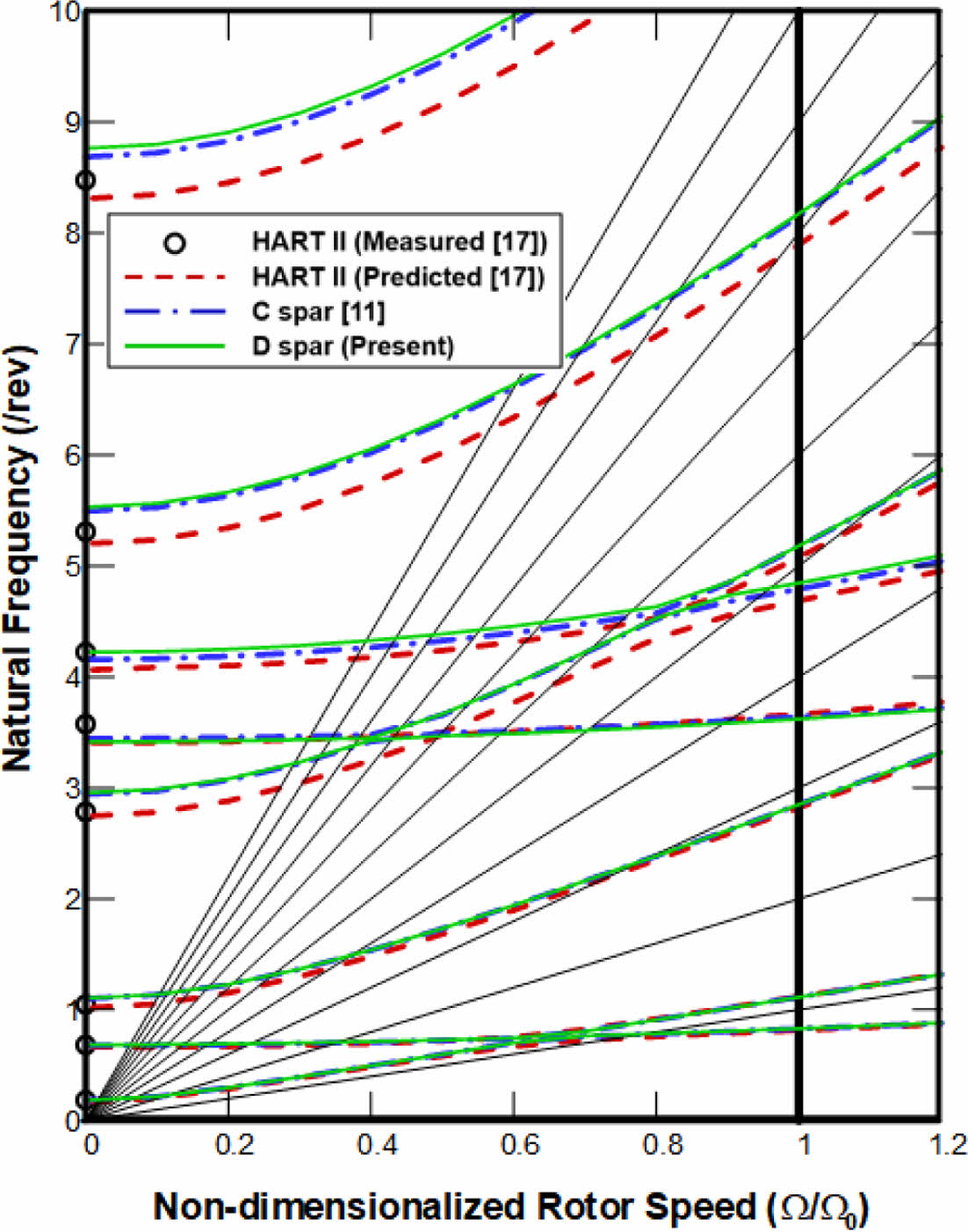
Fig. 14은 비회전 고유진동수 및 회전고유진동수에 대한 fan 선도를 작도한 것이다. C형 및 D형 스파 모델 모두에서 비회전 1차 고유진동수에서 주어진 구속조건을 모두 만족하는 것을 확인할 수 있었다. 또한, 운용 rpm에서 회전고유진동해석 결과들이 로터 회전속도의 정수배에서 최소 ±0.15/rev 이상 차이나는 것을 확인하였으며, 운용 rpm에서의 공진 회피에 대한 구속조건이 만족되었음을 확인하였다.

본 연구에서는 PSGA를 이용하여 단면 유한요소기반 구조해석을 통해 복합재료 블레이드 최적 구조설계 프레임워크를 개발하였으며, C형 및 D형 스파 형상으로 선택할 수 있도록 구성하였다. 최적설계 과정에서 블레이드의 단면 형상은 B-spline을 이용하여 모델링을 하였으며, Gmsh를 통해 유한요소모델을 생성한 후 Ksec2D 및 회전 보 고유진동해석을 통해 최적 구조설계를 수행하였다. 해당 최적설계 프레임워크의 유효성을 검토하기 위해 HART II 블레이드의 단면에 적용하여 기존 물성치와 비교한 결과 최대오차 6.4%에서 수렴된 결과를 얻을 수 있음을 확인하였다.
HART II 블레이드에 대한 최적 구조설계 결과는 C형 스파 모델을 사용한 결과 기준 대비 무게 7.39% 감소 효과를 나타냈고, 전단중심의 경우 앞전으로부터 20.05%에 위치했다. D형 스파 모델의 경우 기준 대비 무게 6.65% 무게 감소 효과를 나타냈고, 전단중심의 경우 21.50%에 위치했다. 해당 최적설계 결과에서는 C형 스파가 무게 감소에 유리했고, 전단 중심의 경우 D형 스파 모델이 공력중심과 더 가까이 있어 공력중심과 전단중심 차이에 따른 모멘트를 줄이는 데 더 유리했다. 이를 통해 C형 스파 모델과 D형 스파 모델을 비교하여 선택할 수 있게 되었고, 본 연구에서 제안한 최적 구조설계 프레임워크의 유효성을 확인하였다.

이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2022R1A4A1018884). 이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF2021R1F1 A104557011).