This study suggests the prediction algorithm for transverse permeability, represented the flow resistance during the manufacturing process of composite, of unidirectional continuous fiber reinforced plastics. The cross-sectional shape of representative volume element (RVE) is considered to reflect fiber arrangement. The equivalent length is used as a factor to express the change of resin flow according to fiber arrangement. The permeability prediction algorithm is created by grafting the Electro-Hydraulic analogy and validity is confirmed. The code for permeability prediction was composed by means of MATLAB and Python, flow analysis was performed by using FLUENT. The algorithm was verified as the permeability results obtained through Algorithm and numerical analysis were almost identical to each other, and the calculation time was reduced around 1/450 compared to the numerical analysis

본 연구에서는 복합재료 제조 공정 과정 중 수지의 유동 저항성을 대변하는 인자인 투수 계수를 예측하는 알고리즘을 개발하였다. 단방향 연속 섬유 복합재료 내부에서 섬유와 수직인 방향 투수 계수의 정확한 예측을 위해 대표 체적 요소의 단면 형상을 고려하였다. 섬유의 유체 유동 저항성을 정량화하기 위한 인지로 섬유 간 간격이 사용되었고, 등가 길이는 섬유 배열에 따른 수지의 유로 변화를 나타내는 인자로 사용되었다. 전기-유압 유사성을 접목하여 투수 계수 예측 알고리즘을 개발하고 그 타당성을 확인하였다. 알고리즘은 Matlab과 Python으로 구성되고, 타당성 검증을 위해 FLUENT를 통해 예측된 투수 계수와 비교하였다. 알고리즘과 수치 해석을 통해 얻은 투수 계수가 거의 일치함을 확인하여 알고리즘을 검증하였으며, 소요 시간은 수치 해석 대비 약 1/450로 감소하였다.

Keywords: 투수 계수(Permeability), 복합재료 제조 공정(Manufacturing process of composite material), 대표 체적 요소(Representative volume element), 등가 길이(Equivalent length), 전기-유압 유사성(Electric-Hydraulic analogy)

단방향 섬유 강화 복합재료는 높은 비강성, 비강도, 피로 강도를 가지며 내식성이 뛰어나 다양한 분야에서 널리 활용되고 있다. 환경 규제의 강화로 경량화에 대한 수요가 높아짐에 따라 섬유강화 복합재료 시장 규모는 더 증가할 전망이며 동시에 제조 공정 관련 연구가 활발히 진행되고 있다. 다양한 공정법이 존재하지만 복합재료의 함침은 수 마이크로미터 크기의 섬유 사이를 통과하는 수지의 유동을 통해 이뤄지며, 함침 과정에서 발생한 공극은 복합재료의 주요 결함으로 작용한다. 따라서 공정 과정에서 공극을 최소화하는 것은 복합재료 제조 공정에서 매우 중요한 과제이며 이를 위해 복합재료 내부의 수지 유동 양상을 정확히 파악할 필요가 있다.
복합재료 제조 공정에서 수지가 복합재료 사이를 통과하는 유동의 양상은 다공성 물질을 통과하는 유체의 유동으로 모사된다. 다공성 물질을 통과하는 유동의 양상은 압력, 점도, 물질의 특성에 지배적인 영향을 받는다. 이 중 물질의 기하학적 특징을 반영한 인자인 투수 계수는 다공성 물질의 미시적인 스케일에서 특성 반영이 필수적이기 때문에 상대적으로 파악이 부정확하다. 따라서 투수 계수를 정확히 예측하는 것은 복합재료 결함 파악 및 최소화에 필수적이다.
투수 계수는 다공성 물질 내부의 유체 유동 저항성을 정량적으로 표현하기 위해 제안되었다. Kozeny-Carman은 가정을 통해 단순화된 Navier-Stokes 식과 Darcy의 법칙 (Darcy’s Law)을 결합하여 등방성 물질에서 투수 계수를 구하는 식을 제안하였다[1]. 이를 Gebert가 발전시켜 수지 이송 형성에서 골고루 배치된 보강재의 투수 계수를 공극률 (Porosity)과 상수들의 적절한 결합을 통해 일차함수로 표현하였다[2]. 이후 다수의 연구가 Kozeny-Carman의 식을 발전시켜 투수 계수를 공극률의 함수로 표현하였지만, 보강재의 기하학적 특징인 섬유 배열 형상을 반영하지 못해 실제 값과 차이를 보인다. 섬유 배열 형상을 반영한 투수 계수를 도출하기 위해 수치 해석이 사용되었다. Bodaghi 등은 시뮬레이션으로 다양한 공극률에서 무작위하게 배치된 대표 체적 요소 22,000개의 투수 계수를 도출하고 확률 밀도 함수를 확인하였다[3]. 이를 통해 섬유 배열이 투수 계수에 영향을 미치는 것을 확인할 수 있다. 이외에도 투수 계수를 예측하는 다양한 연구가 진행되었고 Zarandi 등은 투수 계수를 도출할 수 있는 다양한 연구를 비교하였다[4]. 각 연구는 동일한 조건에서 서로 다른 투수 계수 예측값을 제시한다. 따라서 기존 연구들로 투수 계수를 정확히 예측하기에는 어려움이 있다.
복합재료 제조 공정의 최근 연구 동향은 재료 간 계면 효과 또한 수지의 유동 특성에 영향을 준다고 보고한다. Anastasiadis와 Hatzikiriakos는 폴리머(Polymer) 유동이 진행할 때 고체와의 계면에서 한계 전단 응력 이상의 힘이 작용하면 슬립(Slip)이 발생함을 확인하였다[5]. Lim 등은 표면 자유 에너지(Surface Free Energy)와 표면 거칠기(Roughness)가 낮을수록 탄소섬유 보강재의 함침 속도가 빠른 것을 실험을 통해 확인하였다[6]. 이에 본 연구에서는 수지 유동 양상을 결정하는 복합재료의 특성인 공극률, 내부 섬유 배열, 재료의 표면 특성을 모두 반영하여 투수 계수를 예측하는 알고리즘을 개발하였다.
체적 요소 내부에 탄소섬유 복합재료의 실제 형상을 모사하여 섬유를 배치해 미시적인 스케일에서 전체를 대변하는 대표 체적 요소를 생성하였다. 이후 유효 거리와 유효 공간을 설정하여 대표 체적 요소 내부 공간을 다각형으로 분할하였다. 해당 과정은 MATLAB (MATLAB R2020b, Mathworks, USA) 코드를 통해 구현되었다. 이후 슬립 방지 조건에서 대표 체적 요소의 유동 저항성을 계산하기 위해 전기-유압 유사성을 적용하였으며 해당 알고리즘은 Python (Python 3.10.0, Python Software Foundation, USA)으로 구현되었다.
복합재료의 섬유 부피 분율과 배열에 따른 유로 변화와 재료의 표면 특성을 반영하기 위한 인자로 등가 길이가 도입되었으며, 등가 길이의 도출을 위해 상용프로그램을 통한 수치 해석이 수행되었다. 수치 해석은 동일한 대표 체적 요소로 진행되었으며 FLUENT (FLUENT 2020 R1, Ansys Inc., USA)로 수행되었다. 대표 체적 요소 내 속도 장(Velocity field)을 Darcy의 법칙에 적용해 투수 계수를 계산하여 도출하였다.
알고리즘의 검증을 위해 5개의 서로 다른 대표 체적 요소에서 알고리즘과 상용 시뮬레이션 결과를 비교하였다.

2.1 대표 체적 요소
복합재료는 거시적인 스케일에서 두 가지 이상의 재료가 혼합된 물질이다. 이에 거시적인 스케일과 미시적인 스케일에서 서로 다른 물리적 거동을 보인다. 구성 물질이 골고루 배치된 복합재료의 거시적인 거동은 모든 부분에서 동일하지만 섬유 지름이 마이크로미터 단위를 가지기 때문에 미시적인 스케일에서는 임의로 선정된 부분이 전체를 대표할 수 없다.
복합재료 내부의 모든 섬유를 고려하여 가장 정확한 결과를 도출해 낼 수 있음은 자명하지만, 내부에 많은 섬유를 포함하고 있기 때문에 이는 매우 비효율적이다. 따라서 전체를 대변할 수 있는 적절한 크기의 대표 체적 요소를 선정하는 것이 필수적이다. 본 연구에서는 체적 요소에 포함된 섬유 개수를 기준으로 대표 체적 요소의 타당성을 판단하였다[7].

2.2 섬유 사이를 통과하는 수지의 유동
수지의 높은 점도로 인해 복합재료 내부는 레이놀즈수가 1보다 작은 유동이 형성된다. 따라서 섬유 사이를 수직인 방향으로 통과하는 수지의 유동은 실린더 사이를 통과하는 안정적인 층류 유동으로 취급할 수 있다. 해당 유동은 실린더를 지나는 동안 경계층에서 슬립 방지 조건이 안정적으로 유지되며 압력 구배에 의해 발생하는 유동으로 섬유 중심을 이은 직선을 포함하고 섬유 방향과 평행한 평면에서 유동의 속도 장은 2차 함수로 표현할 수 있다. Continuity 식과 Navier-Stokes 식을 단순화하여 섬유 사이를 통과하는 수지 유동의 속도 장과 평균 속도를 구하면 아래와 같다.



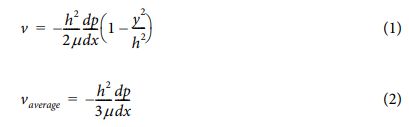
위 식에서 h는 섬유간 최단 거리, μ는 수지의 점도, v는 유동 속도, p는 압력을 나타낸다.

2.3 투수 계수와 Darcy의 법칙
복합재료를 통과하는 수지의 유동은 다공성 물질을 통과하는 유체 유동으로 취급 가능하다. Darcy는 해당 유동에서 유체의 속도 v를 아래의 식과 같이 압력 구배 ∇P, 수지의 점도 μ, 투수 계수 K의 관계로 나타냈다.



위의 식에서 확인할 수 있듯, 투수 계수는 유동의 원활한 정도를 나타내며 다공성 물질의 구조적 특징에 영향을 받는 인자이다.

2.4 전기-유압 유사성과 노달 회로 분석
유압 회로에서 물이 이동하는 현상과 전기 회로 내에서 전자가 이동하는 현상은 매우 유사하며 각 회로에서 물리량의 관계는 Darcy의 법칙과 Ohm의 법칙으로 표현 가능하다. 두 식에서 선속 밀도에 해당하는 물리량은 유동 저항성과 위치에너지의 곱으로 표현된다. 두 회로의 유사성은 전기 회로 분석을 통해 유압 회로에서의 유량 계산을 가능하게 한다.
노달 회로 분석은 전기 회로 분석의 한 방법으로 물리량 사이의 관계식을 통해 회로 내부의 전기적 특징을 분석하는 방법이다. 일정한 전위를 가지는 노드 사이를 통과하는 전자의 위치에너지가 저항에 의해 감소하는 것을 수식으로 표현한 것이며, 이를 유압 회로에 적용하여 선속 밀도에 해당하는 유속을 계산할 수 있다.

3.1 대표 체적 요소 생성
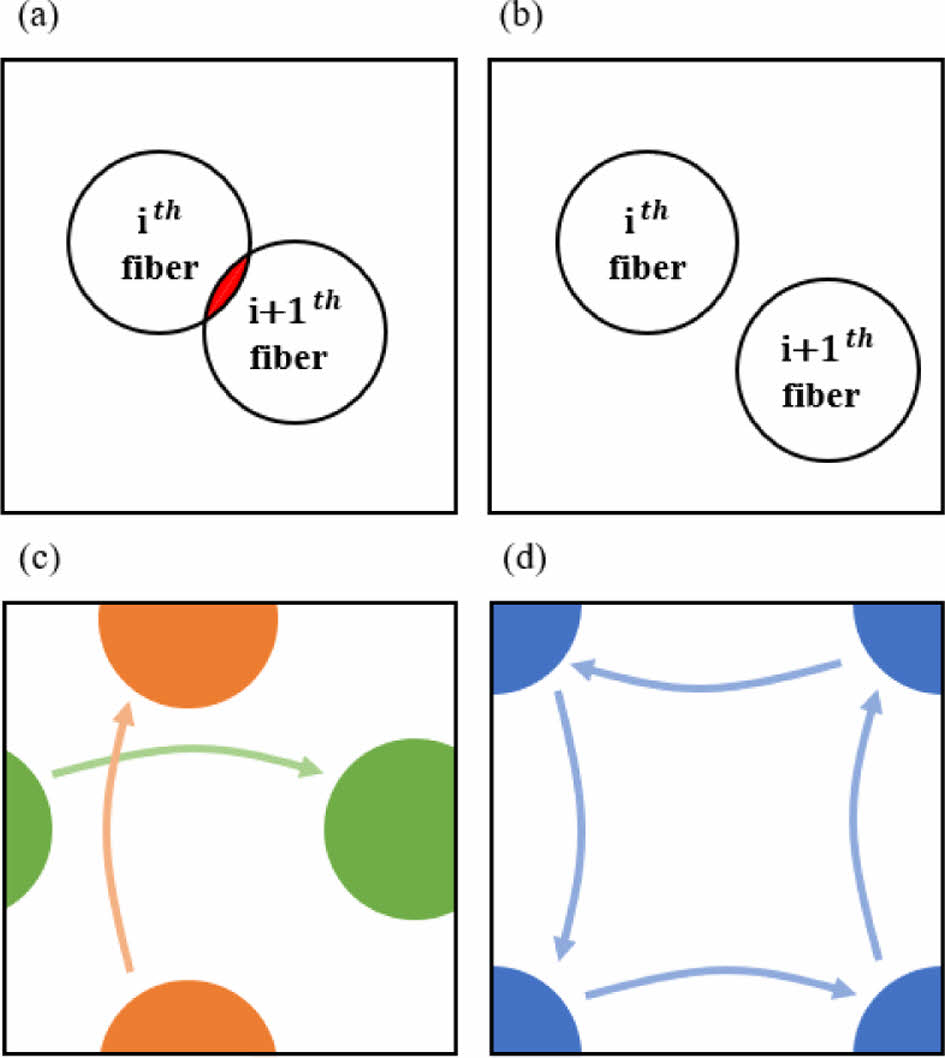
본 연구에서는 최단 이웃 알고리즘으로 다양한 섬유 부피 분율을 가지는 대표 체적 요소를 생성하였다[8]. Fig. 1과 같이 새로운 섬유 배치 시 주기 경계 조건을 만족하며 이미 생성된 섬유와 겹치지 않게 배치하였다.
생성된 대표 체적 요소 내부의 섬유의 지름은 일반적인 탄소 섬유의 지름인 8 μm, 섬유간 간격은 평균 3 μm인 지수 분포를 따른다. 섬유간 거리가 너무 가까울 경우 수치 해석을 위한 메쉬(Mesh) 생성이 불가하기 때문에 최소 거리를 0.1 μm로 설정하였다. 섬유의 생성 각도는 최솟값 0 rad, 최댓값 2p rad인 연속 균등 분포를 따른다. 대표 체적 요소의 생성은 목표한 부피 분율을 초과한 직후 중지된다.

3.2 유효 섬유 쌍 선별 및 유효 거리 도출
대표 체적 요소의 내부에 있는 섬유 중 유동 저항성을 가지는 섬유 쌍을 선별하고 사이의 거리 정보를 유효 거리라 명명한다. 섬유와 수직인 방향으로 발생하는 유동은 섬유 사이를 통과하며 진행하고 섬유 간 거리가 좁을수록 더 큰 유동 저항성을 가지게 된다. 또한, 섬유 쌍 사이에 다른 섬유가 위치하거나 섬유 간 간격이 매우 넓은 경우 해당 섬유 쌍이 형성하는 갭은 유효하다고 판단할 수 없다.
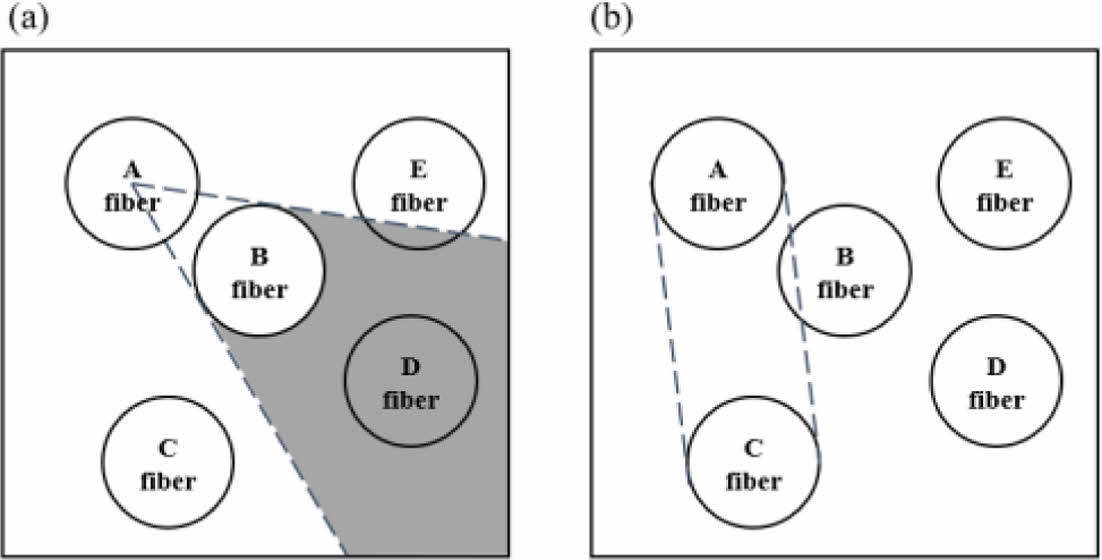
유효 섬유 쌍을 선별하기 위해 Fig. 2와 같이 두 가지 기준을 적용하였다. 첫째로 기준 섬유의 중심에서 주변 섬유에 외접선을 그었을 때 그 사이 면적과 전체 또는 일부가 포함되는 섬유는 유효하지 않다고 판단하였다. 둘째로 두 섬유의 공통 외접선을 그었을 때 그 사이에 다른 섬유의 전체 또는 일부가 포함되는 섬유는 유효하지 않다고 판단하였다.

3.3 유효 거리를 통한 유효 공간 분할
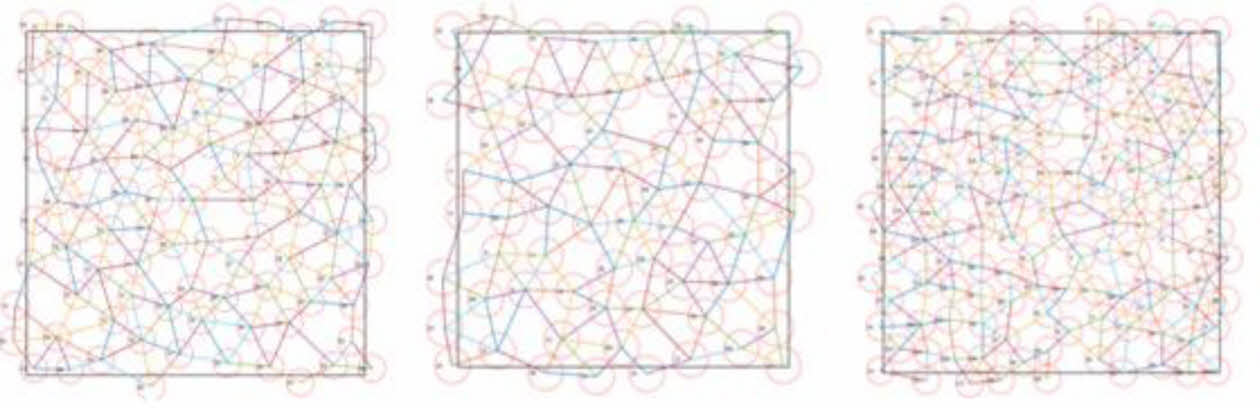
유효 거리를 모두 나타내면 대표 체적 요소 내부의 공간은 다양한 형태의 다각형으로 분할된다. 이때 다각형 내부 공간은 노달 회로 분석의 노드에 해당하고 다각형의 변은 저항으로 취급한다. 주기 경계 조건을 만족시키기 위해 좌우 끝에 위치한 다각형의 각 변을 동일하게 취급하였다. Fig. 3은 한 변의 길이가 100 μm인 대표 체적 요소의 유효 공간 분할 결과이다.

3.4 투수 계수 계산
대표 체적 요소 내부의 복잡한 섬유 배열이 가지는 유동 저항성을 정량적으로 표현하기 위해 노달 회로 분석의 키르히호프(Kirchhoff) 전류 법칙을 이용한다. 다각형 내부의 유효 공간은 노달 회로 분석의 등 전위에 해당하는 노드 (Node)로, 유효 거리는 저항으로 표현할 수 있어 전류 회로에서 등가 저항을 계산하는 과정과 동일하게 유동 저항성을 계산할 수 있다.

스톡스의 역설을 통해 알 수 있듯 실린더 주위에 스톡스 방정식에 대한 해가 존재하지 않는다. 따라서 실험 또는 수치해석을 통해 등가 길이를 도출해야 한다. 본 연구에서는 원형 단면을 가지는 섬유가 슬립 방지 조건을 만족하는 조건에서 등가 길이 도출을 위해 수치 해석을 진행하였다.
섬유에 수직인 방향의 투수 계수를 도출하기 위해 알고리즘으로 2차원 형상의 대표 체적 요소를 생성하였다. 좌우에 주기 경계 조건을 부여하였고, 섬유 표면에는 슬립 방지 조건을 부여하였다. 상하에 10 Pa의 압력 차이를 두어 레이놀즈 수가 1보다 작은 유동이 발생하게 하였다. 유체의 밀도와 점도는 에폭시 수지의 유동이 발생할 때와 유사한 값인 1000 kg/m³와 1 Pa∙s을 부여하였다.
수치 해석을 위한 메쉬의 한 변의 크기는 섬유와 섬유의 간격이 0.1 μm를 가졌을 때도 해석이 가능하도록 생성되었다. 섬유 표면에서 메쉬 한 변의 크기는 0.05 μm로 설정하였고 슬립 방지 조건이 섬유 표면과 인접한 부분에 한정될 수 있도록 인플레이션(Inflation)을 설정하여 2층이 0.025 μm의 두께를 가지고 배치되게 하였다. 계산의 편의를 위해 섬유 표면에서 멀어지면서 메쉬의 크기가 증가하게 설정하였고 그 비율(Growth rate)은 기본 설정인 1.2를 유지하였다.
수치 해석을 통해 얻은 속도 장을 Darcy의 법칙의 속도에 대입하여 투수 계수를 계산하고, 알고리즘을 통해 얻은 결과와 비교하여 등가 길이를 도출하였다.

5.1 임의의 등가 길이를 적용한 알고리즘 결과
본 연구에서는 Fig. 3와 같이 최단 이웃 알고리즘으로 0.4, 0.5, 0.6의 섬유 부피 분율을 가지는 서로 다른 10개의 대표 체적 요소를 생성하였다.
이후 유효 섬유 쌍을 선별하여 유효 거리 정보를 도출하였다. 도출된 유효 거리 정보를 바탕으로 Fig. 4와 같이 대표 체적 요소 내부를 유효 공간으로 분할하였다.
분할된 유효 공간은 대표 체적 요소 내부 공간에서 노드와 저항에 해당하는 정보를 제공해주고 키르히호프 전류 법칙으로 투수 계수를 계산할 수 있게 된다.
해당 알고리즘으로 계산한 0.4, 0.5, 0.6의 섬유 부피분율을 가지는 대표 체적 요소의 투수 계수의 평균값은 3.40 × 10^-13 m², 1.24 × 10^-13 m², 0.37 × 10^-13 m²이며, 표준편차는 4.59 × 10^-14 m², 2.27 × 10^-14 m², 0.21 × 10^-14 m²이다.

5.2 등가 길이 도출
수치 해석 결과와 임의의 등가 길이를 적용한 알고리즘 결과를 비교하여 등가 길이를 도출하였다. Fig. 5와 같이 수지의 속도장은 섬유와 섬유 간격이 넓을수록 높은 값을 나타냈고, 인접한 섬유 사이를 통과하면서 그 유동 특성이 급격하게 바뀌는 것을 확인할 수 있다. 수치 해석을 통해 계산한 0.4, 0.5, 0.6의 섬유 부피 분율을 가지는 대표 체적 요소의 투수 계수의 평균값은 9.77 × 10^-13 m², 3.16 × 10^-13 m², 0.48 × 10^-13 m² 이며, 표준 편차는 1.54 × 10^-13 m², 2.30 × 10^-13 m², 0.06 × 10^-13 m²이다. 조화 평균으로 계산한 등가 길이는 0.363 m, 0.391 m, 0.495 m이다.

5.3 투수 계수 예측
알고리즘의 타당성을 위해 도출한 등가 길이를 적용하여 투수 계수를 예측하였다. 동일한 크기와 섬유 부피 분율을 가지는 대표 체적 요소를 5개씩 추가로 생성하였고, 0.4, 0.5, 0.6의 부피 분율을 가지는 대표 체적 요소의 투수 계수의 평균 값은 9.37 × 10^-13 m², 3.24 × 10^-13 m², 0.48 × 10^-13 m², 표준 편차는 1.26 × 10^-13 m², 0.59 × 10^-13 m², 0.04 × 10^-13 m² 로 예측되어 그 타당성을 확인할 수 있다.

5.4 알고리즘과 수치 해석 프로그램의 소요 시간
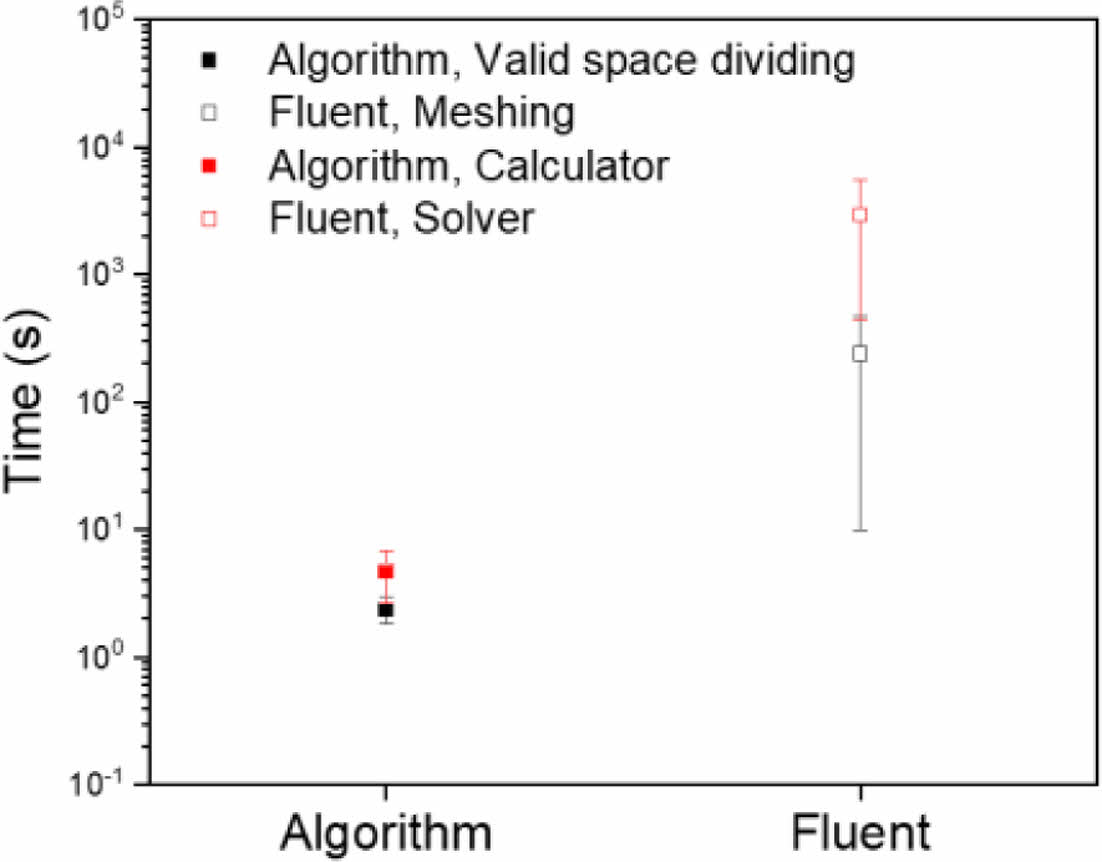
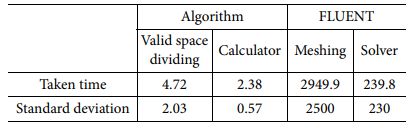
FLUENT와 알고리즘에서 투수 계수를 도출에 소요되는 시간을 확인하였다. Table 1와 같이 알고리즘의 경우 유효 공간 분할과 투수 계수 계산 시간에 큰 차이를 보이지 않았지만, FLUENT의 경우 솔버 구동 시간보다 메쉬 생성 시간에 오랜 시간이 소요되었다. 또한 대표 체적 요소별로 소요 시간의 편차가 매우 큰 것을 확인할 수 있다.
Fig. 6와 같이 두 방법에서 절대적인 구동 시간은 확연한 차이를 보였다. 알고리즘의 유효 공간 분할과 투수 계수 계산은 수 초 내에 완료되었지만 FLENT의 경우 메쉬 생성에 수 시간이 소요되기도 하였다.

본 연구에서는 원형 단면의 섬유가 슬립 방지 조건을 만족할 때 연속 섬유 강화 복합재료의 수직 방향 투수 계수 예측을 위한 알고리즘이 제안되었다. 투수 계수의 정확한 예측을 위해 연속 섬유 복합재료의 함침 특성에 영향을 미치는 인자인 공극률, 내부 섬유 배열, 재료의 표면 특성을 모두 고려할 수 있는 예측 기법을 개발하였다. 공극률과 섬유 배열은 대표 체적 요소 내에 위치한 섬유의 형상을 통해, 재료의 표면 특성은 등가 길이를 통해 알고리즘에 반영되었다.
알고리즘을 통해 다양한 섬유 부피 분율을 가지는 대표 체적 요소의 투수 계수를 예측하였다. 예측 결과는 Darcy의 법칙에 수치 해석 결과를 대입하여 투수 계수를 계산하는 기존 예측 기법의 결과와 잘 일치함을 확인할 수 있었다.
알고리즘은 대표 체적 요소의 유동 저항성을 거리의 함수로 표현하여 투수 계수를 계산한다. 이에, 기존 유한 요소 기법으로는 불가능했던, 접촉한 두 섬유를 포함하는 대표 체적 요소의 투수 계수의 예측이 가능하다.
알고리즘은 상용 시뮬레이션 프로그램에 비해 매우 짧은 구동 시간을 가져 실제 공정 과정에 적용하였을 때 높은 경제성을 가질 것으로 예상하며, 머신 러닝 등의 데이터 기반 연구를 통해 복합재료 공정 관련 해석을 진행함에 있어 높은 활용도를 가질 것이라 기대한다.

본 연구는 산업통상자원부 지원으로 한국산업기술평가관리원의 과제번호 20010509 과제로 수행된 것이며, 지원에 대해 진심으로 감사드립니다.
이 연구는 2022년도 정부(산업통상자원부)의 재원으로 한국산업기술 진흥원의 지원을 받아 수행된 연구입니다. (P0017006, 2022년 산업혁신인재성장지원사업).
이 성과는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2020R1A2C201096512).