PIC (Piecewise Integrated Composite) is a new concept for designing a composite structure with mosaically assigning various types of stacking sequences in order to improve mechanical properties of laminated composites. Also, machine learning is a sub-category of artificial intelligence, that refers to the process by which computers develop the ability to continuously learn from and make predictions based on data, then make adjustments without further programming. In the present study, the tapered box beam type PIC robot arm for carrying and transferring wide and thin LCD display was designed based on the machine learning in order to increase structural stiffness. Essential training data were collected from the reference elements, which were intentionally designated elements among finite element models, during preliminary FE analysis. Additionally, triaxiality values for each finite element were obtained for judging the dominant external loading type, such as tensile, compressive or shear. Training and evaluating machine learning model were conducted using the training data and loading types of elements were predicted in case the level accuracy was fulfilled. Three types of stacking sequences, which were to be known as robust toward specific loading types, were mosaically assigned to the PIC robot arm. Henceforth, the bending type FE analysis was carried out and its result claimed that the PIC robot arm showed increased stiffness compared to conventional uni-stacking sequence type composite robot arm

PIC(Piecewise Integrated Composite)는 적층 복합재의 기계적 특성을 향상시키기 위해 다양한 적층 순서를 모자이크 방식으로 할당하여 복합 구조를 설계하는 새로운 개념이다. 또한 머신 러닝은 인공 지능의 하위 범주로, 컴퓨터가 데이터에서 지속적으로 학습하고 데이터를 기반으로 예측하는 능력을 개발한 다음 추가 프로그래밍 없이 조정하는 과정을 의미한다. 본 연구에서는 구조적 강성을 높이기 위해 기계학습을 기반으로 넓고 얇은 LCD 디스플레이를 운반 및 이송하기 위한 테이퍼 박스형 빔형 PIC 로봇 암이 설계되었다. 필수 학습 데이터는 예비 FE 해석 과정에서 유한 요소 모델 중 의도적으로 배치된 참조 요소에서 수집되었다. 또한 인장, 압축 또는 전단과 같은 지배적인 외부 하중 유형을 판단하기 위해 각 유한 요소에 대한 3축 특성 값을 얻었다. 학습 데이터를 이용하여 머신 러닝 모델을 훈련하고 평가되었으며, 정확도 레벨을 만족한 머신 러닝 모델을 이용해 요소의 로딩 유형을 예측하였다. 특정 하중 유형에 대해 우세한 것으로 알려진 세 가지 유형의 적층 각도 순서가 PIC 로봇 암에 모자이크 방식으로 할당되었습니다. 이후 굽힘형 FE 해석을 수행한 결과 PIC 로봇 암이 기존의 단일 적층 각도 순서로 제작된 복합재 로봇 암에 비해 강성이 증가된 것으로 나타났다

Keywords: LCD 유리패널 디스플레이(LCD glass panel display), 박스 빔(Box beam), 탄소/에폭시 복합재(Carbon/epoxy composite material), 머신 러닝(Machine learning), 구간 조합 복합재(Piecewise integrated composite)

반복적인 작업을 자동화하고 정밀한 작업을 요구하는 산업 자동화에서 산업용 로봇은 빠른 속도, 높은 정밀도, 높은 파워를 장점으로 설치, 조립, 분해, 용접, 도장 등의 광범위한 분야에서 사용되고 있습니다[1,2]. 특히, LCD 생산 공정에서 로봇은 암에 유리 패널을 받쳐서 옮기는 역할을 하는데 패널의 크기가 세대를 거듭하면서 커짐에 따라 로봇 암의 유효 하중과 강성 증가가 요구되었다[3,4]. 로봇 암의 강성을 향상시키기 위해 기존의 알루미늄 로봇 암의 두께를 증가시키면서 유리 패널 적재 카세트 크기 증가와 로봇의 동적 성능을 유지하기 위해 모터의 크기 증가를 야기시켰다[5]. 그래서 유리 패널의 크기가 증가하여도 얇지만 강성을 향상시킬 수 있는 로봇 암의 설계 및 제조가 중요해졌고 철 그리고 알루미늄과 같은 금속에서 얻지 못하는 높은 비강도, 높은 비강성, 가벼운 질량, 긴 피로 수명, 높은 감쇠 특성을 갖는 복합 재료를 이용한 설계 연구가 진행되었다[6-8]. 물질적 문제에 초점을 맞추어 차이점을 비교한 문헌[9]에 따르면 경량, 고강성 및 우수한 정적/동적 성능을 가지는 탄소섬유/에폭시 수지 복합 재료를 사용한 로봇 암이 알루미늄 소재의 로봇 암에 비해 적합하였고 Ghazavi and Gordaninejad[10]는 탄소 섬유/에폭시로 제작된 로봇 암과 알루미늄 로봇 암의 고속 모션에서 위치 정밀도를 비교했고 탄소섬유/에폭시 수지 로봇 암이 보다 안정적인 위치 정밀도를 보이는 것이 확인되었다.
Bicos 등[11]는 로봇 암의 강성 향상과 경량화를 위해 섬유 강화 복합 재료로 box beam 구조를 설계했고 금속재료보다 낮은 중량에서 더 높은 강성 및 강도를 요구할 수 있다는 것을 확인하였다. Wu 등[12,13]은 box beam이 굽힘 하중을 받을 때 전단 지연과 전단 변형을 고려한 수학적 모델을 제한하였다. Loughlan and Ata[14]은 유한요소법과 재료 탄성계수에 의한 Box Beam 굽힘과 비틀림 변형을 예측하였고 Vo 등[8]은 고전 적층판 이론과 유한요소해석을 기반으로 비틀림 하중을 받는 box beam의 거동을 수학적으로 풀었고, 경계조건 및 적층 순서, 섬유 각도를 포함한 다양한 구성에 대한 처짐 및 비틀림 각도를 예측하였다.
Ghiasi 등[15]은 적층 복합 재료로 만들어진 구조물 설계 중 가변 강성 최적화 설계 방법에 대해 검토하였다. Jeong 등[16]은 Piecewise Integrated Composite(PIC)이라는 새로운 개념을 제안하여 자동차 범퍼 빔을 5등분하여 구간 별 나타난 하중 유형에 맞춰 다른 적층 각도 및 순서를 배치하여 범퍼의 강도를 향상시켰다. 또한, Ham 등[17]은 머신 러닝을 적용한 PIC 기법을 이용해 복합 재료 보의 강도를 향상시키는 연구를 진행하였다.
앞서 언급된 연구들은 유리 패널 이송 용 로봇 암의 강성을 향상시키는데 좋은 참고 자료가 된다. 본 연구에서는 세대가 증가할수록 대형화가 되는 유리 패널의 무게로 인한 로봇 암의 처짐을 줄이기 위해 강성을 향상시키는 연구가 진행되었고 복합 재료 로봇 암에 머신 러닝을 적용한 PIC 기법이 이용되었다. PIC 기법에 적합한 머신 러닝 모델을 찾기 위해 다양한 머신 러닝 모델들이 훈련을 통해 비교 및 평가되었다. 예측 정확도 80%이상, 유용성 평가 요소 AUC 값 0.8이상을 보인 머신 러닝 모델들을 이용하여 로봇 암 전체 모델에 작용하는 하중 유형을 예측하고 그에 우세한 적층 각도 순서가 배치되었다. 또한, 머신 러닝 모델들이 제시한 적층 각도가 각각 적용된 로봇 암에 대해 유한 요소 해석이 수행되었고, 이에 따른 처짐 변형량이 분석되었다.

2.1 머신 러닝이란
머신 러닝이란 인공 지능의 한 분야로, 알고리즘 반복을 통해 주어진 데이터 세트에서 입력량과 출력량 사이의 관계를 생성하는 모델링 방법이다. 알고리즘은 과거의 데이터 세트에서 패턴과 상관관계를 찾고 분석을 토대로 최적의 의사결정과 예측을 수행하도록 훈련되고 모델을 구축하여 새로 생성된 입력 정보의 출력 값을 예측할 수 있다[18,19]. 머신 러닝의 종류로는 지도, 비지도, 강화 학습 등의 학습 모델이 있는데 이 중 하나만 적용 가능하고 사용중인 데이터 세트와 원하는 결과에 따라 각 학습 모델 내에서 하나 이상의 알고리즘 기법을 적용할 수 있다.

2.2 머신 러닝 모델
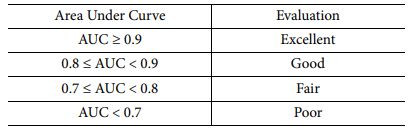
본 논문에서는 정답을 갖고 학습 또는 훈련하여 다른 요소를 예측하는 지도 학습 모델이 사용되었으며 알고리즘은 회귀, 분류 알고리즘들을 사용하여 결과를 비교하는 것이 진행되었다. 회귀 알고리즘으로는 Decision tree, Artificial Neural Network(ANN)과 분류 알고리즘 k-Nearest Neighbor (k-NN), Linear Discriminant Analysis(LDA), Support Vector Machine(SVM) 그리고 분류 및 회귀 알고리즘인 Ensemble (Random Forest) 이용한 훈련이 진행되었고 그 후 머신 러닝 모델 평가 요소 중 참, 거짓을 분류하는 비율을 그래프로 표현한 Receiver Operating Characteristic(ROC) 곡선의 아래 면적인 Area Under Curve(AUC)를 이용하여 모델의 유용성 및 예측 정확도가 평가되었다[20]. AUC의 유용성을 판단하는 기준은 Table 1에서 확인할 수 있다[21].

3.1 PIC box beam 설계
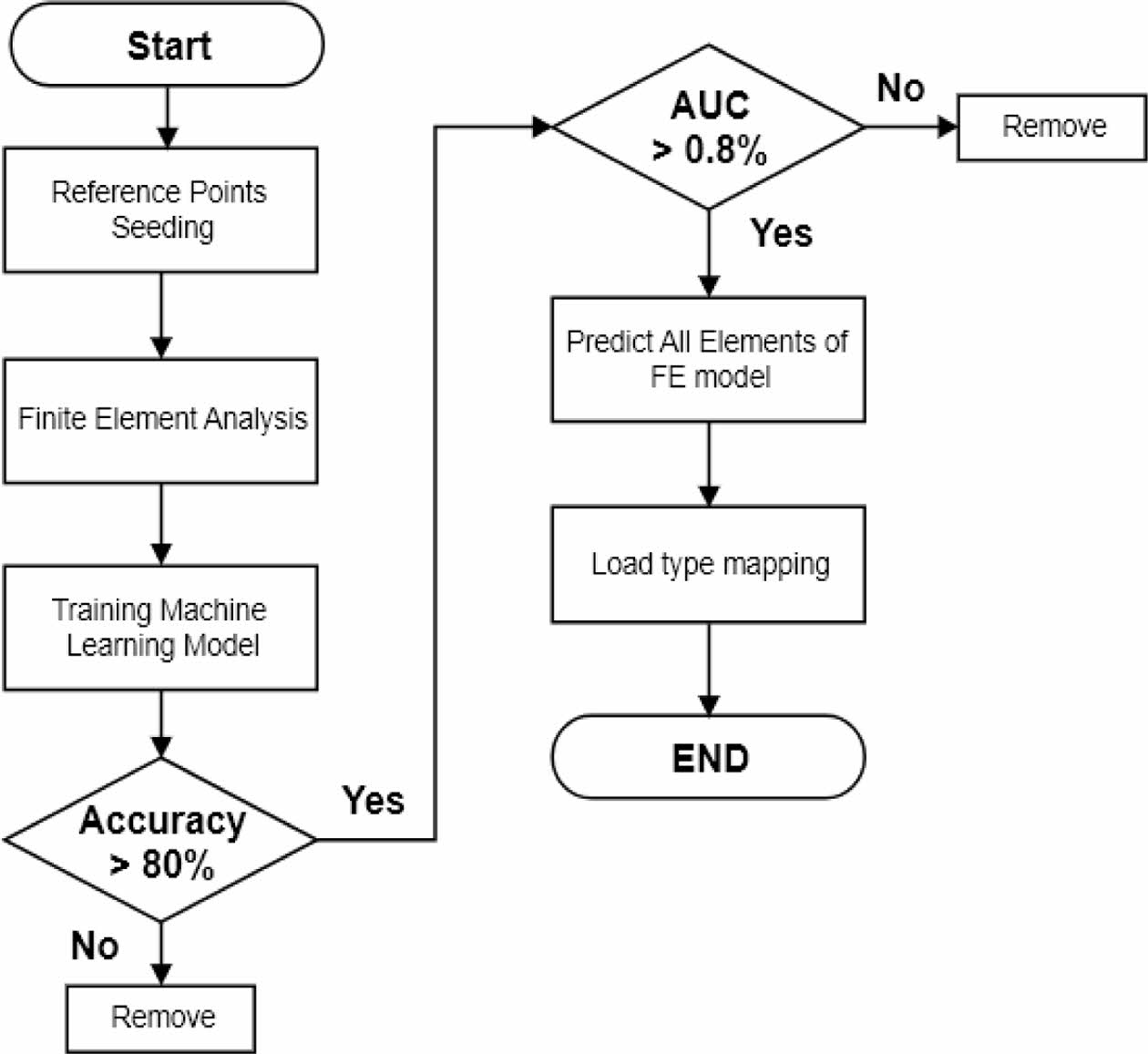
본 연구에서 머신 러닝 모델 생성과정은 Fig. 1의 Flow chat와 같이 진행되었다. 먼저, 학습 데이터 생성을 위해 참조 요소를 일정한 간격으로 유한 요소 모델에 배치시키고 유한 요소 해석이 선행되었다. 해석에서 도출된 참조 요소의 좌표와 하중 유형으로 구성된 학습 데이터가 생성되었고 생성된 학습 데이터를 이용해 머신 러닝 모델 각각 훈련이 진행되었다. 훈련 결과인 예측 정확도와 ROC, AUC를 이용해 머신 러닝 모델 평가가 진행되었다. 훈련에서 예측 정확도를 80%미만으로 도출하거나 AUC 값이 0.8미만으로 신뢰할 수 없는 수준의 머신 러닝 모델은 제외되고 예측 정확도 80%, AUC 값 0.8보다 높은 값을 보인 모델들을 이용해 로봇 암의 전체 요소가 예측되었다.

3.2 Box beam
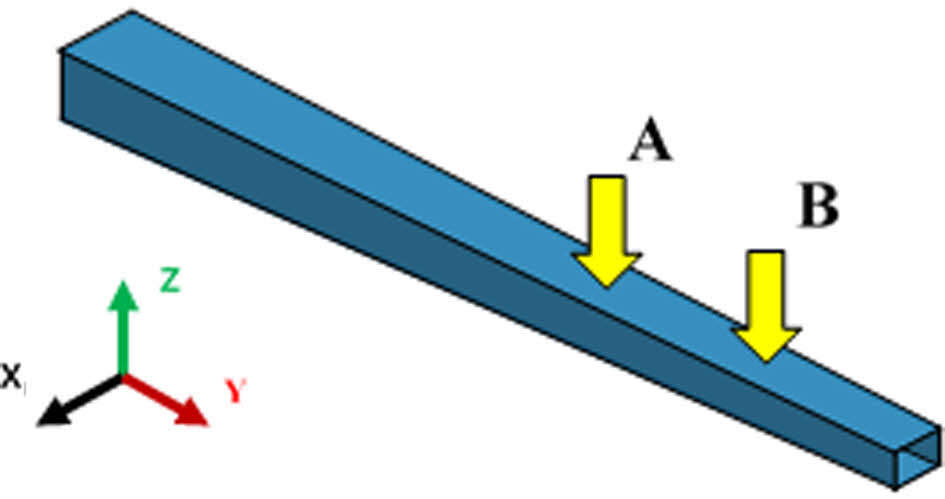
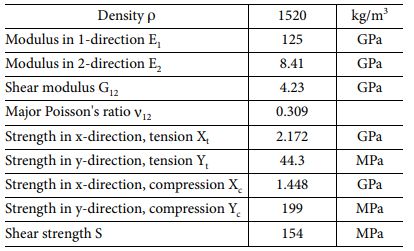
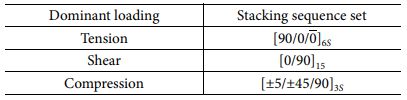
로봇 암은 유리 패널을 4점 지지하는 더블 암형 로봇의 box beam 구조 암을 Fig. 2와 같이 단순화한 모델로 설계되었고 vacuum pad가 장착되는 두 지점에 집중 하중을 가하는 유한 요소 모델로 진행되었다. Box beam의 적층 각도 및 순서는 [±5/±45/90]_3s로 재료는 Carbon/Epoxy이며 Torray사의 T700/2510으로 설계되었고 그 물성치는 Table 2에 나타나있다[22]. 로봇 암에 얹어지는 유리 패널의 경우 크기가 670 mm × 830 mm × 0.7 mm이고 밀도가 2440 kg/m³으로 설계하여 하중 값을 설정하였다.
머신 러닝 모델 훈련을 위한 학습 데이터를 구성하기 위한 참조 요소는 각 면에 630개씩 일정한 간격으로 총 2510개(전체의 약 12%)배치되었다. 학습 데이터에 성분은 3축 특성을 이용하여 구분된 인장, 압축, 전단 각 참조 요소에 우세하게 나타나는 하중 유형과 각 참조 요소별 좌표 값으로 구성되었다. 3축 특성 값(η)은 무차원의 값으로 식 (1)과 같이 정의된다. 구간별로 계산된 η≥0.1 일 때, 인장 하중이 작용하고, η≤-0.1 일 때, 압축 하중, -0.1<η<0.1 일 때, 전단 하중이 작용하는 것을 의미한다[23,24].



3.3 머신 러닝 모델 훈련 결과 및 고찰
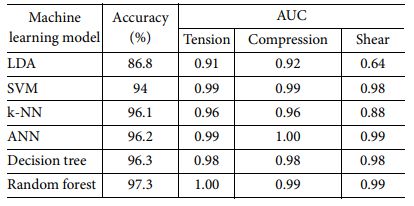
Table 3은 머신 러닝 모델 훈련에서 나타난 예측 정확도와 각 하중 유형을 분류하는 훈련에서의 AUC이다. 모든 모델에서 85% 이상이라는 높은 예측 정확도가 도출되었지만 각 모델의 AUC의 값은 차이가 나타났고 훈련 결과에 대한 고찰은 다음과 같다.
첫 번째로 LDA는 데이터 분포를 학습해 결정경계(Decision boundary)를 생성하여 데이터를 분류하는 모델로 데이터를 특정 한 축에 사영한 후 두 범주를 잘 구분할 수 있는 직선을 찾는 것을 목표로 알고리즘이 진행된다[25]. LDA 모델 훈련 AUC 값을 보면 인장과 압축 하중을 구분할 때 0.91, 0.92로 우수한 결과가 나왔지만 전단 하중을 예측하는 훈련에서 0.64로 신뢰할 수 없는 값이 나타났다. 이는 확률분포를 이용해 decision boundary를 생성하기 때문에 적은 표본을 가진 전단 하중 유형에서 정확도가 떨어진 것으로 판단된다.
다음 SVM은 두 범주 사이의 거리 margin을 최대화하여 분류경계면을 생성하고 분류하는 모델[26]로 본 훈련에서 예측 정확도 94% AUC는 인장, 압축, 전단 하중에서 0.99, 0.99, 0.98로 분류 기준을 생성하여 분류하는 방법이 비슷한 LDA 보다 우수한 결과를 보였는데 이는 데이터 범주 사이에 분류 기준선을 생성하여서 보다 정확한 분류가 진행된 것으로 판단된다.
k-NN은 새로운 데이터가 주어졌을 때 기존 데이터 중 가장 가까운 k개의 이웃 정보로 새로운 데이터를 예측하는 분류 모델[27]로 예측 정확도는 96.1%로 우수했고 AUC 값은 인장, 압축 하중에서는 모두 0.96의 값이 나왔지만 전단 하중에서 0.88로 다소 하락된 결과가 도출되었다. 이는 LDA와 비슷한 원인으로 전단 하중의 데이터가 적어서 이웃의 수가 적게 생성되어 분류하는 데 있어서 인장, 압축 하중이 우위를 가진 것으로 판단된다.
ANN은 생물학의 신경망에서 영감을 얻어 만들어진 회귀 모델로 시냅스 사이의 결합으로 네트워크를 형성하여 학습을 통해 시냅스의 결합 세기를 변화시켜 문제해결능력을 가지는 모델이다[28]. ANN의 예측 정확도는 96.2%로 높은 정확도를 보였고 AUC는 인장, 압축, 전단 하중에서 각각 0.99, 1.00, 0.99로 상당히 우수한 결과가 도출되었다.
Decision tree는 다양한 입력 변수에 기반하여 최종 출력 변수의 값을 예측하는 회귀 모델로 데이터의 입력 변수를 기준으로 출력 변수를 분류하고 분류 과정을 마치면 추정 모델이 생성되는 방법으로 진행된다[29]. 본 모델의 예측 정확도는 96.3%로 k-NN, ANN과 같이 높은 정확도를 보였고 AUC는 인장, 압축, 전단 하중에서 동일하게 0.98로 우수한 결과를 보였다.
마지막으로 decision tree의 overfitting 한계를 극복하기위해 다수의 decision tree를 합하여 만든 Random forest는 훈련을 통해 구성된 다수의 decision tree들로부터 얻은 결과를 취합해서 다수의 결과를 도출하는 분류 회귀 모델이다[30]. Random forest의 예측 정확도는 97.3%로 가장 우수했으며 AUC는 인장, 압축, 전단 하중에서 각각 1.00, 0.99, 0.99로 ANN과 같이 가장 우수한 결과를 보였다.
적은 데이터를 가진 전단 하중 분류 훈련 결과를 보면 분류 모델에서 AUC 값이 회귀 모델에 비해 최대 0.35 떨어진 결과가 나타났고 예측 정확도 또한 최대 10.5% 하락한 결과를 보였다. 이는 적은 수의 데이터를 이용해 생성된 분류 기준이 명확하지 않은 것이 원인으로 판단되며 향후 충분하지 않은 데이터를 이용한 머신 러닝의 경우 가중치를 부여하여 정확도를 향상시키는 연구가 필요할 것으로 보인다.

3.4 Box beam 전체 요소 예측
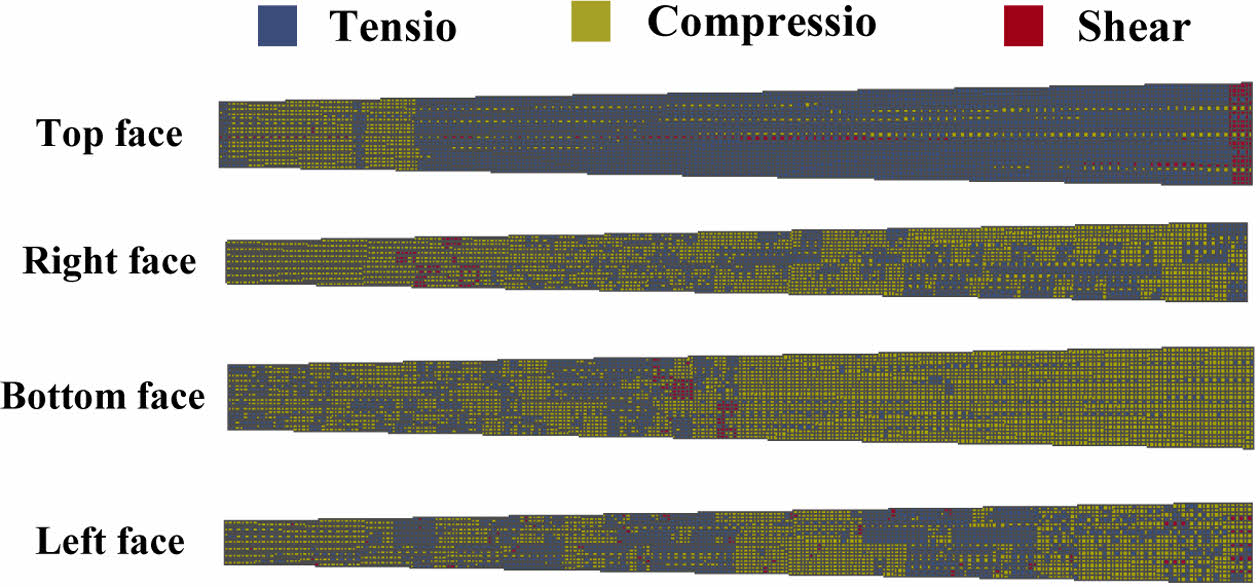
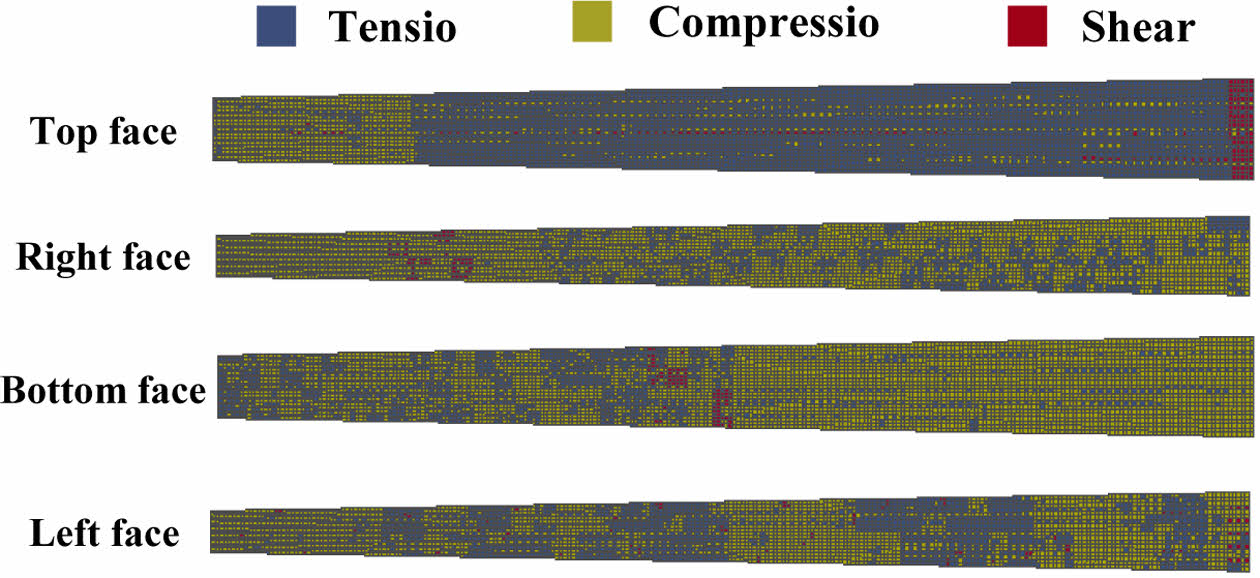
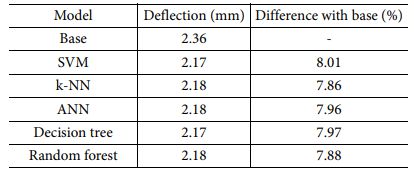
앞서 진행된 훈련과 평가에서 낮은 평가를 받은 LDA를 제외한 5가지 모델을 이용한 전체 요소 예측이 진행되었다. 각 머신 러닝 모델로 하중 유형이 예측된 전체 요소에 PIC 기법에 따라 Table 4에 적힌 각 하중 유형에 강한 특성을 보인 적층 각도 순서[31-33]가 배치되었고 그 모습은 Fig. 3-7과 같으며 모든 모델의 예측 정확도가 비슷하여 하중 유형 예측 결과 또한 유사하게 나타난 것으로 판단된다. 하중 유형에 따라 적층 각도 순서가 배치된 모델들로 유한 요소 해석이 진행되었고 처짐 변형량이 비교되었고 결과는 Table 5와 같다. 기존 모델에 비해 처짐 변형량이 최대 8% 향상된 모습을 보이며 로봇 암의 강성이 향상된 것이 확인되었고 모든 모델의 처짐 변형량의 차이는 최대 0.004 mm로 90% 이상의 높은 정확도와 AUC 값 0.8이상 신뢰할 수 있는 훈련 결과를 도출한 모델들의 변형량은 근사한 것으로 확인됐다. Fig. 4  Fig. 5  Fig. 6
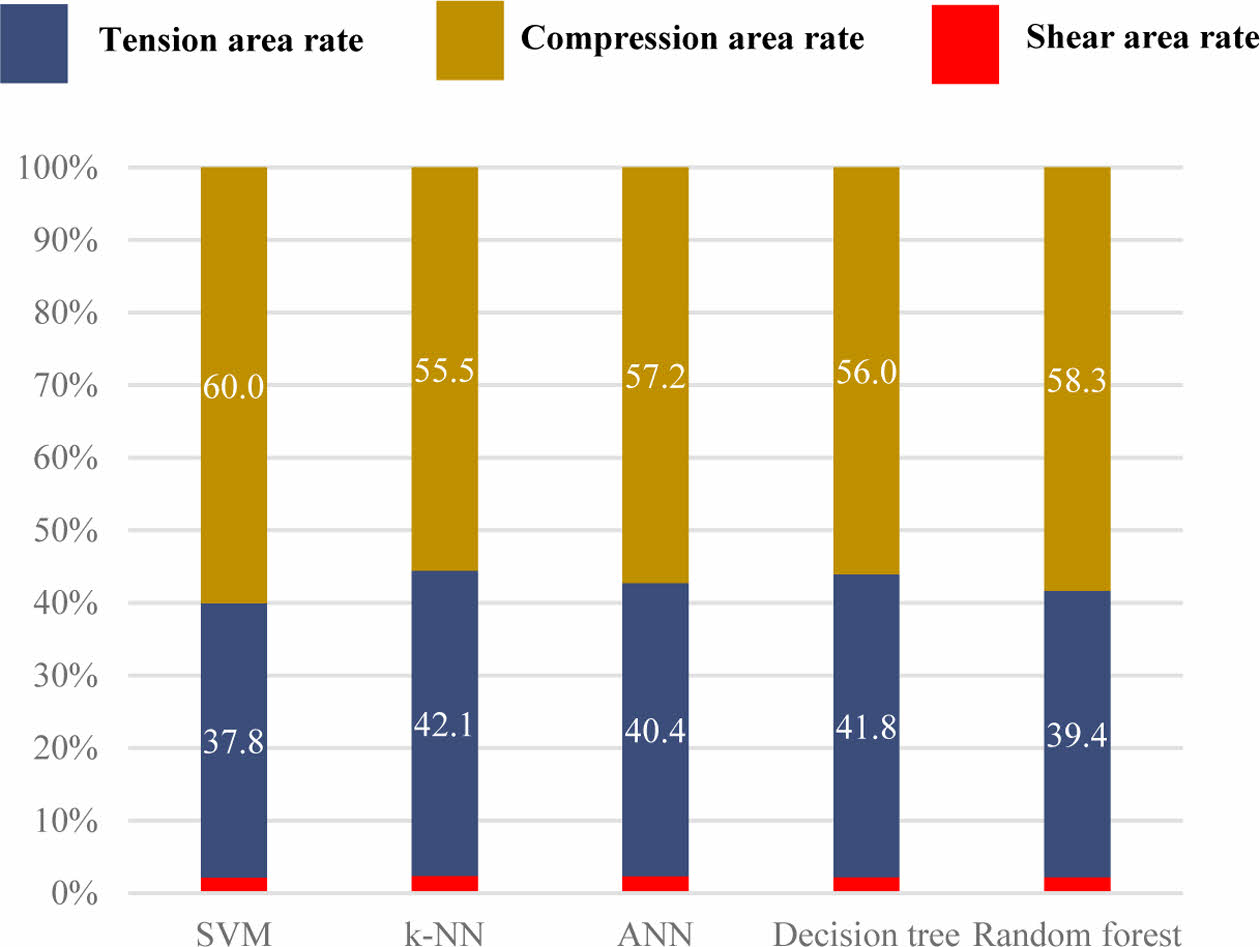
Fig. 8는 각 머신 러닝 모델들이 예측한 전체 요소의 하중 유형 비율로 압축 하중을 받는 요소가 제일 많이 나타난 것으로 확인되었고 그 비율이 높을수록 변형량이 줄어드는 경향을 보였다. 또한, 예측 정확도가 LDA 다음으로 낮았던 SVM이 예측한 로봇 암의 처짐 변형량이 가장 적게 나타났는데 향후 연구에서 분류경계면의 마진을 더 극대화하여 정확도를 향상시킨다면 처짐 변형량을 더 감소시킬 수 있을 것으로 판단된다.

본 연구에서는 복합 재료 로봇 암의 강성을 향상시키기 위해 머신 러닝을 적용한 PIC 기법이 이용되었다. PIC 기법에 적합한 머신 러닝 모델을 찾기 위해 다양한 머신 러닝 모델들이 훈련을 통해 비교 및 평가되었다. 선별된 머신 러닝 모델 모델들이 예측한 결과를 각각 적용한 로봇 암을 유한 요소 해석으로 처짐 변형량이 최대 8% 감소한 것을 확인하며 강성이 향상된 것이 확인되었다. 선별된 머신 러닝 모델들을 이용하여 로봇 암 전체 모델에 작용하는 하중 유형을 예측하고 그에 우세한 적층 각도 순서가 배치되었는데 압축 하중이 제일 많이 예측되었고 압축 하중을 제일 많이 예측한 SVM이 비교적 훈련 정확도는 낮았지만 처짐 변형량이 가장 적게 나타난 것이 확인되었다. 이는 향후 SVM 모델의 분류경계면의 마진을 더 극대화하여 성능을 향상시킨다면 로봇 암의 강성을 향상시켜 처짐 변형을 더 줄일 수 있을 것으로 기대된다. 다만, 적은 데이터를 가진 전단 하중 분류 훈련에서 분류 모델들의 AUC 값은 회귀 모델에 비해 최대 0.35 낮은 결과를 보였고 그로 인해 회귀 모델에 비해 최대 10.5% 낮은 예측 정확도를 보였다. 따라서 충분하지 않은 데이터를 기반으로 머신 러닝이 진행될 경우, 데이터에 가중치를 부여하여 정확도를 향상시키는 연구가 향후 필요할 것으로 사료된다.

이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2018R1D1A1B07051169).