This paper proposes a multiscale process-structural analysis methodology and applies to a battery housing part made of the short fiber-reinforced and fabric-reinforced composite layers. In particular, uncertainties of the material properties within the microscale representative volume element (RVE) were considered. The random spatial distribution of matrix properties in the microscale RVE was realized by the Karhunen-Loeve Expansion (KLE) method. Then, effective properties of the RVE reflecting on spatially varying matrix properties were obtained by the computational homogenization and mapped to a macroscale FE (finite element) model. Morever, through the hybrid process simulation, a FE (finite element) model mapping residual stress and fiber orientation from compression molding simulation is combined with one mapping fiber orientation from the draping process simulation. The proposed method is expected to rigorously evaluate the design requirements of the battery housing part and composite materials having various material configurations

본 논문은 멀티스케일 공정-구조 해석의 방법론을 제안하고 단섬유층과 직물층으로 이루어진 배터리 하우징 파트에 적용한다. 특별히 마이크로스케일 대표체적요소(RVE: Representative Volume Element)안 기지의 불확정성을 고려하였다. 마이크로스케일의 RVE내 기지 물성의 랜덤한 공간내 분포는 KLE(Karhunen-Loeve Expansion)을 통해 구현하였다. 공간상 랜덤분포된 기지 물성을 갖는 RVE의 유효 물성을 전산균질화를 통해 얻어 매크로스케일 유한요소 모델에 매핑하였다. 또한 하이브리드 공정해석을 통해 압축 성형 해석으로부터 얻은 잔류응력과 섬유배향을 매핑한 유한요소 모델과 드레이핑 공정 해석결과로부터 얻어진 섬유배향을 매핑한 모델을 결합하였다. 본 연구에 제안된 방법은 배터리 하우징 뿐만 아니라 다양한 재료 구성을 갖는 복합재료의 공정-구조해석을 통해 설계요구도를 엄밀하게 평가할 수 있을 것이라 기대된다

Keywords: 멀티스케일 해석(Multiscale analysis), 불확실성 정량화(Uncertainty quantification), 압축 성형 해석(Compression molding simulation), 드레이핑 공정 해석(Draping process simulation)

최근 유럽 및 주요 국가들은 온실가스 배출과 석유 의존도 감축 등 국제 환경 규제 강화 추세에 발맞춰, 친환경 자동차 기술 개발에 대한 연구가 활발히 진행되고 있다. 특히, 주행거리의 확장을 위하여 배터리 하우징과 같은 친환경 자동차 주요 부품에 대한 경량화 기술의 중요성이 대두되고 있다. 차량 경량화를 위해, 기존 재료인 금속 소재를 대체하여 복합소재를 활용하는 방향으로 연구 개발이 진행되고 있으며, 재활용이 가능한 열가소성 복합소재 기반 배터리 하우징의 경량화 기술 개발이 필요한 실정이다. 배터리 하우징는 사출, 압출, 압축공정 등 다양한 성형 공법이 활용되어 제작된다[1]. 하지만 시간과 비용이 많이 요구된다는 단점이 있어, 제조 공정을 모사할 수 있는 전산해석 기법들이 제안되고 있다.
Sun 등[2]은 LS-DYNA와 Moldex3D 상용 툴을 활용하여 열가소성 복합소재 기반 Seatback Outer 대한 열 성형공정 이후의 단섬유의 배향, 뒤틀림, 잔류응력을 계산하였고, 이를 실험 결과와의 비교를 통해 검증하였다. Kwak 등[3]은 PCM (Prepreg Compression Molding) 공정에서 발생하는 문제를 해결하기 위해 압력을 서서히 높여가는 다단 압축 성형 방법을 제시했고 복합재 성형 품질에 효과가 있음을 실험적으로 밝혔다. 또한, 성형 공정에서 생성된 기공이나 섬유 배향이 복합재료의 기계적 물성에 영향이 있음을 밝히는 연구도 있었다[4,5]. RTM(Resin transfer molding)과 압축 성형 공정을 통해 생성된 복합재료 시편에 전단 테스트를 실시하여 복합재료의 압축성형에서 미시적으로 생성된 기공이 전단 강도를 감소시키는 요인임을 밝혔다[4]. 이와 다르게, AM(Additive Manufacturing) 공정과 복합재 압축 성형 공정을 연계하여 섬유 배향에 의한 기계적 성능을 실험적으로 확인했다[5]. 결과적으로, 섬유 배향에 따라 인장 강도의 경우 11% 향상되었음을 실험적으로 밝혔다. Isaincu 등[6]는 사출 성형 후 복합 소재 단섬유의 배향 정보를 Moldflow 상용 툴을 활용하여 추출하였고, 이를 Digimat과 Ansys를 통해 단섬유 배향이 기계적 거동에 중요한 인자임을 밝혔다. Song 등[7]는 압축 성형 이후의 단섬유의 배향 정보를 Moldex3D와 Matlab을 통해 유한요소모델에 맵핑하였다. 이를 인장 실험으로부터 획득한 강성 비교를 통해 검증하였다. Haanappel 등[8]는 Aniform 성형해석 툴을 통해 glass 8HS/PPS 장섬유 복합재 보다carbon UD/PEEK 장섬유 복합재의 intra-ply shear에 대한 강도가 높다는 것을 밝혔다. 또한, Khalid 등[9]은 유리 섬유와 천연 섬유를 기반으로 복합재료 압축 성형을 하고 복합재 부품의 휨 실험을 진행했다. 복합재 적층 구성에 따라 휨 거동이 다름을 확인하였고 이를 유한요소 소프트웨어인 ABAQUS를 통해 복합재 강도를 예측했다. 이는 유한요소 기반 성형 해석을 통한 복합재의 강도 예측의 가능성을 보여줬다.
하지만 이러한 연구들은 단일 종류의 섬유에 대해서 성형 해석을 연계한 유한요소해석에 국한되었다. 앞으로 다양한 장/단 섬유가 적용된 하이브리드 복합재에 대해 제조공정을 반영할 수 있는 멀티스케일 공정-구조 연계 해석 기법이 필요하다. 본 연구의 목표는 두 가지(장/단섬유) 복합재 층의 고유 특성을 반영한 압축 성형 해석과 연계한 멀티스케일 구조해석 기법 개발이다. 또한, 각 복합재 층의 특성을 반영한 미소 구조를 생성했고 이를 대표체적요소로 가정했다. 그리고 기지 물성의 불확실성을 고려하기 위해 랜덤 필드 모델링 방법을 활용했다. 원활한 멀티스케일 구조 해석을 위해 확률적 기지 물성 분포를 갖는 RVE에 전산균질화를 통해 유효 물성을 획득했다. 복합재 배터리 하우징 하단 커버를 연구 대상으로, 성형 해석 연계 멀티스케일 구조해석을 수행했다.

2.1 복합재 특성을 고려한 미소 구조 생성
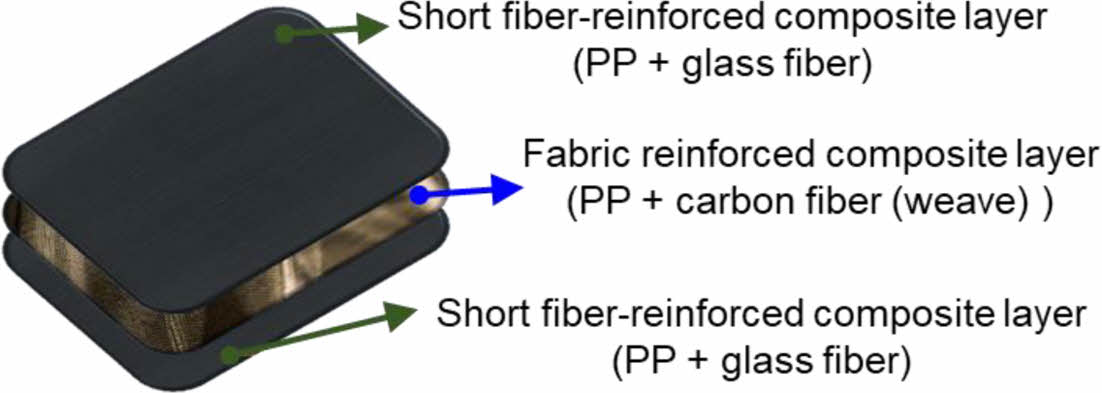
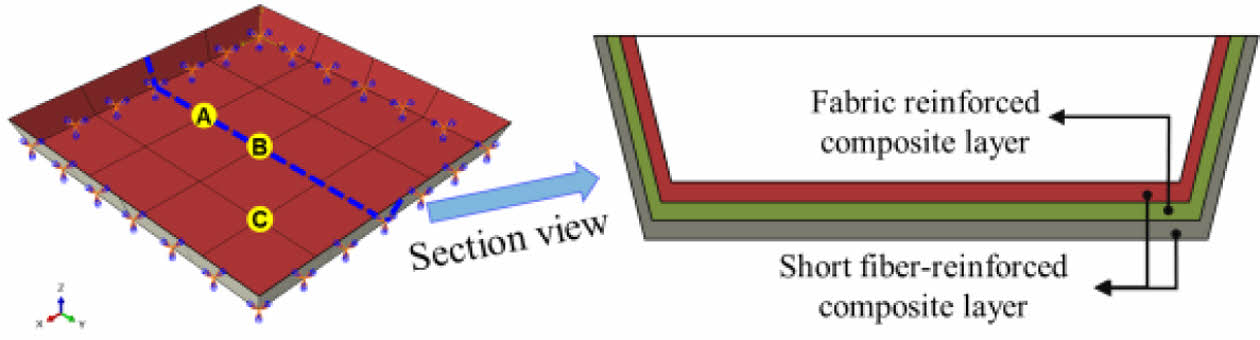
본 연구에선 복합재료 층의 특성을 반영하여 미소 구조물을 생성했다. 배터리 하우징에 포함된 복합재 구조물은 2가지 종류의 복합재료 층을 포함하고 있다. Fig. 1에 명시한 것과 같이 직물 강화 복합재 층을 중심으로 불연속 섬유 강화 복합재 층이 위 아래로 코팅되어 있다. 불연속 섬유 강화 복합재 층은 화재 사고를 대비하기 위해 제작된 층이며, 직물 강화 복합재 층은 구조물의 하중을 견디기 위한 층이다. 본 연구에선 직물 강화 복합재 층을 직물층으로 불연속 섬유 강화 복합재 층을 난연층으로 명명했다.
미소 구조물은 지오딕트[10] 상용 프로그램을 이용하여 생성됐다. 난연층에는 미소 타원체 입자들이 첨가되어 있다고 가정하고 지오딕트의 Graingeo 모듈을 이용하여 형상을 생성했다. 반면, Weavegeo 모듈을 활용하여 강화 섬유 다발이 직물 형태로 짜여진 미소 구조를 생성하여 직물층의 미소 구조로 가정했다.
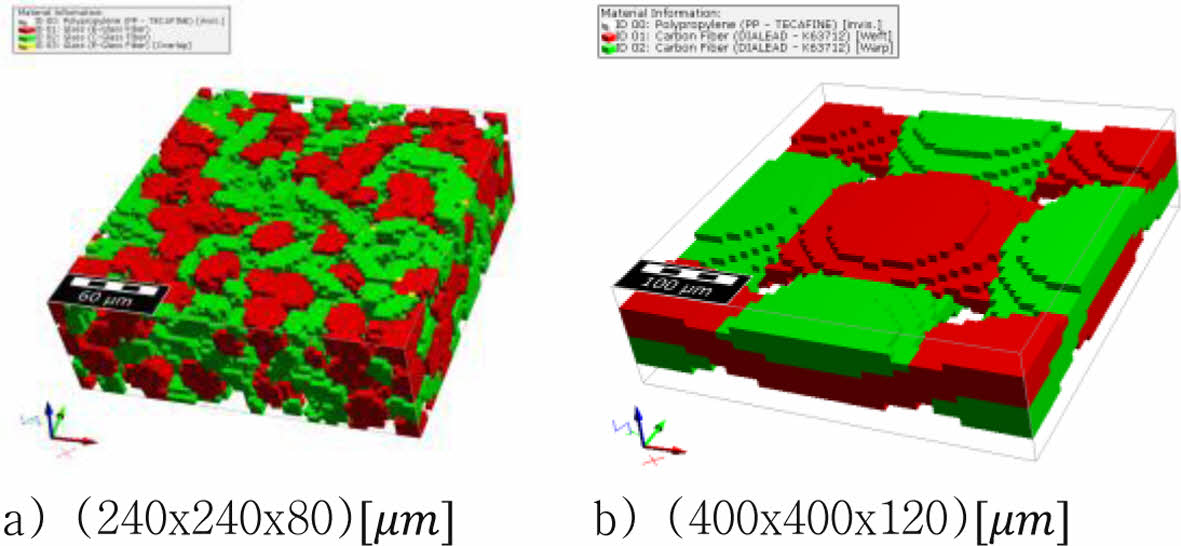
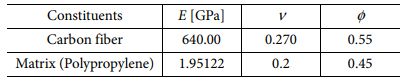
복합재 층 특성을 반영한 미소 구조 형상과 영역 크기를 Fig. 2에 명시했다. 강화제와 기지의 요소 타입은 3차원 8절점 요소(C3D8)이다. 또한, 각 복합재 층의 미소 구조에 반영한 영률 E, 푸아송 비 ν, 부피 분율 φ 값을 Table 1와 Table 2에 표로 정리하였다.

2.2 랜덤 필드 기법을 이용한 확률적 기지 물성 생성
복합재 층의 기지 물성의 불확실성을 고려하기 위해 랜덤 필드 모델링 기법 중 하나인 KLE(Karhunen-Loeve Expansion)를 이용했다. 본 연구에서 랜덤 변수 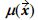는 미소 구조물에 포함된 3차원 공간 상(Ω_m)에 분포된 기지 물성이다. 이를 식으로 나타내면 식 (1)처럼 표현할 수 있다.



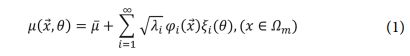
식 (1)의 μ͞͞ 는 랜덤 변수의 공간내 평균값이며 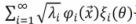는 랜덤 변수의 확률적 효과를 고려하는 항이다. ξ_i는 평균이 0이고 표준편차가 1인 상관관계가 없는 가우시안 랜덤 변수이며, 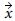는 영역 Ω_m에 포함된 위치 벡터이고, q는 무작위성을 나타내는 기호이다. 또한, 식 (1)에 포함된, λ_i와 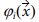은 프레드홀름 적분 방정식 (2)의 고유값 문제을 통해 구해진 고유값과 고유함수이다.

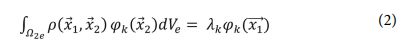
식 (2) 좌변에 포함된 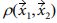는 3차원 공분산 커널이며 3차원 공간 상의 임의의 2개 지점 사이의 상관관계를 나타낸다. 본 연구에선 커널을 다음과 같이 정의했다.



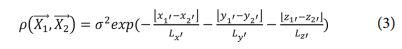
이때, σ²은 랜덤 변수의 분산이며, L_x, L_y, L_z 는 각 방향으로의 상관 길이이다. 상관 길이 값이 클수록 랜덤 변수의 공간상의 분산의 영향은 줄어든다. 반면, 상관 길이가 작아 질수록 분산의 영향은 커지게 된다. 이 연구에선 분산(σ²) 대신 분산 계수(C.O.V.: coefficients of variance)와 평균을 이용하여 나타냈고, 관계식은 C.O.V. = σ/μ이다.

일반적으로 식 (2)는 직접 수식으로 풀기 까다로운 것으로 알려져 있다[11,12]. 따라서, Galerkin 유한요소기법을 활용하여 식 (4)와 같이 이산화하여 고유값과 고유함수를 구하였다. 식 (4)에서 명시한 {d}와[L(x)]는 각각 고유함수의 노달 벡터와 형상 함수를 나타낸다.



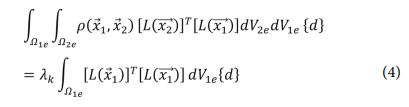
구현한 KLE를 활용하여 미소 구조 기지 물성의 랜덤 분포를 계산했다. 기지 물성의 랜덤 분포만 고려하므로 미소 구조물의 기지 영역에 해당하는 요소에 랜덤물성을 정의하였다. KLE 기법에 활용되는 변수들은 실험적으로 구해야 하지만 여기서는 Table 3과 Table 4와 같이 가정했다. 직물층의 경우 상관 길이를 크게 하여 기지 물성 분포를 난연층보다 적게 했으며 난연층의 경우 작은 입자들의 영향을 고려하여 상대적으로 작은 상관 길이 값을 이용했다.

2.3 미소 구조의 기지 물성 분포 획득 및 대표체적요소의 유효 물성 획득
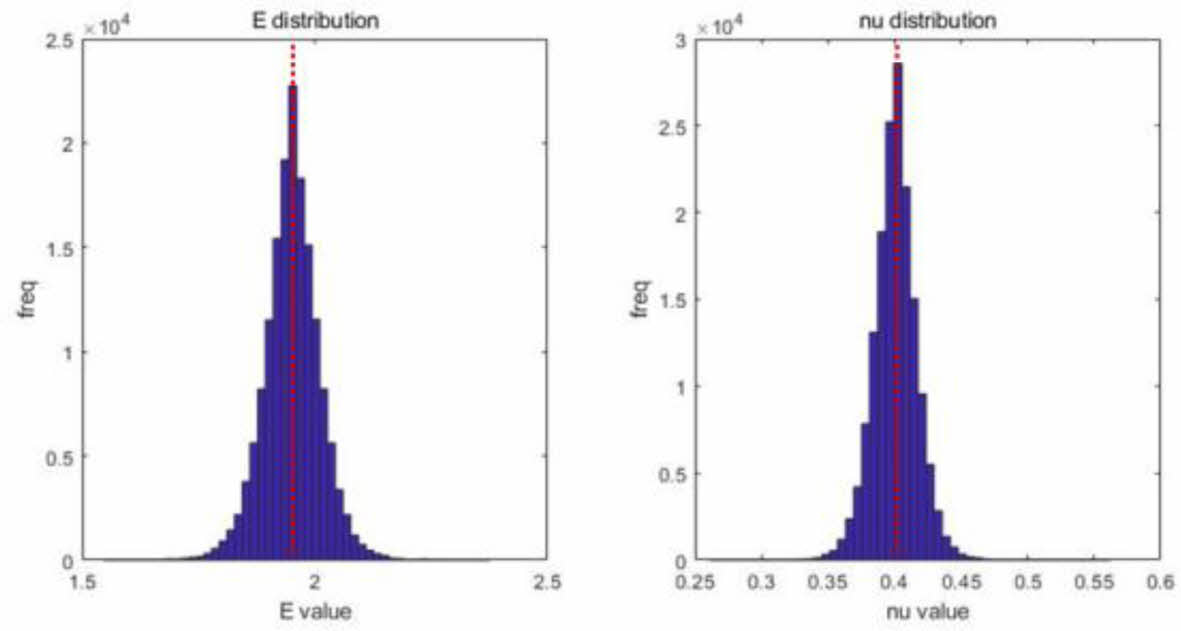
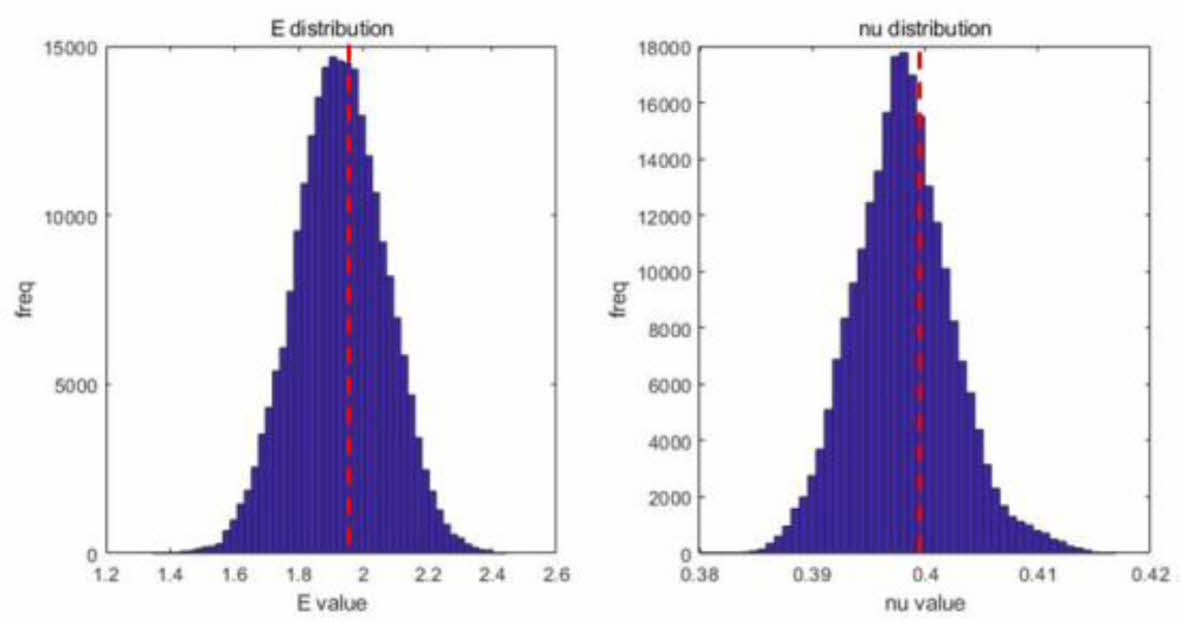
KLE 기법으로 구해진 기지의 랜덤 물성은 기지의 요소와 적분점에 따른 다르게 저장된다. KLE기법을 활용하여 두 종류의 복합재 층의 미소 구조물의 기지 영역에 대한 물성 분포를 획득했다. 자세한 기지 물성 분포는 Fig. 3와 Fig. 4에 나타냈다. 특히, 빨간색 점선으로 KLE 랜덤 변수의 평균값을 표기했으며 히스토그램을 통해 정규 분포의 형태로 기지 물성이 반영됐음을 확인했다. 각 평균값은 Table 3과 Table 4에 명시됐다. 상관 길이에 따라 기지 물성 분포 정도가 달라지는 것을 확인했다. 상대적으로 큰 상관 길이를 이용한 직물층의 기지 물성 분포가 난연층의 기지 물성 분포보다 크다는 것을 확인했다.
KLE 방법을 이용하여 획득한 기지 물성 분포가 균질화 해석에 포함이 되도록 ABAQUS Umat subroutine을 이용했다. 특히, 이 Umat subroutine은 KLE 기법에서 계산된 각 요소와 적분점에 따른 물성 값이 추출되어 이를 통해 강성 행렬이 계산된다. 반면, 강화제의 물성은 Table 1과 Table 2의 값을 그대로 이용했다.
이어서, KLE을 통해 계산된 기지 물성 분포를 바탕으로 미소 구조의 유효 물성을 획득했다. 상용 유한요소 프로그램인 ABAQUS에서 제공하는 Micromechanics plugin을 활용하여 균질화 해석을 실행하고 각 미소 구조물의 유효 물성을 획득했다.

3.1 난연층의 압축 성형 시뮬레이션
배터리 하우징의 복합재 구성은 세 개의 층으로 나뉘며 총 두께는 3 mm이다. 복합재 각 층의 두께는 난연층의 경우 0.5 mm이며 직물층은 2 mm이다. 난연층 재료는 SABIC사의 PPcompound H1020로, 압축 성형 시뮬레이션에 고려된 재료의 물성은 제조사측에서 진행한 실험을 통해 측정된 값을 사용하였다. 측정된 재료의 물성은 유변학적 성질, 열 속성, 기계적 성질 등을 포함한다. 난연층의 압축 성형 공정 해석을 위해 상용 소프트웨어인 Moldflow를 이용했으며 압축 성형 후 섬유 배향 및 잔류응력 값을 획득했다.
Fig. 5a)는 난연층의 압축 성형 후 재배치된 섬유 배향을 나타낸다. 섬유칩을 시트화하여 제조한 재료의 특성에 따라 초기 charge의 섬유 배향을 x-y 평면에 랜덤하게 설정하였고 섬유 배향 예측은 Folar-Tucker 방정식[13]을 기반으로 수치모사 시뮬레이션하였다.
섬유 배향은 보통 2차 텐서로 표현되며 섬유 배향 텐서(T_ij, fiber orientation tensor) (5)는 섬유의 단일 벡터 p의 dyadic product을 배향 분포 함수 ψ(p)로 적분한 것으로 정의한다[13]. 배향 텐서의 정의에 따라 섬유가 특정 배향 p에 있을 확률이 높을수록 1에 가까운 값을 가지며 낮은 확률일수록 0에 가까운 값을 가진다. 섬유 배향 텐서식은 아래와 같다.



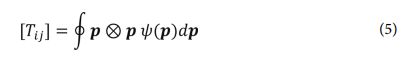
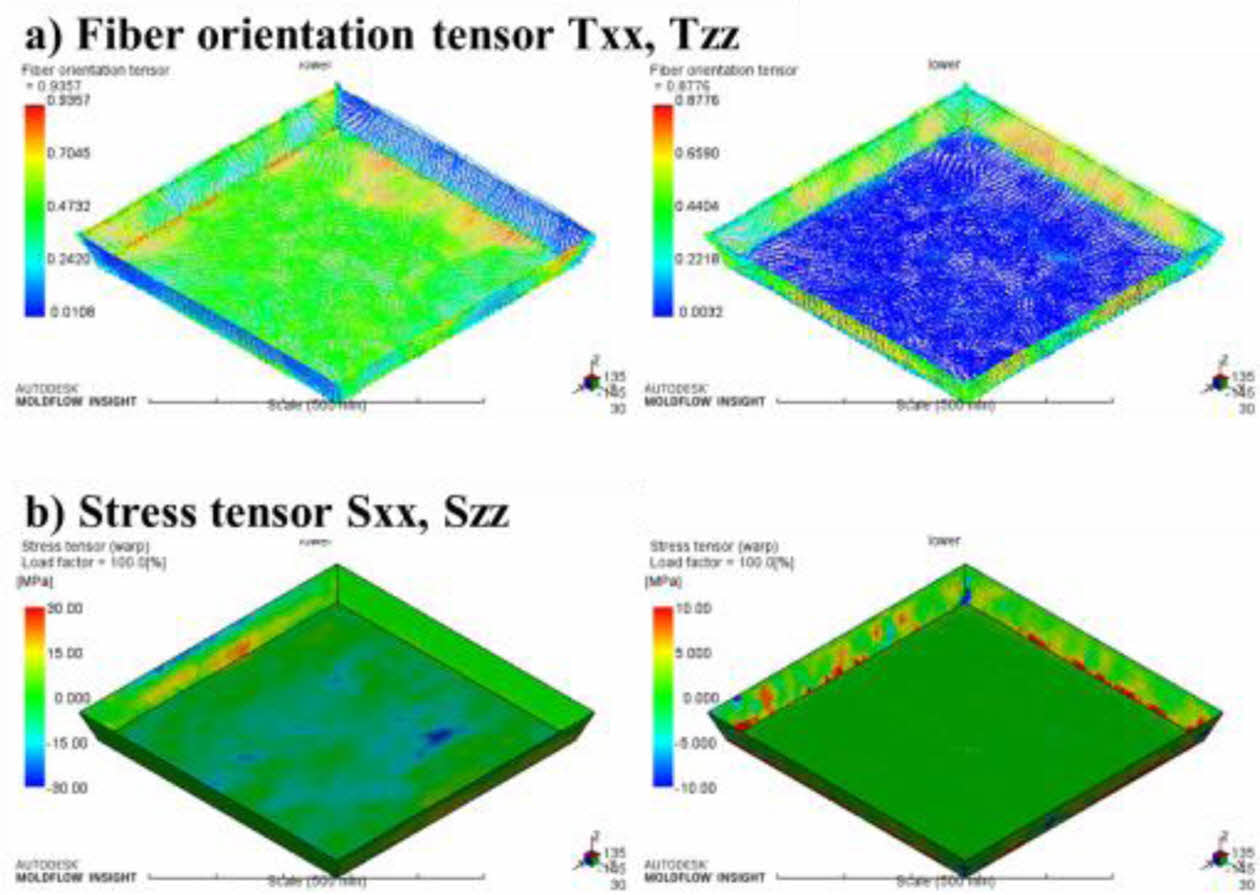
Moldflow 3D 변형해석을 통해 압축 성형 이후 냉각된 복합재에 발생하는 잔류응력을 예측했다. 압축 성형 해석에서 획득한 섬유 배향과 잔류응력을 배터리 하우징 모델에 contour 형태로 Fig. 5에 정리했다. Fig. 5a)의 경우 섬유 배향 값이며 Fig. 5b)의 경우 잔류응력 값이다.
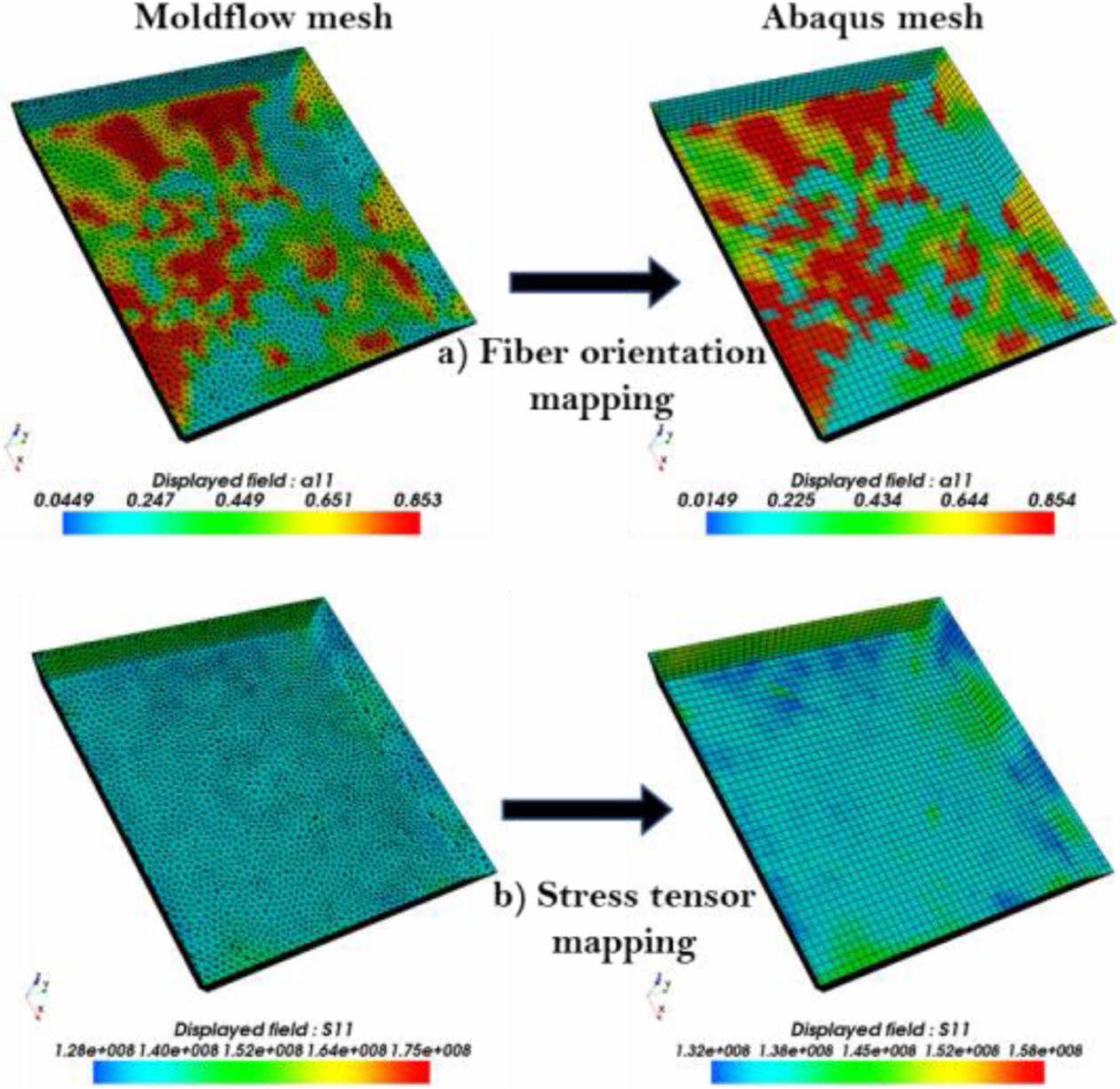
성형해석 결과인 잔류응력을 구조해석 초기 조건으로 성립하여 실제 공정을 고려한 구조해석을 진행할 수 있다. 예측된 섬유 배향과 잔류응력 결과는 Digimat-MAP을 통해 Moldflow 메쉬에서 ABAQUS 메쉬로 맵핑하여 성형 해석 결과 데이터를 구조 해석과 연계할 수 있도록 했다. 자세한 맵핑 결과를 Fig. 6에 나타내었다. Fig. 6a)의 경우 섬유 배향 값의 맵핑 결과이며 Fig. 6b)의 경우 잔류응력 값의 맵핑 결과이다.

3.2 직물층의 드레이핑 공정 시뮬레이션
직물층의 드레이핑 공정을 시뮬레이션 하기 위해 상용 소프트웨어 Aniform을 사용했다. Aniform을 이용한 성형 공정 시, 복합재 플라이의 변형 예측에 인플레인, 벤딩, 계면의 세 가지 메커니즘이 고려된다. 각 메커니즘은 Cross viscosity model 식 (6), Mooney-Rivlin model 식 (7)의 재료 모델로 구성되어 있다.
Cross viscosity model 식 (6)에서 코시 응력 텐서(σ)는 변형률 속도 텐서 D, 변형 구배의 자코비안 J, zero-shear점도 η₀, infinite shear 점도 η_∝와 전단 변형률 속도 γ̀, 유체상수 m과 n으로 구성되어 있으며, 이는 non-Newtonian 유체에 사용되는 전단 변형률 속도 의존 점도 모델이다. Mooney-Rivlin 모델 식 (7)은 초탄성 모델로, C₁₀과 C₀₁는 재료 상수, B는 코시-그린 변형 텐서, I는 변형 불변량이다. 본 연구에서는 각 재료 모델에 동일한 가중치를 둔 혼합 모델을 사용했다.



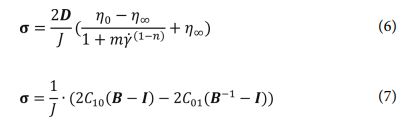
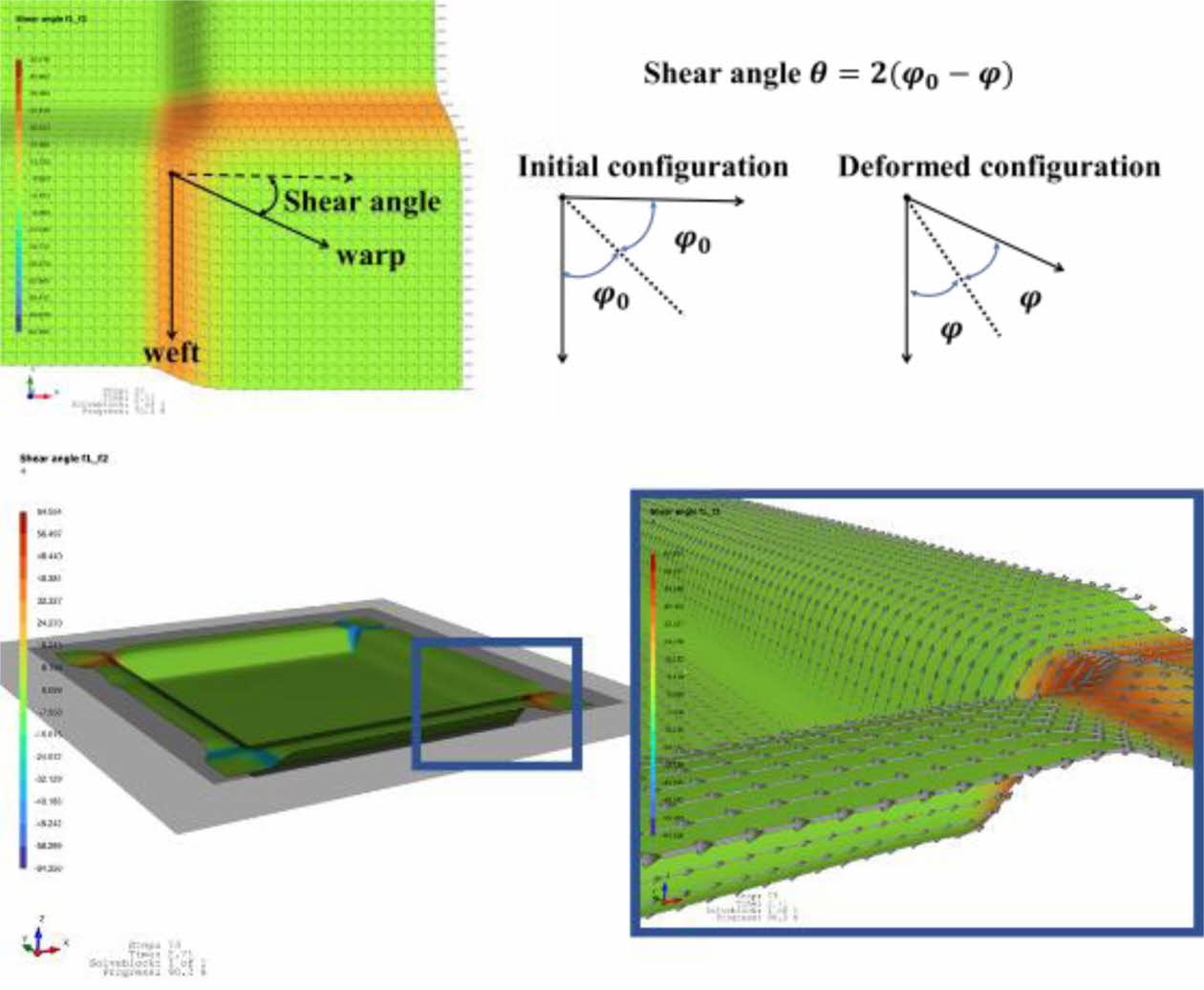
Fig. 7는 Aniform의 드레이핑 시뮬레이션을 통해 예측한 전단 각도 및 평직의 경사 방향의 섬유 배향을 보여주고 있다.
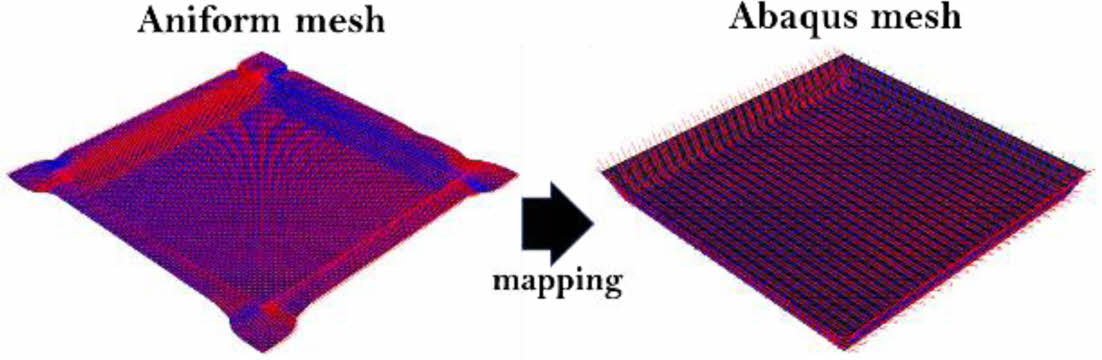
성형 공정 해석을 연계한 구조 해석을 하기 위해 Aniform의 드레이핑 해석 결과인 직물 배향 정보를 유한요소에 매핑했다. 자세한 매핑 결과를 Fig. 8에 나타냈다.

4.1 복합재 층을 반영한 유한요소 모델링
압축 성형 시뮬레이션의 결과인 섬유 배향과 잔류응력의 유무에 따른 복합재의 구조 응답을 확인하기 위해 멀티스케일 구조해석을 수행했다. 이때 이용한 소프트웨어는 ABAQUS이다. 멀티스케일 구조해석을 하기 위해 미소스케일에서 획득한 유효 물성을 이용했다. 이 유효 물성은 2장에서 설명한 확률적 기지 물성이 반영됐으며, 배터리 하우징의 복합재 층마다 다른 유효 물성이 Digimat을 통해 구조 해석에 활용된다. 성형 공정 해석 결과인 섬유 배향은 Fig. 6과 Fig. 8에 명시된 것처럼 ABAQUS 유한요소 모델에 매핑이 된다. 반면, 잔류응력은 ABAQUS의 구조 해석에서 초기 응력으로 구조 해석에 이용할 수 있다. ABAQUS의 Predefine 조건의 초기 응력 값으로 성형 해석 결과물인 잔류응력 값을 넣어 배터리 하우징 구조 해석 이전에 잔류응력에 의한 변형을 반영할 수 있었다.
배터리 하우징 하단부에 포함된 복합재 층을 반영하기 위해 Fig. 9와 같이 유한요소 모델링을 진행했다. Fig. 9 좌측은 배터리 하우징 하단부를 단순화한 유한요소 모델이며 원활한 후처리를 위해 세 개의 노란색 지점을 선정했다. Fig. 9 우측은 유한요소 모델에 반영된 각 복합재 층을 단순화하여 표현한 것이다. 모든 복합재 층 사이에 타이 구속조건을 적용했다. 직물 강화 복합재료 층에 이용한 요소 타입은 삼각형 쉘 요소(S3)이고 불연속 섬유 강화 복합재료 층에는 3차원 10절점 테트라 요소(C3D10)를 이용했다.

4.2 섬유 배향과 잔류응력 영향 검토
앞서 정의한 유한요소 모델에 진동해석 실시하여 섬유 배향과 잔류응력의 유무에 따른 modal 값과 동적 응답을 검토했다. Modal 해석을 선행적으로 실시하고 추출된 modal 값들을 기반으로 주파수 응답 해석을 수행했다. 여기서 외력으로 Z방향으로 5G 가속도를 부여했다. 결과적으로 주파수 응답 함수(FRF: Frequency response function)을 2000(Hz) 범위 내에서 획득할 수 있었다. 잔류응력을 반영하기 위해 ABAQUS의 Predifine field를 이용하였고 이 잔류응력 값들이 평형 상태로 도달하기 위해 modal 해석 전에 외력이 없는 정해석을 실시했다[14]. 해석 대조군으로 섬유 배향과 잔류응력을 모두 고려하지 않은 경우와 섬유 배향은 그대로 적용하고 잔류응력만 제한한 경우를 고려하여 총 세 종류의 해석을 실시했다. 반면, 물성치, 경계 조건, 외력 등 모든 조건은 세 가지 해석에 동등하게 적용했다.
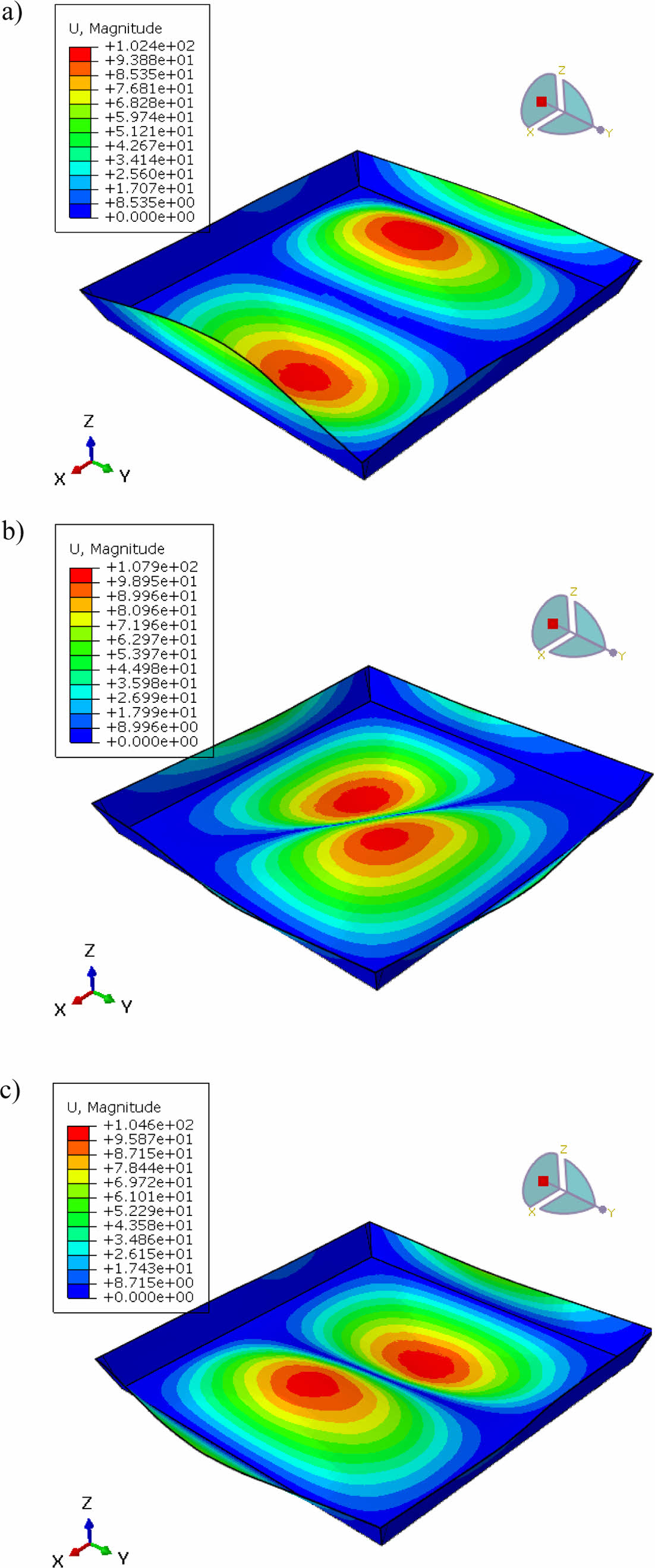
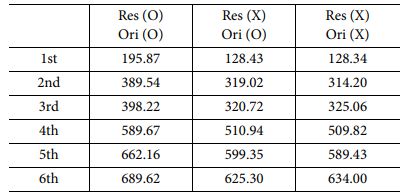
세 가지 모든 경우의 해석에 대해 2000(Hz) 범위에서 modal 값은 25개씩 나왔으며 첫번째 mode부터 여섯 번째 mode까지에 대한 결과를 정리하여 Table 5에 명시했다. Table 5의 첫 행은 본 연구에서 시행한 세 가지 해석을 명시한 것이다. Res와 Ori의 의미는 각 잔류응력과 섬유 배향을 의미하며, 괄호 안의 O와 X는 잔류응력과 섬유 배향의 포함 유무를 표기하는 기호로써 이용했다. 또한, 3번째 mode에 대해 mode 형상 이미지를 Fig. 12에 정리하였다.
수치적으로 비교했을 때 잔류응력과 섬유 배향을 모두 포함한 해석에서 다른 경향의 고유 주파수를 획득할 수 있었다. 섬유 배향의 유무의 해석 결과 차이는 고유 주파수 값으로 비교했을 때 큰 차이는 없어 보였으나, mode 형상을 비교했을 때 차이가 있다는 것을 확인했다.
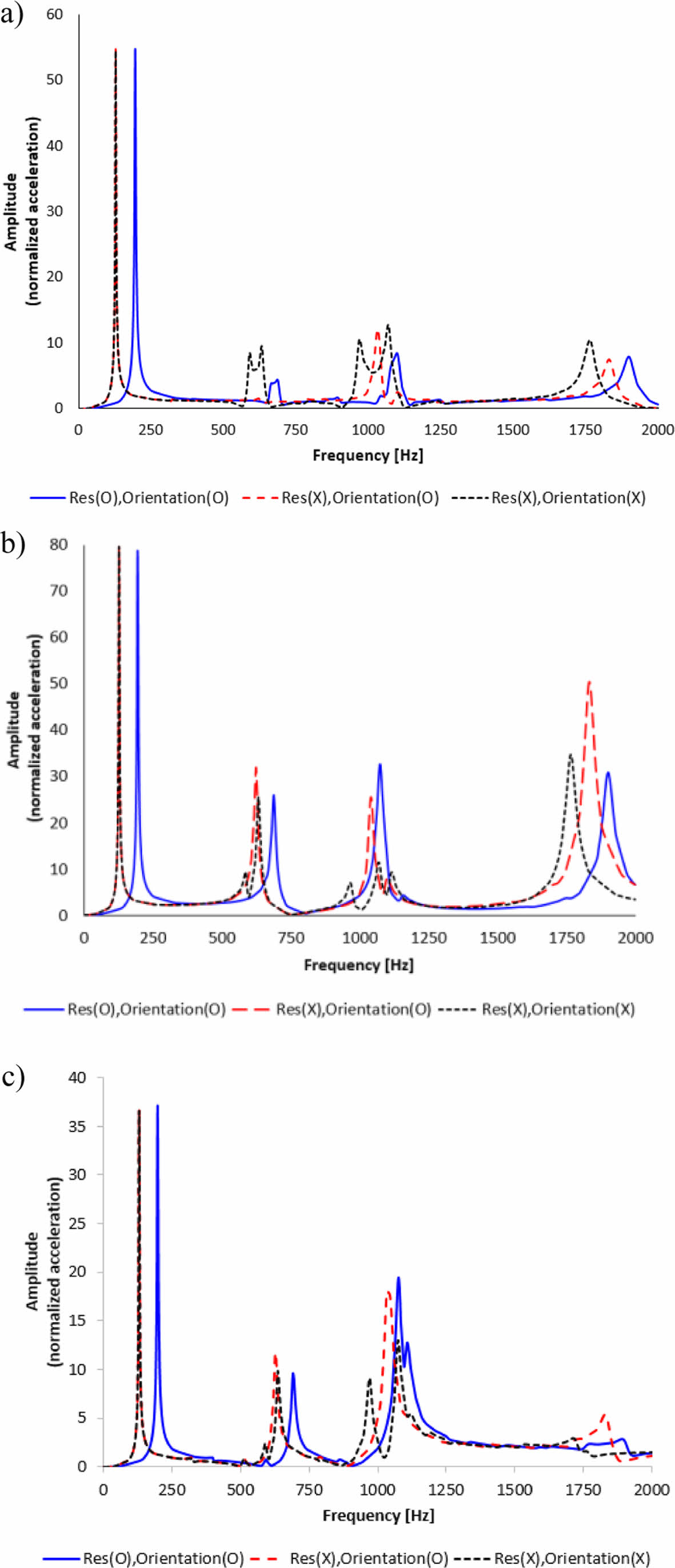
Fig. 9 좌측에 명시한 해석 모델의 세 지점에 대하여 진동 응답 결과 중 하나인 가속도 크기를 추출하고 인가한 5G가속도로 나누어 FRF를 획득했다. 그리고 각 해석 결과를 하나의 그래프로 묶어서 비교했다. 상세한 결과 비교는 Fig. 11에 나타냈다. 파란색 실선은 잔류응력과 섬유 배향을 모두 고려한 경우이고 빨간색 점선은 섬유 배향만 고려한 경우이다. 마지막으로 검정색 점선은 압축 성형 해석 결과를 모두 고려하지 않은 경우이다.
잔류응력을 고려하지 않고 섬유 배향 만 고려한 FRF 결과와 잔류응력과 섬유 배향을 모두 고려하지 않은 FRF 결과와 비교하면 1차나 2차 mode 수준에서 비슷한 경향을 보였지만, 고차 mode로 갈수록 mode의 위치나 응답의 크기가 다름을 확인했다. 하지만, 잔류응력과 섬유 배향을 모두 고려한 경우 저차 mode까지 상이한 결과를 얻을 수 있었다.
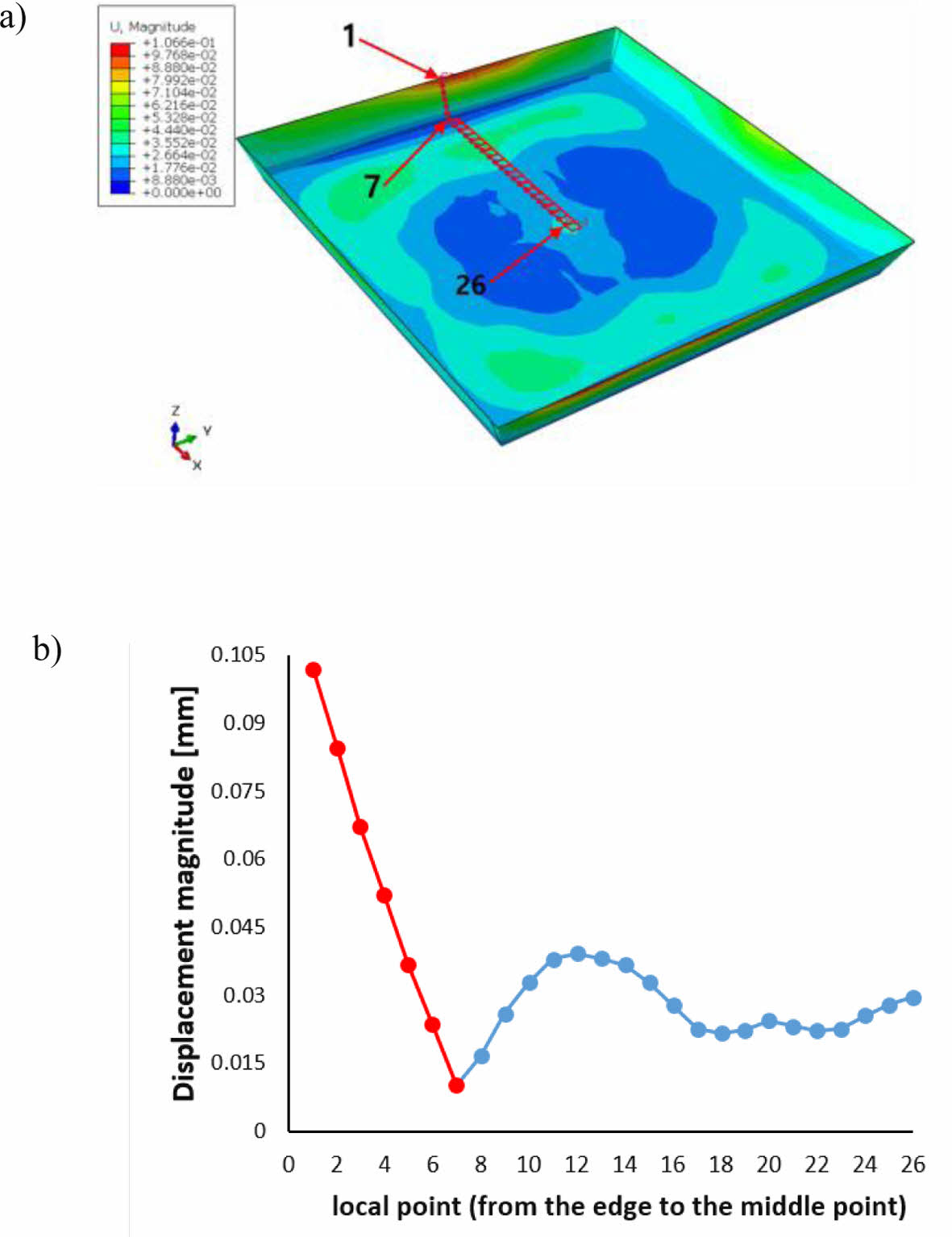
고온 고압 환경에서 이뤄지는 복합재료 압축 성형 과정 중에 공간상의 섬유 배향 분포가 달라지고 압축 성형 이후 필연적으로 잔류응력이 잔존하게 된다. 이 잔류응력은 구조물에 warpage와 shrinkage를 일으켜 구조물의 변형을 일으키는 것으로 알려져 있다[15,16]. 본 연구에서도 압축 성형 해석 이후 Moldflow에서 6개의 잔류응력 성분 값들을 획득할 수 있었으며 잔류응력에 의한 변형이 관측되었다. 잔류응력에 의한 구조물 변형을 가시적으로 나타내기 위해 Fig. 10a)에 크기에 대한 변위장을 넣었으며 Fig. 10b)에는 구조물 표면에 따른 변위값 선도를 그렸다. 하우징 옆면을 따라 1번부터 6번 노드까지 있으며 하우징 밑 면을 따라 8번부터 26번 노드까지 있다. 7번 노드는 옆 면과 밑 면의 모서리 점을 나타낸다. Fig. 10b)와 같이 위치에 따른 변위 크기 차이가 존재하기 때문에 잔류응력에 의한 구조물의 변형을 무시 할 수 없다는 것을 확인 할 수 있다. 따라서, 잔류응력에 의한 구조물의 변형은 복합재 구조물의 고유 주파수를 변화하게 하는 요인으로 작용하여 FRF의 전체적인 경향이 잔류응력이 없는 FRF 경우와 달라지게 된다. 따라서, 압축 성형 해석 결과인 섬유 배향과 잔류응력을 복합재료의 구조 해석에 모두 반영해야 엄밀한 구조 해석 결과를 얻을 수 있다고 판단된다.

본 연구는 미소 구조물 단위에서 기지 물성의 확률적 분포를 고려하고 성형 해석과 연계하여 멀티스케일 구조해석을 진행했다. 특히, 복합재 배터리 하우징에 포함되는 복합재 층을 특성마다 구분하여 연구를 진행했다. 첫째로, 미소 구조물의 형상을 고려하여 복합재 층마다 다른 미소 구조물을 생성했으며 기지 영역에 대해 랜덤 필드 모델링 기법 중 하나인 KLE를 이용하여 기지 공간에 대한 물성 분포를 획득했다. 이를 토대로 확률적 기지 물성 분포가 고려된 RVE에서 유효 물성을 획득할 수 있었다. 또한, 복합재 층마다 다른 압축 성형을 고려하여 각 복합재 층에서 섬유 배향과 잔류응력을 구했다. 직물층의 경우 Aniform을 이용하여 압축 성형중 하나인 드레이핑 공정 해석을 했으며 난연층의 경우 Moldflow를 이용하여 압축성형 공정 해석을 했다. 마지막으로 성형 해석 결과와 균질화 된 물성값을 모두 ABAQUS에 포함하여 배터리 하우징 하단부에 대해 멀티스케일 구조 해석을 진행했다. 해석 결과를 바탕으로 성형 해석 결과인 잔류응력, 섬유 배향의 유무에 따라 고유 진동수와 FRF의 경향성이 크게 차이가 있다는 것을 확인했다. 향후 연구로 제시한 연구 결과의 실험적 검증을 위한 실험을 계획하고 있다. 또한, 본 연구에서 제시한 방법을 확장 및 응용하여 압축 성형 공정을 통해 생산된 복합재 부품에 대한 구조 내구도를 엄밀하게 평가할 수 있을 것이라 기대한다.

이 연구는 산업통상자원부의 산업기술혁신사업(No.20013598)과 서울대학교 공학연구원의 지원을 받아 수행된 연구 결과입니다.