- Study on Mode I Fracture Toughness and FEM analysis of Carbon/Epoxy Laminates Using Acoustic Emission Signal
Hyun-jun Cho*, Min-Hyeok Jeon*, Hae-Ri No*, In-Gul Kim*†
Department of Aerospace Eng., Chungnam National University
- 음향 방출 신호를 이용한 탄소/에폭시 적층판의 Mode I 파괴 인성 및 유한요소해석에 관한 연구
조현준*· 전민혁*· 노해리*· 김인걸*†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Composite materials have been used in aerospace industry and many applications because of many advantages such as specific strength and stiffness and corrosion resistance etc. However, it is vulnerable to impacts, these impact lead to formation of cracks in composite laminate and failure of structures. In this paper, we analyzed Mode I fracture toughness of Carbon/Epoxy laminates using acoustic emission signal. DCB test was carried out to analyze Mode I failure characterization of Carbon/Epoxy laminates, and AE sensor was attached to measure AE signal induced by failure of specimen. Fracture toughness was calculated using cumulative AE energy and measured crack length using camera. The calculated fracture toughness was applied in FE model and the result of FE analysis compared with DCB test results. The results show good agreement with between FEM and DCB test results.
복합재료는 비강도, 비강성 및 내부식성 등이 우수하여 항공우주산업뿐만 아니라 다양한 산업에서 사용되고 있다. 그러나 복합재료는 충격에 취약하고 이러한 충격은 복합 재료 내부의 균열 형성과 균열 성장으로 이어져 구조 파단의 원인이 된다. 본 논문에서는 음향 방출 신호 및 유한요소해석(Finite element analysis, FEA)을 이용하여 복합재 적층판의 Mode I 파괴 모드의 특성을 분석하였다. DCB 시험은 탄소/에폭시 적층판의 Mode I 파괴 특성을 분석하기 위하여 수행되었고 시편의 파괴에 의해서 발생되는 탄성파를 측정하기 위하여 시편에 음향 방출 센서를 부착하였다. 누적 음향 방출 에너지와 균열 선단 위치의 관계를 이용하여 시편의 파괴 인성(Fracture toughness, GI)을 계산하였다. 계산된 파괴 인성 값을 유한요소모델에 적용하여 해석을 수행하였고 하중-변위 곡선 및 균열 길이-변위 곡선을 통하여 DCB 시험 결과와 비교/분석하였다. 유한요소해석 및 DCB 시험의 결과가 잘 일치함을 보였다
Keywords: 음향 방출 센서(Acoustic emission sensor), 누적 음향 방충 에너지(Cumulative acoustic emission energy), 균열 길이(Crack length), 파괴 인성(Fracture toughness), 유한요소해석(Finite element analysis)
복합재료는 비강도, 비강성 및 내부식성 등이 우수하여 항공우주산업뿐만 아니라 다양한 산업에서 사용되고 있다. 그러나 복합재료는 충격에 취약하고 이러한 충격은 복합 재료 내부의 균열 형성과 균열성장으로 이어져 구조 파단의 원인이 된다. 이러한 구조 파단 주요모드는 Mode I 파손이다. Mode I 균열 성장을 표현하기 위한 주요 인자로는 균열 길이가 있으며 이를 정확히 측정할 방법이 필요하다. 카메라를 활용하여 시편 측면에서의 균열 길이를 측정하는 것이 가장 일반적이나, 시편의 폭 방향으로 균열 선단의 형상이 어떻게 전파되는지 측정이 어렵다. 따라서 본 논문에서는 시편에 부착이 가능하며 시험 중 시편의 균열 성장으로 발생하는 탄성파를 측정할 수 있는 음향 방출 센서를 활용하였다.
음향 방출 센서는 복합재료의 파괴 인성에 관한 연구를 수행하는데 있어서 수십 년 동안 사용되고 있는 가장 효과적인 비파괴센서이다. 구조물 파단 시 발생하는 음향 방출 신호는 Signal-based data 및 Parametric-based data를 통하여 분석할 수 있다. 본 논문에서는 Parametric-based data의 한 종류인 누적 음향 방출 에너지(Cumulative acoustic emission energy)를 활용하여 균열 선단의 위치를 예측하였다. Oskouei와 Ahamadi[1]는 Glass/Polyester의 Mode I 시험을 수행하였고 음향 방출 신호 및 Power spectrum density (PSD)를 이용하여 파괴 모드에 따른 주파수 영역을 식별하였다. Yousefi외 저자[2]는 일방향 프레프레그를 사용하여 제작된 [0o] 시편 및 직물 형태의 섬유를 사용하여 제작된 [0-90o] 시편에 대하여 누적 음향 방출 에너지와 균열 선단 사이에 멱함수 관계를 가진다고 보고하였다.
많은 연구자들[4-8]은 유한요소해석과 응집 영역 모델(Cohesive zone model, CZM)을 활용한 연구를 수행해왔으며, 응집 영역 모델은 복합재료의 균열 성장을 모사하는데 있어서 가장 적합한 방법으로 사용되어왔다[8]. Zhao 외 저자[8]는 응집 영역 모델에서 초기 계면 강성(Initial interface stiffness, K0), 계면 강도(Interface strength, s), 응집 요소의 수 및 Viscosity coefficient(m)에 관한 매개변수 연구를 수행하였다. 결과적으로 Viscosity coefficient의 값이 충분히 작다면 초기 계면 강성이 균열 성장 모사에 끼치는 영향은 무시될 수 있다고 보고하였다. 그리고 유한요소모델에서 균열 길이에 따라 변화하는 파괴 인성을 유한요소모델에 대입할 경우, 정확한 해석 결과로 이어짐을 밝혔다. 0o/5o, 45o/-45o and 90o/90o 시편에 대하여 균열 길이에 따라 변화하는 파괴 인성의 유한요소모델에 대입하여 시험 결과와 비교하였으며 매우 유사한 경향을 보였다. Gong 외 저자[5]는 Fiber bridging 효과를 가지는 Mode I을 모사하기 위하여 물리법칙에 기반한 새로운 응집 영역 모델을 제안하였고 새로운 응집 영역 모델을 이용하여 계면 강도의 민감도를 조사하였다. 수행된 연구를 통하여 계면 강도는 유한요소해석에서 미치는 영향이 적으며, 새롭게 제시된 응집 영역 모델을 이용하여 실험 결과와 유사한 결과를 제시하였다.
본 논문에서는 유한요소해석과 음향 방출 센서를 통하여 다양한 계면 각도를 가지는 Carbon/Epoxy 적층판에 대한 파괴 인성 특성을 분석하였다. 앞서 언급된 유한요소해석을 통한 연구에서 균열 길이에 따라 변화하는 파괴 인성의 대입을 위해서는 R-곡선에서 파괴 인성이 수렴하는 구간을 필요로 한다. 하지만 본 연구에서 수행된 시험에서는 R-곡선에서 파괴 인성이 수렴하는 구간을 보이지 않았기 때문에 누적 음향 방출 에너지와 카메라를 통하여 얻은 광학상의 균열 선단 위치와의 관계를 통하여 균열 선단 위치에 따른 파괴 인성 값을 세분화하여 계산하였다. 이를 유한요소모델에 적용하여 시험 결과와의 비교/분석하였다.
2.1 재료 및 시편 제작
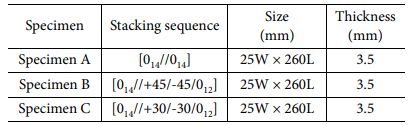
본 논문에서는 SK 케미칼㈜의 USN 125 A(탄소/에폭시 일방향 프리프레그)를 사용하여 시편을 제작하였다. 모든 시편은 Hand lay-up으로 적층되었고 시편의 중앙 면에는 두께 0.013 mm의 폴리이미드 필름(인공 결함)을 삽입하여 오토클레이브를 사용하여 성형하였다. Table 1은 시편의 사양이며, '//'은 인공 결함이 삽입된 층을 의미한다. 계면 사이의 상대적인 섬유 각도가 파괴 인성에 미치는 영향을 확인하기 위하여 계면의 각도가 0o, 30o 및 45o가 되도록 시편을 제작하였다. 균열 길이를 확인하기 위하여 시편의 측면부에 노란색 물감을 이용하여 코팅하였고 1 mm 간격으로 눈금을 표시하였다.
2.2 시험 방법
2.2.1 시험 절차
DCB 시험은 ASTM 5528에 따라 수행되었다. Fig. 1은 DCB 시험의 개략도이다. 시험은 INSTRON 5900R을 사용하여 수행되었고 cross-head의 변위 속도가 1 mm/min인 변위 제어 조건에서 수행되었으며, 하중 및 변위 데이터는 10 Hz의 속도로 기록되었다. 인공 결함이 삽입된 시편에 하중을 부과하여 초기 균열(a0)을 55 mm 진전시킨 후 하중을 제거하였다. 이후 다시 하중을 부과하였고 균열 선단 위치가 100 mm지점에서 시험이 종료되었다. 균열 선단의 위치를 기록하기 위하여 시편의 측면부에 캠코더를 설치하였고, 하중 작용점으로부터 120 mm 떨어진 지점에 음향 방출 센서를 DCB 시편 윗면에 양면테이프를 사용하여 부착하였다.
2.2.2 음향 방출 센서
재료가 파괴되면서 발생하는 탄성파를 측정하기 위하여 Physical Acoustic Corporation에서 제작된 음향 방출 센서(UT1000)를 사용하였다. 음향 방출 신호를 기록하기 위하여 최대 샘플링 속도 20 MHz와 최대 전압 범위 ±5 V를 가지는 PXI-5102 디지털 오실로스코프를 사용하였다. 재료가 파괴되면서 발생하는 탄성파는 매우 작은 신호이기 때문에 신호 증폭을 위하여 40 dB gain을 가지는 프리앰프를 통하여 신호를 증폭하였다. 적용된 샘플링 속도는 2 MHz이고 샘플 수는 200k(0.1초)이다.

|
Fig. 1 Schematic of DCB Test |
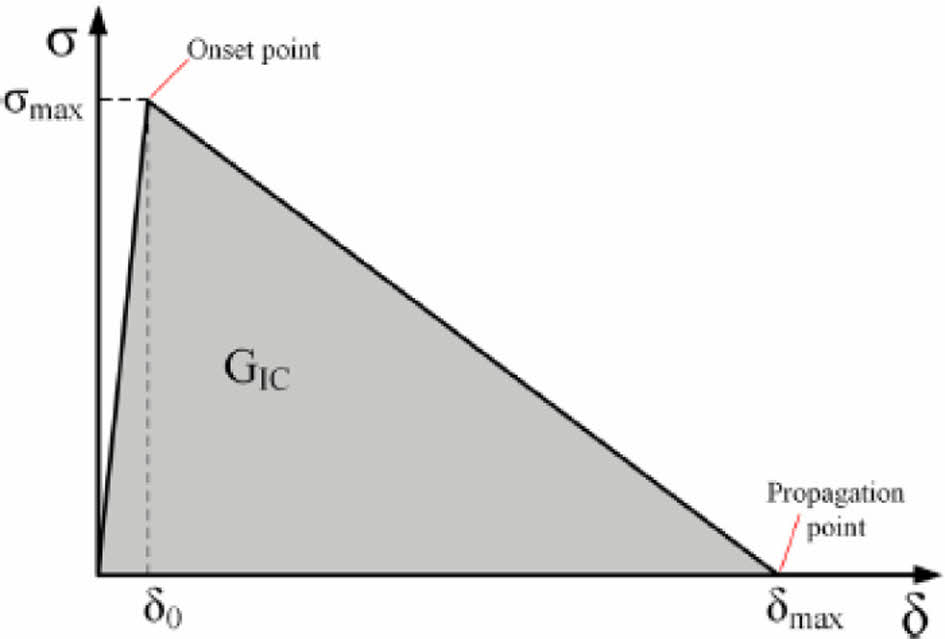
응집 영역 모델은 복합재 적층판의 Mode I 균열 성장을 모사하는 방법 중에 가장 효과적이라고 알려져 있다[8]. Fig. 2는 일반적인 bi-linear 응집 영역 요소이다. 응집 영역 요소는 파괴 인성(G0), 초기 계면 강성(K0) 및 계면 강도(σ0)로 구성된다. 하중이 증가함에 따라 응집 영역 요소가 받는 응력은 초기 계면 강성(K0)을 따라 증가하며 요소의 파괴는 발생하지 않는다. 이후, 응집 영역 요소가 받는 응력이 계면 강도(σ0)에 이르면 응집 영역 요소가 손상되기 시작하고 계면 강성은 감소한다. 최종적으로 응집 영역 요소의 손상과정에서 소실된 에너지가 파괴 인성 값(GIC)과 같아지는 시점에서 응집 영역 요소의 파괴가 발생한다.
복합재료의 경우, Bi-liner 응집 영역 요소은 DCB 시험에서 보이는 다양한 물리적인 거동으로 인하여 DCB 시험 모사에 있어 제한적이다. 따라서, 많은 연구자는 변형된 응집 영역 요소(Tri-liner, Quad-liner 및 Multi-liner)를 제안해 왔고 파괴 인성 값을 균열 성장 길이에 따른 함수로 표현하였다. 본 논문에서는 Bi-linear 응집 영역 요소 및 Saeedifar[2]에 의해서 제안된 누적 음향 방출 에너지 및 광학 장비로 측정된 균열 길이의 관계를 이용하여 유한요소해석을 수행하였다.
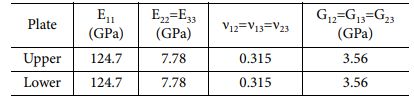
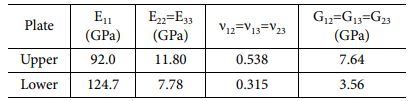
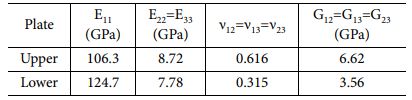
ABAQUS를 이용하여 DCB 시험을 모사하였고, Fig. 3은 2D 요소(CPE4)를 활용한 유한요소모델이다. 응집 영역 요소의 길이와 두께는 각각 0.1 mm와 0.01 mm이며 Table 2-4는 각 시편을 모사하기 위하여 사용된 시편의 Upper plate와 Lower plate의 재료 물성 값이다. 복합재는 층별 모델링하지 않고 단일 적층판으로 가정하여 Engineering constant 물성을 적용하였다. Specimen B와 specimen C의 경우, 굽힘 거동을 층별 모델링과 유사하게 구현하게 하기 위하여 식 (1)을 사용하여 적층판의 굴곡 강성도 D11 값이 층별 모델링과 같은 값을 가지도록 등가의 E11을 계산하여 적용하였다. Table 3
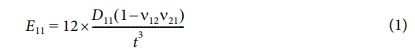
여기서 n12, n21는 포아송 비, t는 시편의 절반 두께이다. Table 5는 응집 영역 요소의 입력 매개변수로 GIC 값은 균열 길이에 따라 변화하는 값을 적용하였기 때문에 ‘-’로 입력하였다. 이에 대한 결과는 결과 및 토론에서 제시하였다.
|
Fig. 2 Bi-linear constitutive equation of cohesive element[2] |

|
Fig. 3 FEM model for DCB specimen |
4.1 DCB 시험 결과
4.1.1 하중, 균열 길이 및 누적 음향 방출 에너지-변위 곡선
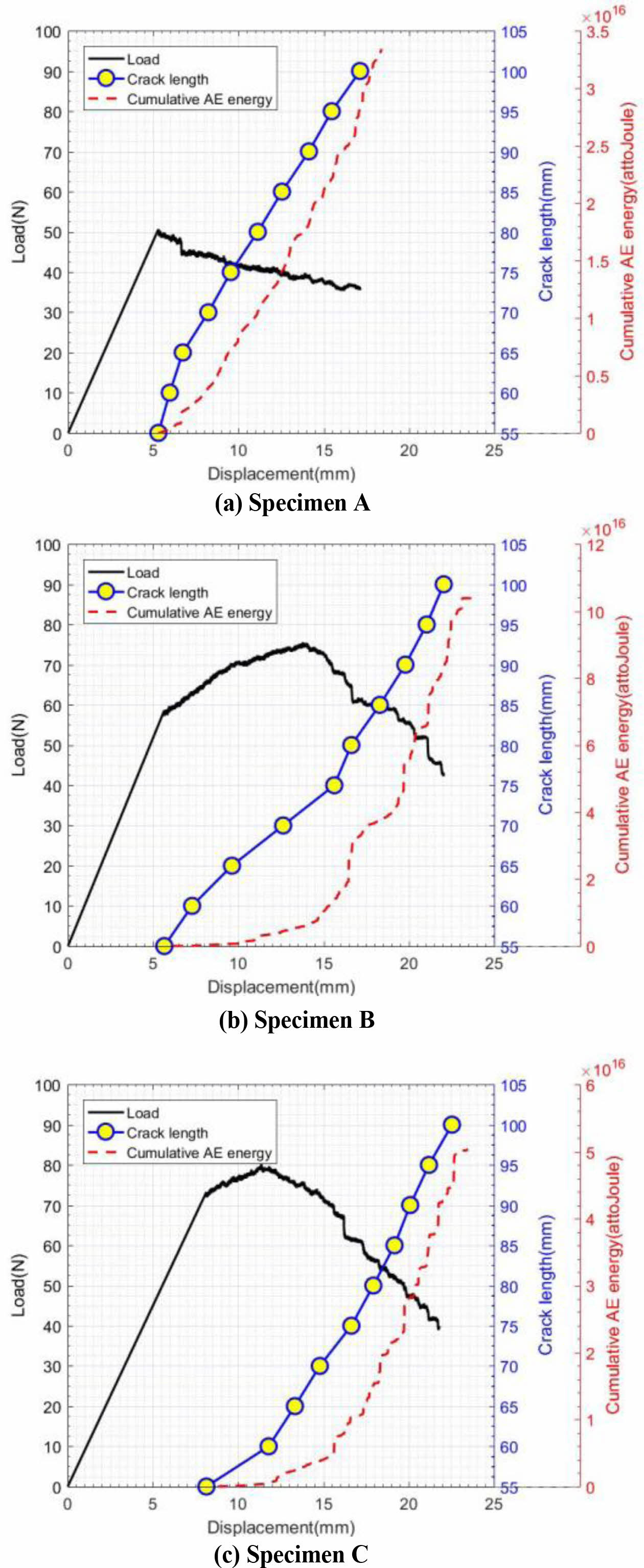
Fig. 4는 Specimen A, B 및 C에 대하여 각각의 하중-변위, 균열 길이-변위 및 누적 음향 방출 에너지-변위 곡선 결과를 보여준다. 모든 균열 길이는 하중을 부여하는 지점을 기준으로 55 mm부터 100 mm까지 5 mm 간격으로 측정되었다. Specimen A의 경우, 균열 개시 이후 하중이 점진적으로 감소하는 경향을 보였다. 반대로 specimen B와 specimen C의 경우 균열 개시 이후 하중이 계속 증가하다가 특정 변위 이후 하중이 점진적으로 감소하는 경향을 보였다. 이는 균열 개시 이후 섬유 가교(Fiber bridging) 현상으로 인하여 균열 진전 속도가 지연되고 하중이 증가하다 섬유 가교의 섬유가 시편이 떨어져나가면서 하중이 점진적으로 감소하고 균열 진전 속도가 빨리지는 경향을 보였다.
4.1.2 누적 음향 방출 에너지 및 균열 길이의 상관 관계
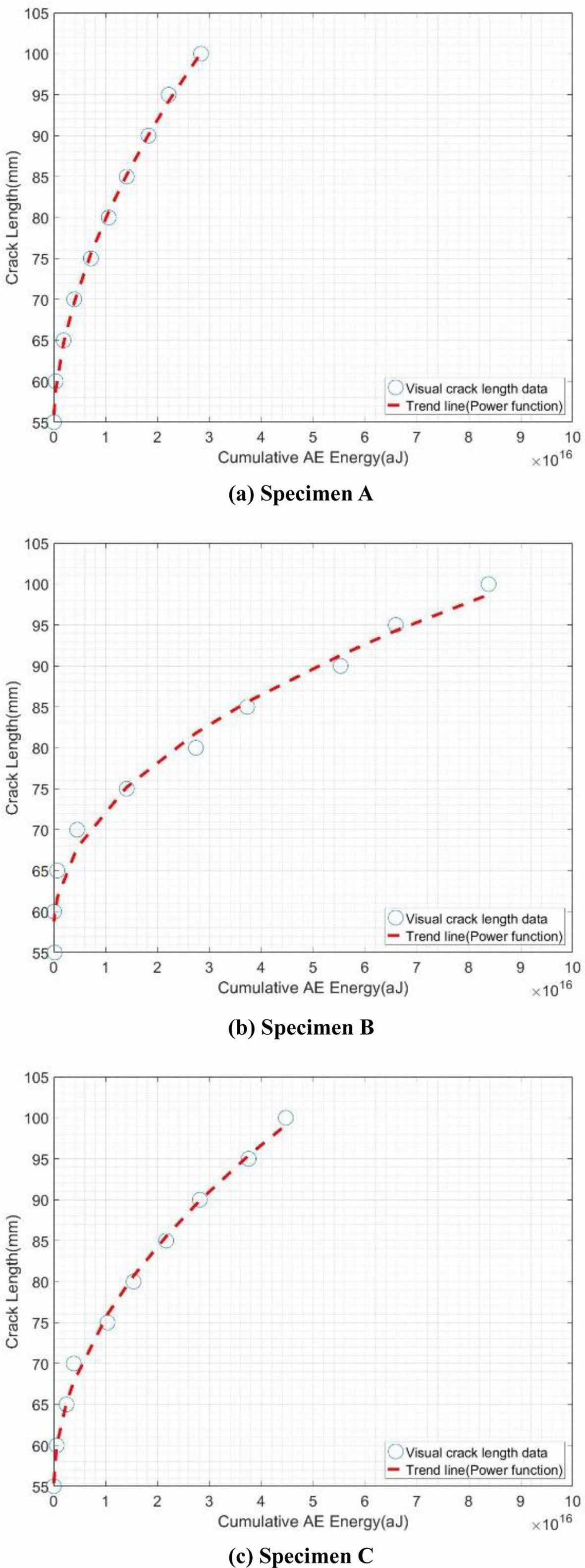
Saeedifar[2]는 누적 음향 방출 에너지와 균열 길이 사이의 관계를 식 (2)와 같이 멱함수 형태로 제안하였다.

여기서 α는 균열 길이, CE는 누적 음향 방출 에너지, α, β 및 γ는 Fig. 5와 같이 곡선 피팅에 의해서 얻어진 계수들이다.
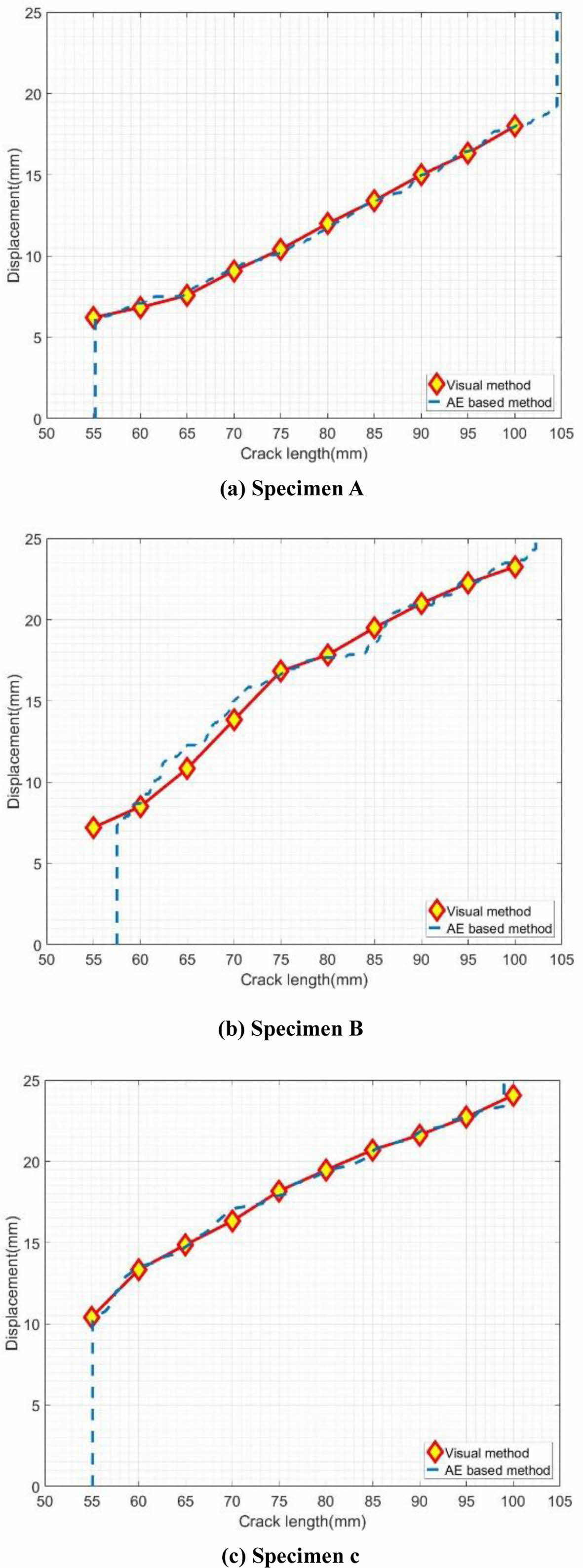
Fig. 6은 식 (2) 및 누적 음향 방출 에너지를 이용하여 계산된 균열 길이 및 광학으로 측정된 균열 길이를 비교한 결과이다. Specimen A와 specimen C는 계산된 균열 길이 및 측정된 균열 사이에 잘 일치하는 경향을 보였다. 그러나 specimen B는 다른 시편에 비하여 상대적으로 높은 오차를 보였다. 이는 45o 섬유 방향 존재로 인한 전단 성분에 의하여 불안정한 균열 성장에 기인한 것으로 보인다[6].
4.2 유한요소해석 결과
4.2.1 누적 음향 방출 에너지를 이용한 파괴인성 계산
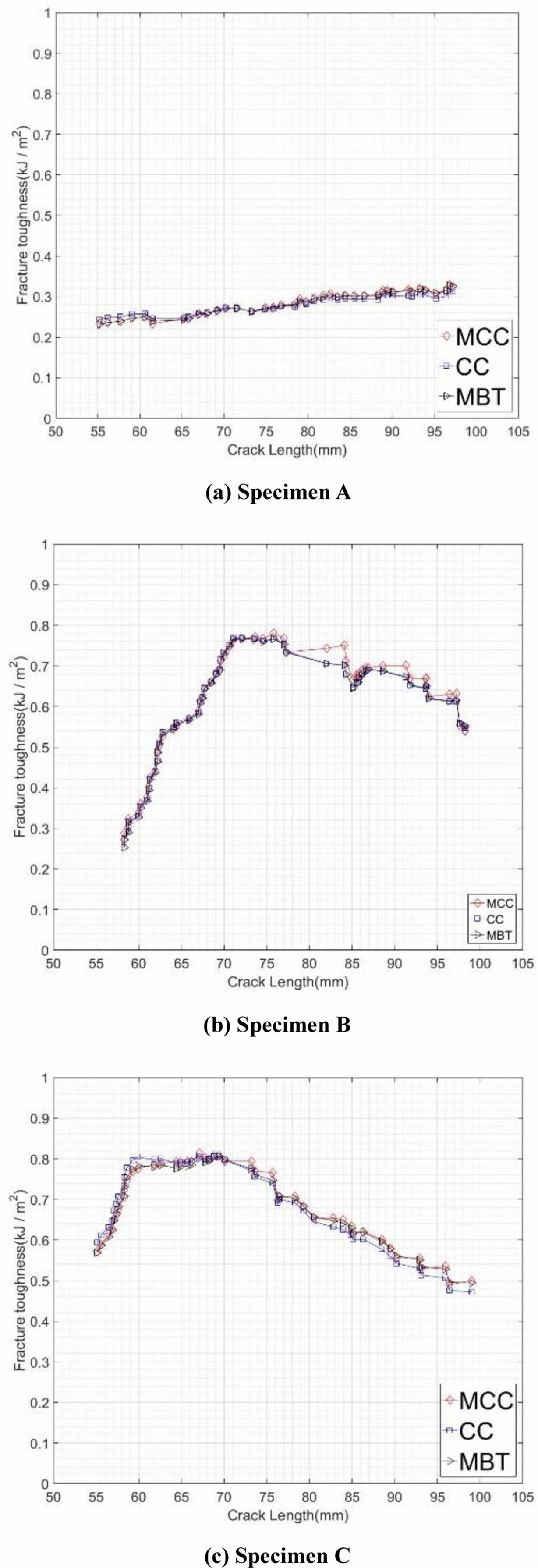
일정한 파괴 인성 값과 Bi-linear 응집 영역 요소를 사용하는 것은 Mode I 균열 성장을 모사하는데 가장 간단한 방법이다. 그러나 이러한 방법은 복합재료의 정확한 균열 성장을 모사하기에는 한계점을 가지고 있다. 본 연구에서 DCB 시험을 통하여 얻은 R-곡선에서 파괴 인성이 수렴하는 구간을 보이지 않았기 때문에 균열 길이에 따른 파괴 인성 값을 적용하였다. 균열 길이에 따른 파괴 인성 값을 적용하기 위하여 누적 음향 방출 에너지 및 식 (2)를 통하여 계산된 균열 길이 및 시험에서 얻은 하중 및 변위를 이용하여 파괴 인성을 계산하였다. Fig. 7은 ASTM D 5528에서 제시된 Modified Compliance Calibration (MCC), Compliance Calibration (CC) 및 Modified Beam Theory (MBT)를 이용하여 계산된 파괴 인성 값이다[13]. Specimen A는 상대적으로 안정적인 R-곡선을 보였으나, 균열 개시(α0 = 55 mm) 및 시험 끝 지점(α= 100 mm)에서의 파괴 인성의 값이 차이가 나는 것을 확인하였다.
Specimen B와 specimen C와 같은 비대칭 적층판의 경우, Angle ply층으로 균열이 전이되는 현상이 발생하고 이 현상은 가교 현상의 원인으로 파괴 인성 증가로 이어진다. 이로 인하여 specimen B와 specimen C는 specimen A에 비하여 높은 파괴 인성 값을 보였으며, 유사한 최대 파괴 인성 값을 보였다. 하지만 specimen B가 specimen C보다 낮은 초기 파괴 인성 값을 보였으며, 반대로 균열이 진전될수록 specimen B는 specimen C에 비하여 상대적으로 높은 파괴 인성 값을 보였다.
4.2.2 유한요소해석을 이용한 하중-변위 및 균열 길이-변위 예측
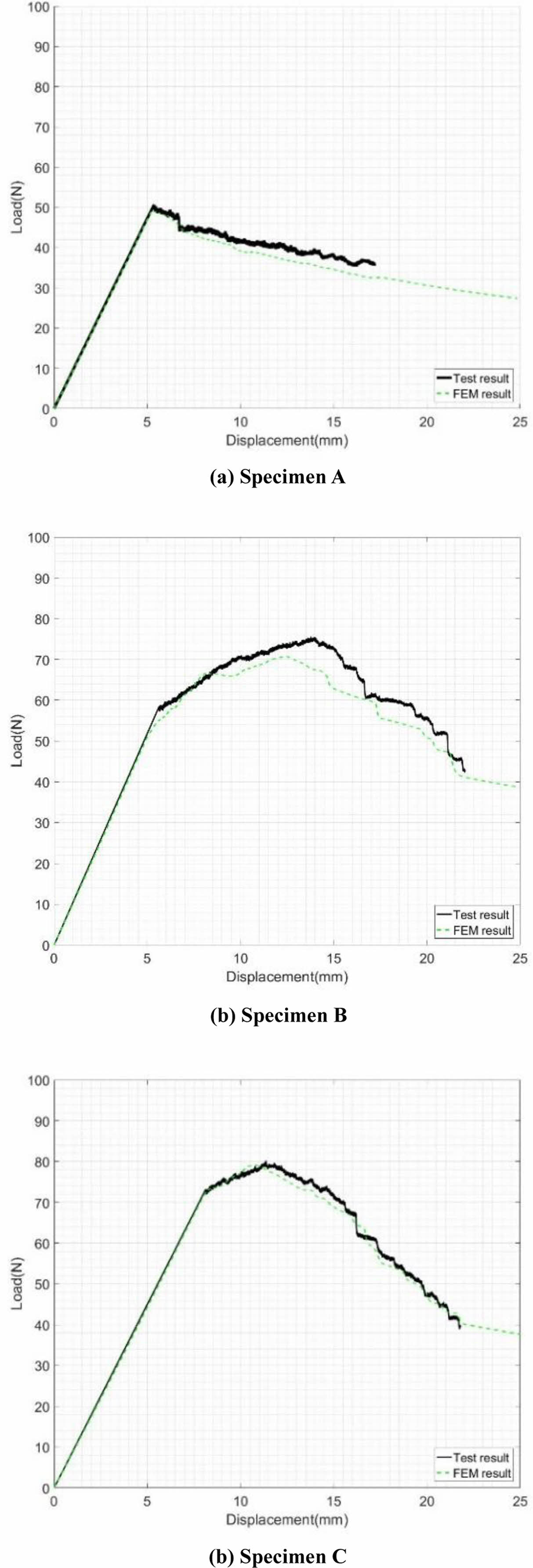
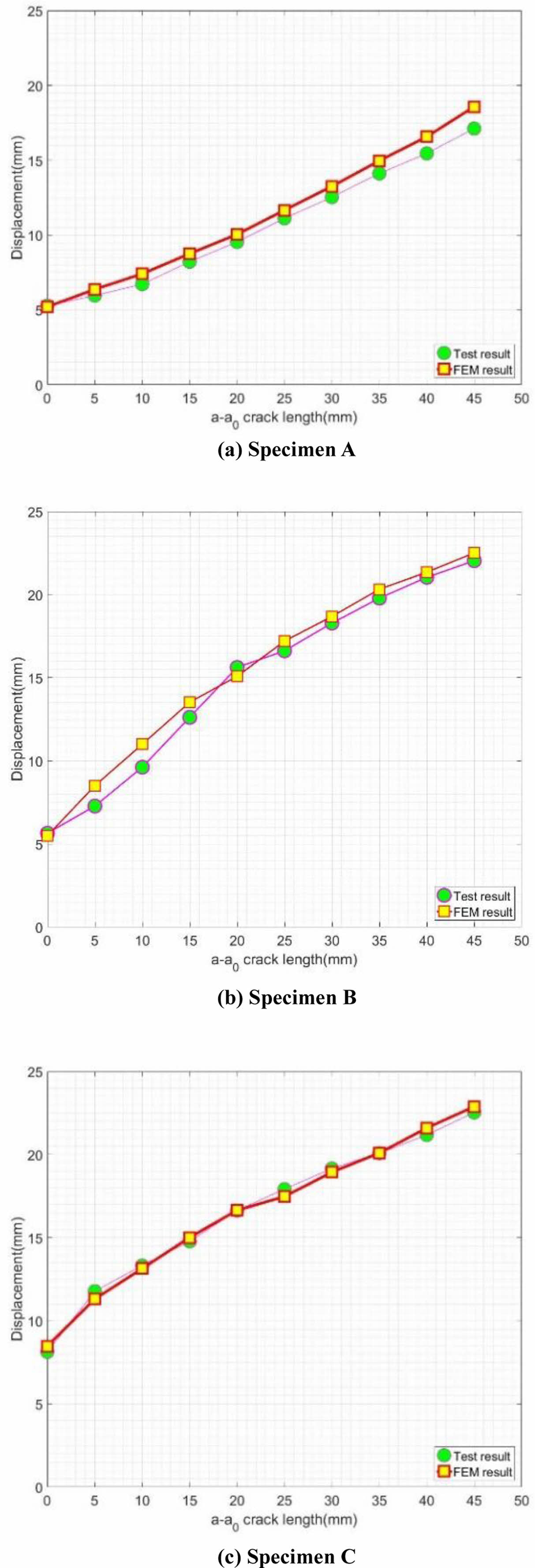
Fig. 8과 9는 유한요소해석 및 DCB 시험의 하중-변위 곡선 및 변위-균열 길이를 비교한 그래프이다. 모든 시편에서 유한요소해석 및 시험 결과 사이에 유사한 경향을 보였다. 하지만 specimen B는 다른 시편에 비하여 시험 및 유한요소해석 결과 사이의 오차가 크게 나타났다. 앞선 4.1.2절에서 언급된 것처럼 전단 성분에 의한 불안정한 균열 성장에 기인한다.
|
Fig. 4 Load, crack, and cumulative AE energy-displacement curve |
|
Fig. 5 Relation between cumulative AE energy and visible crack length |
|
Fig. 6 Predicted crack length versus measured crack length |
|
Fig. 7 R-curve using cumulative AE energy |
|
Fig. 8 Comparison of load-displacement curve |
|
Fig. 9 Comparison of crack length-displacement curve |
본 논문에서는 음향 방출 신호 및 유한요소해석을 통하여 다양한 적층각을 가지는 탄소/에폭시 복합재 적층판의 파괴 인성에 관한 연구를 수행하였다. 복합재 적층판의 파괴 인성을 평가하기 위하여 DCB 시험을 수행하였으며, 시편의 파단으로 인하여 발생하는 탄성파를 측정하기 위하여 음향 방출 센서를 시편의 윗면에 부착하였다. 측정된 음향 방출 신호 및 광학 장비로 측정된 균열 길이의 상관관계를 멱함수 형태로 가정하였고 음향 방출 신호를 이용하여 균열 길이를 예측하고 이를 광학 장비로 측정된 균열 길이와 비교/분석하였다. 모든 시편에서 예측된 균열 길이와 측정된 균열 길이가 잘 일치하는 경향을 보였으나, 45o 계면을 가지는 시편에서 다른 시편에 비하여 상대적으로 높은 오차를 보였다. 이는 섬유 방향으로 인한 전단 성분에 의한 모재의 불안정한 균열 성장에 기인한 것으로 보인다.
DCB 시험을 모사하기 위하여 Mode I 균열 성장을 모사하는 방법 중에 가장 효과적이라고 알려진 응집 영역 모델을 사용하였다. 균열 길이에 따라 변하는 파괴 인성 값을 적용하기 위하여 음향 방출 신호를 통하여 계산된 균열 길이를 이용하여 파괴 인성을 계산하고 이를 유한요소모델에 적용하여 해석을 수행하였다. 유한요소해석을 통하여 얻은 하중-변위 곡선 및 균열 길이-변위 곡선을 시험 결과와 비교/분석 하였으며 모든 시편에서 해석 및 시험 결과가 잘 일치하는 경향을 보였다.
향후, 계면의 상대적 섬유 각도는 동일하나 시편 길이 방향의 섬유 각도가 다른 시편에 대하여 DCB시험을 수행할 예정이며 길이 방향의 섬유 각도 차이의 의한 파괴 거동을 분석할 예정이다. Specimen B는 다른 시편에 비하여 상대적으로 높은 오차를 보였다. 이는 계면에서 섬유의 상대적 각도가 커질수록 계면층 내의 파손으로 인하여 균열 길이와는 무관한 음향방출신호의 발생때문이라고 판단된다. 따라서 균열 길이와는 무관한 신호를 제거할 수 있는 방법에 관한 연구를 수행할 예정이다.
이 논문은 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(2020R1I1A3071845).
- 1. Oskouei, A.R., and Ahmadi, M., “Acoustic Emission Characterization of Mode I Delamination in Glass/Polyester Composites”, Journal of Composite Materials, Vol. 44, No. 7, 2010, pp. 793-807.
-

- 2. Yousefi, J., Mohamadi, R., Saeedifar, M., Ahmadi, M., and Hosseeini-Toudeshky, H., “Delamination Characterization in Composite Laminates Using Acoustic Emission Features, Micro Visualization and Finite Element Modeling”, Journal of Composite Material, Vol. 50, No. 22, 2016, pp. 3133-3145.
-

- 3. Barile, C., Casavola, G., Pappalettera, G., and Vimalathithan, P.K., “Damage Characterization in Composite Materials Using Acoustic Emission Signal-based and Parameter-based Data”, Composite Part B, Vol. 178, 2019, 107469.
-

- 4. Davila, C.G., Rose, C.A., and Camanho, P.P., “A Procedure for Superposing Linear Cohesive Laws to Represent Multiple Damage Mechanisms in The Fracture of Composites”, International Journal of Fracture, Vol. 158, 2009, pp. 211-223.
-

- 5. Gong, Y., Hou, Y., Zhao, L., Li, W., Zhang, J., and Hu, N., “A Modified Mode I Cohesive Model for Delamination Growth in DCB Laminates with the Effect of Fiber Bridging”, International Journal of Mechanical Sciences, Vol. 176, 2020, 105514.
-

- 6. Saeedifar, M., Najafabadi, M.A., Yousefi, J., Mohammadi, R., Toudeshky, H.H., and Minak, G., “Delamination Analysis in Composite Laminates by Means of Acoustic Emission and Bi-liner/Tri-liner Cohesive Zone Modeling,” Composite Structures, Vol. 161, 2017, pp. 505-512.
-

- 7. Shokrieh, M.M., Daneshjoo, Z., and Fakoor, M., “A Modified Model for Simulation of Model I Delamination Growth in Laminated Composite Materials”, Theoretical and Applied Fracture Mechanics, Vol. 82, 2016, pp. 107-116.
-

- 8. Zhao, L., Gong, Y., Zhang, J., Chen, Y., and Fei, B., “Simulation of Delamination Growth in Multidirectional Laminates under Mode I and Mixed Mode I/II Loadings Using Cohesive Elements”, Composite Structure, Vol. 116, 2014, pp. 509-522.
-

- 9. Arumugam, V., Sajith, S., and Stanley, A.J., “Acoustic Emission Characterization of Failure Modes in GFRP Laminates under Mode I Delamination”, Journal of Nondestructive Evaluation, Vol. 30, 2011, pp. 213-219.
-

- 10. Fotouhi, M., and Najafabadi, M.A., “Acoustic Emission-Based Study to Characterize the Initiation of Delamination in Composite Materials”, Journal of Thermoplastic Composite Materials, Vol. 29, No. 4, 2016, pp. 519-537.
-

- 11. Groot, de P.J., Wijnen, P.A.M., and Janssen, R.B.F., “Real-Time Frequency Determination of Acoustic Emission for Different Fracture Mechanisms in Carbon/Epoxy Composites”, Composite Science and Technology, Vol. 55, 1995, pp. 405-412.
-

- 12. Nikbakht, M., Toudeshky, H.H., and Minak, G., “Delamination Evaluation of Composite Laminates with Different Interface Fiber Orientations Using Acoustic Emission Features and Micro Visualization”, Composite Part B, Vol. 113, 2017, pp. 185-196.
-

- 13. ASTM D-5528-13, “Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composite”, ASTM International, West Conshohocken, PA, 2013.
-

 This Article
This Article
-
2022; 35(2): 61-68
Published on Apr 30, 2022
- 10.7234/composres.2022.35.2.061
- Received on Dec 6, 2021
- Revised on Feb 3, 2022
- Accepted on Mar 4, 2022
 Services
Services
Shared
 Correspondence to
Correspondence to
- In-Gul Kim
-
Department of Aerospace Eng., Chungnam National University
- E-mail: igkim@cnu.ac.kr






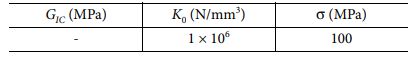
 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.