In this study, when the carbon fiber composite was manufactured, the correlation between the porosity and mechanical properties according to the number of glass fiber felts laminated together and the stacking sequence was confirmed. The carbon fiber composite was manufactured by stacking glass fiber felts, which are highly permeable materials, and using vacuum assisted resin transfer molding (VARTM). Porosity was measured by photographing the cross-section of the specimen with an optical microscope and then using porosity calculation code of MATLAB, and mechanical properties were measured for tensile strength, modulus by tensile test. Furthermore, Pearson correlation coefficient between porosity and mechanical properties was calculated to confirm the correlation between two variables. As a result, the number of glass fiber felt increased and the distance from the center of laminated composites increased, the porosity increasing were confirmed. In addition, tensile strength/modulus showed a weak positive correlation with porosity. Also, in order to confirm the effect of only porosity on tensile strength and modulus, mechanical properties calculated by CLPT (Classical Laminate Plate Theory) and experimental values were compared, and the difference in tensile strength showed a strong positive correlation with porosity and the difference in modulus showed a weak positive correlation with porosity

탄소섬유 복합재를 제작하였을 때, 함께 적층되는 유리섬유 부직포 개수 및 적층 순서에 따른 기공률과 기계적 물성 간의 상관관계를 확인하였다. 탄소섬유 복합재는 고 투과성 물질인 유리섬유 부직포를 함께 적층 하여 진공 수지 이송 성형 법(vacuum assisted resin transfer molding, VARTM)을 통해 제작하였다. 기공률은 시편의 단면을 광학현미경으로 촬영 후 MATLAB의 기공률 계산 코드를 통해 측정하였고, 기계적 물성은 인장시험을 통해 인장 강도 및 인장 강성, 굽힘 강도, 굽힘 강성을 측정하였다. 또한, 기공률과 기계적 물성 간의 상관관계를 확인하기 위해 두 변수간 피어슨 상관계수를 계산하였다. 결과적으로 유리섬유 부직포의 개수가 증가할수록, 적층 시 중심에서 멀어질수록 기공률이 증가하는 것을 확인할 수 있었다. 또한, 인장 강도 및 인장 강성은 기공률과 약한 양의 상관관계를 보였다. 또한, 인장 강도 및 강성에 기공률만이 미치는 영향을 확인하기 위해 고전 적층 판 이론으로 계산한 기계적 물성과 실험값을 비교하였으며, 인장 강도의 차이는 기공률에 강한 양의 상관관계를 인장 강성은 약한 양의 상관관계를 보였다.

Keywords: 탄소섬유 복합재료(Carbon fiber composite), 진공 수지 이송 성형 법(Vacuum Assisted Resin Transfer Molding, VARTM), 미세기공(Microscopic voids), 피어슨 상관계수(Pearson correlation coefficient), 고전 적층판 이론(Classical laminate plate theory)

진공 수지 이송 성형 법(vacuum assisted resin transfer molding, VARTM)은 탄소섬유 프리프레그를 사용하는 압축성형공정에 비해 고온, 고압 장비가 필요하지 않기 때문에 낮은 비용으로 탄소섬유 복합재료를 제작할 수 있는 장점이 있다[1]. 하지만 수지의 입출구간의 절대 압력차가 최대 1기압이라는 특성 때문에 수지 유동속도의 최댓값이 낮아 내부의 기공이 자주 발생하고 이를 해결하기 위해 유동속도 향상을 위해 플로우 미디어를 사용하거나 적층 시 유리섬유 부직포를 사용하여 유동속도를 높이려는 연구가 진행되고 있다. 이를 이용 시 유동속도가 높아지지만 유리섬유 부직포내에 육안으로 확인되지 않는 미세기공이 형성된다. 형성된 미세기공은 제작된 복합재가 설계된 복합재보다 낮은 기계적 물성을 갖게 하는 원인이 된다. 따라서 실제 복합재 제품 설계 시 기공률에 따른 기계적 물성 저하를 고려해야 한다. 본 연구에서는 유리섬유 부직포의 개수 및 적층 순서에 따른 복합재료의 기공률을 측정하고 그에 따른 인장 강도, 인장 강성을 확인하였다. 또한, 기공률과 기계적 물성 간의 상관관계를 피어슨 상관계수를 통해 정의하였고, 기계적 물성에 기공률 만의 영향을 확인하기 위해 실험값과 고전 적층 판 이론을 통해 계산된 이론 값의 차이와 기공률 간의 경향성을 확인하였다.

2.1 시편제작
2.1.1 재료
실험에는 탄소섬유 복합재료의 보강재로 사용할 탄소섬유(CF, carbon fiber twill woven fabric 3K 245gsm, Chomarat)와 고 투과성 재료로 사용할 유리섬유 부직포(GF, glass fiber surface mat 30gsm, 근영실업)를 선정하였다. 진공 수지 이송 성형법 진행 시 수지로는 에폭시 수지(KFR-120V, 근영실업)와 그에 맞는 경화제(KFH-163, 근영실업)를 경화비율 10:3의 중량비로 혼합하여 사용하였다.

2.1.2 적층법
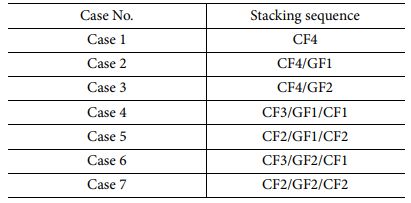
고 투과성 재료로 사용한 유리섬유 부직포의 개수 및 적층 방법에 따른 기공률 및 기계적 물성을 확인하기 위해 Table 1과 같은 7가지 케이스의 적층 순서로 탄소섬유 복합재료를 제작하였다. CF(carbon fiber fabric)와 GF(glass fiber felt)는 각각 탄소섬유 및 유리섬유 부직포를 나타내고 후술된 숫자로 적층된 섬유의 개수를 표현하였다. Case 1, 2, 3을 통해 유리섬유 부직포 개수에 따른 기공률 및 기계적 물성을 확인할 수 있었고 Case 2, 4, 5과 Case 3, 6, 7을 통해 유리섬유 부직포의 위치에 따른 기공률 및 기계적 물성을 확인할 수 있었다. Fig. 1

2.1.3 진공 수지 이송 성형법(vacuum assisted resin transfer molding, VARTM)
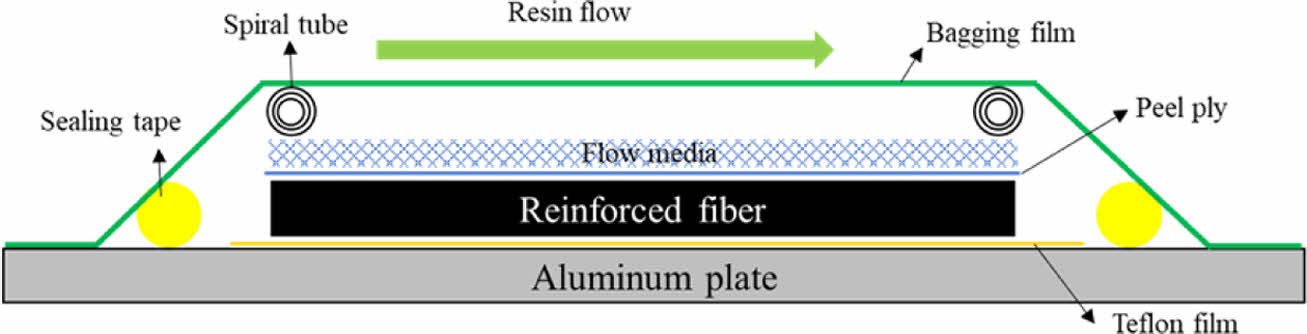
진공 수지 이송 성형법은 기존의 수지 이송 성형 법(RTM)에서 닫힌 몰드가 아닌 진공성형백을 사용하여 성형성을 높인 복합재료 제작 방법이다. Fig. 2와 같이 적층 시 몰드에 이형제를 도포하고 탄소섬유와 같은 보강재를 적층한다. 적층된 보강재 위에 수지가 경화된 후 진공백을 분리하기 쉽도록 필플라이를 적층하고 수지의 이송속도를 증가시키기 위해 플로우 미디어를 위치시킨다. 이후 실링 테이프를 사용하여 진공백으로 밀봉한 후, 스파이럴 튜브 및 우레탄 튜브를 사용하여 수지 입출구를 형성한다. 진공펌프로 진공을 형성한 후, 수지를 주입시키고 어느정도 수지가 함침되는 것을 확인후 입출구를 닫아 진공을 유지시킨다. 수지가 경화된 후 제작된 복합재료 이외의 것들을 제거하여 복합재를 완성시킨다[2].
Fig. 3, 4
2.2 기공률 측정
본 연구에서는 진공 수지 이송 성형법으로 제작한 복합재료 평판의 중심부를 워터젯 가공을 통하여 단면을 획득하고 이를 광학 현미경을 통해 촬영하였다[3]. 촬영된 이미지를 MATLAB의 이미지 프로세싱 및 기공률 계산 코드를 통해 10um 이상의 기공을 판별하였다. 판별한 기공률을 이용하여 기공률에 따른 기계적 물성을 분석하였다.

2.3 인장시험
기계적 물성을 측정하기 위해 인장시험을 ASTM D3039 참조하여 물성시험 진행하였으며[4], 인장시험의 경우 만능 인장 시험기(100kN, UNITECH-M)를 사용하였고, 길이 250 mm, 폭 15 mm의 시편을 테스트속도 2 mm/min로 진행하였다.

2.4 피어슨 상관계수(Pearson correlation coefficient)
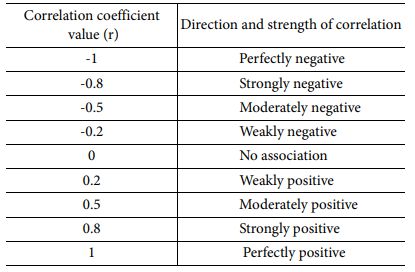
피어슨 상관계수(Pearson correlation coefficient)는 두 변수 간의 상관관계를 계량화한 수치이다[5]. 다음 수식에 의해 결정되며, Table 2와 같이 상관계수 값에 따라 상관관계를 결정할 수 있다. 상관계수가 1에 가까워질수록 두 변수가 강한 양의 상관관계를 갖게 되고 반대로 -1에 가까워질수록 두 변수가 강한 음의 상관관계를 갖게 된다. 상관계수가 0에 가까워질수록 두 변수 간의 상관관계는 없다.



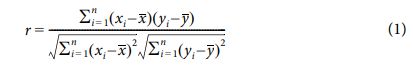
2.5 고전 적층판 이론
고전 적층판 이론(Classical Laminate Plate Theory, CLPT)은 복합 적층판의 문제를 간단하게 해석하기 위해정립된 이론으로 다음과 같은 세가지의 가정을 필요로 한다[6,7].
1) 복합 적층판이 인장이나 압축 및 전단만을 받는 경우에는 적층판의 두께 방향으로 변형률이 일정하다.
2) 각 플라이의 변형률과 전체 적층판의 변형률이 서로 같다.
3) 각 플라이마다 탄성계수가 다르기 때문에 플라이마다 다른 값의 응력을 갖는다.
평면응력상태의 경우에 k번째 플라이의 응력을 적층판 축으로 나타내면 식 (2)와 같이 표시할 수 있다.



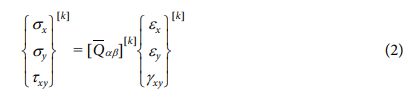
여기서 σ및 t는 적층판 축에 관하여 k번째 플라이의 응력 성분을 나타내며, ε및 γ는 적층판 축에 관하여 k번째 플라이의 변형률 성분을 나타낸다.

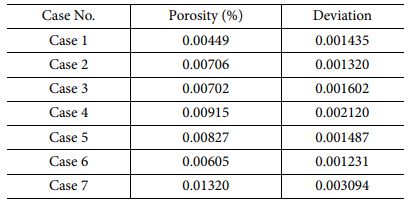
3.1 유리섬유 부직포 개수 및 적층 순서에 따른 기공률
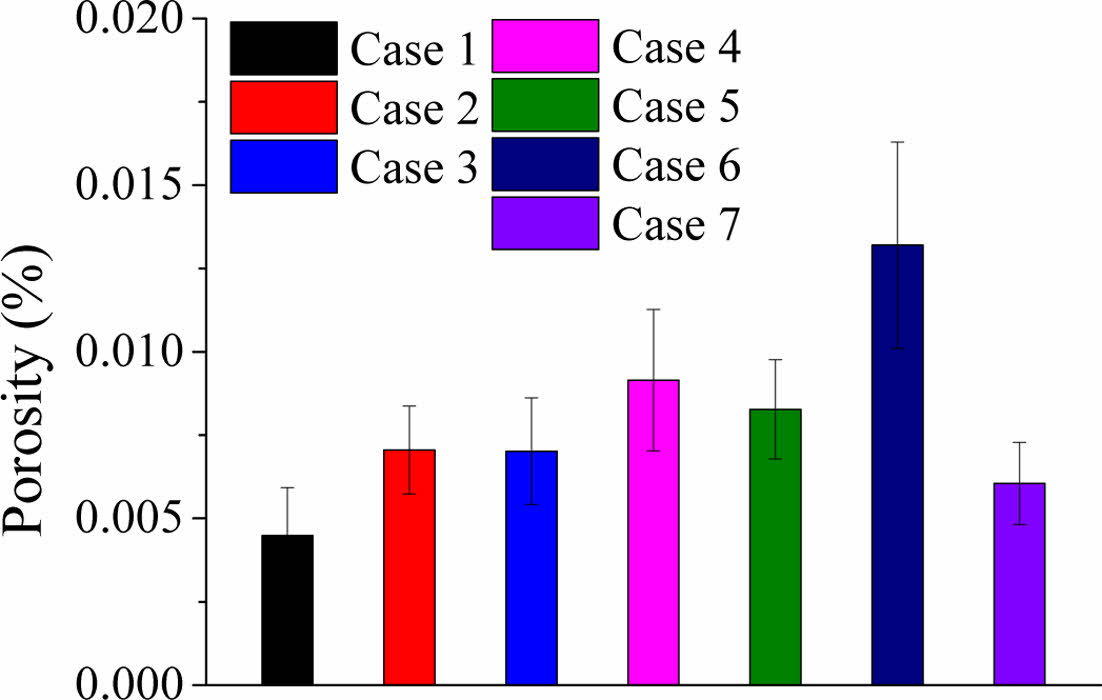
이미지 프로세싱을 통해 계산된 기공률은 Fig. 5 및 Table 3에 나타내었다. 기공률은 유리섬유 부직포의 개수가 늘어날수록, 적층 위치가 중심에서 멀어질수록 증가하는 경향을 보였다. 진공 수지 이송 성형법 공정 시 유리섬유 부직포의 개수가 늘어날수록 수지가 경화되는 동안 복합재 내부에서 빠져나가지 못하는 미세기공이 많아지고, 부직포의 위치가 중심에서 멀어질수록 진공백과 섬유사이로 지나가는 미세기공이 갇혀 기공률이 증가하는 결과가 나타났다.

3.2.1 기공률에 따른 인장 강성
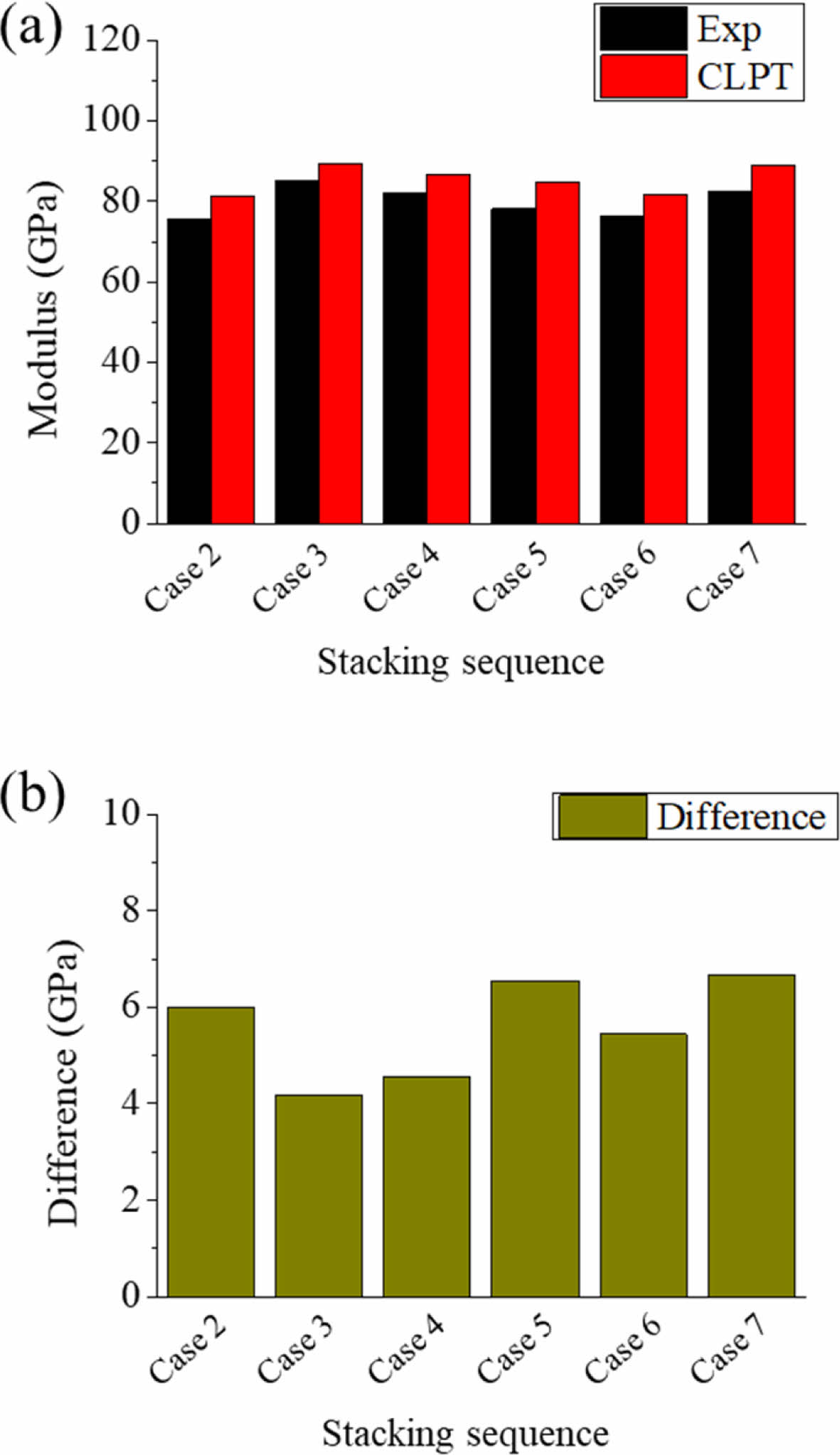
인장 시험을 통해 측정한 적층 순서(stacking sequence) 별 인장강도와 고전 적층 판 이론을 통해 계산된 인장 강성은 Fig. 6(a)에 나타나 있다. 이론값과 실험값의 차이는 Fig. 6(b)에 나타나 있으며, 기공률과 경향성이 낮았다. 또한 기공률과 이론값 및 실험값 차이의 피어슨 상관계수의 경우 0.11로 약한 양의 상관관계를 보였다. 기공률은 복합재료내에서 수지의 물성에 영향을 끼치게 된다. 하지만 유리섬유 부직포 및 수지의 강성보다 탄소섬유의 강성이 매우 강하기 때문에 기공률에 의해 저하되는 물성이 복합재의 물성에 매우 작은 영향을 미치게 된다.

3.2.2 기공률에 따른 인장 강도
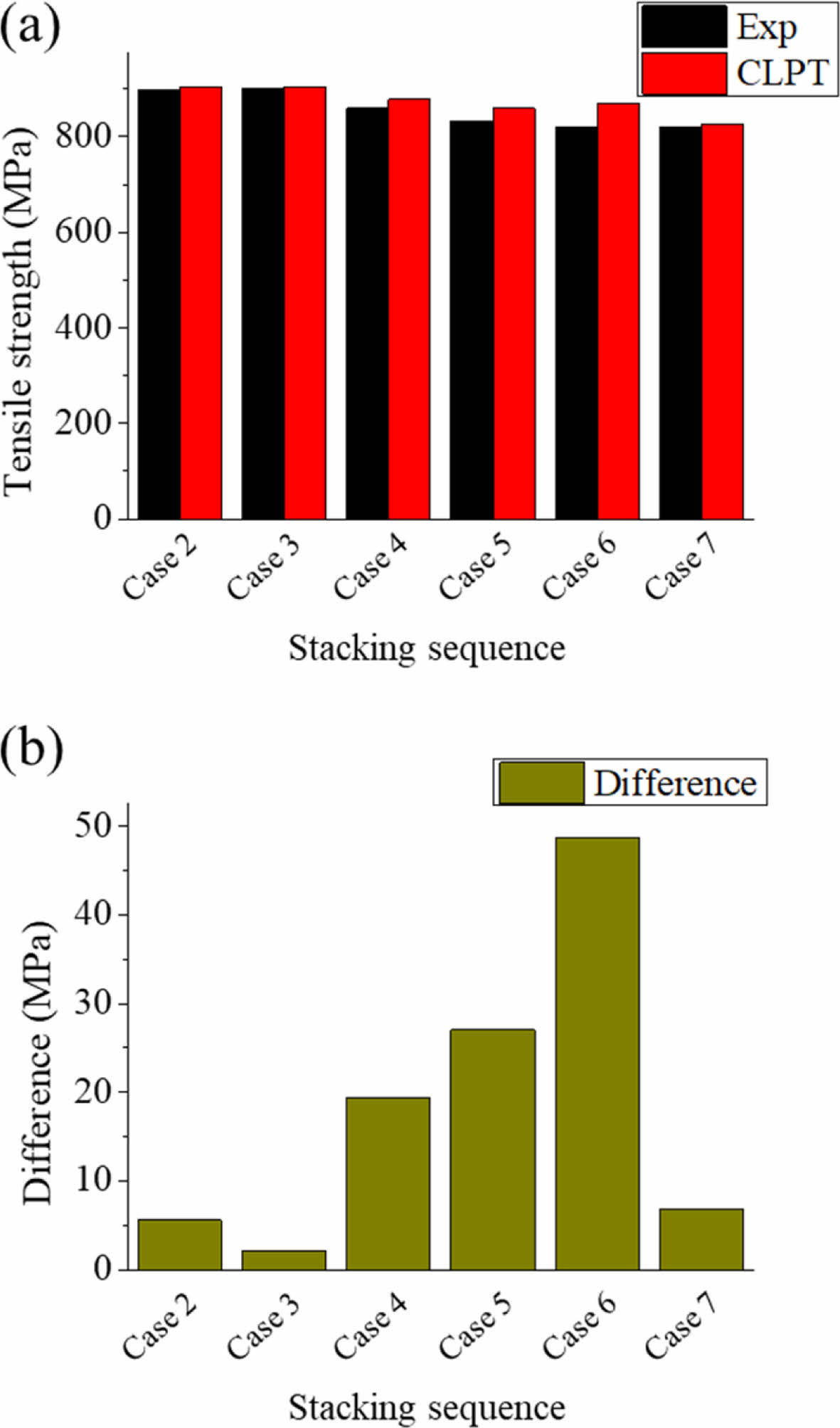
인장 시험과 고전 적층 판 이론으로 각각 측정 및 계산된 인장 강도는 Fig. 7(a)에 나타나 있다. 또한, 실험값과 이론값의 차이는 Fig. 7(b)에 나타나 있으며, 두 값의 차이는 기공률과 비례하는 경향을 보였다. 피어슨 상관계수의 경우 0.97의 강한 양의 상관관계를 보였다.

본 연구에서는 탄소섬유 복합재의 유리섬유 부직포의 개수 및 적층 순서에 따른 기계적 물성을 분석하였다. 기공률은 MATLAB의 이미지 프로세싱 및 기공률 계산 코드를 사용하였으며, 기계적 물성은 인장강도 및 강성, 굽힘 강도 및 강성을 측정하였다. 유리섬유의 개수가 많아질수록 기공률이 증가하였으며, 같은 개수의 유리섬유 부직포를 사용했을 때는 부직포의 위치가 복합재 중심에서 멀어질수록 기공률이 증가하였다. 인장 시험으로 측정한 인장 강도 및 강성과 고전 적층 판 이론으로 계산한 인장 강도 및 강성의 차이로 기공에 의해 감소되는 기계적 물성을 확인할 수 있었다. 인장 강성의 경우 실험값과 이론값의 차이와 기공률 간의 상관관계가 약한 양의 상관관계를 보였으나, 인장 강도의 경우 두 변수 간의 상관관계는 강한 양의 상관관계를 보였다. 즉, 인장 강도는 기공률이 증가할수록, 이론 값과 실험값의 큰 편차를 보였다. 본 연구로 제품 설계 시 기공률에 따른 강도의 저하를 예상할 수 있으며, 실제 제품 설계 시 강도 저하를 고려한 설계가 가능할 것으로 기대된다.

본 연구는 방위사업청과 국방과학연구소의 지원으로 수행된 수중운동체 장기체류 특화연구실(UD200012DD)의 연구비 지원 및 2020년도 정부(산업통산자원부)의 재원으로 한국에너지기술평가원의 지원을 받아 수행된 연구임 (20202020800360, 기존 공공건물 에너지 효율 진단 및 리모델링 기술 개발 실증).