In this study, we measure the initial electrical conductivity of SCF/rubber specimens and SCF/rubber specimens with nickel particles respectively. The corresponding electrical conductivity with compressive strain on the specimens is also measured. Through this experiment, we observed the effects of the volume fraction of carbon fiber, nickel particles and external strain on the electrical conductivity. Experiments show that even a small difference in the volume fraction of SCF plays a major role in the change of the electrical conductivity and that the piezoresistivity increases due to fiber reorientation respond to external strain. In addition, the nickel particles contribute to improving the electrical conductivity in specimens with carbon fibers above the threshold volume fraction. It was confirmed that there is an effect of offsetting the increment in the piezoresistivity caused by the reorientation of carbon fibers according to external strain.

본 연구에서는 탄소 단섬유를 천연고무 기지에 혼합한 탄소섬유/고무 시편과 그에 니켈입자를 추가한 탄소섬유-니켈입자/고무 시편의 초기 전기전도도를 측정하고, 그 시편에 압축스트레인을 가하면서 변화하는 전기전도도를 측정하였다. 실험을 통해 탄소섬유의 체적분율 및 추가된 니켈입자, 외부스트레인 등이 전기전도도에 미치는 영향을 관찰하였다. 탄소섬유 체적분율은 작은 차이로도 시편의 전기전도도의 변화에 매우 큰 역할을 하였고, 외부스트레인에 따른 탄소섬유 재배열에 의해 압저항이 증가하는 것을 알 수 있었다. 또한, 니켈입자의 추가는 탄소섬유가 임계체적분율 이상인 시편에서 전기전도도를 개선하는데 기여하는 것을 볼 수 있었는데, 이로부터 외부변형에 따른 탄소섬유의 재배열에 의해 압저항이 증가하는 현상을 상쇄하는 효과가 있음을 확인하였다.

Keywords: 압저항(Piezoresistivity), 퍼콜레이션 모델(Percolation model), 탄소 단섬유(Short carbon fiber, SCF), 탄소섬유-니켈입자/고무복합체(Carbon fiber-nickel powder/rubber matrix composite)

천연고무와 같은 부도체인 매트릭스에 전도성 물질인 충전재를 혼합한 복합재료의 전기전도도는 매트릭스 내부에 충전된 소재의 종류, 양 및 형상에 따라 영향을 받는다. 본 연구에서는 최신 기술로서 탄소나노튜브(CNT)가 우수한 물리적 특성과 화학적 안정성을 지녀 높은 전기 전도성을 갖음에도, 실제적으로 적용하는 대형 구조물의 경우에는 비용이 중요한 변수로 작용하기에 탄소나노튜브가 아닌 탄소 단섬유를 이용한 복합체를 대상으로 하였다. Fig. 1(a)는 천연고무 매트릭스에 탄소 단섬유(short carbon fiber, SCF)를 충전재로 혼합한 복합재료의 한 예시이며, 전기전도는 재료 내부의 전류 이동통로가 되는 SCF들 사이의 네트워크 구성의 완전성에 따라 결정된다. 매트릭스 내부에서 충전재의 체적분율이 점차 증가함에 따라 전류가 흐르는 통로가 점차 확장되고, SCF가 일정 체적분율 이상으로 개재되면 SCF들이 직접 접촉하거나 터널링 효과(tunneling effect)를 기대할 수 있는 거리로 접근하여, Fig. 1(a)와 같이 원활한 네트워크 연결이 가능해진다. 퍼콜레이션(percolation) 모델은 이 과정을 설명하는 이론이고 소재가 부도체에서 전도체로 전환하는 지점 또는 복합재료의 전기전도도가 급격히 상승하는 지점에서 SCF의 체적분율을 임계체적분율(threshold volume fraction)이라 부른다.
Kirkpatrick가 전도체와 부도체가 혼합된 격자구조를 퍼콜레이션 모델에 처음 응용한 이후 다수의 연구자들에 의해 각기 제안한 퍼콜레이션 모델들을 연구하였다[1-4].
퍼콜레이션 네트워크가 완성되어 전도체인 Fig. 1(a)와 같은 소재에 외부 하중에 의한 스트레인이 발생하면, 그 스트레인의 증가에 따라 Fig. 1(b)처럼 매트릭스 내부 네트워크가 점차 분리되어 전기전도도가 점차 떨어진다. 이러한 성질을 소재가 갖는 압저항성(piezoresistivity)이라고 부르며, 여기서 SCF들 사이의 네트워크 분리는 터널링 효과가 없는 거리 이상을 의미한다[5]. 이후 Taya는 결합가능성이 도입된 식을 보완하여 이에 대한 해석을 수행하였다[6,7].
초기 퍼콜레이션 모델에서는 매트릭스에 입자상이나 섬유상 가운데 한 종류의 충전재를 사용한 복합재료에 관한 연구를 위주로 하였으나, 최근에는 두 종류의 충전재를 하나의 매트릭스에 혼합한 복합재료에 대한 연구가 비교적 활발하다[8-10].
전기전도성을 갖는 고무나 수지기반 복합재료는 전기적으로나 기계적으로 독특한 물성치를 갖고, 특히 외부 스트레인의 증가에 따라 전기저항이 증가하는 압저항성을 갖는다. 이러한 성질을 활용하여 그동안 압력센서에 많이 활용되었고, 현재는 MEMS(micro electro mechanical system) 구성 장치로 상당한 비중을 차지하고 있으며, 비교적 최근에는 구조물의 건전성을 진단 또는 감시하는데 많이 이용되고 있다[11-13].
본 연구에서는 기존 인장방향의 전기전도도 측정이 아닌, 시편에 압축이 가해질 때 그와 수직한 방향에서의 전기전도도 변화를 측정하였다. 시편은 SCF의 체적분율 변화를 갖도록 제작하고, 각 시편에 대응하는 니켈입자가 추가된 시편의 니켈입자 체적분율은 0.05로 고정하였다. 실험은 시편의 초기 전기전도도 측정후 압축이 가해질 때 실시간으로 변화하는 전기전도도를 측정하였다.
이 실험결과를 바탕으로 임계체적분율을 찾고 Cohen의 식을 완성하였다. 그 과정에서 매트릭스에 대한 SCF의 체적분율과 추가된 니켈입자가 전기전도도에 미치는 영향 및 두 충전재 사이의 상호작용을 등을 고찰 하였으며, Taya의 식을 이용하여 외부스트레인에 따라 변하는 전기전도도를 살펴보았다.

2.1 압저항성을 복합재료의 전기전도도에 관한 퍼콜레이션 이론
Taya는 압저항성을 갖는 탄성복합재료의 전기전도도에 관한 모델로 Eshellby의 모델과 퍼콜레이션 모델을 비교하고, 매트릭스에 충전되는 전도체가 섬유상이고 매트릭스와 전도체 사이의 전기전도도 차이가 클 때는 퍼콜레이션 모델이 적합함을 확인하였다[6]. Kirkpatrick 연구 이후 제안된 여러 형태의 퍼콜레이션 모델들이 있지만, 본 연구에서는 Cohen의 식과 이를 보완한 SCF 재배열 모델을 이용하여 실험결과를 해석하였다.

2.1.1 Cohen의 식
Cohen이 제안한 아래의 식 (1)은 퍼콜레이션 모델에서 고전이론으로 일컬어지고 있지만, 다양한 조건에 대응하는 일반형이 없는 현재의 상황에서 여전히 유용한 식이며, 실제로 많은 논문에서 인용하고 있다[7].



위의 식에서 σ는 소재의 전기전도도, σ_f는 소재 내부에 혼합된 충전재의 전기전도도, f는 매트릭스에 대한 충전재의 체적분율, f^*는 충전재의 임계체적분율, t는 전도도 지수이다. 부도체인 매트릭스에 전도성 충전재를 계속 추가하면, 전기전도가 일어날 때의 f와 전기전도도의 상승률이 급격하게 떨어질 때의 f가 존재한다. Taya는 그 중간 값을 임계체적분율로 정의하였다[2]. t는 3차원 모델일 때 최대 2이고, 시편 또는 충전재의 형상이나 크기와 관련을 갖는다. 여러 형태의 모델들 가운데, 식 (1)은 구성이 간단하고 몇 번의 실험을 통해 쉽고 빠르게 f^*와 t의 근사값을 찾을 수 있는 장점이 있다. 식 (1)과 유사한 형태이지만, 충전재들 사이의 결합가능성(probability of bond)을 도입하여 변수를 수정한 식 (2)는 몬테카를로 시뮬레이션에 이용되고 있다.



식 (2)에서, σ는 소재의 전기 전도도, σ_f는 소재 내부에 개재된 충전재의 전기전도도, t는 전도도지수, p는 섬유들 사이의 결합 가능성이다. 충전재가 섬유상일 경우 p는 Taya에 의하면 아래의 식 (3)으로 계산한다[14].



식 (3)에서 N_f는 시편 내부에 혼합된 SCF들의 개수, N_i는 SCF들이 서로 만나는 점의 개수이다. P_c는 퍼콜레이션 한계를 뜻하는 임계값이고 3차원 모델일 경우 0.44이다[2]. N_i는 일반적으로 충전재의 형상, 크기, 배열되는 각도와 밀접한 관련을 갖는다. 예를 들어, 두 복합재료의 SCF 체적분율이 같더라도 종횡비가 큰 쪽에서 SCF들이 만나는 점이 더 많을 확률이 크다. 따라서, 식 (3)은 퍼콜레이션 모델에서 충전재의 형상이 일정한 역할을 하고 있음을 내포한다. N_f는 시편과 충전재 각각의 체적과 충전재의 종횡비 및 체적분율을 알면 쉽게 계산이 가능하고, N_i는 몬테카를로 방법을 이용하여 얻는다.

2.1.2 SCF 재배열 모델
앞서 간략하게 살펴본 두 식은 퍼콜레이션 모델에서 소재의 전기전도도를 예측하는데 사용되지만, 소재에 스트레인을 가할 때 전기전도도의 변화 양상을 반영하지는 못한다. 이를 해결하기 위해 Taya는 SCF 재배열(fiber reorientation) 모델을 제안하였다[7].
본 연구의 실험에서는 Taya의 전개조건과 달리 압축 스트레인이 가해지므로, 식 (9)와 (10)으로 수정하였다.
매트릭스 내부에서 SCF가 제한된 각도 범위로 배열되는 경우와 무작위 배열인 경우를 비교해 보면 SCF 사이의 접촉 가능성은 후자가 높다고 보는 것이 타당하다. 예를 들어, 배열 각도를 10° 이내로 제한할 때와 90° 이내로 제한 할 때를 비교해 보면 이해가 쉽다.
따라서 각도의 제한에서 벗어나 무작위 배열에 가까울수록 임계체적분율은 줄어들고, 반대의 상황에서는 커진다. 만약 외부 스트레인이 가해져 각도 배열에 제한이 주어지는 경우와 동일한 상태가 된다면, 그에 대응하는 임계 체적분율이 증가하는 만큼 식 (1)에서 전기전도도가 떨어질 것이다. 이러한 착상을 바탕으로 내부 SCF의 배열 각도와 외부스트레인과의 관계를 찾는다.
Fig. 2는 시편에 스트레인이 가해지기 전에 시편 내부에 개재된 SCF의 위치를 표현한 것이다.
여기서 u는 SCF의 길이, (x, y, z)는 무작위로 배열된 어떤 SCF의 중심점의 좌표, f는 SCF와 Z축이 이루는 각도,θ는 SCF가 X-Y평면에 투영되었을 때 X축과 이루는 각도이다.
Fig. 3은 Fig. 2의 SCF를 포함한 미소정육면체에 압축스트레인을 가할 때, 변형 전후를 나타낸다. 이 과정에서 SCF의 위치변화는 천연고무의 위치변화와 같은 비율로 변화하고 천연고무가 비압축성이라고 가정하면, Fig. 3과 같은 미소체적의 변형을 고려하여 다음의 관계식을 얻을 수 있다.



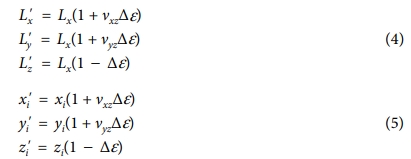
식 (4)와 (5)에서, L은 SCF를 포함한 미소정육면체의 한 변의 길이, ν는 프와송의 비, ∆ε는 Z방향의 압축스트레인, 위 첨자(')는 압축스트레인이 가해진 후 변화된 값, 아래 첨자(_i)는 i번째 SCF를 의미한다.



식 (6)과 (7)은 i번째 섬유에 스트레인을 가할 때 그 전후로 섬유의 길이가 u에서 u'로 변하는 것을 나타낸다. 식 (4) ~(7)로부터 다음 관계식을 얻는다.




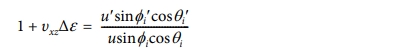
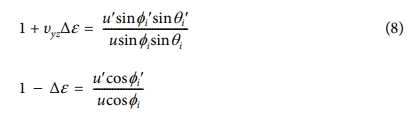
식 (8)을 이용하여 SCF의 초기각도와 스트레인을 받은 후 각도 사이의 관계식을 식 (9), (10)과 같이 구할 수 있다. 식 (11)은 SCF가 X-Y 평면과 이루는 각도이다.



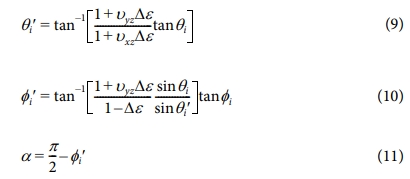
전도체인 시편의 높이 방향을 Z축과 일치시켰을 때, Y축 방향의 단면에서 SCF의 배열은 Fig. 1(a)와 같은 상태이다. 시편에 Z방향 압축스트레인을 가하면, 시편의 반경방향으로 인장스트레인이 나타나므로 Fig. 1(b)와 같은 상태로 점차 옮겨간다. 식 (9)와 (10)은 그 과정에서 SCF들이 재배열될 때 나타나는 각도의 변화를 표현하고, 각도의 변화는 원래 무작위 배열이었던 SCF들이 점차 방향성을 띄게 된다는 것을 의미한다. 만약 시편을 등방성 소재로 가정하면, φ의 변화만 나타나므로 방향성의 변화가 더 선명하다. 이로부터, Z방향 압축스트레인을 가할 때, 측정한 반경방향 전기전도도의 변화는 식 (2), (3), (9), (10)으로 설명할 수 있다.

3.1 시편 준비
매트릭스로 사용된 소재는 천연고무(SMR CV60)이고 내부에 개재된 섬유상 소재는 TORAY사의 T300을 짧게 절단한 SCF이다. SCF의 길이는 0.8~1 mm, 직경은 7 μm(종횡비, 약 130)이다. 추가된 니켈입자의 직경은 약 70 μm이다. 천연고무의 조성은 미국재료실험학회(ASTM)의 천연고무 배합법을 따랐다. SCF와 천연고무의 배합은 0.30 Liter Banbury(internal mixer)를 이용하였고, 배합 단계는 ASTM 기준에 따라 진행되었다. 제작된 시편의 형상은 직경 17 mm, 높이 25.4 mm인 원통형이다. 시편의 종류는 천연고무 내부에 개재되는 SCF의 체적분율에 따른 3종류와 니켈입자의 유무에 따른 2종류로 구분하여 총 6종류이다. 시편에 혼합된 SCF의 체적분율은 각각 0.01, 0.02, 0.03이고, 각각의 시편에 니켈입자를 체적분율 0.05로 추가하여 비교 시편을 제작하였다.
Table 1은 천연고무를 매트릭스로 제작된 시편의 조성을 나타낸 환산표이다. 조성물의 양을 나타내는 단위는 고무 100 g당 조성물의 g수를 뜻하는 PHR(per hundred rubber)이다. SCF와 니켈입자의 조성은 퍼콜레이션 모델에서 전기전도도에 주요 변수인 체적분율로 환산한 수치이다.
전기저항을 측정하기 위해 시편과 접촉할 전극은 실버페이스트를 활용하여 시편의 형상에 가깝게 제작하였다. 실버페인팅은 시편과 전극의 전기적 접촉도를 향상 시키는 효과도 있었다[15]. 전극의 단면적은 0.075 cm²(0.15 cm × 0.5 cm)이다.

3.2 실험장치 구성 및 실험
압축 실험을 위한 장비 구성은 Fig. 4와 같다. 시편을 압축했을 때 나타나는 반경방향 인장스트레인에 의해 변화하는 전기저항을 측정하기 쉽도록 MTS Alliance RT/1을 이용하여 1 mm/min의 속도로 변위제어 압축실험을 하였다. 시편 높이의 1/2지점에 전극을 접촉시키고 반경방향에서 초기 전기저항을 측정한 후, 가중되는 스트레인에 따라 변하는 전기저항을 압축스트레인 1%마다 측정하였다.
원통형 시편의 반경방향 전기전도도를 측정하므로, 전극의 접촉점이 시편의 원주면과 일치하여야 하지만, 압축시 전극의 파손 및 변형 방지를 위하여, 전극의 높이를 0.5cm로 하였고, 전극과 피측정체의 동일한 접촉압력을 유지하기 위하여 시편에 전극을 부착한 형태로 실험을 진행하였다.
Table 1의 시편들 가운데 시편 1, 3, 5를 실험하여 SCF의 체적분율이 다를 때 나타나는 전기전도도의 차이를 살펴보고, 이후 시편 2, 4, 6을 실험하여 SCF의 체적분율이 동일한 시편들에 니켈입자를 추가한 영향을 비교하였다.

4.1 실험 결과
4.1.1 전기전도도
전기전도도는 비저항의 역수로 표시하며 단위는 S(Siemens,지멘스)/cm나 1/Ωcm를 사용한다. 아래의 식은 그 관계를 나타낸다.



식 (12)에서 σ는 전기전도도, R은 전기저항 측정값, d는 전극 사이의 거리, A는 전극의 면적이다. 본 연국의 실험에서는 시편에 축방향(Z방향) 압축스트레인을 가하면, 반경방향에 인장스트레인이 발생하여 전극사이의 거리가 점차 멀어진다. 그러나 압축스트레인을 가할 때 나타나는 반경방향의 배럴링(barreling) 때문에, 그것을 정확하게 반영하기가 매우 어려웠다. 이에 전극사이의 거리를 초기 시편의 직경과 근사적으로 같은 값으로 고정하여 전기전도도를 계산하였다.

4.1.2 실험데이터
SCF의 체적분율이 0.01인 시편(SP1, SP2)들은 니켈입자의 유무와 상관없이 시편의 전기저항이 순수 천연고무일 때와 비슷하였고, 스트레인을 가해도 변화가 거의 없었으므로 실험 분석대상에서 제외하였다. SCF의 체적분율이 전기전도도에 미치는 영향은 시편 4와 6을 비교하면 관찰이 가능하고, 니켈입자가 전기전도도 개선에 기여하는 정도는 시편 3, 4와 시편 5, 6에서 비슷한 결과를 보였다. 따라서 중복된 해석을 피하기 위해 SCF의 체적분율이 0.02이고 니켈입자가 없는 시편 3도 실험 분석대상에서 제외하였다.
Table 2는 시편제작에 쓰인 소재와 제작된 시편 가운데 SP4, SP5, SP6의 초기 전기전도도를 각각 정리한 것이다.
Table 3의 데이터는 세 시편(SP4, SP5, SP6)에 외부스트레인이 가중될 때 변화하는 전기전도도이다. 종류별로 동일한 사양의 시편들에 대해, 축방향 압축실험을 실시하면서 측정한 전기저항의 평균값들을 식 (12)를 사용하여 전기전도도로 환산한 값이다. 전반적으로 Z축 방향에서 압축을 가할 때 반경방향의 인장스트레인에 따라 측정되는 저항이 점차 커지는 경향을 보였다. 스트레인을 10% 정도 가한 이후에는, 시편 표면에 나타나는 배럴링 형상이 시편 마다 불규칙 했기 때문에, 시편들 사이의 적절한 비교 검토를 위해서 이후 측정값을 생략하였다.
Fig. 5~Fig. 7은 Table 3의 내용을 그래프로 나타낸 것이다. 그래프의 수직축은 측정된 저항의 평균값들을 전기전도도로 환산한 후 가독성을 높이기 위해 상용로그를 취한 값이다. 시편의 전기전도도는 시편에 가해진 스트레인과 직접적인 상관 관계가 있으므로 스트레인을 수평축에 표시하였다. 그리고 압축이 가해질 때 그 수직방향의 전기전도도를 얻는 것이 목적이므로 압축 방향의 스트레인을 그대도 반영하였다. Fig. 8은 시편 5와 시편 6을 비교하여 니켈입자의 영향을 관찰하기 위해 Fig. 6과 Fig. 7을 동시에 나타낸 그래프이다.
퍼콜레이션 모델에서 고려해야 할 변수들은 터널링 효과가 발행하는 거리(경우에 따라서는 전극 사이에 걸리는 전압) 및 충전재의 종류 그리고 매트릭스 종류와 양단에 걸리는 전류의 종류 등이다.
추가적으로 매트릭스의 프와송의 비(ν), SCF와 Z축이 이루는 각도(f) 그리고 SCF를 X-Y 평면에 투영했을 때 X축과 이루는 각도(θ) 등도 고려해야 한다. 그러나 시편을 등방성소재로 가정하면, 천연고무이므로 방향에 관계없이 ν = 0.5이고 Z축 방향 압축스트레인이 가해질 때 θ_i' = θ_i이다. 따라서, 본 연구에서는 SCF와 Z축 사이의 각도 φ의 변화만 고려하여 식 (9)과 (10)이 외부 스트레인과 전기전도도사이의 관계를 설명할 수 있는지 살펴보았다.

4.2 고찰
4.2.1 SCF-Ni/Rubber 퍼콜레이션 모델과 SCF 체적분율의 영향
두 충전재를 혼합한 시편 2, 4, 6의 실험 데이터를 활용하여 Cohen의 식에서 임계체적분율과 전기전도도지수를 결정한다. 시편에 스인 니켈입자의 체적분율이 자력으로 퍼콜레이션 네트워크를 구성하려면 대략 0.43이상은 되어야 한다[15]. 그러나 시편에 쓰인 니켈입자의 체적분율은 0.05에 불과하므로, SCF의 체적분율이 전기전도도의 변화를 주도한다고 가정하고 해석한다.
Fig. 9는 SCF 체적분율의 변화가 전기전도도에 주는 영향을 나타내는 그래프이며, SCF의 체적분율이 0.012정정일 때 시편에서 전기전도도의 변화가 나타나고 이후 급격히 증가하다 0.026정도에서 증가율이 급격히 감소하는 것을 보여준다. 그간의 실험이나 연구논문을 참고하면, 이후 0.03의 오른쪽 구간은 충전재를 계속 채워도 전기전도도의 상승이 매우 작고 정체된다. 이것은 충전재 들이 네트워크를 구성할 때 필연적인 접촉저항이 증가하기 때문이고, 실제로 충전재를 계속 추가해도 복합재료의 전기전도도가 충전재의 고유 전기전도도에는 미치지 못한다.
Fig. 9에서 전도도지수를 추출하기 위해, 식 (1)의 양변에 상용로그를 취하여 식을 변형하면 다음과 같은 식 (13)를 얻었다.



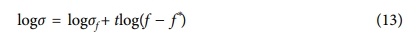
Fig. 9에서 시편이 부도체에서 전도체로 전환되는 구간(threshold region)을 대략 0.012~0.026로 보면, 이 구간을 포함한 근처에서 SCF 체적분율의 차이가 전기전도도의 변화를 주도하는 것은 명백하다. Taya의 정의에 의하면 그 중간값 0.019를 임계체적분율(f^*)로 잡을 수 있다[2,16]. 이 값을 이용하여 식 (13)로부터 Fig. 10의 관계를 얻는다.
Fig. 10에서 전기전도도지수(t)는 그래프의 기울기이므로 t = 3.38이다. 지금까지 구한 것을 종합하면, 천연고무 매트릭스에 SCF와 니켈입자를 혼합한 복합소재의 전기전도도는 다음의 식 (14)과 같다.



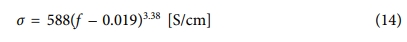
식 (14)는 니켈입자의 체적분율은 0.05이고 SCF의 체적분율이 변할 때 소재가 갖는 전기전도도를 예측하는 식이다. 단, 식 (14)는 시편이나 충전재의 형상과 크기를 포함하여 시편과 모든 조건이 동일할 때만 사용할 수 있다. 예를 들어, 니켈입자의 체적분율이 0.05인 것을 포함하여 시편과 모두 동일한 조건이고 SCF의 체적분율이 0.025이면 전기전도도는 약 1.82 × 10^-6 [S/cm]가 될 것이다. 만약 실험에 쓰인 시편의 조건과 달리 추가되는 니켈입자가 임계체적분율에 가까울 경우, 두 충전재의 체적분율을 반영할 수 없으므로 식 (14)와 같은 표현을 얻기가 어렵다.
식 (14)에서 3차원 시편일 때 이론적인 전기전도도지수(t)의 최대값은 2이다. 그러나 에폭시 매트릭스에 길이 1.15~2.85 mm인 SCF를 혼합한 복합재료의 실험데이터로부터 찾은 전기전도도지수가 3.0 ± 0.6인 결과[17]를 참고하여, 식 (14)을 기반으로 니켈입자의 영향을 살펴보았다.
먼저 SCF의 체적분율은 식 (14)를 완성하는 과정에서 그 영향은 이미 드러났지만, Fig. 5와 Fig. 7을 비교하면 전기전도도에 매우 큰 영향을 주고 있는 것을 관찰할 수 있다. 두 시편에서 전기전도도의 차이는 결합가능성에 관한 식 (2)로부터 예상할 수 있다. SCF의 체적분율은 식 (3)의 변수인 SCF 개수(N_f)와 직접 관련을 갖는데, 체적분율이 증가하면 SCF의 개수(N_f)와 SCF들이 만나는 점의 수(N_i)도 증가한다. 이 N_i는 식 (3)에서 분모(4N_f + 2N_i)의 변화율 보다 분자(N_f + 2N_i)의 변화율에 더 크게 작용하므로 결합 가능성(p)가 커지고, 이 값을 식 (2)에 대입하면 전기전도도가 상승한다.
이러한 사실은 그간의 연구에서 같은 종횡비를 갖는 SCF일 때 부도체에서 전도체로 전환하는 구간 근처에서 체적분율 0.02의 차이는 상용로그를 취한 전기전도도가 매우 큰 차이를 보이는 것과 일치하고[14], 이 실험의 결과에서도 시편 4(또는 시편 3)와 시편 6을 비교해 보면 그것과 잘 일치한다.

4.2.2 압축스트레인에 따른 수직방향 전기전도도(σ)의 변화
Table 1의 시편 1, 2를 제외한 나머지 시편들에 스트레인을 가하였을 때, 전반적인 전기전도도의 변화는 스트레인이 더해질수록 떨어지는 경향을 보인다. Fig. 5~Fig. 7에서 세 시편들 사이에 나타나는 전기전도도의 큰 차이는 SCF의 체적분율과 니켈입자의 유무에 따라 달라진 결과이다. 시편에 압축이 주어짐에 따라 길이방향으로 압축스트레인이 증가하게 되고, 그에 대응하여 반경방향으로 인장스트레인이 나타난다. 이때 시편내부에서는 Fig. 1(b)와 같은 현상이 발생하여 전류의 이동 통로가 단절되므로 전기저항이 증가하고 전기전도도가 떨어지는 것이다.
이와 같이 외부스트레인에 의해 시편의 압저항이 커지는 과정은 앞서 살펴본 SCF 재배열 모델로 설명될 수 있다. 원통형 시편의 축방향에 가해진 압축스트레인은 시편 내부에서 SCR가 배열되었던 각도의 변화를 가져온다. Fig. 3(b)와 식 (9)~(11)로부터 SCF와 X-Y 평면이 교차하는 각도 (π/2 - f)가 점차 작아지는 것을 알 수 있다. 이와 같이 무작위였던 SCF의 배열이 방향성을 띄면 식 (3)의 결합 가능성(p)는 작아지고, 이 값을 식 (2)에 반영하면 전기전도도는 떨어진다. 이것은 다른 모든 조건이 동일할 때, SCF가 배열되는 각도를 작게 제한할수록 임계체적분율은 커진다는 Taya의 연구에서 확인할 수 있다[14].
SCF의 배열 각도 제한과 관련하여, 시편을 제작할 때 SCF가 무작위로 배열되는 것이 중요함을 알 수 있다. 매트릭스 내부에 SCF가 배열될 때 그 중심부와 표면 근처를 비교해 보면, 한 면에 제약이 있는 표면 근처는 중심부에 비해 자유도가 떨어질 것이다. 이것은 이론적인 해석에서 무작위 배열로 가정하는 것을 어렵게 한다.

4.2.3 니켈 입자의 영향
시편 5와 시편 6사이에 존재하는 니켈입자의 영향을 다음의 식 (15)와 (16)를 통해 살펴 본다.



식 (15)에서 f는 충전재의 체적분율, 하 첨자(c)는 SCF, 하 첨자(n)은 니켈입자, 상 첨자(^*)는 해당 충전재의 임계체적분율이다[8]. 위 식은 좌변이 1보다 클 때 복합재료가 전기전도성을 띄게 되는 것을 의미하며, 두 종류의 충전재를 한 매트릭스에 혼합할 때 그 배합량을 예상하는데 쓰인다. 보통 두 충전재의 임계체적분율은 다수의 연구를 통해 알려진 경우가 많거나 새로운 시도인 경우 앞서 기술된 몇 번의 실험을 통해 간단하게 찾을 수 있다.
식 (15)는 두 충전재 사이의 단순한 선형관계를 나타내므로 둘 사이에 있을 수 있는 상승효과를 알 수 없다. 식 (16)는 그와 관련된 최근의 연구 결과이다[9].



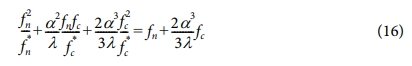
식 (16)에서 α = d_n/d_c는 니켈입자와 SCF의 직경비, λ = l/d는 SCF의 종횡비이고 나머지 문자는 식 (15)와 동일하다. 식 (16)도 앞의 식 (15)와 마찬가지로, 좌변이 우변보다 큰 값을 가질 때 전기전도가 가능함을 의미한다. 주어진 데이터로 SCF의 체적분율을 계산하면 계산값이 두 식에서 차이를 보이는데, 이것은 식 (16)의 좌변에서 두 번째 항이 표현하는 상승효과 때문이다. 식 (16)은 식 (15)와 달리 비선형이므로 단순히 중첩할 수 없다. 따라서 좌변의 두 번째 항을 계산한 값이 그 차이와 일치하지는 않는다. 종합하면, 추가된 니켈입자는 SCF와의 사이에서 상승효과를 가져오므로, 니켈입자가 추가된 시편은 각각 혼합된 소재의 전기전도도를 단순히 합한 것 보다 큰 값을 갖는다는 것을 알 수 있다.
Fig. 8은 시편 5와 시편 6을 비교한 것으로, 추가된 니켈입자가 외부스트레인 전영역에 걸쳐 전기전도도의 개선에 기여하고 있는 것을 나타내고 있다. 또한, 스트레인이 가중 될수록 그 격차가 커지는 경향을 보이는데, 두 시편을 센서에 응용한다면 민감도 면에서는 니켈입자를 추가하지 않는 것이 나은 선택일 수 있다. 시편 5의 초기 전기전도도는 스트레인 0.03지점에서 시편 6의 전기전도도와 비슷한 값을 보인다. 이것은 시편 6에 외부변형이 주어질 때, 탄소섬유의 재배열에 의해 압저항이 증가하는 현상을 추가된 니켈입자가 상쇄하는 효과가 있음을 의미한다.
SCF만 사용한 시편 1, 3, 5도 Fig. 9와 유사한 양상을 보인다. 여기에 니켈입자를 추가했을 때, 앞서 살펴본 결과를 고려하면, 전기전도도의 상승이 어려운 SCF의 체적분율이 0.03이후인 구간에서도 전기전도도가 개선되는 효과를 기대할 수 있다.

본 연구에서는 천연고무 매트릭스에 SCF(탄소 단섬유)와 니켈입자를 혼합한 복합재료에서 외부 변형에 따른 전기전도도의 변화를 실험을 통해 측정하고, Cohen 및 Taya의 퍼콜레이션 모델을 적용하여 비교 검토한 결과, 다음과 같은 결론을 얻었다.
(1) SCF와 천연고무 매트릭스를 혼합한 원통형 시편에 니켈입자를 체적분율 0.05만큼 추가한 경우, SCF의 임계체적분율은 0.019이다.
(2) 같은 종횡비일 때, 섬유상 충전재인 SCF의 체적분율은 복합재료의 전기전도도에 매우 큰 역할을 하고 있음을 알 수 있다.
(3) SCF가 임계체적분율 이상으로 혼합된 시편에서, 추가된 니켈입자는 두 충전재 사이의 상승효과와 함께 전기전도도의 개선에 기여하는 것을 볼 수 있다.
(4) 니켈입자가 추가된 시편에 외부스트레인이 가해질 때, 외부변형에 따른 탄소섬유의 재배열에 의해 압저항이 증가하는 현상을 추가된 니켈입자가 상쇄하는 효과가 있음을 알 수 있다.
(5) 시편에 외부스트레인이 가해지면 시편 내부에 형성된 섬유상 충전재들의 재배열로 인한 각도 변화로 퍼콜레이션 네트워크가 점차 불완전해진다는 모델로 압저항이 점차 증가하는 실험 결과를 설명할 수 있다.
(6) 니켈입자가 SCF의 체적분율이 비슷할 경우와 같이 추가된 충전재의 체적분율이 유의미할 때, 이것을 Cohen의 수식에 반영하기가 어렵다. 이에 대한 연구가 필요하다.

본 연구는 2021년도 산업통상자원부 및 한국산업기술평가관리원이 지원하는 디자인혁신역량강화사업(과제번호 : 20015596)으로 수행된 것이며, 지원에 대해 진심으로 감사드립니다.