This paper derives numerically the buckling Knockdown factors using two different initial imperfection models, such as geometric and loading imperfection models, to investigate the unstiffened composite cylinder with an ellipse pre-buckling deformation pattern. Single Perturbation Load Approach (SPLA) is applied to represent the geometric initial imperfection of a thin-walled composite cylinder; while Single Boundary Perturbation Approach (SBPA) is used to represent the geometric and loading imperfections simultaneously. The buckling Knockdown factor derived using SPLA is higher than NASA’s buckling design criteria by approximately 84%, and lower than buckling test result by 9%. The buckling Knockdown factor using SBPA is higher than NASA’s buckling design criteria by about 75%, and 14% lower than the buckling test result. Therefore, it is shown that the buckling Knockdown factors derived in this study can provide a lightweight design compared to the previous buckling design criteria while they give reasonably a conservative design compared to the buckling test for both the initial imperfection models.

본 연구에서는 압축력을 받는 얇은 복합재 원통 구조에 대하여 기하학적 혹은 하중에 대한 초기 결함 모델을 이용하여 수치해석적으로 좌굴 Knockdown factor를 새롭게 도출하였다. 전역 좌굴이 발생하기 이전에 타원 형상의 변형 형상을 갖는 복합재 원통 구조를 사용하였다. 복합재 원통 구조의 기하학적 초기 결함만 고려하기 위하여 Single Perturbation Load Approach를 이용하였으며, 기하학적 초기 결함과 더불어 하중 불균일을 함께 구현하기 위하여 Single Boundary Perturbation Approach를 사용하였다. 기하학적 초기 결함 모델의 좌굴 Knockdown factor는 NASA의 기존의 좌굴 Knockdown factor보다 약 84% 높게 도출되었으며, 좌굴 시험에 비하여서는 약 9% 낮게 도출되었다. 기하학적 초기 결함과 하중 불균일을 함께 고려하는 모델의 좌굴 Knockdown factor는 NASA의 좌굴 Knockdown factor에 비하여서는 약 75% 높게, 그리고 좌굴 시험보다 약 14% 낮게 계산되었다. 따라서, 본 연구의 좌굴 설계 기준은 고려된 초기 결함 모델과 상관없이 기존의 좌굴 설계 기준에 비하여 경량 설계의 제공이 가능함과 동시에 좌굴 시험 대비 적절히 보수적인 설계 기준을 제공할 수 있음을 확인하였다.

Keywords: 복합재 원통(Composite cylinder), 좌굴 Knockdown factor(Buckling knockdown factor), 기하학적 초기 결함(Geometric imperfection), 하중 불균일(Loading imperfection)

최근 다양한 위성의 발사와 민간 우주 개발이 활발해지면서 우주 발사체의 우수한 경쟁력 확보가 요구되고 있다. 발사체 경쟁력에는 발사 비용 절감 및 탑재 중량의 증가가 중요한 요인이며 이를 위하여서는 보다 높은 수준의 발사체 구조 경량화가 필요하다. 특히, 최근 각광받는 재사용 발사체는 귀환 비행을 위한 추가적인 추진제 및 착륙 장비로 인한 중량 증가로 구조 경량화가 더욱 중요하다. 발사체 구조물 중에서 추진제를 제외하고 우주 발사체 탱크 구조가 대부분의 중량을 차지한다[1]. 이러한 이유로, 발사체 구조 중량을 낮추기 위하여 발사체 탱크 구조의 중량을 절감해야 한다[2]. 따라서, 우주 발사체 탱크 구조의 경량화를 위하여 비강도 및 비강성이 우수한 복합재료를 발사체 탱크 구조에 적용하는 연구가 활발히 수행 중이다[3].
우주 발사체 추진제 탱크와 더불어 고체 모터 케이스 및 동체에 사용되는 얇은 원통 구조는 압축력에 의한 좌굴(buckling)에 매우 취약하며, 제작 및 운용 시 필연적으로 발생하는 초기 결함(initial imperfection)으로 인하여 실제 좌굴 하중은 선형 이론 해에 비하여 낮다. 이를 고려하기 위하여, 좌굴 Knockdown factor(KDF)를 좌굴 설계 기준으로 사용한다. 좌굴 Knockdown factor는 초기 결함이 없는 완벽한 쉘 구조의 전역 좌굴 하중((N_cr)_perfect)에 대한 초기 결함이 있는 쉘 구조의 전역 좌굴 하중((N_cr)_imperfect)의 비율로 식 (1)과 같이 정의된다. 좌굴 Knockdown factor의 값이 낮을수록 얇은 쉘 구조가 무겁게 설계되므로, 좌굴 Knockdown factor는 얇은 쉘 구조의 구조 경량 설계와 직결된다.



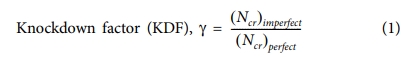
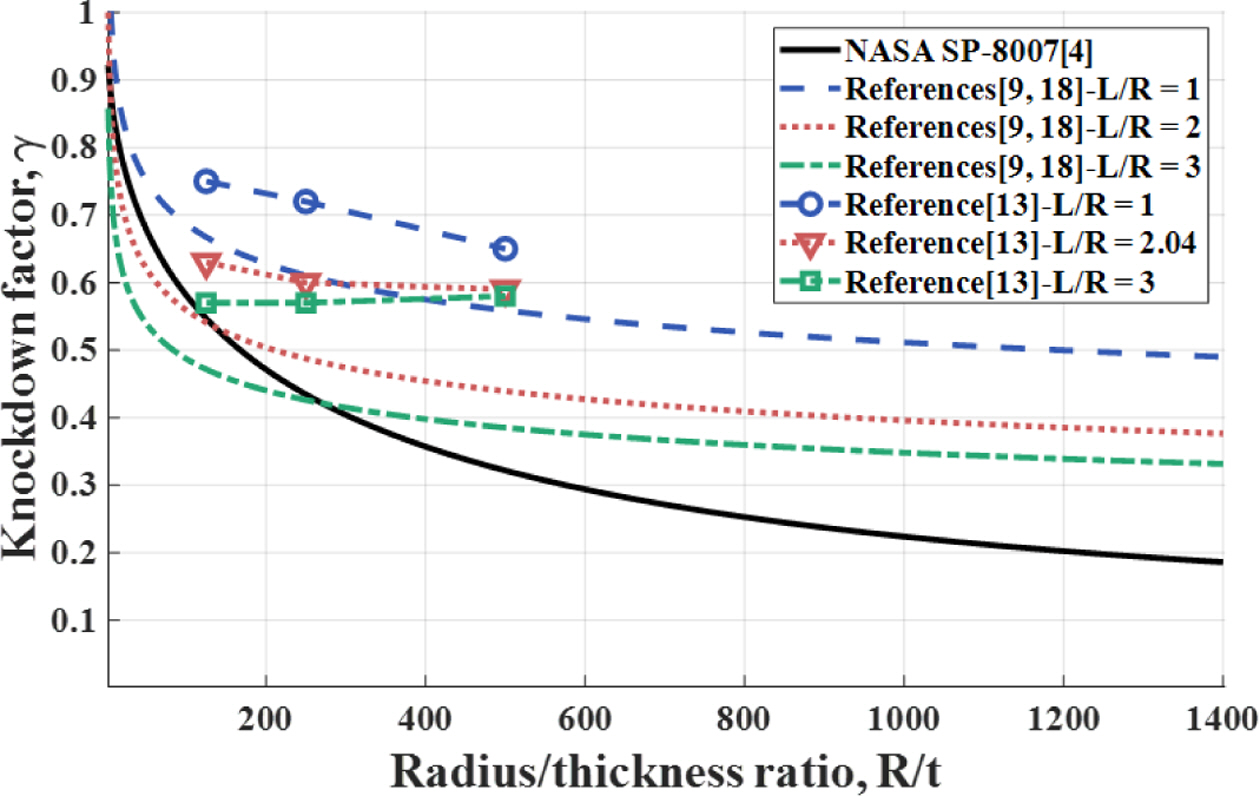
얇은 원통 구조에 대한 좌굴 설계 기준으로 지금까지 이용되고 있는 NASA의 좌굴 Knockdown factor[4]는 1930~ 60년대 압축력에 대한 좌굴 시험결과의 하한값을 이용하여 정립되었다. 그러나, NASA의 기존 좌굴 Knockdown factor [4]는 다음과 같은 한계점으로 인하여, 이를 이용할 경우 비교적 최근에 제작되는 얇은 쉘 구조가 과도하게 보수적으로, 즉 무겁게 설계된다[5-7]. 첫째, NASA의 좌굴 Knockdown factor는 주로 금속재 원통 구조의 좌굴 시험에 대한 결과로 이루어져 복합재 구조의 좌굴 거동을 적절히 고려하지 못한다. 둘째, 현대에 사용되는 첨단 재료 및 정밀 제작 기술의 특성을 반영하지 못한다. 셋째, 얇은 원통 구조의 반지름(R)과 두께(t)의 비율인 두께비(R/t)에 대한 함수로만 표현되었으며, 길이(L)와 반지름(R)의 비율인 세장비(L/R)의 좌굴 하중에 대한 영향이 무시되어 다양한 두께비(R/t)와 세장비(L/R)를 갖는 원통 구조에 대하여 세분화되지 않았다. 따라서 이를 보완 및 개선하기 위하여 NASA의 Shell Buckling Knockdown Factor(SBKF, [8]) 프로젝트, DLR의 New Robust Design Guideline for Imperfection Sensitive Composite Launcher Structures(DESICOS, [9]) 프로젝트, 중국[10-12], 및 한국[13-17]의 연구진들에 의하여 최소한의 좌굴 시험과 정교한 수치 해석 기반의 새로운 좌굴 Knockdown factor의 개선 및 도출 연구가 수행되고 있다. 특히, Fig. 1에서 보이듯, 등방성(isotropic) 및 링 패턴(ring pattern)의 pre-buckling 변형 형상을 갖는 준-등방성(quasi-isotropic) 복합재 원통 구조에 대한 수치 해석 기반의 새로운 좌굴 Knockdown factor의 하한 값이 정립되었으며[9,18], 복합재 원통 구조에 대한 다양한 두께비(R/t)와 세장비(L/R)에 대한 새로운 좌굴 Knockdown factor가 도출되었다[13].
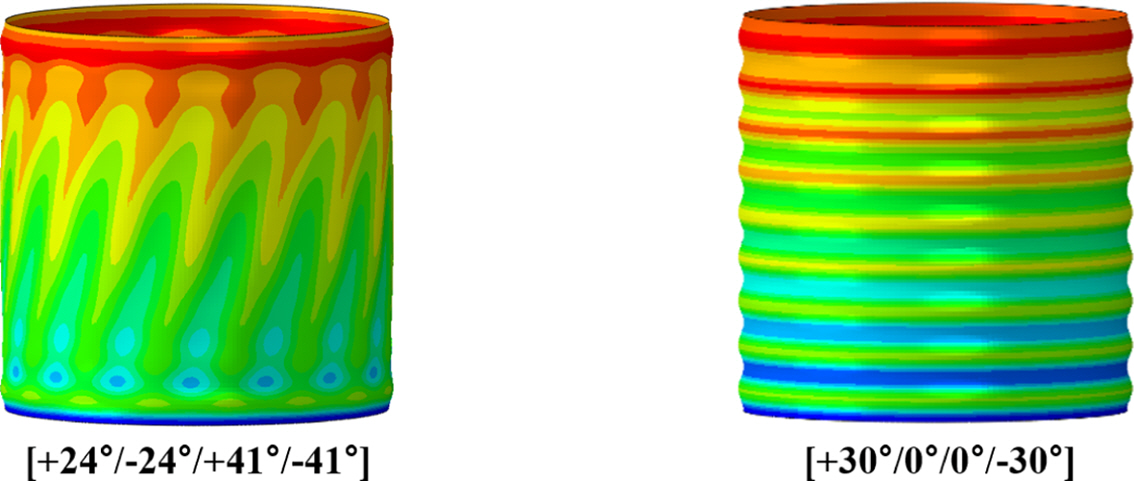
그러나, 복합재 원통 구조는 금속재 원통 구조와 달리, 기하학적 형상(두께비 및 세장비)이 동일하더라도 적층 각 및 적층 순서와 같은 적층 조건(lay-up condition)에 따라 다른 좌굴 하중을 갖는다[19]. 또한, Fig. 2의 초기 결함이 없는 복합재 원통 구조의 전역 좌굴이 발생하기 이전의 거동인, pre-buckling 단계에서의 타원(ellipse) 및 링(ring) 패턴의 변형 형상의 예시와 같이, 복합재 원통 구조의 적층 조건에 의한 pre-buckling 변형 형상이 좌굴 하중의 감소와 동반하는 좌굴 파형에 대한 영향을 끼치며, 이러한 pre-buckling 거동에 따라 기하학적 혹은 하중 불균일에 대한 서로 다른 민감도를 갖는다[18]. 따라서, 복합재 원통 구조의 좌굴 설계 시, 적층 조건(lay-up condition) 혹은 pre-buckling 패턴에 대하여, 적절한 기하학적 혹은 하중 불균일 모델에 대한 비선형 후좌굴 해석을 이용한 심도 있는 좌굴 Knockdown factor의 도출 연구가 필요하다.
본 연구에서는 복합재 원통 구조에 대하여 기하학적 초기 결함을 구현하는 Single Perturbation Load Approach (SPLA, [20])와 기하학적 초기 결함과 더불어 하중 불균일을 고려하는 Single Boundary Perturbation Approach(SBPA, [21])의 초기 결함 모델을 이용하여 복합재 원통 구조의 좌굴 Knockdown factor를 수치해석적으로 각각 도출하고, 이를 상호 비교하고자 한다. 상용 비선형 유한요소 해석 프로그램인 ABAQUS(ver 6.16)를 이용하여 복합재 원통 구조의 유한요소 모델링, 초기 결함 모델링, 및 비선형 후좌굴 해석을 수행하였다. 이때, 기하학적 혹은 하중 불균일에 대한 복합재 원통 구조의 좌굴 거동을 확인하기 위하여, 전역 좌굴이 발생하기 이전의 pre-buckling 거동에서 타원형의 좌굴 형상(Fig. 2(left))을 갖는 선행 연구[20]의 Z07 복합재 모델을 해석 모델로 선정하였다. 또한, 기하학적 초기 결함 모델인 SPLA 모델의 좌굴 Knockdown factor의 값은 동일한 초기 결함 모델을 이용한 본 연구진의 선행 연구[13]의 결과를 이용하였다. 본 연구를 통하여 SPLA 및 SBPA의 초기 결함 모델을 이용하여 도출된 좌굴 Knockdown factor를 NASA[4] 및 DLR에서 제안한 새로운 좌굴 Knockdown factor의 하한 값[9,18]과 상호 비교하여, 각각의 초기 결함 모델을 이용한 좌굴 Knockdown factor를 복합재 원통 구조에 적용할 경우, NASA[4] 및 DLR[9,18]의 기존의 좌굴 Knockdown factor 보다 경량 구조 설계가 가능함을 확인한다.

2.1 복합재 원통 구조 모델링
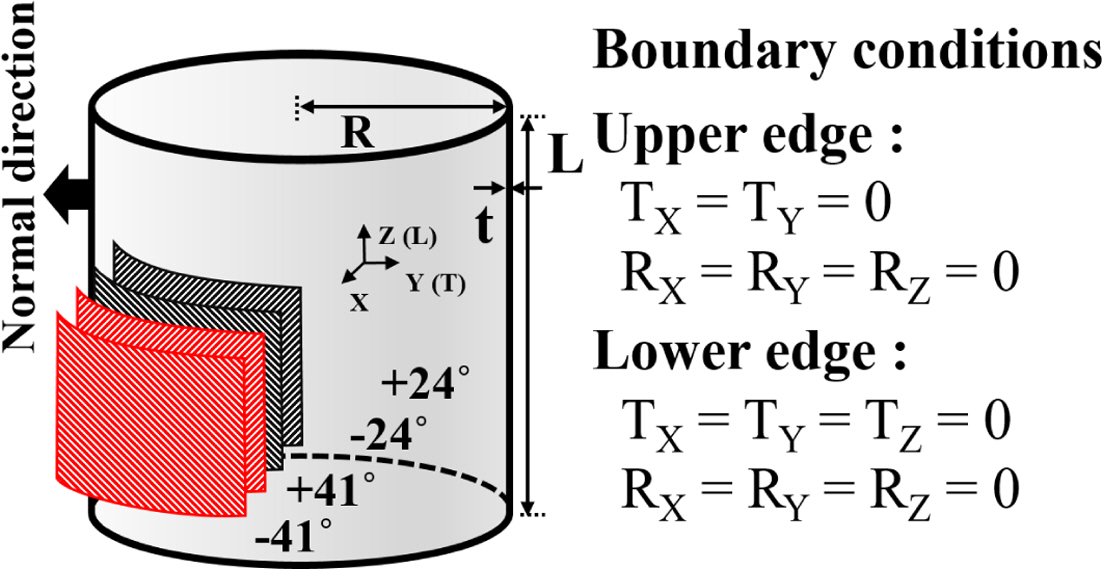
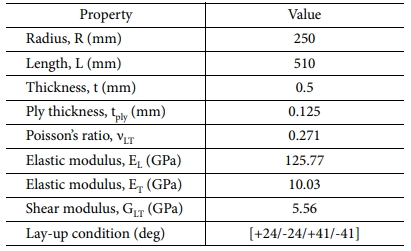
본 연구에서는 압축력에 대하여 초기 결함이 없는 완벽한 복합재 원통 구조의 좌굴 하중((N_cr)_perfect)이 최대값을 갖기 위하여 최적 설계된 DLR의 Z07 복합재 원통 구조[20]를 연구 모델로 선정하였다. Fig. 3 및 Table 1에 Z07 복합재 원통 구조(두께비(R/t)=500 및 세장비(L/R)=2.04)의 제원, 경계 조건, 및 재료 물성치를 나타내었다. ABAQUS의 4절점의 쉘 요소(S4R)를 이용하여 복합재 원통 구조의 유한요소 모델을 구축하였으며, 적층판의 섬유 방향은 원통 구조의 Z축의 길이 방향을 기준으로 정의하였다. 적층 순서는 원통 구조의 안쪽에서 바깥쪽으로 적층하였다. 유한요소의 크기는 선형 좌굴 해석의 좌굴 하중의 수렴을 통하여 5.6 mm로 선정하였다.

2.2 SBPA를 이용한 초기 결함 모델링
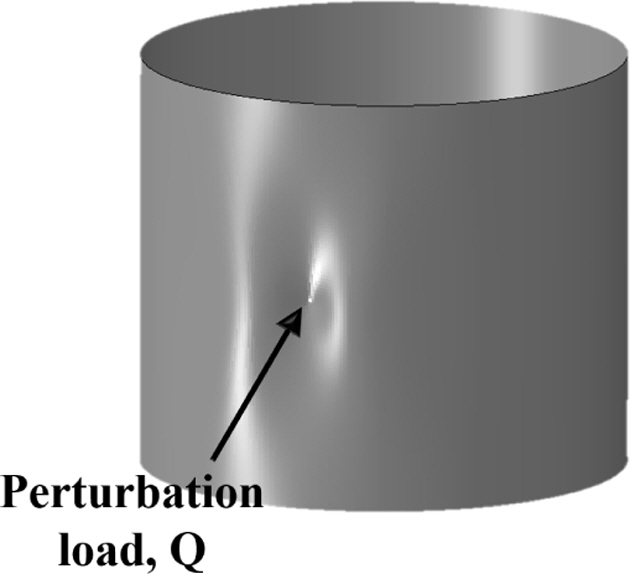
좌굴 Knockdown factor가 적용되는 원통 구조의 초기 설계 단계에서는 실제 구조물의 찍힘(dent), 불균일한 두께, 및 진원도(out of roundness)의 형상 편차와 같은 기하학적 초기 결함 혹은 우주 발사체의 단과 단 사이의 연결부에 의한 불균일한 하중의 작용 등과 같은 실제 결함 정보를 정량적으로 정의하는 것을 불가능하다. 그러므로, 본 연구에서는 SPLA[20] 및 SBPA[21]를 이용하여 얇은 복합재 원통 구조의 기하학적 혹은 하중 불균일의 초기 결함을 수치해석적으로 모델링한다. SPLA[20] 및 SBPA[21]의 초기 결함 기법은 실제 얇은 쉘 구조의 기하학적 혹은 불균일한 하중이 가해지는 초기 결함 특성을 적절히 구현할 수 있으며, 초기 결함의 모델링이 용이하여 다양한 선행 연구[8,9,12-18]에서 사용된 기법이다. Fig. 4는 원통 구조 길이의 중간에서 원의 중심 방향으로 교란 하중(perturbation load, Q)을 가하여 구현한 원통 구조의 single dimple 형상의 기하학적 초기 결함 모델(SPLA 모델)을 나타낸다. SPLA[20]의 기하학적 초기 결함 모델을 이용한 비선형 후좌굴 해석 과정은 본 연구진의 선행 연구[13-17]에 상세히 주어져 있다.
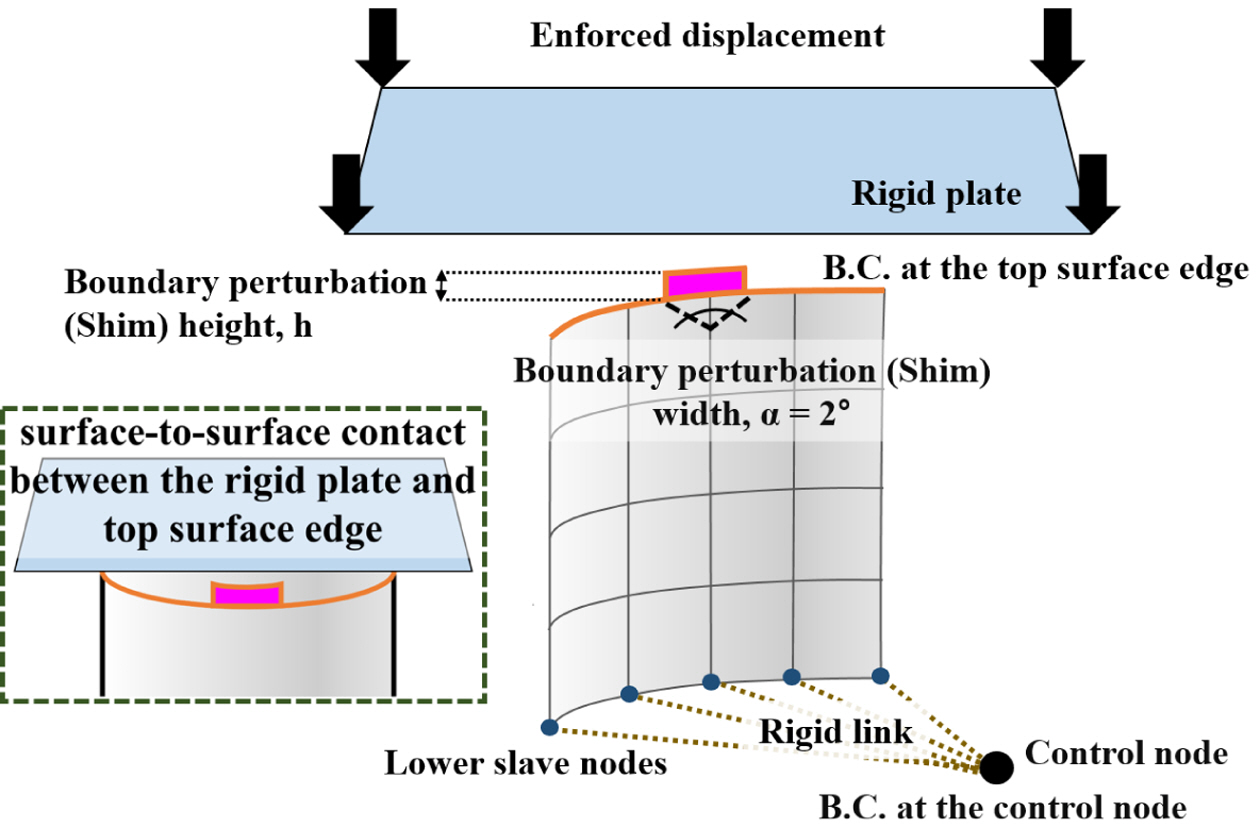
SBPA[21]를 이용한 초기 결함 모델은 single dimple 형상의 기하학적 초기 결함과 더불어 하중 불균일을 동시에 구현할 수 있다. 이를 위하여 강제 변위가 가해지는 강체 평판과 끝 단에 얇은 쉘 단편(shim)이 있는 원통이 접촉되도록 모델링한다(Fig. 5). DLR의 선행 연구[21]를 기반으로 하여, 쉘 단편의 폭은 원통의 원주 방향에 대하여 2°로 설정하였으며, 쉘 단편의 높이(h)를 증가시키면서 후좌굴 해석을 반복 수행한다. 강체 평판과 원통 상단(top surface edge)의 접촉 모델링은 ABAQUS의 surface-to-surface contact을 이용하였으며, 원통의 상단에 Fig. 3에서 주어진 경계 조건을 적용하였다. 원통 하단에는 고정 지지를 가하기 위하여, 하단에 있는 부절점(lower slave nodes)들을 원통의 중심에 있는 제어 절점(control node)에 강체 연결(rigid link)하였다. 강체 연결로 구속된 절점들은 제어 절점과 6자유도를 공유하며, 제어 절점에 경계 조건을 부여하였다.

2.3 비선형 후좌굴 해석 기법
본 연구에서는 주어진 SBPA의 초기 결함 모델에 대하여 얇은 복합재 원통 구조의 국부, 전역, 및 후좌굴 상태의 좌굴 거동을 살펴보기 위하여 변위 제어(displacement control)기반의 뉴턴-랩슨(Newton-Raphson) 방법을 이용하여 비선형 후좌굴해석을 수행한다[13-17].
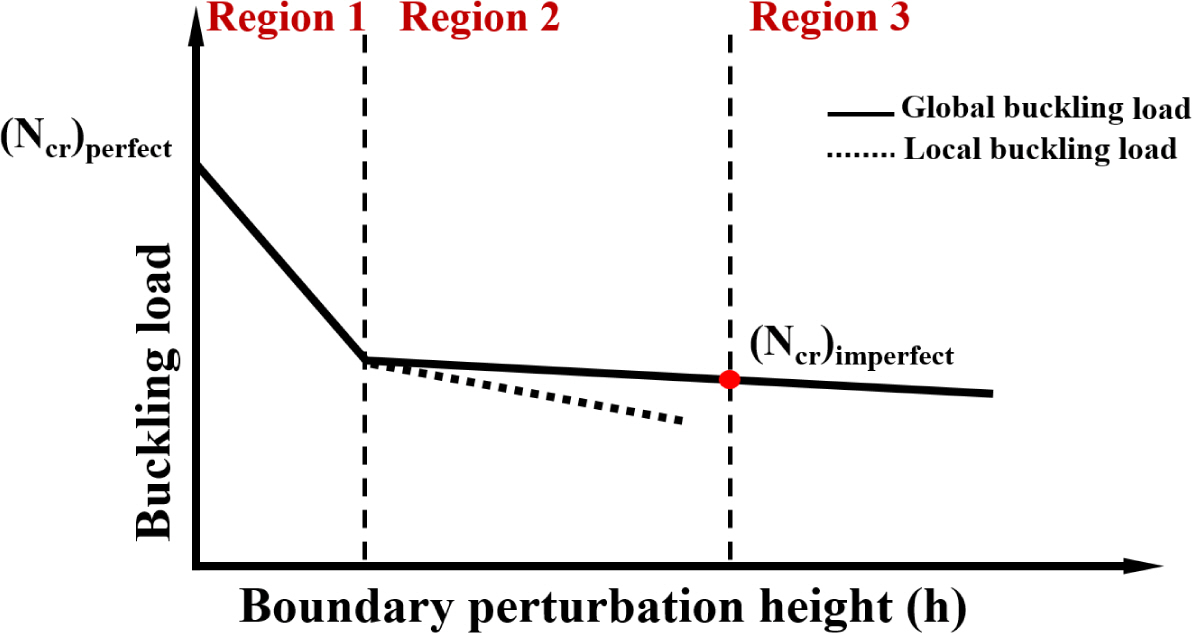
선행 연구[22]에서는 본 연구의 복합재 원통 구조 모델[20]과 동일한 적층 조건을 갖지만 세장비가 다소 작은 (L/R=2) 복합재 원통 구조에 대하여 좌굴 Knockdown factor를 도출하였으나, 좌굴 형상, 하중-변위 선도, 및 쉘 단편(shim)의 높이(h)에 따른 좌굴 거동에 대한 결과가 상세하게 제시되지 않았다. 따라서, 본 연구에서는 Z07 복합재 원통 구조[20]에 대하여 Fig. 6과 같이 초기 결함을 고려한 좌굴 거동의 특성을 상세하게 조사하기 위하여 쉘 단편의 높이(h)에 따라 하중-변위 선도 및 좌굴 형상을 3 종류의 영역(Region)으로 분류하고 그 결과를 상세하게 살펴본다. Region 1은 쉘 단편의 높이(h)가 증가하면서 전역 좌굴 하중((N_cr)_imperfect)이 급격히 선형적으로 감소하는 구간이다. Region 2에서는 쉘 단편의 높이가 일정 크기보다 커지면, 국부 좌굴이 발생하고 동시에 전역 좌굴 하중((N_cr)_imperfect)이 점근적으로 수렴한다. Region 3에서는 쉘 단편의 높이가 증가될 때, 비교적 완만한 스냅-스루(smooth snap-through)가 발생하며, 전역 좌굴 하중((N_cr)_imperfect)만 발생하여 그 크기가 점근적으로 수렴한다. 마지막으로, Region 3에서의 수렴된 전역 좌굴 하중((N_cr)_imperfect)과 식 (1)을 이용하여 좌굴 Knockdown factor를 도출한다.
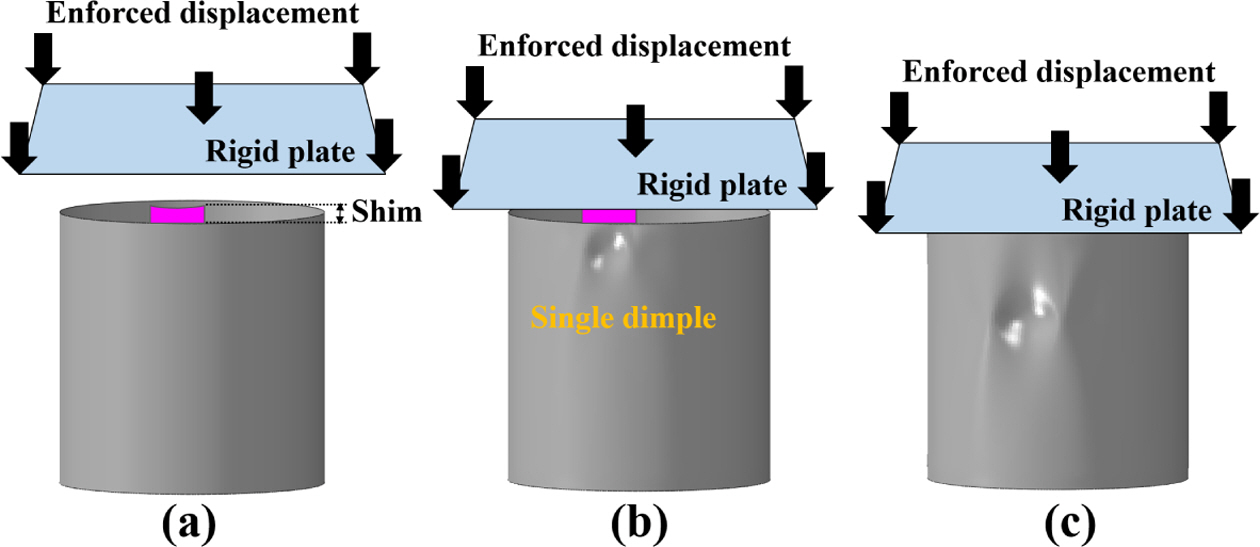
전술한 내용을 기반으로, 얇은 복합재 단순 원통 구조의 기하학적 초기 결함과 하중 불균일을 동시에 고려할 수 있는 SBPA 결함 모델의 비선형 후좌굴 해석 절차는 다음과 같이 요약된다(Fig. 7).
1) 초기 결함이 없는 완벽한 원통 구조 모델의 끝 단에 얇은 쉘 단편과 강체 평판을 모델링하며, 강체 평판에 강제 변위를 적용하여 뉴턴-랩슨 기반의 후좌굴 해석을 수행한다(Fig. 7(a)).
2) 강체 평판과 끝 단에 얇은 쉘 단편이 있는 원통 구조가 접촉하면서 기하학적 초기 결함(single dimple)과 불균일한 하중이 동시에 구현된다(Fig. 7(b)). 이후, 원통에 가해지는 강체 평판에 의한 강제 변위가 증가하면서, 원통 구조 끝단의 기하학적 초기 결함이 원통의 길이 방향의 중앙으로 이동함과 동시에 전역 좌굴 및 후좌굴이 발생한다(Fig. 7(c)).
3) 앞의 1)-2)의 해석 절차를 쉘 단편의 높이(h)를 증가시키면서, 전역 좌굴 하중((N_cr)_imperfect)의 수렴 및 Fig. 6의 Region 3에 도달할 때까지 반복 수행한다.
4) 3)에서 얻어진 전역 좌굴 하중((N_cr)_imperfect)과 식 (1)을 이용하여 좌굴 Knockdown factor를 도출한다.

3.1 쉘 단편의 높이에 따른 좌굴 거동
3.1절에서는 2.2 및 2.3절에서 전술한 내용을 바탕으로, 쉘 단편의 높이(boundary perturbation height, h)에 따른 좌굴 거동을 3가지의 영역으로 나누어서 확인한다. 본 연구에서 이용한 복합재 원통의 초기 결함이 없는 모델의 전역 좌굴이 발생하기 이전의 형상, 즉 pre-buckling 형상은 Fig. 2의 타원형의 변형 형상이다.
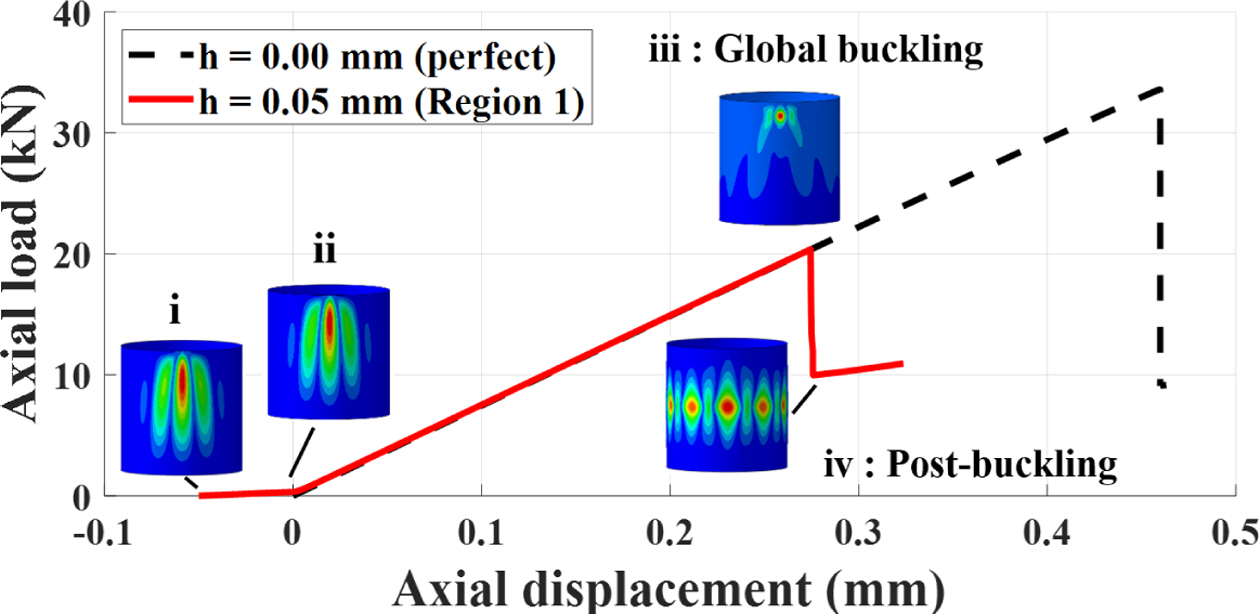
Region 1(h=0.05 mm)에서의 하중-변위 선도 및 좌굴 형상을 Fig. 8에 나타내었다. 그림에서 보이듯, 강체 평판에 강제 변위가 가해지면서, 강체 평판과 쉘 단편이 있는 원통과의 접촉이 발생한다(i). 다음으로, 강체 평판이 쉘 단편의 높이(h)만큼 원통 구조의 축 방향으로 이동하여 원통 끝 단의 상단 부와 강체 평판의 전체 접촉(full-contact)이 발생한다(ii). 이후, 축 방향의 강제 변위가 더욱 증가하면서 압축력이 증가한다(ii-iii). 축 방향의 하중이 원통 구조의 전역 좌굴 하중 크기에 도달하면, 축 방향의 강성이 급격히 감소하며 좌굴 파형이 복합재 원통 구조의 원주 방향으로 확산된다(iii-iv). Region 1에서의 전역 좌굴 하중은 20.37 kN으로 계산되었다.
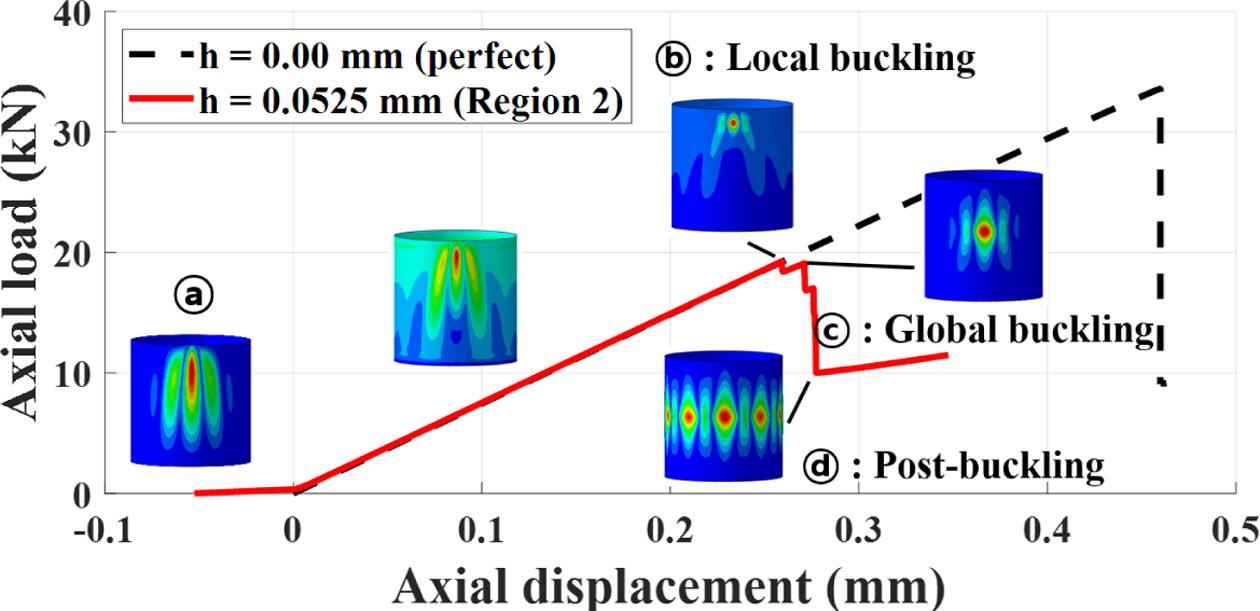
Region 2(h=0.0525 mm)의 경우에도(Fig. 9), 앞의 Fig. 8의 결과와 유사하게 강체 평판이 쉘 단편의 높이만큼 이동하는 축 방향의 압축 거동이 발생한다. 압축력이 더욱 증가하며(ⓐ-ⓑ), 전역 좌굴이 발생하기 이전에 국부 좌굴(local snap-through)이 발생한다(ⓑ). 국부 좌굴이 발생한 이후, 축 방향 강성의 감소 및 좌굴 형상(single dimple)의 크기 증가와 함께 전역 좌굴이 발생한다(ⓑ-ⓒ). 축 방향의 강제 변위가 더욱 증가하면서, 전역 좌굴 이후에 축 방향 강성이 감소하고 좌굴 파형이 원주 방향으로 급격히 확산되는 후좌굴이 발생한다(ⓒ-ⓓ). h=0.0525 mm의 Region 2에서 얻어진 국부 좌굴 하중은 19.25 kN이며, 전역 좌굴 하중은 19.09 kN으로 계산되었다.
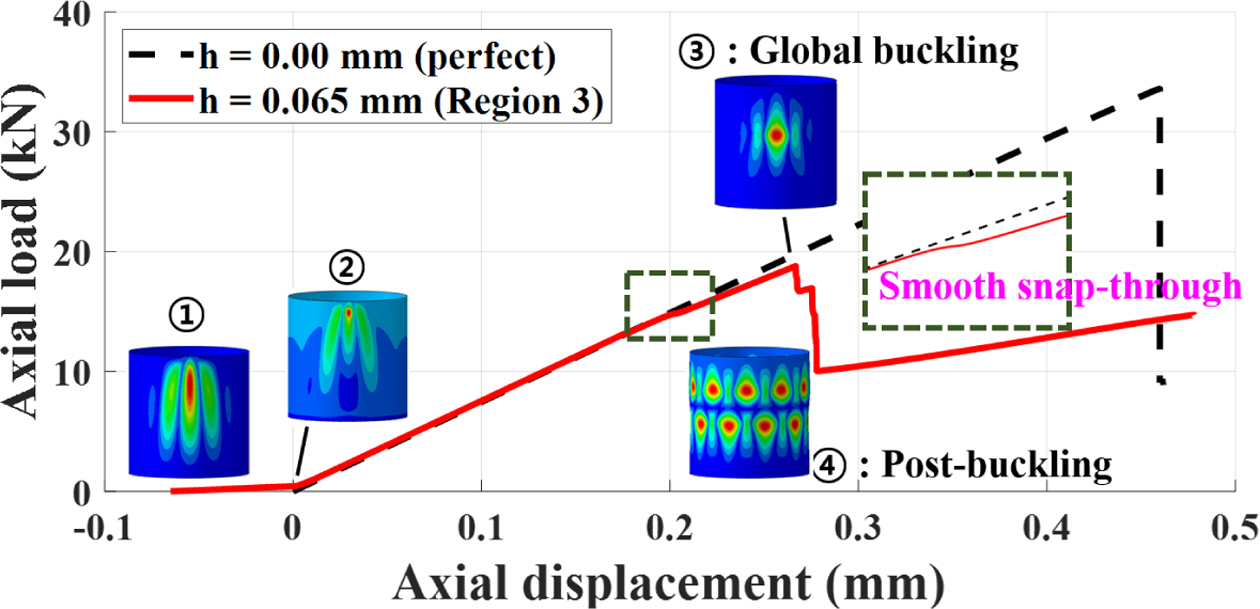
마지막으로, 좌굴 Knockdown factor 도출을 위한 초기 결함을 고려한 전역 좌굴 하중의 기준이 되는 Region 3(h=0.065 mm)의 비선형 후좌굴 해석 결과를 Fig. 10에 정리하였다. Region 3에서는 Fig. 8 및 9의 결과와 동일하게 강체 평판과 쉘 단편이 있는 원통의 접촉 거동이 발생한다 (①-②). 그러나, 국부 좌굴은 관찰되지 않으며, 비교적 완만한 스냅-스루가 발생하며, 전역 좌굴(③)만 발생하였다. 계산된 전역 좌굴 하중의 크기는 18.78 kN으로, 전역 좌굴이 발생한 이후, 원통 구조의 축 방향 강성 및 하중-지지 능력(load-carrying capacity)이 급격히 감소하며 후좌굴(④)이 발생하였다.
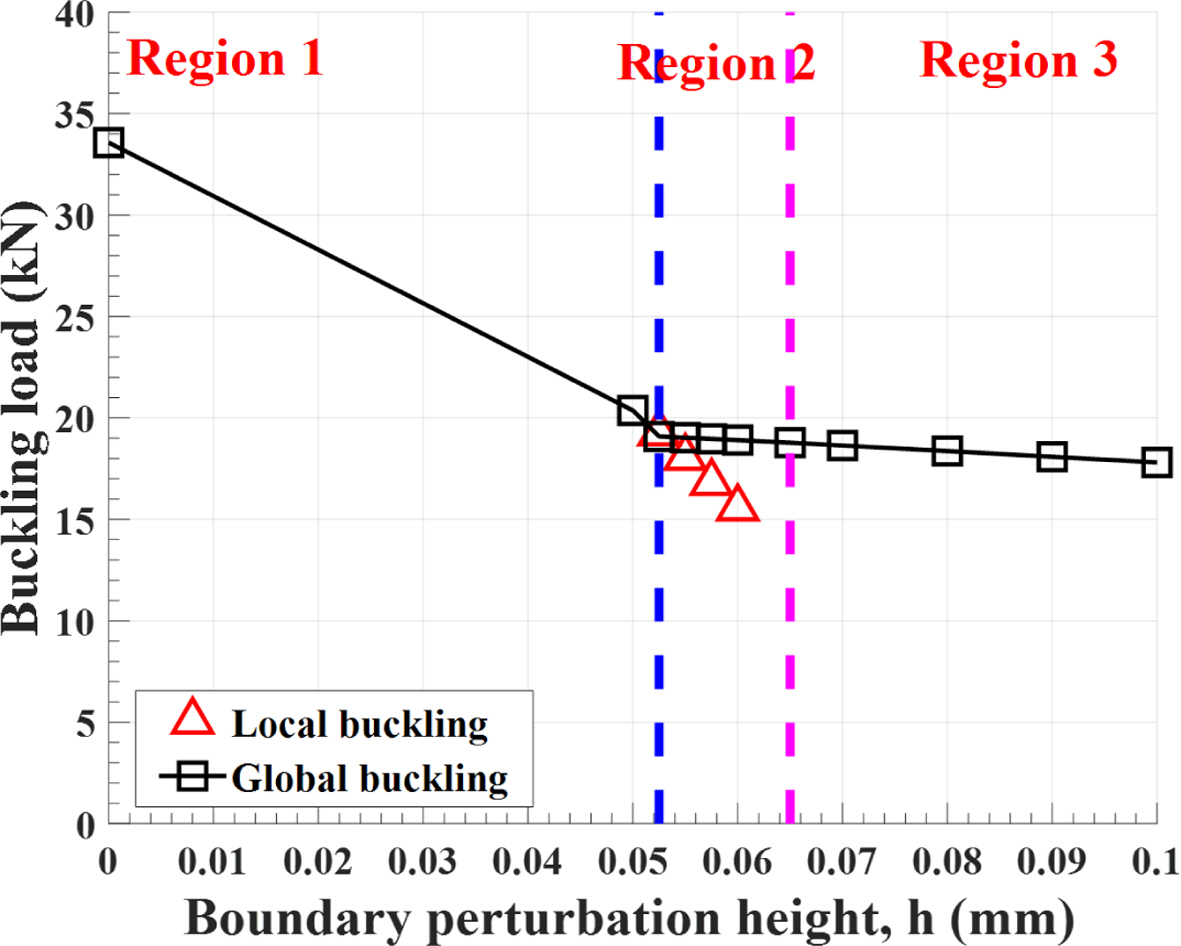
Fig. 8~10에 주어진 쉘 단편의 높이(h)의 증가에 대한 비선형 후좌굴 해석 결과를 요약하여 Fig. 11에 정리하였다. 그림에서 보이듯, Region 2에서 국부 좌굴이 전역 좌굴과 동시에 발생하며, 전역 좌굴 하중이 점근적으로 수렴하는 것을 확인할 수 있다. Region 3에서는 전역 좌굴만 발생하며, 여전히 전역 좌굴 하중이 쉘 단편의 높이의 증가에 따라 점근적으로 수렴한다. Fig. 11에서 사용된 쉘 단편의 높이(h)의 크기는 Table 1에 정리된 복합재 원통 구조의 크기에 비하여 상당히 작은 값이나, Fig. 8~10의 후좌굴 해석의 하중-변위 그래프에서 전역 좌굴 발생 시의 축 방향 변위의 크기와 비교 시, 19~25%에 해당되므로 좌굴 거동의 관점에서는 큰 결함임을 알 수 있다.
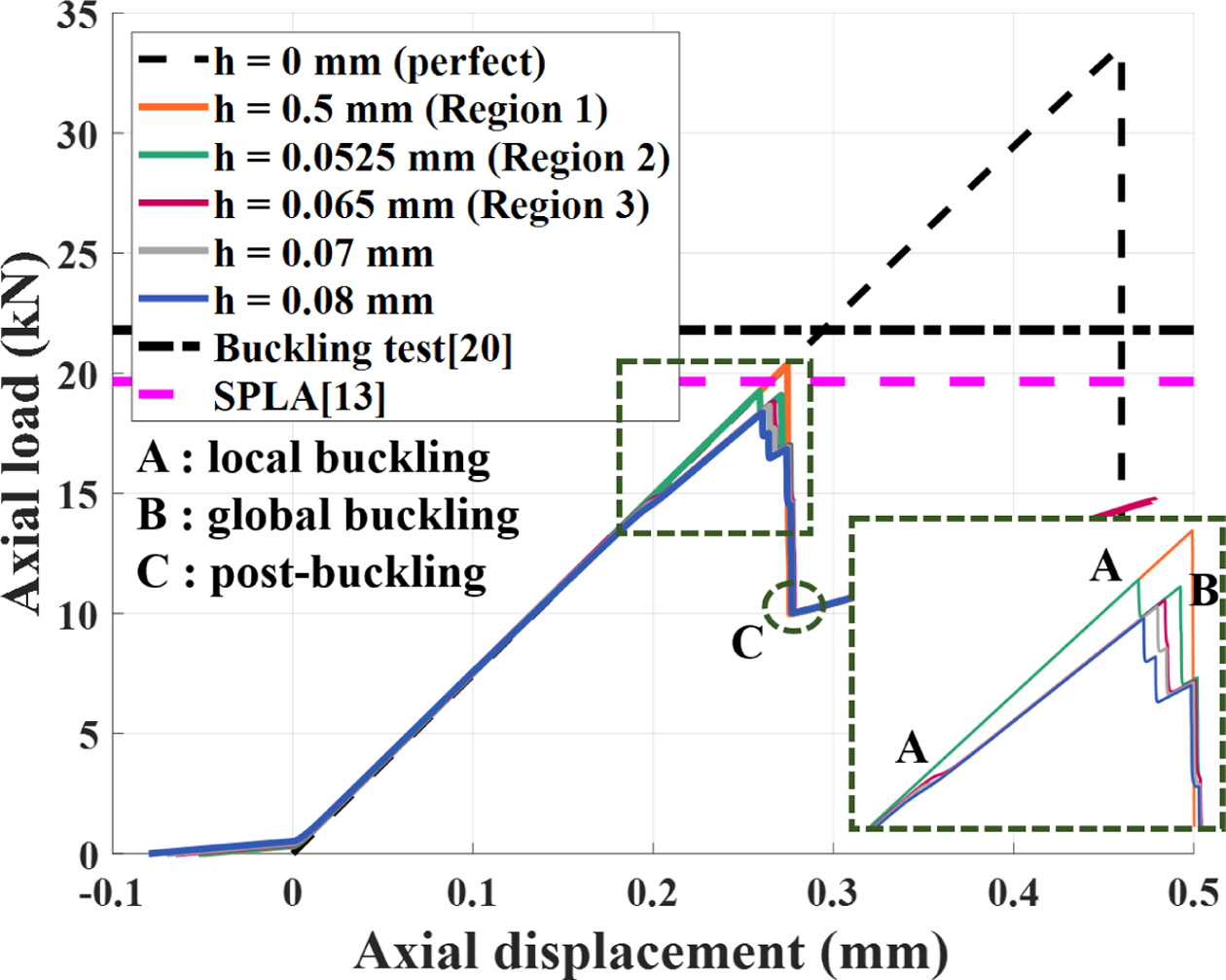
Fig. 12는 본 연구의 SBPA 모델을 이용한 하중-변위 선도를 좌굴 시험[20] 및 SPLA 모델[13]을 이용한 전역 좌굴 하중 결과와 함께 나타낸 결과이다. 초기 결함이 없는 완벽 구조의 전역 좌굴 하중((N_cr)_perfect)은 33.57 kN으로 계산되었다. 주어진 그림에서도 SBPA 모델의 쉘 단편의 높이에 따른 Region 2 및 3에서의 전역 좌굴 하중의 수렴을 확인할 수 있으며, 본 연구에서는 Region 3(h=0.065 mm)의 전역 좌굴 하중(18.78 kN)을 수렴한 전역 좌굴 하중, 즉 초기 결함을 고려한 전역 좌굴 하중((N_cr)_imperfect)으로 정의하였다. 좌굴 시험[20]과 SPLA 모델[13]의 전역 좌굴 하중((N_cr)_imperfect)은 각각 21.80 kN 및 19.66 kN으로, SBPA 모델의 전역 좌굴 하중이 좌굴 시험[20]대비 약 14% 그리고 SPLA 모델[13]대비 약 4%만큼 낮게 즉, 보수적으로 계산되었다.

3.2 좌굴 Knockdown factor
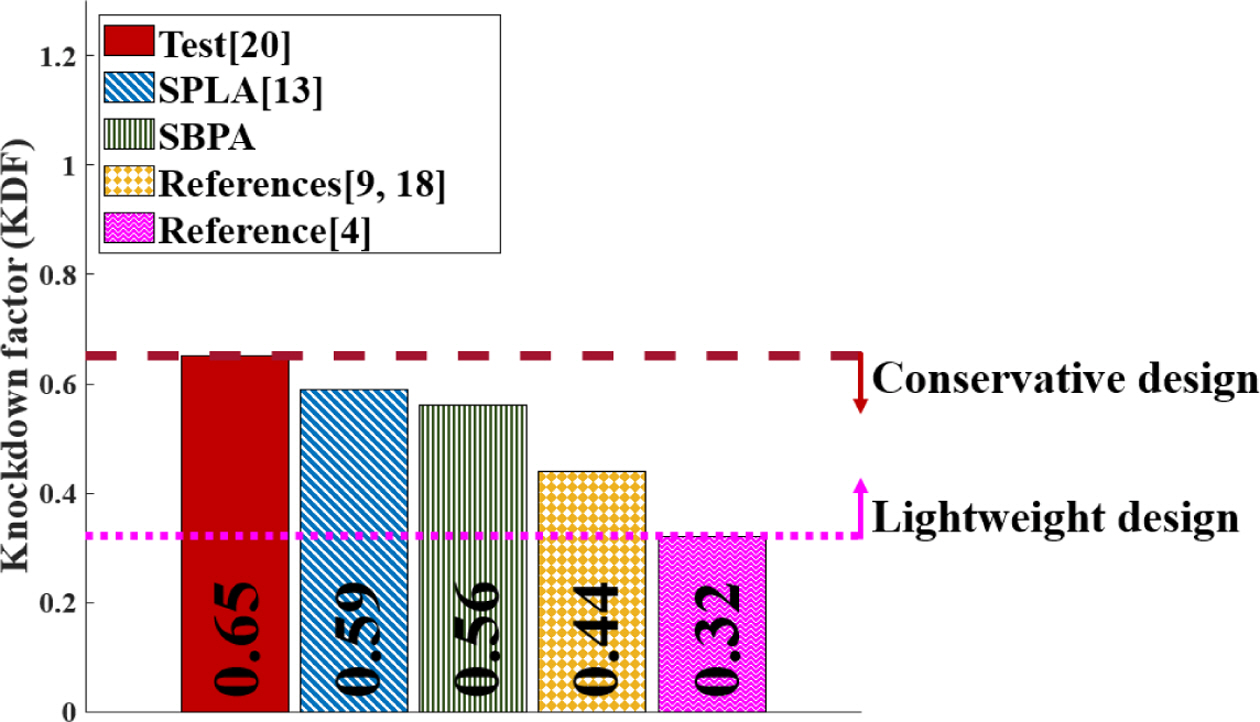
Fig. 13에 본 연구진의 SPLA 모델[13]과 SBPA 모델의 좌굴 Knockdown factor를 좌굴 시험[20], DLR에서 제안한 좌굴 Knockdown factor의 하한 값[9,18], 및 NASA의 좌굴 Knockdown factor[4]와 함께 정리하여 비교하였다. Z07 복합재 원통 구조[20]에 대하여 기하학적 초기 결함을 구현한 SPLA 모델[13]과 기하학적 초기 결함과 더불어 하중 불균일을 함께 고려한 본 논문의 SBPA 모델의 좌굴 Knockdown factor는 각각 0.59 및 0.56으로 얻어져, 좌굴 시험[20] 대비 약 9% 및 14% 낮게 계산되었다. 도출된 좌굴 Knockdown factor는 NASA의 좌굴 Knockdown factor[4]보다 모두 높은 값으로, 주어진 타원형의 pre-buckling 거동을 갖는 Z07 복합재 모델에 대하여 SPLA 및 SBPA 모델이 좌굴 시험보다 보수적인 설계의 제공이 가능하며, 동시에 NASA의 좌굴 Knockdown factor[4]에 비하여 복합재 원통 구조의 경량 구조 설계가 가능함을 알 수 있다. 또한, DLR에서 제공한 새로운 좌굴 Knockdown factor의 하한 값[9,18]에 비하여서도 여전히 SPLA 및 SBPA 모델의 좌굴 Knockdown factor가 약 34% 및 27% 높은 값으로 보다 높은 수준의 경량 설계가 가능함을 알 수 있다. 주어진 복합재 모델에 대하여서는 SPLA와 SBPA 모델의 좌굴 Knockdown factor는 매우 유사하게 얻어졌다.

본 연구를 통하여 타원 형상의 pre-buckling 거동을 갖는 얇은 복합재 원통 구조에 대하여 SPLA와 SBPA의 초기 결함 모델을 이용할 경우, 초기 결함 모델에 상관없이 NASA의 좌굴 Knockdown factor 대비 경량 구조 설계와 좌굴 시험 대비 보수적인 설계를 동시에 제공할 수 있는 좌굴 Knockdown factor를 도출할 수 있음을 확인하였다. 또한, 주어진 복합재 원통 모델에 대하여서는 SBPA 모델이 SPLA 모델에 비하여 보다 보수적인 설계를 제공함을 확인하였다. 그러나, 실제 우주 발사체 구조에 적용되는 복합재 원통 구조는 설계되는 적층 조건에 따라 다양한 pre-buckling 변형 형상을 가질 것이므로, 이를 고려한 심도 있는 후좌굴 해석 및 시험 연구가 수행되어야 할 것으로 사료된다. 따라서 본 연구를 바탕으로 링(ring) 패턴의 pre-buckling 거동을 갖는 복합재 원통 구조에 대하여 해석 및 시험 연구와 함께, 발사체 복합재 탱크 구조의 내부 압력을 압축력과 함께 고려한 연구를 심층적으로 수행될 필요가 있다.

본 연구는 과학기술정보통신부에서 시행한 한국형발사체개발사업의 지원을 받아 수행된 연구 결과입니다. 본 연구의 일부는 2021년도 한국복합재료학회 춘계학술대회 우수발표논문상으로 선정된 논문에서 발표되었습니다.