Composite materials have been widely applied for fabricating pressure vessels used for storing gaseous and liquid fuel because of their high specific stiffness and specific strength. Accordingly, the accurate measurement of their mechanical property, particularly the burst pressure or fracture strain, is essential prior to the commercial release. However, verification of the safety of composite pressure vessels using conventional test methods poses some limitations because it may lead to the deformation of the load transferring media or provoke an additional energy loss that cannot be ignored. Therefore, in this study, the segment-type ring burst test device was designed considering the theoretical load transferring ratio and applicable displacement of the vertical column. Moreover, to verifying the uniform distribution of pressure of the segment type ring burst test device, the hoop stress and strain distribution of ring specimens were compared with that of the hydraulic pressure test method via FEM. To conduct a simulation of the fracture behavior of the composite pressure vessel, a Hashin failure criterion was applied to the ring specimen. Furthermore, the fracture strain was also measured from the experiment and compared with that of the result from the FEM

복합재료는 높은 비 강성 및 비 강도 특성으로 인해 기체 혹은 액체 연료를 저장하기 위한 압력용기의 설계 및 제작에 널리 활용되고 있다. 이에 따라, 압력용기의 파열 압력 또는 파단 변형률의 기계적 특성의 보다 정확한 측정은 상용화 전 필수적 요소이다. 그러나, 복합재료 압력 용기의 안전성 검증을 위한 기존의 시험 방법은 하중 전달 매체의 변형으로 인한 추가적인 에너지 손실과, 불필요한 하중 및 모멘트의 발생 등의 한계가 있다. 따라서 본 연구에서는, 이론적인 하중 전달정도와 적용가능한 수직방향 변위를 고려하여 세그먼트 형 링 버스트 시험장치를 설계하였다. 또한, 원주 방향의 균일한 압력분포를 검증하기 위해 수치해석을 활용하였고, 수압 시험법과 세그먼트 형 링 버스트 시험법의 원주 방향 응력 및 변형률 분포를 비교하였다. 복합재료 압력용기의 파괴 거동을 모사하기 위해 Hashin 파단 기준을 적용하였고, 실험적으로 파단 변형률을 측정하여 이를 수치해석 결과와 비교하였다

Keywords: 복합재료(Composite materials), 압력용기(Pressure vessels), 시험 장치(Test methods), 파괴 압력 (Burst pressure)

물이나 모든 에너지 원에서 생성될 수 있는 수소 연료는 주요한 대체 친환경 에너지로 기대된다. 하지만 수소 기체는 고압(30~70 MPa)으로 압축되어 압력 용기에 저장되어야 하기에 압력 용기의 설계 시 파열없이 고압 조건을 견딜 수 있는지 검증해야 한다[1,2]
. 압력용기의 설계 시, 높은 비 강도와 비 강성을 가진 복합 재료가 금속의 대체재로서 널리 활용되고 있다. 이전 연구에 따르면 복합 재료를 활용하는 압력 용기의 제작은 기존 금속 압력 용기에 비해 그 중량을 최대 40%까지 줄일 수 있어 무게 대비 더 나은 성능을 보여줌을 확인하였다[3,4]. 그러나 재료의 특성과 제조 공정의 차이로 인해 복합 재료의 신뢰성을 예측하는 것은 기존의 금속 압력 용기와 비교할 때 큰 어려움이 있다는 단점이 있다[5]. 따라서 고압 조건에서 사용되는 압력 용기 제작에 복합 재료를 사용하기 위해서는 그 안전성을 필수로 검증해야 하며 관련 연구가 활발히 진행 중이다.
기존의 전통적인 압력용기 시험 방법은 수압을 가하여 압력 용기의 파단 특성을 평가하였고, 이 경우 전체 모델의 필라멘트 와인딩(Filament winding) 압력 용기가 활용된다 [6,7]. 하지만, 전체 모델을 사용하여 수압 시험을 수행하는 것은 매우 정확하지만 상대적으로 긴 제작시간과 높은 비용이 발생한다는 단점이 있다. 따라서 본 연구에서는 전체 모델이 아닌 링 모양의 표본을 사용하여 보다 경제적으로 파열 압력을 평가하는 방법을 고안하였다.
일반적으로 링 시편에 내압을 가하기 위해 PTFE (Polytetrafluoroethylene) 혹은 고무 관을 활용하여 유압을 가하는 방법과 기계적 구조를 활용하는 방법이 있다. 유압을 활용한 시험방법은 직접적으로 링 시편에 내압을 전달하지만, 하중 전달 재료의 시험 중 영구적 변형으로 인해 초기 형상으로 복원시 추가적으로 고온에서 긴 시간동안 풀림 작업이 필요하다는 단점이 있다[8,9]. 또한, 시편 모서리에서 고무 관의 과도한 팽창은 응력 집중을 유발하고 이는 원치 않는 조기 파단을 유발한다. 따라서 링 시편의 양쪽 모서리에 추가적인 보강재가 필요하고, 이를 위해 유한 요소 분석(FEA)을 활용하여 시편 유형에 따른 보강층의 재료 유형과 치수를 결정해야 하는 단점이 있다.
한편, 기계적 구조를 활용한 링 버스트 시험 방법 또한 여러 연구를 통해 개발이 진행되었다. 분할 원반(Split disk) 시험 장치는 링 시편의 원주방향 겉보기 인장 강도를 평가하기위한 표준 시험방법이다[10]. 본 방법은 분할 원반을 통해 링 시편에 원주방향 인장 하중을 부과하고, 링 시편의 게이지(Gage) 영역에서 파단이 발생한다. 하지만 링 시편에 압력을 가할 때 두 개의 분할 원반 사이에서 링 시편의 굽힘 모멘트가 발생 가능하고, 시험 장치와 시편사이의 마찰에 의한 에너지 손실을 고려하지 못하는 단점이 있다. 따라서, 일반적으로 본 시험 방법을 통해 도출한 시험 결과는 이론적 결과보다 낮은 값을 보인다[11].
이와 더불어, 분할 된 금속 세그먼트(Segmented metallic disks)를 사용하여 링 시편의 반경 방향으로 보다 균일 한 압력을 가할 수 있는 시험법이 개발되었다[12-14]. 이 시험 방법은 만능 시험기에 의한 압축 하중을 금속 세그먼트를 통해 링 시편의 반경 방향으로 전달하는 시험법으로서, 세그먼트 사이의 틈으로 인해 균일 한 압력이 전달되지 못하는 단점이 있다. 또한 예상치 못한 조기 파손과 불안정한 응력 및 변형률의 측정을 방지하기 위해 링 시편에 추가 보강재가 필요하였다.
기존의 세그먼트 형 링 버스트 시험 장치의 한계를 극복하기 위해 본 연구에서는 링 시편에 균일 한 압력의 전달이 가능한 시험장치를 개발하였다. 이를 위해 이론적인 하중 전달률을 고려하였고, 이를 유한 요소(FE) 모델의 결과와 비교하여 세그먼트 수에 따른 변형률 분포를 확인하였고, 이를 통해 최적의 세그먼트의 수를 결정하였다. 또한, 변형률 오차를 더욱 줄이기 위해 링 시편과 세그먼트 사이에 PTFE를 두어 설계하였다. 실제 링 버스트 시험에서는 변형률 분포를 확인하기 위해 스트레인 게이지(Strain gage)를 활용하여 파단 변형률을 측정하였다.

2.1 세그먼트 형 링 버스트 시험법의 하중 관계
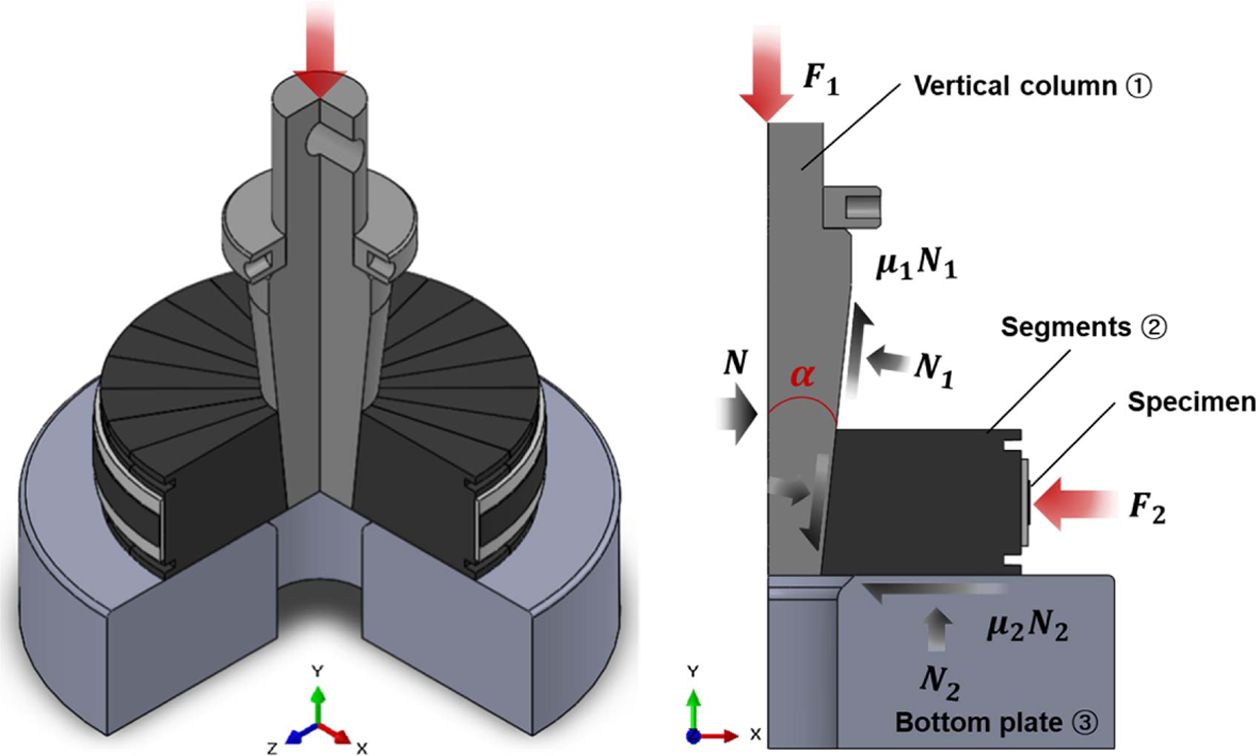
링 시편의 이론적 응력 및 변형률의 도출을 위해 링 시편에 가해지는 내부 압력을 계산하였다. Fig. 1은 축 대칭 링 버스트 시험 장치의 자유 물체도이다. 만능 재료 시험기를 통해 장치에 압축 하중(F₁)이 부과되고, 결과적으로 반경방향으로 하중(F₂)이 전달된다. a는 수직기둥과 세그먼트 사이의 접촉각을 의미한다. 또한, 각 접촉면에서 수직 하중(N₁, N₂)에 의해 마찰력이 발생하고, 부품의 연속적인 미끄러짐 거동을 고려하여 동적 마찰계수(μ₁, μ₂)를 활용하였다.
링 시편에 적용되는 내압의 도출을 위해 각 부품에서의 하중 평형방정식을 유도하여 최종적으로 F₁과 F₂ 하중사이의 하중 관계식을 도출하였고, 이는 식 (1)과 같다.



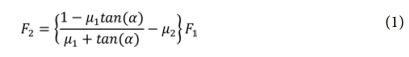
최종적으로 유도된 하중(F₂)을 링 시편 내부 면적으로 나누어 시편에 가해지는 내부 압력(P)의 도출이 가능하다.

2.2 링 시편의 이론적 응력 및 변형률 도출
두께가 있는 원통형 실린더 형상에서의 응력 및 변형률은 반경방향의 하중 평형 방정식을 유도하여 도출 가능하고, 이는 식 (2)와 같이 복합재료의 재료 물성 및 적층 수 그리고 와인딩 각도(Winding angle)를 고려하여 유도 가능하다[15].



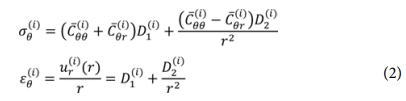
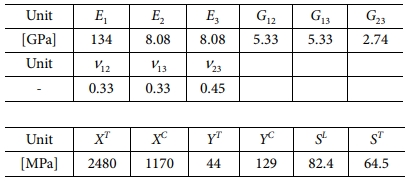
i는 각 적층 수를 의미하고 C͞͞는 축외 강성계수 그리고 D₁과 D₂는 경계조건으로부터 결정되는 적분상수를 의미한다. 따라서 Table 1의 실험을 통해 측정된 탄소섬유 복합재료의 강성 값을 활용하여 복합재료 링 시편에 작용하는 내압에 의한 원주방향 응력 및 변형률의 도출이 가능하다. 본 연구에서는 제작된 복합재료 압력용기의 와인딩 각도 [±89.4]₂를 고려하여 이론식에 적용하였다.

3.1 수치해석 모델
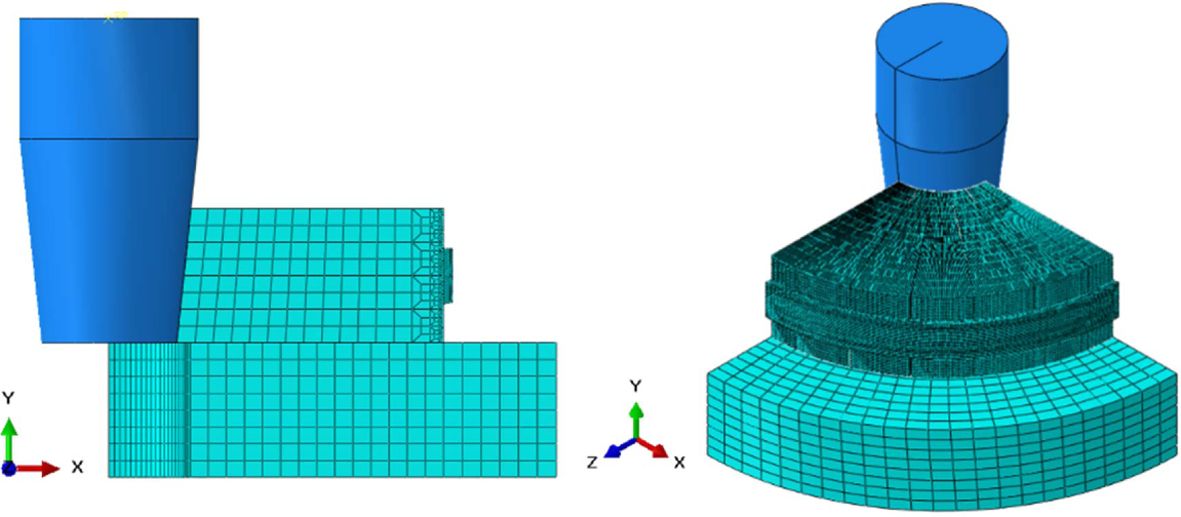
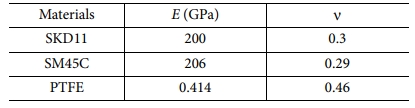
복합재료 압력용기의 기계적 물성 시험을 위해, 링 버스트 시험 장치를 설계하고 검증하기 위해 본 연구에서는 ABQUS/CAE (Dassault Systemes, USA) 응용 프그램을 활용하여 유한 요소 분석을 수행하였다. 3D, 8 절점 요소를 활용하여 1/4의 링 버스트 장치 모델을 구성하였고 이는 Fig. 2에 도시하였다. 또한 2D, 4 절점 면 요소를 사용하여 링 시편의 파괴 거동을 모사하였고, Hashin 파손 기준을 적용하였다. FEA에 활용된 복합재료 및 금속재료의 탄성 물성과 파괴 강도는 Table 1 그리고 Table 2에 명시하였다[16].

3.2 수치해석 기법 및 재료 물성 정보
링 버스트 시편의 파단 현상을 모사하기 위해 재료의 강성 저하의 시작점으로서 Table 3에 명시된 것과 같이 Hashin 파손 기준을 활용하였다. 이 방법은 탄성 취성 재료의 이방성 조건에서 파손을 예측하며 주로 섬유 강화 복합 재료에 활용된다. 복합 재료의 파괴를 모사하기 위해 섬유 인장, 압축 그리고 수지의 인장 및 압축거동의 총 4가지 파손 모드를 고려 가능하다. Hashin과 Rotem이 제안한 계수 값에 따라 계수는 α = 0 and S^T = 0.5Y^C로 설정하였다[17,18]. 또한, FEA의 수치적 오차를 조정하기 위해 링 시편의 원주 길이에 따른 요소의 크기를 조절하여 수치해석을 수행하였다.

4.1 링 버스트 시험 장치 설계
일반적으로 링 버스트 시험 장치는 복합재료 링 시편의 치수를 기반으로 설계되고, 본 연구에서는 반지름 150Φ 두께 0.5t의 시편을 기준으로 제작되었다.
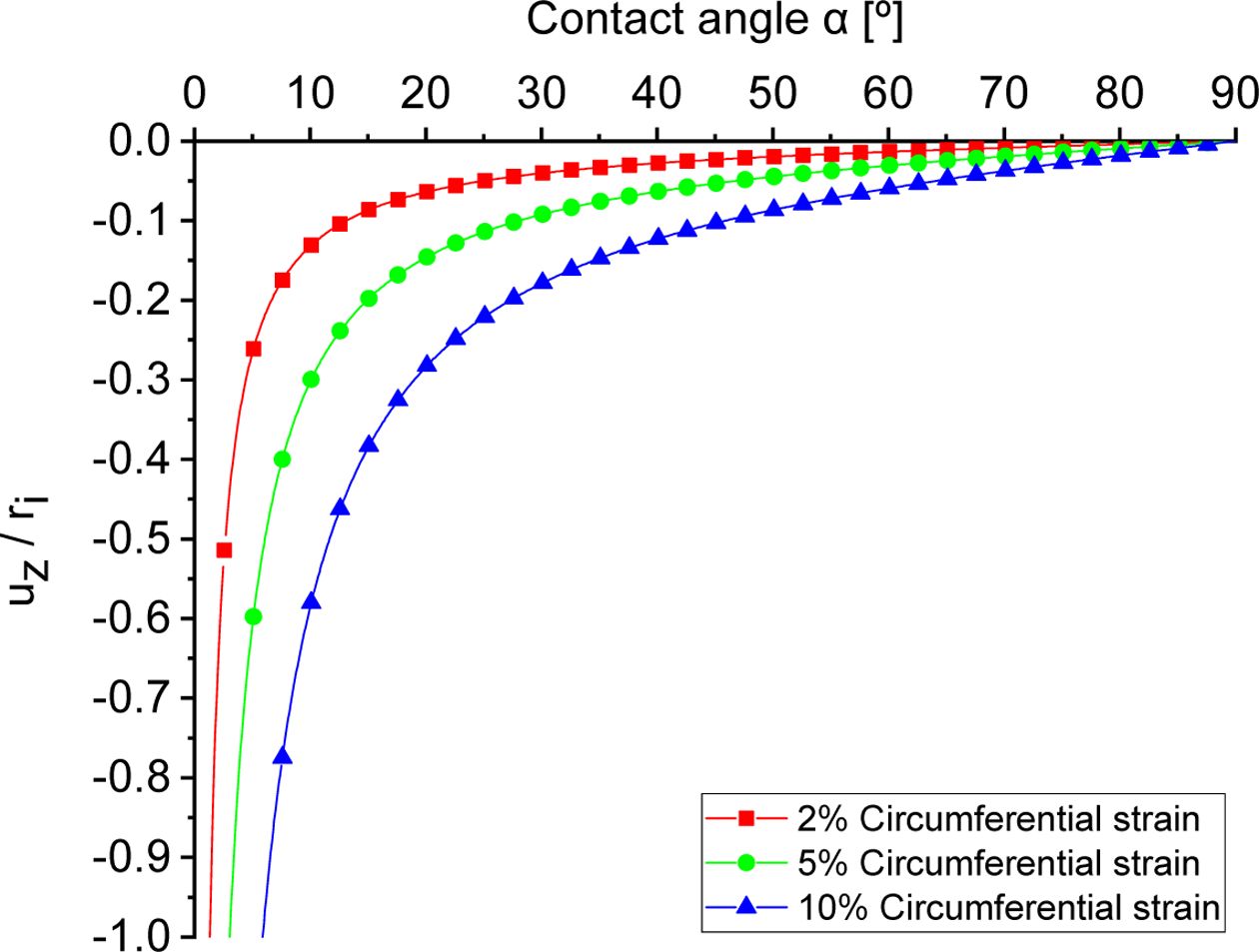
Fig. 1에서 확인할 수 있듯이, 수직 기둥과 세그먼트 사이의 접촉각(α)은 수직 기둥의 최대 변위(u_z)의 범위와 하중 전달률을 결정하는 요소이다. 접촉각 대비 수직 기둥의 변위 사이의 관계는 Fig. 3에 도시하였고, 접촉각 특성이 작아질수록 또는 요구되는 링 시편의 파단 변형률이 증가될수록 수직기둥에 더 큰 변위가 필요함을 확인 가능하다. 이와 같은 특성을 고려하여 2% 파단 변형률 조건에서 수직기둥이 시편의 반지름(r_i) 대비 약 20% 이내 (약 20 mm 이내)의 변위가 필요한 조건으로 장치를 설계하였고(α = 6°), 이 경우 식 (1)을 활용한 하중 전달률을 계산하면, 윤활조건 (μ₁ = μ₂ = 0.1)이라 가정하였을 때 적용 하중(F₁) 대비 약 5배 하중의 전달이 가능하다.
수압 시험 장치와 달리 세그먼트 형 링 버스트 시험 장치는 여러 세그먼트를 활용하는 구조적인 특징으로 인해 그 사이의 간격은 실험 중에 더욱 확장된다는 단점이 있다. 이와 같은 특징은 접촉 면적 주변에 국부적인 응력집중으로 인한 예측할 수 없는 조기 파손을 유발할 수 있다. 이러한 원주방향의 비 균일 응력 및 변형 분포는 링 시편의 정확한 파손 압력 및 변형을 측정하기 어렵게 만들기 때문에, 세그먼트 형 링 버스트 시험 장치를 설계하기 위한 FE 모델을 세그먼트 수에 따라 세분화하고, 링 시편의 원주방향 변형 분포를 조사하여 그 결과를 비교하였다.
또한 변형률 오차를 더욱 줄이기 위해 세그먼트와 링 시편 사이에 PTFE를 위치하였다. PTFE의 낮은 마찰 계수는 마찰에 의한 불필요한 에너지 손실을 감소시기는 장점이 있고, 낮은 강성으로 인해 기존의 금속재료에 비해 추가적으로 요구되는 불필요한 하중의 부과를 줄일 수 있다.

4.2 링 버스트 시험 조건
복합재료 링 시편은 탄소 섬유(T700, Toray, Japan)와 에폭시 수지(Epon826, Miller-Stephenson, USA)를 사용하여 제조되었다. 필라멘트 와인딩 장치를 활용하여 에폭시 수지가 함침 된 토우(Tow)를 알류미늄(Aluminium) 원통(A6061, 외경: 150 mm, 두께: 5 mm)에 1 kgf 장력 조건으로 원주 방향을 따라 5 mm 간격으로 감아 제작하였다. 복합재료의 경화 사이클은 6 h, 85^oC 그리고 6 h, 150^oC로 설정하였고, 온도 변화율은 ±1^oC/min이다. 제작된 총 길이 200 mm의 원통형 복합재료를 링 형상으로 가공하고, 시편의 모서리를 연마 처리하여 가공 과정에서 발생 가능한 결함을 줄였다. 최종적으로 제작된 링 시편의 제원은 내경 150 mm, 폭 12.7 mm, 두께 0.5 mm로 결정하였다. 링 버스트 시험 장치는 수직 기둥 및 세그먼트에 SKD11를 활용하고 하부 지지판에 SM45C를 활용하여 제작되었다. 수직 기둥을 범용 재료 시험기(5969, 미국 Instron)에 체결하여 압축 하중을 부가하였고, 크로스 헤드(Cross head)의 속도는 7.5 mm/s로 설정하였다.

4.3 링 버스트 시험 결과
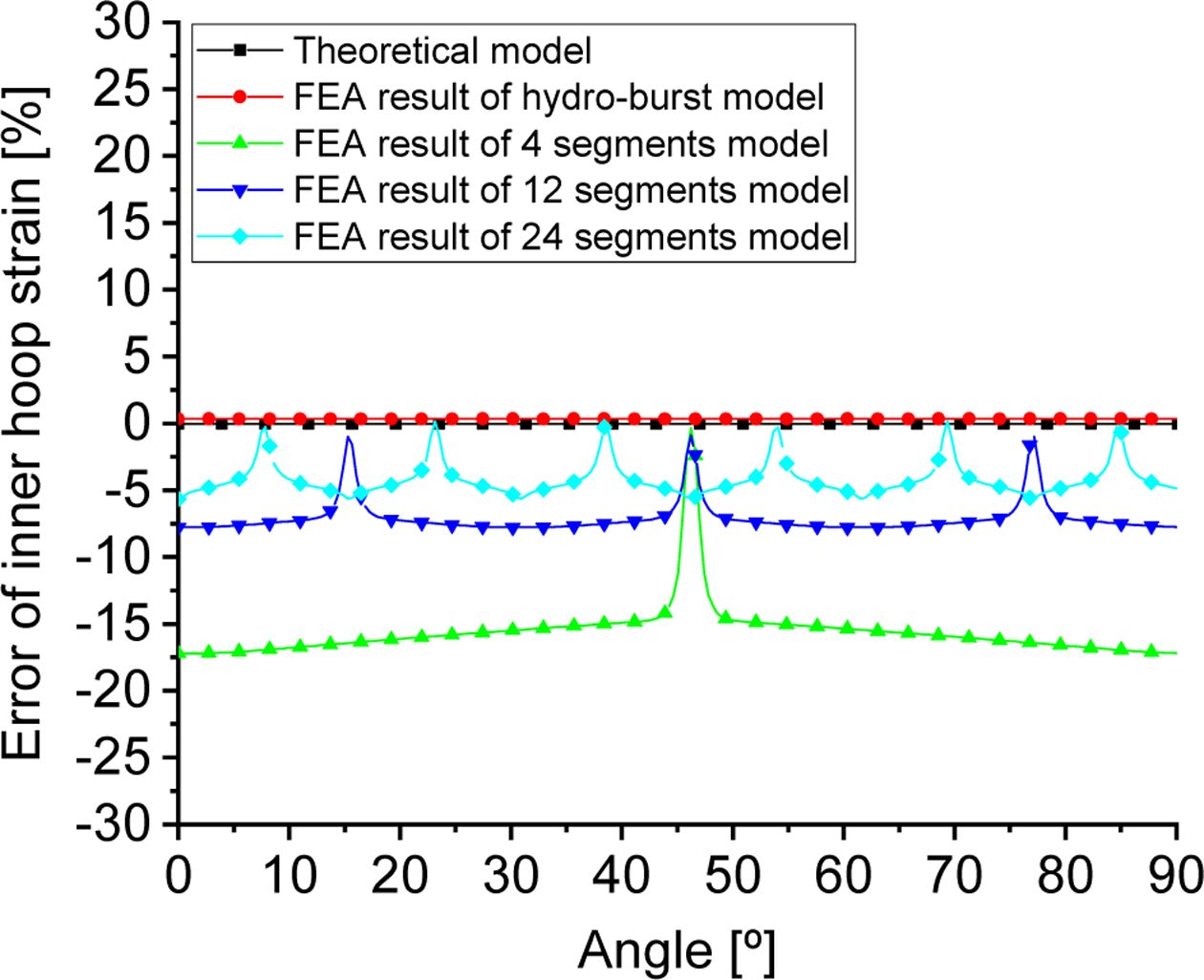
수압 시험과 마찬가지로 여러 세그먼트를 사용하여 링 버스트 시험 장치를 설계할 때 가장 중요한 문제는 장치가 링 시편에 대한 보강없이 균일 한 압력을 전달할 수 있는지 여부이다. 따라서 세그먼트 형 링 버스트 장치를 활용한 링 시편의 신뢰할 수 있는 시험평가를 위해 Fig. 4와 같이 수치해석을 통해 링 시편의 변형 분포를 세그먼트 수에 따라 비교하였다. 유압 시험에서의 이론적 수식에 의한 결과와 수치해석적 결과는 1% 오차 이내임을 확인하였다. 식 (1)을 이용한 링 시편의 원주방향 응력 및 변형률 또한 세그먼트 형 링 버스트 시험 장치의 수치해석 결과와 수압 시험 결과를 비교하면 세그먼트의 수를 증가할수록 변형률 불일치를 줄일 수 있음을 확인하였다. 그 결과 세그먼트 수가 증가할수록 유압 시험 결과에 근접하는 것을 확인하였다. 링 시편의 원주방향 변형률의 최대 백분율 오차는 적용된 세그먼트 수가 각각 4, 12 그리고 24개일 때 약 18%, 8% 그리고 6% 이내임을 확인하였다. 따라서 세그먼트의 가공 가능여부와 취급 가능성을 고려하여 24개의 세그먼트를 활용한 모델을 설계 및 제작하였다.
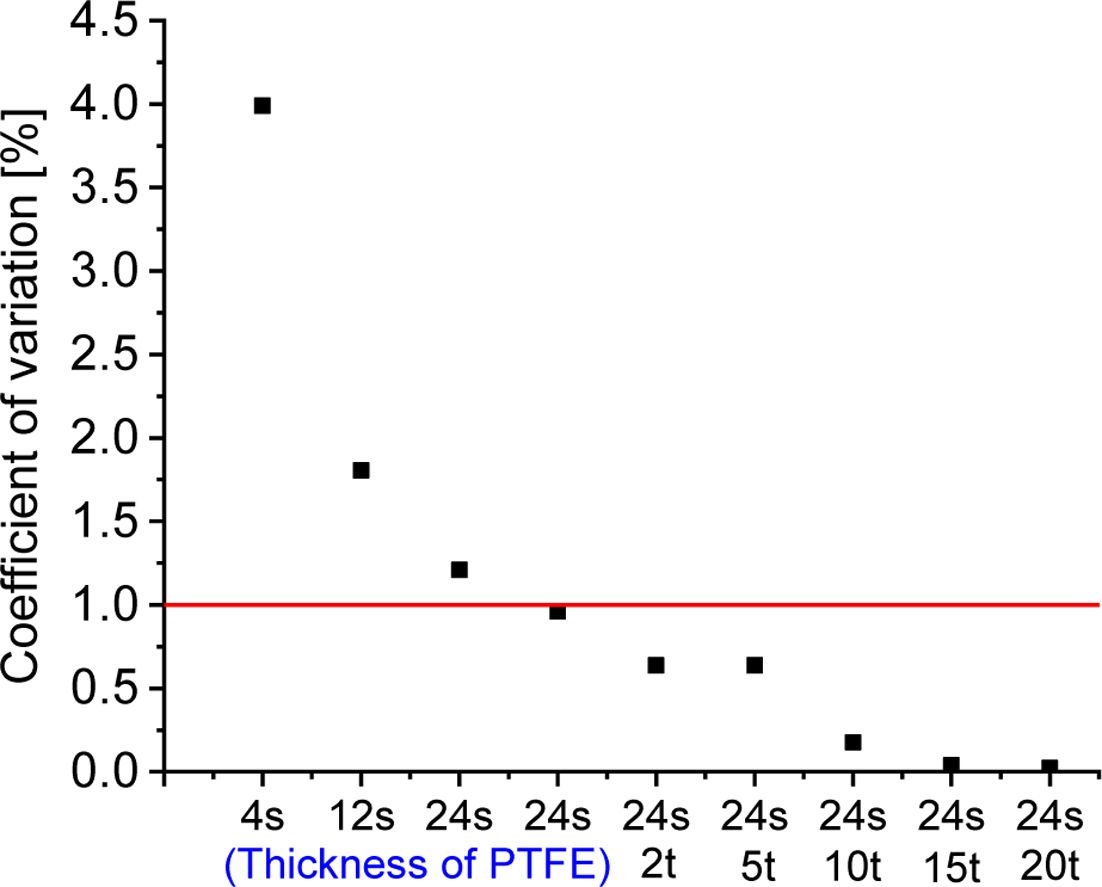
세그먼트와 시편 사이에 마찰을 줄이고, 보다 균일 한 압력을 가하기 위해 세그먼트와 시편 사이에 PTFE를 위치하였고, PTFE의 두께에 대한 영향을 Fig. 5에 도시하였다. PTFE의 활용은, 낮은 마찰 계수와 낮은 강성 특성으로 인해 세그먼트 사이 틈에서의 응력 집중의 완화를 야기한다. 변형률 불일치에 대한 보다 자세한 분석을 위해 PTFE의 두께에 따른 원주방향 변형률의 변동 계수를 비교하였을 때, PTFE의 두께가 증가하면 변형률의 변동 계수가 감소함을 확인하였다. 2t PTFE를 활용한 24개의 세그먼트 모델의 경우 변동 계수는 약 1% 미만이었고 이 경우 PTFE의 영구 변형도 최소화 하면서 보다 신뢰할 수 있는 파단 특성을 도출이 가능하므로, 본 연구에서는 2t의 PTFE를 활용하여 시험장치를 설계 및 제작하였다.
수치해석을 활용한 파단 특성과 실제 시험 결과를 통한 파단 특성을 비교하기위해 Hashin 파손 조건을 활용하였다. 보다 정확한 분석을 위해 수치해석 수행 시, 요소의 크기에 따른 파단 특성에의 영향을 분석 및 비교하였다.
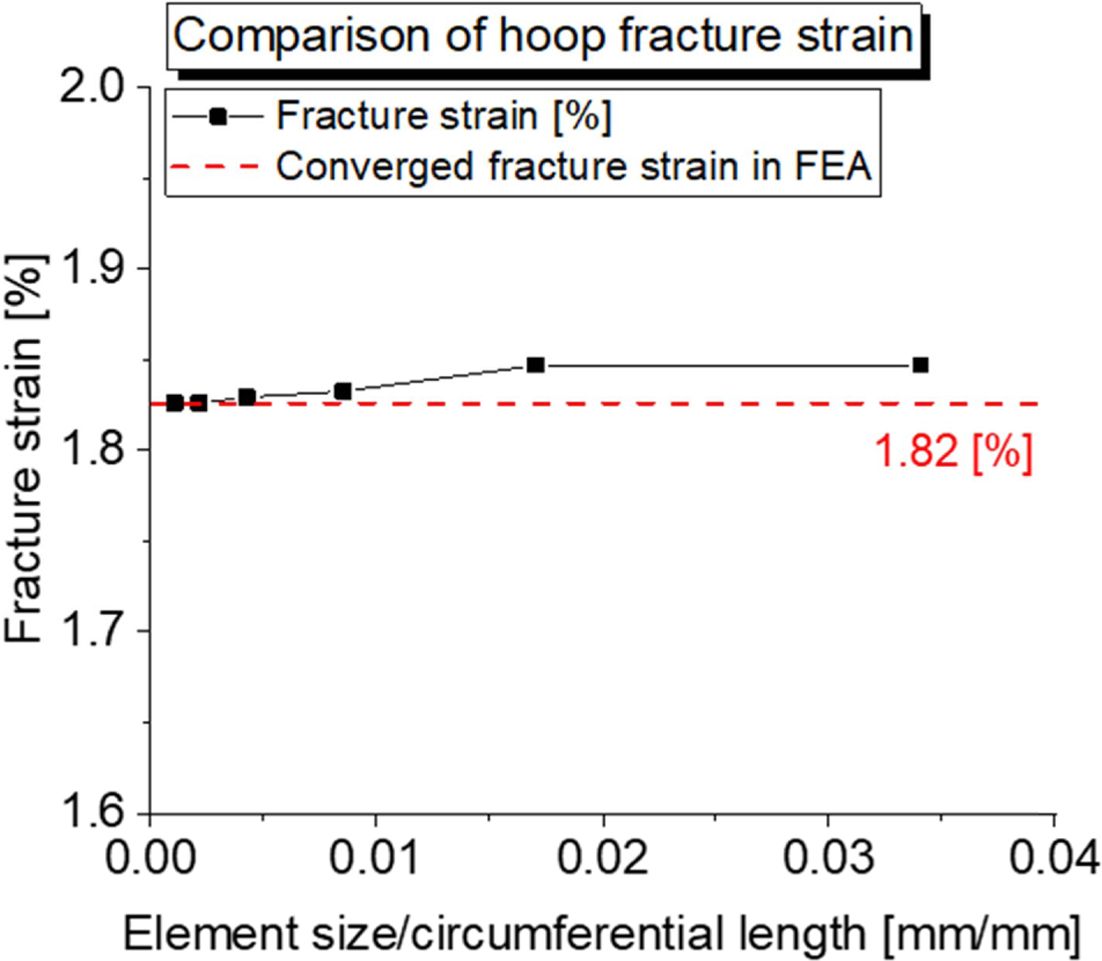
Fig. 6에서 요소의 크기가 작아질수록 링 시편의 파단 변형률은 특정 값으로 수렵하였다. 따라서 수치해석의 수행 조건을 고려하여 링 시편의 원주방향 길이 대비 약 1% 이내의 요소 크기를 설정하여 수치해석을 수행하였다.
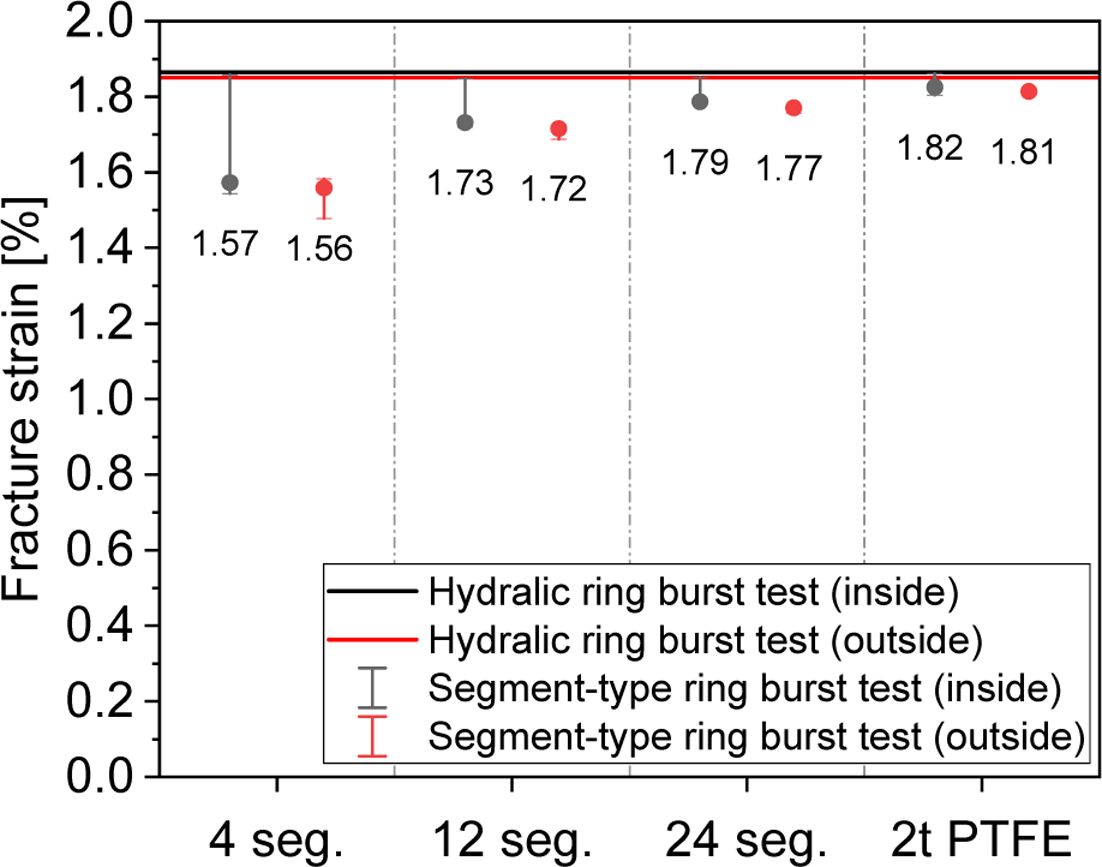
세그먼트를 활용한 링 버스트 시험 장치를 수치해석적으로 모사한 후 그 파단 변형률의 비교를 수행하였다. Fig. 7에서 확인 가능하듯이 세그먼트의 수가 증가할수록 파단 변형률은 식 (2)의 이론적 수식으로 도출한 결과 혹은 수압 조건에서의 수치해석 결과에 근접하는 것을 확인하였다. 이를 통해 24개의 세그먼트를 활용하고 2t의 PTFE를 활용하였을 때 파단 변형률이 가장 작은 오차를 보임을 확인하였다.
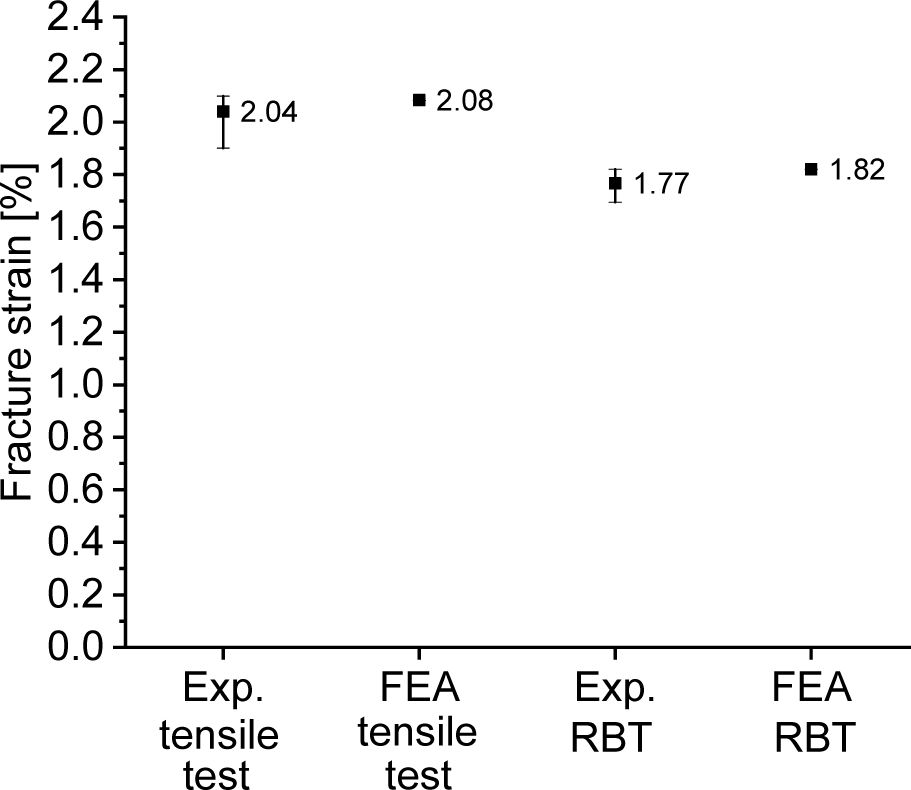
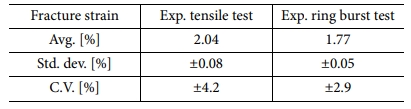
최종적으로 도출한 수치해석 결과를 활용하여 실제 실험을 통해 확보한 파단 변형률 값의 비교를 수행하였다. 우선적으로 동일 섬유 및 수지를 활용하였을 때 인장 시험 및 링 버스트 시험을 수행하여 파단 변형률을 도출하였고 이를 Table 4, Fig. 8에 도시하였다. 인장 시험 및 링 버스트 시험 모두 실제 시험 결과와 수치해석 결과를 비교하였을 때, 실험결과가 상대적으로 낮은 값을 갖으며 분포함을 확인하였다. 이는 실험에 사용된 복합재료 시편의 제작 공정 시 주변 환경 등에 영향을 받기 때문에 시편마다 물성의 차이가 발생함을 예측할 수 있다. 또한 인장시험 결과와 비교하여 링 버스트 시험에서의 파단 변형률이 상대적으로 낮은 값을 보이는 이유는 링 시편의 원통형 구조 형상이기 때문에, 내부에서의 응력 분포가 외부에서의 응력분포보다 상대적으로 높아 내압 시험 시 인장시편보다 상대적을 낮은 파단 변형률 분포를 보임을 예측 가능하다. 그리고 평균 파단 변형률의 비교 시 인장시험보다 링 버스트 시험에서 수치해석 결과와 시험 결과를 비교하였을 때, 그 불일지 정도가 더 높은 요인은 복합재료 링 시편의 제작 시 상대적으로 인장시편보다 더 높은 비율의 기공(Void)이 분포하여 조기 파단을 야기한 결과라 예측할 수 있다.

본 연구에서는 실린더 형상의 복합재료 압력용기의 보다 신뢰성 있는 물성 평가를 위해 세그먼트 형 링 버스트 시험 장치를 설계 및 분석하였다. 이론적 하중 관계식을 활용하여 실린더 형상의 링 시편에 부과되는 응력 및 변형률 분포를 도출하였고, 이를 FEA를 활용한 수치해석과 실제 실험을 수행하여 파단 변형률의 비교를 수행하였다. 그 결과 다음과 같은 결론의 도출이 가능하다.
1) 3 차원의 횡 등방성 및 두꺼운 실린더 형상의 복합재료 압력용기 모델을 기반으로 링 시편의 하중 관계에 관한 이론적 방정식을 유도하여 보다 정확한 응력 및 변형 값을 예측할 수 있다.
2) 유압조건 그리고 세그먼트 형 링 버스트 시험 장치의 수치해석 결과를 비교할 시, 세그먼트 수를 증가할수록 변형률 오차가 줄고, 평균 파단 변형률이 유압 시험 결과에 근접해질 수 있음을 확인하였다.
3) 실제 링 버스트 시험을 통한 파단 변형률을 확인하였을 때, 상대적으로 작은 표준편차와 변동계수를 갖음을 확인하였기에, 본 장치를 활용하였을 때, 균일한 내압의 전달을 통한 신뢰성 있고 보다 경제적인 압력 용기의 물성 평가의 수행이 가능함을 검증하였다.

본 연구는 대한민국 정부(산업통상자원부 및 방위사업청) 재원으로 민군협력진흥원에서 수행하는 민군기술협력사업의 연구비 지원으로 수행되었습니다(협약번호 UD100044TU).