- A Study on Simplification of Flow Analysis in VaRI Process
Yeongmin Kim*, **, Jungwan Lee*, Jungsoo Kim*, Sehoon Ahn*, **, Youngseok Oh*, Yi Jin Woo*, Wiedae Kim**, Moon-kwang Um*†
* Composites Research Division, Korea Institute of Materials Science, Changwon, Korea
** Department of Aerospace Engineering, Pusan National University, Pusan, Korea- VaRI 공정 유동해석 간소화 방법에 대한 연구
김영민*, ** · 이정완* · 김정수* · 안세훈*, ** · 오영석* · 이진우* · 김위대** · 엄문광*†
This article is an open access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
VaRI(Vacuum assisted Resin Infusion) process, which is cost effective and suitable for manufacturing large-sized composites, is an OoA(Out-of Autoclave) process. For rapid resin infusion in the VaRI process, a DM(distribution media) is placed on top of the fabric. The resin is rapidly supplied in plane direction of the fiber along the DM, and then the supplied resin is impregnated in the out-of-plane direction of fiber. It is difficult to predict the flow of resin because the flow of in-plane direction and the out-of-plane direction occur together, and a 3D numerical analysis program is used to simulate the resin infusion process. In 3D flow analysis, many elements are required in the out-of-plane direction of fabric. If part size becomes larger, longer analysis time needs. Therefore, in this study, a method was suggested to reduce the time required for flow analysis by simplifying the 3D flow analysis to 2D flow analysis. The usefulness was verified by comparing the 3D flow analysis with the simplified 2D flow analysis at the same conditions. The filling time error was about 7% and the reduction of flow analysis time was about 95%. In addition, by utilizing the constant difference in the flow front between the top, middle, and bottom of the fabric of the 3D analysis, the flow front of the top, middle, and bottom of the fabric can be also predicted in the 2D flow analysis
VaRI(Vacuum assisted Resin Infusion) 공정은 공정비용이 저렴하며, 크기가 큰 복합재 제작에 적합한 OoA(Out of Autoclave) 공정이다. VaRI 공정에서는 원할한 수지 주입을 위해 섬유 상단에 유로망을 적층한다. 수지는 이 유로망을 따라 섬유의 면 방향으로 빠르게 공급되고, 공급된 수지는 다시 섬유의 두께방향으로 함침된다. 면방향의 유동과 두께방향의 유동이 동시에 일어나기 때문에 수지의 유동을 예측하기 힘들며, 수지 주입과정을 예측하기 위해 3D 수치해석 프로그램이 사용되고 있다. 하지만, 3D로 해석하기 위해서 섬유와 유로망의 두께방향에 많은 Element가 필요하고, 이로 인해 제품의 크기가 클수록 해석시간이 오래 걸린다. 따라서 본 연구에서는 3D 유동해석을 2D 해석으로 간소화하여 유동해석에 소요되는 시간을 줄이는 방법을 제시하였다. 3D 유동해석과 간소화된 2D 유동해석을 동일조건에서 비교하여 효용성을 검증하였고, 충진시간 오차율은 약 7%, 유동해석시간 감소율은 약 95%로 나타났다. 또한 3D 해석에서 섬유 상, 중, 하단 간의 유동 전진 거리의 차이가 일정하다는 것을 활용하여 간소화된 2D 유동해석에서도 상, 중, 하단의 유동 전진 거리를 예측할 수 있었다
Keywords: 유동해석(Flow analysis), VaRI 공정(Vacuum assisted Resin Infusion process), OoA 공정(Out of Autoclave process), 유로망(Distribution media)
온실가스 배출이 기후변화의 주원인으로 지목되며, 세계 여러 국가에서는 다양한 산업분야의 탄소배출량을 지금의 수준으로 동결하거나 감축하는 방안으로 정책을 수립하고 있다. 항공분야에서는 매년 평균 4.1%씩 항공 교통량이 늘어날 것으로 예상되고, 탄소 배출량도 연 평균 5% 가량 증가하고 있다. 이에 따라 국내·외 항공사는 CORSIA(국제항공탄소상쇄제도)를 도입하여 국제항공 온실가스 배출량을 2020년 수준으로 동결하는 것을 목표로 하였다. CORSIA에 참여한 항공사는 항공기 운항시 온실가스 배출량을 모니터링하여 매년 검증기관으로부터 검증받아야 하며, 배출기준량을 초과하면 탄소배출권을 구매하여 상쇄해야 한다[1]. 이에 따라 여러 항공사에서는 연료효율 개선 방법으로 항공기 부품 경량화를 진행중이며, 기존 항공기 부품으로 주로 쓰였던 알루미늄 합금을 비강도 및 비강성이 우수한 탄소복합재료로 대체하고 있다[2].
탄소복합재 성형에 주로 사용되었던 오토클레이브(Autoclave) 공정은 고품질의 제품을 생산할 수 있지만 장비 가격 및 운용 비용이 높고 생산성이 낮다는 단점이 있다. 이러한 문제점을 해결하기 위해 탈 오토클레이브(Out of Autoclave) 공정이 많이 연구되고 있다[3].
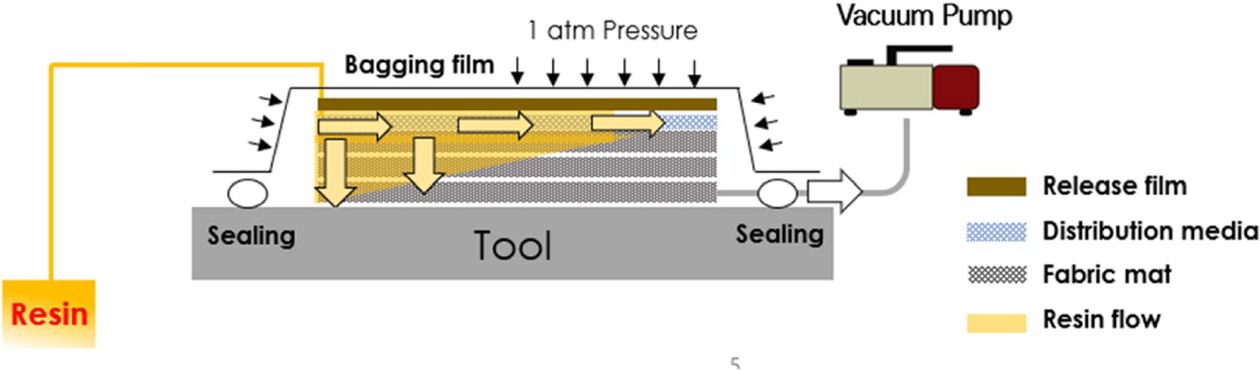
그 중 VaRI(Vacuum assisted Resin Infusion) 공정은 Fig. 1과 같이 진공압을 이용하여 섬유에 수지를 직접 주입하는 액상성형 공정으로 크기가 큰 제품을 우수한 품질로 생산할 수 있고, 공정비용이 저렴하다는 장점이 있다. VaRI 공정의 이러한 장점은 섬유 상단에 적층되는 유로망(Distribution Media)을 통해 실현된다. 유로망은 기하학적 형상으로 인해 높은 투과성을 가진 유동매체로, 액상수지를 주입할 때 수지를 면내방향(X, Y-axis)으로 빠르게 공급한 후 두께방향(Z-axis)으로 함침을 유도하는 역할을 한다[4].
유로망의 특성으로 인해 VaRI 공정의 수지주입은 모든 방향에서 동시다발적으로 이루어지며, 이렇게 복잡한 수지유동을 예측하고 공정설계를 최적화하기 위해 3D 유동해석이 사용되고 있다[5-7]. 하지만, 제품의 크기와 두께가 커질수록 3D 해석을 위해 생성해야할 두께방향 Element 수는 매우 많아지며, 이는 해석에 소요되는 시간을 증가시킨다. 이러한 이유로 3D 유동해석 계산시간을 줄이기 위해 Park 등[8]은 Dual-Scale 기법을 도입하여 전체영역은 2.5D로 해석하고 주요 관심영역만 3D로 해석하는 방법을 제시하였고, Chen 등[4]은 유로망과 섬유의 등가투과성계수 모델을 사용하여 유동해석을 간소화하였다. Dong 등[9]은 더 나아가 두께방향 투과성을 반영한 등가 투과성 모델을 연구하였다. 세 연구의 핵심은 유로망과 섬유의 유효 투과성계수를 결정하고, 이를 활용하여 유동해석에 필요한 차원을 낮추는것이다. 하지만 이 방법에서는 3D 유동해석의 섬유 상/하단의 유동을 예측하기가 어렵다.
따라서 본 연구에서는 VaRI 공정에서 기존 3D 유동해석을 2D 해석으로 간소화하는 방법을 제시하였고, 간소화된 2D 해석과 3D 해석을 동일한 조건에서 수행하여 그 효용성을 검증하였다.
|
Fig. 1 Schematic diagram of VaRI process |
2.1 섬유직물 압착실험
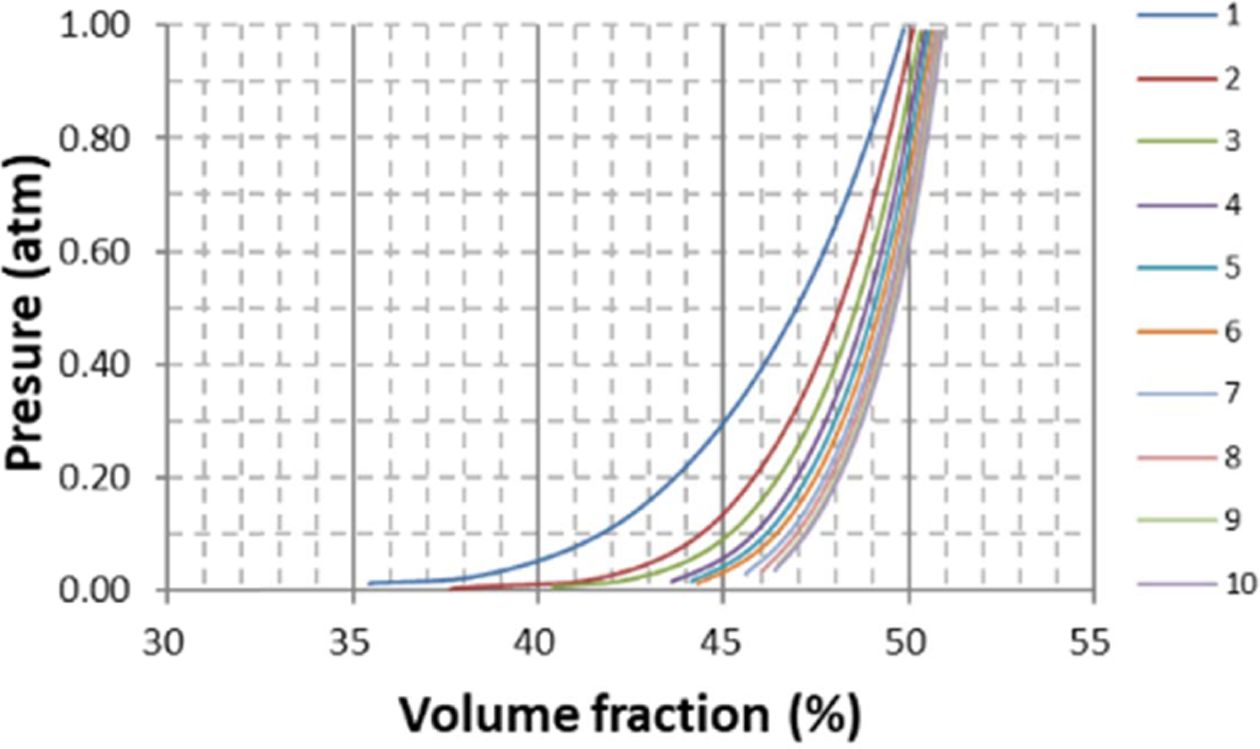
수지 주입압에 해당하는 1 atm에서 섬유의 두께와 체적율을 섬유 압착실험을 통해 계산하였다. 실험에 사용된 섬유는 Hexcel 社의 T700급 섬유로 5H Satin 형태로 직조된 섬유직물이다. 섬유직물을 100 × 100 (mm2)로 40장 재단하여 적층한 후 만능재료시험기로 1 atm에 해당하는 하중을 10회 가하여 변위를 측정하였다. 실험은 총 3회를 수행하였다. 측정된 변위와 식 (1)~(3)을 통하여 체적율로 환산하였고 결과를 Fig. 2에 나타내었다.

V, W, ρ는 체적율(%), 면중량(g/m2), 밀도(kg/m3)를 나타내고 아래첨자 f, r은 각각 섬유와 바인더를 의미하며, n은 섬유의 장수, t는 압착실험에서 측정된 두께(mm)이다. 그리고 총 체적율 Va는 섬유와 바인더의 체적율을 합한 값이다. 실험결과 1 atm에서 총 체적율은 51.0%, 섬유의 두께는 1 Ply당 0.443 mm로 측정되었다.
2.2 섬유 투과성계수 측정
VaRI 공정의 핵심은 수지가 섬유 내부의 공간(Space)을 완전히 채우는것이다. 섬유직물과 같은 다공성매질의 수지유동에 관한 가장 일반적인 식은 Darcy 식이고 식 (4)와 같이 표현된다.

여기서 U, μ, ∇P, K는 각각 유체의 표면 속도벡터, 유체의 점도, 압력구배, 투과성계수 텐서를 뜻한다. 위 식과 같이 수지의 유동은 배출구와 주입구의 압력차이에 의해 생기고, 주입유체의 점도와 섬유의 투과성에 따라 유체의 속도가 정해진다. 투과성계수는 VaRI 공정에서 섬유의 유동저항 특성을 나타내는 섬유의 고유한 값이고, 섬유의 면내방향 투과성과 두께방향 투과성으로 나누어 구할 수 있다.
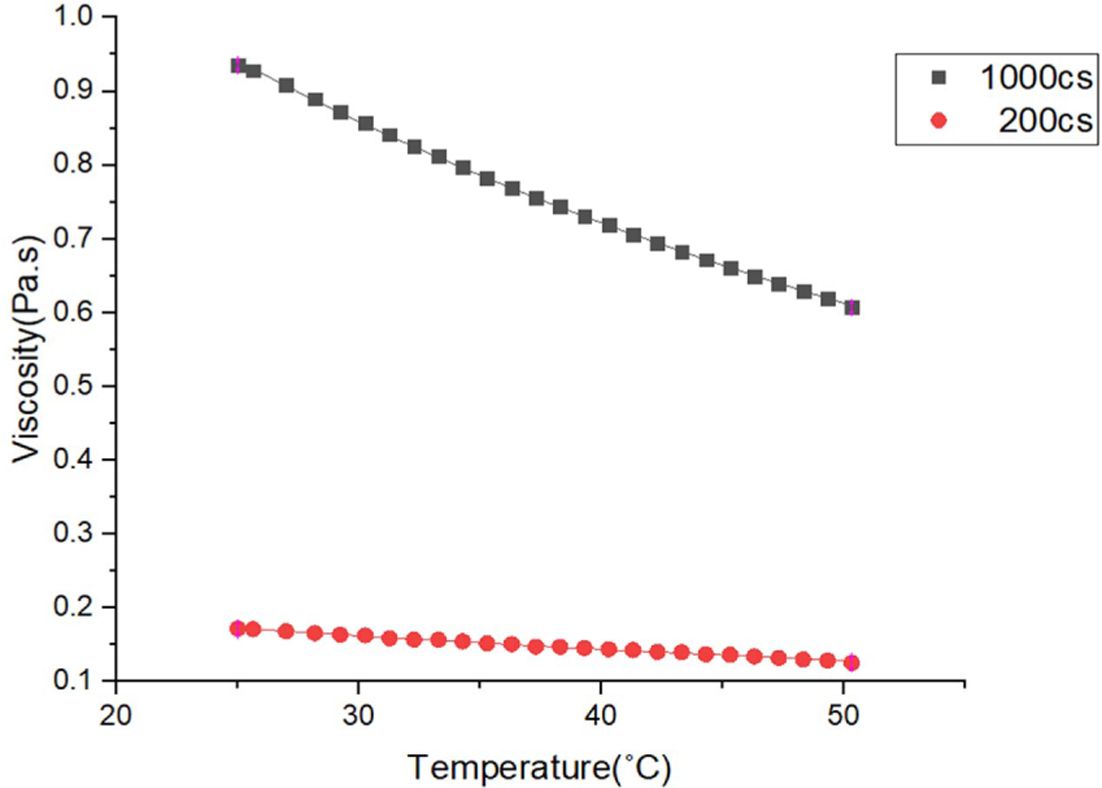
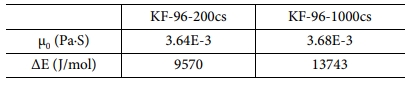
섬유의 투과성계수 측정 실험에 사용될 유체는 화학반응이 없고 상온에서 점도가 일정한 Shinetsu 社의 실리콘 오일을 사용하였다. 실리콘 오일은 Rotational Rheometer에서 1oC/min의 승온 속도로 온도별 점도를 측정하였고 식 (5)를 이용하여 Curve-Fit 하였다. 오일의 점도와 Fitting 결과는 각각 Fig. 3, Table 1에 나타내었다.

위 식에서 μ는 유체의 점도(Pa·S), μ0는 실험에서 얻어지는 점도상수, ∆E는 활성화 에너지(J/mol), R은 기체상수(J/K×mol), T는 절대온도(K)를 나타낸다.
섬유의 면내 투과성은 섬유를 300 × 350 (mm2)로 6 Ply를 재단하여 적층하였고, 면내방향으로만 유체가 주입될 수 있도록 Ø15(mm) Hole을 내었다. Fig. 4와 같이 주입 Port로 실리콘 오일(200cs)를 주입하였고, 실험 시 압력, 온도(∝점도), 섬유 상/하단의 유동선단을 기록하였다. 그 후 Chan 등[10]이 제안한 방법으로 면내투과성계수를 계산하였다. 실험은 총 3회 수행하여 평균을 냈다. 면내투과성계수 계산결과는 K1 = 7.57E - 11(m2), K2=5.99E - 11(m2)으로 나타났다.
두께방향 투과성계수는 Fig. 5에 나타낸 방법으로 측정하였다. 섬유를 원형으로 컷팅 후 다공체 사이에 적층했고 두께조절이 가능한 투과성계수 측정치구에 삽입하였다. 1 atm에 해당하는 두께로 치구의 높이를 설정하였고 다공체를 통해 실리콘오일(200cs)를 주입하였다. 유량, 압력, 온도를 기록하여 두께방향 투과성계수 계산식 (6)으로 계산하였다. 실험은 총 6회 수행하여 평균을 냈고, 결과는 K3 = 1.03E -11(m2)로 나타났다.

위 식에서 μ는 유체의 점도(Pa·S), Q는 유체의 유량(m3/s), h는 섬유의 두께(m), A는 다공체의 면적(m2), ∆P는 주입 압력(Pa)에 해당한다.
2.3 유로망 투과성계수 결정
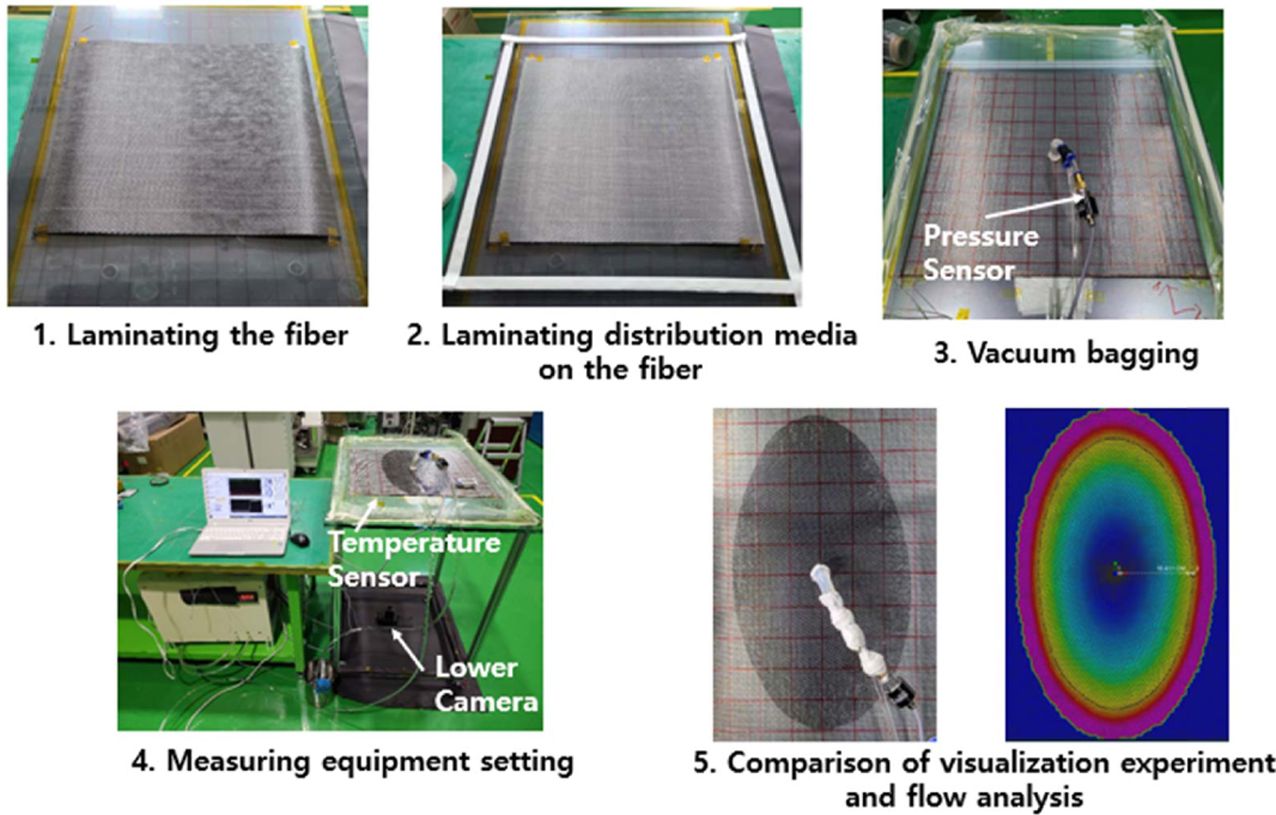
유로망은 섬유의 상단에 적층되며, 섬유에 비해 투과성이 수십배 높은 특징이 있기 때문에, VaRI 공정에서 수지의 원할한 공급을 통해 유동거리를 증가시키는 역할을 한다. 하지만, 유로망은 투과성계수 측정 시 접촉면의 상태에 따라 기하학적 형태가 변하기 때문에, 실제 섬유에 적층된 상태에서의 투과성을 결정하는 작업이 필요하다. 본 연구에서는 실제 섬유에 유로망을 적층하여 수행한 유동 가시화 실험과 유동해석과의 비교를 통해 유로망의 투과성계수를 결정하였다.
시험에 사용된 소재는 앞서 투과성계수를 측정한 5H Satin으로 직조된 섬유, 주입 유체는 KF-96-1000cs를 사용하였다. 유동해석 프로그램은 ESI 社의 PAM-RTM을 사용하였고, 실험시 주입압력, 실리콘오일의 온도를 측정하여 유동해석의 입력값으로 사용하였다. 유로망 투과성계수에 임의의 값을 입력한 후, 유동해석 결과가 가시화 실험의 유동 거리와 오차가 제일 작을 때의 투과성 값을 유로망의 투과성계수로 결정하였고 그 값은 K1 = 2.40E - 8(m2), K2 = 8.19E -9(m2), K3 = 1.00E - 6(m2)이다. Fig. 6에 유로망의 투과성계수 결정방법을 요약하였다.
|
Fig. 2 Results of fabric compaction test |
|
Fig. 3 Silicone oil viscosity as a function of temperature |

|
Fig. 4 Resin flow experiment for in-plane permeability : (a) upper and (b) lowe |

|
Fig. 5 Test procedure for measuring an out-of plane permeability |
|
Fig. 6 A Procedure to determine permeability of distribution media |
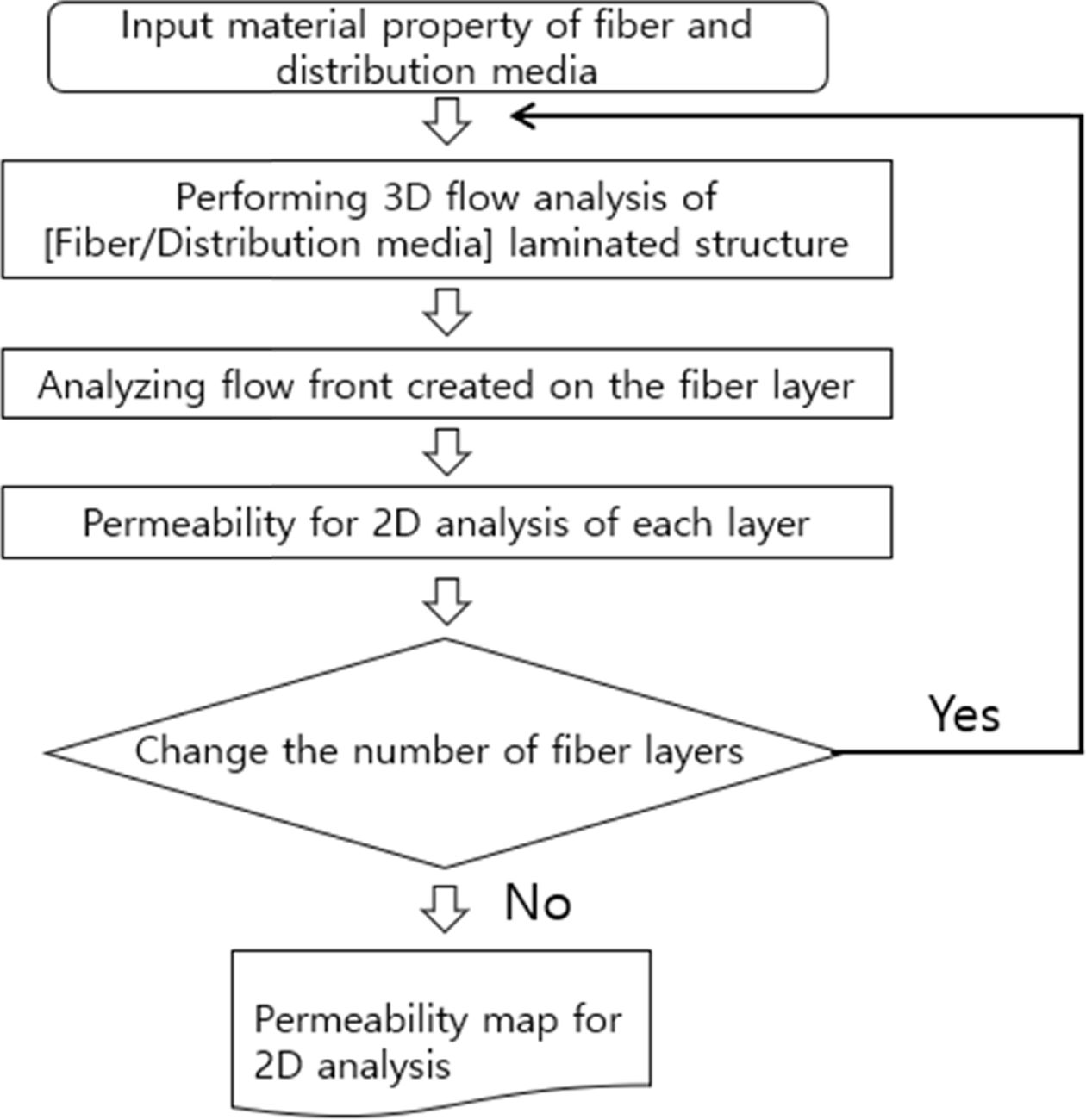
본 연구에서는 VaRI 공정의 3D 유동해석을 간소화하여 2D로 해석하는 방법을 제시하였다. 2D 해석용 투과성계수를 결정하는 방법은 Fig. 7에 나타내었다. 실험으로 결정된 섬유와 유로망의 물성을 유동해석에 입력하고 섬유/유로망 적층구조의 3D 유동해석을 수행한다. 해석결과에서 섬유와 유로망의 면방향 및 두께방향 투과성이 복합적으로 반영된 섬유 Layer에서 유동선단을 분석한다. 2D 해석용 투과성계수는 섬유 Layer에 생성된 유동선단과 유체의 점도, 주입압력 등을 반영하여 Chen 등[10]이 제안한 방법으로 계산된다. 섬유의 적층수를 변경하고 2D 해석용 투과성계수를 결정하는 작업을 반복하여 다양한 섬유적층수에 대한 2D 해석용 투과성계수 Map을 그린다. 이렇게 결정된 투과성계수를 활용하여 각 섬유 Layer에서 두께방향 Element가 없는 2D로 유동 해석이 가능하다. 단, 섬유나 유로망의 소재가 바뀌거나 적층각의 변경이 있다면 해당하는 조건에 대해 투과성계수 Map을 다시 그려야 한다.
3.1 2D 투과성계수 Map의 활용 및 검증
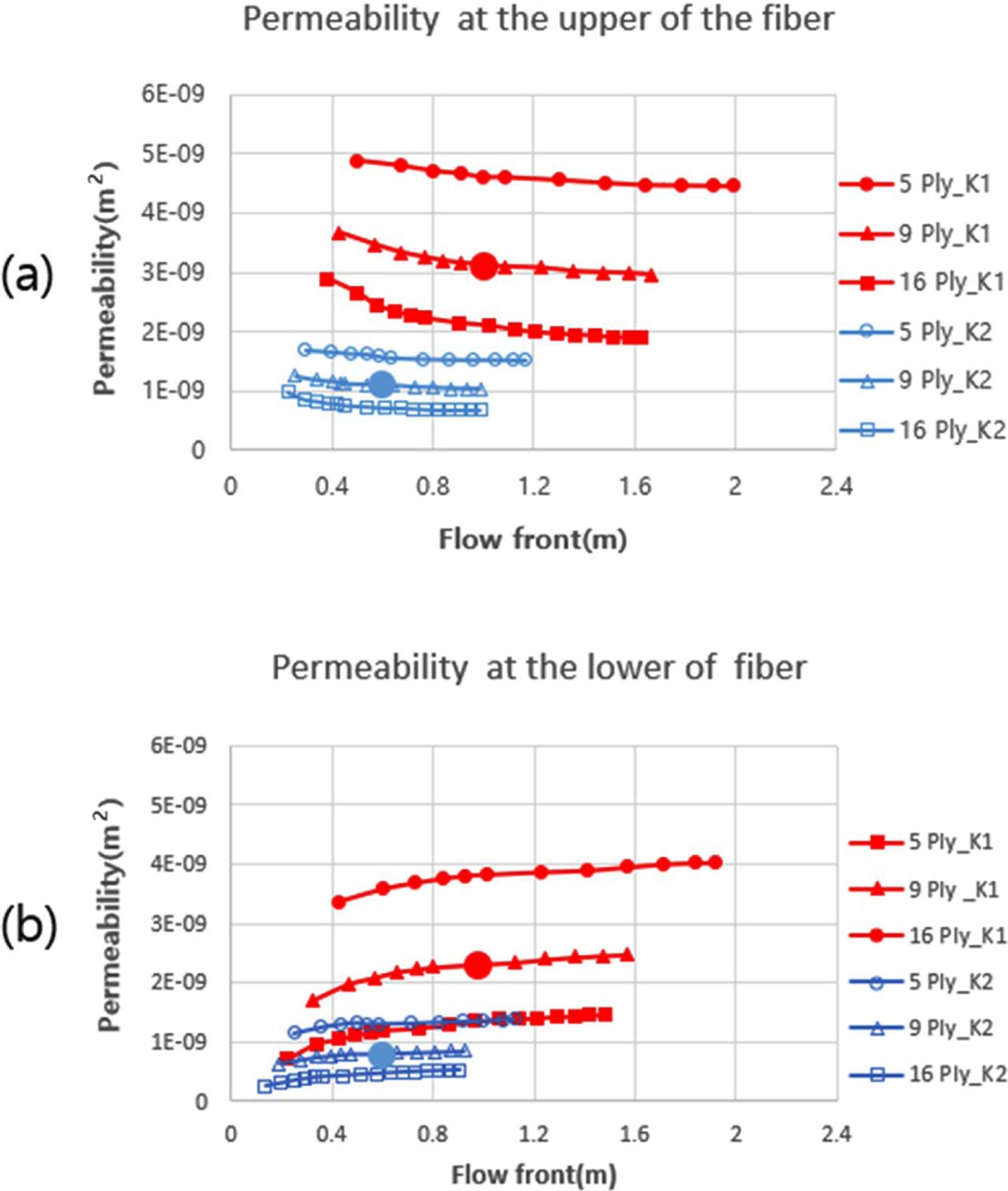
2D 해석용 투과성계수의 효용성을 검증하기 위해 섬유 5, 9, 16 Ply에 유로망 1 Ply가 0o 방향으로 적층 된 구조를 예시로 들었고, 섬유 상단과 하단 Layer의 유동을 분석하여 Fig. 8과 같이 투과성계수 Map을 그렸다. 결정된 투과성계수를 활용한 2D 해석과 기존 방식의 3D 유동해석을 각각 수행하였고, 유동 양상 및 유동 전진 거리를 비교하여 효용성을 검증하였다.
해석해야 할 형상의 주입구에서 형상경계까지의 거리를 알면 2D 투과성계수 Map에서 그 거리에 해당하는 투과성계수를 선택할 수 있다. 섬유 적층수 9 Ply에서 2000 × 1200 mm2 형상의 주입구 위치를 정가운데로 가정하면 주방향의 유동거리는 1000 mm, 부방향의 유동거리는 600 mm가 된다. Fig. 8의 9 Ply 투과성계수 Map에서 원으로 표시된 것 처럼 K1은 유동 전진 거리 1000 mm에서 선택하고 K2는 600 mm에서 선택하였다. 따라서 2D 해석용 투과성계수는 섬유 상단에서 K1 = 3.14E - 9(m2), K2 = 1.10E - 9(m2),섬유 하단에서 K1 = 2.32E - 9(m2), K2 = 8.11E - 10(m2) 으로 결정된다. 해당 형상에서 섬유 상단과 하단의 투과성계수를 각각 입력하여 2D 해석을 수행했고 3D 해석은 섬유 9 Ply, 유로망 1 Ply에 적층조건에서 수행하였다. 주입구 크기는 Ø5(mm)이고, 압력과 점도는 각각 100(kPa), 1072(cP)로 일정한 값을 입력하였다. 그리고 유동이 형상의 끝에 닿기 전까지 2D 해석과 3D 해석에서 시간에 따른 유동 전진 거리를 비교하였다. 결과는 Fig. 9에 나타냈고, 유동 전진 거리의 오차는 약 5% 미만으로 나타났다.
3.2 2차원 형상의 적용
위의 2D, 3D 해석 결과는 유동이 형상끝에 도달하기 전까지의 결과이다. 하지만, 실제 VaRI 공정과 3D 유동해석에서는 한 방향의 유동이 형상의 경계에 도달하면 경계에 도달하지 못한 다른 방향으로 유량이 증가한다. 2D 해석에서는 이러한 효과를 반영하기 어려우며 본 연구에서는 2D 해석에서 섬유 상단 Layer와 하단 Layer의 투과성계수를 평균하여 형상경계의 효과를 보정하고자 하였다. 이에 대한 검증으로 1000 × 1000 mm2의 평면형상에서 섬유 5, 9, 16 Ply, 유로망 1 Ply를 적층했을 때의 3D 해석과 투과성계수 Map을 활용한 2D 해석에서 총 충진시간과 해석 계산시간을 비교하였다.
우선 평면형상에서 주입구를 중앙에 설치했을 때를 검증하였다. 마찬가지로 주입구 크기는 Ø5(mm), 주입압력, 유체의 점도는 각각 100(kPa), 1072(cP)이다.
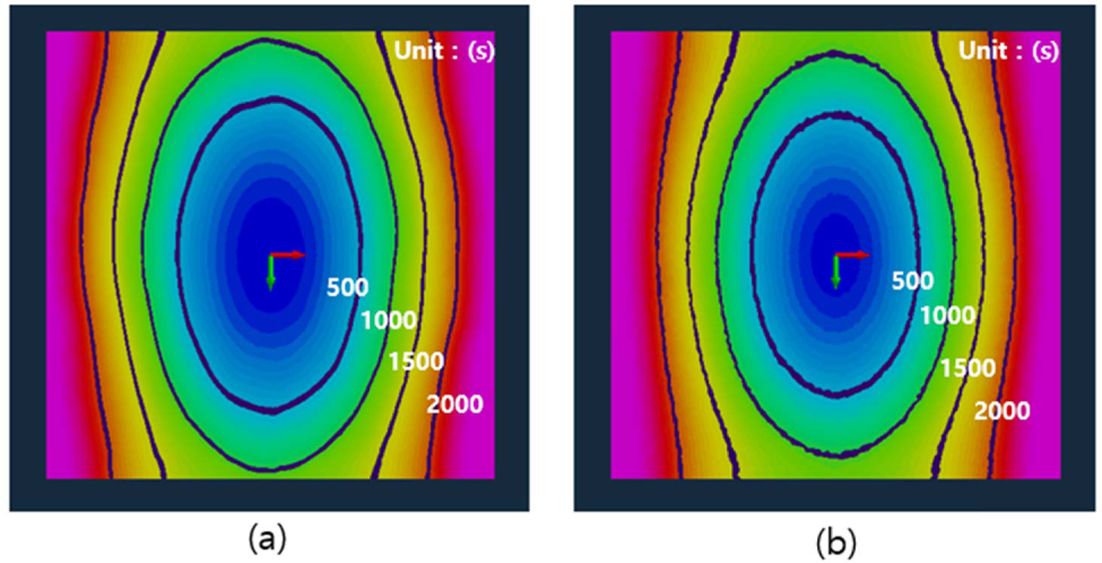
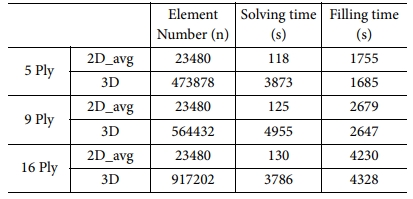
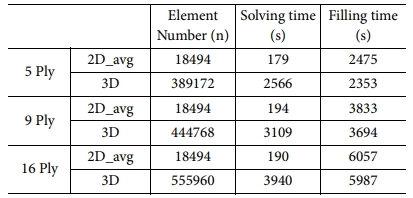
세가지 적층수 중, 대표적으로 섬유 9 Ply 해석의 유동선단 결과를 Fig. 10, Fig. 11에 나타내었다. Fig. 10의 하얀색 숫자는 주입시간(s)을 뜻한다. 상단 Layer와 하단 Layer 투과성계수 평균값을 입력한 2D 해석 결과는 3D 해석에서 섬유 중단 Layer의 유동양상과 비슷했다. 총 충진시간은 오차율 약 4% 미만으로 나타났고, 해석시간은 96%가량 단축할 수 있었다. 다른 섬유 적층수의 비교결과는 Table 2에 요약하였다.
주입구가 가장자리에 있는 형상에도 같은 방법으로 비교하였다. 주입구의 위치는 형상의 가장자리에서 50(mm) 떨어진 위치에 설치되었고, 주입조건은 동일하다. 2D 해석결과는 3D 해석결과와 비교하여 충진시간 오차율은 약 5% 미만을 나타냈으며 해석시간은 약 94% 단축되었다. 가장자리 주입구 형상의 해석 결과는 Fig. 12, Fig. 13과 Table 3에 요약하였다.
3.3 3차원 형상의 적용
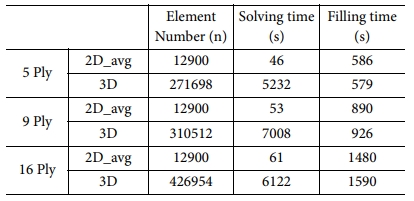
굴곡이 있는 3차원 형상에서도 2D 해석의 실효성을 검증하였다. 250 × 250 × 250 (mm3)의 Cube 형상에서 마찬가지로 섬유 5, 9, 16 Ply, 유로망이 1 Ply 적층된 구조를 예시로 들었다. 2D 해석은 섬유 상단과 하단 투과성계수의 평균값을 입력하여 수행하였고 3D 해석은 섬유 중단 Layer를 관찰하였다. 주입구는 Cube 형상의 상부 중앙에 설치하였고 주입구의 크기, 점도, 압력은 2차원 형상의 해석조건과 동일 하다. 해석결과에서 충진시간 오차율은 약 7% 미만으로 나타났고, 해석시간은 약 99% 단축되었다. 자세한 해석결과의 비교는 Fig. 14과 Table 4에 요약하였다.
3.4 섬유 상, 하단 유동 전진 거리 예측
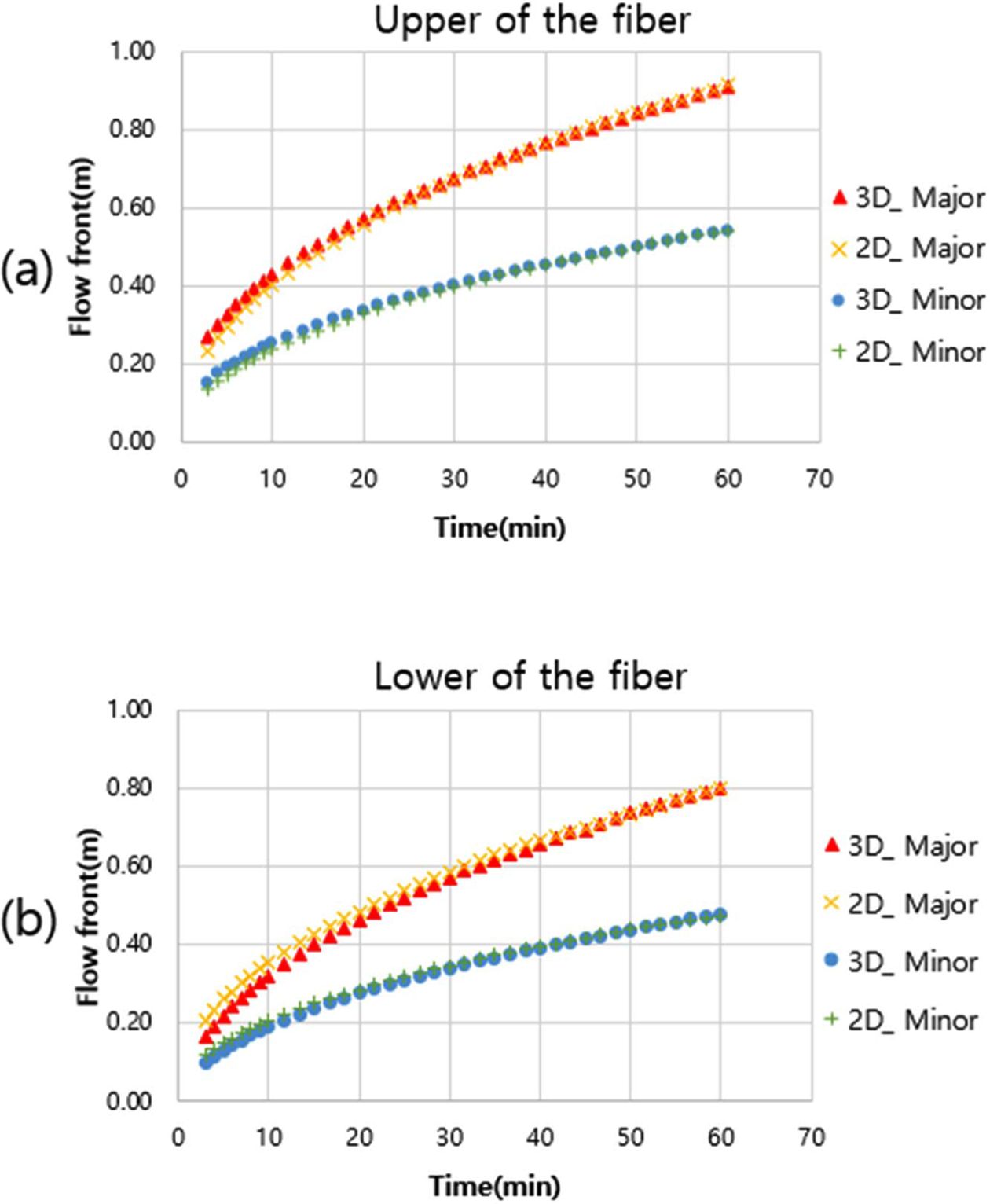
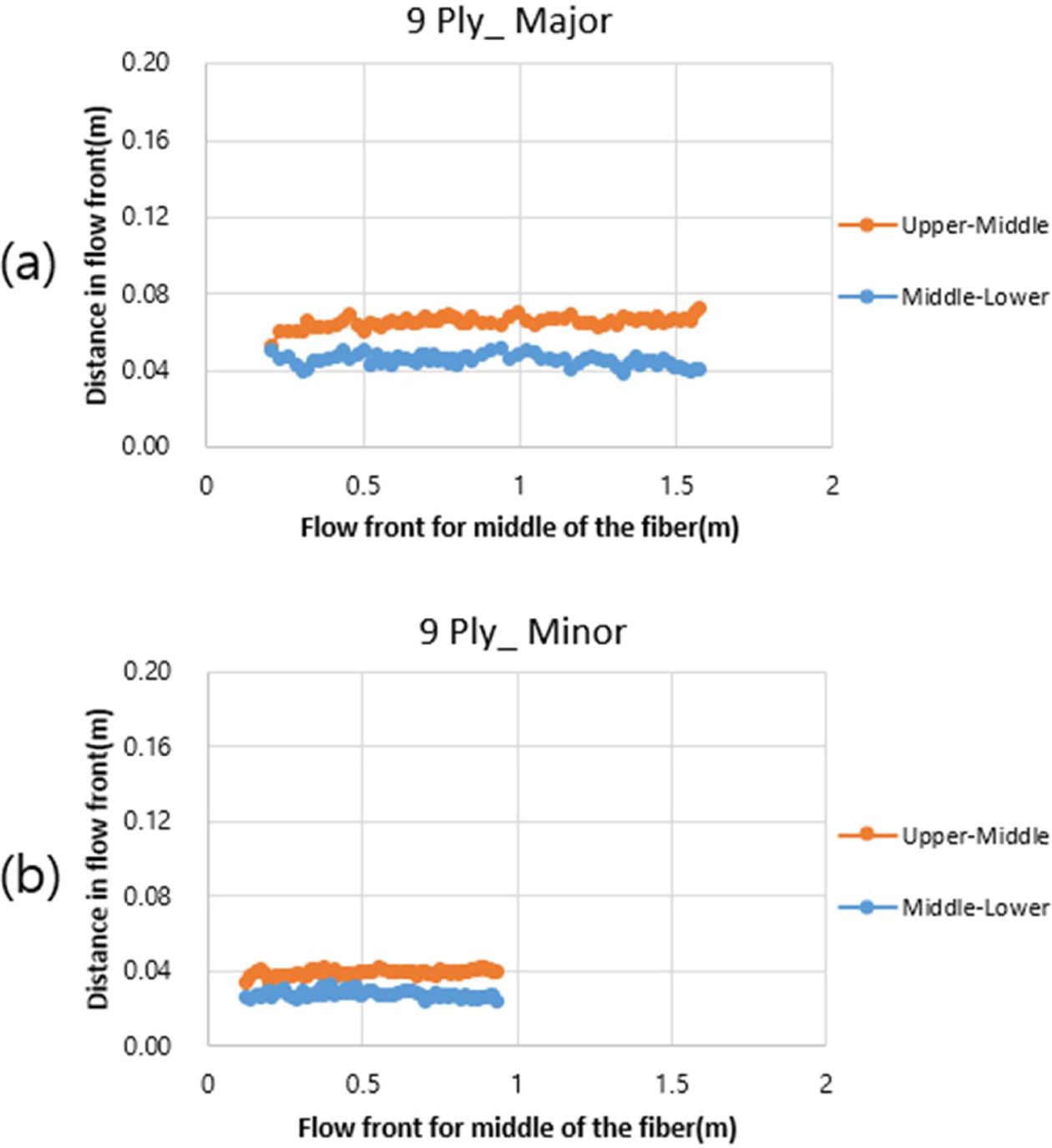
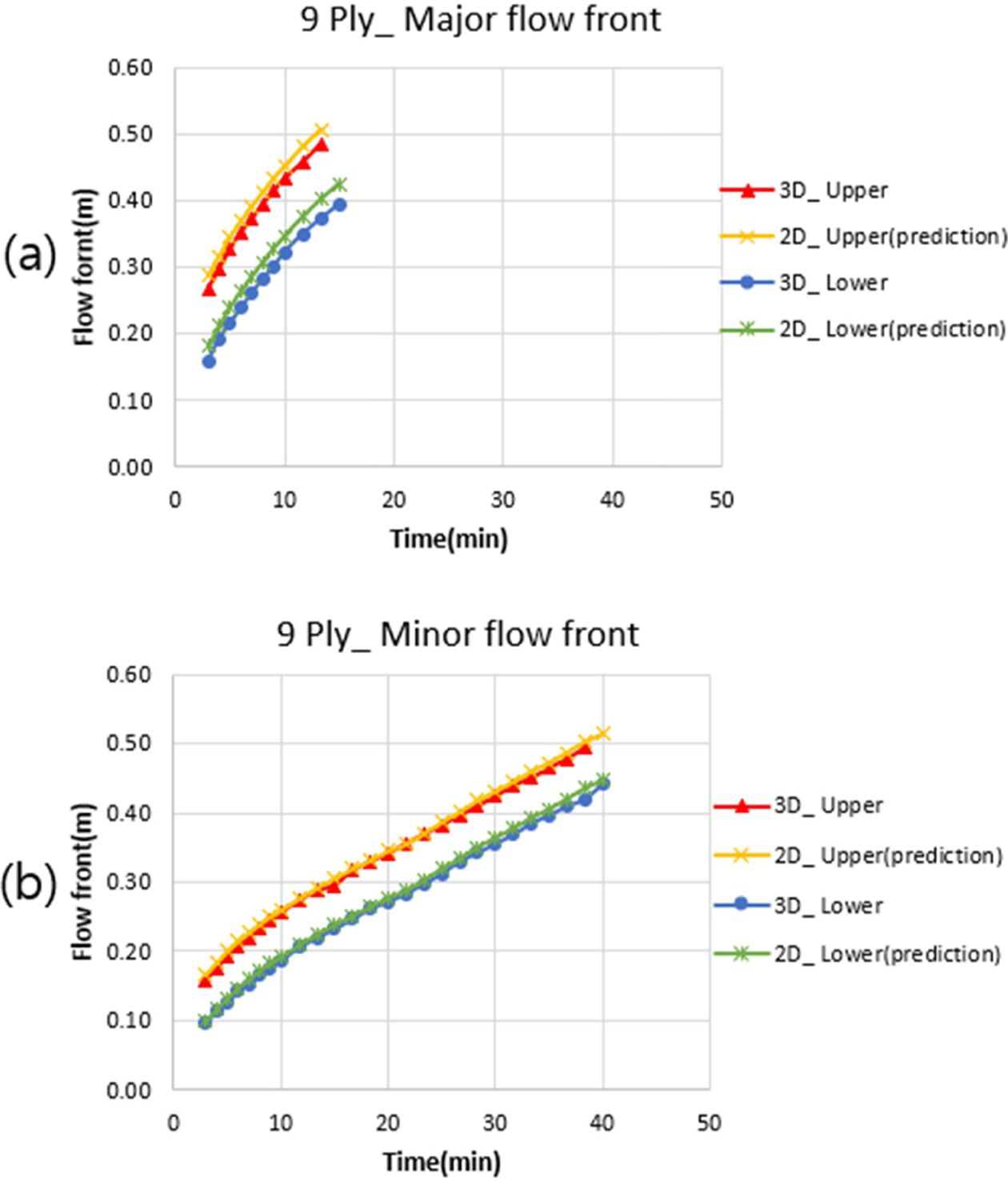
평면형상의 3D 해석에서 유동 전진 거리를 분석하면 Fig. 15에 나타난 것처럼 섬유 상단에서 중단과 중단에서 하단의 유동거리 차이는 거의 일정하다는 것을 확인할 수 있다. 상/하단 Layer의 투과성계수 평균값을 입력한 2D 해석이 3D 해석의 중단 Layer의 유동과 일치하므로 2D 해석 결과에서 상단-중단의 거리차이를 더하면 3D 해석의 섬유 상단의 유동, 중단-하단의 거리차이를 빼면 3D 해석의 섬유 하단의 유동과 비슷한 결과가 나올 것으로 예상할 수 있다. 3D 해석에서 섬유 상, 하단의 유동 전진 거리와, 2D 해석에서 Fig. 15 값을 반영하여 유동 전진 거리를 예측한 결과와 비교하였다. 결과는 충진시간 오차율 약 5% 미만으로 나타났고 자세한 유동전진거리 결과는 Fig. 16에 요약하였다.
|
Fig. 7 Flow chart for determining permeability used in 2D analysis |
|
Fig. 8 Results of determined permeability : (a) upper and (b) lower |
|
Fig. 9 Comparison of flow front between 3D and 2D analysis : (a) upper flow front and (b) lower flow front |
|
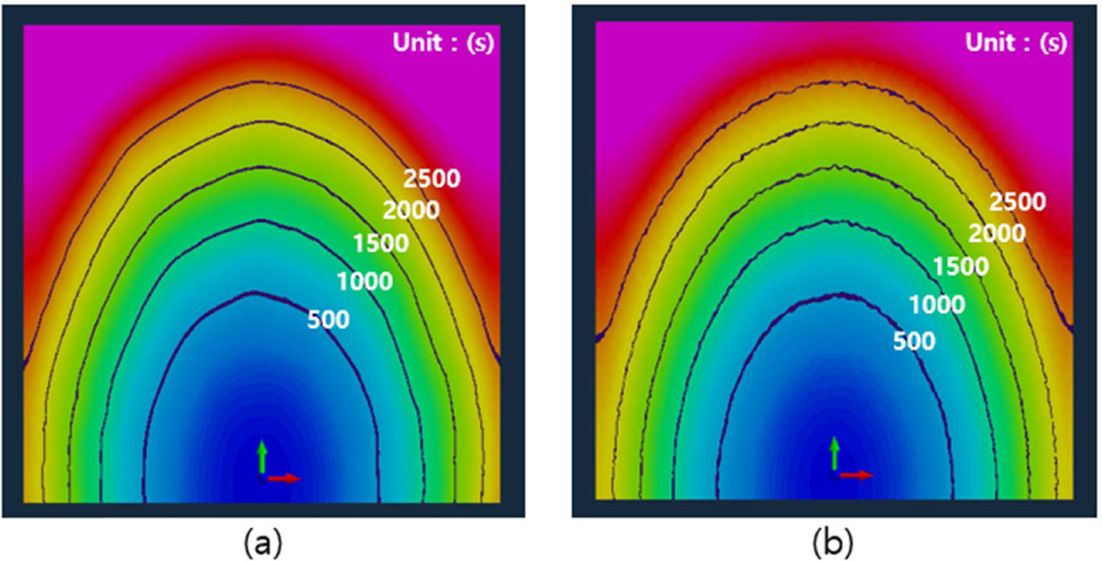
Fig. 10 Results of flow front in case of central infusion : (a) 2D analysis with average permeability and (b) 3D analysis at middle layer of 9 ply laminate |
|
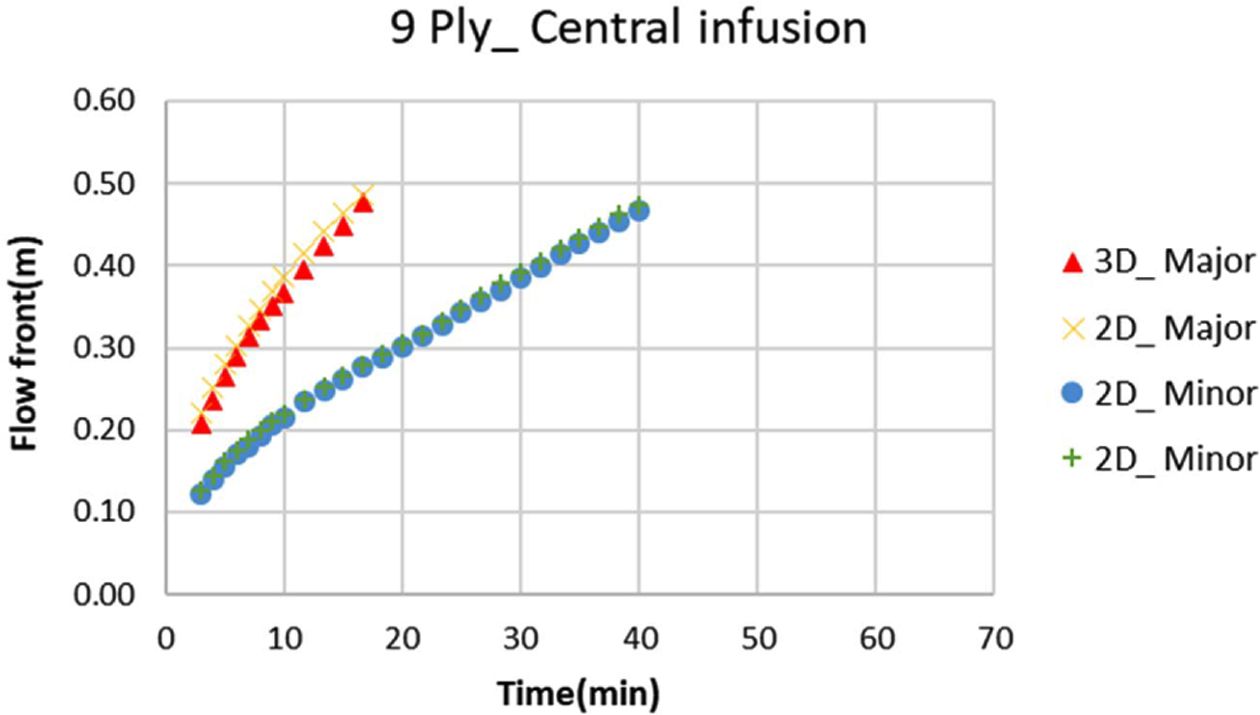
Fig. 11 2D and 3D flow fronts results of 9 ply laminate central infusion |
|
Fig. 12 Results of flow fronts in case of edge infusion : (a) 2D analysis with average permeability and (b) 3D analysis at middle layer of 9 ply laminate |
|
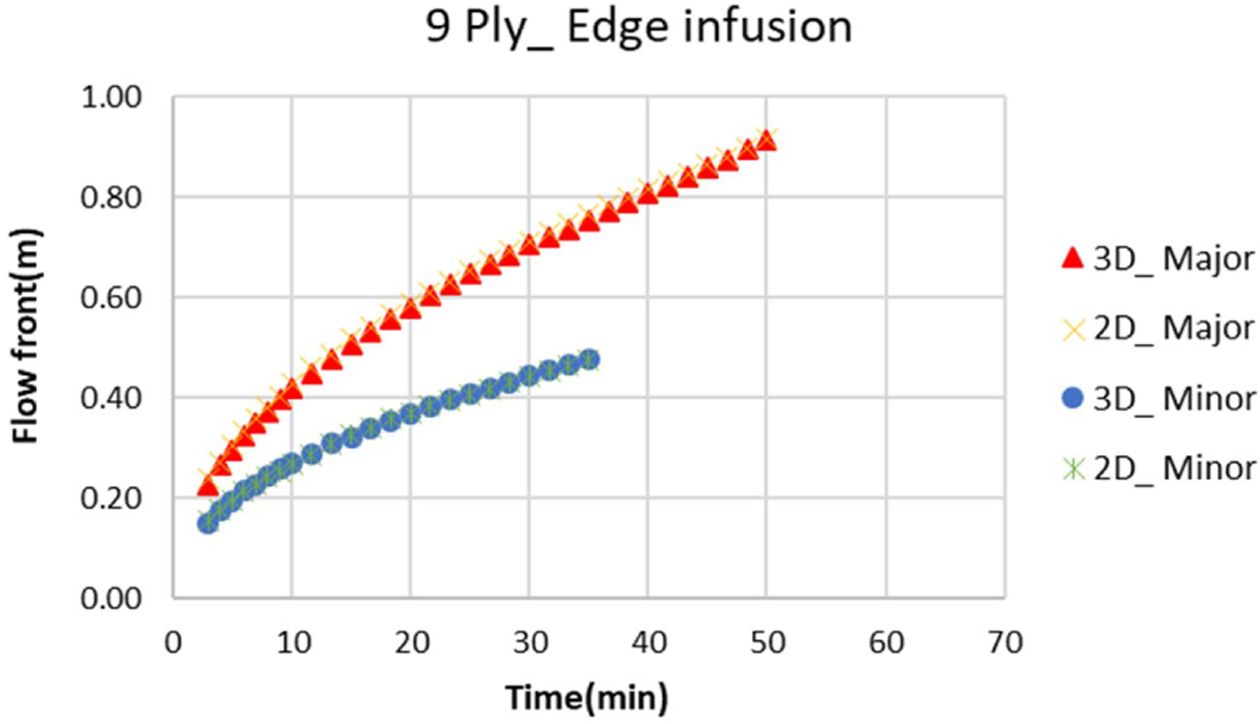
Fig. 13 2D, 3D flow front result of 9 ply laminate edge infusion |
|
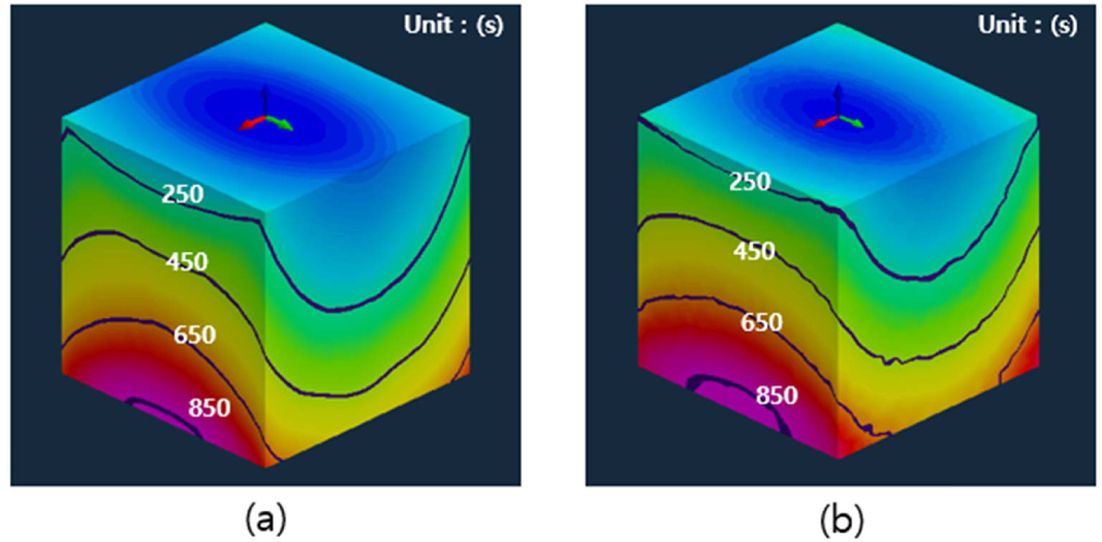
Fig. 14 Results of flow front in case of cube shape : (a) 2D analysis with average permeability and (b) 3D analysis at middle layer of 9 ply laminate |
|
Fig. 15 Flow front difference at upper-middle, middle-lower of 9 Ply : (a) major direction and (b) minor direction |
|
Fig. 16 Comparison of flow front between 3D analysis and 2D analysis (prediction) in 9 ply : (a) major direction and (b) minor direction |
|
Table 2 Solving time comparison of 2D and 3D analysis in case of central infusion |
본 연구에서는 VaRI 공정에서 유동해석에 소요되는 계산시간을 줄이고자 3D 유동해석을 2D 유동해석으로 간소화하는 방법을 제시하고 효용성을 검증하였으며 과정은 다음과 같다.
1. 섬유 압착실험을 통해 1 atm의 하중이 가해졌을 때 섬유 두께를 측정하여 섬유 총 체적율을 계산하였고, 섬유의 면내방향, 두께방향 투과성계수 측정 시 반영하였다. 측정하기 어려운 유로망의 투과성계수는 가시화실험과 유동해석을 비교하여 결정하였다.
2. 섬유/유로망 적층구조에서 다양한 섬유적층수에 대해 3D 유동해석을 수행하였고, 유동선단을 분석하여 2D 투과성계수 Map을 결정하였다.
3. 제시된 2D 투과성계수 Map은 임의의 섬유/유로망 소재와 임의의 각도에서 그려진 결과이며, 소재와 적층각이 다른경우 해당 소재에 대해 투과성계수 Map을 새로 그리는 작업이 필요하다.
4. 2차원 형상, 3차원 형상에서 동일한 주입 조건으로 2D 해석과 3D 해석을 비교하였고 충진시간에서 오차율은 약 7% 미만으로 나타났고, 해석시간을 약 95% 단축할 수 있었다.
5. 3D 해석에서 섬유 상, 중, 하단의 유동거리차이가 일정하게 나타난다는 점을 활용하여 2D 해석에서도 3D 해석 섬유 상, 하단의 유동거리를 예측할 수 있다.
간소화된 2D 유동해석은 기존 3D 유동해석에 비해 계산시간이 대폭 줄어들어 구조물의 크기가 큰 항공기, 선박, 풍력블레이드 등의 VaRI 유동해석에 적용이 가능가능할 것으로 예상된다.
본 연구는 산업통상자원부(No.20011022)의 지원을 받아 수행되었으며 이에 감사드립니다.
- 1. Lee, J.H., Kim, W.H., Kim, Y.S., and Choi, S.W., “A Study on the Approach to Reduce in the Aviation GHG Emissions in Korea,” Jounal of the Korean Society for Aviation and Aeronautics, Vol. 24, No. 1, 2016, pp. 47-54.
-

- 2. Kim, K.S., and Park, S.J., “Technique Status of Carbon Fibers-reinforced Composites for Aircrafts,” Elastomers and Composites, Vol. 46, No. 2, 2011, pp. 118-124.
-

- 3. Harshe, R., “A Review on Advanced Out-of-Autoclave Composites Processing,” Journal of the Indian Institute of Science, Vol. 95, No. 3, 2015, pp. 207-220.
- 4. Chen, R., Dong, C., Liang, Z., Zhang, C., and Wang, B., “Flow Modeling and Simulation for Vacuum Assisted Resin Transfer Molding Process with the Equivalent Permeability Method,” Polymer Composites, Vol. 25, No. 2, 2004, pp. 146-164.
-

- 5. Trochu, F., Gauvin, R., and Gao, D.M., “Numerical Analysis of the Resin Transfer Molding Process by the Finite Element Method,” Advances in Polymer Technology: Journal of the Polymer Processing Institute, Vol. 12, No. 4, 1993, pp. 329-342.
-

- 6. Fuqua, M., and Glancey, J.L., “A Port Injection Process for Improved Resin Delivery and Flow Control in Vacuum-assisted Resin Transfer Molding,” ASME International Mechanical Engineering Congress and Exposition, Vol. 4773, 2006, pp. 45-57.
-

- 7. Jhan, Y.T., Lee, Y.J., and Chung, C.H., “Experimental and Numerical Investigation of the VARTM Process with a Sandwich Structure,” Journal of composite materials, Vol. 46, No. 12, 2012, pp. 1417-1430.
-

- 8. Park, Y.H., Kang, M.G., and Lee, W.I., “A Dual-Scale Analysis of Macroscopic Resin Flow in Vacuum Assisted Resin Transfer Molding Process,” Journal of the Korean Society for Composite Materials, Vol. 15, No. 6, 2002, pp. 1-7.
- 9. Dong, C., “An Equivalent Medium Method for the Vacuum Assisted Resin Transfer Molding Process Simulation,” Journal of Comaterials, Vol. 40, No. 13, 2006, pp. 1193-1213.
-

- 10. Chan, A.W., and Hwang, S.T., “Anisotropic In-plane Permeability of Fabric Media,” Polymer Engineering & Science, Vol. 31, No. 16, pp. 1233-1239.
-

 This Article
This Article
-
2021; 34(4): 233-240
Published on Aug 31, 2021
- 10.7234/composres.2021.34.4.233
- Received on Jul 21, 2021
- Revised on Aug 3, 2021
- Accepted on Aug 4, 2021
 Services
Services
Shared
 Correspondence to
Correspondence to
- Moon-kwang Um
-
Composites Research Division, Korea Institute of Materials Science, Changwon, Korea
- E-mail: umk1693@kims.re.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.