Metamaterials are complexes of elements that can create properties not found in naturally occurring materials, such as changing the direction of forces, creating negative stiffness, or altering vibration and impact properties. In the case of wood pile metamaterials that are easy to manufacture and have excellent performance in reducing vibration and shock in the vertical direction, basic research on variables affecting shock transmission is needed to reduce shock. Although research on impact reduction according to geometrical factors is being conducted recently, studies on the effect of material variables on impact reduction are insufficient. In this paper, finite element analysis was carried out by variablizing the geometrical properties (lamination angle, diameter, length) and material properties (modulus of elasticity, specific gravity, Poisson's ratio) of wood pile cylinders. Through finite element analysis, the shape of the wooden pile cylinder delivering impact was confirmed, and the effect of each variable on the reduction of impact force and energy was considered through main effect diagram analysis, and frequency band analysis was performed through fast Fourier transform. proceeded In order to reduce the impact force and vibration, it was found that the variables affecting the contact area of ​​the cylinder have a significant effect

메타물질은 자연발생 물질에서 발견되지 않는 특성을 만들 수 있는 여러가지 요소들의 복합체로, 힘의 방향을 변환하거나, 음의 강성을 만들거나, 진동 및 충격 특성을 바꿀 수 있다. 제작이 용이하고, 수직방향의 진동과 충격을 저감시키는데 탁월한 성능을 지닌 우드파일 메타물질의 경우, 충격 저감을 위해 충격 전달에 영향을 끼치는 변수에 대한 기초 연구가 필요하다. 최근 기하학적 요소에 따른 충격저감에 대해 연구가 진행되고 있지만, 재료적 변수가 충격저감에 끼치는 영향에 대한 연구는 미흡하다. 본 논문에서는 우드파일 실린더의 기하학적 특성(적층각도, 직경, 길이)과 재료적 특성(탄성계수, 비중, 포아송 비)을 변수화하여 유한요소해석이 진행되었다. 유한요소해석을 통해 우드파일 실린더가 충격을 전달하는 양상을 확인하고, 주효과도 분석을 통해 충격 힘과 에너지의 저감에 대한 변수 별 영향이 고찰되었고, 고속 푸리에 변환(FFT)을 통해 주파수 대역에 대한 분석이 진행되었다. 충격 힘과 진동을 저감시키기 위하여 실린더의 접촉 면적에 영향을 주는 변수들이 크게 영향을 끼치는 것으로 나타났다

Keywords: 우드파일 메타물질(Woodpile Metamaterial), 파라 메트릭 연구(Parametric Study), 충격 저감(Impact Reduction), 고속 푸리에 변환(Fast Fourier Transform)

메타물질이란, 자연발생 물질에서 발견되지 않은 특성으로 설계된 물질로, 금속 및 플라스틱과 같은 재료로 만들어진 여러가지 요소의 복합체로 알려져 있다. 메타물질은 특정 방향으로 입력된 힘을 다른 방향의 힘으로 전환하거나[1], 음의 강성(유전율, 굴절률, 벌크 모듈러스, 유효질량밀도, 포아송 비 등)을 만들거나[1-4] 입력된 충격 힘이나 에너지를 저감시키고, 파동의 전파 특성을 제어하는 등 다양한 목적으로 사용되며, 다방면에서 사용되는 만큼 많은 메타물질의 연구가 진행되어왔다. 힘의 방향을 전환시키기 위한 메타물질의 예로는 다단계 메타물질(MSM) 있다. MSM은 압축상태에서 전역 하중을 여러 변형 경로로 변환하여 미세 단위 셀에 순차적인 접촉과 좌굴을 통해 응력-변형률 그래프에서 다중 평탄의 특징을 보인다. 파단 응력이 작은 경우에는 낮은 응력 안정기가 필요하지만 큰 충격에서 물체를 보호하기 위해서는 높은 응력 안정기가 필요하다고 알려져 있다. 이 때 다중 고원 기능을 통해 다목적 에너지 흡수 장치를 위한 설계에 사용될 수 있다[5]. 음의 포아송 비, 음의 강성, 음의 압축성 등 직관에 반하는 기계적 특성을 가진 인공 구조인 기계적 메타물질은 기존의 허니콤 재료와 비교하여 보조 메타재료로써 충격 과정동안 증가된 안정 응력과 시편의 부피 감소로 인해 충격에너지 흡수 응용 분야에서 크게 각광받고 있다[4]. SMP(Shape Memeory Polymer, 다중 안정 메타물질)는 강성과 변형 복구 효과를 자동으로 조정할 수 있다. 복합 격자 미세 구조 기울기 설계를 통해 다중 안정 메타물질의 변형 및 복구 효과를 조정할 수 있으며 공진 영역 이전의 저주파에서 음의 진동 레벨 차이를 나타내어 강도 저하 없이 우수한 방진 성능이 입증되었다[6,7]. 이중 나선 메타물질(DDHM)은 선택적 레이저 소결 기술을 기반으로 한 적층 제조기계를 통해 뛰어난 복구 능력과 완화 능력을 지닌다. 충격속도와 단위 셀의 수를 변수로 하여 비선형 거동을 고려한 spring-mass 모델을 수립하여 단위 셀의 공진에 의한 bandgap을 통해 충격완화 성능에 대하여 연구되었다[8]. 이와 같은 많은 메타물질의 특성 중 시스템의 감쇠에 의존하지 않고 강한 감쇠와 응력 파형의 주파수 변조가 가능한 우드파일 메타물질[9]은 적층된 원형 실린더의 형상을 띄고 있으며, 수직 방향의 진동 및 충격저감에 탁월한 효과를 지니고, 단순한 형상으로 인해 쉽게 제작할 수 있다는 장점이 있다[10,11]. 이전의 연구는 우드파일 메타물질의 요소 배열이나 기하학적 특성만을 변환하여 충격특성을 해석하는 방향으로 진행되었다. 최근 메타물질의 재료를 변경하여 에너지 흡수 및 충격특성을 비교하는 연구가 진행되었으나, 그 재료의 특성이 메타물질의 충격저감에 영향을 미치는지에 대하여 분석되지 않았다[7,12]. 진동 및 충격특성에 대해 많은 연구가 진행중인 우드파일 메타물질에서, 각 변수들이 어떻게 작용되는지에 대한 연구가 진행된다면 메타물질의 재료적 변수들이 어떠한 영향을 끼치는지에 대한 좋은 선행연구가 될 것이라고 생각된다. 본 논문에서는 메타물질의 기하학적, 재료적 특성에 따른 충격 및 진동 특성을 분석하였다. 기하학적 변수와 재료적 변수를 선정하여 각 변수 별 충격특성을 확인할 수 있는 우드파일 메타물질의 단일 유닛 모델을 제작하여 유한요소해석이 진행되었고, 충격 전달 양상이 확인되었다. 바닥에서 올라오는 반사파를 고려하지 않기 위해 응력파 이론을 적용하여 충격전달속도 및 출력충격을 확인하고, 유한요소해석 결과와 이론식을 비교하여 해석의 신뢰성을 높였다. 충격 힘과 에너지의 충격저감을 확인하기 위하여 주효과도 분석이 진행되었고, 저감되는 주파수 대역을 확인하기 위하여 고속 푸리에 변환(FFT)이 진행되었다.

2.1 우드파일 메타물질 모델
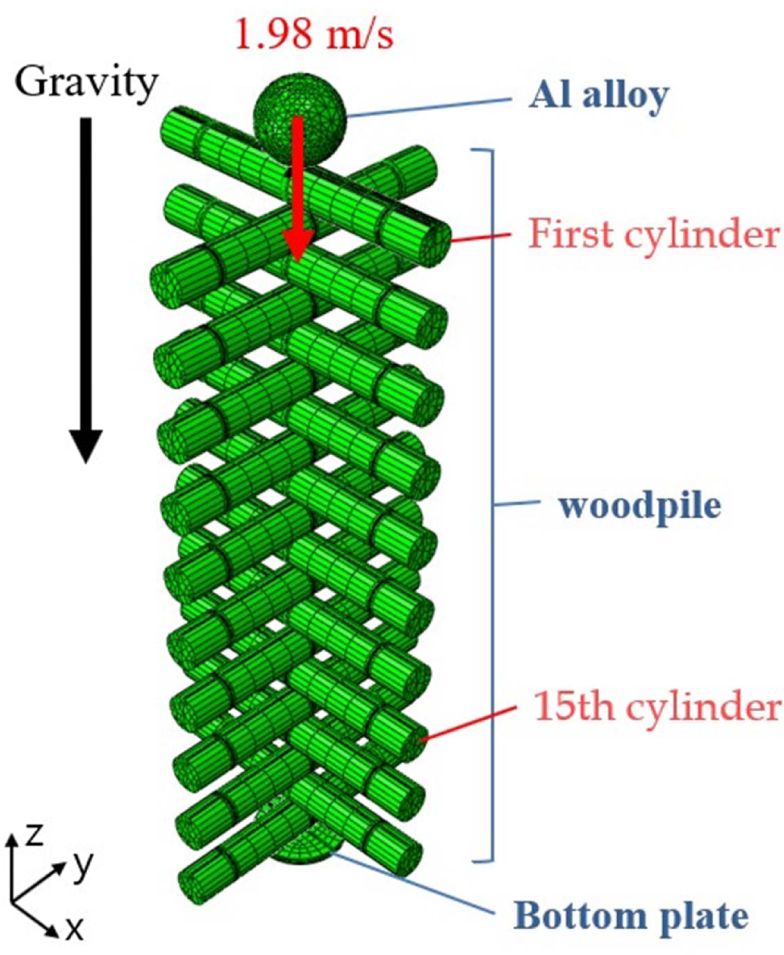
우드파일 메타물질은 적층된 나무토막들과 같은 형상에서 붙여진 이름으로, 적층 방향의 충격이 증가하거나 감소된다. 우물 정(井)의 모양처럼 우드파일들이 여러 개 겹쳐있는 것이 전체 모델이지만, 유한요소해석을 진행하여 충격 변화량을 계산하기 위해 Fig. 1과 같이 우드파일 메타물질의 단일 유닛 모델이 제작되었다. 입력 에너지를 동일하게 적용하기 위해 적층된 20개의 실린더 중 첫번째 우드파일 실린더 위에 -z 방향으로 1.98 m/s의 속도를 가진 알루미늄 합금의 강구를 모델링하였다. 강구가 첫번째 실린더에 전달한 충격을 입력 충격으로 지정되었다. 출력충격을 지정하기 위하여 응력파 이론을 적용하였다. 바닥판에서 올라오는 반사파와 바닥판이 받는 충격이 중첩으로 인해 이것이 정확한 출력충격인지 판단하기 어렵다[9]. 중첩을 고려하지 않고 출력 충격을 확인하기 위하여 바닥판까지 응력파가 도달하는 시간이 계산되었고 바닥까지 응력파가 도달하기 전인 15번째 실린더가 받은 충격을 출력충격으로 지정되었다.

2.2 충격저감을 위한 해석변수
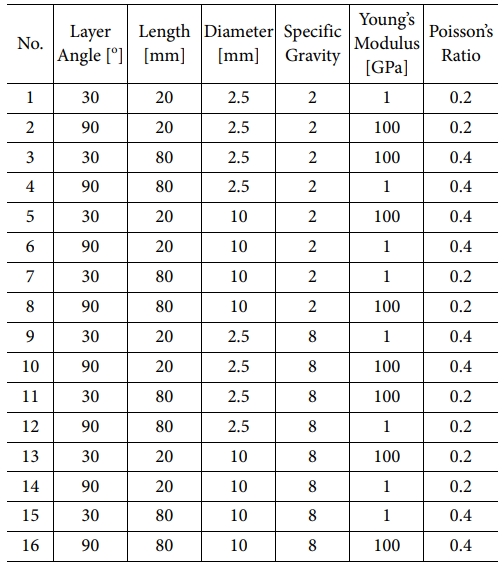
이전의 우드파일 메타물질 연구들은 기하학적 변수만을 조절하여 충격저감이 얼마나 발생되는지 확인했지만, 본 논문에서는 기하학적 변수와 재료적 변수를 동시에 조절하여 충격저감에 주는 영향이 확인되었다. Table 1에 나타난 것과 같이 기하학적 변수로는 우드파일의 각도, 길이, 지름을 두었고, 재료적 변수로는 영률, 포아송 비, 비중이 지정되었다. 총 6가지 변수마다 2개의 인자를 두어 총 16가지의 케이스의 유한요소해석이 진행되었다.

3.1 유한요소해석 결과
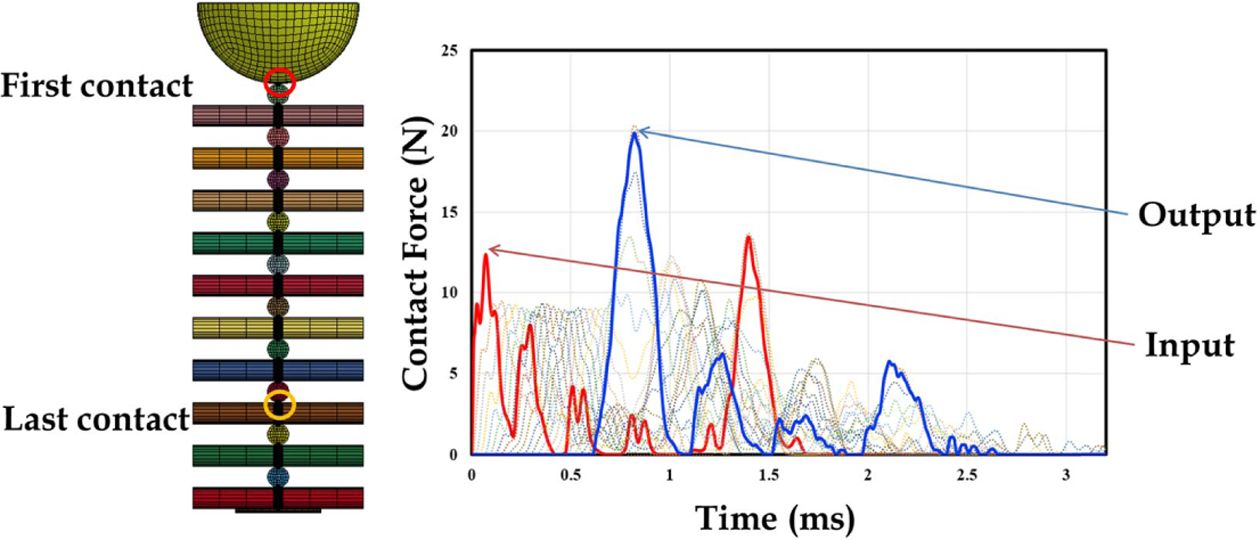
본 연구에서 강구의 질량과 속도를 동일하게 주어 입력에너지가 동일하지만, 우드파일의 변수가 다르기에 입력 충격 힘은 모두 다르다. 따라서 충격저감을 확인하기 위해서는 충격저감비를 확인할 필요가 있다. 입력충격은 강구가 첫번째 실린더에 준 충격을, 출력충격은 14번째 실린더가 15번째 실린더에 준 충격으로 지정되었다. Fig. 2에 나와있는 것처럼 출력충격이 실린더의 진동에 의해 여러 개의 극값을 가질 경우, 응력파가 도달하기 전까지의 최댓값이 출력충격으로 지정되었다. 응력파의 속도를 구하기 위하여 식 (1)이 사용되었다.



C는 응력파의 속력을 나타내고, E는 탄성계수를, ρ는 V_f/V_s를 나타낸다. V_f = 5πD²L이고 우드파일의 실제 부피를 나타낸다. 겉보기 부피의 계산식은 V_s = 20DL²이다. 충격저감량은 입력충격에서 출력충격을 뺀 값이며, 입력충격 대비 출력충격을 충격저감비로 본 연구에서 충격 힘에 대한 저감을 확인하기 위한 지표로 사용되었다.

3.2 충격 힘 분석
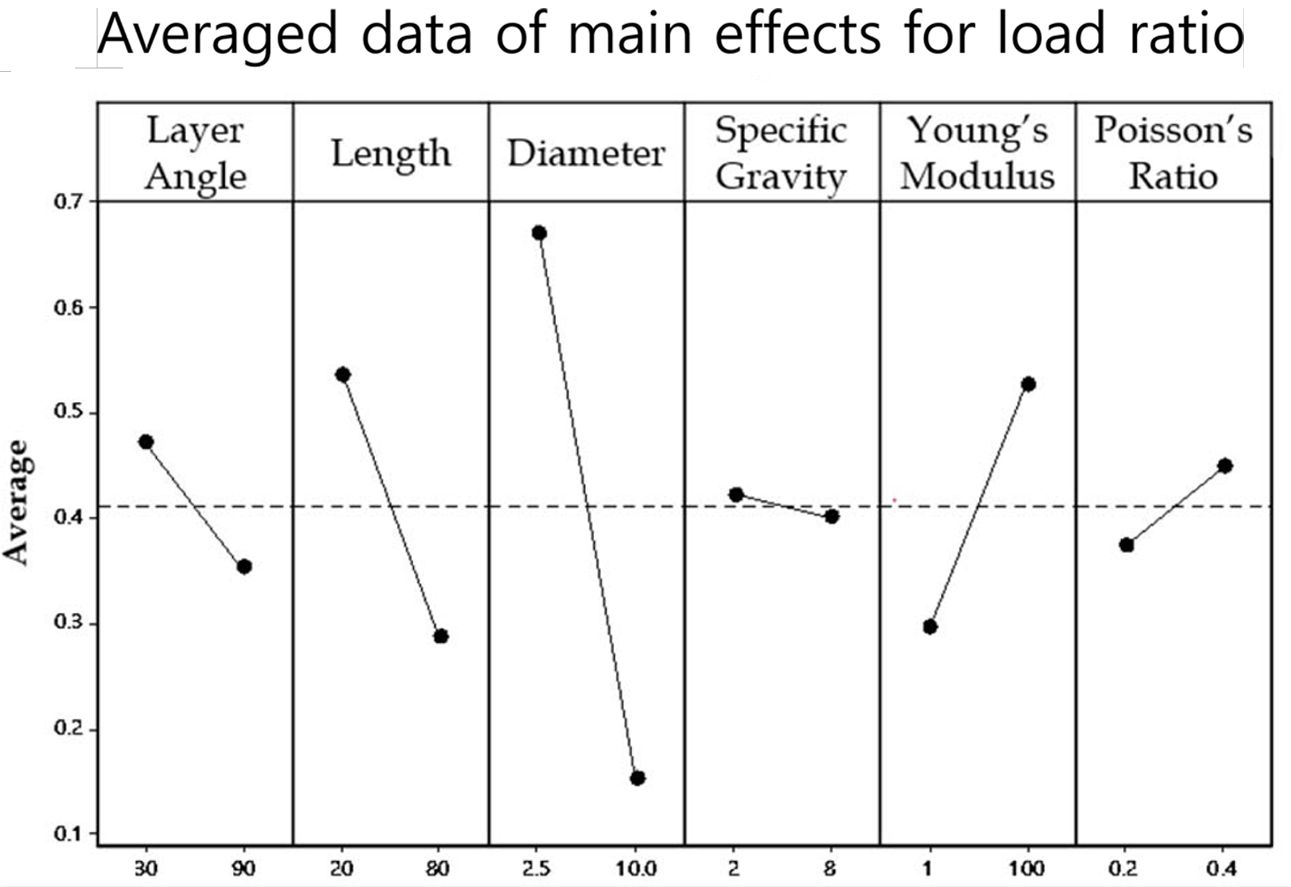
충격저감비에 대한 DOE 분석을 사용하여 주효과도를 분석하였다. 각 변수별 주효과도는 Fig. 3에 나타난 것과 같다. 그 결과, 길이, 적층각도, 지름 그리고 비중이 클수록, 탄성계수, 포아송 비가 작을수록 충격저감이 더 큰 것으로 나타났다. 이는 우드파일 사이의 접촉 면적이 넓을 수록 충격저감에 더 좋다고 사료된다. 특히 직경과 길이가 가장 큰 영향을 끼치는 것으로 나타났는데, 접촉 면적에 가장 크게 영향을 끼치는 인자라고 사료된다. 재료적 변수는 탄성계수가 가장 큰 영향을 끼치는 인자로, 연성이 큰 재질일수록 충격저감이 클 것으로 사료된다.

3.3 충격 에너지 분석
충격 에너지의 저감량을 보기 위하여 각 실린더의 내부 에너지 변화량이 확인되었다. 에너지의 경우는 비중과 포아송 비가 클수록, 적층각도, 길이, 지름 그리고 탄성계수가 작을수록 충격에너지가 더 잘 저감된 것으로 나타났다. 충격 힘과는 다르게 접촉면적이 작을수록 충격 에너지의 저감에 좋을 것으로 사료된다. 하지만 영향력이 큰 인자는 지름과 길이로 충격 힘과 동일한 것으로 나타났다.

3.4 주파수 대역 분석
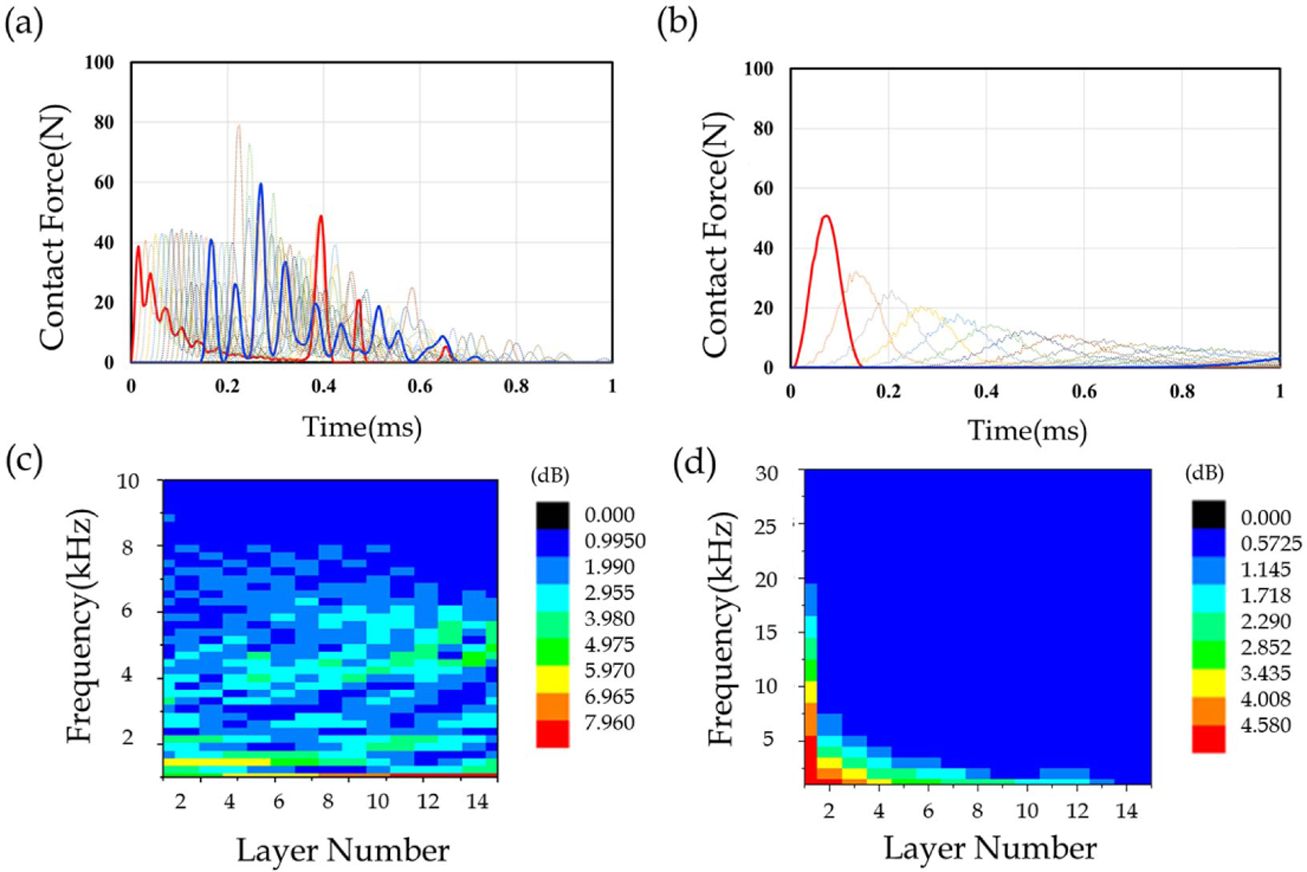
충격 힘을 고속 푸리에 변환하여 주파수 대역에 대한 분석이 진행되었다. Fig. 4에서 (a)는 다중 충격을 받은 실린더의 전달양상을, (b)는 단일 충격을 받은 우드파일 실린더의 전달양상을 나타내며, 빨간 선으로 입력충격을, 파란 선으로 출력충격을 나타냈다. (c)는 다중충격을 받은 실린더의 고속 푸리에 변환을, (d)는 단일 충격을 받은 실린더의 고속 푸리에 변환을 나타내었다. 첫 번째 우드파일이 다중 충격을 받는 경우에는 저주파 대역의 진동이 증폭되는 것으로 나타났고, 고주파의 진동은 거의 유지되었다. 단일 충격을 받는 경우 모든 주파수 대역의 진동이 저감되는 것으로 나타났다. 첫 번째 우드파일이 다중 충격을 받는 경우, 강구가 첫 번째 우드파일에 진동 충격을 주는 것으로 나타났다. 이 때, 첫번째 우드파일이 받는 충격의 진동수가 클수록 일정한 진폭을 지니며 지수적으로 작은 파동열을 갖는 비국소 독방파인 나노프테라(Nanoptera)[13]의 진폭이 더 큰 것으로 나타났다. 다중 충격이 발생하는 경우는 우드파일의 길이가 짧고 각도가 크며, 직경이 작은 경우에 발생되었다. 재료적 변수는 탄성계수가 작을수록 강구의 진동이 많은 다중충격이 발생되었다.

4.1 헤르쯔 접촉식과 굽힘에 관한 이론적 분석
강구와 우드 파일 실린더의 접촉 힘, 각각 실린더 사이의 접촉 힘을 확인하기 위해 헤르쯔 접촉식을 사용하여 강구가 우드파일에 가한 충격과 우드 파일이 전달하는 충격들을 계산되었다[14]. 헤르쯔 접촉 힘은 식 (2)로 알려져 있다.



이 때의 β는 접촉계수로, β_cc는 실린더와 실린더 사이의 계수이고, β_cs는 강구와 실린더 사이의 계수이다. 그에 대한 식은 식 (3)와 (4)에 나타내었다.



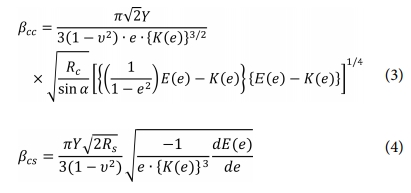
식에서 R_c는 실린더의 반지름을, R_s는 강구의 반지름을 나타내고, K(e)와 E(e)는 제1차, 제2차 완전 타원 적분의 값이다. e는 두 실린더의 타원접촉면적의 면적의 이심률이며, 식 (5)를 따른다.



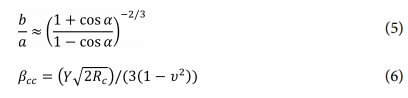
α는 두 실린더의 접촉각을 나타내며, 그 값이 90도일 때의 접촉계수는 식 (6)를 통해 간략하게 표현될 수 있다[15].
헤르쯔 접촉식 외에도 실린더들은 입력충격에 대해 굽힘 이론이 적용되었다[16]. 실린더 상부의 양 끝단의 길이가 감소하는 경우에는 굽힘모멘트가 위 방향으로 발생되고, 길이가 증가하는 경우에는 아래 방향으로 발생되는 것으로 나타났다. 유한요소해석을 통해 얻은 실린더 길이의 변화량으로 식 (7)을 통해 ρ를 구하고, 식 (8)을 통하여 굽힘모멘트가 도출되었다.



위 식에서 ρ는 실린더의 중립면에서 원점까지의 거리이고, R은 실린더의 반지름을, L은 처음 실린더의 길이, L'은 나중 실린더의 길이이다.

4.2 이론식에 따른 결과 그래프 비교
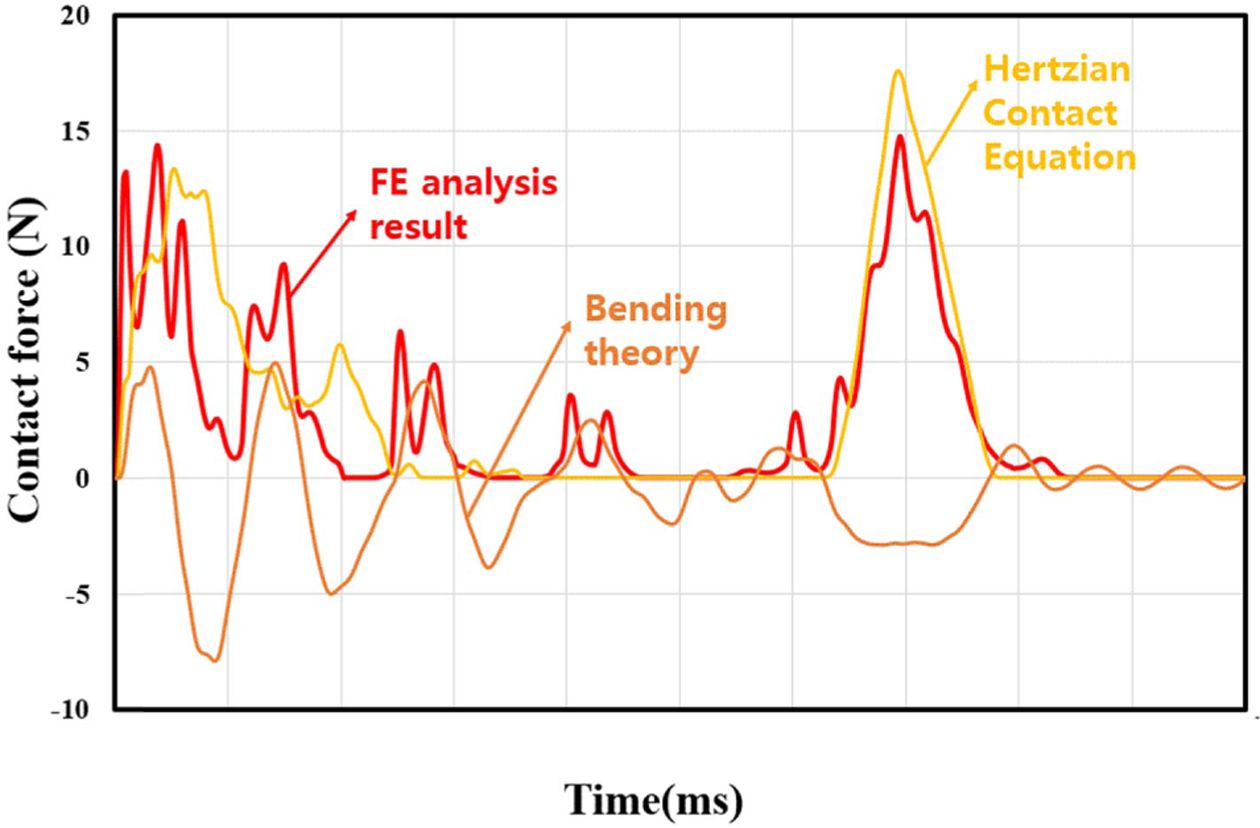
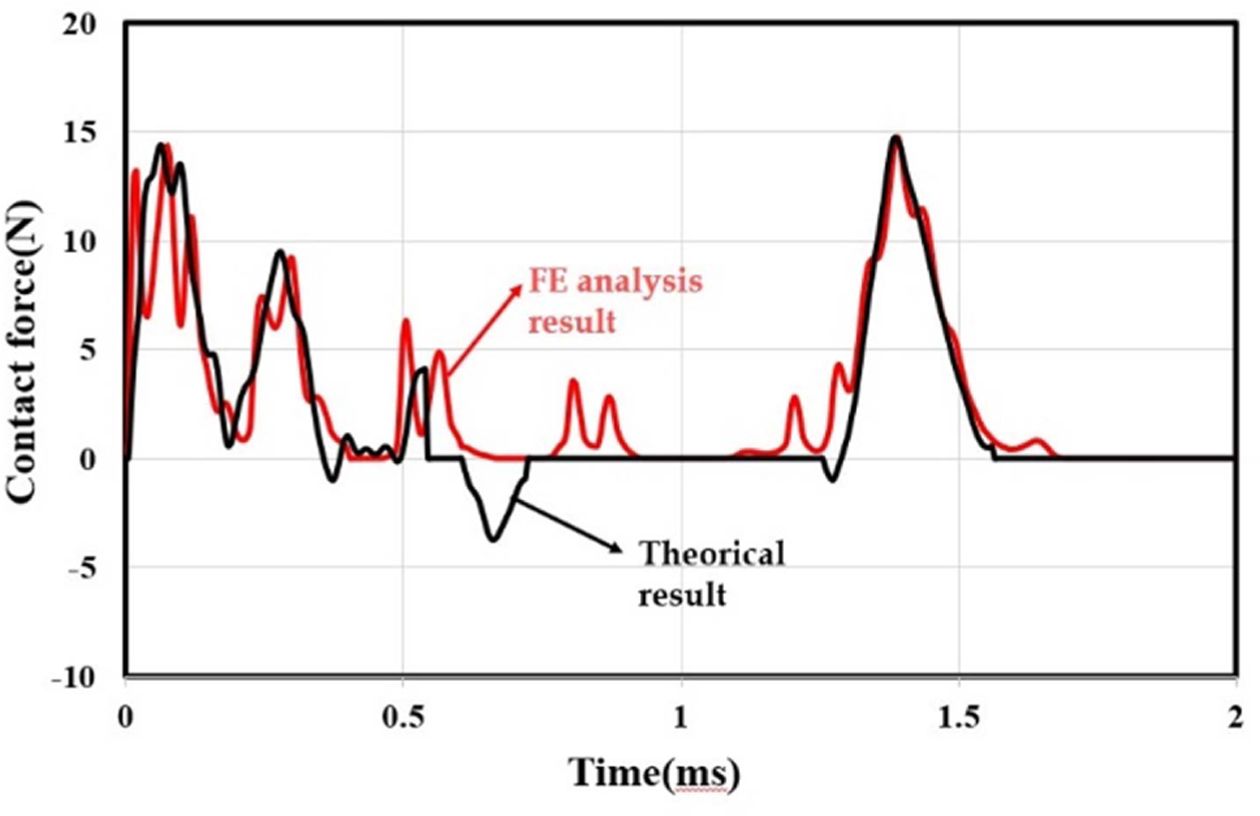
Fig. 5은 총 16가지 케이스의 헤르쯔 접촉식과 굽힘식, 그리고 유한요소해석 결과에 대한 그래프이다. 우드파일 실린더의 충격전달은 헤르쯔 접촉식과 굽힘에 대한 영향을 받는 것으로 사료된다. 유한요소해석에서 실린더가 받은 충격은 헤르쯔 접촉식과 가장 유사한 형태를 지니고 있었고, 굽힘모멘트가 위 방향으로 주어질 때에는 헤르쯔 접촉식보다 큰 해석 값이, 아래 방향으로 주어질 때는 헤르쯔 접촉식보다 작은 해석 값이 도출되었다. Fig. 6을 통해 헤르쯔 접촉식과 굽힘식의 합을 유한요소해석 결과와 비교하였으며. 그래프의 양상이 유사한 것으로 나타났다. 우드파일 실린더는 헤르쯔 접촉식과 굽힘식에 의해 충격이 전달된다고 사료된다.

우드파일 메타물질의 충격저감을 확인하기 위하여, 단일 유닛 모델이 제작되었고, 기하학적, 재료적 변수를 선정하여 총 16가지 케이스의 유한요소해석이 진행되었다. 유한요소해석 결과를 통한 충격 힘과 에너지의 변수 별 주효과도 분석과 고속 푸리에 변환을 통해 얻은 주파수 대역 저감에 대한 분석으로 다음과 같은 결과를 얻었다. 우드파일 메타물질을 통해 z 방향의 진동 및 충격을 크게 혹은 작게 제어될 수 있다고 사료된다. 충격 저감에 가장 민감한 반응을 보인 것은 우드파일의 지름이고, 가장 적게 영향을 끼친 것은 비중임이 확인되었다. 대체적으로 접촉면적에 많은 영향을 끼치는 변수일수록, 충격저감에 더 크게 영향을 끼치는 것으로 사료된다. 우드파일의 접촉면적이 작은 경우에 첫 번째 우드파일 실린더에 다발성 충격이 발생되며, 저주파 대역의 진동을 증폭시키는 경향이 있다고 사료된다. 단일 충격인 경우, 주파수 전역에서 진동 저감에 탁월한 성능을 지닌다고 나타났다. 우드파일의 접촉 면적이 클수록 충격저감에 효과적이라고 사료되었다.

이 논문은 2018년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2018R1D1A1B07051169).