In this paper, in order to examine the effect of fiber volume fraction non-uniformity in thickness direction on the buckling load of cylindrical composite lattice structures, we modified the equation of buckling load of the cylindrical composite lattice structures proposed by Vasiliev. The thickness of each layer of the rib was varied by fiber volume fraction, and material properties were applied differently by using the rule of mixture. Also, we performed linear buckling analysis by varying the structure size, thickness, and average value of the fiber volume fraction of finite element model. Finally, by comparing the calculation results of the buckling load of the equivalent model using the modified buckling load equation and the results of the finite element analysis, we found that the fiber volume fraction non-uniformity in thickness direction can reduce the buckling load of the cylindrical composite lattice structure

본 논문에서는 필라멘트 와인딩 공정에서 발생하는 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴하중에 미치는 영향을 확인하기 위해서 Vasiliev가 제안한 원통형 복합재 격자 구조 좌굴하중 이론식을 변형하여 섬유체적비에 따른 좌굴하중 저하를 확인하였다. 섬유체적비에 따라 격자 구조 리브의 각 층의 두께를 달리하였으며, 혼합법칙을 사용하여 각 층별로 물성치를 다르게 적용하였다. 구조물 크기, 두께, 섬유체적비 평균값을 달리한 유한요소모델에 대한 선형좌굴해석을 수행하였다. 최종적으로 이론식을 사용한 등가모델의 좌굴하중 계산 결과와 유한요소해석 결과를 비교하여 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴하중 저하의 원인이 될 수 있음을 확인하였다

Keywords: 원통형 복합재 격자 구조(Cylindrical Composite Lattice Structures), 필라멘트 와인딩(Filament Winding), 섬유체적비(Fiber Volume Fraction), 좌굴 하중(Buckling Load), 유한요소해석(Finite Element Analysis)

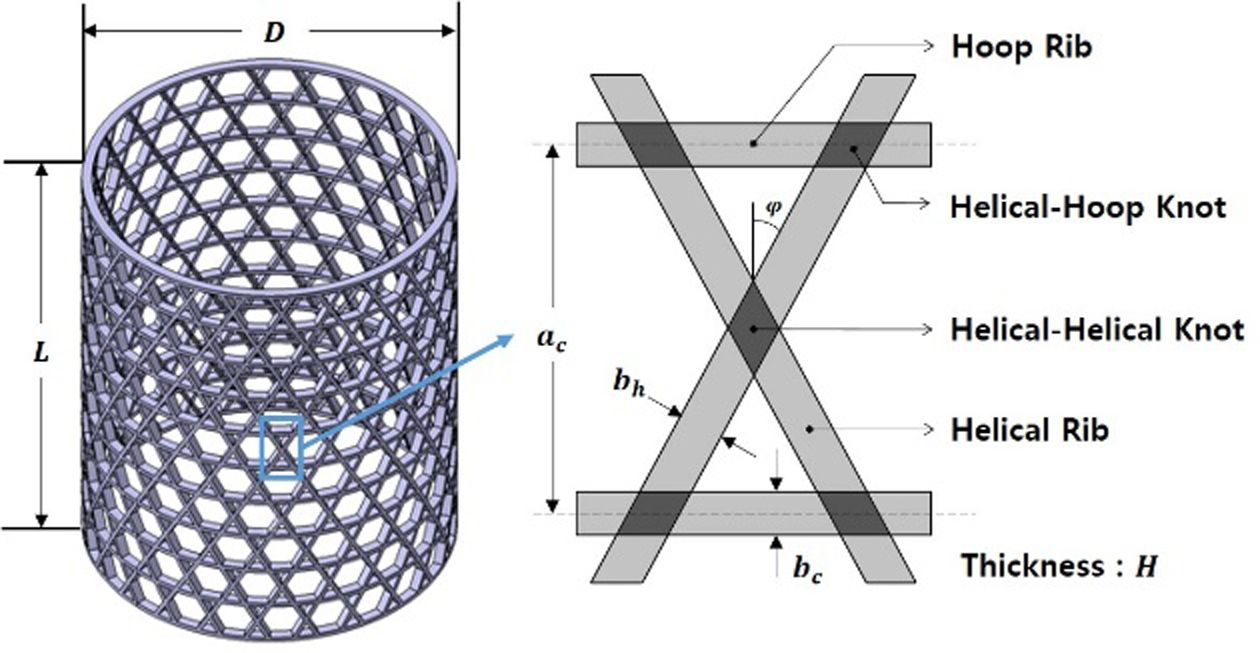
발사체의 인터스테이지, 위성, 항공기의 동체 구조와 같이 항공우주분야의 여러 구조에 적용가능한 복합재 격자 구조는 금속재 격자 구조보다 비강성, 비강도에서 우수한 성질을 갖으며 주로 압축 하중을 받는 대상에 효과적인 구조물이다[1]. 복합재 격자 구조물은 Fig. 1과 같이 헬리컬 리브(Helical Rib)와 후프 리브(Hoop Rib), 각 리브의 교차부(Knot)로 구성된 복합재 격자 구조는 에폭시 수지에 함침시킨 탄소섬유 토우(Tow)를 회전하는 몰드에 감아 적층하는 필라멘트 와인딩(Filament Winding) 기법을 주로 사용한다.
와인딩 시 작용하는 장력으로 인해 몰드에 지속적으로 압력이 작용하게 되고 이로 인해 복합재 격자 구조의 외경보다 내경에서 더 큰 섬유체적비를 갖게 된다. 복합재로 구성된 구조물의 강성은 섬유체적비의 영향을 받으며 공정상에서 발생한 섬유체적비 불균일은 구조물의 강성을 저하시켜 구조적 불안정성을 가져올 수 있고, 특히 압축 하중을 주로 받는 복합재 격자 구조의 경우 구조물의 좌굴 하중에 영향을 줄 수 있다. 원하는 수치로 내경에서 외경으로 불균일한 섬유체적비가 적용된 구조물을 제작하여 압축 시험을 하는 것은 어려우므로 이론적 계산 및 유한요소해석을 통한 예측이 필요하다.
Morozov 등[2]은 구조물의 높이 및 헬리컬 리브 각도를 달리하여 다양한 종류의 하중이 작용할 때 복합재 격자 구조의 좌굴 거동을 비교하였다. Terashima 등[3]은 CT검사를 통해 각 요소의 섬유체적비를 확인하였다. 또한 물성 시험을 통해 구한 강성 및 강도를 적용하여 유한요소해석을 수행, 이를 시험 결과와 비교하여 해석 모델의 타당성을 확인하였다. 강 등[4]은 광학 장비를 사용한 단면 검사를 통해 섬유체적비를 측정하였으며, 후프 리브와 헬리컬 리브의 강성을 확인하였다. 전 등[5]은 원통형 복합재 격자 구조의 단위 요소에 대한 압축 시험 및 후프 리브의 휘임 시험을 진행하였으며, 단면검사를 통해 측정된 섬유체적비를 적용하여 유한요소해석을 수행, 시험 결과와 비교하여 제시한 시험법의 타당성을 확인하였다. 이 밖에도 격자 구조의 최적 설계, 구조물 평가 시험에 관련된 다양한 연구가 진행되었으나[6-10], 두께 방향으로 불균일한 섬유체적비의 영향에 대한 연구는 그 수가 적은 편이다.
본 논문에서는 구조물의 크기 및 두께 방향 섬유체적비를 달리하여 이론적 계산 및 유한요소해석을 통해 원통형 복합재 격자 구조의 좌굴 하중을 계산하여 그 차이를 비교하였다. 이를 통해 두께 방향 섬유체적비 불균일이 복합재 격자 구조의 좌굴 하중에 미치는 영향에 대하여 고찰하였다.

2.1 이론식을 사용한 등가모델 좌굴하중
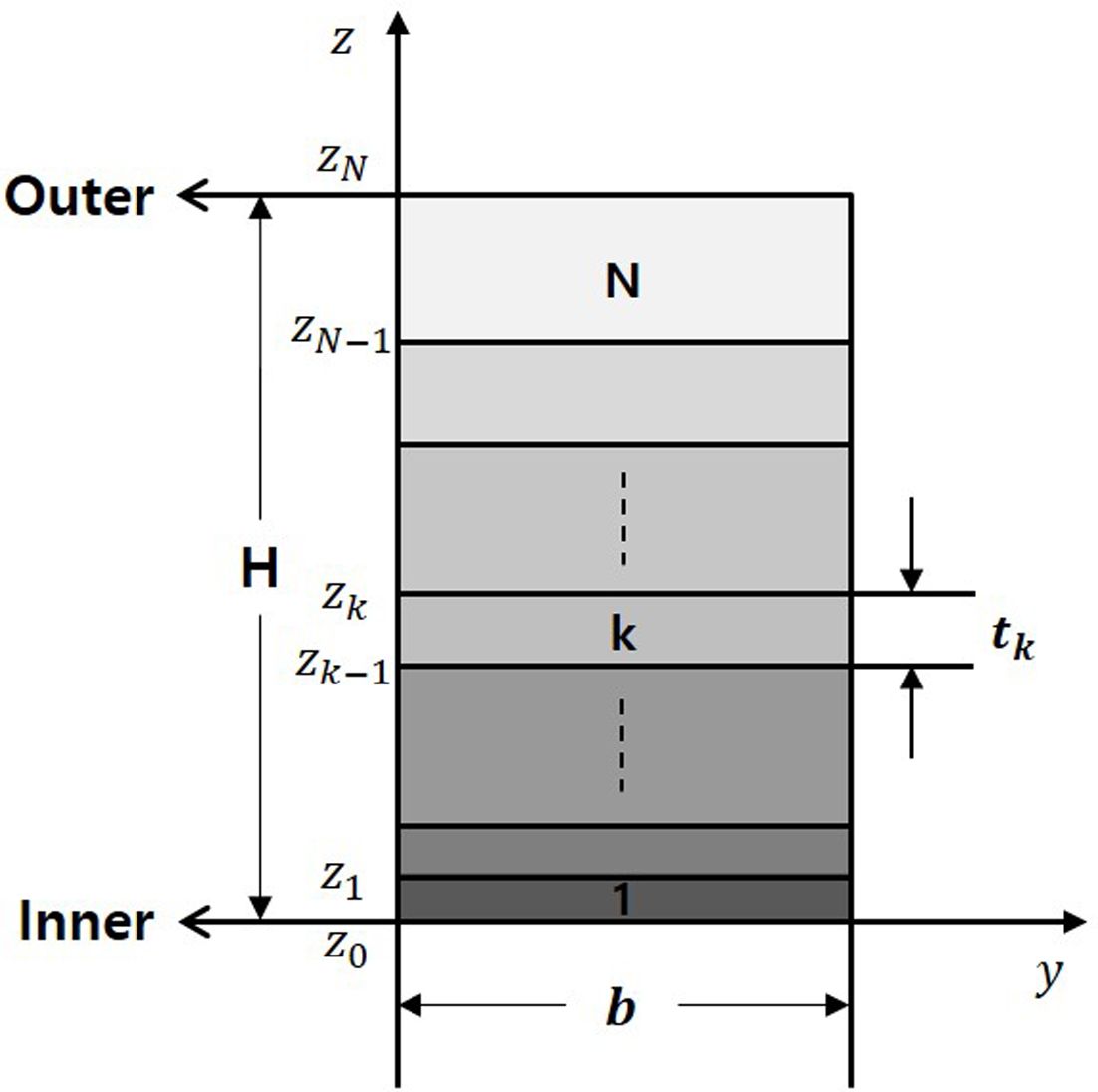
복합재 격자 구조의 경량 설계를 위해서 미국, 러시아 등에서는 Vasiliev[1]가 정립한 설계 기법을 바탕으로 복합재 격자 구조를 설계하고 있으며, 특히 압축 하중을 주로 받는 구조물로써 좌굴하중을 고려하여 설계한다. 원통형 복합재 격자 구조의 구성요소는 Fig. 1과 같다. Fig. 1의 형상요소와 제작에 사용된 재료의 물성치를 통해 격자구조의 축대칭 좌굴하중을 유도할 수 있다. 일반적으로 격자 구조 설계에는 두께 방향으로 불균일한 섬유체적비를 고려하지 않고 평균값을 사용하며 각 층의 두께를 일정하게 설정하여 좌굴하중을 결정한다. 실제 와인딩 구조물은 각 층의 섬유량은 같으나 작용하는 압력에 의해 섬유체적비는 내경에서 더 높아지므로 두께는 이에 반비례하여 얇아진다[4]. 식 (1)을 이용하여 각 층의 섬유체적비가 높아질수록 각 층의 두께가 얇아짐을 수식적으로 고려하였다. 내경에서 섬유체적비가 높아짐에 따라 두께가 얇아짐을 표현한 그림은 Fig. 2와 같다.



V_f는 섬유체적비, 하첨자 N은 전체 적층수를 의미하며, k는 k번째 층을 의미한다. k번째 층의 두께(t_k)는 해당 층의 섬유체적비와 반비례한다고 가정하였고, 이에 리브 평균 두께(t_mean)와 평균 섬유체적비(V_fmean)를 곱하여 표현하였다.
각 층의 물성치는 섬유체적비에 따라 식 (2)~(4)의 혼합법칙(Rule of Mixture)을 사용하여 계산하였으며 이때 사용한 섬유(fiber)와 기지재(matrix)의 물성치는 Table 1과 같다.



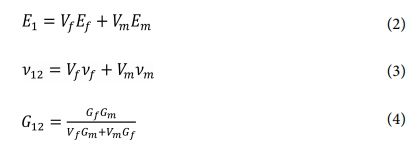
Vasiliev는 좌굴하중을 계산하기 앞서 격자 구조의 구성방정식을 식 (5)와 같이 설정하였다.



여기서 N과 ε은 기준면(reference surface)에 작용하는 막응력의 합(membrane stress resultant)과 변형률(strain), M과 κ는 모멘트(moment)와 그에 따른 휘임(bending)과 비틀림 변형(twisting deformations)을 의미하며, V과 γ는 횡방향 전단력(transverse force)과 전단 변형률(shear strain)을 의미한다. B, C, D는 각각 3×3 행렬로, B행렬은 membrane stiffness, C행렬은 coupling stiffness, D행렬은 bending stiffness를 나타낸다. B, C, D행렬의 요소는 I행렬의 요소로 식 (6)~(8)과 같이 구성된다.



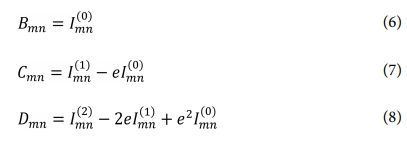
여기서 e는 기준면의 위치이며 이는 C행렬의 요소가 0이 되는 위치를 의미한다. 또한 I행렬의 요소는 식 (1)의 두께 및 강성 변화를 고려할 수 있도록 Vasiliev의 식을 변형하여 식 (9)~(20)으로 나타내었다.




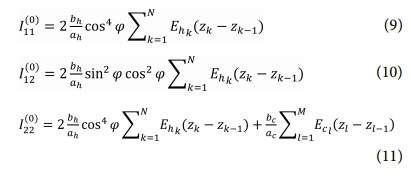
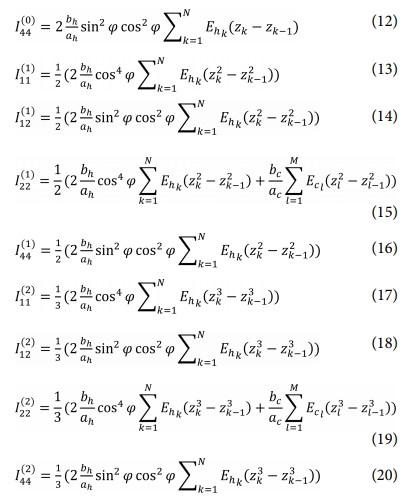
여기서 하첨자 h는 헬리컬 리브, c는 후프 리브를 의미하며, N과 M은 전체 층의 수, k와 l은 각각 k번째 층과 l번째 층을 의미한다.b는 리브의 두께, a는 리브 사이의 간격, φ는 헬리컬 리브 각을 의미하며 E는 탄성계수(Young’s modulus)를 의미한다. k번째 층의 두께 방향 위치 z_k는 앞서 가정한 두께를 통해서 식 (21)과 같이 나타낼 수 있다.



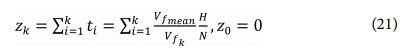
Vasiliev는 B행렬과 D행렬의 요소를 사용하여 격자 구조의 축대칭 좌굴하중을 식 (22)로 정의하였다.



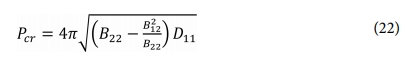
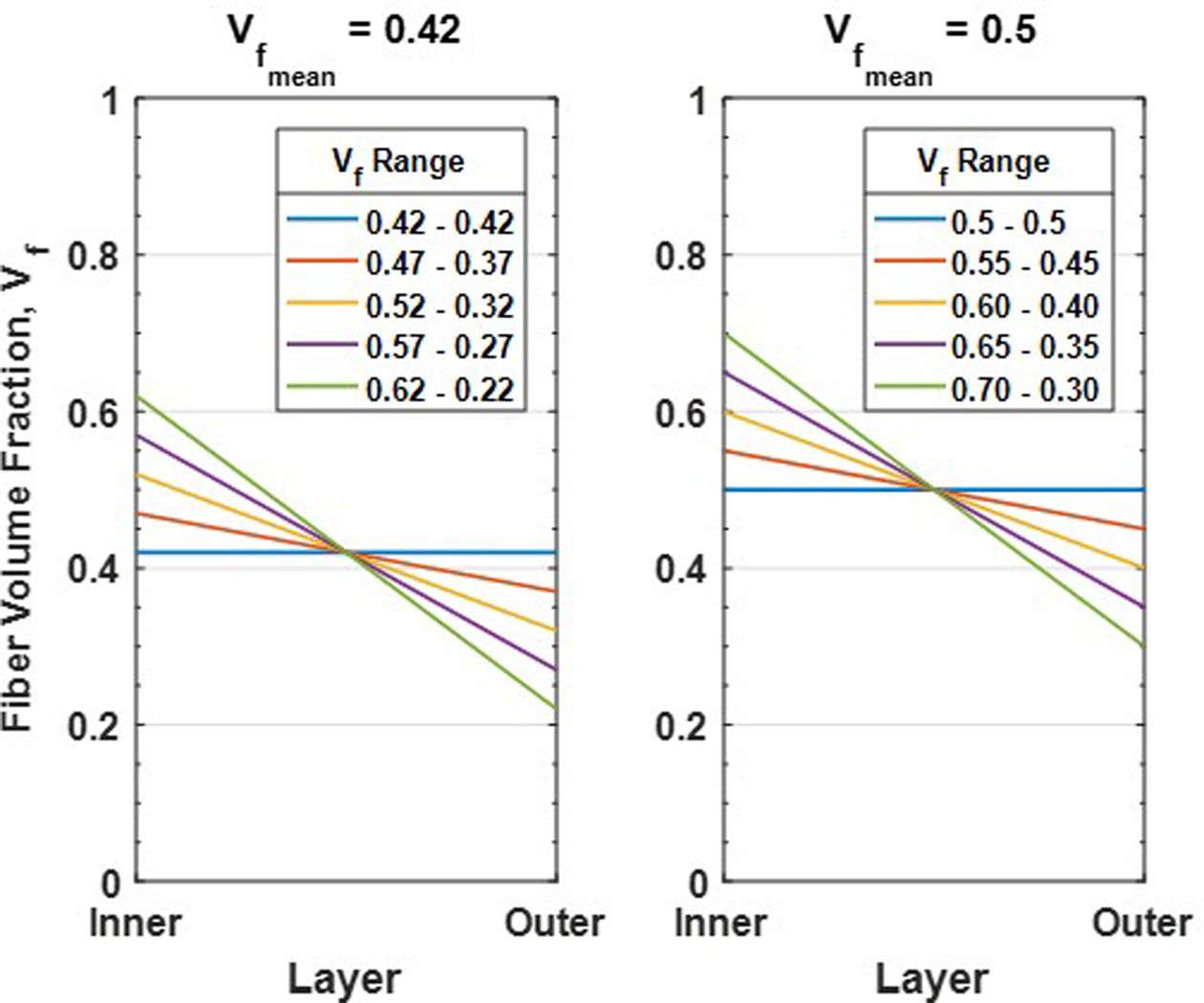
지름 600 mm, 높이 618 mm의 원통형 복합재 격자 구조에 대하여 리브 두께 및 평균 섬유체적비를 Table 2와 같이 달리하여 좌굴하중을 계산하였다. Fig. 3는 섬유체적비 평균이 0.42, 0.5일 때 두께 방향 섬유체적비 범위를 다섯 가지로 나타낸 것이다.
섬유체적비 차이를 0.1씩 증가시켜 계산하였으며 차이가 커질수록 섬유체적비가 더 불균일하게 분포한 것으로 볼 수 있다. 이와 같이 구조물의 크기가 동일할 때, 리브 두께 및 섬유체적비 평균을 달리하여, 구조물의 좌굴하중 변화에 대한 영향을 파악하였다.
2.2 유한요소해석
2.1절의 이론식을 사용하여 원통형 복합재 격자 구조 등가모델의 좌굴하중을 계산할 경우, 교차부의 적층수와 강성이 고려되지 않는다. 또한 원통형 격자 구조의 축대칭 모드는 일반적으로 고차 모드로, 구조물의 좌굴은 더 낮은 하중에서 발생할 수 있다[3]. 따라서 축대칭 좌굴 이외의 모드를 고려하여 해석적으로 두께방향 섬유체적비 불균일의 영향을 검증할 필요가 있다. 이를 위해 유한요소법을 활용한 좌굴해석을 수행하였으며, 모델링 및 해석에는 상용 해석툴인 MSC.Patran/Nastran을 사용하였다.
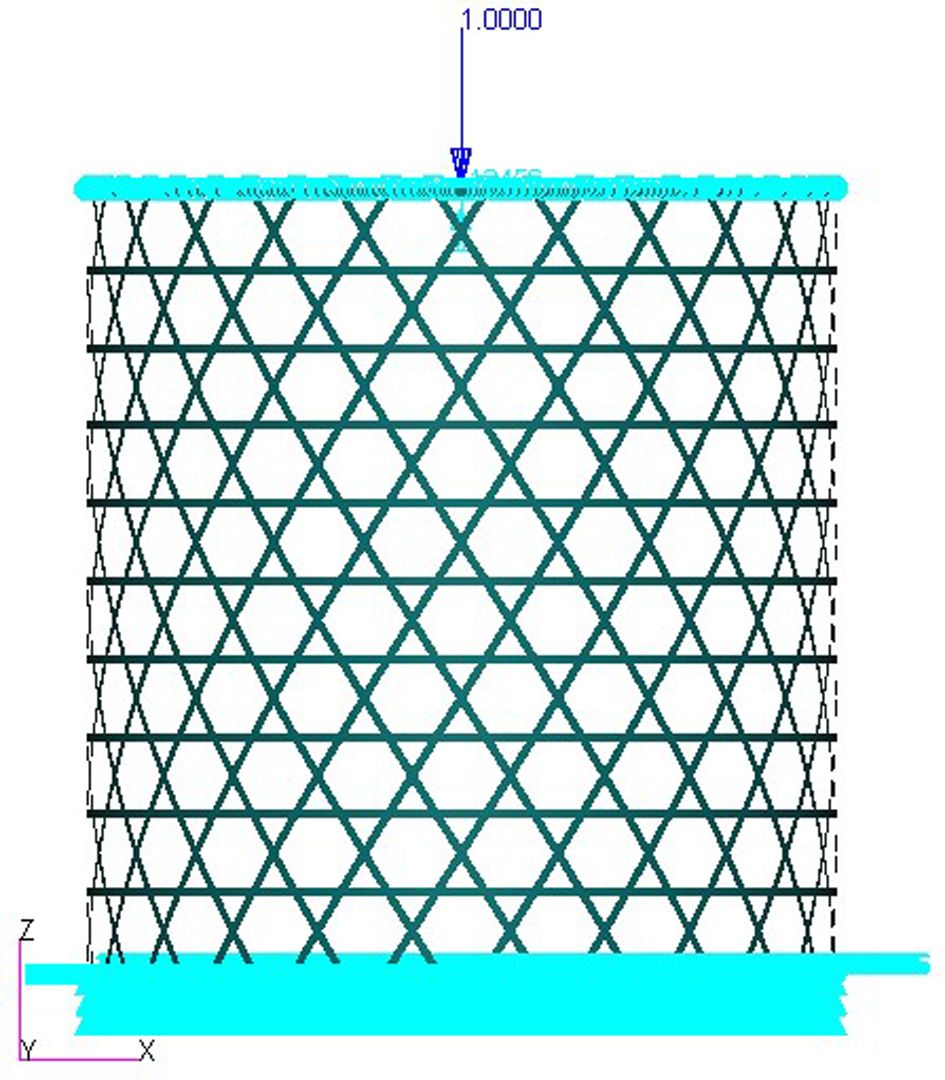
구조물의 형상은 Table 2의 형상 조건에 따라 헬리컬 리브의 각도 및 각 리브의 수를 모든 모델에 동일하게 적용하여 Fig. 4와 같이 모델링하였다.
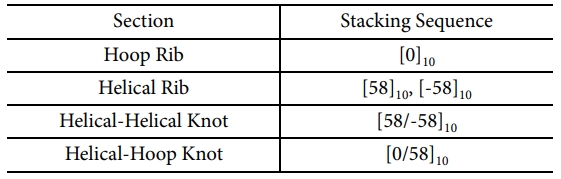
모델링에는 2D Orthotropic Laminated Shell 요소(CQUAD4)를 사용하였고, 2.1절에서 설정한 섬유체적비에 따른 두께와 물성치를 사용하였다. 각 리브 및 교차부의 적층패턴은 Table 3과 같다. 섬유교차부의 전체 적층수는 리브의 두배, 각 층의 두께는 인접 리브의 반으로 설정하였다.
경계조건은 Fig. 4와 같이 격자 구조의 하단부의 6자유도를 모두 구속하였다. 구조물의 상단부는 MPC(Multi Point Constraints) 절점에 RBE2(Rigid Body Element)요소를 사용하여 구조물 높이 방향인 z방향 병진변위를 제외한 모든 자유도를 구속하였다. 압축 하중을 받는 구조물을 묘사하기 위해 하중조건은 상단의 MPC 절점에 단위 하중을 적용하였다. 모델링된 원통형 복합재 격자 구조에 대하여 선형좌굴해석(MSC.Nastran Sol.105 Linear Buckling Analysis)을 수행하였다.

3.1 등가모델 좌굴하중
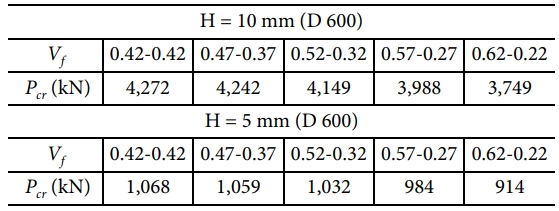
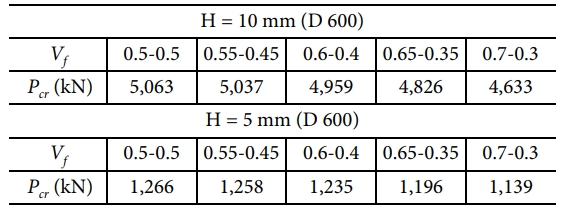
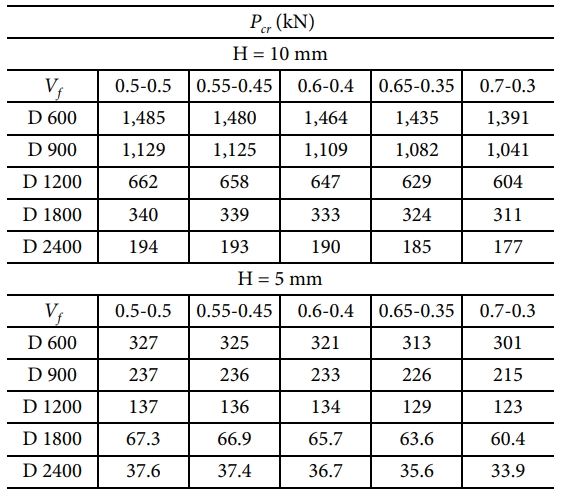
이론식을 사용하여 계산한 원통형 복합재 격자 구조 등가모델의 섬유체적비에 따른 좌굴하중을 Table 4, 5로 나타내었다. 섬유체적비는 내경-외경으로 표현하여 비교하였다. 섬유체적비가 균일한 모델에 비해 내경에서 외경으로 섬유체적비 차이가 커질 경우 좌굴하중이 낮아진다. 또한 두께가 얇은 경우 구조물의 좌굴하중이 섬유체적비 불균일에 더 영향을 받아 좌굴하중이 더 낮아짐을 확인할 수 있으며, 내경에서 외경으로 섬유체적비의 차이가 같을 때 섬유체적비의 평균값이 작을 경우 좌굴하중이 더 낮게 나타났다.
등가모델의 좌굴 하중을 정의할 때 섬유체적비를 통해 구조물의 형상 변수를 변화시킬 수 없기 때문에 구조물의 크기가 변화하여도 섬유체적비 불균일에 따른 좌굴하중 감소비가 거의 같게 나타난다. 이는 이론식을 사용하여 등가모델의 좌굴하중을 계산할 경우 구조물의 크기에 따른 두께 방향 섬유체적비 불균일이 원통형 복합재 격자구조의 좌굴하중 저하에 미치는 영향을 확인하는데 한
계점으로 작용한다. 따라서 등가모델의 좌굴하중 차이만으로는 두께 방향 섬유체적비 불균일의 영향을 정의하는 것은 어려움이 있음을 확인하였다.
3.2 유한요소해석 결과
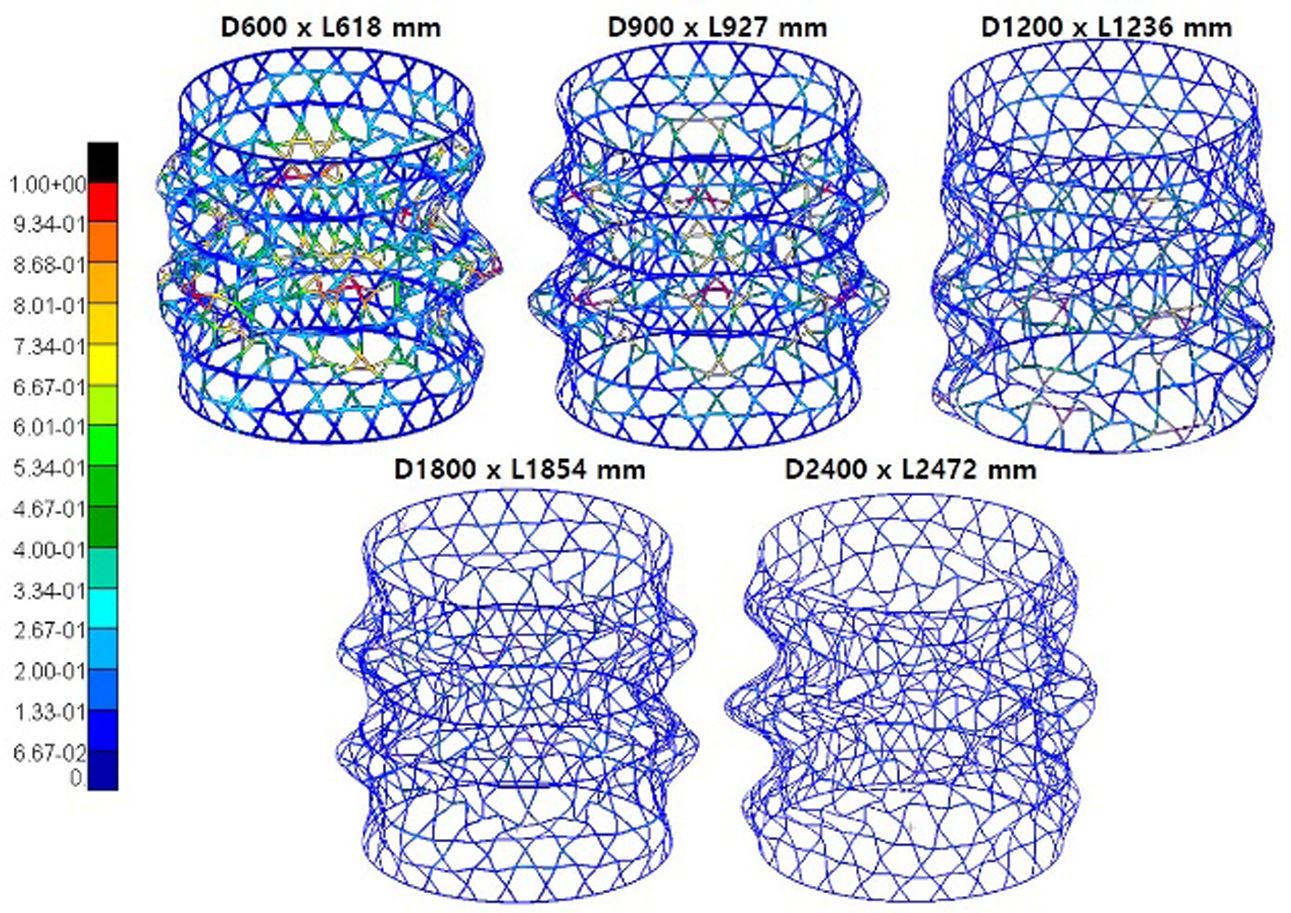
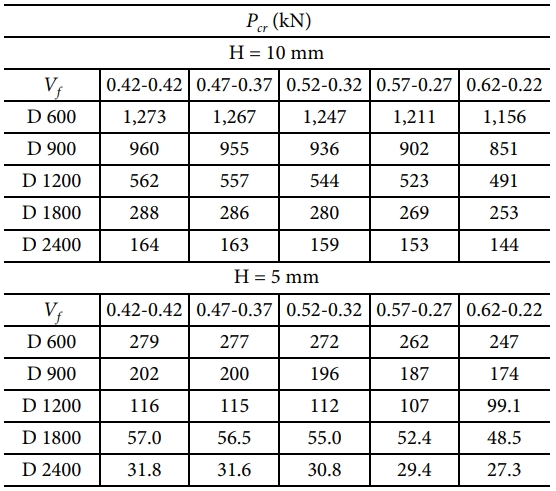
유한요소해석을 통해 얻은 원통형 복합재 격자 구조의 좌굴하중을 두께 및 크기에 따라 Table 6, 7로, 모델의 크기에 따라 1차 좌굴 모드의 좌굴 형상을 Fig. 5로 나타내어 비교하였다. Fig. 6, 7을 통해 섬유체적비가 일정한 구조물의 좌굴하중에 대한 섬유체적비가 불균일한 분포를 가진 구조물의 좌굴하중 감소비를 비교하였다.
Fig. 5의 원통형 복합재 격자 구조의 좌굴 형상을 살펴보면 3가지 모델 모두 축대칭 모드가 아닌 나선방향으로 비틀어진 비축대칭 모드로 좌굴이 발생한 것을 확인할 수 있다. 2.2절에서 언급했듯이 일반적으로 원통형 격자 구조의 좌굴은 축대칭 모드가 아닌 더 낮은 하중에서 비축대칭 모드로 나타나기 때문이다[3].
Table 4, 5와 Table 6, 7의 지름 600 mm, 길이 618 mm 모델의 결과를 비교하여 축대칭 모드의 좌굴하중이 더 높음을 확인할 수 있다.
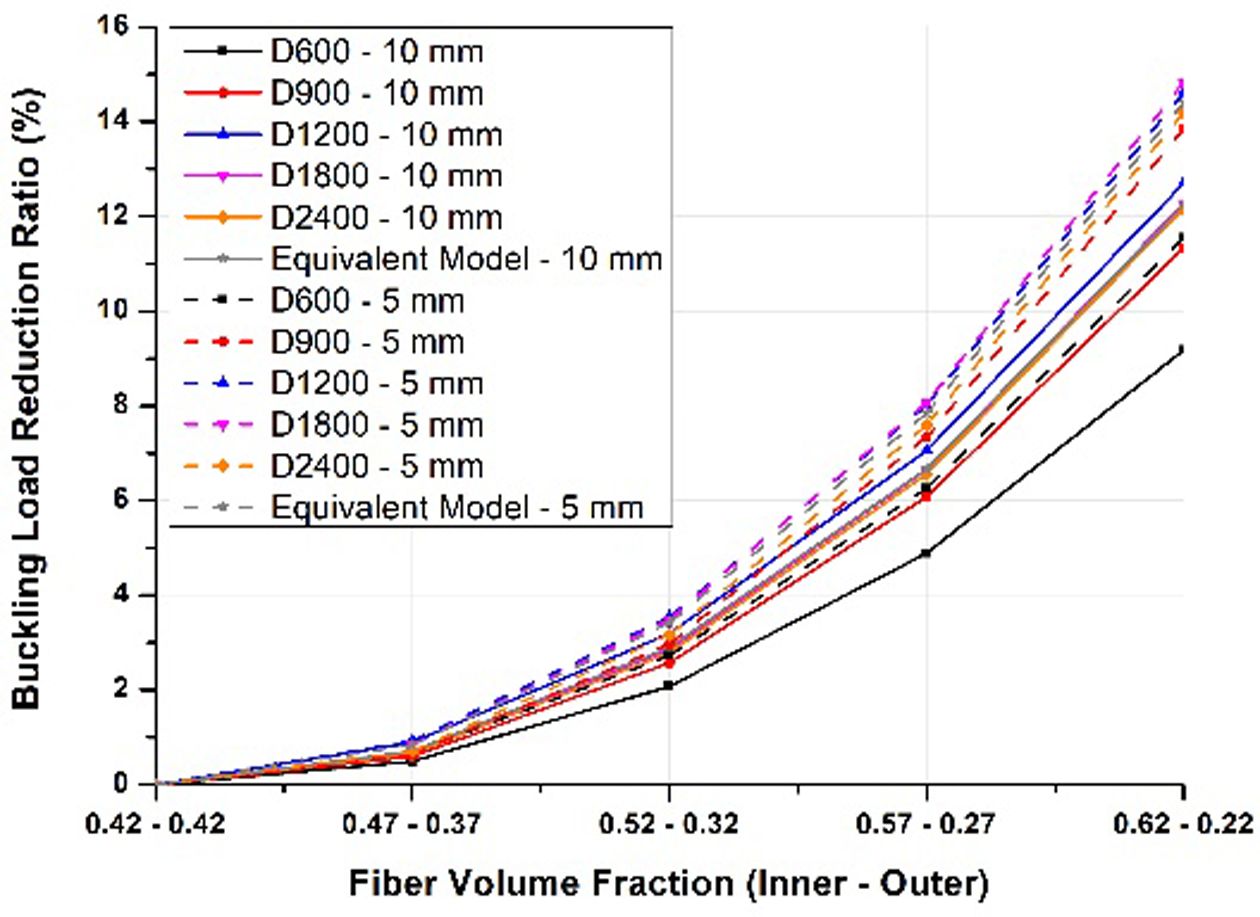
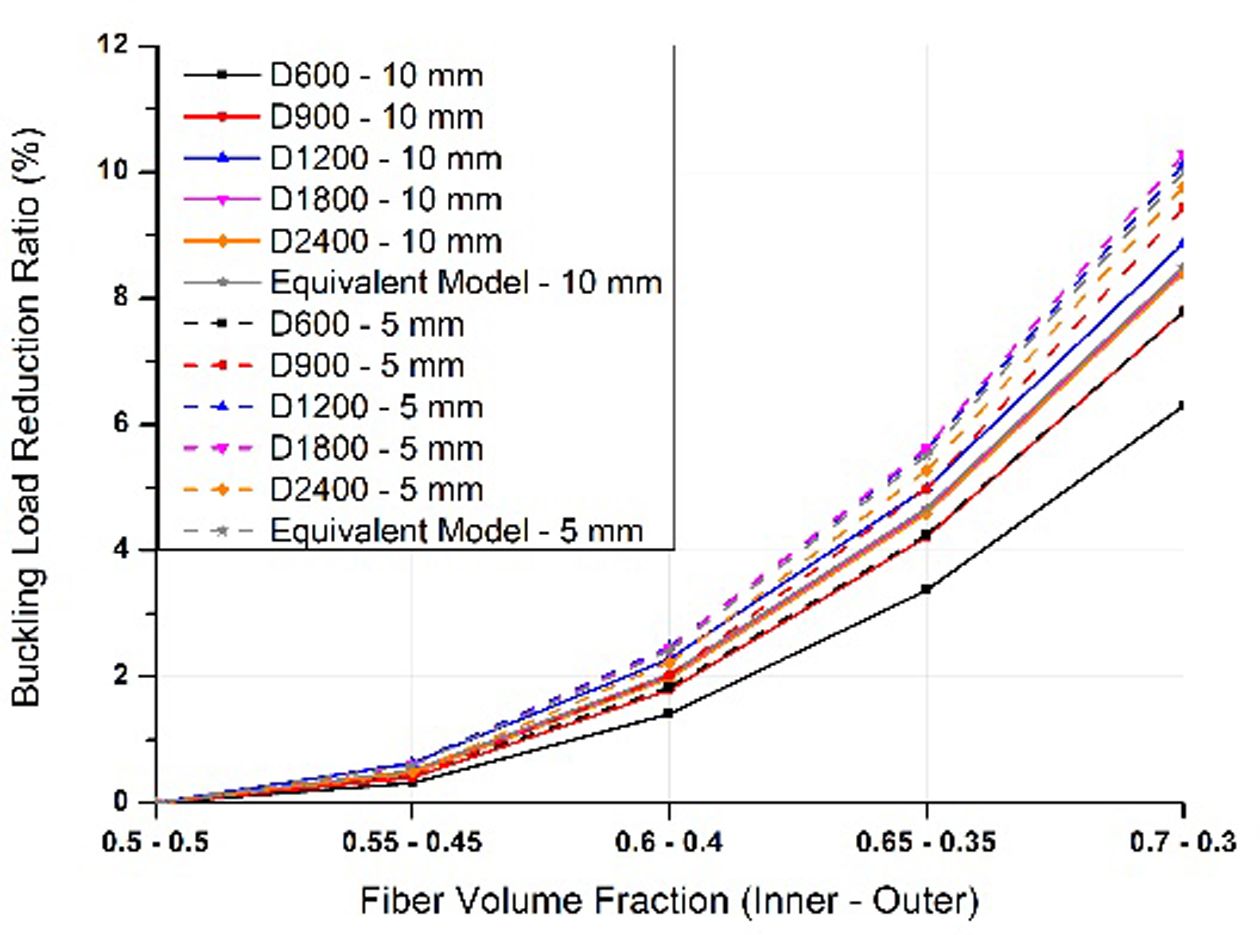
평균 섬유체적비가 0.42와 0.5일 때 두께 별 좌굴하중 차이를 Fig. 6, 7로 비교하였다. 등가모델과 FEA 모델 모두 섬유체적비가 균일하지 않을수록 균일한 모델에 비해 좌굴하중이 낮게 계산되었다. 실선으로 표현된 리브 두께 10 mm 모델과 점선으로 표현된 두께 5 mm 모델을 비교하였을 때 두께가 얇은 모델이 좌굴하중이 더 큰 폭으로 낮아졌다. 또한 Fig. 6, 7을 비교하였을 때 평균 섬유체적비가 높은 모델이 좌굴하중 저하가 더 낮게 나타났다. 지름과 길이, 두께를 제외한 모든 기하학적 변수들이 일정하므로, 구조물의 크기가 커질수록 좌굴에 더 취약하다. 이를 두 그래프를 통해 확인할 수 있으며, 구조물의 크기가 커졌을 때 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴하중 저하에 더 큰 영향을 미치는 것을 확인할 수 있다.
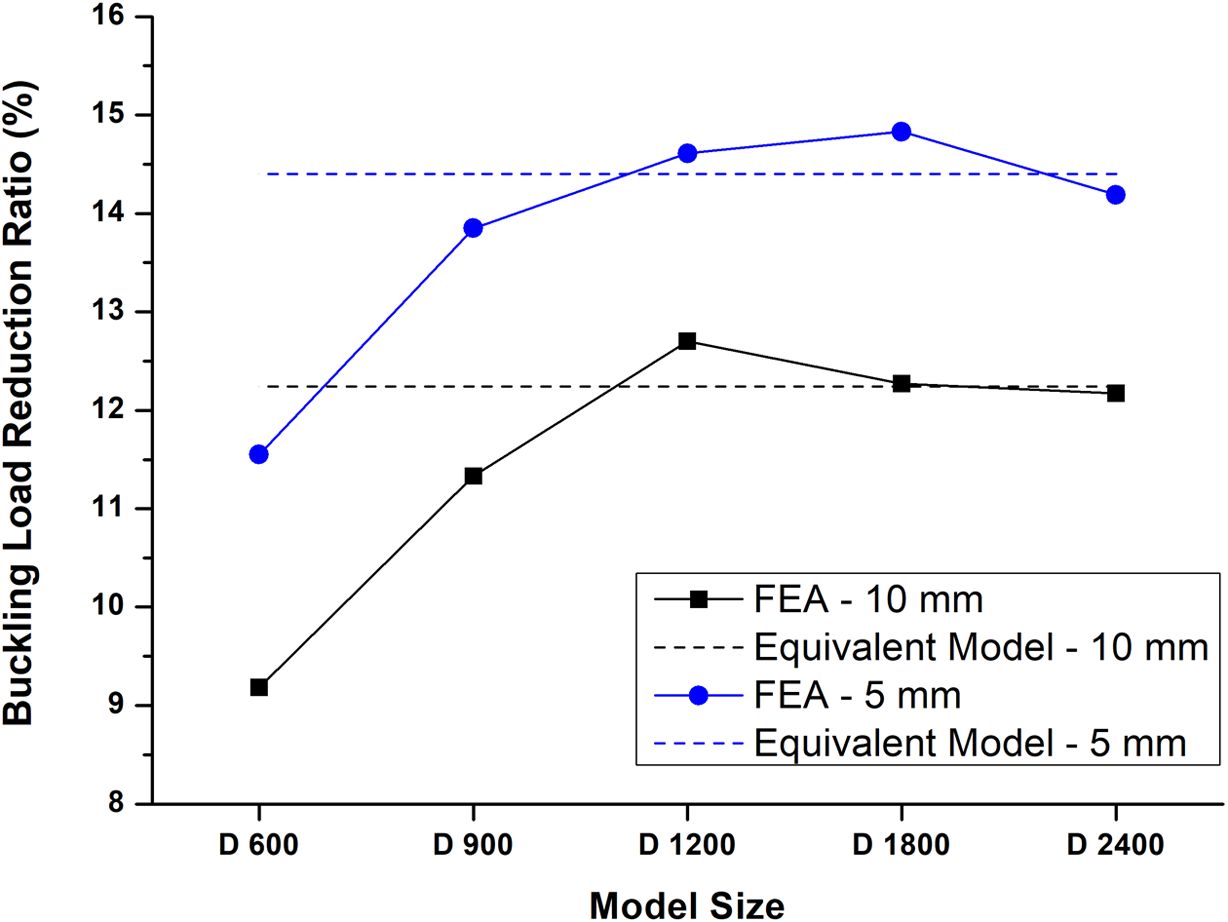
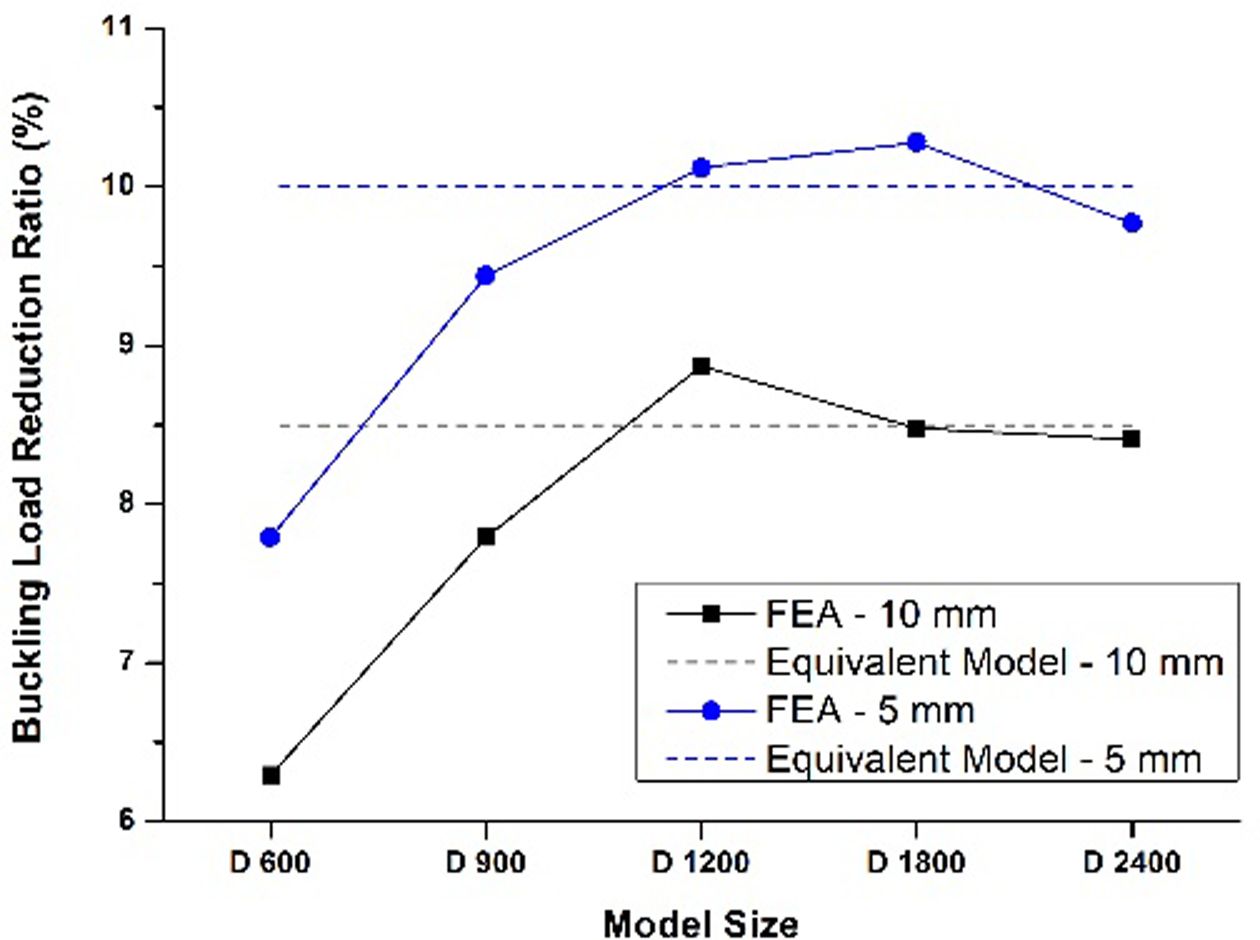
섬유체적비 평균 0.42인 경우와 0.5인 경우의 가장 불균일한 분포를 가진 모델의 좌굴하중 감소비를 Fig. 8, 9로 표현하여 모델의 크기에 따라 유한요소해석의 결과와 등가모델의 결과를 비교하였다. 모델의 크기가 작을수록 등가모델과 섬유체적비가 일정한 구조물의 좌굴하중 값에 대한 감소비는 차이가 나타났으나, 크기가 커질수록 섬유체적비와 두께에 관계없이 등가모델의 결과로 수렴하였다.
이와 같이 이론식을 사용하여 계산한 등가모델의 축대칭 모드 좌굴하중과 유한요소해석을 통해 계산한 1차 좌굴 모드의 좌굴하중을 비교하여 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴하중 저하에 대한 영향을 확인하였다.

본 논문에서는 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴거동에 미치는 영향을 확인하기 위해 복합재 격자 구조 경량 설계에 사용되는 Vasiliev의 격자 구조 좌굴하중 이론식을 섬유체적비에 따라 두께 및 물성치를 달리하여 변형하였다. 변형된 이론식을 통해 좌굴하중을 계산하여 섬유체적비 불균일에 따른 좌굴하중 저하를 확인하였다. 그러나 이론식을 사용하여 등가모델의 좌굴하중을 계산할 경우 두께에 이외의 형상변수에 대하여 섬유체적비 불균일을 적용할 수 없어 격자 구조체 크기에 따라 좌굴하중 감소비가 일정하게 나타나는 한계점이 존재한다.
이를 보완하기 위해 등가모델과 마찬가지로 섬유체적비에 따라 두께와 물성치를 달리하여 유한요소모델의 크기 및 전체 두께를 달리하여 모델링하여 선형좌굴해석을 수행하였다. 좌굴해석 결과 구조물의 크기에 따라 최대 약 14%의 좌굴하중 저하를 확인하였고, 구조물의 크기가 커질수록 두께방향으로 불균일한 섬유체적비가 구조물의 좌굴하중 저하에 더 큰 영향을 줄 수 있음을 확인하였다. 또한 등가모델의 계산 결과와 해석 결과를 비교하여 구조물 크기가 커짐에 따라 섬유체적비가 균일한 모델과 불균일한 모델의 좌굴하중 감소비가 이론식을 사용한 등가모델 계산 결과에 수렴함을 확인하였다. 그러나 원하는 범위의 섬유체적비 불균일을 설정하여 구조물을 제작할 수 없기 때문에 실험을 통한 비교검증이 어렵다는 한계점이 존재한다.
본 연구를 통해 두께 방향 섬유체적비 불균일이 원통형 복합재 격자 구조의 좌굴하중을 저하시킬 수 있음을 확인하였다. 필라멘트 와인딩 공정에 적용되는 변수들을 개선하기 위하여 몰드에 탄소섬유 토우를 감을 때 발생하는 장력을 조절하여 구조물에 섬유체적비를 일정하게 할 수 있는 성형 기술이 필요하다. 그러나 이러한 성형 기술이 성숙될 때까지는 많은 비용과 시간이 요구될 것이다. 따라서 공정에서 발생하는 두께 방향 섬유체적비 불균일을 설계 제한치로 제시하며, 이를 적용하여 저하된 좌굴하중을 고려하여 원통형 복합재 격자 구조를 설계한다면 보다 정확하고 안전한 복합재 격자 구조물 성능 평가가 가능할 것으로 예상된다.

본 연구는 민군협력진흥원(ICMTC)의 지원을 받아 수행한 연구입니다(15-CM-MA-12).