This paper dealt with multi-scale natural frequency characteristics of wavy CNT (carbon nanotube) reinforced composites by applying the Mori-Tanaka method, rule of mixture, and Halpin-Tsai equation. By compelling benefit of an ad-hoc Eshelby tensor, the load-transfer characteristics of CNT with a waviness implanted in the polymer matrix was determined. The numerical results obtained are in good agreement with those reported by other investigators. Furthermore, the new results reported in this paper show the interactions between CNT weight, waviness ratios and layup sequences of laminated composites. Key observation points are discussed and significant considerations are given in practical designing of CNT reinforced composites

본 논문은 Mori-Tanaka법, 혼합법칙 및 Halpin-Tsai 이론식을 적용하여 굴곡진 탄소나노튜브(CNT)로 보강된 복합재의 멀티스케일 고유진동 특성을 규명하였다. Eshelby 텐서를 이용하여 곡률을 갖는 CNT가 함유된 폴리머의 하중 전달 특성값이론을 유도하였다. 도출된 수치해석 결과는 기존의 연구결과와 잘 일치하였다. 본 연구에서 제시한 새로운 결과는 적층 복합재의 CNT 함유량, 굴곡성 및 적층배열의 상호작용 특성을 규명하였다. 주요 결과에 대하여 분석하였으며, CNT 보강 복합재의 실용적 설계를 위한 중요 고려사항을 제시하였다

Keywords: 굴곡진 CNT(Wavy CNT), 멀티스케일(Multi-scale), 적층복합재(Laminated Composites), 고유진동(Natural frequency)

탄소나노튜브(CNT)는 1990년대 최초 발견 이후 다양한 적용성에 관한 연구가 수행되어 왔다[1]. CNT는 기존의 산업분야 적용되는 강재 등과 비교하였을 때 매우 경량이며 뛰어난 기계적인 특성을 가진 이상적인 재료이다. 이론 및 실험으로 측정한 CNT의 탄성계수는 1.2 TPa이상, 인장 강도는 50~200 GPa 나타낸다[2]. 강철과 단순 비교하였을 경우, 탄성계수가 약 5배, 인장강도는 100배 이상 높으며 CNT를 에폭시와 같은 고분자에 첨가하였을 경우에는 탄소나노튜브 강화 복합체(Carbon Nanotube Reinforced Composite, CNTRC)를 형성할 수 있다[3]. 이를 기반으로 다양한 실험과 이론적 연구가 수행되어 왔다. 더욱 우수한 기계적, 열적 및 전기적 특성으로 인하여 재료 과학을 시작으로 다양한 공학에 이르기까지 다양한 분야에서 유용한 응용 방법이 제안되었다[4,5]. 예를 들면, Zhang 등[6]은 고분자 구조에 소량의 CNT 필러를 추가하여 CNT/고분자 복합체의 전반적인 기계적 특성을 크게 향상시키는 연구를 수행하였다. Choi와 Lee는 다중벽 CNT 복합재로 보강된 콘크리트 구조체의 고에너지 충격거동에 대하여 규명하였다[7].
반면, CNT 분산 복합재에 대한 연구는 해결해야 할 여러문제를 내포하고 있다. 불충분한 분산, 폴리머와 CNT 간의 상호작용 특성, CNT의 크기, 불규칙한 형태와 방향성 등은 CNT가 결합된 복합재 구조의 역학적 거동 특성에도 영향을 줄 수 있다. 특히, CNT의 직경은 매우 작고 유연한 특성 을 보이며, 직선이 아닌 말려 있거나 고리가 있는 형태로 분포하고 있는 경우도 자주 발생한다[8]. 미세한 CNT의 굴곡성은 직선형 CNT에 비하여 복합재의 보강 효과를 감소시킬 수 있다[9]. 섬유의 파형과 말려있는 형태는 각각 진폭과 나선 반경이 다른 사인파 및 나선형 모델로 설명된다. 이에 대한 영향은 유한요소 기반의 균질화 방법, 분석 모델 및 분자역학 시뮬레이션을 통하여 분석이 가능하다.
한편, Mori-Tanaka 모델은 잘못된 필러 분포, 곡률 및 응집 효과와 같은 CNT의 보다 복잡한 구성의 시뮬레이션을 비교적 간편하게 가능하게 한다[10]. Yanase 등은 미세역학적 모델링 기법을 사용하여 CNT 강화 고분자의 탄성 특성에 미치는 곡선형 CNT의 영향을 연구하였다[11]. 이들은 기존의 Mori-Tanaka 방법으로는 시뮬레이션 하지 못하기 때문에 특정한 물결 모양의 미세구조에 대하여 Eshelby의 텐서를 이용하여 확장 적용할 필요가 있다는 것을 밝혀냈다. 이를 기반으로 CNT로 강화된 경사진 판 구조의 사례 연구가 최종적으로 제시되어 거시적인 진동거동에 대한 곡률과 응집의 결합효과를 입증하였다[12].
멀티스케일 기반의 CNT 함유로 강화된 직교이방성 또는 등방성 복합재에 대한 다양한 동적 거동 규명 연구가 수행되었으나, CNT 효과가 고려되지 않았거나 직선형태의 이상적인 CNT 분산을 고려한 경우가 대부분이었다[13-16]. 따라서, 본 연구에서는 Mori-Tanaka 모델으로부터 평균체적법을 기반으로 CNT의 굴곡 특성을 고려하였으며, 복합재에 대하여 직선의 경우와 비교하여 물리적 변화를 추정하도록 모델링하였다. 다음으로 적층판 구조를 대상으로 다양한 매개변수에 대한 고유진동 특성을 분석한다. 기본 해석결과는 기존 문헌과 비교하여 검증하며, CNT의 굴곡성, 함유량 및 보강섬유의 배열 변화가 적층판의 고유진동 특성에 미치는 영향을 상세 규명한다.

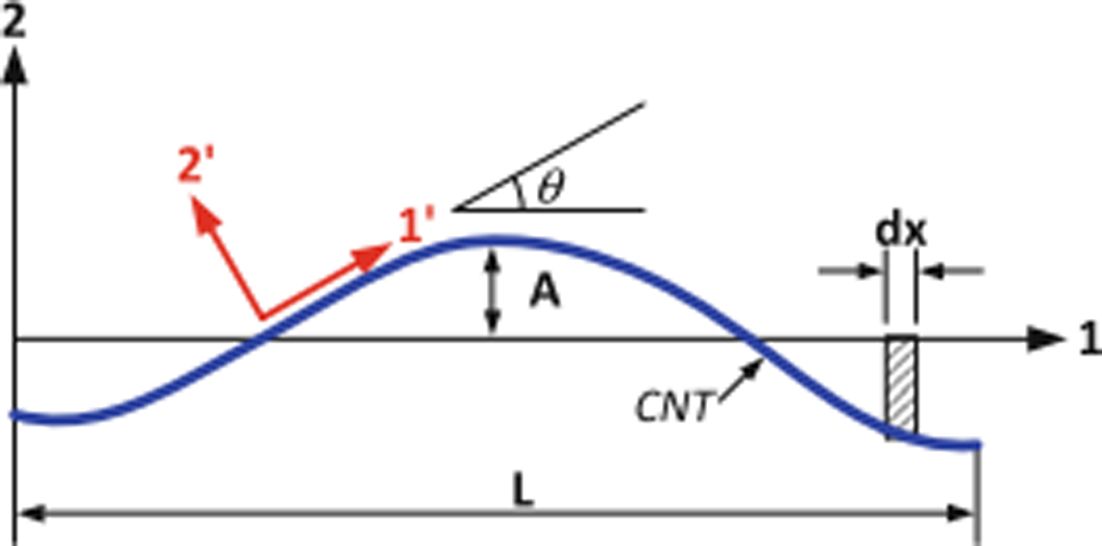
본 연구에서 다루는 굴곡진 CNT의 가정된 형상은 Fig. 1과 같다. Mori-Tanaka 모델을 기반한 굴곡진 CNT 분산 복합재의 유효강성행렬은 다음과 같이 표현된다[10,11].



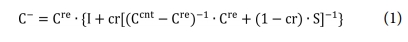
여기서 C^re 와 C^cnt 는 모재(Resin)와 CNT의 강성을 의미하며 I는 단위행렬, cr는 CNT의 부피 함유율이다. CNT의 높은 가로 및 세로 비율을 나타내기 위하여, 식 (1)에서 긴 원형 섬유에 대한 Eshelby 4차 텐서 S는 다음과 같이 나타낼 수 있다.



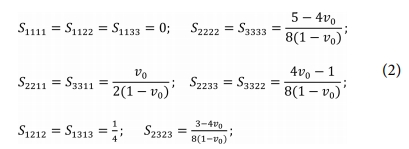
여기서 v₀ 는 행렬의 푸아송 비이다. 상기식에서 굴곡진 CNT는 다음과 같이 정현파 형상(sinusoidal shape)을 갖으며, 나란하게 배열되었다고 가정한다.



여기서 A와 L은 각각 파형 CNT 섬유의 진폭과 길이를 나타낸다(Fig. 1 참조). 연속 좌표 변환을 적용함으로써 정현파 굴곡형상을 갖는 CNT 섬유 강화 복합재의 강성은 다음과 같이 나타낼 수 있다[11].



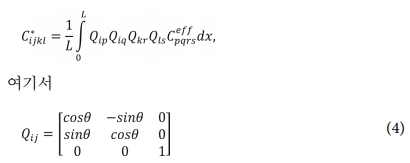
섬유보강 각도 q 는 A와 L의 함수로 다음과 같이 표현된다.



여기서 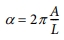이며, 최종적으로 각 방정식의 구성요소는 다음과 같이 명시적으로 표현할 수 있다[11].



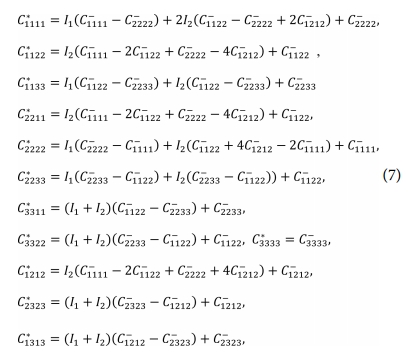
한편, 길이방향으로의 복합재 유효탄성계수 E₁은 다음과 같이 주어진다.



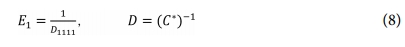
여기서 식 (9)와 단순 부피의 합산에 의하여 파형 굴곡을 갖는 CNT 효과가 고려된 복합재의 탄성계수는 다음과 같은 식으로 요약 정리할 수 있다.



상기 식으로부터 혼합법칙(Rule of mixture) 및 Halpin-Tsai 이론식을 적용하면 CNT 분산된 섬유보강 복합재의 멀티스케일 기반 물성 및 강도 등을 추정할 수 있다[17].

3.1 기존문헌과의 결과 검증
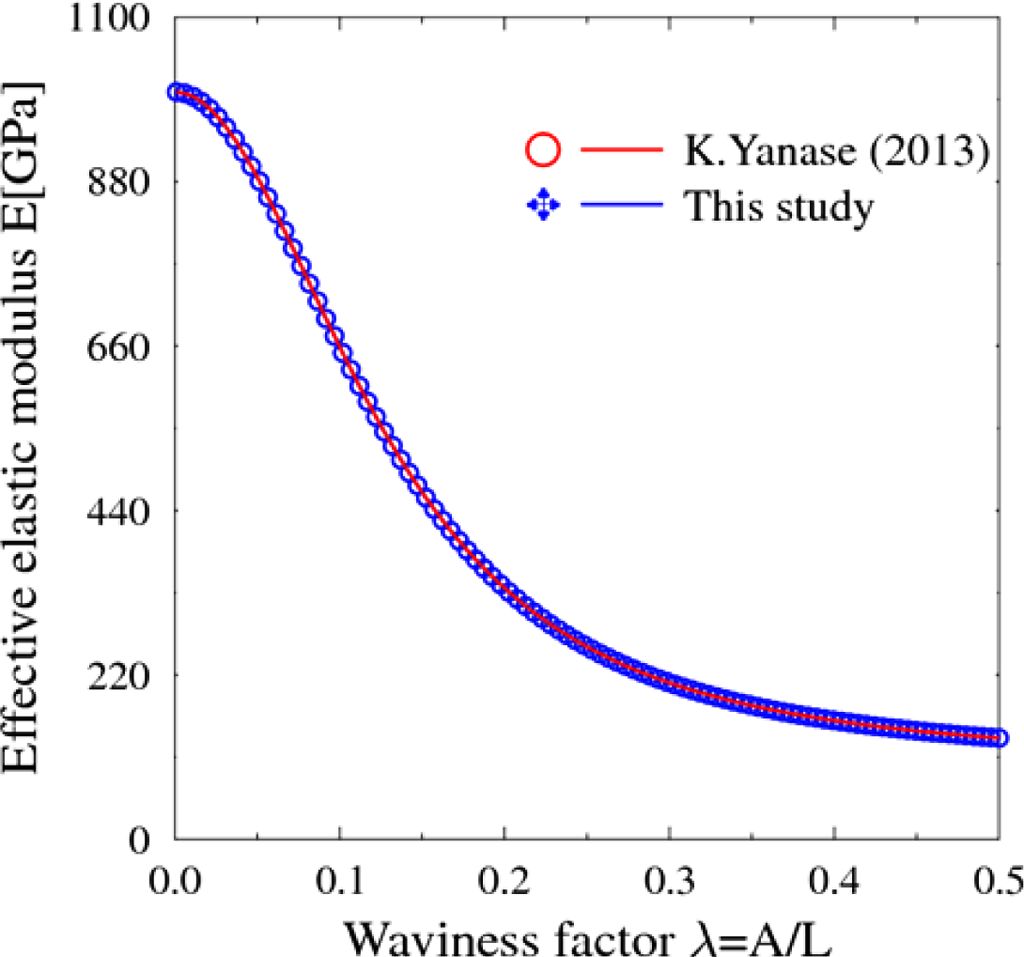
먼저, 전술한 이론을 기반으로 굴곡진 CNT 보강 복합재의 유효강성을 추정하였으며, 기존 문헌과 비교 검증하였다. Fig. 2는 굴곡비율변화에 따른 복합재의 유효 강성변화를 그림으로 나타낸 것이다. 본 예제에 대한 복합재의 탄성계수(E)는 6.9 GPa, 질량은 p = 2,720 kg/m³, 프아송 비는 0.36이며. 판의 두께는 2.0 mm, 길이는 a = b = 500 mm이다. 또한, 경계조건은 4변 고정지지이다. Fig. 2에서와 같이 CNT의 곡률이 증가할 수록 탄성계수는 가파르게 감소함을 알 수 있으며, λ = 0.2~0.3부터 다소 완만하게 감소하였다. 도출된 결과는 기존문헌과 잘 일치하였다.
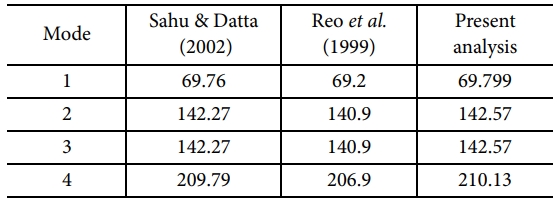
Table 1은 CNT 효과가 고려되지 않은 복합재 평판의 고유진동 해석결과를 기존 문헌과 비교한 것이다. 표에서 보는 바와 같이 본 CNT 보강 폴리머 복합재 평평한 판의 1~4번 모드의 고유 진동에 대한 본 해석 결과와 기존문헌의 결과는 잘 일치하는 것을 알 수 있다.
3.2 CNT 굴곡 비율에 따른 물성 및 강도 추정 비교
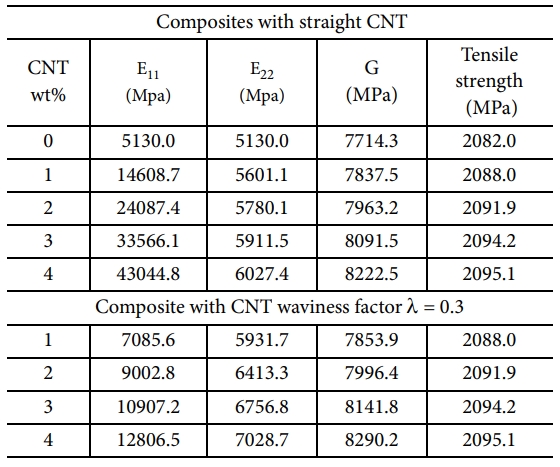
CNT 굴곡 비율 변화에 따른 복합재 판구조의 각 물성과 강도를 추정하였으며, 직선 CNT의 결과와 비교하였다. 해석에 사용한 CNT의 탄성계수는 953 GPa, 질량은 1,300 kg/m³, 프아송 비는 0.33이다. 또한 CNT의 두께는 20 nm, 직경은 30 nm, 그리고 길이는 2 nm 이다. Table 2은 직선 및 굴곡(l=0.3) CNT에 대하여 CNT 함유량에 따른 물성 및 인장강도 추정 결과를 보여준다. 여기서, E₁₁, E_22, G, 및 Tensile strength는 CNTRC 구조의 길이방향 탄성계수, 횡방향의 탄성계수, 면내전단탄성계수 및 인장강도를 각각 의미한다. 표에서 보는 바와 같이 CNT의 함유량이 증가함에 따라 재료적 물성은 일정하게 증가함을 알 수 있다. 그러나 직선에 비하여 굴곡진 CNT의 경우는 상대적으로 소폭 증가함을 알 수 있다. 특히, E₁₁ 경우에는 직선형보다 증가 비율이 작은 경향을 보였다. 반면, E₁₁를 제외한 재료 물성 및 인장강도의 경우는 직선 또는 굴곡진 경우 보다 유사하였으며, CNT 함유량 증가에 따라 큰 영향을 받지 않았다. 이는 E₁₁의 경우는 실험식으로부터 CNT 함유 증가에 따른 직선증가의 혼합법칙을 통하여 추정하며, 나머지 물성 및 강도는 Hapin-Tsai 이론식에서 가정한 완만한 비선형성 증가를 갖는 실험식으로부터 추정되었기 때문이다. 이러한 특성은 CNT의 굴곡성과 결합되어 직선형과는 다른 결과값을 보임에 유의해야 한다.
3.3 복합재 적층판 구조의 고유진동
이 절에서는 CNT의 굴곡비율, 함유량 및 복합재 적층배열 변화에 따른 고유진동 특성을 비교 분석하였다. 해석에 사용된 에폭시의 탄성계수는 5.13 GPa, 질량은 1,030 kg/m³, 프아송 비는 0.33이다. 또한, 평판의 두께는 2 mm, 양변 길이는 1,000 mm이며, 4변 고정지지로 설정하였다.
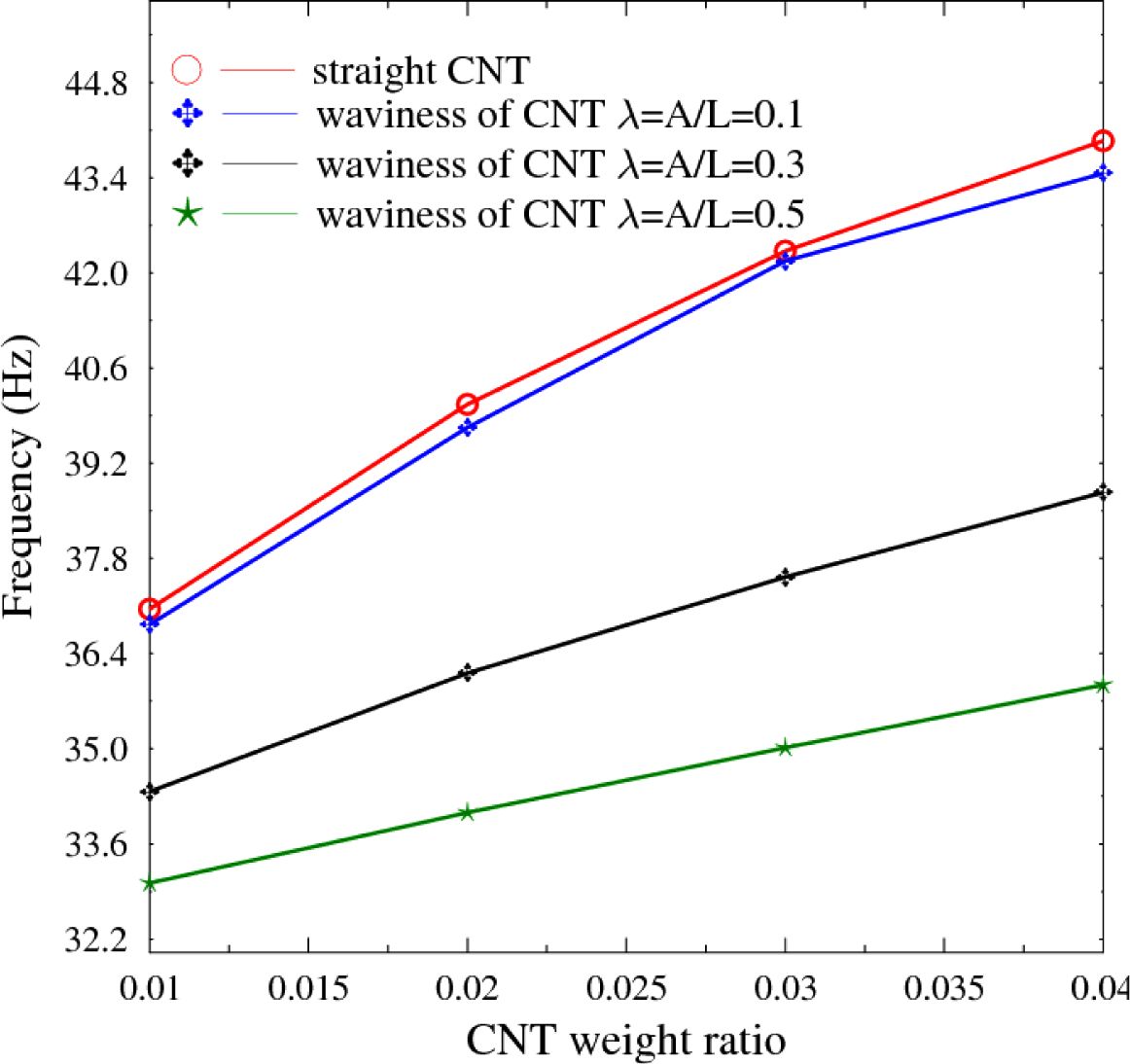
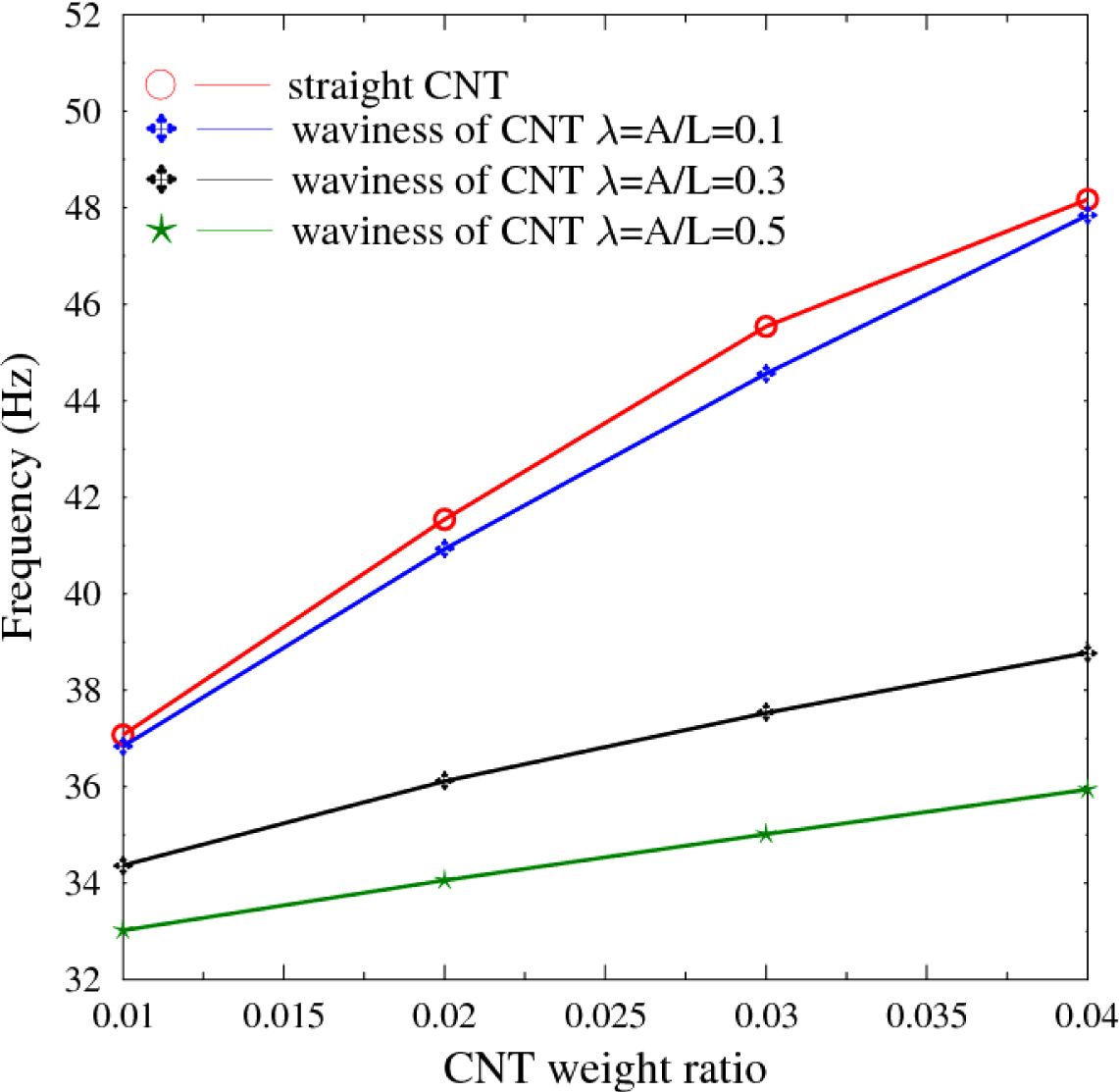
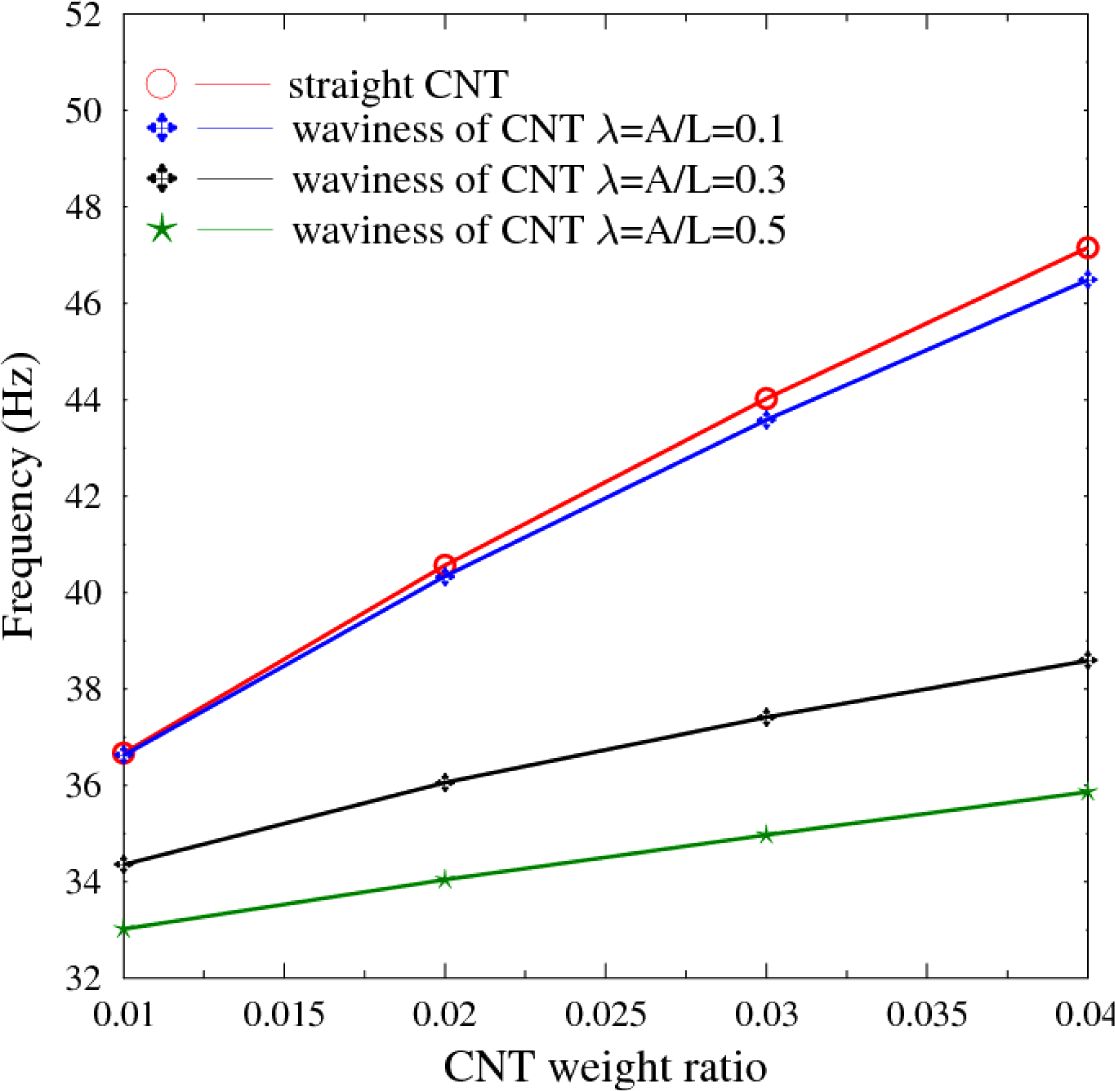
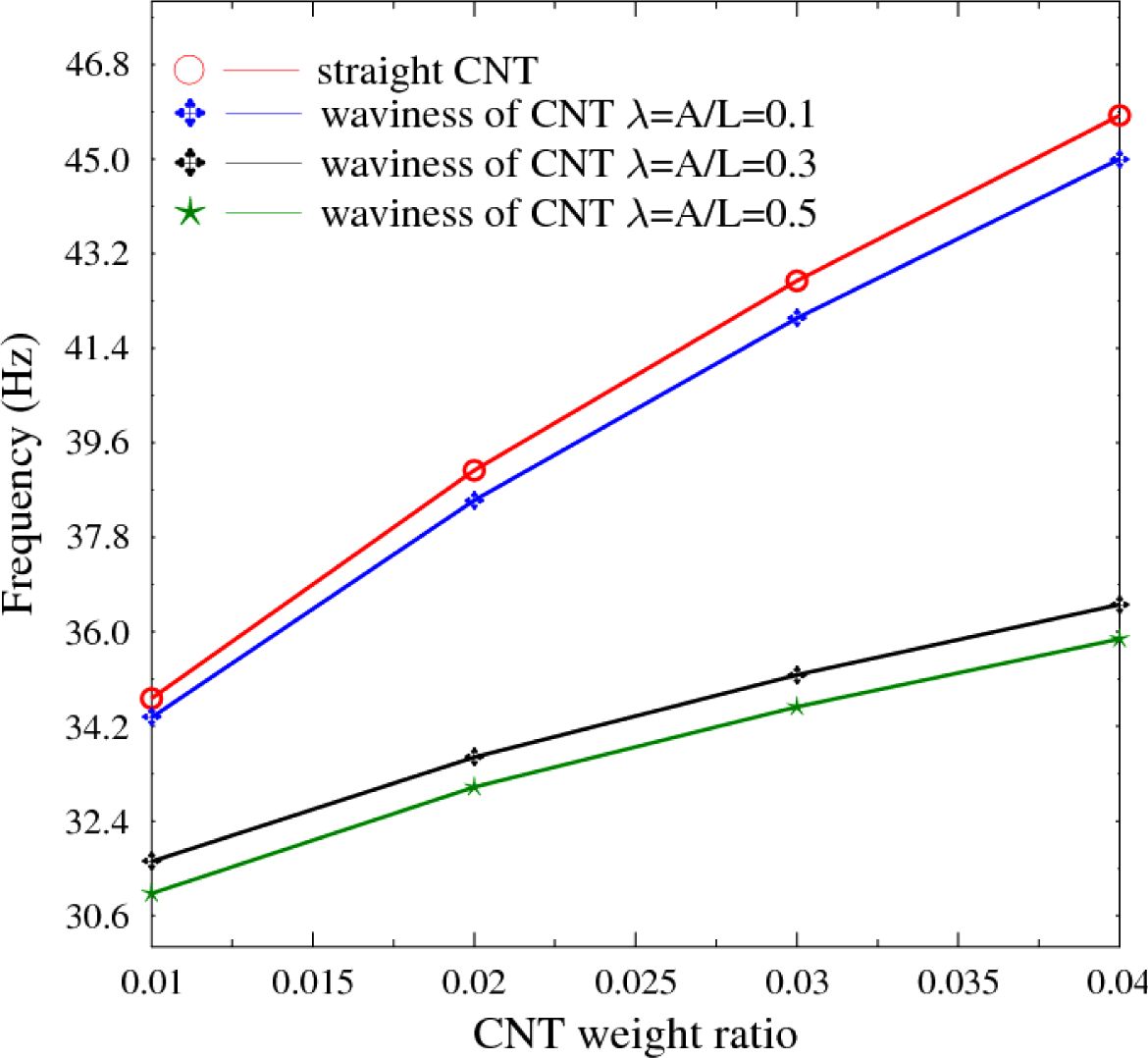
Fig. 3은 CNT 함유량 비율 및 곡률 영향에 따른 [0/0/0/0]으로 적층된 복합재 평판의 고유진동 결과를 비교한 것이다. CNT의 함유량이 증가할수록 판의 강성은 증가하여 고유진동수는 일정하게 증가하는 것으로 나타났다. 반면, CNT 곡률이 증가하는 경우, 고유진동수는 감소하며, 함유량이 증가할수록 감소 비율로 증가하는 것으로 나타났다. 직선형과 λ = 0.1 경우를 비교하면 고유진동수가 감소하는 비율은 크지 않으나, 약 4% CNT 함유량에 대하여 약 4-6%의 감소를 보였다. 이러한 차이는 λ = 0.3 이상부터 14~15% 이상 크게 증가하는 경향을 보였다. 이러한 경향은 [0/90/90/0] 및 [0/90/0/90]으로 적층된 Figs. 4~5의 경우도 유사한 결과를 보였다. 반면, [45/-45/-45/45]로 적층된 경우는 Fig. 6에서와 같이 λ = 0.3와 λ = 0.5의 결과 차이는 약 2% 내외로 미미하였다. 이러한 결과는 CNT의 굴곡성이 적층판의 자유진동 특성에 중요한 영향을 미치고 있다는 것을 보여준다. 이러한 영향은 적층배열과도 연관성이 있으며, 45°방향으로 섬유보강된 경우 λ = 0.3 이상의 곡률을 갖는 경우는 고유진동수 차이가 직각 방향보강보다 크게 감소한다는 점에 유의해야 한다.
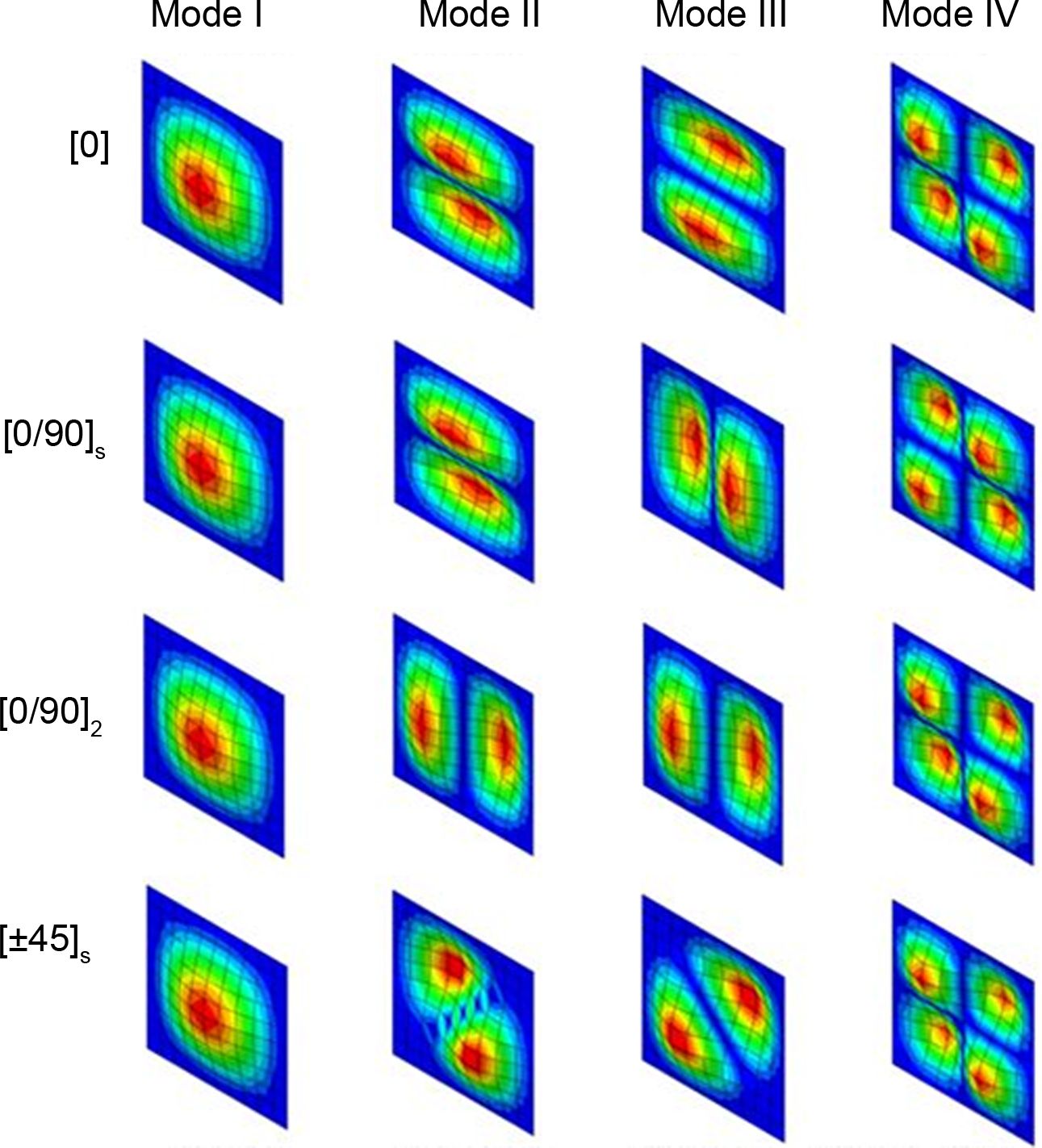
Fig. 7은 CNT 함유율 2.0%와 λ = 0.3에 대하여 적층배열 변화에 따른 고유모드를 보여준다. 동일한 물성을 갖는 경우데도 적층배열 변화에 따라 다양한 자유진동 특성을 보임을 알 수 있다. 이러한 특성은 CNT의 곡률에 직접적으로 연관되므로 곡률 특성은 중요한 고려사항으로 판단된다.

본 연구에서는 탄소나노튜브의 굴곡성을 고려하여 보강된 복합재 적층판구조의 고유진동 특성을 규명하였다. Mori-Tanaka 모델을 기반으로 파형 CNT의 물성을 계산하였으며 Halpin-Tsai 이론식을 적용하여 적층판구조의 멀티스케일 강성 및 강도값을 추정하였다. 본 해석결과는 기존 연구문헌과 비교 검증하였다. 수치해석 예로부터 도출한 결과를 요약하면 다음과 같다.
(1) CNT의 곡률이 증가할 수록 추정된 일방향 탄성계수는 가파르게 감소하였다. 이후 λ = 0.2~0.3부터 다소 완만하게 감소하였다. CNT의 굴곡성은 보강된 구조체의 일방향 강성에 중요한 영향을 미치므로 해석 시 고려되어야 한다.
(2) CNT의 함유량이 증가함에 따라 재료적 물성은 직선형에 비하여 굴곡진 CNT의 경우가 증가하였으며, 특히, E₁₁ 경우에는 직선형보다 증가 비율이 작은 경향을 보였다. 반면, E₁₁를 제외한 재료 물성 및 인장강도의 경우는 직선 또는 굴곡진 경우 보다 유사하였으며, CNT 함유량 증가에 따라 큰 영향을 받지 않았다. 이러한 특성은 CNT의 굴곡성과 결합되어 직선형과는 다른 결과값을 보임에 유의해야 한다.
(3) CNT의 함유량이 증가할수록 판의 강성은 증가하여 고유진동수는 일정하게 증가하였다. 반면, CNT 곡률이 증가하는 경우, 고유진동수는 감소하며, 함유량이 증가할수록 감소 비율로 증가하였다. 직선형과 λ = 0.1 경우를 비교하였을 때, 고유진동수가 감소하는 비율은 크지 않으나, 약 4% CNT 함유량에 대하여 약 4~6%의 감소하였다. 이러한 차이는 λ = 0.3 이상부터 14~15% 이상 크게 증가하는 경향을 보이므로 곡률 효과가 반영되어야 한다.
(4) [45/-45/-45/45]로 적층된 경우는 λ = 0.3와 λ = 0.5의 결과 차이는 약 2% 내외로 미미하였다. CNT의 굴곡성이 적층판의 자유진동 특성에 중요한 영향을 미친다. 이러한 영향은 적층배열과도 연관성이 있으며, 45°방향으로 섬유보강된 경우 λ = 0.3 이상의 곡률을 갖는 경우는 고유진동수 차이가 직각 방향보강보다 크게 감소한다는 점에 유의해야 한다.
본 연구결과로부터 CNT의 굴곡성이 구조체 전체의 동적 특성에 영향을 미치고 있으며, 이는 CNT 함유량 및 섬유적층배열 변화와 연동하여 민감한 특성을 보이는 것을 알 수 있었다. 따라서, CNT의 실제적 분산 형태를 반영하는 본 연구결과는 CNT 보강 멀티스케일 복합재의 동적거동 규명에 기여할 수 있을 것으로 기대된다. 향후 랜덤한 방향으로 배열된 CNT의 보다 실제적인 분산 특성을 고려한 연구가 필요하다.

본 연구는 중소기업벤처부에서 지원하는 2019년도 창업성장기술개발사업(No.S2797130) 및 한국연구재단 기초연구사업의 지원을 받아 수행된 연구(No.2018R1D1A1B07050080)임.