Composite structures have components and joints. Theses connections or joints can be potentially weak points in the structure. The failure mode of the composite bolted joint is designed as a bearing failure mode for structural safety. The load-displacement relation exhibits bearing failure mode shows a nonlinear behavior after the initial failure and progressive failure behavior. In order to accurately predict the failure behavior of composite bolted joints, this study modified the shear damage variable calculation process in the existing progressive failure analysis model. The results of the bearing stress-bearing strain of the composite bolted joint were predicted using the modified progressive failure analysis model, and the modified model was verified through comparison with the previous progressive analysis model

복합재료를 활용하여 설계되는 구조물은 각 부품들의 조립, 체결부를 갖게 된다. 이러한 연결 또는 조인트는 구조에서 잠재적으로 취약 부분이 될 수 있다. 복합재료 볼트 조인트의 파손모드는 구조 안전성을 위해 베어링 파손모드로 설계된다. 베어링 파손모드로 파괴되는 복합재료 볼트 조인트의 하중-변위 관계는 초기 파손 발생 후 비선형 거동을 보이며, 점진적인 파손을 보인다. 이러한 비선형적이고 점진적인 복합재료 볼트 조인트의 파손거동을 정확히 예측하기 위해 본 연구에서는 기존의 파손해석 모델에서 전단 손상변수 계산 과정에 수정을 수행하였다. 수정된 파손해석 모델을 이용하여 복합재료 볼트 조인트의 베어링 응력-베어링 변형률 결과를 예측하였으며, 기존 수정되지 않은 해석모델과 비교를 통해 수정된 모델의 유효성을 입증하였다

Keywords: 복합재료(Composite material), 복합재료 볼트 조인트(Composite bolted joint), 점진적 파손해석(Progressive failure analysis), 비선형 전단거동(Nonlinear shear behavior)

복합재료는 비강성 및 비강도, 부식 저항성, 피로 저항성 등이 기존 재료들에 우수하여 항공, 기계 등 다양한 산업 분야에서 활용되고 있다. 현대의 항공기의 50% 이상이 탄소 섬유 복합재료로 구성되며 보잉 787 드림라이너의 경우 복합재료를 활용하여 20% 정도의 무게를 줄일 수 있었다. 자동차와 같은 운송 수단에서도 연료 소모량의 75% 정도가 차량 무게에 관계되는 것과 관련하여, 복합재료의 우수한 비강성 및 비강도 특성은 설계에 큰 이점을 불러온다. 이러한 기계 구조를 이루는 복합재료는 다양한 체결부를 가지며 결합된다. 대표적인 복합재료 체결부는 접착(adhesive)과 기계적(mechanical)인 체결을 통해 만들어지며, 접착과 기계적 체결을 혼합하기도 한다[1]. 항공기 구조에서는 수 많은 볼트 및 리벳을 활용하여 기계적 체결부를 구성하고 부품들을 조립한다. 보잉 787 항공기의 경우에는 조립을 위해 240만개 정도의 패스너를 사용한다. 이런 연결부는 잠재적으로 구조의 가장 취약한 부분이 되기도 하며 전체 구조물의 수명을 결정하는 요인이 되기도 한다. 따라서 체결부를 포함하는 기계 구조물을 설계할 때, 체결부의 기하학적 불연속이나 체결력, 체결되는 패스너 등의 결정이 신중히 고려되어야 한다. 또한, 복합재료로 구성되는 볼트 조인트의 경우에는 안전한 설계를 위해 파손모드와 체결력, 하중 및 응력의 비선형적인 거동을 정확히 예측하여야 한다. 복합재료 볼트 조인트의 파손거동에 관하여 다음과 같은 시험적, 해석적인 연구들이 수행 되었다. Hundley 등[2]은 복합재료 볼트 조인트의 파손거동을 점진적 파손해석 도구를 통해 예측하였다. 예측 결과는 조인트 시험결과와 비교를 통해 검증하였으며 연구를 통해 복합재료의 적절한 파손모드를 불러올 수 있는 최적 설계 변수를 획득하였다. 또한 복합재료의 실제 파손거동과 예측된 파손거동의 비교를 수행하였다. 정강우 [3]등은 원공 공차를 가지는 볼트 및 핀 조인트의 강도 변화에 관한 연구를 수행하였다. 공차가 증가함에 따라 볼트 및 핀 조인트의 강도가 저하되는 것을 관찰하였으며, 이를 유한요소해석을 통해 상호 비교하였다. 유한요소해석은 Tsai-Wu 파손판정식과 접촉 요소의 정의를 통한 비선형 유한요소해석을 수행하였다. 파손거동의 분석은 파손기준식의 파손지수를 통해 수행하였다. 피 등[4]은 선박용 복합재 에어 스포일러의 체결부의 설계를 수행하며 복합재료 볼트 조인트에 관해 연구하였다. 유한요소해석을 통해 각 볼트에 걸리는 하중을 예측하고 실제 시험을 통해 구조물이 견딜 수 있는 하중을 평가하였다. 연구 결과, 설계된 에어 스포일러의 충분한 강도와 정적 강도 대비 우수한 피로 강도를 확인하였다. 이를 통해 실제 선박에 적용할 수 있는 기술적 기반을 마련하였다.
본 연구에서는 기계적으로 체결된 복합재료 볼트 조인트의 파손거동을 점진적 파손해석 도구를 이용하여 예측하였다. 복합재료의 비선형 거동을 보다 정확히 예측하기 위해 기존 제안된 Lapczyk의 모델의 전단 손상변수 계산 과정을 수정하였으며, 수정된 모델을 활용하여 복합재료 볼트 조인트의 비선형 적인 파손거동을 예측하였다. 예측된 결과는 시험결과와 상호 비교하였으며 그 유효성을 입증하였다.

2.1 복합재료 볼트 조인트
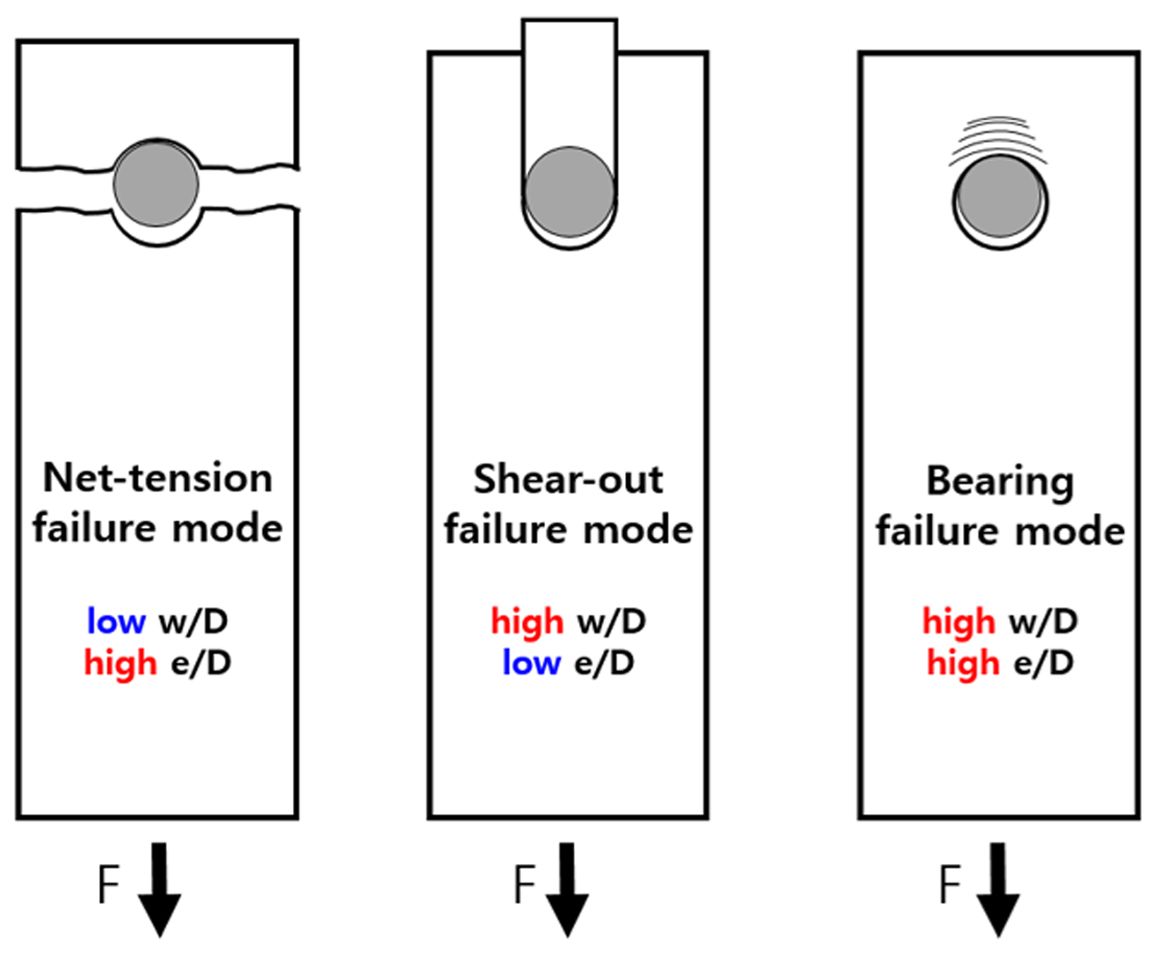
복합재료 볼트 조인트는 몇 가지 파손모드를 보이며 파손이 진행된다. 복합재료 볼트 조인트에서 볼트의 파손과 복합적인 파손을 제외하면 대표적으로 세 가지의 파손모드를 관찰할 수 있다. Fig. 1은 복합재료 볼트 조인트의 대표적인 파손모드를 보여준다. Net-tension, shear-out 파손모드는 초기 발생된 파손이 빠르게 최종 파단으로 연결되며 급격하게 조인트의 하중전달능력이 상실된다. 반면에, bearing 파손모드는 파손이 시작되면서 섬유 및 기지가 점차 구겨지게 되고 점진적인 파손 진전 형태를 보여준다. 이러한 파손모드는 복합재료 볼트 조인트의 기하학적 설계 요인들에 의해 결정될 수 있다. 복합재료 부품의 폭(w), 끝 단에서 볼트 구멍 중심까지의 거리(e), 그리고 볼트 구멍의 직경(D) 와 같은 설계 변수들에 의해 파손모드가 달라지게 된다. ASTM D5961[5]에서는 bearing 파손모드의 설계를 위해 e/D 비를 3 이상으로 제시하고 있다. 대체적으로 w/D 비가 작고, e/D 비가 큰 경우에는 net-tension 파손모드가 발생되며, w/D 비가 크고, e/D 비가 작은 경우에는 shear-out 파손모드가 발생된다. Bearing 파손모드는 다른 파손모드들과 다르게 비선형 응력-변형률 관계를 보여준다. 볼트 조인트에서 응력-변형률 거동은 베어링 응력-베어링 변형률 관계로 표현하며, 그 계산방법은 아래와 같다.



위 식에서 σ_br는 베어링 응력을 의미하며 P는 조인트 시험 중 측정되는 하중을 의미한다. k, D, h는 각각 볼트 구멍의 개수, 볼트 구멍의 직경, 복합재료 시편의 두께를 의미한다. ε_br는 베어링 변형률을 의미하며 δ는 시험 중 측정되는 변위를 나타낸다.
2.2 점진적 파손해석
본 연구에서는 Lapczyk가 제안한 점진적 파손해석 모델을 이용하였다[6,7]. Lapczyk의 모델은 복합재료의 선형 거동만을 고려하여 제안된 모델로 재료의 선형 거동만을 예측한다. 하지만 보편적으로 사용되고 있는 MLT 모델[8,9] 보다 메쉬에 따른 계산 결과에 차이가 적고 하중 예측에 정확하다는 장점이 있다. 이러한 장점은 Lapczyk 모델이 재료의 손상 거동을 예측하는 과정에서 등가 응력-등가 변위 관계를 이용하기 때문이다. 등가 변위를 계산하는 과정에서 유한요소해석(FEA)의 요소 크기가 반영이 되며, 손상변수(damage variable) 계산시에 재료의 파괴에너지가 고려된다. 이 두 절차가 Lapczyk 모델에서 메쉬 독립성과 정확한 하중 예측 장점에 영향을 준다[6]. 점진적 파손해석은 기본적으로 손상이 발생함에 따라 강성행렬을 감소시키면서 재료의 손상거동을 예측한다. 본 연구에서는 Hashin 파손기준식을 이용하여 파손의 발생 유무를 판단하였다[10]. Lapczyk의 모델에서는 다음과 같은 방법으로 손상변수를 계산하여 강성행렬에 손상의 정도를 반영해주고, 점진적 파손해석을 수행한다.



여기서 d는 손상변수, δ는 변위를 의미하며, 위 첨자 0와 f은 각각 파손 초기 시점과 최종 파단 시점을 나타낸다. 아래 첨자 I는 손상변수가 계산되는 각 파손모드를 의미하며 복합재료의 파손모드에 따라 ft(섬유 인장), fc(섬유 압축), mt(기지 인장), mc(기지 압축)로 바뀔 수 있다. 아래 첨자 eq는 등가(equivalent)를 의미한다. 손상변수 d는 0에서 1 사이의 값을 가지며 (1 - d_I)의 형태로 강성행렬 성분들에 고려된다. 재료 내에 파손이 발생하지 않은 경우에는 손상변수가 0의 값으로, 강성행렬은 본래의 값을 유지하지만 손상변수가 1로 점차 증가하면서 손상변수가 반영된 강성행렬의 성분들은 점진적으로 감소하게 되며 점진적 파손해석이 수행된다. 완전히 파단 된 경우에는 손상변수의 값이 1이 되어 강성행렬의 성분이 0이 되고, 재료는 기능을 할 수 없게 된다. 섬유 인장/압축, 기지 인장/압축의 파손모드에서는 계산된 손상변수가 곧바로 강성행렬 성분에 반영된다. 하지만 전단 손상변수는 계산된 섬유 인장/압축, 기지 인장/압축 손상변수들의 곱으로 다음과 같이 계산되어 강성행렬의 전단강성 성분들에 반영된다.



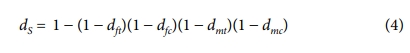
여기서 d_S는 전단 손상변수를 의미한다. 위와 같은 방법을 이용하여 많은 연구들에서 전단 손상변수를 계산하여 점진적 파손해석을 수행하였다. 하지만, 이러한 계산방법을 이용하면 Lapczyk의 모델은 재료의 선형 거동만 예측하다는 한계점이 있다. 따라서 본 연구에서는 전단 손상변수 계산 과정을 수정하여 해석을 수행한다.
2.3 전단 손상변수 계산의 수정
탄소섬유강화 복합재료의 인장 및 압축 거동은 일반적으로 선형 거동을 보인다. 하지만 재료의 전단 거동은 비선형 거동을 보이며 이를 정확히 예측하기 위해 다양한 연구들이 수행되었다[11,12]. 본 연구에서는 점진적 파손해석 방법을 이용하며 손쉽게 전단 손상변수를 계산하고, 재료의 비선형 전단 거동을 예측하기 위해 Lapczyk 모델의 전단 손상변수 계산 과정에 수정을 수행하였다. 식 (4)에서 보여지는 전단 손상변수 식에서 각 손상변수에 1 이하의 값을 곱해주어 각 손상변수의 전단 손상변수 계산에 대한 영향을 감소시켜 주었으며, 이러한 방법은 기존 연구들[13,14]에서 사용되기도 하였다. 곱해지는 1 이하의 값들을 손상 저하계수라고 명명하기도한다. 수정된 전단 손상변수의 계산식은 다음과 같다.



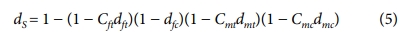
여기서, C_ft, C_mt, C_mc는 각각 섬유 인장, 기지 인장, 기지 압축 모드에서의 손상 저하계수를 의미한다. 기존 연구[13] 에서는 기지 인장과 기지 압축 모드 손상변수에만 저하계수를 0.9과 0.5로 각각 접목하였으나, 본 연구에서는 보다 정확한 전단 거동을 예측하기 위해 섬유 인장 손상변수까지 포함하여 계수들을 도입하였다. 각 손상 저하계수들을 구하기 위해 반복적인 작업을 수행하며 본 연구에서 사용된 재료에 맞는 계수들을 획득하였고, 그 값들은 섬유 인장, 기지 인장, 기지 압축 손상모드에서 각각 0.8, 0.2, 0.2 이다. 섬유 압축 파손모드의 경우에는 전단 상황에서 영향이 없기 때문에 따로 손상 저하계수를 곱해주지 않았다.

3.1 재료 및 시편
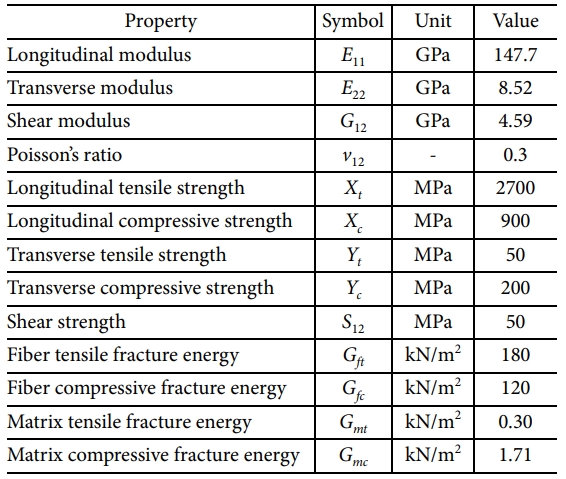
본 연구에서는 T700/Epoxy 복합재료를 사용하였으며 탄소섬유는 TORAY사, 에폭시 기지는 국도 화학에서 제조되었다. 해석을 수행하기 위해 필요한 기계적 물성치와 재료의 파괴에너지는 ASTM 규정[15-19] 및 관련 문헌[20-22]을 참고하여 시험을 통해 획득하였으며, Table 1에서 볼 수 있다. 각 기계적 물성치를 획득하기 위해 인장, 압축 및 전단 시험을 수행하였다. 시편은 해당 복합재료의 프리프레그를 이용하여 vacuum bagging 공정을 통해 제작되었다. 프리프레그 한 장의 두께는 0.15 mm이다. 최종적으로 제작된 복합재료의 섬유 체적 분율은 areal method[23,24]을 통해 계산되었고, 평균적으로 61.37%의 값을 보였다.
복합재료 볼트 조인트 시험을 수행하기 위해 시편을
제작하였다. 복합재료 시편의 치수는 Fig. 2에서 볼 수 있다. e/D 비는 2.8로 설계되었다. 시편의 두께는 6 mm로 [0/+45/0/-45]_5S의 적층으로 제작되었다. 볼트가 체결되는 구멍의 직경은 11.10 mm이며 볼트와 구멍의 공차는 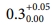mm로 고정되었다.
3.2 복합재료 볼트 조인트 시험 절차
복합재료 볼트 조인트 시험은 ASTM D 5961[5]의 Procedure C를 참고하여 설계되었다. 단일 접합 볼트 조인트를 구성하여 시험을 수행하였으며, MP35N 고강도 볼트를 이용하여 체결하였다. 볼트의 체결은 체결력을 20, 500, 700 kgf-cm로 달리하여 시험을 수행하였다. 시편의 체결시에는 공차의 영향을 무시할 수 있도록 시편 구멍 가장자리에 볼트를 밀착하여 체결하였으며 체결시 시편의 손상을 방지하기 위해 볼트 헤드 아래에 와셔를 삽입하였다. 전체적인 시험 모습은 Fig. 3을 통해 볼 수 있다. 시험은 MTS810 만능재료시험기를 이용하여 수행되었으며, 시험 속도는 1 mm/mm으로 변위 제어를 통해 수행하였다. 하중 데이터를 얻기 위해 250 kN 용량의 로드셀을 이용하였으며, 시험 중 시편에서 발생되는 변위를 측정하기위해 별도의 게이지를 Fig. 3과 같이 부착하였다. 변위 및 하중 데이터는 100 Hz로 획득하였다.
3.3 복합재료 볼트 조인트 해석 절차
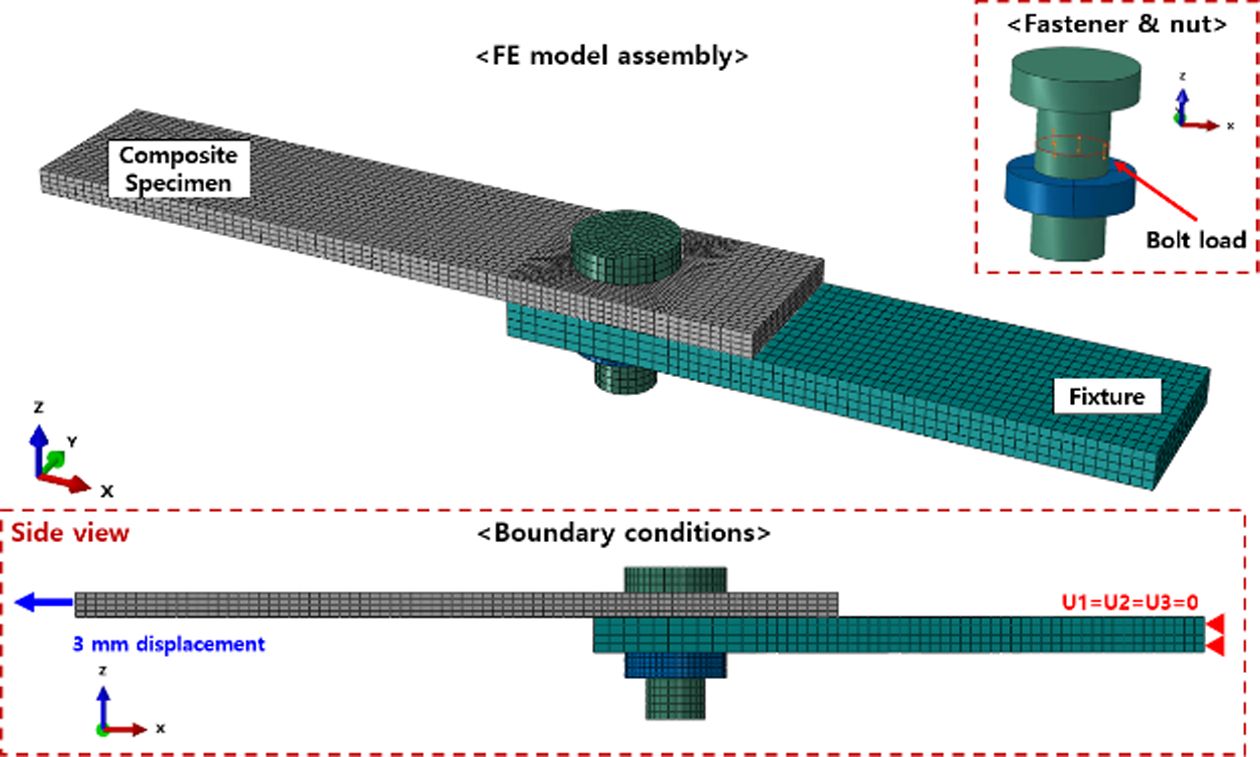
복합재료 볼트 조인트의 파손거동을 예측하기 위해 2장에서 설명된 수정 Lapczyk 파손해석 모델을 이용하여 유한요소 (FE) 해석을 수행하였다. FE 해석은 Abaqus와 사용자 정의 부 프로그램 UMAT을 이용하여 수행되었으며, 해석 모델에는 복합재료 시편, 금속 치구, 볼트, 그리고 너트가 포함되었다. 복합재료 모델은 8절점 선형 요소를 사용하였으며 8,544개의 요소로 구성되었다. 전체적인 해석 모델은 Fig. 4을 통해 볼 수 있다. 재료물성치는 Table 1의 값들을 이용하였고, 복합재료 시편의 적층 또한 시험과 동일하게 구성하였다. 볼트에 가해지는 체결토크 설정은 Abaqus에 내장된 볼트 체결력 도구를 사용하였으며, 볼트 기둥 중간의 절단면에 계산된 힘을 가하여 체결 조건을 설정하였다. 볼트에 가해지는 체결력은 다음의 식을 통해 계산되었다.



여기서 F_bolt는 볼트에 가해지는 체결력이며, t는 볼트에 가해지는 체결 토크이다. k는 토크 계수로 일반적으로 0.2의 값을 갖는다[25]. d는 볼트의 직경이다. 각 부품들의 접촉 조건을 설정하기 위해 surfaced-based 접촉 조건에 linear penalty method를 이용하였다. 접촉 조건은 복합재료-볼트 헤드, 복합재료-볼트 기둥, 복합재료-금속 치구, 볼트 기둥-금속 치구, 금속 치구-너트 사이에 구성되었다. 복합재료와 금속간 마찰계수는 관련 논문의 값을 인용하여 0.114의 값을 이용하였다[26]. 해석 절차는 크게 두 단계로 나뉜다. 처음 스텝는 볼트에 체결력이 가해지는 단계, 그 다음은 복합재료 볼트 조인트에 인장력이 가해지는 단계이다. 두번째 스텝에서는 Fig. 4에서 보여지는 것과 같이 금속 치구 끝 단의 변위를 고정(U₁ = U₂ = U₃ = 0)하고, 복합재료 시편의 끝 단에 3 mm의 변위 조건을 부여해 시험과 같은 절차를 수행하였다. 본 연구에서는 층간에서 발생되는 파괴 거동은 고려되지 않는다.

4.1 단일요소(single-element) 해석을 통한 검증
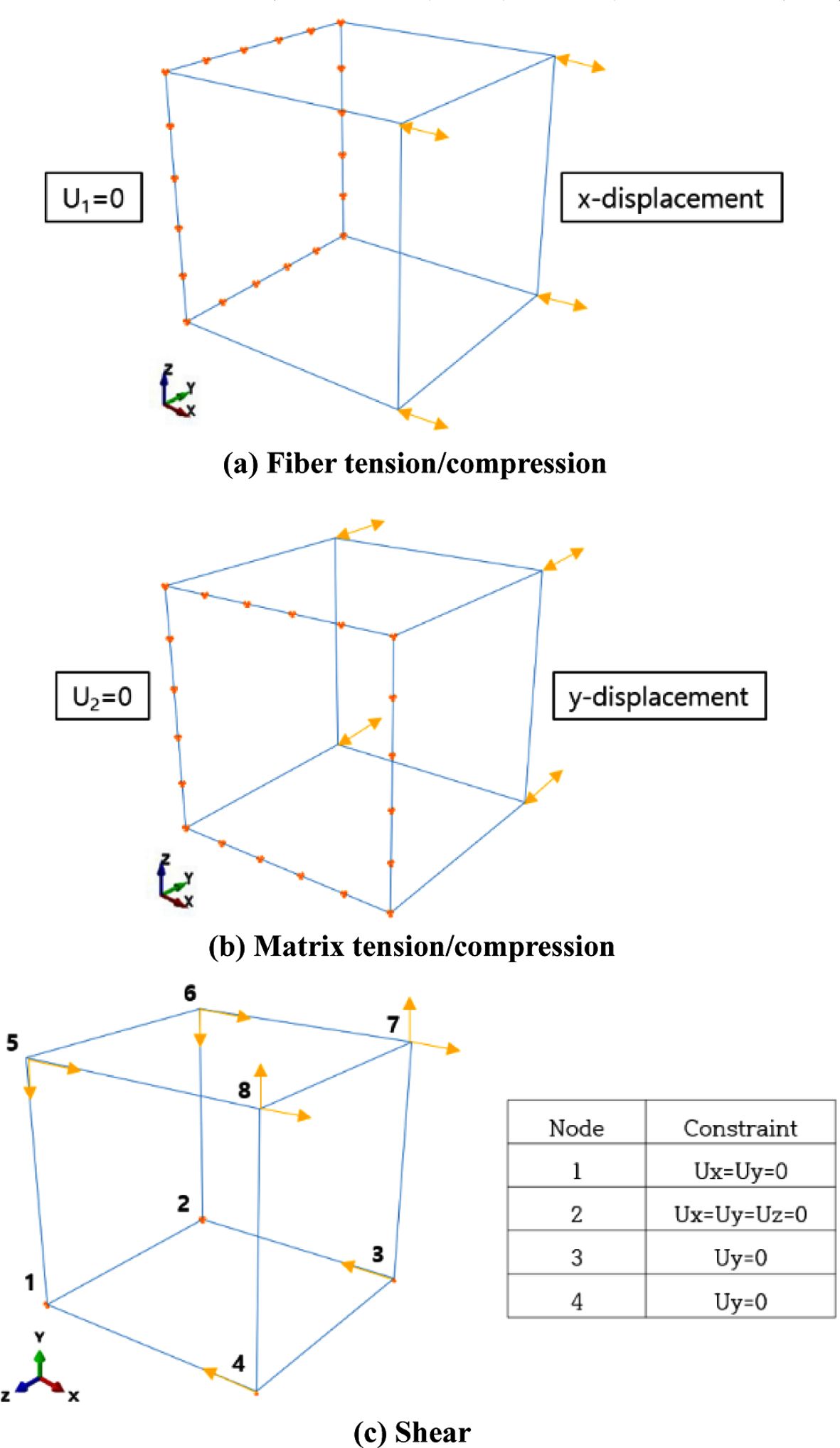
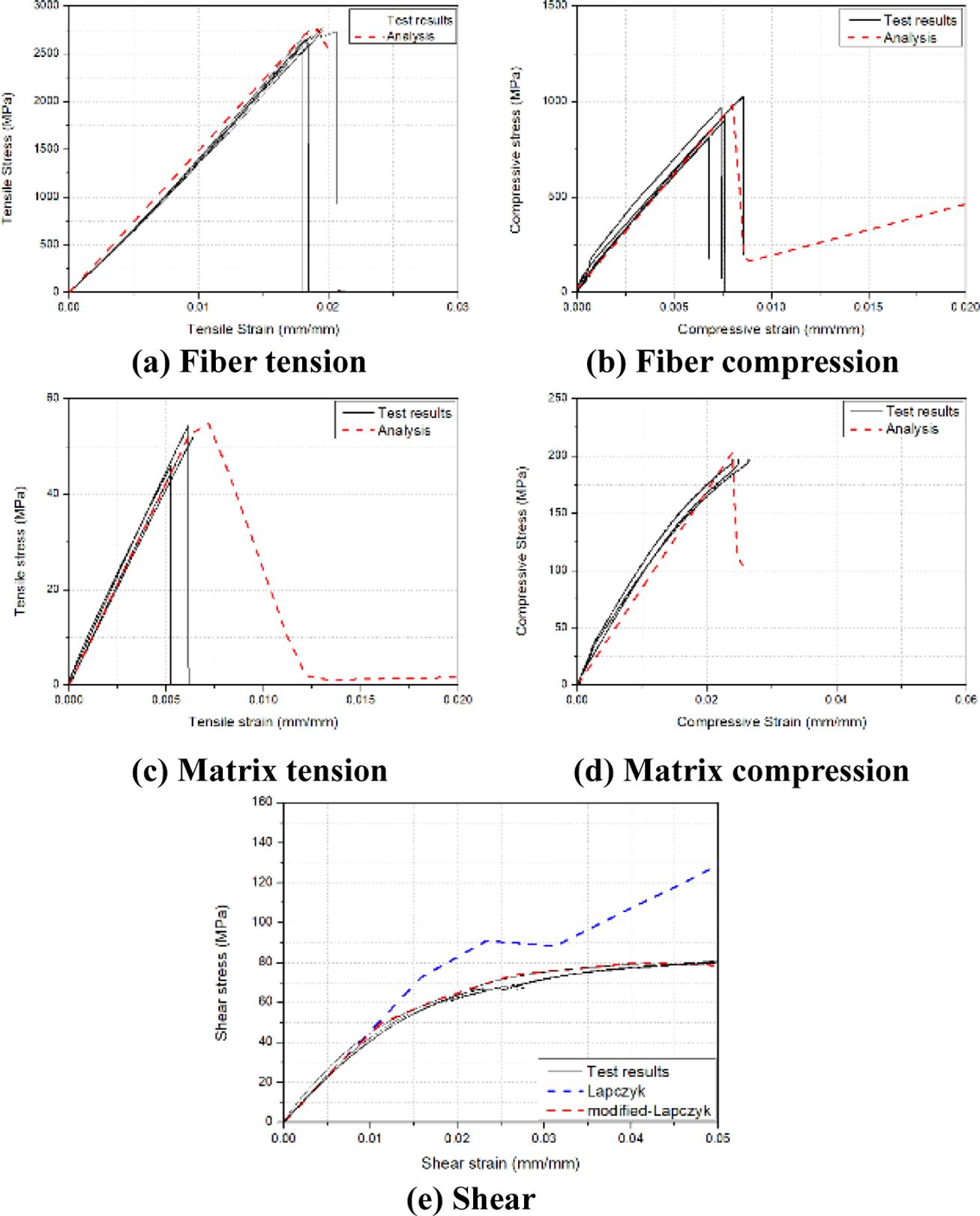
2장에서 수정된 Lapczyk 파손해석 모델의 검증과정을 수행하였다. 검증 과정은 단일요소를 통해 각 파손모드(섬유 인장/압축, 기지 인장/압축, 전단)에서 수행되었다. 단일요소 및 각 파손모드 해석을 위해 단일요소에 가해진 경계 조건은 Fig. 5을 통해 확인할 수 있다. 해석결과는 기계적 물성치를 얻기 위해 수행된 시편 시험결과와 비교되었다. Fig. 6은 단일요소해석과 시험을 통해 획득한 응력-변형률 결과를 보여준다. 각 파손모드에서 강성 및 강도가 정확하게 예측되는 것을 확인하였다. Fig. 6(e)의 전단 파손모드 경우에는 기존 Lapczyk 모델과 수정된 모델에서 획득한 결과를 모두 나타냈으며, 전단 손상변수 계산 과정의 수정을 통해 전단 응력-전단 변형률 거동이 정확하게 예측되는 것을 확인할 수 있다. 이런 과정을 통해 수정된 파손해석 모델이 복합재료의 각 파손 거동을 정확히 예측할 수 있음을 검증하였다.
4.2 복합재료 볼트 조인트 시험 및 해석 결과
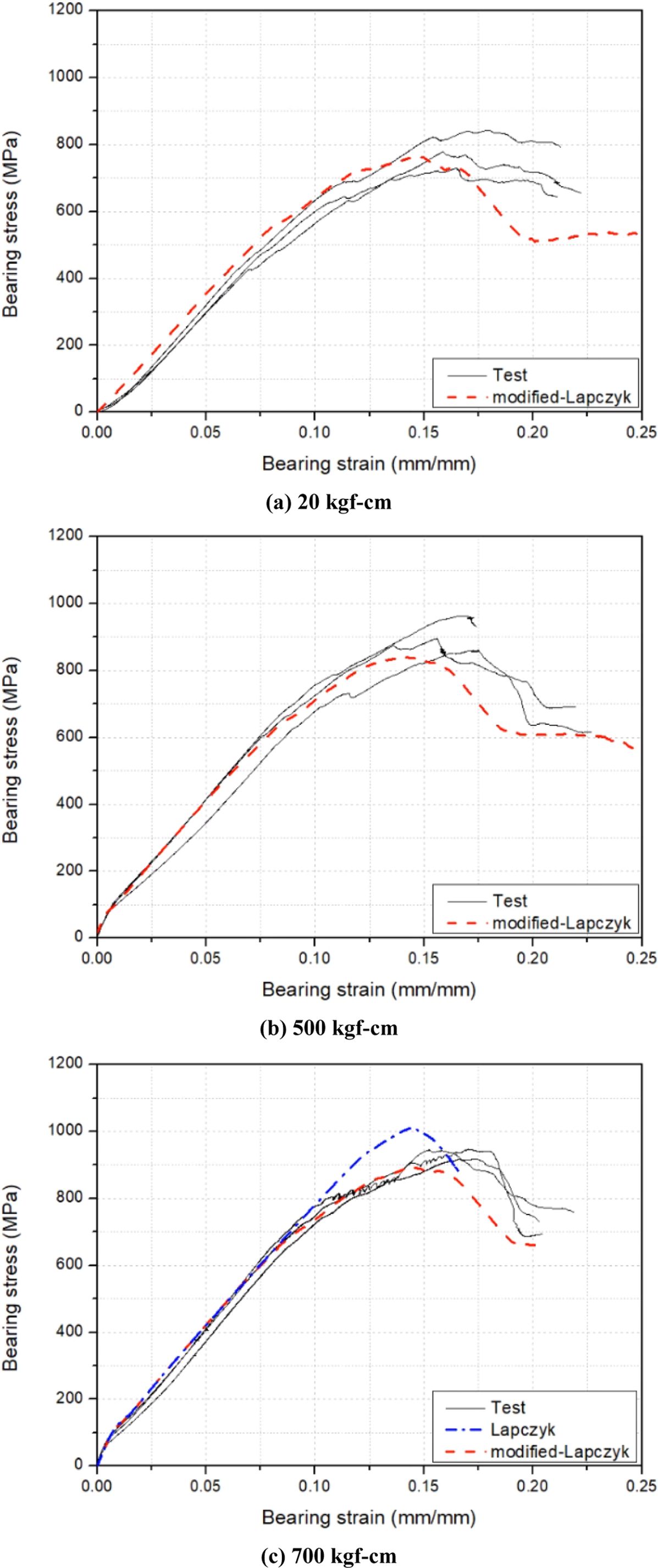
복합재료 볼트 조인트의 시험과 해석을 통해 획득한 베어링 응력-베어링 변형률 거동은 Fig. 7에서 볼 수 있다. 초기 구간에서 체결력에 의해 베어링 응력-베어링 변형률 관계가 달라짐을 확인할 수 있다. 증가된 체결력은 보다 큰 마찰력을 복합재료와 금속 치구 사이에 가하게 되고, 그에 따라 초기 강성이 변화하였다. 그 후, 복합재료 볼트 조인트의 베어링 응력은 초기 파손까지 선형 거동을 보였다. 파손의 발생 후 볼트 조인트의 베어링 응력은 비선형 거동을 보이기 시작하였으며 베어링 강도지점까지 증가하다가 최대 점을 기점으로 감소하는 경향을 보였다. 기존 Lapczyk 모델과 수정된 모델을 시험결과와 비교하기 위해 Fig. 7(c)에 나타내었다. 파손의 발생을 기점으로 두 모델이 큰 차이를 보였다. 기존 Lapczyk 모델은 전체적으로 선형적인 거동을 보이는 반면에 수정된 모델은 시험 결과와 상당히 유사한 거동을 보이는 것을 확인하였다. 수정된 모델은 비선형 거동과 복합재료 볼트 조인트의 강도를 유효한 범위 내에서 예측하였다. 이런 결과를 바탕으로, 비선형 전단 거동을 정확하게 예측할 수 있는 수정 Lapczyk 모델이 기존의 Lapczyk 모델보다 복합재료 볼트 조인트의 파손거동을 정확하게 예측할 수 있다는 것이 확인되었다.
4.3 복합재료 볼트 조인트의 파손모드 관찰
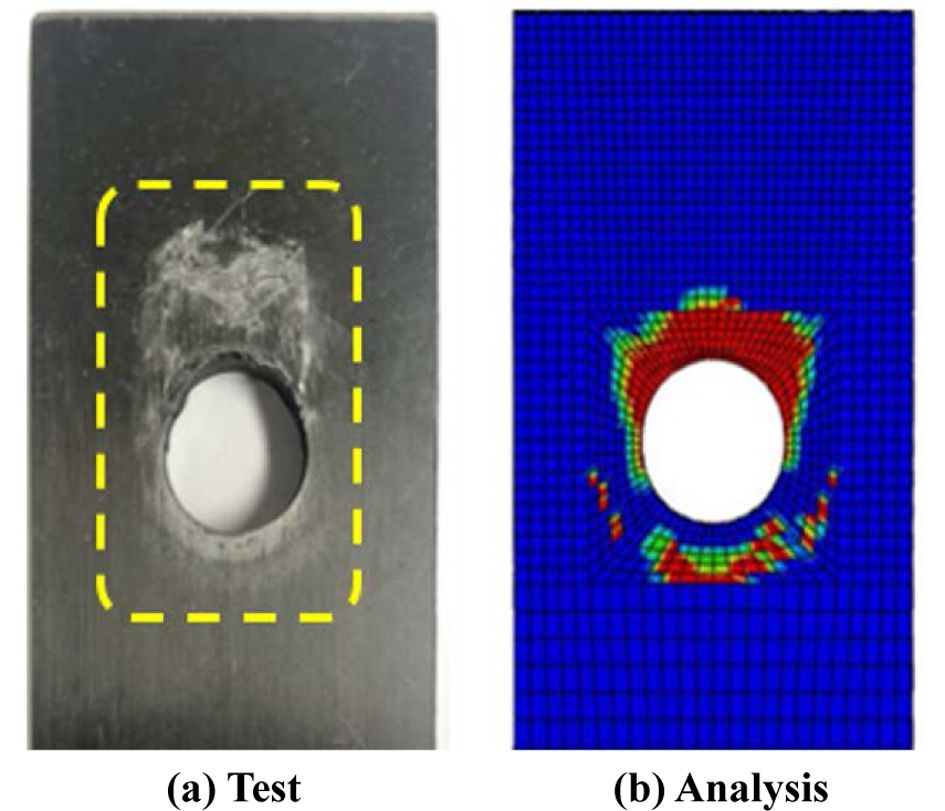
수정된 Lapczyk 모델을 이용하여 예측한 복합재료 볼트 조인트의 파손모드를 확인하였다. 시험된 시편의 파손모드를 파손해석을 통해 예측된 파손모드와 비교하였으며, Fig. 8을 통해 나타냈다. 해석결과는 손상변수를 나타낸 그림으로, 파손이 없는 손상변수가 0의 경우는 파란색, 완전 파단 된 1의 경우는 빨간색으로 나타내었다. 시험된 시편의 파손모드와 파손해석 모델을 통해 예측한 파손모드 모두 bearing 파손모드로 관찰되었다. 파손해석 결과 예측된 컨투어에서 볼트 구멍 아래쪽의 손상은 볼트 헤드에 의한 표면의 손상이다. 수정된 파손해석 모델을 이용하여 수행된 해석 결과가 파손모드를 예측하기에 유효함을 확인할 수 있다.

본 연구에서는 복합재료의 파손거동을 보다 정확히 예측하기 위해 기존 제시된 Lapczyk의 손상해석 모델을 수정하였고 이를 이용하여 복합재료 볼트 조인트의 파손해석을 수행하였다. 그 결과는 다음과 같다.
(1) 기존 선형 거동만 예측이 가능한 Lapczyk 모델의 전단 손상변수 과정을 수정하여 복합재료의 비선형 전단 거동 또한 예측할 수 있게 되었다. 이는 단일요소해석 결과와 시험결과를 비교하여 검증하였으며, 수정된 모델은 섬유 및 기지의 인장/압축 거동과 비선형적인 전단 거동을 정확히 예측하였다.
(2) 수정 Lapczyk 모델을 이용하여 예측한 베어링거동과 복합재료 볼트 조인트 시험결과로부터 획득한 베어링 응력-베어링 변형률 거동을 상호 비교하였으며 예측된 결과가 시험결과를 유효한 범위에서 예측하는 것을 확인하였다.
(3) 복합재료 볼트 조인트 시험결과에서 관찰된 복합재료의 파손모드와 수정된 Lapczyk 모델로 예측한 파손모드는 모두 베어링 파손모드로 나타났으며 수정된 Lapczyk 모델이 복합재료 볼트 조인트의 파손모드를 예측하는 데에도 적절하게 사용될 수 있음을 확인하였다.
결과적으로, 수정된 Lapczyk 모델은 연구된 복합재료 볼트 조인트의 파손거동을 충분히 예측할 수 있으며, 보다 큰 비선형 거동을 보이는 구조들에 유용하게 적용될 수 있을 것으로 판단한다.

본 연구는 ㈜한국화이바가 지원하는 연구과제로 수행된 것이며, 지원에 대해 진심으로 감사드립니다.