The free vibration characteristics of corrugated laminated composite plates with axial stiffeners is investigated using the Rayleigh-Ritz method. The plate is stiffened by beams with open cross-section area. The equivalent homogenization model is used for the corrugated laminated composite plates. This homogenization model is treated a corrugated plate as an orthotropic plate that has different material properties in two perpendicular directions. The motion of equivalent plate is represented on the basis of the first order shear deformation theory (FSDT) to account for the effect of rotary inertia and transverse shear deformation. Stiffeners are considered as discrete elements to predict the local vibration mode to be generated by the presence of stiffeners. To validate the proposed analytical approach, natural frequencies and vibration mode shapes from the analytical method are compared with those from the FEA by ANSYS.

본 연구에서는 Rayleigh-Ritz 법을 이용하여 열린 단면보로 보강된 복합재료 주름판의 자유진동 특성을 연구하였다. 복합재료 주름판에 대해 등가균질모델을 이용하였으며, 이 등가모델은 주름판을 두 수직방향에 대해 서로 다른 재료특성을 갖도록 직교이방성판으로 취급한다. 등가 직교이방성판의 운동은 회전 관성 및 횡전단변형을 고려하기 위해 1차 전단변형이론을 기초로 표현된다. 또한 진동형상에서 보강재의 위치에 따른 국부 형상을 표현하기 위해 이산보강이론이 적용되었다. 제안된 해석 방법에 대한 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하였으며, 두 방법을 이용해 얻은 진동수 및 진동형상을 비교하였다.

Keywords: 적층 복합재료(Laminated Composite), 주름판(Corrugated Plate), 균질 모델(Homogenization Model),   이산 보강재(Discrete Stiffener), 1차 전단변형이론(FSDT)

주름판은 주름방향에 대해서는 매우 유연하고 횡방향으로는 매우 단단하다. 이와 같은 구조특성을 갖는 주름판을 한쪽 방향에 대해서만 큰 강성이 요구되는 구조물에 적용하면 구조물의 큰 비강성을 얻을 수 있다. 이러한 장점때문에 주름구조가 고강성 및 경량화가 요구되는 항공우주, 자동차, 토목 및 건축 등의 구조물에 널리 이용되고 있다. 특히 복합재료를 구조물에 적용할 경우 그 장점은 더욱 커진다. Thill 등[1]은 실험을 통해 국부 파손 메카니즘에 대해, Winkler와 Kress[2]는 유한요소법을 적용해 주름 형상에 따른 영향을 연구하였다. Xia 등[3] 및 Park 등[4]은 복합재료 주름판에 대해 등가강성을 유도하였다. Park과 Kim[5,8]은 적층 복합재료 주름판에 대해 진동 및 좌굴 특성에 대해 연구하였다. Bai 등[6]은 가변익의 표피를 주름 구조로 대체하기 위해 이론 및 실험을 통해 주름 요소의 신장특성을 연구하였다. Karakoti와 Kar[7]은 유한요소법을 이용하여 굽힘 거동에 대해 연구하였다. 주름 구조는 횡하중에 의해 큰 변형이 발생될 수 있다. 또한 주름방향으로의 내평면 또는 전단 하중에 의해 쉽게 좌굴될 수 있다. 그러나 보 형태의 구조요소로 주름판을 보강하면 이와 같은 현상을 방지할 수 있다. Tong과 Guo[9]는 보강된 전단벽에 대한 전단저항을, Maleki와 Mehretehran[10]은 보강 사일로의 좌굴 거동에 대해 유한요소법을 이용하여 연구하였다. Wang 등[11]은 실험을 통해 거더의 중량을 줄일 수 있는 새로운 형태의 보강 주름 웨브를 제안하였다.
\본 연구에서는 해석적 방법을 이용하여 균일 단면보로 보강된 복합재료 주름판의 자유 진동 특성을 분석하였다. 이론 전개과정에서 횡전단변형과 회전관성을 고려하였으며, Rayleigh-Ritz법을 이용하여 진동수 방정식을 유도하였다. 주름판은 직교이방성판으로 등가시켰으며, 주름 방향에 평행하게 개방 단면보로 보강된 판을 고려하였다. 보강재 사이에 국부 진동형상을 나타낼 수 있도록 보를 이산요소로 취급하는 이산 보강이론을 적용하였다. 해석해의 결과를 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하였다. 다양한 수치 예가 복합재료 보강 주름판의 진동특성을 이해할 수 있도록 제시되었다.

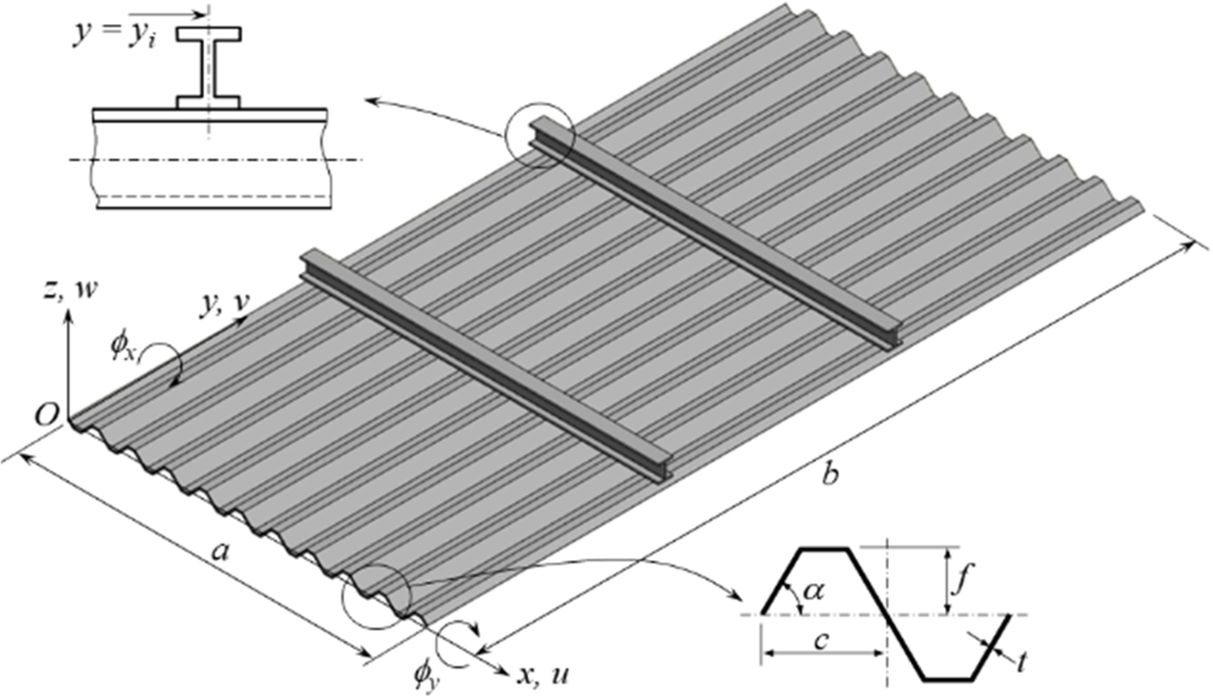
본 연구에서는 보로 보강된 복합재료 주름판을 고려하였다. 직사각판의 크기는 a×b로 나타냈으며, 단위 주름요소에 대해 반 주기는 c, 반 진폭을 f 및 판의 두께를 t로 표기하였다(Fig. 1). 보강재는 판의 한쪽 면에만 주름방향에 평행하게 위치한다. 본 연구에서는 사다리꼴 주름을 기준으로 주름각 a를 조절하여 삼각꼴, 사각꼴 및 요각꼴 형상의 4가지 주름 형상을 고려할 수 있다.
연구에서 주름판을 균일한 두께를 갖는 직교이방성판으로 등가시켜 해석에 적용하였다. 해석에서 횡전단변형과 회전 관성을 고려하기 위해 1차 전단변형이론(FSDT)을 적용하였다.
1차 전단 변형 이론으로부터 등가 이방성판의 변위장을 다음과 같이 쓸 수 있다.
 

 
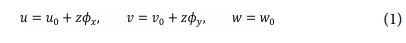
여기서 u, v 및 w는 x, y 및 z 방향 변위이다. 그리고 u₀, v₀ 및 w₀는 중립면에서 한 점의 변위이다. 또한 f_x, f_y는 y 및 x 축에 대한 회전을 나타낸다.
등가판의 구성 방정식을 다음과 같이 쓸 수 있다.
 

 
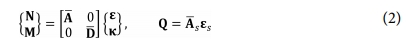
여기서 N = {N_x N_y N_xy}, M = {M_x M_y M_xy} 및 Q = {Q_y Q_x}^T 는 단위길이당 내평면력, 모멘트 및 횡전단력을 나타내는 합력들이다. 그리고 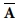, 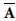_s및 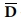는 복합재료 주름판을 직교이방성판으로 등가시켜 얻은 등가 신장 및 굽힘 강성계수이다[5]. 또한 ε, k 및 ε_s는 1차 전단변형 이론에 따른 수직 변형률, 곡률 및 횡전단 변형률이다.
 

 
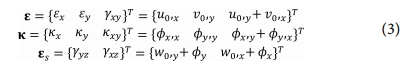
식에서 (,)는 다음에 나타나는 첨자에 대한 미분을 의미한다.
등가 직교이방성판의 두께 t_e를 2f로 등가시킬 경우 등가 직교이방성판의 변형 및 운동에너지를 다음과 같다.
 

 
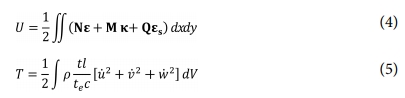
식 (5)에서 (∙)는 시간에 대한 미분을 나타내며, r는 주름판의 밀도, l은 반 주기의 주름 펼친 길이이다.
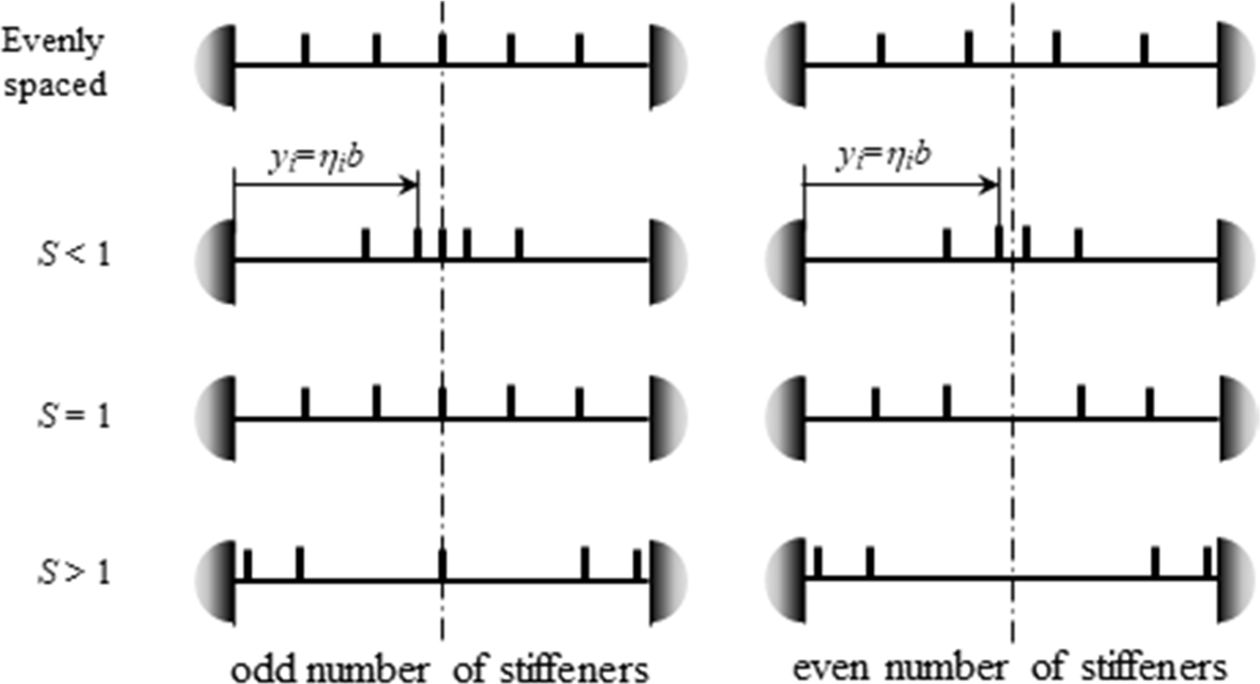
여러 개의 보강재로 보강될 경우 보강재는 y 방향으로 등간격 또는 비등간격으로 위치할 수 있다. 본 연구에서는 식 (6)과 같이 정의된 함수 η_i에 따라 보강재가 위치하며, 간격비 S의 함수이다. 식에서 N_S는 보강재의 수이며, c_i 는 식 (7)과 같이 정의되어 S에 따라 비등간격 보강에서 보강재의 분포 형태가 결정된다.
 

 
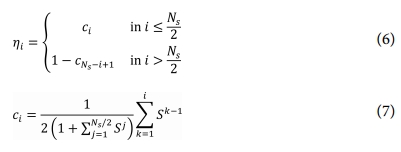
Fig. 2는 간격비 S에 따른 보강재의 개략적인 위치를 가시적으로 나타낸 것이다. 보강재들은 y = b/2를 기준으로 대칭으로 분포한다. 홀수 개로 보강될 경우 보강재 하나는 항상 y = b/2에 위치하며, 짝수 개인 경우에는 y = b/2에 위치하지 않는다. 그림에 나타난 것처럼 S > 1인 경우에는 양쪽 경계 근처에 보강재가 위치하며, S < 1인 경우에는 판의 중앙에 가깝게 위치한다. S = 1에 대해서는 보강재가 홀수 개인 경우에는 등간격으로, 짝수 개인 경우에는 판의 중앙을 기준으로 각 측면의 보강재들이 등간격으로 위치한다.
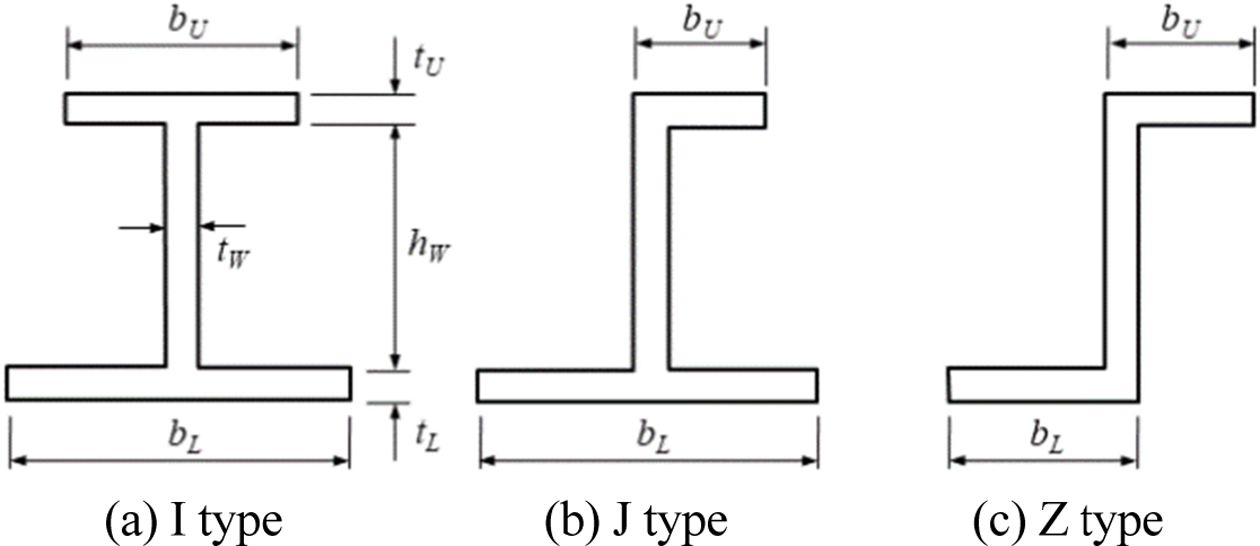
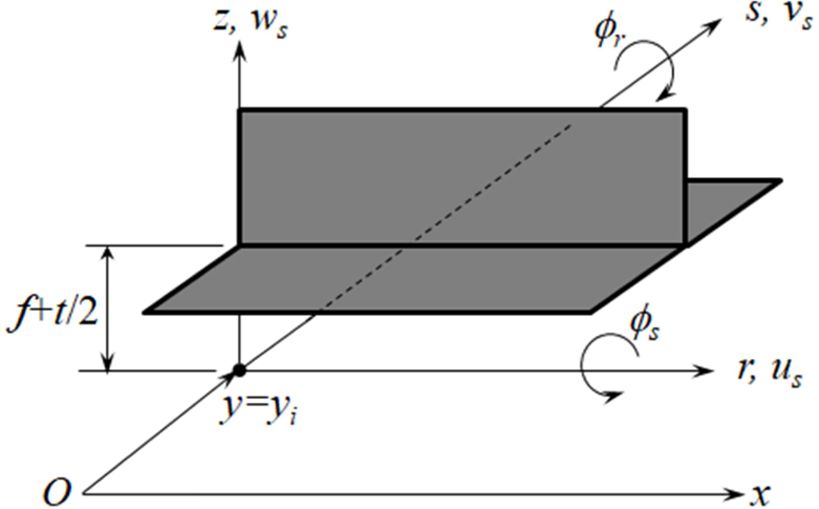
보강재는 Fig. 3처럼 3가지의 열린 단면보가 고려되었다. 웨브, 상단 플랜지, 하단 플랜지의 두께를 각각 t_W , t_U, t_L로 나타냈다. 보강재의 거동을 나타내기 위해 Fig. 4에서처럼 국부 좌표계(r, s, z)를 이용하였다. 국부 좌표계의 원점은 전역 좌표계의 (x, y_i, z)와 일치한다. 보 형태의 보강재에 대해 등가판의 중립면으로부터 수직방향 거리 z에서의 변위장을 다음과 같이 쓸 수 있다.
 

 
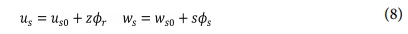
여기서 u_s0, w_s0는 판의 중립면에서 보강재의 변위를 나타낸다. 따라서 중립면에서 판과 보강재 사이에는 다음과 같은 관계를 갖는다.


 
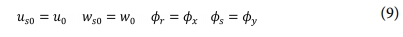
한편 보강재에 대한 변형률과 변위의 관계를 다음과 같이 쓸 수 있다.
 

 
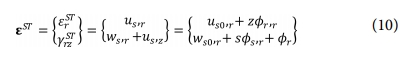
y = y_i에 위치하는 i번째 보강재의 변형에너지 및 운동에너지는 다음과 같다.
 

 
여기서 δ는 디랙 델타(Dirac delta) 함수로 진동형상에서 보강재의 위치에 따른 영향을 나타내기 위해 사용되었다. 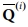는 적층 보강재의 각 층의 강성도 행렬이다.
임의의 경계조건을 갖는 판에 대한 변위식을 다음과 같이 급수 형태로 쓸 수 있다.
 

 
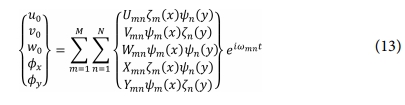
여기서 ω_mn은 고유 모드(m, n)에서의 고유 각진동수이며, U_mn, V_mn, W_mn, X_mn, Y_mn는 진폭을 나타내는 계수이다.
본 연구에서는 다음 식과 같이 모든 단이 고정된 경계조건을 고려하였다.
 

 
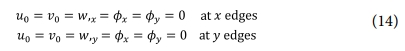
식에서 사용된 변위함수는 다음과 같다.
 

 
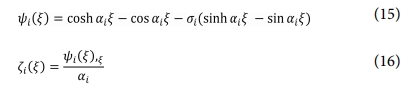
여기서 i = m, n이며 ξ = x, y이다. 그리고 α_i = β_i/L (여기서 L은 판의 폭 또는 길이), β_i는 반파수와 관계된 수, σ_i은 경계조건을 만족시키는 계수이다. 
보강된 주름판에 저장된 총 포텐셜 에너지는 다음과 같이 표현할 수 있다.
 

 
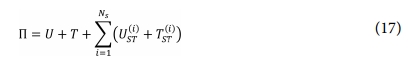
가정된 변위식 (13)을 총에너지식 (17)에 대입한 다음 그 결과를 Rayleigh-Ritz 과정을 적용하면 다음과 같은 고유값 문제를 얻을 수 있다.


 
여기서 M, K는 고려된 계의 질량 및 강성행렬 이며, P는 진동형상을 결정하는 계수행렬이다. 각각의 행렬은 (5×5)의 부분 행렬로 구성되며, 부분행렬은 (M+N) × (M+N) 크기를 갖는다. 식 (18)로부터 고유 진동수 및 진동형상을 구할 수 있다.

본 연구에서는 주름판 및 보강재에 대해 모두 AS4/3501-6 carbon/epoxy 복합재료를 고려하였다[3]. 복합재료의 물성은 E₁ = 148 GPa, E₂ = 10.5 GPa, G₁₂ = 5.61 GPa, G₂₃ = 3.17 GPa, ν₁₂ = 0.3, ν₂₃ = 0.59 및 ρ = 1590 kg/m³이다. 이때 각 층의 두께는 일정하다. 제시된 모든 수치예에서 주름판 및 보강재에 대한 적층밥법은 [±45°/0°/90°]_S이며, 보강재의 각 부분 두께는 t_L = t_U = t_W = t이다.
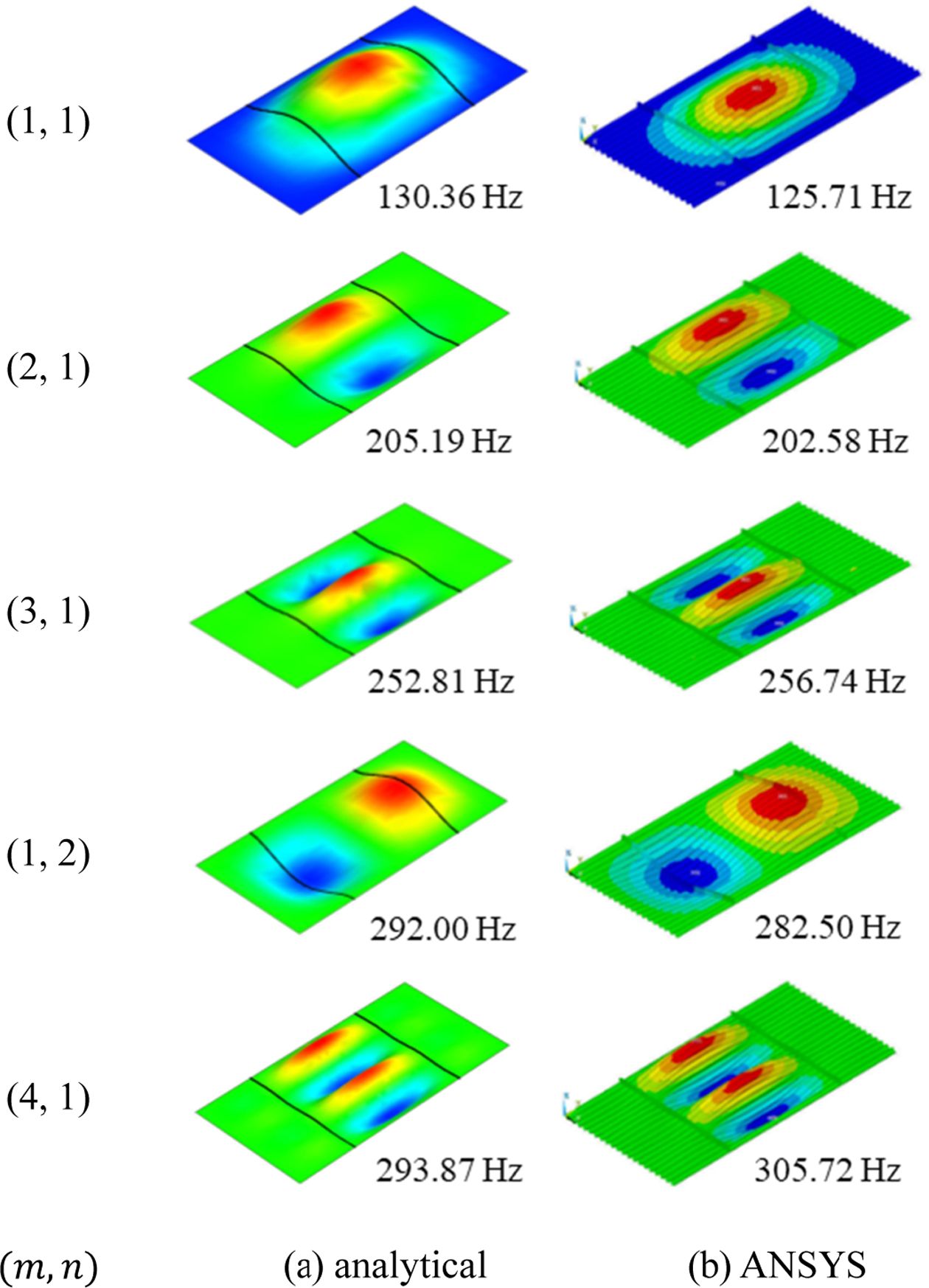
제안된 해석방법의 타당성을 검증하기 위해 ANSYS를 이용하여 유한요소해석을 수행하였다. 유한요소 모델링을 위해 SHELL281 요소가 이용되었다. Fig. 5는 사다리꼴 주름판 (σ = 60^o)에 대해 이론해석해와 유한요소해를 진동형상과 함께 제시하여 비교하였다. 이 때 형상비 b/α = 2인 주름판은 t = 1.0 mm, f = 5.0 mm, c = 12.5 mm 및 N_c = 20이다. 판은 두 개의 I형 보가 간격비 (S) 1로 보강되었다 (y₁ = 0.25b, y₂ = 0.75b). 보강재의 기하형상은 b_L = b_U = c, h_W/f = 2이다. 그림에서처럼 두 해석 방법 간의 진동수 차이는 최대 4% 미만으로 잘 일치하고 있다. 또한 진동형상의 경우에도 본 이론해석과 유한요소해석 결과가 매우 잘 일치하는 것을 볼 수 있다. 이론해석의 진동형상에서 굵은 실선은 보강재의 위치를 나타낸다. 모드 (2, 1), (3, 1) 및 (4, 1)의 경우 보강재 간에 국부 진동형상이 나타나는 것을 볼 수 있으며, 이론해석 방법에서도 국부 진동형상이 잘 표현되고 있다.
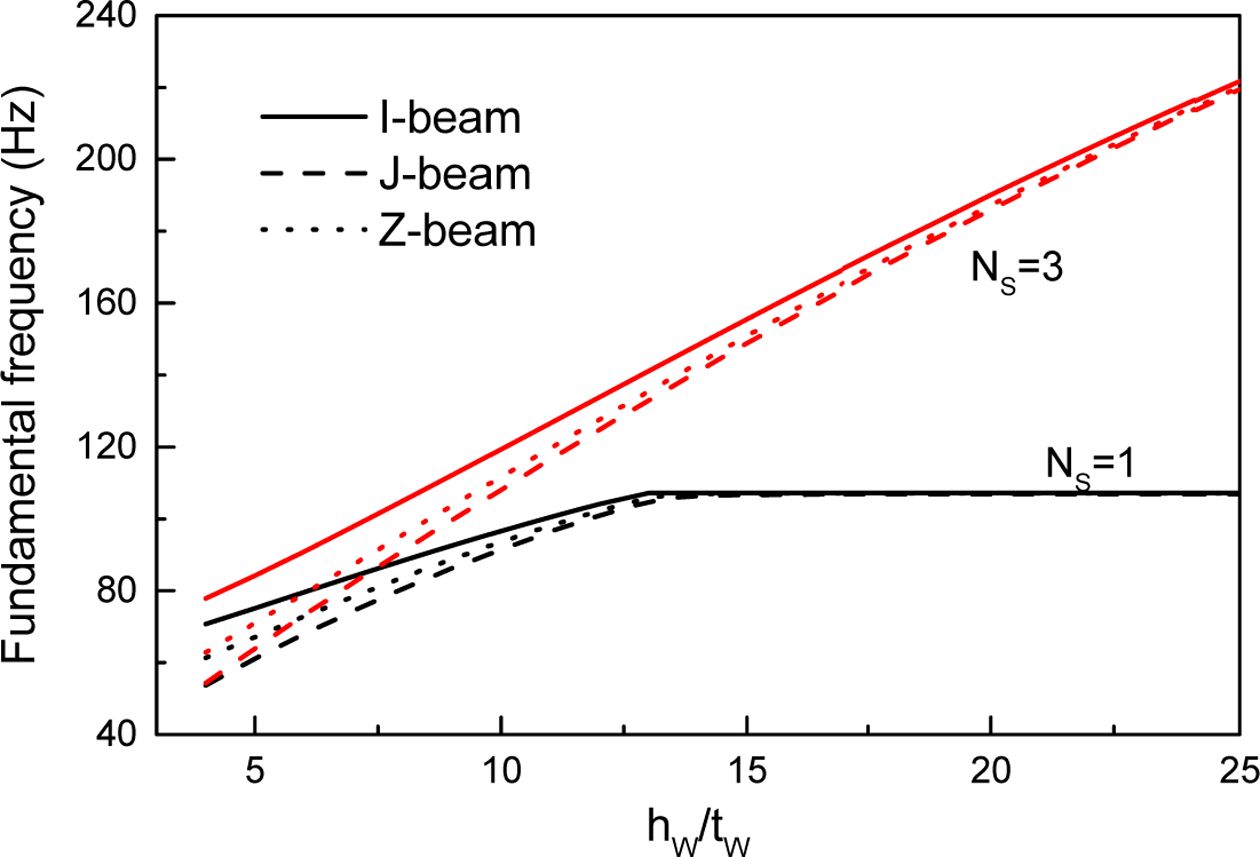
보강재의 높이 대 두께 비(h_W/t_W)가 기본진동수에 미치는 영향을 알아보기 위해 Fig. 6이 제시되었다. 사용된 기하 자료는 b/α = 3, N_c = 20, α = 60°, f = 5t, b_U = c 및 b_L = c/2이다. 보강재는 등간격으로 분포하며 보강재의 단면적은 보강재 단면 형상에 관계없이 같은 h_W/t_W에서는 모두 같다. 진동수는 h_W/t_W 비의 증가와 함께 증가하는 것을 볼 수 있다. 그러나 N_S = 1인 경우 어느 비 이상이 되면 진동수는 증가하지 않고 일정한 값을 갖게 되어 보강재의 높이에 따른 보강효과를 얻을 수 없다. 초기의 작은 높이비에서는 보강재의 단면형상에 따라 진동수의 크기가 달라지지만 어느 비 이상에서는 단면 형상에 관계없이 거의 같은 값을 갖는다.
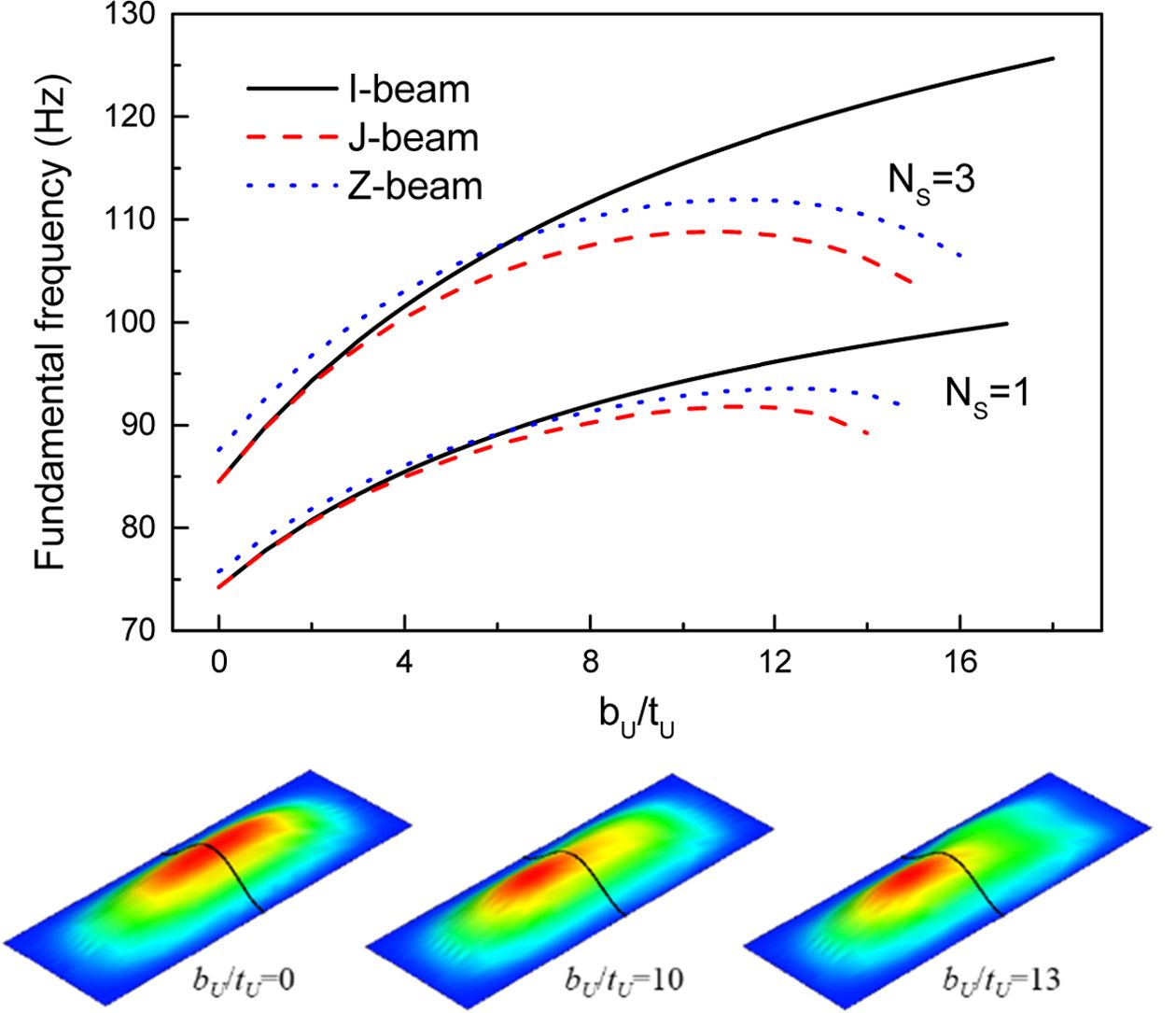
Fig. 7에서는 등간격으로 보강된 주름판에 대해 상단 플랜지의 길이 대 두께 비(b_U/t_U)가 기본 진동수에 미치는 영향을 알아 보았다. 사용된 판의 기하형상은 b/α = 3, N_c = 20, α = 60°, f/t = 5, b_L = c/2 및 h_W/f = 2이다. 동일한 b_U/t_U 비에서 보강판의 질량은 보강재의 단면 형상에 관계없이 모두 같다. 전반적으로 b_U/t_U 비가 증가함에 따라 진동수도 증가하지만 J 및 Z 형의 경우 진동수가 최대값까지 증가하다가 감소하는 거동을 한다. 이와 같은 현상은 보강재의 비대칭성 때문으로 제시된 진동형상(J형 보, N_S=1)에서처럼 b_U/t_U 비에 따라 진동형상에서의 변화가 나타나기 때문이다. 또한 보강재의 단면 형상에 따른 진동수의 차이는 b_U/t_U 비의 증가와 함께 커진다. 이와 같은 이유는 보강재의 단면 형상에 따라 회전관성이 달라지기 때문이다.
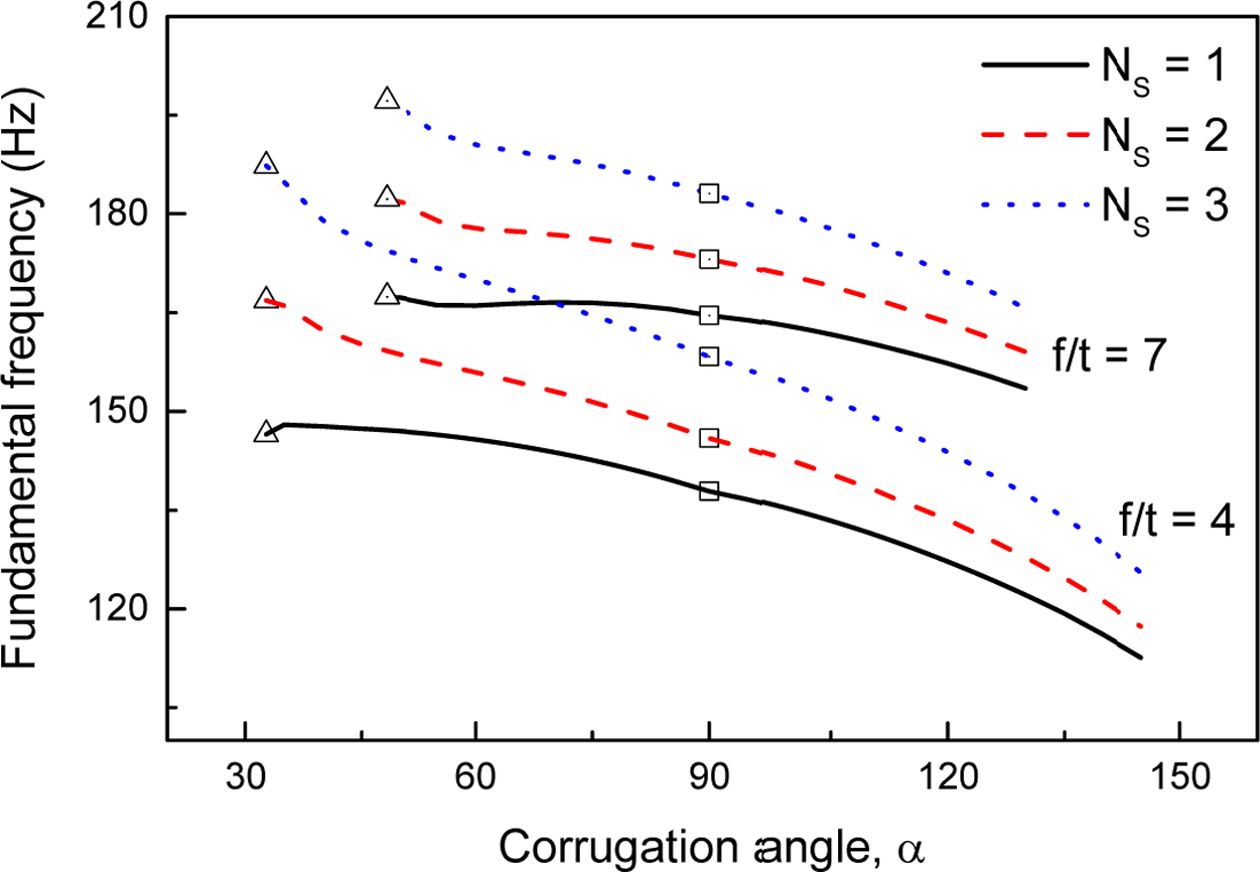
Fig. 8에서는 I형 보(b_L = b_U = c, h_W/t_W = 10)로 보강된 주름판의 주름각에 따른 기본진동수 변화를 보이고 있다. 여기서 판의 형상비 b/α = 2, 주름수 N_c = 20이 고려되었으며, 보강재는 등간격으로 보강된다. 그림에서 기호 ‘9’와 ‘#’는 삼각형 및 사각형 주름형상의 주름판에 대한 진동수를 의미한다. 비보강 주름판의 경우 주름각을 증가시키면 판의 강성 증가와 함께 질량도 증가하지만 강성효과가 질량효과보다 커 주름각 증가와 함께 진동수가 증가를 한다[5]. 그러나 보강판의 경우 보로 보강을 함으로써 강성이 충분히 증가하기 때문에 주름각 증가에 따라 진동수에 미치는 질량효과가 강성효과보다 크기 때문에 진동수는 오히려 감소한다. 또한 보강 주름판에 대해서도 비보강판의 경우처럼 가장 큰 기본진동수를 얻기 위해서는 주름형상을 삼각형에 가깝게 하는 것이 좋은 안임을 알 수 있다.
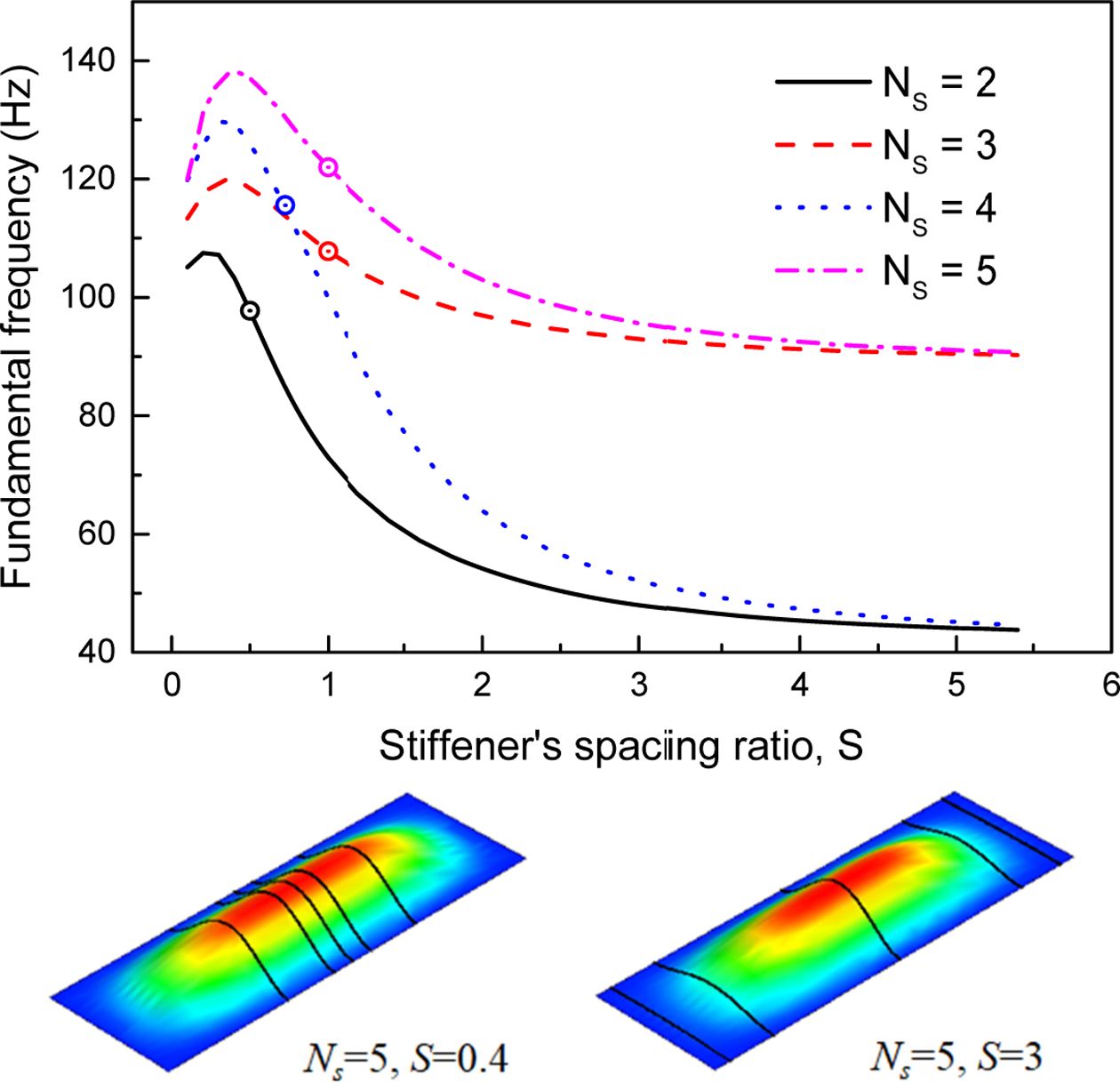
Fig. 9에서는 I 형 보로 보강된 주름판에 대해 보강재의 위치가 기본 진동수에 미치는 영향을 알아 보았다. 고려된 기하변수는 b/α = 3, N_c = 20, α= 60°, f/t = 5, b_L = b_U = c/2 및 h_W/ t_W = 10이다. 그림에서 기호 ‘’는 보강재가 등간격으로 분포된 주름판의 진동수를 나타낸다. 그림에서처럼 보강재들이 판의 중앙 근처에 위치하는 보강판(S < 1)의 진동수가 보강재가 판의 양단 부분에 집중이 되는 보강판(S > 1)의 진동수보다 큰 값을 갖는다. 이와 같은 현상은 보강재의 위치에 따라 진동형상에서 보강재의 변형 여부에 따라 나타나는 것이다. 제시된 진동형상에서처럼 보강재가 중앙에 위치하는 경우(S = 0.4)에는 보강재가 많이 변형되지만, 판의 양단에 위치하는 경우(S = 3)에는 중앙에 위치한 보강재를 제외하고 다른 보강재는 거의 변형이 되지 않는다. 또한 간격비 S가 증가함에 따라 진동수는 특정 값으로 접근을 한다. 이 특정 값은 짝수 개 보강인 경우에는 비보강판의 진동수에 해당되며, 홀수 보강인 경우에는 판의 중앙에 보강재가 하나 있는 경우의 진동수이다. 이와 같은 현상으로부터 보다 큰 진동수를 얻기 위해서는 보강재를 등간격으로 배열시키기보다는 비등간격으로 배열시키는 것이 보다 효과적이다고 할 수 있다. 

개방형 단면 보로 보강된 적층 복합재료 사다리꼴 주름판의 진동특성을 얻기 위해 이론해석 및 유한요소해석을 수행하였다. 이를 통해 제안된 이론해석방법이 구조물의 진동특성인 고유 진동수 및 진동형상을 적절히 예측할 수 있음을 보였다. 특히 보강재 사이에 나타나는 국부 진동형상까지도 예측할 수 있었다. 제시된 수치예로부터 보강재의 웨브 높이가 작은 경우에는 보강재의 단면 형상에 따라 진동특성이 달라지지만 큰 경우에는 그 차이가 거의 없으며, 특정 높이 이상에서는 진동수 변화가 없음을 알았다. 또한 보강재의 플랜지 크기가 어느 이상이 되면 진동수는 오히려 감소함을 보였다. 주름판에서 보강재의 보강 효과는 작은 주름각에서 더욱 크다는 것을 알았으며, 보다 큰 기본진동수를 얻기 위해서는 주름형상을 삼각형에 가깝게 하는 것이 좋은 방안임을 알 수 있었다. 또한 보강재를 등간격으로 배열시키기보다는 비등간격으로 배열시키는 것이 보다 효과적임을 알았으며, 보강재가 존재함으로써 1차 진동형상이후에 보강재 사이에서 국부 진동형상이 발생되는 것을 확인하였다.