In this work, a contour-based section analysis method incorporating the use of Bézier curves is attempted for the construction of optimal structural design framework of composite helicopter blades. The suggested section analysis method is able to analyze composite blades with solid cores made of arbitrary materials and geometric shapes. The contour-based section analysis method is integrated into a blade structural optimization framework to confirm the efficiency of the present approach. The numerical simulation result demonstrates that the optimized blade configurations are obtained with a reduction in mass by 52%, compared to the baseline blade. For the structural optimization of composite blades with 19 subsections, it takes about one hour for the successful optimization while satisfying all the design constraints considered in this study, which reveals the efficiency of the present approach.

본 연구에서는 매개변수곡선의 일종인 Bézier 곡선을 이용한 단면해석법을 개발하고, 이를 이용한 블레이드 최적구조설계 프레임워크를 구성하였다. 개발된 단면해석기법은 기존의 직선 세그먼트를 이용한 중심선기반 단면해석법의 효율성을 유지하면서 고형 블레이드 단면에 대한 해석이 가능한 특징이 있다. 본 연구에서 제안한 단면해석법을 예제 블레이드에 적용하고 구조 최적설계를 수행하여 설정된 구속조건을 모두 충족함과 동시에 기준형상대비 약 52% 질량이 감소된 최적 블레이드 형상을 도출하였다. 최적설계에는 총 19개의 블레이드 단면을 고려하였으며, 결과를 도출하는 데 대략 1시간 정도의 계산시간이 소요되었다. 본 연구를 통해 개발된 단면해석기법과 최적설계 프레임워크의 효율성을 확인하였다.

Keywords: Bézier 곡선(Bézier curves), 로터 블레이드(Rotor blade), 구조 최적화(Structural optimization)

헬리콥터 및 풍력발전기 분야에서 사용되는 블레이드는 블레이드의 단면 크기에 비해 길이가 매우 긴 기하학적인 특징을 갖고 있다. 따라서, 반복적인 계산이 많이 요구되는 블레이드의 초기구조설계 단계에서는, 효율적인 해석을 위해 블레이드의 3차원 구조 형상을 블레이드의 여러 지점에 위치한 단면과 1차원의 보 유한요소모델로 분리하여 해석을 진행하는 것이 효율적이다. 일반적으로 블레이드의 최적 구조설계는 여러 지점에서 단면의 강성과 관성치를 계산한 후, 이를 블레이드의 1차원 유한요소모델에 대입하여 블레이드의 구조동역학적 해석을 진행하며, 초기 설계요건을 만족하는 블레이드 형상이 도출될 때까지 이 과정을 반복수행하게 된다.
블레이드의 단면해석기법은 크게 2차원 유한요소기반 단면해석법과 중심선 기반 단면해석법으로 구분할 수 있다.
2차원 유한요소기반 단면해석법[1-5]은 2차원 평면유한요소를 이용하여 이산화 된 단면의 주요 물성을 도출하는 방식이다. 이 방법을 이용할 경우 모델링 가능한 형상 및 재료분포에 제약이 없기 때문에, 대부분의 블레이드 단면 구조설계 연구들[6-8]이 이 방법을 이용하고 있다. 하지만, 최적설계 프레임워크 구축 과정에서 반복적인 단면해석을 위한 자동화된 유한요소모델링과정 구축에 많은 준비작업이 필요하고 계산시간이 많이 소요되는 단점이 있다.
한편, 중심선(contour) 기반의 단면해석법[9-14]은 속이 빈 박벽(thin-walled) 블레이드의 단면해석에 사용하기 적합한 방법으로, 단면 벽을 1차원 곡선으로 근사화하고, 이들을 단순 선적분하여 블레이드의 단면 물성을 계산하는 방법이다. 블레이드를 구성하는 각각의 벽을 1차원적인 선으로 모델링하여 해석을 수행하므로 2차원 유한요소기반 단면해석법에 비해 효율적인 단면 모델링 및 해석이 가능하다. 그러나, 2차원 유한요소기반 단면해석법에 비해, 고형(solid) 블레이드 단면에 대해서는 해석이 어려우며, 중심선의 수학적 표현식을 도출하기가 쉽지 않다는 단점이 있다. 이러한 문제점을 극복하기 위해, 일부 선행연구[11,13,14]에서는 임의의 곡률을 갖는 단면의 중심선들을 수학적으로 표현하기 쉬운 여러 개의 직선 세그먼트(segment)로 이산화하여 모델링하는 방법을 제안한 바 있다. 선 세그먼트 기반의 접근법은 임의의 곡률을 갖는 곡선을 효과적으로 모델링하는 것이 가능하나, 반복적인 내부형상변경(단면 벽의 두께 등)이 요구되는 최적설계 프레임워크에 적용하기에는 비효율적인 측면이 있다.
본 연구에서는 앞서 언급된 중심선 기반의 단면해석법의 한계점을 보완하는 단면 모델링 기법을 제안하였다. 개발된 단면 모델링 기법은 기존 중심선 기반 단면해석법이 다루지 못했던 고형 단면형상에 대한 해석이 가능하며, 최적설계에서 요구되는 반복적인 내부 구조형상 변경에 효과적으로 대응할 수 있다. 모델링 기법의 정확성 검증을 위해, 임의의 예제 단면을 이미 검증이 완료된 2차원 유한요소기반 단면해석법과 비교하여 본 연구에서 개발된 단면 해석법의 유효성을 확인하였다. 개발된 단면해석법을 이용하여 회전익기 최적 구조 설계 프레임워크를 구축하고, 이를 기존 헬기 블레이드 구조설계에 적용하였다.

2.1 Bézier 곡선을 이용한 단면 형상 모델링
본 연구에서는 직선 세그먼트 기반 단면해석법의 단점을 해소하기 위해 매개변수 곡선의 일종인 Bézier 곡선을 단면 모델링에 도입하였다. Bézier 곡선의 수식은 다음과 같다[15].
 


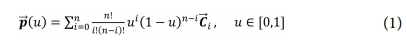
여기서, 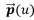는 Bézier 곡선 위에 놓인 점의 자취를 의미한다. u는 매개변수 좌표, n은 곡선의 차수, 그리고 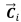는 제어점(control point)을 의미한다.
Bézier 곡선은 차수와 제어점의 위치를 조절하여 임의의 곡률을 갖는 곡선을 자유롭게 표현할 수 있다. 따라서 곡선을 표현하는데 필요한 선 세그먼트의 개수를 효과적으로 줄일 수 있다. 또한, 직선 세그먼트들을 오프셋할 때 수반되던 트림 작업[14]의 횟수 역시 줄일 수 있다. 매개변수식으로 표현된 오프셋 곡선의 일반식은 다음과 같다.
 

 
여기서, 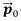는 곡선 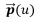에서 거리 t만큼 떨어진 곳에 위치한 오프셋 곡선을 나타낸다. 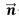은 매개변수 좌표 u에서의 법선벡터를 나타낸다.
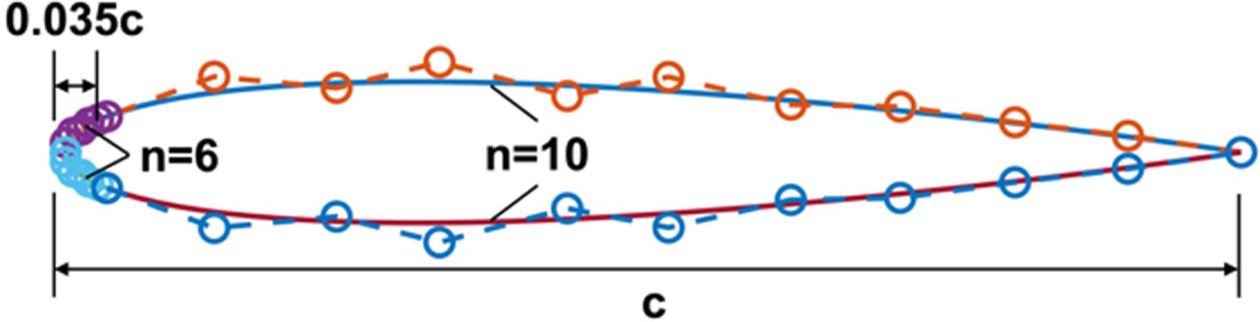
Fig. 1은 NACA0012 에어포일의 외형을 Bézier 곡선으로 나타낸 것이다. 앞전부근에서 곡률이 급격히 변하므로, 윗면 아랫면 각각 0.035c(c: 시위길이) 지점을 기준으로 곡선을 두 개로 구분하였다. 0.035c 기준으로 왼쪽의 곡선들은 6차, 오른쪽의 곡선들은 10차의 Bézier 곡선을 이용하여 표현하였다.
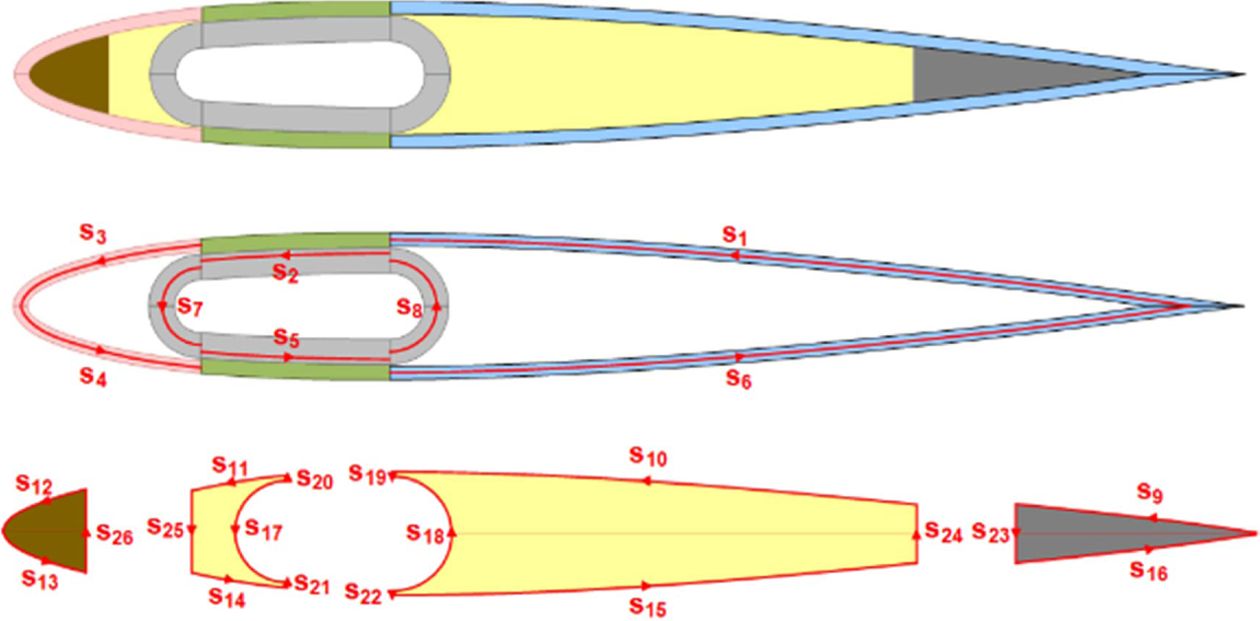
Bézier 곡선과 같은 매개변수 곡선을 이용하여 기존 중심선 기반 단면해석법이 다루지 못한 고형 단면에 대한 해석을 편리하게 수행할 수 있다. Fig. 2는 외피와 전단웹, 그리고 심재(core)로 구성된 임의의 단면을 외피와 전단웹으로만 구성된 단면과 심재 영역으로 분리한 것이다. 외피와 전단웹으로 이루어진 단면의 물성은 중심선기반 단면해석법을 이용하여 계산되며, 심재영역의 단면 물성은 심재들의 경계선을 나타내는 매개변수 식들을 선적분하여 계산된다. 심재에서는 단면적 A, 단면일차모멘트 Q_y , Q_z, 단면이차모멘트 I_y , I_z, 및 단면 면적곱 I_yz 등이 계산되며, 이를 각각 수식으로 나타내면 식 (3)부터 (8)과 같다.
 

 
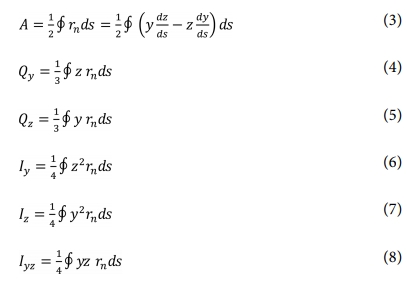
여기서 y와 z는 각각 단면의 수평과 수직방향 좌표축을 의미한다.
2.2 최적설계 프레임워크
본 연구에서 제안한 단면해석 기법의 효율성을 확인하기 위해, 미국 Sikorsky사에서 제작된 동축반전 헬리콥터인 XH-59A의 블레이드를 활용하여 단면 최적 구조 설계를 수행하였다. 참고문헌[16]에 제시된 데이터를 토대로 계산된 XH-59A의 블레이드의 질량은 152 kg이며, 블레이드의 공진회피조건을 만족함과 동시에 무게가 감소된 블레이드의 획득을 목표로 하였다.
정식화된 최적화 문제는 다음과 같다.
 

 

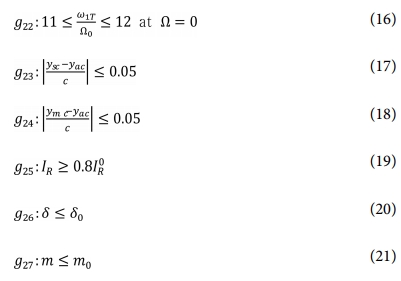
여기서 x는 설계변수 벡터를 의미한다. m은 블레이드의 질량, m₀는 기준형상의 m을 나타낸다. 식 (10)부터 (12)까지는 로터의 공진회피조건을 나타낸다. N은 로터 회전수의 정수배수를 의미한다. ω_i, ω_j 및 ω_k는 제자리 비행 시 로터 회전수의 69%, 78% 및 100%에서의 블레이드의 주요 회전고유진동수(1, 2, 3차 플랩(flap)모드, 1, 2차 래그(lag), 1차 비틀림 모드)들을 의미한다. y_sc, y_mc 및 y_ac는 각각 단면의 앞전 기준 전단중심, 질량중심 및 공력중심의 시위방향 위치이다. I_R은 블레이드의 익근(root)을 기준으로 한 굽힘축기준 관성모멘트이며, 상첨자 0이 붙은 값은 기준형상의 값(548.43 kgm²)을 의미한다. δ는 블레이드의 끝단에 작용한 단위전단하중에 의한 블레이드의 끝단 변위이며, 상첨자 0이 붙은 값은 기준형상의 값을 의미한다. 단위 전단하중에 의한 끝단 변위확인 시, 블레이드의 익근에는 외팔보(cantilever)조건을 적용하였으며, 기준 블레이드의 끝단변위는 1.58×10^-4 m이다.
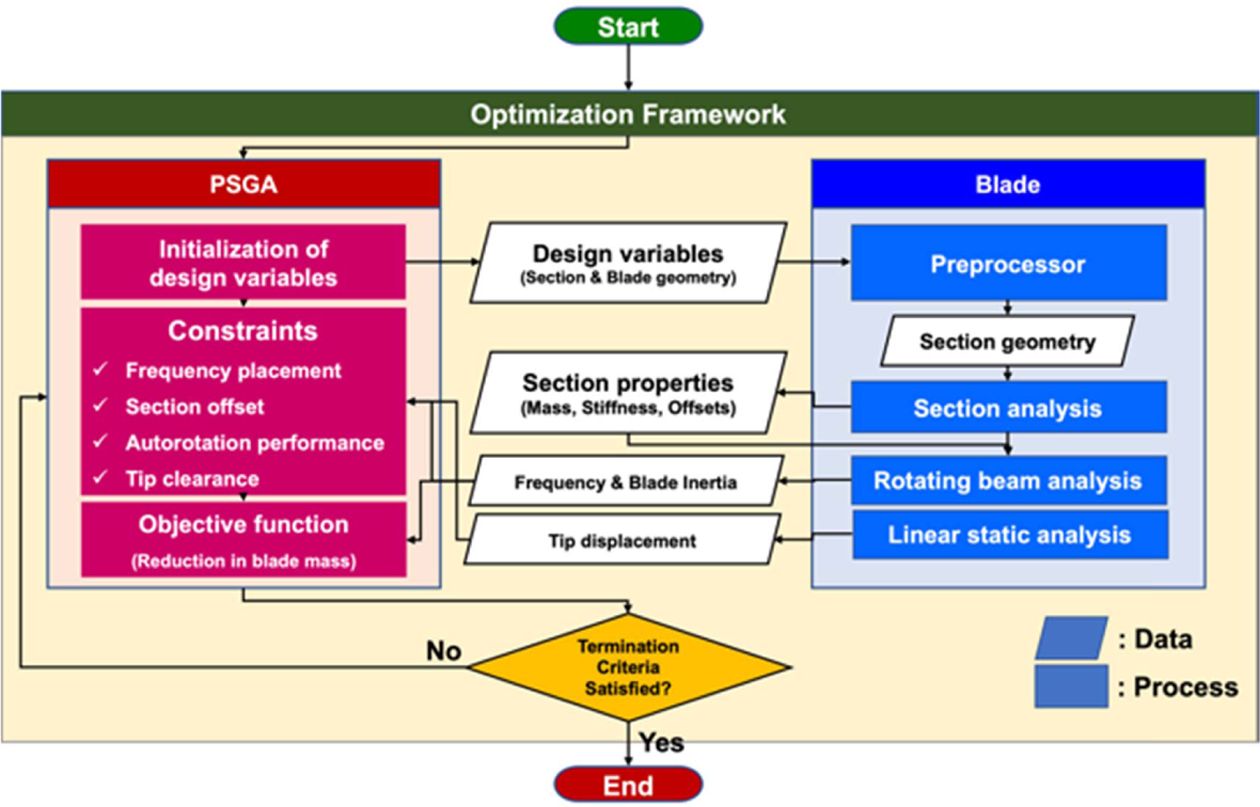
최적구조설계를 위한 프레임워크를 그림으로 나타내면Fig. 3과 같다. 프레임워크는 설계변수들을 생성하는 최적화 알고리듬과 블레이드 구조해석 모듈로 구분할 수 있다. 최적화 알고리듬은 Dhadwal 등[17]이 제안한 전역탐색알고리듬인 PSGA(Particle Swarm assisted Genetic Algorithm) 알고리듬을 사용하였다. PSGA는 유전알고리듬과 군집알고리듬을 혼합한 최적화 알고리듬으로, 설계변수 공간 전역을 탐색하여 구속조건이 있는 비선형 최적화 문제의 해를 구한다. 블레이드 구조해석 모듈은 Bézier 곡선을 이용하여 단면을 생성하는 전처리기 모듈, 단면해석 모듈, 회전고유진동해석 모듈과 선형정적해석 모듈로 구성되어 있다. 단면해석 모듈은 Jung 등[12]이 제안한 박벽 복합재료 보 이론을 바탕으로 제작되었으며, 보의 회전고유진동해석 및 선형정적해석에 필요한 (5×5)의 강성행렬, (4×4)의 질량행렬과 단면의 주요 중심치(전단중심, 질량중심 등)의 위치를 계산한다. 회전고유진동해석[18] 및 선형정적해석 모듈에서는 주요회전고유진동수와 블레이드의 끝단변위를 계산한다.
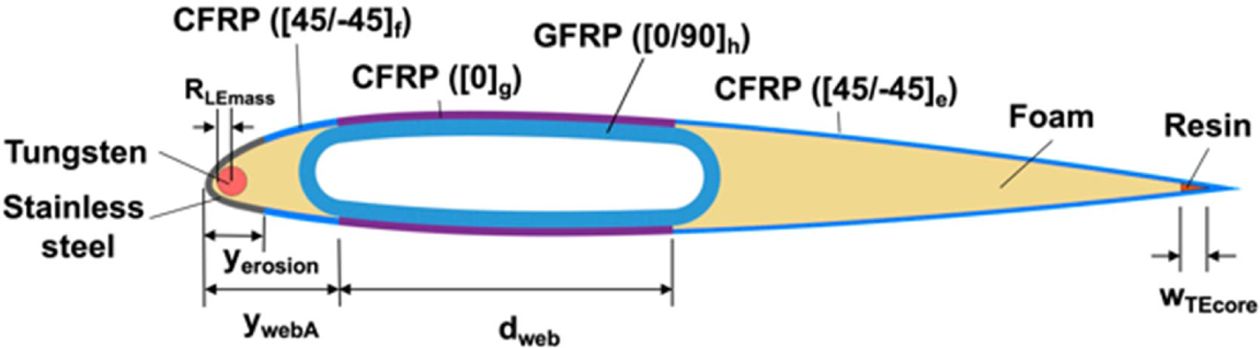
기준 단면형상을 참고하여 Fig. 4와 같이 설계변수들을 설정하였다. 설계변수는 외피 및 스파 복합재의 적층수, 앞전 erosion shield와 뒷전 레진보강재의 폭, 전단웹의 위치 등으로 구성된다.
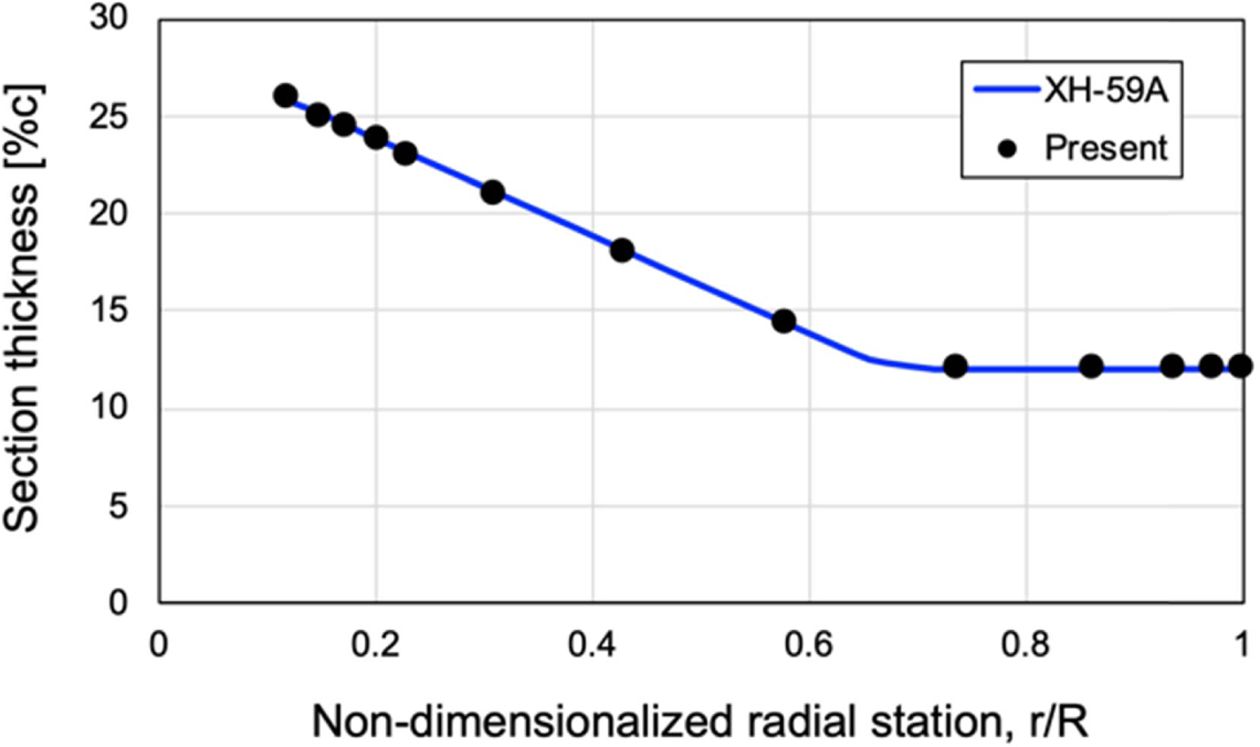
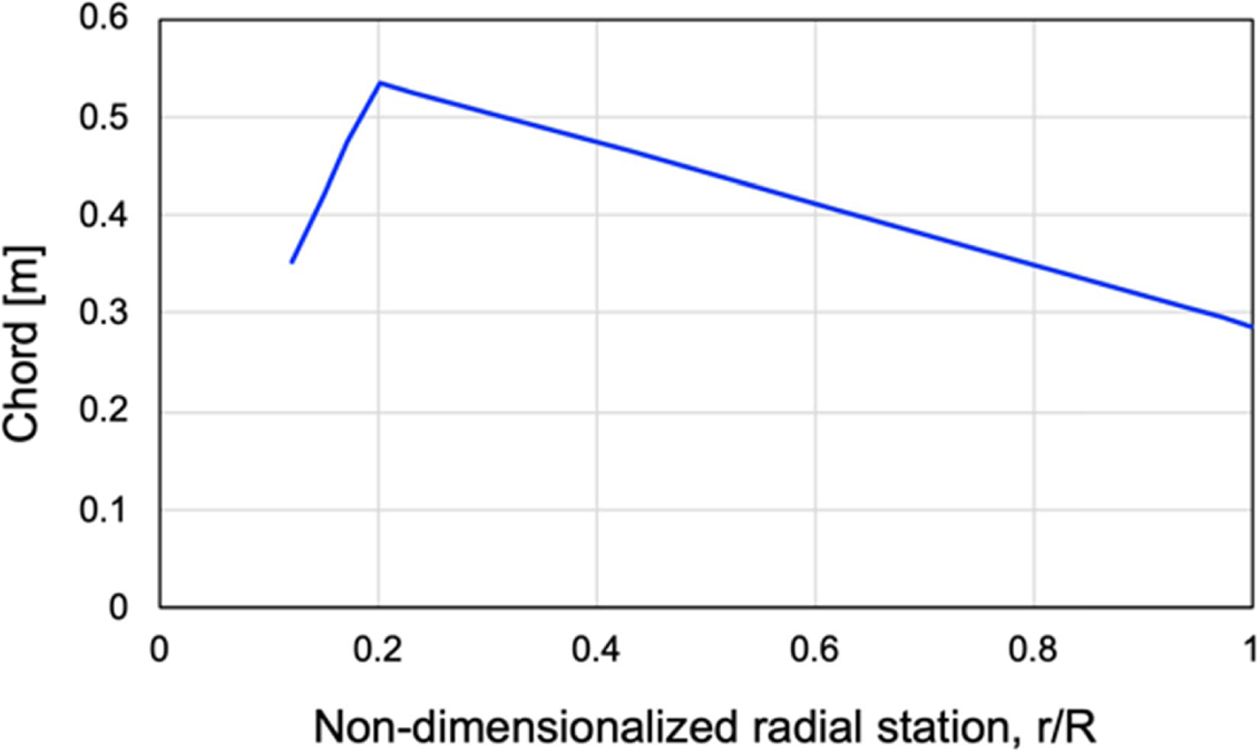
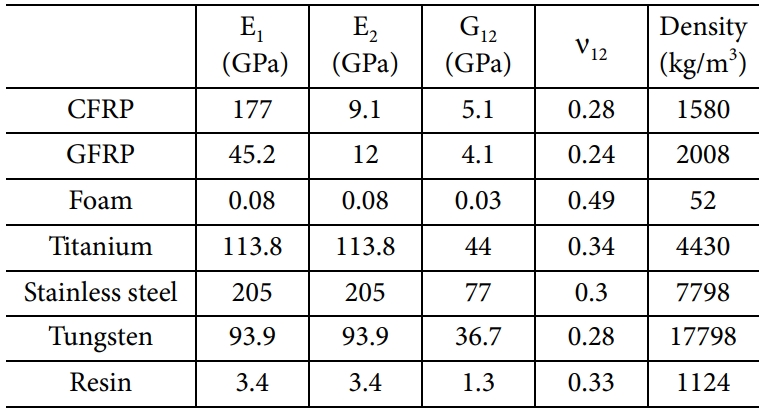
단면의 두께분포와 시위길이 분포는 각각 Fig. 5 및 6과 같다. 참고문헌[7]을 참고하여 0.12R부터 0.73R까지의 단면에는 NACA00xx 계열 에어포일을, 0.73R 이후 지점의 단면에는 NACA23012 에어포일을 이용하였다. 단면의 초기비틀림각 분포는 참고문헌[16]의 데이터를 그대로 이용하였다. 단면에 사용된 재료들의 주요 물성치는 Table 1에 정리되어 있다. Stainless steel의 물성치는 참고문헌 [6]의 데이터를 이용하였다.

3.1 단면모델링 기법 검증
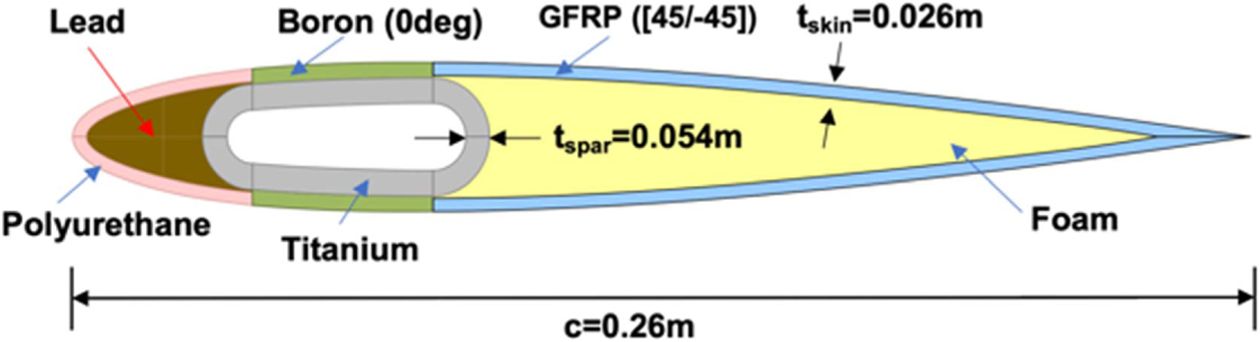
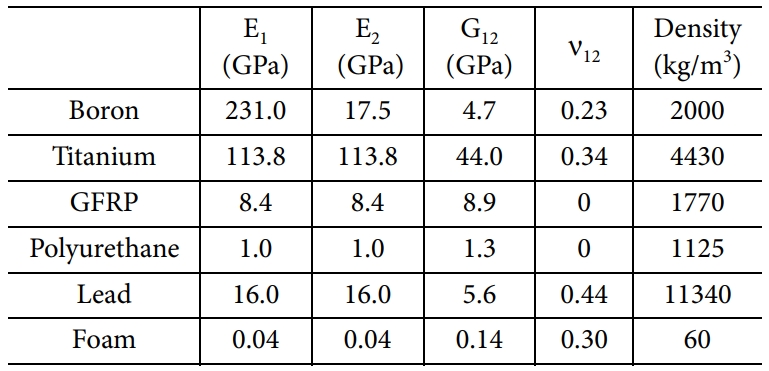
제안한 단면 모델링 기법의 신뢰성을 검증하기 위해 임의의 블레이드 단면에 대하여 검증을 수행하였다. 단면형상과 재료분포를 나타내면 Fig. 7과 같다. 단면의 외형은 NACA0012 에어포일을 이용하여 생성하였다. 외피에는 앞전에서부터 polyurethane, boron, GFRP 등이 사용되었다. GFRP는 [45/-45]로 적층된 라미네이트(laminate)의 등가물성을 이용하였다[3]. 심재는 앞전의 납(lead)과 뒷전의 폼(foam)으로 구성된다. 재료들의 주요 물성치를 표로 나타내면 Table 2와 같다. Boron, polyurethane의 물성은 각각 참고문헌 [19]와 [20]의 데이터를 이용하였다. Titanium은 Table 1에 제시된 물성을 이용하였다. 이외 나머지 재료들의 물성은 참고문헌[3]의 값을 이용하였다.
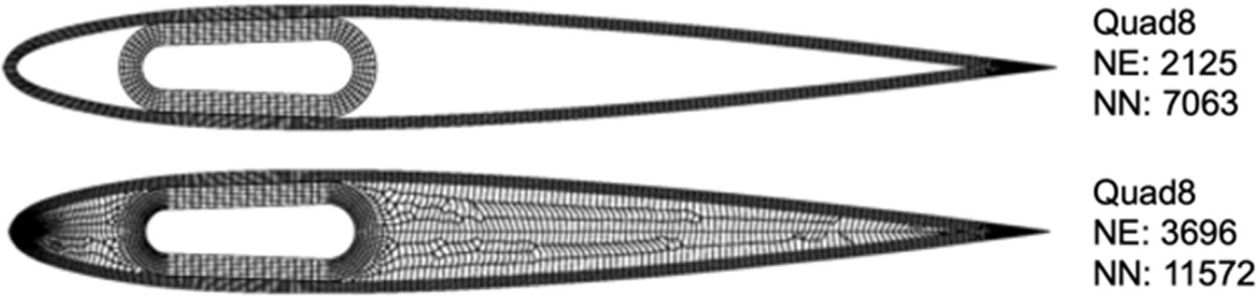
검증은 실험과의 비교 연구를 통해 신뢰성이 검증된 2차원 유한요소기반 단면해석 코드(Ksec2d-AE)[3]의 결과와 비교하는 방법으로 진행되었다. Fig. 8은 예제 단면의 유한요소 모델이며, 심재 반영유무를 고려하여 심재가 포함된 모델과 포함되지 않은 모델을 각각 제작하였다. 심재가 없는 모델은 2125개의 8절점 사각형요소와 7063개의 절점, 심재가 있는 모델은 3696개의 8절점 사각형요소와 11572개의 절점으로 이루어져 있다.
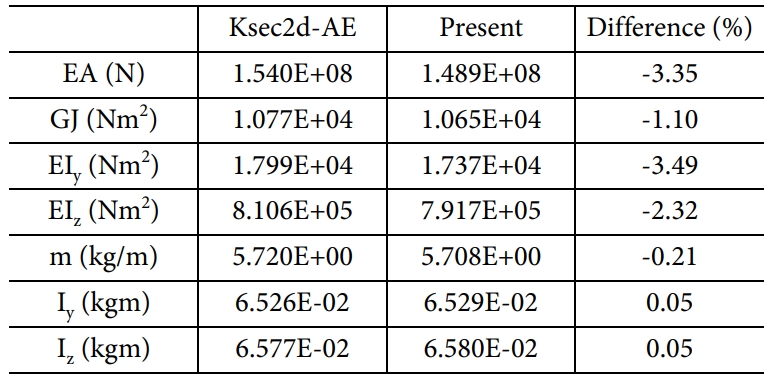
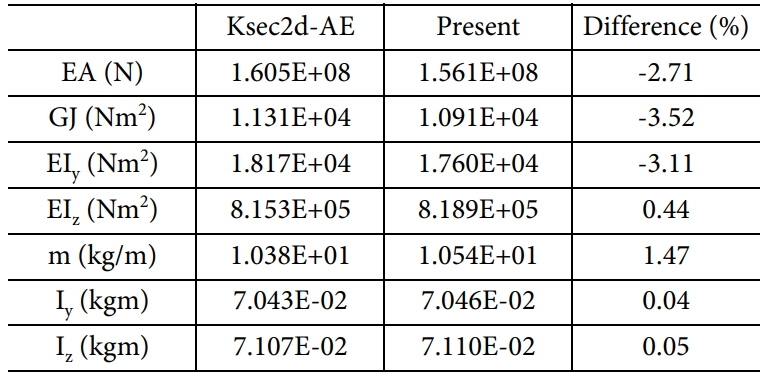
Table 3과 4는 각각 심재가 미 포함 및 포함된 단면에 대한 해석결과를 비교한 것이다. 강성 비교는 축강성(EA), 비틀림강성(GJ), 그리고 굽힙강성(EI_y, EI_z)에 대해 진행하였고, 관성치는 블레이드의 단위길이당 질량(m), 그리고 y축과 z축에 대한 관성모멘트(I_y, I_z)를 비교하였다. 상대오차는 Ksec2d-AE의 결과를 기준값으로 설정하여 계산하였다. 심재가 미 포함된 경우 해석코드 간 최대오차가 약 3.49%, 심재가 포함된 경우, 두 해석 코드 간 최대오차가 약 3.52%임을 확인하여, 본 연구에서 개발된 해석코드의 유효성을 확인할 수 있었다.
3.2 블레이드 구조 최적설계
블레이드의 구조 최적설계를 위해 60개의 인구수를 적용하였다. 최대 인구수는 50,000, 목적함수의 최대 계산횟수는 100,000회로 설정되었다. 수렴 시 각 인구의 목적함수값의 차이가 1×10^-4 이내로 수렴할 경우 또는 최적해가 반복된 세대가 30세대 이상이 될 경우, 계산이 종료되도록 하였다. 블레이드의 익근에 위치한 실린더형 단면을 포함하여 총 19개의 단면을 블레이드 구조 최적 설계에 투입하였다.
최적설계 결과 블레이드의 질량은 기준형상 대비 약 52%가 감소된 79 kg을 기록하였다. I_R의 경우 약 439 kgm²을 기록하여, 식 (19)의 경계값을 만족하였다.
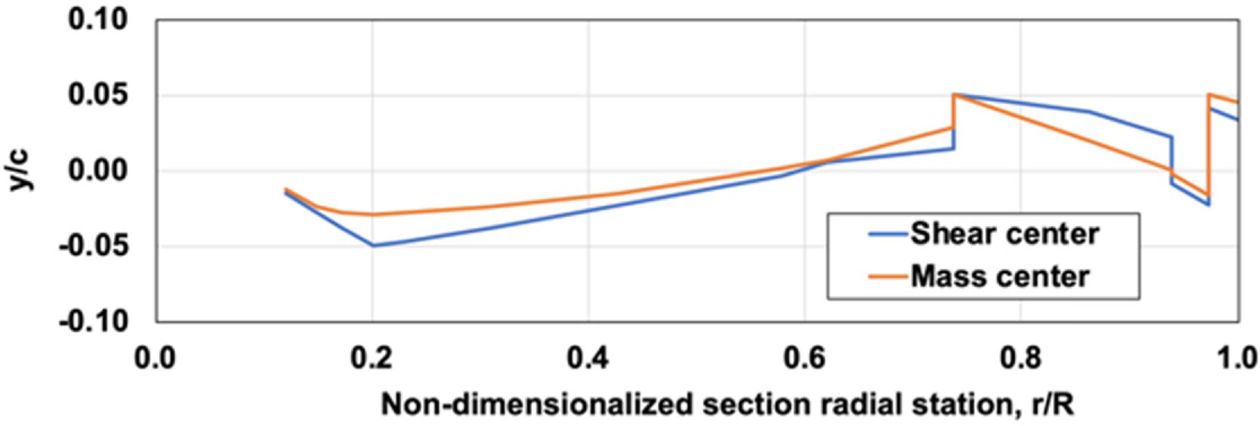
Fig. 9는 블레이드 단면의 전단중심과 질량중심의 위치를 공력중심 기준으로 나타낸 것이다. 에어포일 영역의 모든 단면에서 주요 중심치 구속조건을 모두 만족하는 것을 확인할 수 있다.
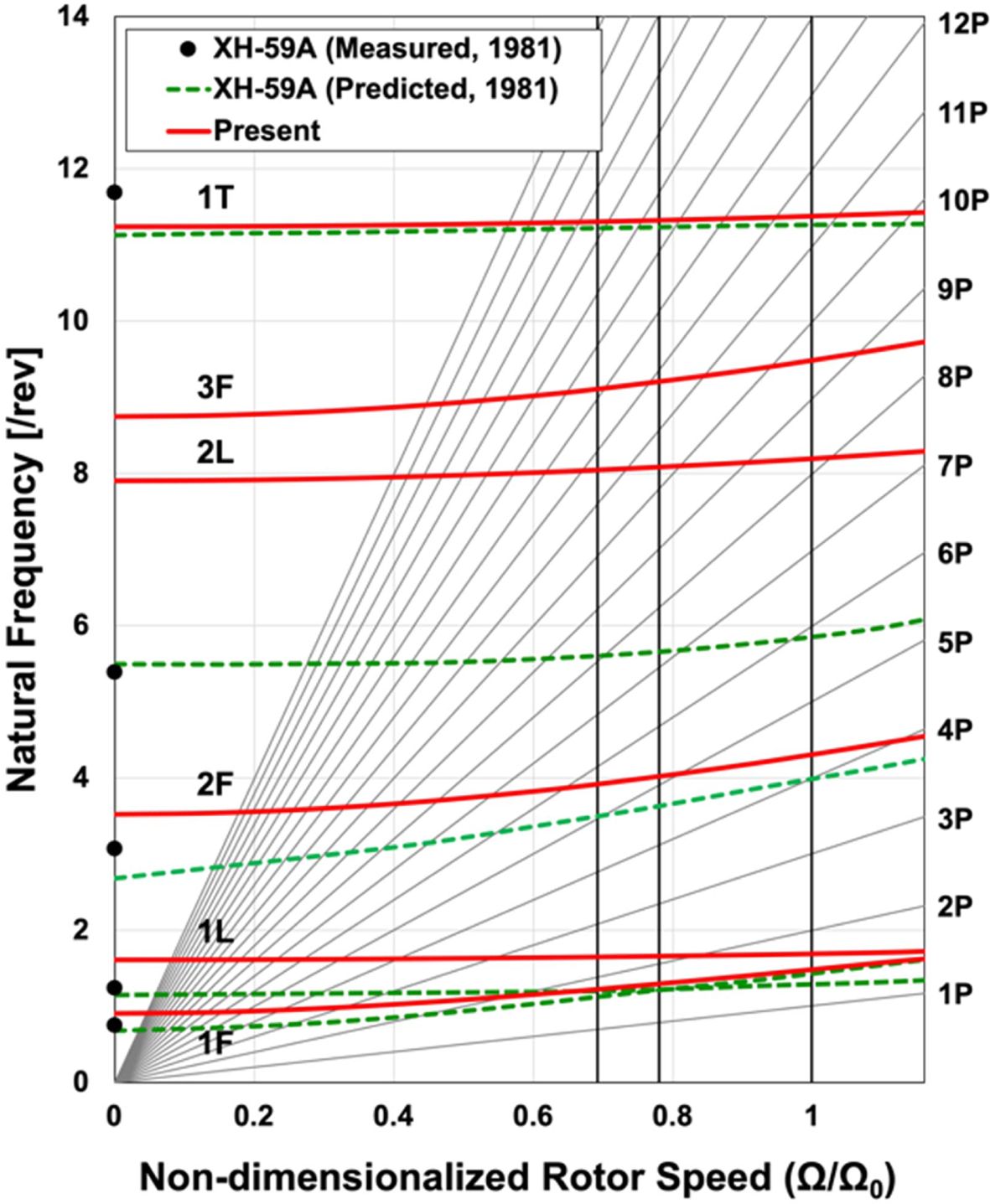
Fig. 10은 로터 회전속도에 따른 고유진동수의 분포를 나타내고 있다. 로터의 주 운용 회전수에서 공진회피 구속조건을 만족하였다.
19개의 단면을 최적화하는 동안 소요된 시간은 약 3919초(약 1시간 5분)이며, 본 연구에서 개발된 블레이드 최적 구조설계 프레임워크의 효율성을 확인하였다.

본 연구에서는 블레이드의 고효율 최적 구조 설계를 위해 Bézier 곡선과 중심선 기반 단면해석법을 결합한 단면 해석 기법을 개발하였으며, 이를 활용한 블레이드 최적구조설계 프레임워크를 구축하여 기존 블레이드에 대한 최적 구조 설계를 수행하였다.
Bézier 곡선을 적용한 결과, 본 연구에서 다룬 에어포일들을 6차 및 10차의 Bézier 곡선을 이용하여 표현하였다. 임의의 고형단면에 대한 단면해석 결과 기존 2차원 유한요소기반 단면해석법 대비 최대 3.5%의 오차를 기록하였다. 이를 통해 제안된 단면해석기법의 유효성을 확인하였다. 최적 블레이드의 질량은 약 79 kg으로, 기존 XH-59A 기체의 블레이드 질량 대비 52% 감소된 결과를 얻었다. 최적설계 결과 설정한 구속조건들을 모두 만족하였으며, 19개의 단면들을 최적화하는데 총 1시간 정도가 소요되었다. 이를 통해, 본 연구에서 제안한 최적설계 프레임워크가 매우 효율적임을 확인하였다. 

본 연구는 국방과학연구소의 지원으로 차세대 고속 복합형 무인 회전익기 특화연구실에서 수행되었습니다. 이 성과는 2018년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(2018R1A4A1024191).