- Design of Composite Laminates Using Enumeration Method
Chanwoo Joung*, Il-Joon Bae**, Young-Bin Park*†
* Department of Mechanical Engineering, Ulsan National Institute of Science and Technology
** Materials and Processing Research Lab, Research Institute of Science and Technology (RIST)- 나열법을 이용한 복합재 적층판 설계
정찬우* · 배일준** · 박영빈*†
Fiber-reinforced composite laminates have high
specific stiffness and strength and are expected to be useful for weight
reduction in weight-sensitive industries, such as automotive and aerospace.
However, designing composite laminates is often dependent on designer’s experience
and intuition because of difficulties in determining the number of plies and
stacking sequence, which tends to lead to over-design. In this study, optimal
design of composite laminates was performed to minimize weight, while withstanding
the given load. Based on the enumeration method, all combinations of stacking
sequence satisfying the design guideline for composite laminates were
considered. Composite laminates were discretized into panels. Optimal number of
plies and stacking sequence for each panel were determined considering local
load on each panel and contiguity across adjacent panels. Failure index from
Tsai-Wu criteria was optimized for strength and buckling analysis was performed
for compressive load. Stacking angles of 0, ±45 and 90° were used.
섬유강화 복합재 적층판은 높은 비강성과 비강도를 가지고 있으며, 자동차
및 항공과 같은 무게에 민감한 산업에서 경량화에 유용할 것으로 기대되고 있다. 하지만 복합재 적층판의
설계는 적층 개수와 적층 순서를 모두 결정해야 하는 어려움으로 인해 설계자의 축적된 경험과 직관에 의존하는 경우가 많고, 이는 필요 이상으로 제품의 중량이 증가하는 과설계로 이어질 수 있다. 본
연구에서는 주어진 하중을 견디고 최소 무게를 갖는 복합재 적층판의 최적설계를 수행하였다. 나열법을 기반으로, 복합재 적층판의 설계 지침을 만족하는 모든 경우의 적층 조합을 고려하였다. 복합재
적층판을 여러 개의 패널로 나누고, 각 패널의 응력 분포와 인접한 패널 간 연결성을 고려하여 최적의
적층 수와 적층 순서를 결정하였다. 강도를 고려하기 위해
Tsai-Wu 파손 이론으로부터 파손 지수를 최적화하였고, 압축 하중에 대해서는 좌굴 해석을
수행하였다. 적층각은 일반적으로 사용하고 있는 0, ±45, 90°를 사용하였다.
Keywords: 복합재 적층판(Composite laminate), 최적 설계(Optimal design), 나열법(Enumeration method), 설계 지침(Design guideline)
자동차 및 항공과 같이 중량에 민감한 산업에서 경량화에 대한 노력이 점점 증가하는 가운데, 섬유강화 복합재에 대한 수요가 점차 증가하고
있다. 높은 비강성과 비강도를 갖는 섬유강화 복합재는 제품의 중량을 줄임과 동시에 요구되는 기계적 물성을 만족시키기에 유용하다. 이때 섬유강화
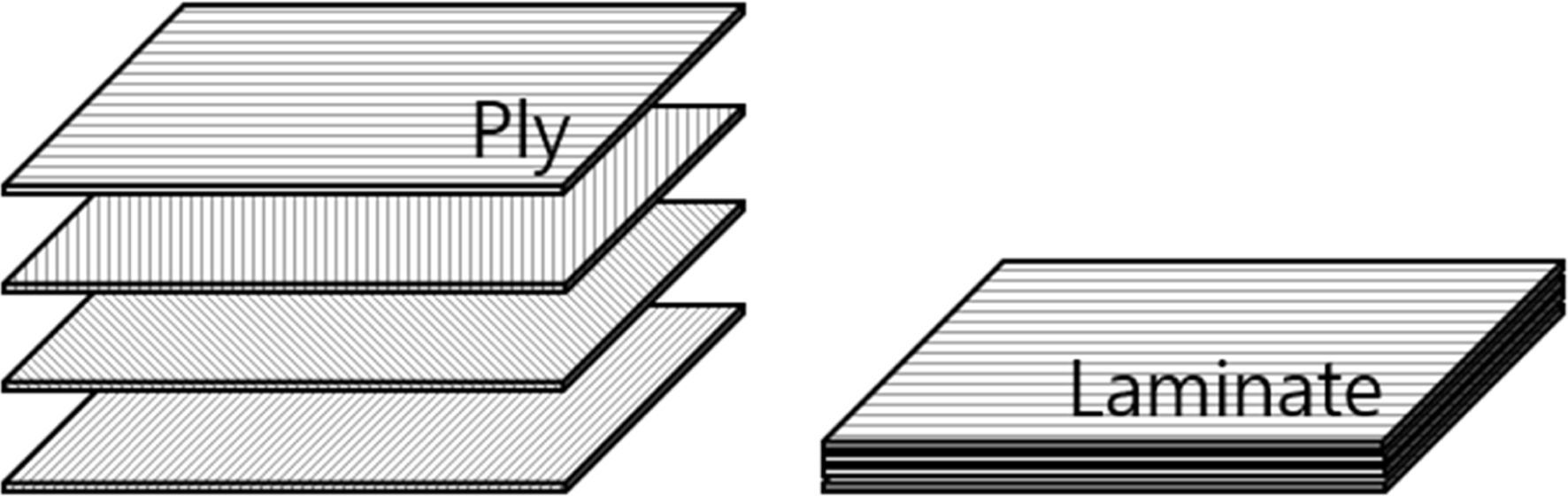
복합재는 Fig. 1과 같이 단방향 섬유강화복합재가 플라이(ply)를 구성하고 이러한 플라이가 층층이 쌓인 적층판(laminate)의
형태로써 주로 이용된다.
하지만 이러한 복합재 적층판의 설계는 적층 개수, 적층각, 적층 순서와 같은 많은 설계 변수들을 모두 결정해야 하는 어려움을 가지고 있기 때문에, 설계자는 자신의 축적된 경험에 의존하여 설계 변수를 줄이고 단순화하여 설계하고자 많은 노력을 해왔다.
Chung[1]와 Hwang[2]은 비행기 날개의 설계에서 적층각과 적층 순서를 미리 정하고 주어진 하중을 견딜 수 있는 적층 두께를 결정하였다.
Lee[3], Je[4]와 Kim[5]은 각 복합재료 제품에 대해 여러 가지 적층각과 적층 순서들을 미리 정하고 유한 요소 해석을 통해 주어진
하중을 견딜 수 있는 최적의 적층 구조와 적층 개수를 결정하였다. Kim[6]은 블레이드 설계에서 적층 구조를 [02/902/±θ]s와 같이 정하고 블레이드
tip의 변형을 최소화하는 적층각 θ를 구하였다. Kong[7]은 소형 위그선의 주익 구조 설계에서 하중을 견딜 수 있는 0° 플라이의 개수를 먼저 계산한 뒤, ±45, 90° 플라이를 보완하고 유한
요소 해석을 통해 구조 안정성을 평가하였다. Kim[8]과 Park[9]은 복합재 제조 공정과 구조적 안정성을 고려하여 미리 적층 구조를 정한
후 유한 요소 해석을 통해 구조 안정성을 평가하였다.
하지만 복합재 적층판의 주된 설계 목적이 경량화일 때, 위와 같은 방법은 제품의 중량이 필요 이상으로 증가하게 되는 과설계의 원인이
될 수 있다. 과설계를 방지하고, 주어진 하중을 견디면서 최소 무게를 갖는 복합재 적층판을 설계하기 위해서 유전 알고리즘과 설계 민감도 해석
등과 같은 최적화 기법들이 연구되어왔다[10]. 한편, Kim[11]은 이산화된 적층각 0, ±45, 90°을 가지고 적층판의 설계 지침과 변형률 요구 조건을
모두 만족하는 적층 구조를 최소 층수부터 한 층씩 더해가며 모두 나열하였다. 이 중에서 가장 낮은 변형률을 갖는, 즉 최대강성을 갖는 최적의 적층
구조를 결정하였다.
본 논문에서는 [11]과 같이
나열법(enumeration method)을 기반으로 복합재 적층판의 최적 설계를 수행하였다. 중량 최소화를 설계 목적으로, 적층 개수와 적층
순서를 설계 변수로, 파손 지수, 좌굴 하중 계수 및 설계 지침들을 설계 제한 조건으로 설정하였다. 복합재 적층판의 중량을 더 줄이기 위해, 복합재료
적층판을 여러 개의 패널로 나누어 응력 분포가 낮은 곳의 적층 개수를 줄였다. 동시에 편집 거리(edit distance) 알고리즘을 기반으로
패널 간 적층 순서의 유사도가 가장 높도록 최적화를 수행함으로써 패널간 두께 변화에 따른 제조 가능성의 어려움을 해소하고자 하였다.
|
Fig. 1 Composite laminate formed by stacking plies |
2.1 고전 적층판 이론
두께가 얇은 적층판에 대하여 평면 응력 상태(plane stress state)를 가정하고, 고전 적층판 이론(classical
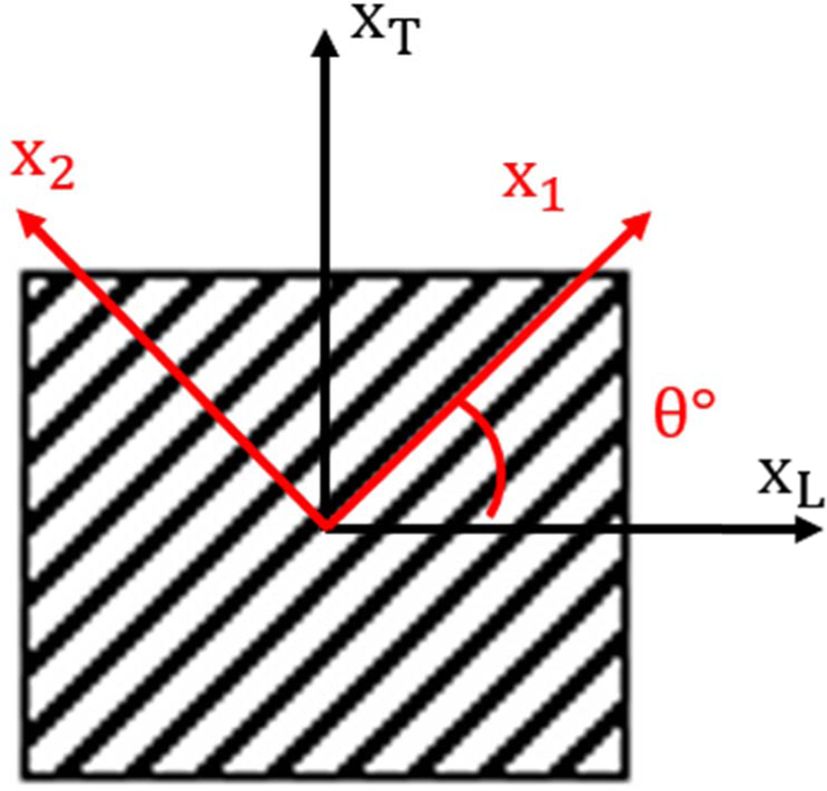
laminate theory)을 바탕으로 복합재 적층판의 구조해석을 수행하였다[12]. Fig. 2에서 기준 좌표계(reference
coordinate system or laminate axis)에 대하여 적층각 θ를 갖는 플라이는 방향코사인 ![]() 을 이용하여 다음의 강성
을 이용하여 다음의 강성 ![]() 를 갖는다.
를 갖는다.

각 플라이에 작용하는 응력 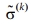 은 다음 식으로 구할 수 있다.
은 다음 식으로 구할 수 있다.

위 식에서 ε0 z k0 은 각각 변형률, 적층판 중간 평면으로부터의 위치, 곡률을 의미한다. 식 (4)로부터
합력을 이용하여 다음과 같은 구성 방정식을 표현할 수 있다.

위 식에서 N, M은 면내 응력과 모멘트, A는 인장강성, B는 커플링강성, D는 굽힘강성이며 다음과 같이 정의된다.
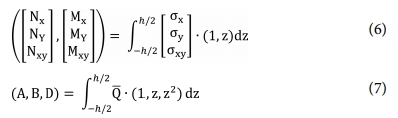
위 식에서 h는 적층판의 두께를 의미한다.
2.2 Tsai-Wu 파손 이론
Tsai-Wu 파손 기준을 이용하여 복합재 적층판의 파손 여부를 평가하였다. 평면 응력 상태(σ33 = τ23 = τ13 = 0)에 대한 2차원 Tsai-Wu 파손 식은 아래와 같다.
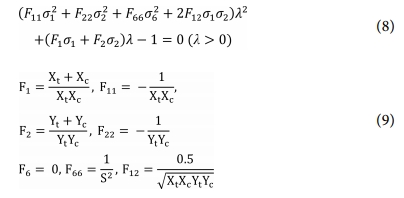
위 식에서 Xt, Xc, Yt, Yc, S는 섬유 방향의 인장강도, 압축강도, 섬유에 수직한 방향의 인장강도, 압축강도 그리고 전단 강도를 의미한다. (8)로부터 구해진 파손
지수 l에 대하여 l≤1은 파손이 발생했음을 의미한다.
2.3 좌굴 해석
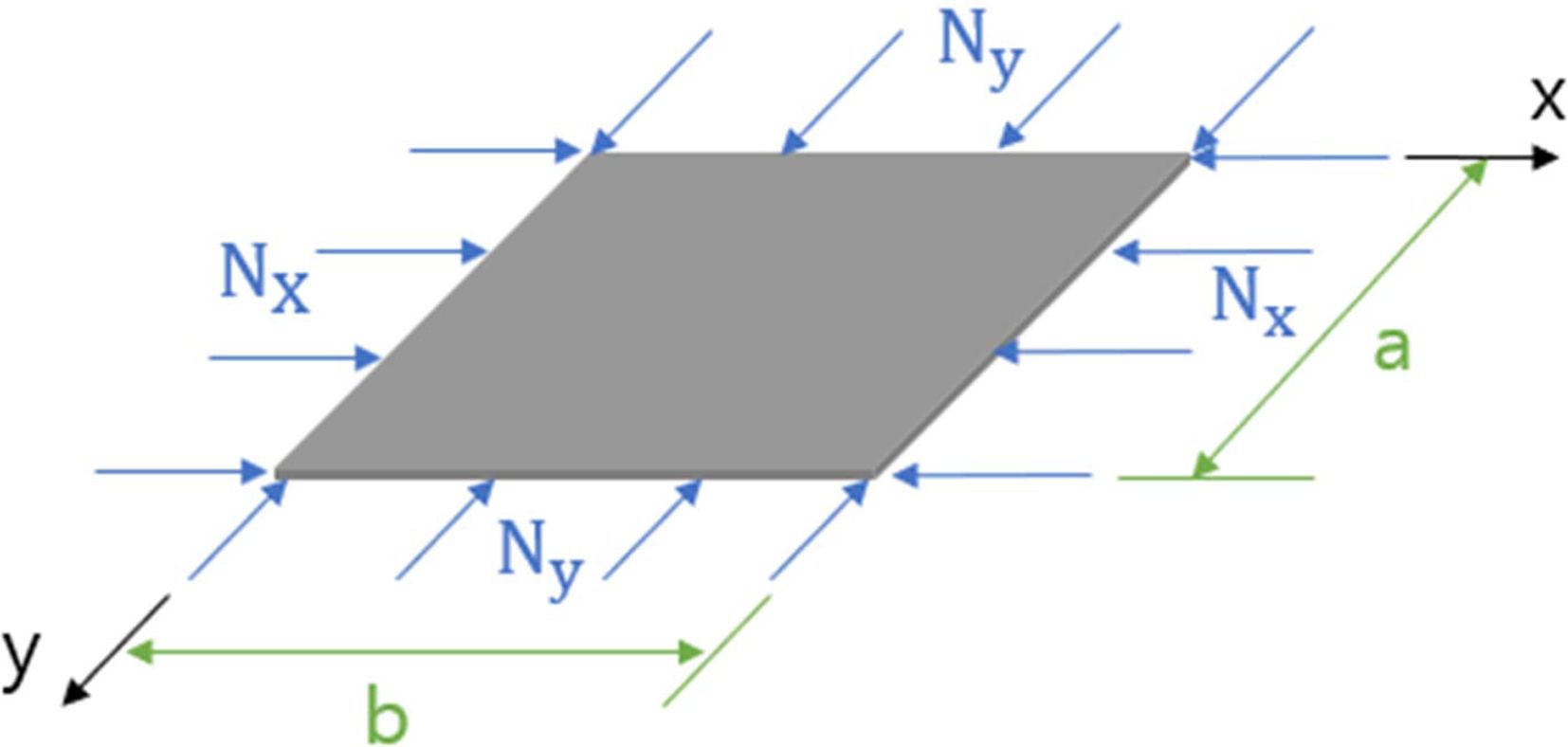
압축 하중이 가해질 때, 복합재 적층판의 좌굴에 의한 파손 여부를 평가하기 위해 좌굴 해석을 수행하였다. Fig. 3과 같이 길이 a, b를 갖고 4개의 모서리가 단순 지지된(simply supported) 적층판에
압축 하중 Nx, Ny이 가해질 때, x방향으로의
m개의 반파장(half-wave) 그리고 y방향으로의 n개의 반파장을 갖는 좌굴 모드(buckling mode)에 대한 식은 아래와 같다[12].
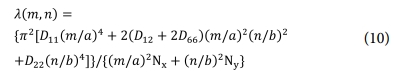
위 식에서 Dij는 (7)에서 구한 굽힘
강성이다. (10)로부터 구한 좌굴 하중 계수 l에 대하여 l≤1은 좌굴에 의한 파손이 발생했음을 의미한다. 본 논문에서는 m, n 값을 각각 1~10까지 적용하여 총 100가지 경우에 대해 l 값들을 계산 후 그 중에 최솟값을 사용하였다. x 방향으로(y 방향으로만)만 압축 하중이 가해지는
경우에는 (10)에서 Ny = 0, n = 1(Nx = 0, m = 1)을 적용하여 좌굴 하중 계수를 구하였다.
2.4 편집 거리(edit
distance) 알고리즘
패널 간 적층 순서의 유사도를 평가하기 위해 동적 프로그래밍을 이용한 편집 거리 알고리즘을 적용하였다[13]. 본래 편집 거리 알고리즘은
두 문자열의 유사도를 판단하는 알고리즘이다. 한 문자열이 다른 문자열이 되기 위해 문자를 삽입, 삭제, 변경하는 최소 횟수가 편집 거리가 된다.
예를 들어, 문자열 abcde가 bbdef가 되기 위해서 a를 b로 변경하고, c를 삭제하고, 마지막에 f를 삽입하면 되므로 편집거리는 3이 된다.
본 논문에서는 적층 순서와 적층각을 각각 문자열과 문자로 보고 패널 간 적층 순서의 유사도를 평가했고, 전체 패널에 대한 유사도를 구하는 식은
아래와 같이 정의하였다.
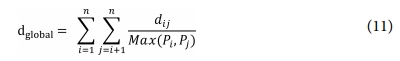
위 식에서 n은 패널의 개수, dij는 i번째 패널의 적층
순서와 j번째 패널의 적층 순서의 편집 거리, Max(Pi,
Pj)는 i번째 패널의 적층 개수 Pi와 j번째 패널의 적층 개수 Pj 중 큰 값을 의미한다.
dglobal이 작을수록 패널 간 적층 순서의 유사도가 높음을 의미한다.
2.5 복합재 적층판의 설계 지침
복합재 적층판의 설계 시 중요하게 고려되는 설계지침들이 존재한다[14]. 아래의 설계 지침들은 복합재 적층판의 최적 설계에 관한 많은
문헌에서 고려되었으며, 본 논문에서도 또한 고려되었다.
1. Symmetry: 평면 하중과 굽힘 하중의 연계 및 열부하에 의한 뒤틀림을 방지하기 위해 적층
순서는 적층판의 중립 축에 대해서 대칭이여야 한다(커플링 강성 B = 0).
2. Balance: 인장과 전단 하중의 연계를 방지하기 위해 적층판은 0와 90°를 제외한 θ 플라이 개수에 대해 같은 개수의 -θ 플라이를 가짐으로써 중립
축에 대해 균형이여야 한다(인장강성 A에서 A16 = A26 = 0).
3. 10% rule: 하중이 가해질 때 모재 방향으로 취약한 점을 보완하기 위해 0, ±45,
90° 방향으로 최소한 10% 적층 비율을 갖도록 적층 순서를 정해야 한다.
4. Contiguity: 적층판의 강도를 증가시키고, 모재 균열과 층간 분리를 방지하기 위해 동일한 적층각으로 연달아 4장 이상(자유 경계단의 경우 3장 이상) 적층하지 않아야 한다. 본 논문에서는 동일한 적층각으로
3장 이상 적층하지 않는 것으로 통일하였다.
5. Disorientation: 섬유 파손 혹은 층간 분리를 방지하기 위하여 인접층 사이에서 적층각의
차이는 45°를 초과하지 않아야 한다.
6. 가장자리에서 층간 분리가 일어나는 것을 방지하기 위해 최외각층은 복합재 적층판을 모두 덮어야
한다.
2.6 복합재 적층판의 최적 설계
과정
본 연구에서 수행한 복합재 적층판의 최적 설계는 총 3단계로 구성되어 있다(Fig. 4~6).
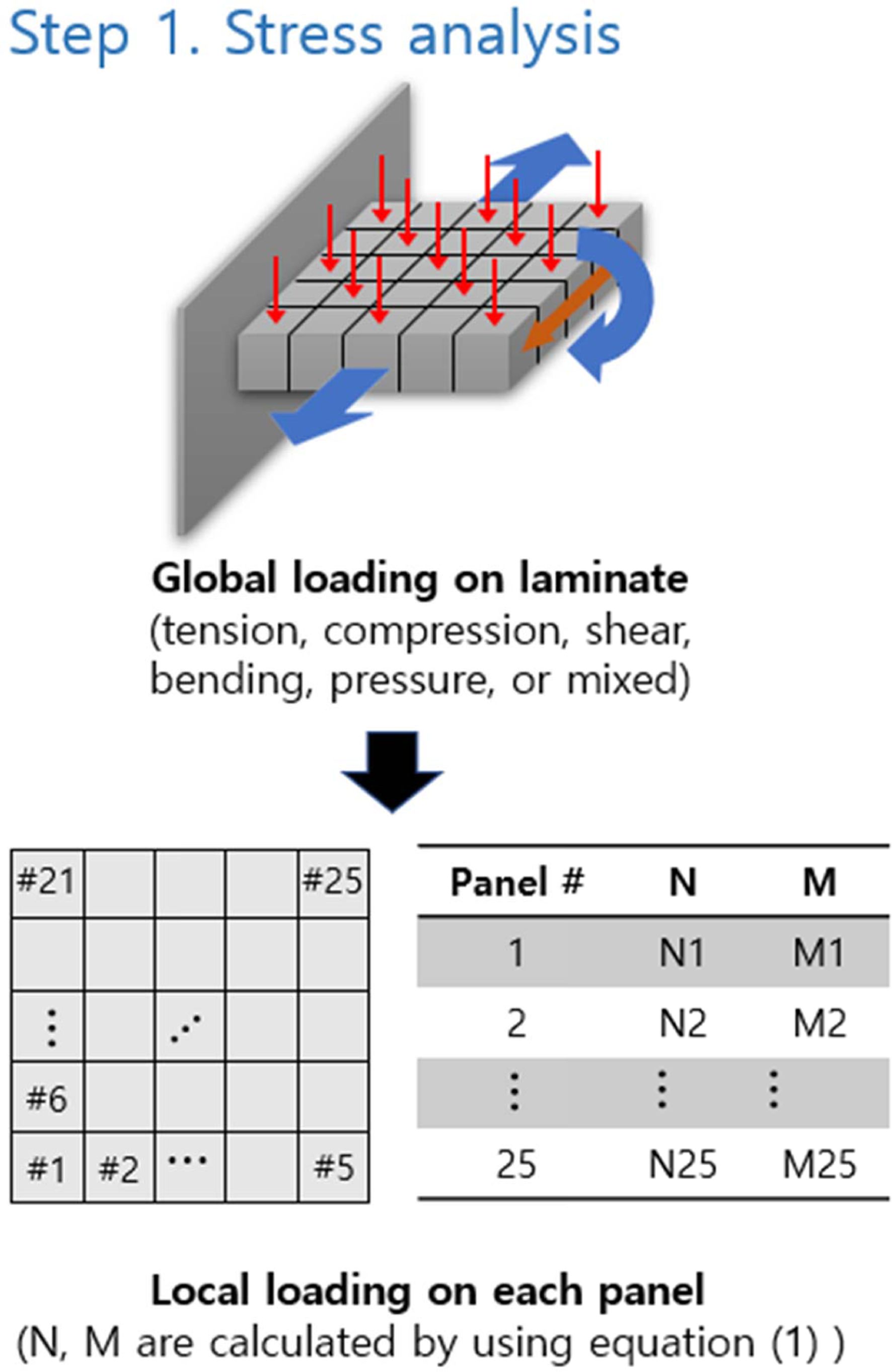
Step 1: Fig. 4에서, 복합재 적층판을 여러 개의 패널로 나누고, 구조해석을
통해 전체 하중(global loads)에 대한 각 패널의 국부 하중(local loads)을 구하였다. 사실 패널의 적층 구조가 바뀌어 강성이
변하게 되면 전체 패널에 작용하는 응력 분포가 달라지지만, [15]에 따르면 이는 적층 구조의 설계와 응력 분포 계산을 패널에 걸리는 국부 하중의
변화가 무시 가능할 때까지 반복함으로써 해결할 수 있다.
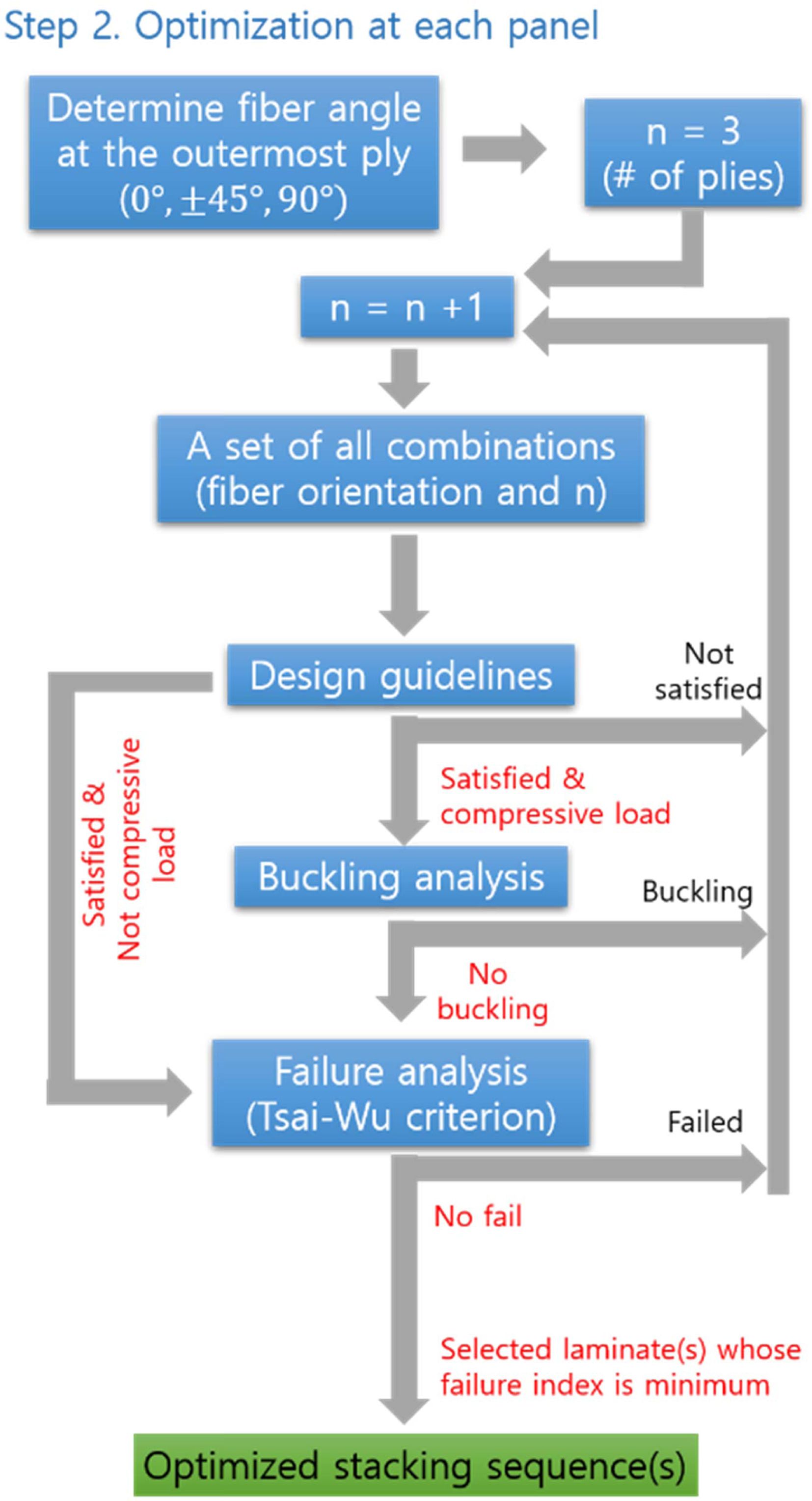
Step 2: Fig. 5에서, 각 패널에 대해 최적 설계를 수행하였다. 이때
적층각은 일반적으로 사용하고 있는 0, ±45, 90°를 사용하였다. 설계지침 6번을 만족하기 위해서 최외각층의 적층각을 미리 정하고, 설계지침
3번을 만족시킬 수 있는 최소한의 적층 개수 4장(대칭조건에 의하여 실제로는 8장)에서 최적화를 시작하였다.
적층각 4개와 적층 개수 4개로 만들 수 있는 모든 가능한 적층 순서에 대하여 설계 지침을 만족하고, Tsai-wu 파손 이론과 좌굴 해석을 기반으로
주어진 하중에 대해 파손되지 않는 적층 순서들을 정하였다. 강도를 고려하여 이 중 파손 지수가 가장 낮은 적층 순서들을 최적의 적층 순서로 정하였다.
만약 적층 개수 4장에서 설계 제한 조건들을 만족할 수 없는 경우, 적층 개수를 1장씩 늘려가면서(대칭조건에 의하여 실제로는 2장) 위의 과정을
반복하였다. 결과적으로 각 패널에 대해 주어진 하중을 견딤과 동시에 최소의 적층 개수를(혹은 무게) 갖는 적층 순서를 얻을 수 있었다.
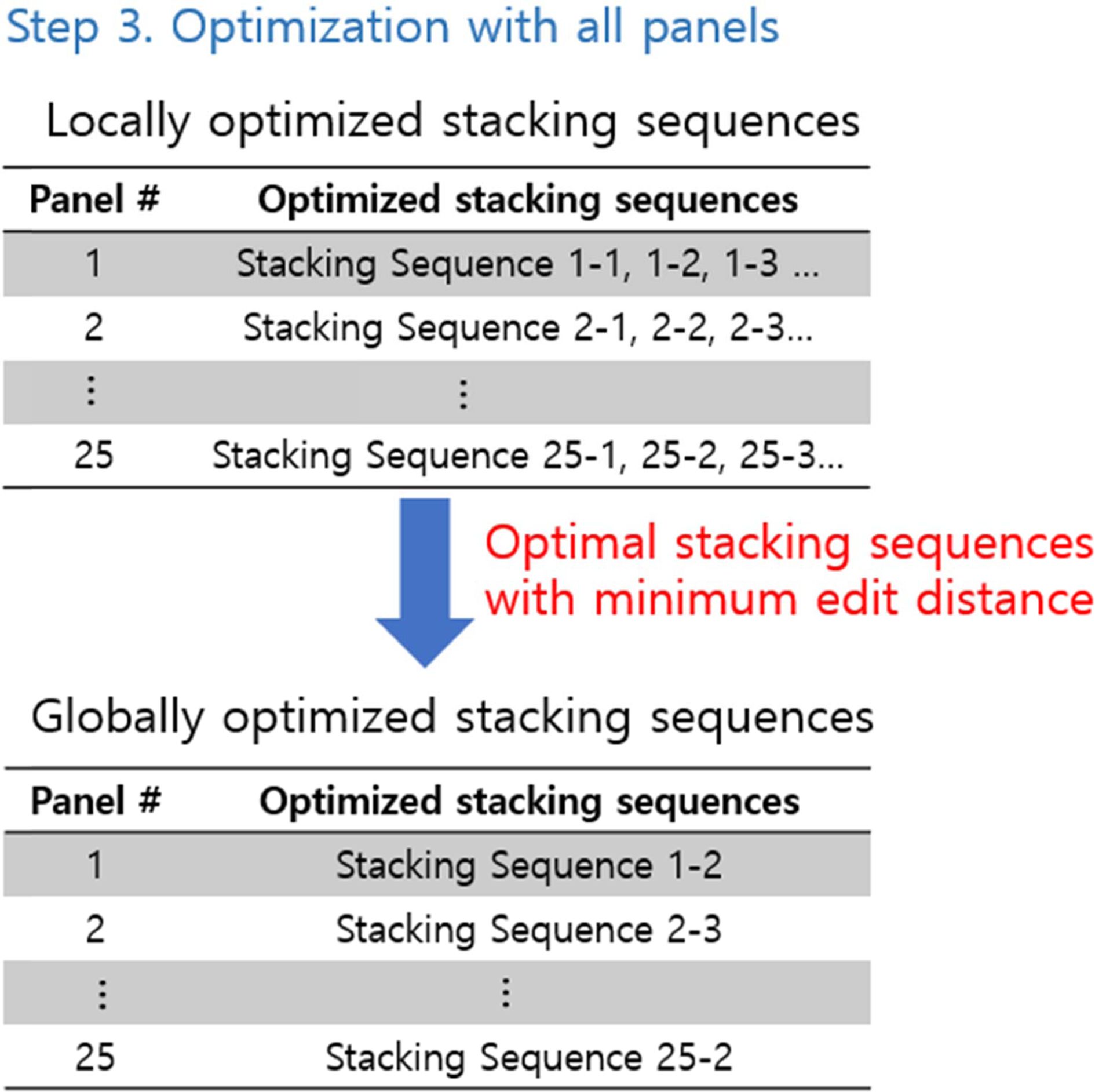
Step 3: Fig. 6에서, 2번에서 최적해가 2개 이상인 패널이 존재하는
경우, (11)을 이용하여 전체 패널 간 적층 순서의 유사도가 가장 높은 적층 순서들의 조합을 구하였다. 최외각층의 적층각이 0, ±45,
90°인 4가지 경우에 대해 1~3번의 과정을 수행하고, 이 중 가장 가볍고 유사도가 높은 해를 선정하였다.
2.7 최적 설계 시 추가 고려
사항
본 논문에서 나열법과 설계 지침을 바탕으로 최적화를 수행할 때 추가로 고려할 사항과 제한점들을 아래에 정리하였다.
1) 설계지침 1번을 만족하지 않아 커플링 강성 Bij가 0이 아닌 경우에도 최적화를 수행할 수 있다.
2) 하중의 종류와 구속조건의 종류에 상관 없이 복합재 적층판 내 응력 분포를 구할 수 있는 경우에는
최적화를 수행할 수 있다. 다만 적층판의 두께방향으로의 파손을 무시할 수 없는 경우(특히 면외 하중 또는 충격 하중), 두께방향으로 파손을 고려하는 이론을 설계 제한
조건에 추가해야 한다.
3) 두꺼운 복합재 적층판에 대하여 최적화를 수행하는 경우, 평면 응력 상태를 가정할 수 없으므로
최적화 과정에서 필요한 구조 해석, Tsai-wu 파손이론, 좌굴 해석을 3차원으로 확장하여야 한다.
4) 복합재 적층판이 샌드위치 패널의 면재로 사용되는 경우 코어와 분리하여 면재에 작용하는 응력 분포를
따로 구할 수 있는 경우에만 최적화를 수행할 수 있다.
|
Fig. 2 Fiber angle definition (XT, XL ; reference coodinate system) |
|
Fig. 3 Buckling of rectangular laminate (4 edges are simply
supported) |
|
Fig. 4 Step 1 of optimization process of composite laminate |
|
Fig. 5 Step 2 of optimization process of composite laminate |
|
Fig. 6 Step 3 of optimization process of composite laminate |
설계에 사용된 탄소섬유강화 복합재 UD/carbon epoxy의 물성은 Table 1에 정리하였다[16]. Fig. 7에서 응력 분포를 고려하기 위해 50 cm * 50 cm 크기의 복합재 적층판을
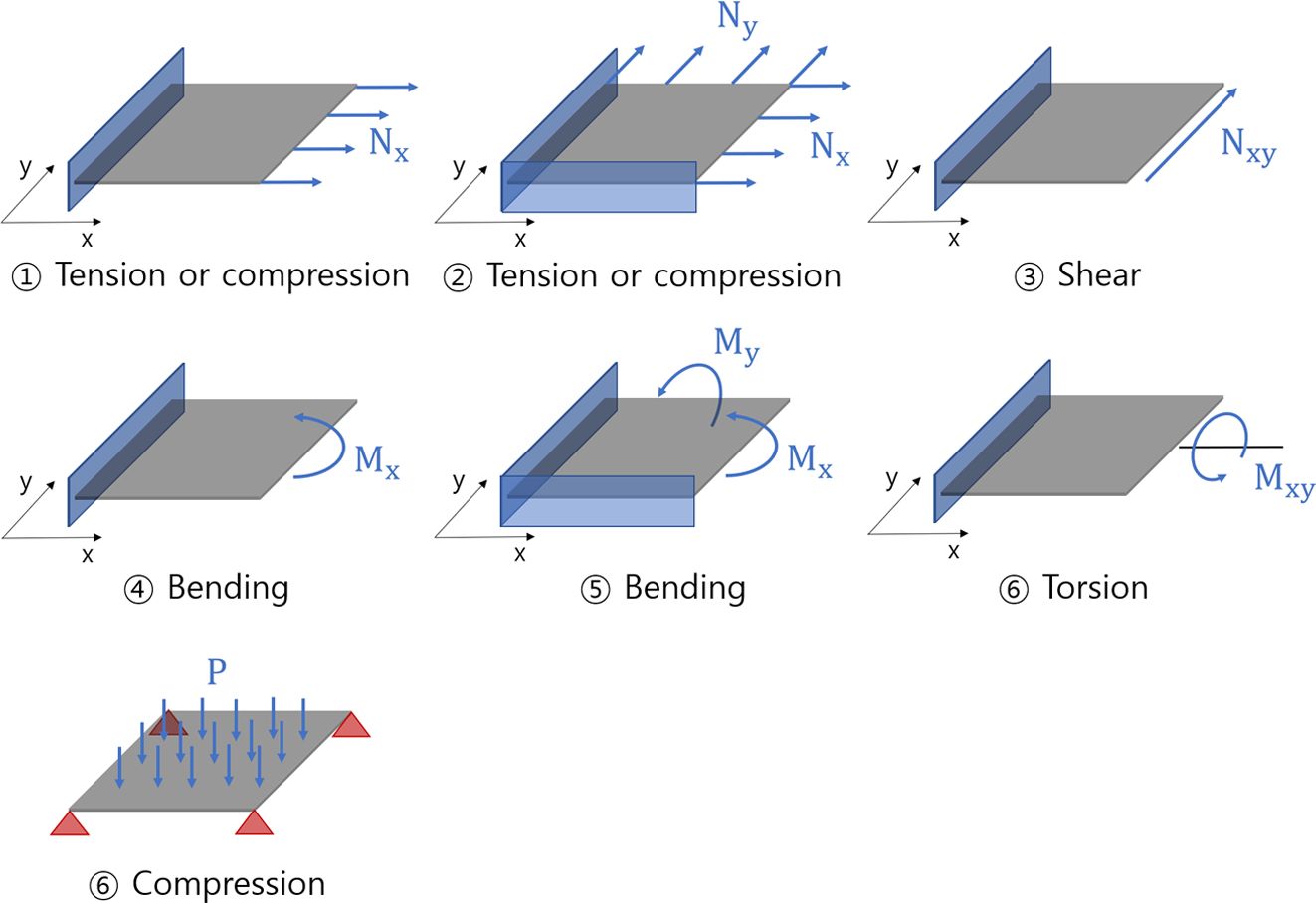
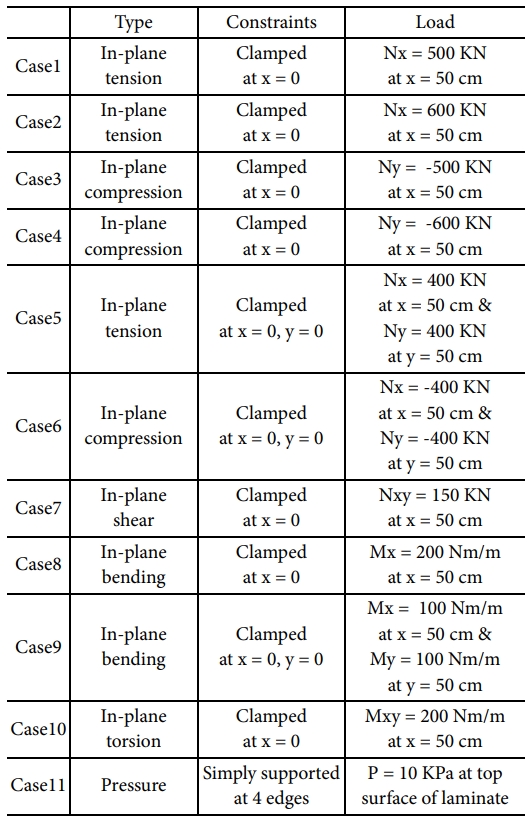
25개의 정사각형 패널로 나누었다. Fig. 8에서 임의의 하중 조건에 대해 최적 설계가 가능한지
확인하기 위해서 면내 인장, 압축, 전단, 굽힘, 비틀림 하중 그리고 면외 압축 하중에 대해 최적 설계를 수행하였다. 하중 및 구속 조건은
Table 2에 정리하였다.
3.1 면내 인장 및 압축 하중
Case 1에 대하여, 유한요소법을 기반으로 각 패널에 작용하는 응력 분포를 구하고 (5)를 이용하여 면내 응력 N과 모멘트 M을 계산하였다.
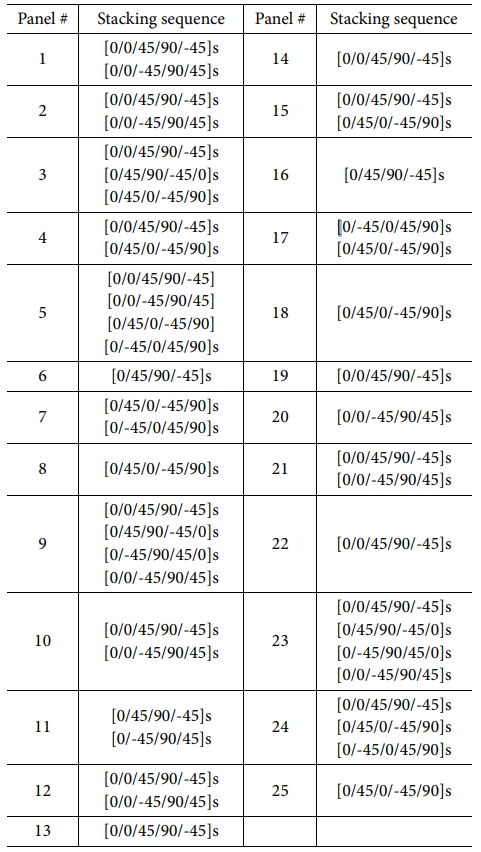
이때 응력 분포를 계산하기 위한 용도로 준등방성 적층판(quasi-isotropic laminate) [0/90/-45/45]s를 이용하였다.
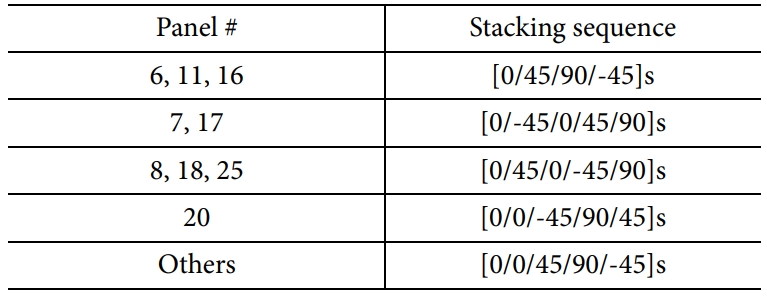
Step 2에서 최외각층의 적층각을 0°로 정하고 각 패널의 최적의 적층 개수와 적층 순서를 결정하였다(Table 3). Table 3에서 2개의
이상의 해가 존재하는 패널이 있으므로, step 3에서 전체 패널 간 적층 순서의 유사도가 가장 높은 적층 순서 조합을 결정하였다(Table
4). 다른 최외각층의 적층각에 대해서도 최적화를 수행하였다(Table 5). Table 5에서 적층판의 무게가 가장 가볍고 유사도가 높은 해(case 1의 경우, 최외각층의 적층각이 -45°거나 45°)를 최적해로 결정하였다. 적층판
내에 응력 분포를 고려하여 6, 11, 16번
패널의 적층 개수를 줄임으로써 기존 대비 중량이 2.4% 감소하였다.
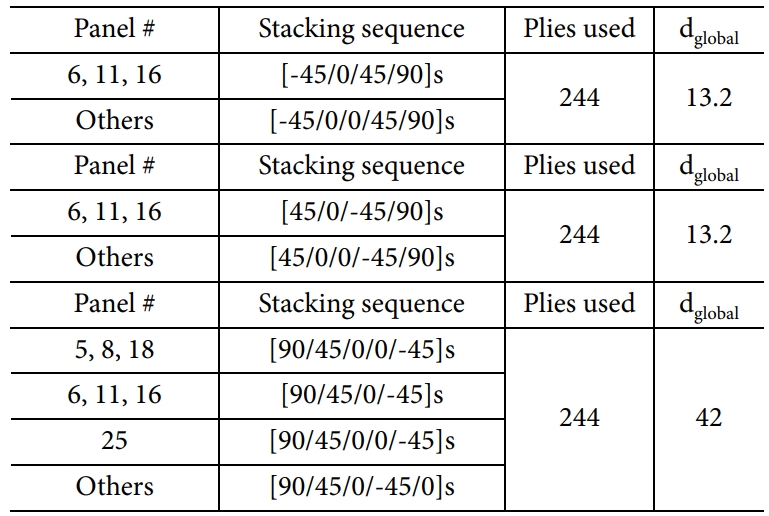
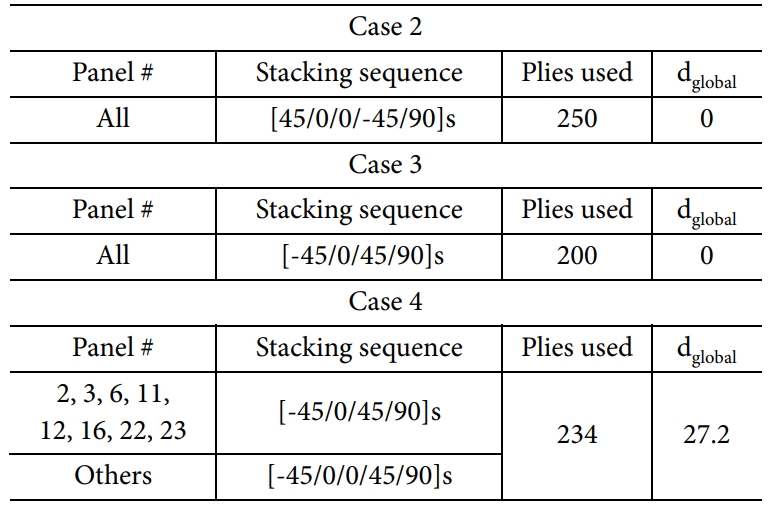
이어서 case 2, 3, 4에 대한 전역 최적해를 Table 6에 정리하였다. Case 2는 case 1과 비교하여 인장 하중 Nx가 500 KN에서 600 KN으로 증가하였다. 가장 두꺼운 패널의 적층 개수는 10장으로 동일하나, case 2의 경우 모든 패널이 같은 적층 순서 및 적층
개수를 가지므로 응력 분포를 고려하기 전과 비교하여 중량 감소의 효과는 없다. 이는 600 KN 인장 하중에 의해 발생하는 적층판 내 응력 분포의 차이가 패널 간
적층 개수를 조정할 수 있을 만큼 충분히 크지 않기 때문으로 보인다. Case 3, 4의 최적화 결과도 case 1, 2와 비슷한 양상을 보인다. 한편, case 4의 경우 기존 대비 중량이 6.4% 감소하였다.
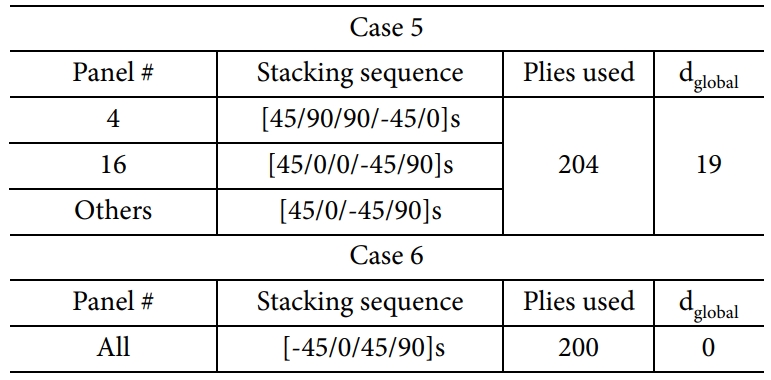
Case 5, 6에 대한 전역 최적해를 Table 7에 정리하였다. Case 1~4과 비교하여 고정된 모서리가 1개 더 증가하고, 가해지는 하중의 방향도 1개 더 증가하였으나 적층판 내 응력 분포만 구할 수 있다면 최적화를 수행할 수 있음을 알 수 있다. Case 5의 경우 기존 대비
중량이 18.4% 감소하였다.
3.2 다양한 하중 조건
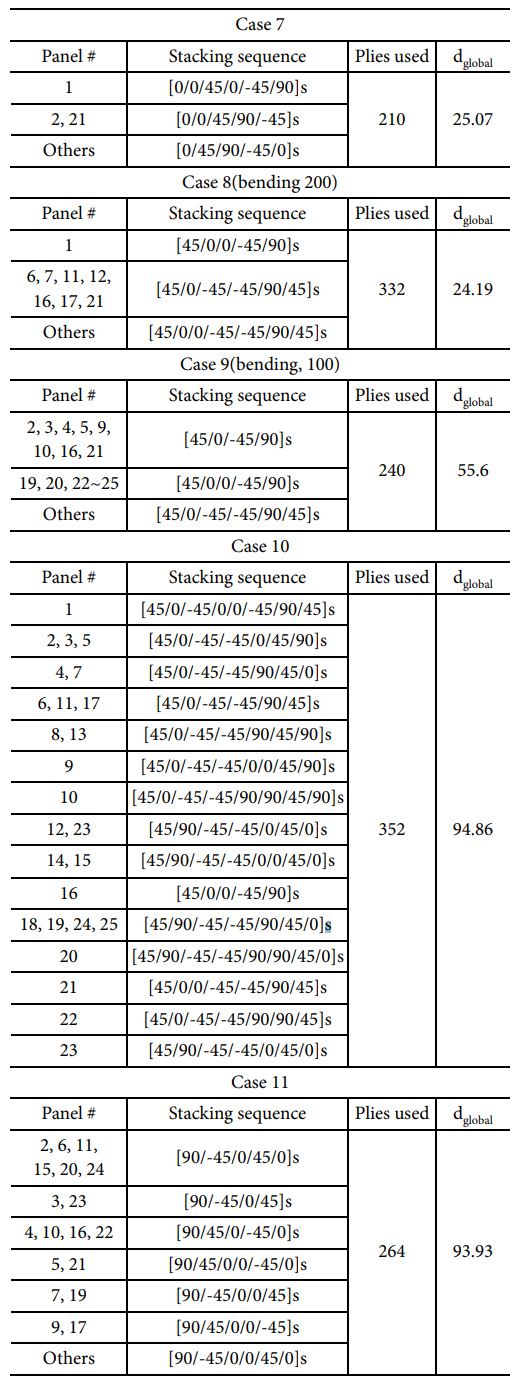
Fig. 8에서 전단, 굽힘, 비틀림 및 면외 압축 하중에 대한
최적화를 수행하였다(Table 8). Case 10과 11의 결과에서 패널 간 적층 순서가 많이 상이함을 알 수 있는데, 이는 비틀림과 면외 압축
하중에 의해 적층판 내에 응력 분포의 차이가 매우 크기 때문으로 보인다.
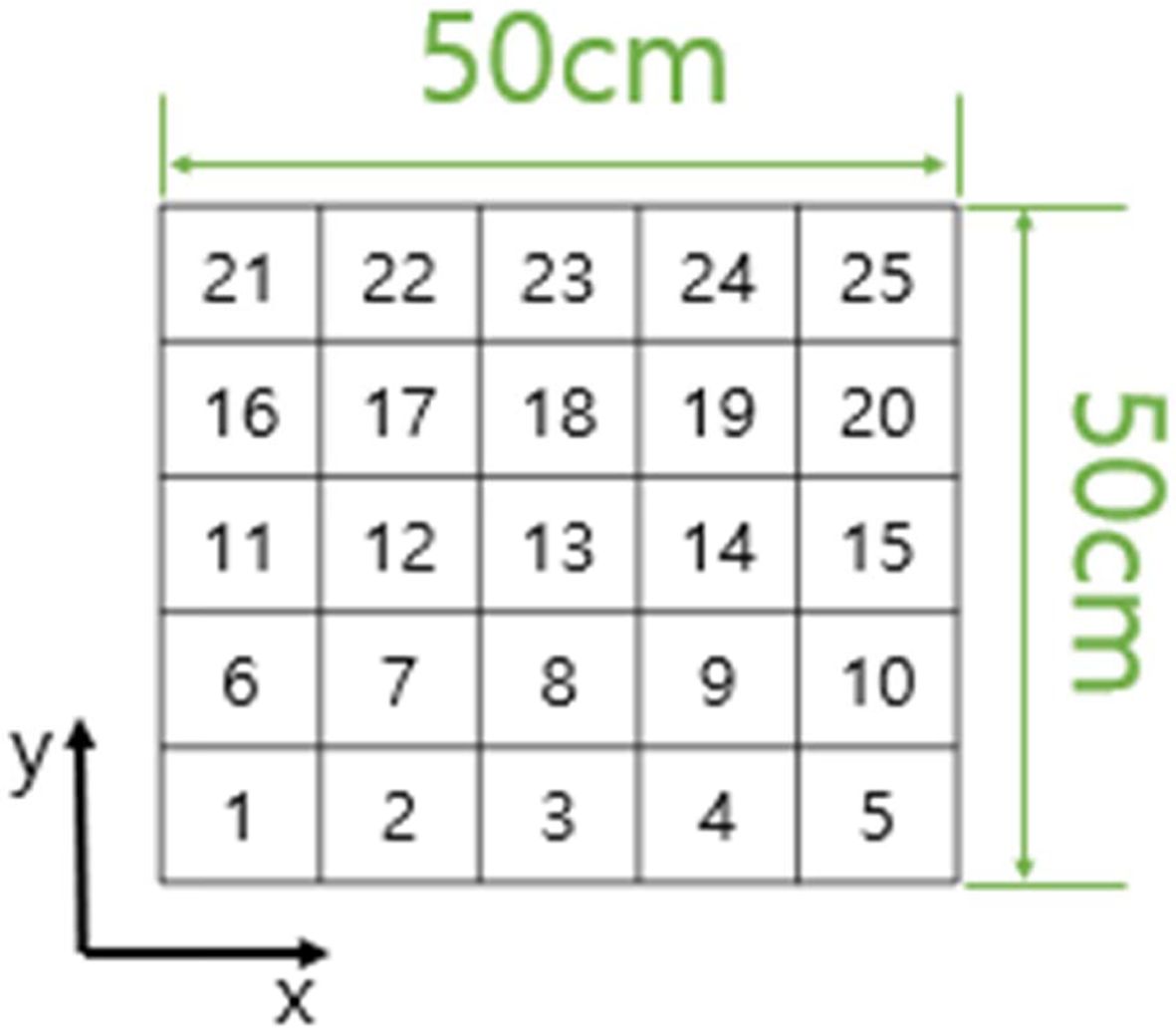
|
Fig. 7 Laminate size and panel numbering |
|
Fig. 8 Various load types and constraints |
|
Table 4 Global optimization results of case 1 with 0 degree at
the outermost layer (dglobal= 71.4, Plies used = 244) |
|
Table 5 Global optimization results of case 1 with ±45 and 90° at
the outermost layer |
본 연구에서는 나열법과 설계지침을 기반으로 적층각과 적층 순서의 조합 가능한 모든 경우에 대해, 복합재 적층판이 주어진 하중을 견딤과
동시에 최소 무게를 갖도록 하는 최적 설계를 수행하였다. 인장, 압축, 굽힘, 비틀림 등과 같은 다양한 하중 조건에 대해서 최적화를 수행하였으며,
이때 복합재 적층판을 여러 개의 패널로 나누어 응력 분포를 고려하고 낮은 응력 분포가 작용하는 패널의 적층 개수를 줄임으로써 무게 절감 효과를
얻을 수 있었다. 패널 간 적층 순서가 상이하여 발생하는 제조상의 어려움을 최소화하기 위해 편집 거리 알고리즘을 이용하여 패널 간 적층 순서의
유사도를 높였다. Case 1, 4, 5, 7, 8, 9의 최적화 결과와 같이 패널 간 적층 순서의 유사도가 비교적 높은 경우에는 automated tape laying 기술[17]을 이용하여
제작할 수 있을 것으로 보인다. 다만 case 10, 11의 최적화 결과와 같이 패널 간 적층 순서가 많이 상이한 경우, 유사도를 평가하는 dglobal가
일정 값을 넘어가지 않도록 제한하여 제조 가능한 적층 구조를 갖도록 최적화를 수행해야 할 것으로 사료된다.
본 연구는 산업통상자원부의 재원으로 한국산업기술진흥원을 통해 지원하는 국제공동기술개발사업(P007800016) 및 국가혁신클러스터사업(P0006669)으로
수행된 연구결과입니다.
- 1. Chung, T.E., and Yang, S.U., “Design of Lightweight Composite Main Wing and Aileron by the Panel Analysis,” Composites Re-search, Vol. 10, No. 3, 1997, pp. 109-118.
- 2. Hwang, C.H., and Joo, J.H., “Initial Design of Simplified Composite Wing Box Structure,” Composites Research, Vol. 10, No. 4, 1997, pp. 11-17.
- 3. Lee, J.A., Hong, H.T., Kang, K.T., and Chun, H.J., “Design of Composite Laminate Bicycle Wheel Considering Stacking Se-quence,” Composites Research, Vol. 25, No. 5, 2012, pp. 141-146.
- 4. Je, H.M., and Kim, W.D., “Stress Analysis of Composite Double Lead Spiral in 20mm Universal Ammunition Loading System,” Composites Research, Vol. 31, No. 6, 2018, pp. 340-346.
- 5. Kim, T.H., and Kim, W.D., “Analysis and Design of Composite Ladder for Pilot,” Composites Research, Vol. 32, No. 2, 2019, pp. 108-112.
- 6. Kim, S.J., Lee, H.K., and Lee, M.H., “Study on the Structural Design of Composite Propfan Blade,” Composites Research, Vol. 1, No. 1, 1988, pp. 18-25.
- 7. Kong, C.D., Park, H.B., and Kang, K.J., “Structural Design and Analysis for Carbon/Epoxy Composite Wing of A Small Scale WIG Vehicle,” Composites Research, Vol. 9, No. 5, 2006, pp. 12-19.
- 8. Kim, J.B., Um, M.K., Lee, S.Y., Kim, T.U., and Shin, J.W., “Study on Design of the Composite Torque Link for a Landing Gear System of a Helicopter,” Composite Research, Vol. 22, No. 2, 2009, pp. 30-36.
- 9. Park, H.B., “Study on Structural Design of Glass/Epoxy Composite Blade and Tower of Vertical Axis Wind Turbine System,” Composites Research, Vol. 31, No. 3, 2018, pp. 104-110.
- 10. Awad, Z.K., Aravinthan, T., Zhuge, Y., and Gonzalez, F., “A Review of Optimization Techniques Used in the Design of Fibre Com-posite Structures for Civil Engineering Applications,” Materials and Design, Vol. 33, 2012, pp. 534-544.
- 11. Kim, J.S., Kim, C.G., and Hong, C.S., “Design of Composite Laminates Using Expert System and Enumeration Method,” Compo-site Research, Vol. 11, No. 2, 1998, pp. 48-57.
- 12. Barbero, E.J., Introduction to Composite Materials Design, Taylor & Francis., Washington, 1999.
- 13. Gusfield, D., Algorithms on Strings, Trees, and Sequences, Cambridge University Press, New York, NY, 1997.
-

- 14. Bailie, J.A., Ley, R.P., and Pasricha, A., “A Summary and Review of Composite Laminate Design Guidelines,” Technical Report NASA, NAS1-19347, Northrop Grumman Military Aircraft Systems Division, 1997.
- 15. Adams, D.B., Watson, L.T., and Gürdal, Z., “Optimization and Blending of Composite Laminates Using Genetic Algorithms with Migration,” Mechanics of Advanced Materials and Structures, Vol. 10, No. 3, 2003, pp. 183-203.
-

- 16. Hong, H.T., Chun, H.J., and Choi, H.S., “Optimal Strength Design of Composite Bicycle Wheels,” International Journal of Precision Engineering and Manufacturing, Vol. 15, No. 8, 2014, pp. 1609-1613.
-

- 17. Grimshaw, M., Grant, C., and Diaz, J., “Advanced Technology Tape Laying for Affordable Manufacturing of Large Composite Structures,” Proceeding of 46th International SAMPE Symposium and Exhibition, 2001, pp. 2484-2494.
 This Article
This Article
-
2020; 33(5): 288-295
Published on Oct 31, 2020
- 10.7234/composres.2020.33.5.288
- Received on Dec 8, 2019
- Revised on Sep 6, 2020
- Accepted on Sep 11, 2020
 Services
Services
Shared
 Correspondence to
Correspondence to
- Young-Bin Park
-
Department of Mechanical Engineering, Ulsan National Institute of Science and Technology
- E-mail: ypark@unist.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.