This paper analyzed the degradation behaviors of silica nano epoxy composite based on the isoconversional method. The size of the silica nano particle was about 12 nm and the particles were mixed by three different weight ratios to make the degradation test samples. The thermogravimetric analyses were performed under six different temperature increase rates to measure the weight changes. Four different methods, Friedman, Flynn-Wall-Ozawa, Kissinger and DAEM (Distributed Activation Energy Method), were employed to calculate the activation energies depending on the conversion ratios, and their calculation results were compared. The results represented that the activation energy was increased when the silica nano particles were mixed up to 10%, indicating the definite contribution of the particles to the degradation behavior enhancements. However, the enhancement was not proportional to the particle mixture ratio by demonstrating the similar activation energies between 10% and 18% samples. The calculation results by the different methods were also compared and discussed.

이 연구에서는 에폭시 수지에 나노 실리카 입자의 농도가 열화 거동에 미치는 영향에 대해 알아보았다. 약 12 nm 크기의 실리카 입자를 에폭시 수지에 세가지 무게비로 섞은 나노 복합소재를 제작하여 열중량분석 (Thermogravimetric Analysis, TGA)을 이용하여 여섯 가지의 서로 다른 승온률 하에서 열화거동 변화를 분석하였다. 등변환법(Isoconversional Method)에 기초한 Friedman, Flynn-Wall-Ozawa, Kissinger 그리고 DAEM(Distributed Activation Energy Method) 방식으로 활성화에너지를 정량적으로 계산하였다. 계산 결과에 의하면 순수 에폭시와 비교했을 때, 실리카 입자가 함유될 경우 활성화에너지가 상승한다는 것을 확인할 수 있었다. 그러나 10%와 18%의 활성화에너지 값이 유사함에 따라 반드시 함유랑에 비례하지는 않는 것으로 나타났다. 또한 각 방법에 의한 계산방식을 분석하여 그 결과를 비교하였다.

Keywords: 에폭시(Epoxy), 실리카 나노복합재료(SiO₂ nano composite), 열화(Thermal degradation), 등변환법(Isoconversional method)

나노복합소재는 모재에 첨가하는 재료를 원자/분자 수준의 크기로 작게 하여 차별화된 기능을 구현하고자 하는 시도로써 많은 연구가 이루어졌고 현재에도 주목받고 있다 [1]. 나노 복합소재는 기지(matrix materials) 재료에 나노크기(10~100 nm)의 이종 소재를 혼입시켜 기존의 복합소재의 특성을 강화한 소재를 말한다. 그중에서도 가공이 쉽고, 경량화 측면에서 강점이 있는 고분자소재를 모재로 한 연구가 활발히 진행되어오고 있으며 대표적인 나노 재료로는 나노클레이(Nano-clay), 나노실리카(Nanosilica) 그리고 나노 탄소튜브(Carbon nanotubes) 등이 있다. 이는 기존의 마이크로미터(10^-6m) 크기의 물질들과 비교해 보았을 때, 훨씬 높은 표면적과 짧은 소재 간 거리로 모재의 물성을 더 효율적으로 향상시킬 수 있는 것으로 알려져 있다.
에폭시 수지는 기계적 물성과 내열성 및 전기 절연성 등의 성질도 우수하여 전기/전자 산업분야에 많이 사용되고 있는 열경화성 고분자이다. 특히 경화 후 성형이 용이하기 때문에, 이를 기지재료로 실리카 나노입자등과 같은 충전재를 첨가하는 연구가 수행되고 있다[2].
최근에는 우수한 열경화성 수지의 개발로 고성능 고분자 나노복합소재가 항공기용 재료로 주목받기 시작하고 있다[3]. 기존 금속재료와 비교하여 높은 무게 대비 강도와 경량성은 중량 감소 효과를 낳아 연료절감과 환경보호의 요구에도 부합한다. 하지만 고분자계 재료는 다른 재료와 비교하여 부정형 분자구조의 특성으로 인해 열화에 취약하기 때문에 내열성이 요구되는 구조재료로써 사용되기 위해서는 재료의 열적 거동에 대한 해석이 필수적이다[4]. 이러한 이유에서 본 연구는 실리카 에폭시 나노복합소재의 열화 거동에 대해 실험으로 검증하고 이론적으로 해석하고자 한다.
이 연구에서 사용된 나노입자 실리카(SiO₂)는 일찍이 고분자 화합물의 기계적, 물리적 특성을 보강하기 위해 사용되기 시작했다[5]. 금속산화물 나노입자가 가지고 있는 불연속적이고 극히 좁은 전자 에너지 분포상태에 의한 광학적 특성 그리고 높은 비표면적에 기인하는 화학적 특성 등을 활용하여 형광체, 촉매, 분리막, 약물전달 등 다양한 분야로 그 적용을 넓혀가고 있다. 특히 실리카 나노입자는 값싸고 화학적으로 안정하며 투명한 특성 때문에 유기-무기 나노복합재료에 가장 빈번히 사용되고 있는 충진재의 하나이다. 그동안 실리카 나노 복합소재에 대한 기계적 거동 변화에 대해 여러가지 연구가 있었지만 입자가 열화 거동에 어떻게 영향을 미치는지에 대한 연구는 미미한 실정이다.
이 연구에는 에폭시 수지를 기지로 하여 0%, 10%, 그리고 18%의 실리카 나노입자를 혼합하여 열중량분석 (Thermogravimetric Analysis, TGA) 데이터를 기반으로 Arrhenius 방정식과 등변환법(Isoconversional Method)을 이용하여 실리카 농도에 따른 열적 거동과 활성화에너지 변화를 정량적으로 계산하였다. 

2.1 Arrhenius Equation
일반적으로 물질의 특성 거동 모델에 대한 반응식은 다음과 같이 표현된다[6].
 

 
여기서 k는 반응상수(rate constant)이며 전환값(conversion rate) a는 시간에 따른 변화를 나타내는 물리적 양으로써 이 연구에서는 온도에 따른 열화에 의한 무게의 변화이고 다음과 같이 정의된다.
 

 
W_i와 W(t), W_f 는 각각 시편의 초기 질량, t 시간경과에 따른 질량, 열화 실험 후 잔여 질량을 의미한다. 만약 반응 상수 k를 무게와 무게 변화율의 선형 비례상수로 가정하면, 식 (1)은 다음과 같이 나타낼 수 있다.
 

 
비례상수 k는 아레니우스 모델을 적용한다. 아레니우스 방정식은 온도와 반응률의 관계식에서 도출되었으며 이는 수명이 반응률의 역수에 비례하며 식 (4)로 표시된다.
 

 
A: 반응속도정수(min^-1)
E: 활성화에너지(kcal/mole)
R: Universal gas constant(8.314 kcal/molK)
T: 절대온도(K)
 
따라서 식 (4)를 (3)에 대입하면 다음과 같다.
 

 
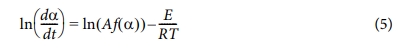
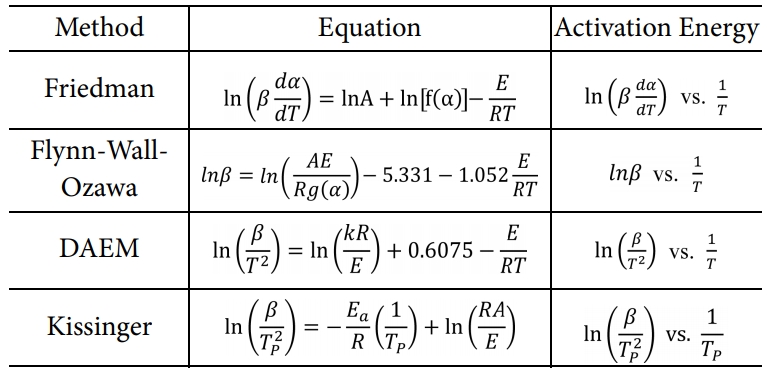
식 (5)에서 반응역학을 나타내는 함수 f(a)는 실험데이터의 거동 현상을 바탕으로 추정된다. 본 논문에서는 등변환법에 의해 정립된 Friedman[7], Kissinger[8], Flynn-Wall-Ozawa [9], 그리고 DAEM 방식[10]을 사용하여 활성화 에너지를 구하였다. 각각의 모델을 Table 1에 정리하였다. 이 표에서 b는 승온률 dT/dt을, 그리고 Tp는 최대반응률이 나타나는 온도이다. 그 밖의 변수는 식 (4)에 설명되어 있다.

나노입자는 Nissan chemical에서 만든 메틸에틸케톤 (Methylethylketon)에 30% 용해되어 있는 평균 직경 12 nm의 실리카 나노입자(MEK-ST, Nissan Chemical)를 이용하였다. MEK-ST의 상세 물성은 Table 2에 기술되어 있다. 고분자 기지재료는 낮은 점도의 액체 수지인 EPON Resin 862 (Diglycidyl Ether of Bisphenol F)를 사용했고, EpiCure-W (diethyldiamino toluene)을 사용하여 경화시켰다. 두 재료 모두 Miller-Stephenson Chemical Company, Inc로부터 구매 가능하다. 이 결합 방식은 낮은 점성과 높은 작동온도 및 물성으로 항공우주분야에서 많이 연구되고 있고 특히 Chen등에 의해 그 물성에 대해 자세히 연구되어 발표되었으며 시편도 그에 따라 제작하였다[11].
위의 재료를 토대로 실험에 사용될 나노복합재료 시편들을 무게비로 각각 0, 10, 18%의 실리카 함량을 갖도록 제작하였고 그 계산식은 식 (6)과 같다.
 

 
시편 제작은 Epon 862 에폭시와 MEK-ST를 무게비로 섞어 섭씨 50도에서 초음파 세척기에 넣어 교반기로 약 3시간 섞은 후 진공 오븐에 넣어 섭씨 70도에서 공기방울을 제거하였다. 그 다음 경화재인 Epicure W를 조성비에 맞추어 다시 교반기로 배합한 후 필요에 따라 진공 오븐을 이용해 공기방울을 제거하였다. 그 후 권장한 경화 싸이클을 따라 섭씨 121도까지 30분에 걸쳐 올린 후 3시간동안 유지하고 그 후 177도까지 30분동안 온도를 올린 후 2시간동안 경화 하였다.
제작된 시편 내의 나노입자 분산도와 농도를 확인하기 위해 Philps CM200 (TEM)을 이용하여, 시편 내부의 나노입자 분포를 확인하였다. 시편은 울트라 마이크로 톱을 이용하여 샘플의 두께를 대략 100 nm 이하로 절편하여 그리드에 올려서 촬영하였다.
시편의 열화 과정을 측정하기 위해 NETZSCH TG 209 F3 TGA를 사용하였으며, 6가지 다른 승온률(2.5, 5, 10, 15, 20, 25^oC min^-1)을 설정하여 질소기체 하에서 시료를 열화시키면서 이에 따른 무게감소를 측정하였다. 이 실험들로 구한 데이터는 활성화에너지 계산에 사용되었다.

4.1 투과전자현미경 관찰
Fig. 1은 TEM을 이용하여 투과된 상을 보여준다. 이를 통해 시편 내부구조와 각각의 농도 내에서 나노 실리카 입자의 분산도와 비중을 확인할 수 있었으며, 보는 바와 같이 입자가 잘 분포되어 있음을 확인하였다.
 
4.2 활성화에너지 계산
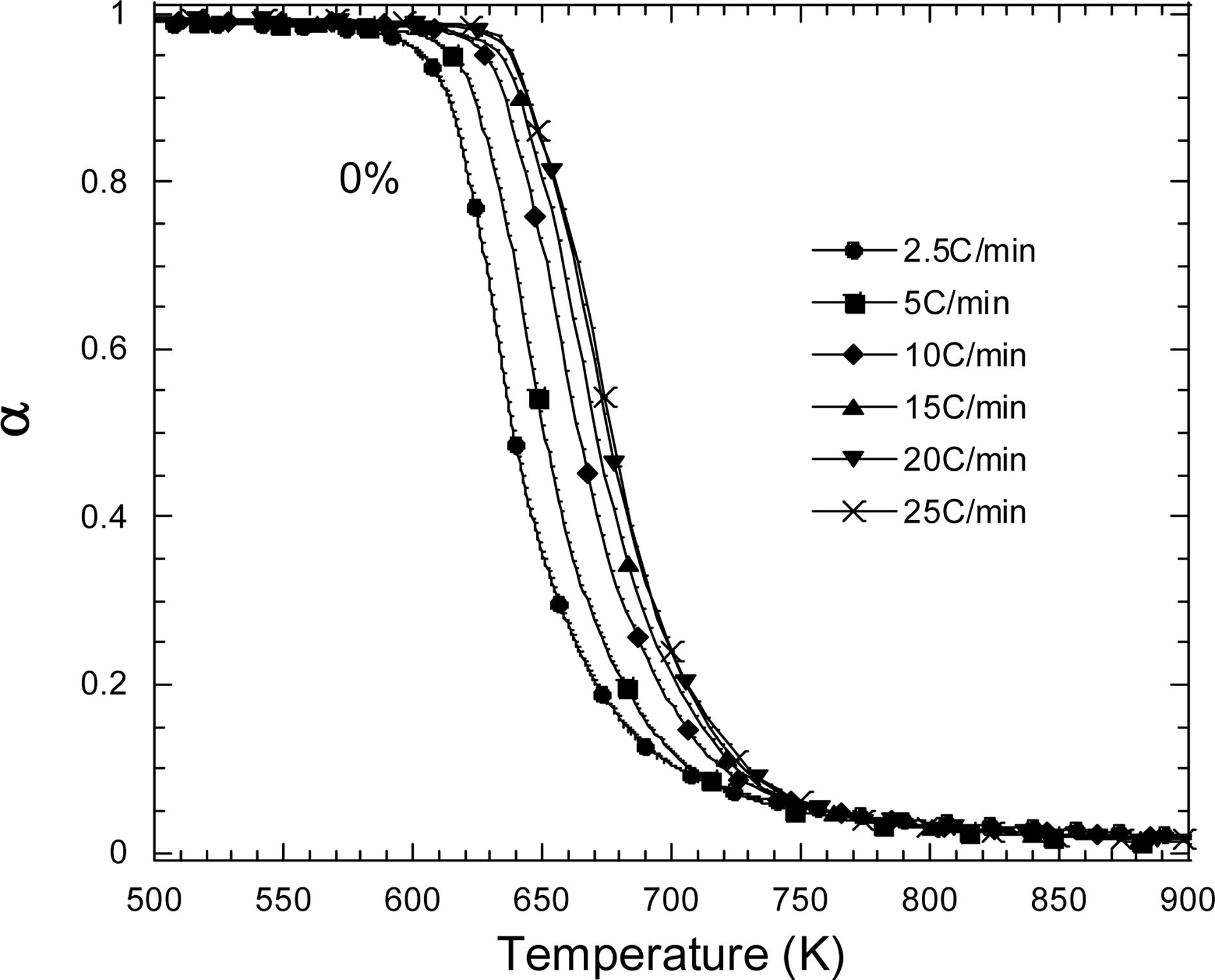
Fig. 2은 0% 시편이 주어진 6가지 승온률에 따라 열화될 때 측정된 무게 변화를 (2) 식에 따라 전환값 a로 나타낸 그래프이다. 승온률이 높을수록 그래프가 오른쪽으로 이동하며 더 높은 온도에서 열화가 시작되는 경향을 보인다. 10%와 18%의 시편 역시 동일한 경향성을 나타낸다.
열중량분석 실험 결과로부터 활성화에너지를 계산하기 위해 질량감소구간(0.2≤a≤0.9)의 데이터를 0.05 간격으로 각각의 전환값에 대한 da/dt, da/dT 그리고 T 값을 구하였다. 이 데이터를 이용하여 앞에서 소개된 네 가지 방법으로 활성화에너지를 계산하였다.
 
4.2.1 Friedman Method
Friedman 방법은 등변환법에 의한 미분 형태의 방정식이다. 위의 식 (5)에서 승온률 b를 고려하면, 다음과 같이 정리될 수 있다.
 

 
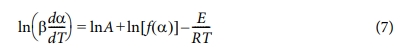
따라서 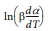 실험값을 1/T에 대하여 정리한 그래프로부터 활성화에너지 E 값을 계산할 수 있다.
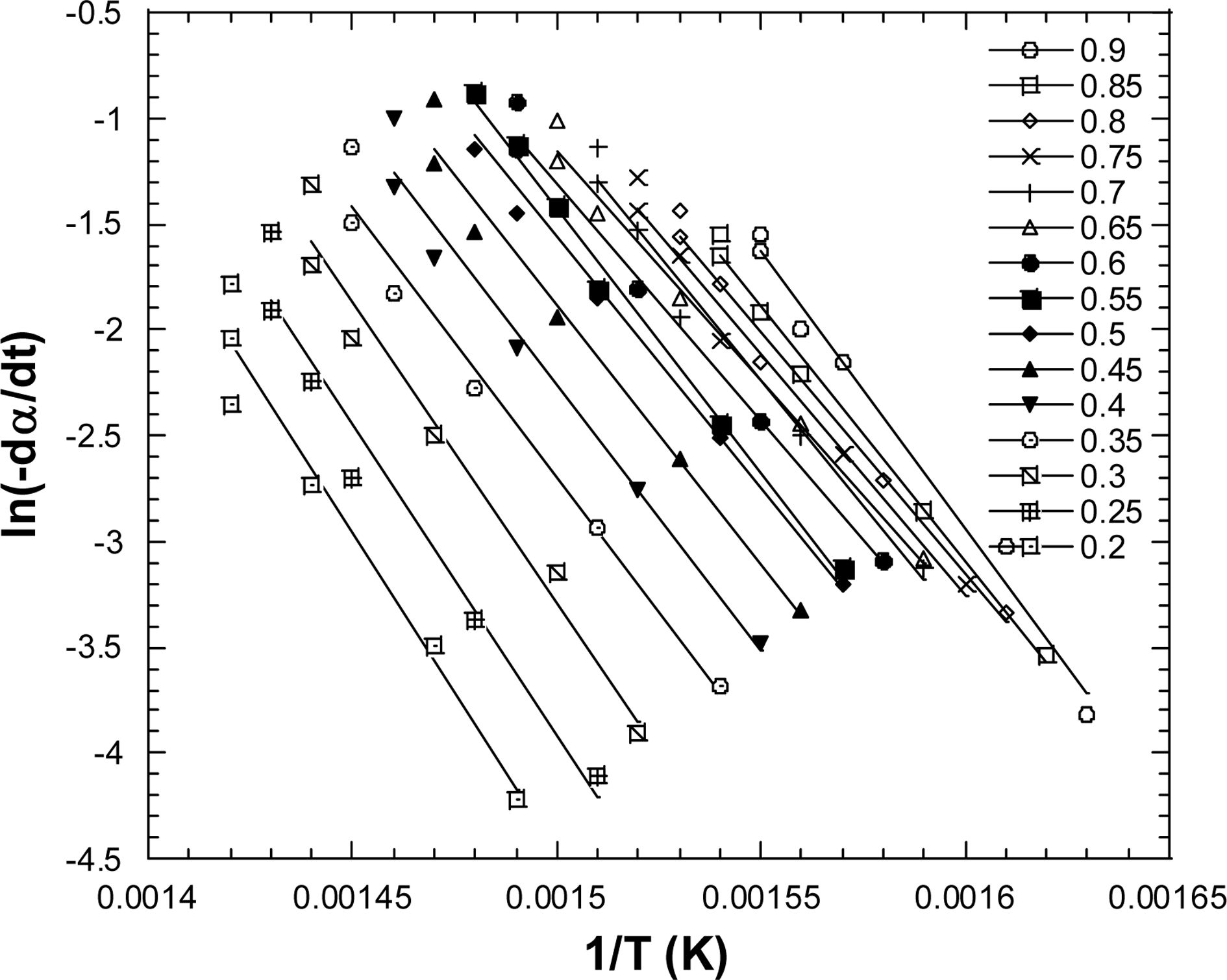
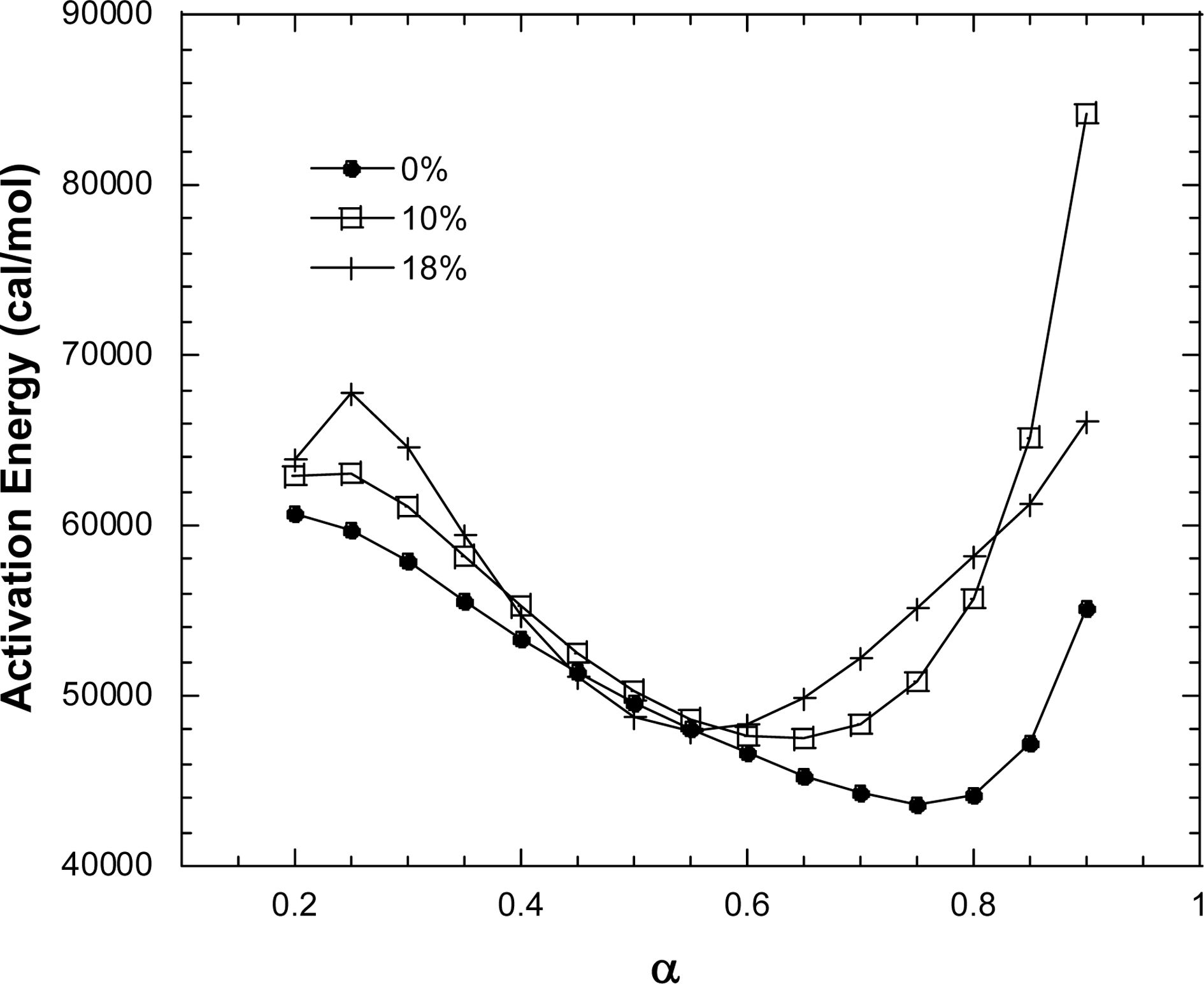
Fig. 3은 Friedman 방법에 따라 활성화에너지를 구하기 위해 ln(da/dt)를 1/T에 따라 그린 그래프이다. 각기 다른 승온률에 대해 전환값이 같은 데이터를 대상으로 선형 추세선을 생성하면, 식 (7)에 의해 기울기에 기체상수를 곱한 값이 활성화에너지로 계산된다. 이렇게 열화구간내에서 계산된 활성화에너지 결과를 Table 3과 Fig. 4에 나타내었다.
계산된 결과에 따르면, 열화 초반(0.6≤a≤0.8), 열화 중반(0.4≤a≤0.6) 그리고 열화 후반(0.2≤a≤0.4)으로 나눠봤을 때, 열화 초반과 후반에서는 실리카 농도에 비례하는 활성화에너지값을 보이는 반면 열화 중반에서는 실리카 농도에 관계없이 거동이 비슷하게 진행되는 경향을 확인할 수 있다. 또한, 열화 극초반(a>0.8)에서는 10%의 활성화에너지 값이 상대적으로 높음을 알 수 있다.
 
4.2.2 Flynn-Wall-Ozawa(FWO) Method
Flynn-Wall-Ozawa(FWO) 방법은 등변환법에 의한 적분형태의 방정식이며, 그 식은 다음과 같다.
 

 
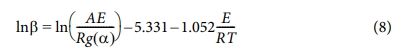
여기서 g(a)=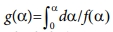는 적분 전환 공식이다. 따라서 a가 일정할 때 여러 승온률에 대한 ln(b) vs. 1/T 그래프의 기울기로부터 활성화 에너지를 얻을 수 있다.
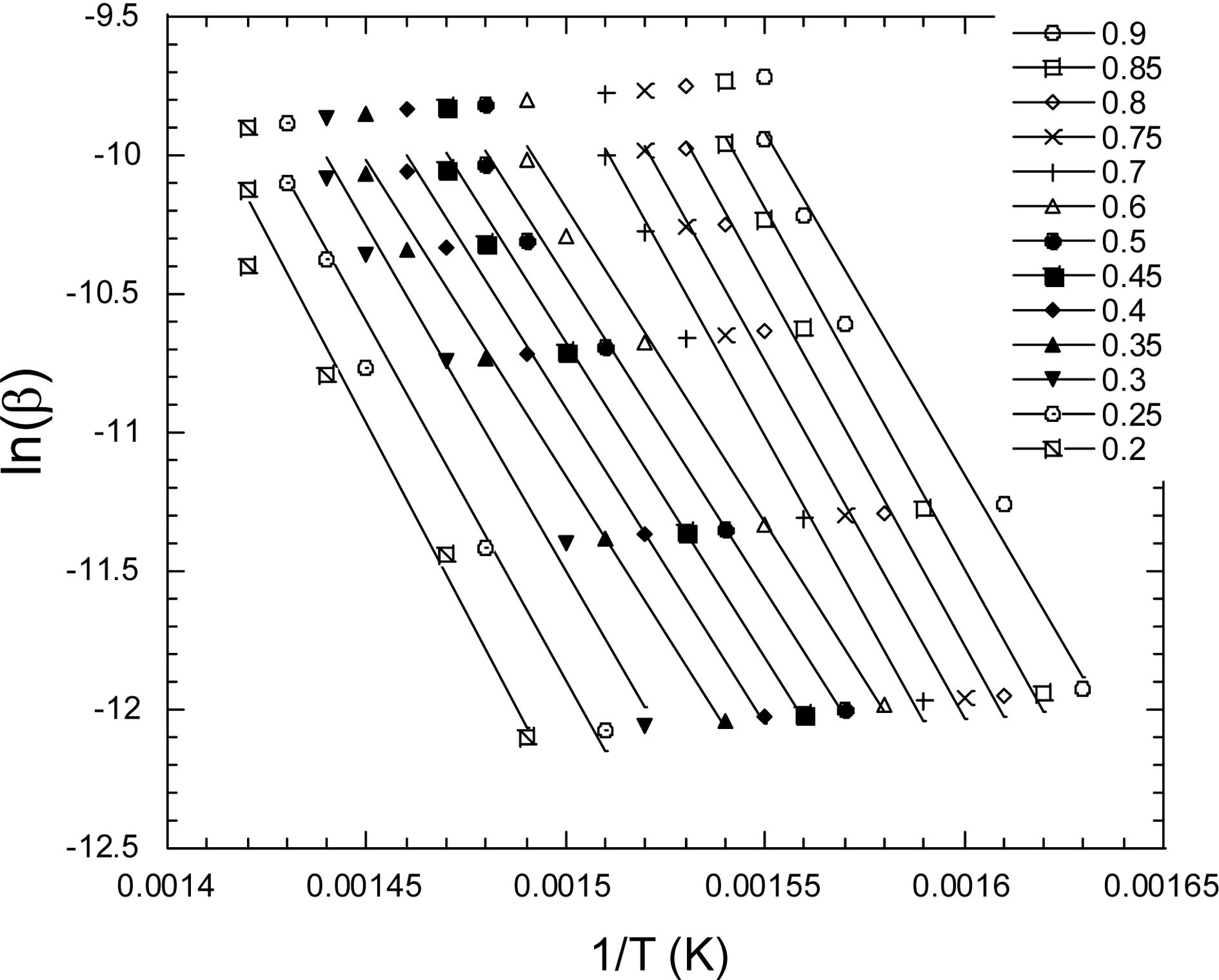
Fig. 5는 식 (8)에 의해 구해진 그래프로써 기울기에 기체상수를 곱하고 -1.502 상수를 나눠줌으로써 활성화에너지 값을 구할 수 있다.
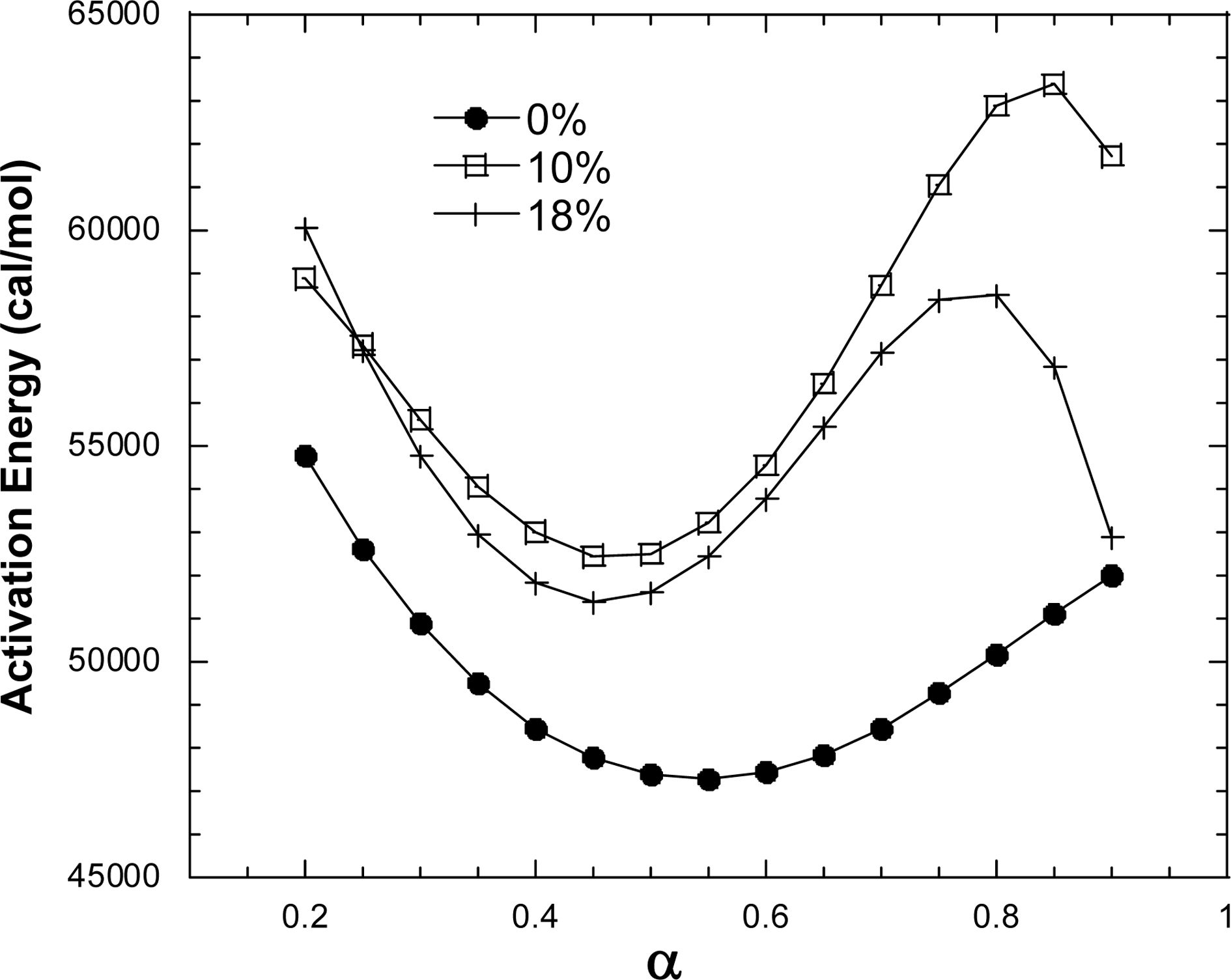
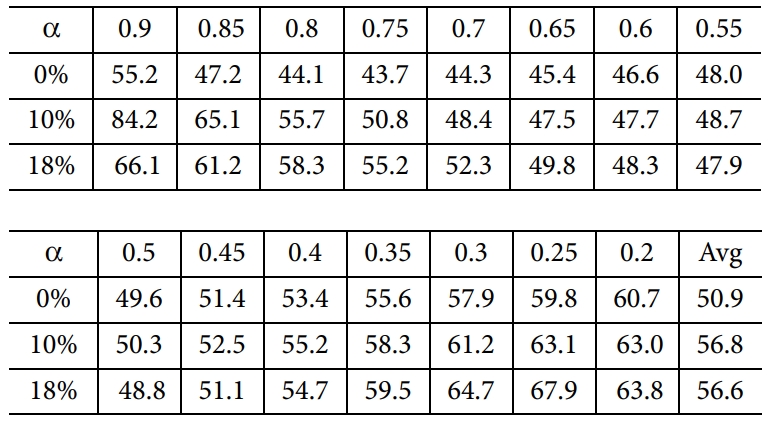
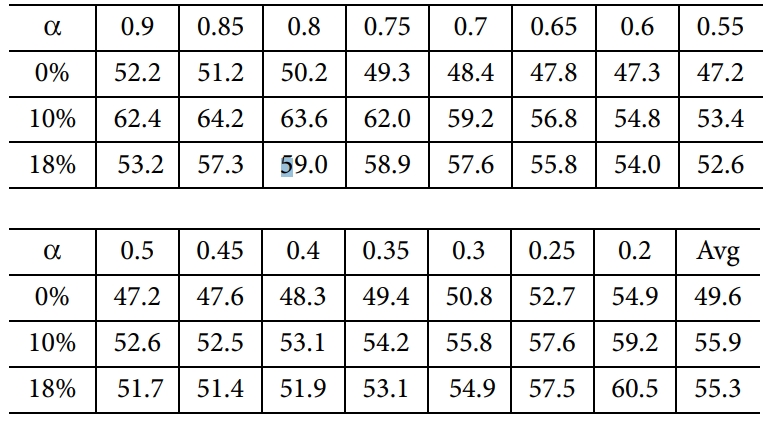
Fig. 6은 Fig. 5를 바탕으로 계산된 활성화 에너지를 전환률에 따라 나타낸 그래프이다. 보는 바와 같이 10%일 때 가장 높은 값을 보이며, 18%인 경우 조금 낮아지는 계산결과를 보여 준다. 또한 Friedman 방법으로 계산된 결과와 달리 초기열화 부분에서 높은 활성화 에너지를 보이지 않았다. 전체적으로 실리카 입자가 포함된 경우가 순수 에폭시의 열화거동에 비해 항상 높은 값을 가지며 따라서 우수한 열적 물성을 보이는 것은 Friedman 방법에 의한 결과와 동일하였다. 열화 극초반(a > 0.8)의 활성화에너지는 10%일 때 61.7 kcal/mole 값으로 가장 높은 값을 보이는 반면, 18%의 경우 52.9 kcal/mole으로 0%인 52.0 kcal/mole과 비교해보았을 때 큰 차이가 없는 것으로 확인된다.
 
4.2.3 DAEM(Distributed Activation Energy Method)
DAEM 방법은 역학반응이 다중적으로 일어날 때, 전체 반응 내 활성화 에너지의 변화를 고려하여 계산하며, 다음과 같은 식으로 표기된다.
 

 
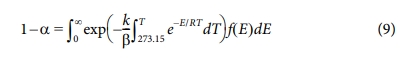
여기서 f(E)는 다른 반응을 나타내는 활성화에너지 분포이고, k는 해당 활성화에너지에 따른 주파수 계수이다. 해당 공식은 이후 함수 f(E)가 Gaussian 분포에 기반한다는 가정으로 이론적인 전개를 통해 다음과 같이 간략화 되었다[12].
 

 
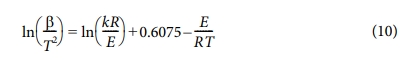
여기서 E와 k 값은 ln(b/T²) 실험값을 1/T에 대하여 정리한 그래프로부터 찾을 수 있다.
DAEM 방법을 적용하기 위해 적어도 3번의 다른 승온률에 대한 실험값이 필요하지만, 본 논문에서는 이미 6가지의 서로 다른 승온률에 대하여 실험하였고 이를 통해 계산의 정확도를 높이고자 하였다.
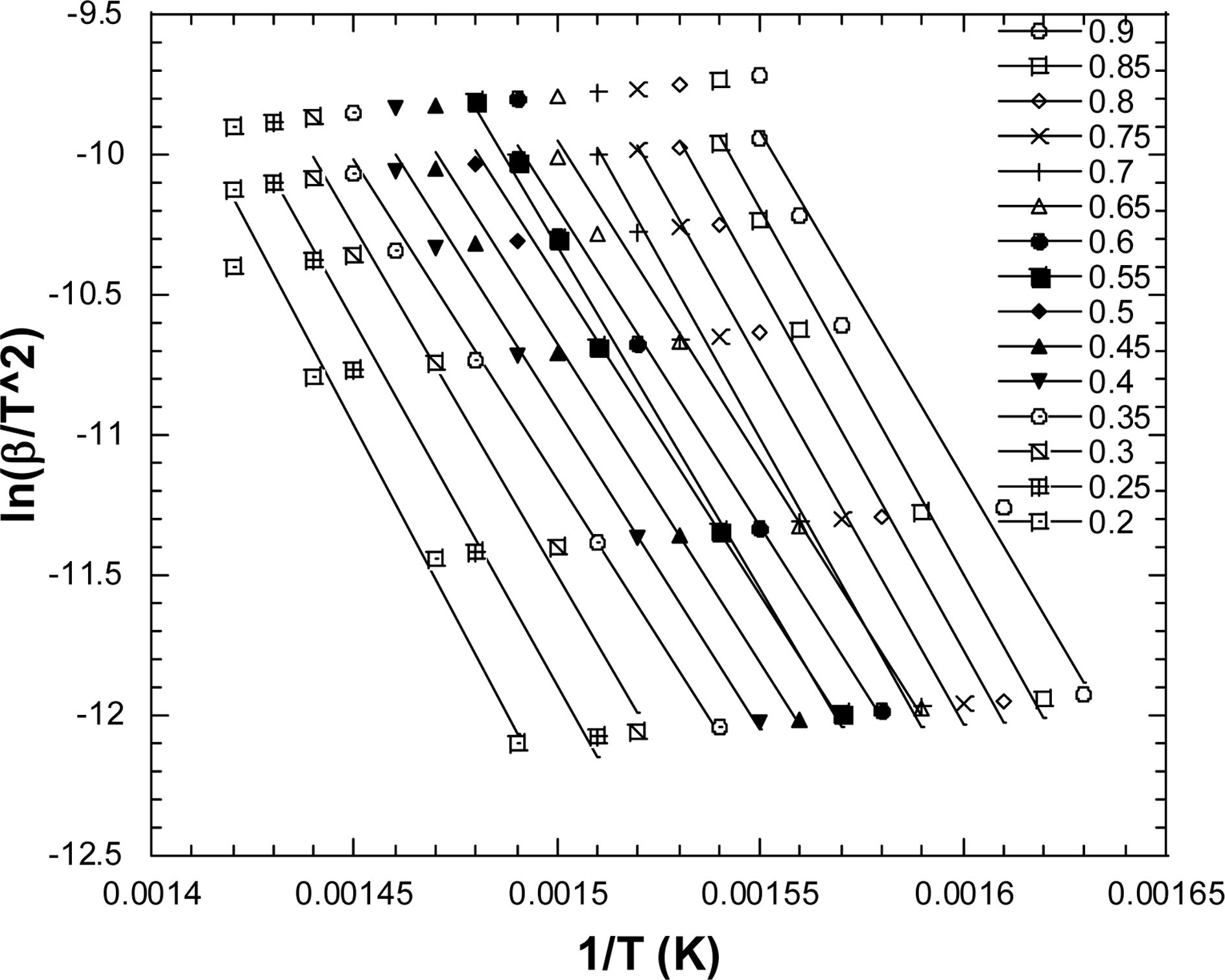
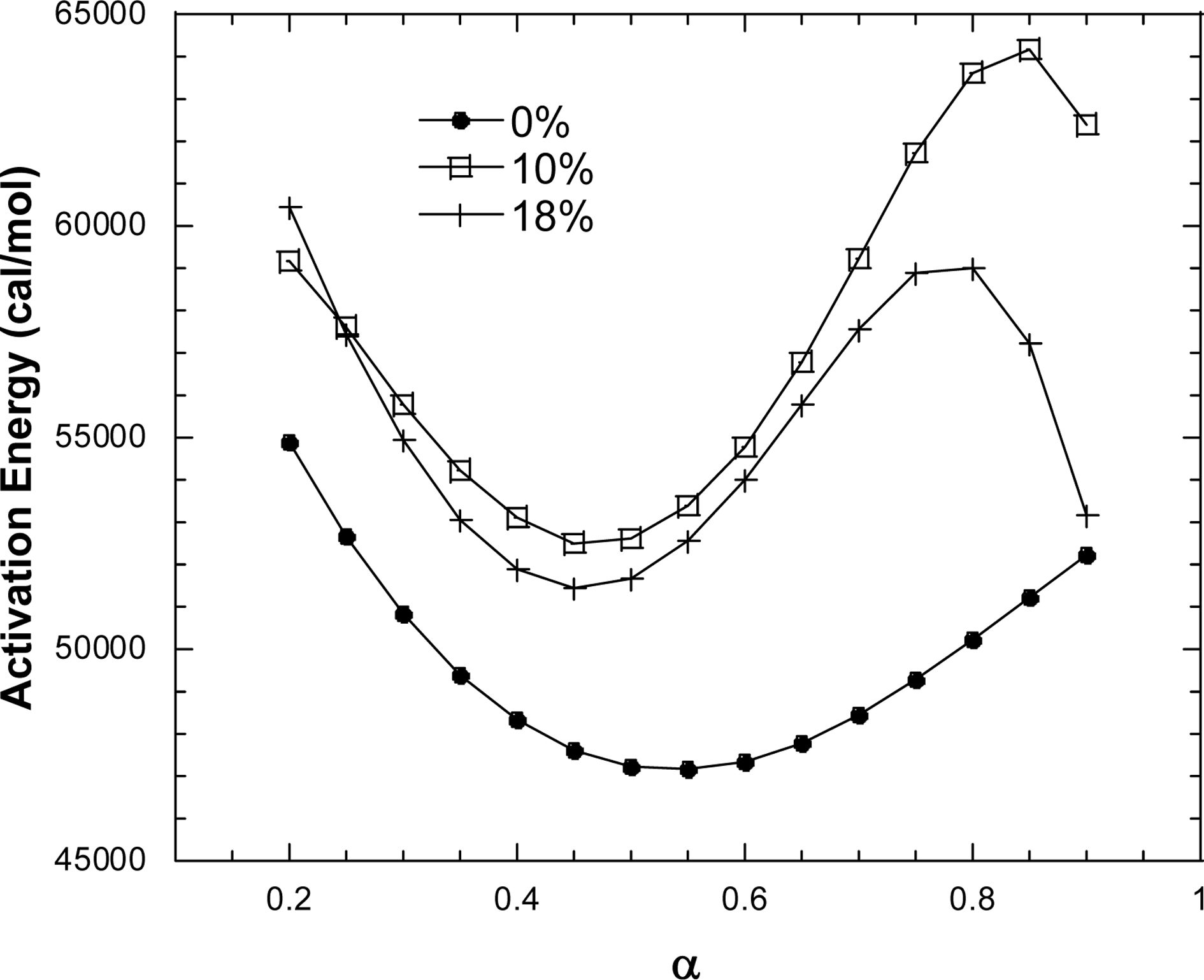
Fig. 7은 DAEM 방법에 따라 구해진 그래프이다. 보는 바와 같이 Fig. 5의 Flynn-Wall-Ozawa 계산법과 유사한 결과를 보임을 알 수 있으며 따라서 Fig. 8과 같이 전환값에 따른 활성화 에너지도 Fig. 6과 거의 유사함을 알 수 있다. 이는 Fig. 5와 Fig. 7에서 동일하게 x축은 1/T로 설정되고 y축은 ln(b) 와 ln(b/T²)으로 데이터가 정리되었는데 실험에서 사용된 온도범위(295~1000K)에서는 1/T²의 값이 너무 작아서 큰 영향이 없기 때문이다. Table 5는 DAEM으로 계산된 에너지값이며 Table 4와 비교하면 거의 같은 값으로 계산됨을 알 수 있다.
 
4.2.4 Kissinger Method
Kissinger는 최대반응속도 지점의 온도는 열분석 곡선의 최대 변곡점 온도와 같다고 가정하며 각기 다른 승온속도의 열분석 곡선으로부터 반응 활성화에너지를 구하는 방법이다. f(a) = 1 - a 인 경우에 대하여 최대반응속도 조건에 따라 유도된 Kissinger 방정식은 다음과 같다[13].
 
 

 
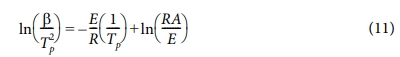
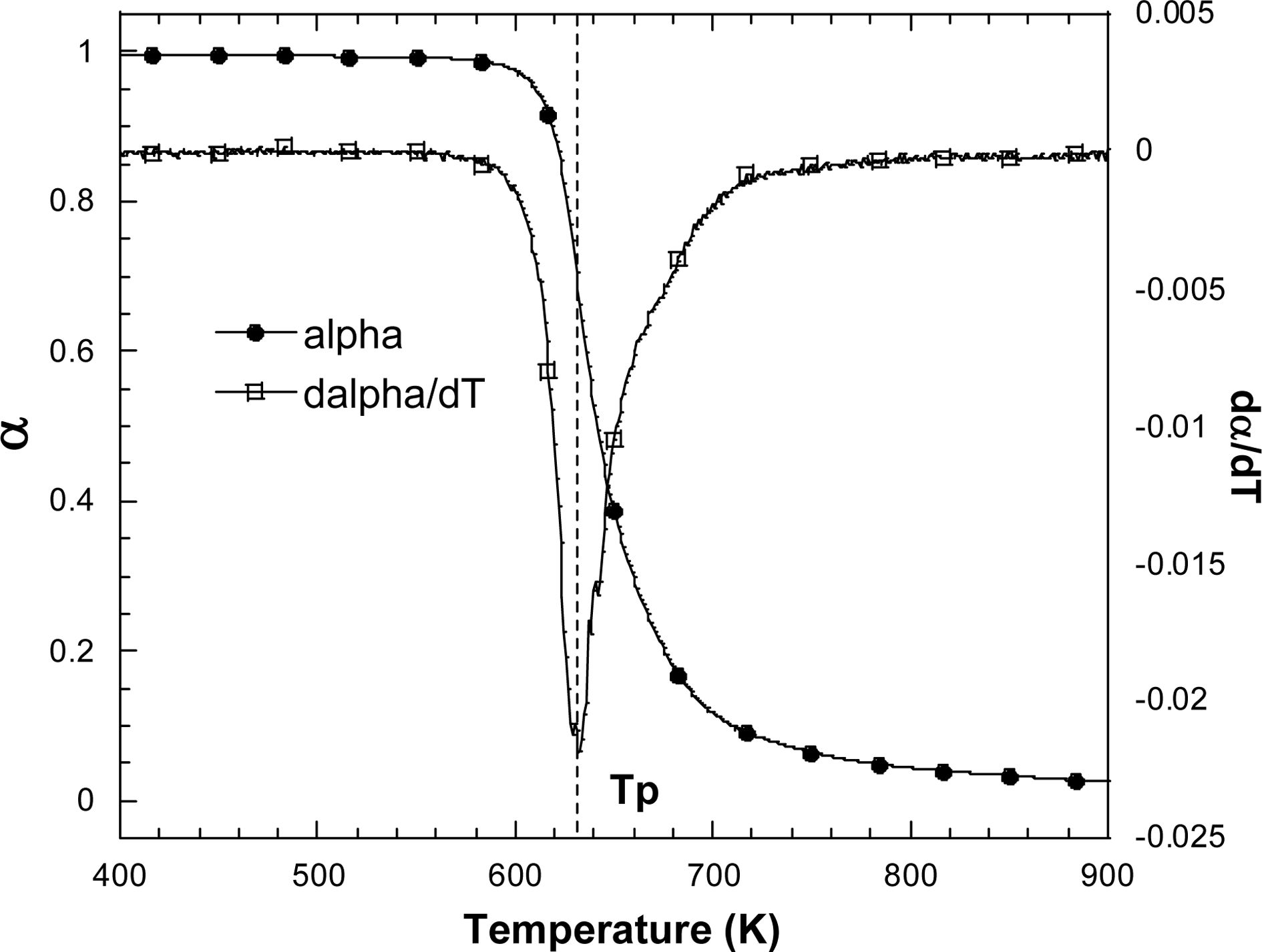
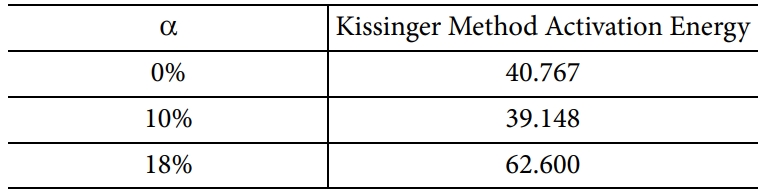
여기서 T_p는 반응 변화율이 최대인 지점에서의 온도이다. Fig. 9는 일반적으로 나타나는 최대 반응률에서의  온도를 보여준다. 그래프에서 확인할 수 있듯이 |da/dT|가 최대인 지점의 온도를 T_p로 설정하여 ln(b/T_p) vs. 1/T_p의 그래프의 기울기로부터 활성화에너지 E를 구하였다. 이 방법의 특징에 따라 각 함량에 따른 활성화 에너지는 하나의 값으로 도출되고 그 결과는 Table 6에 나타나 있다. 결과에서 보는 바와 같이 0%와 10% 샘플의 값이 유사하고 18%의 값이 크게 증가함으로써 이는 앞의 세 방법에 의해 계산된 결과와 상당히 다르다는 것을 알 수 있다.
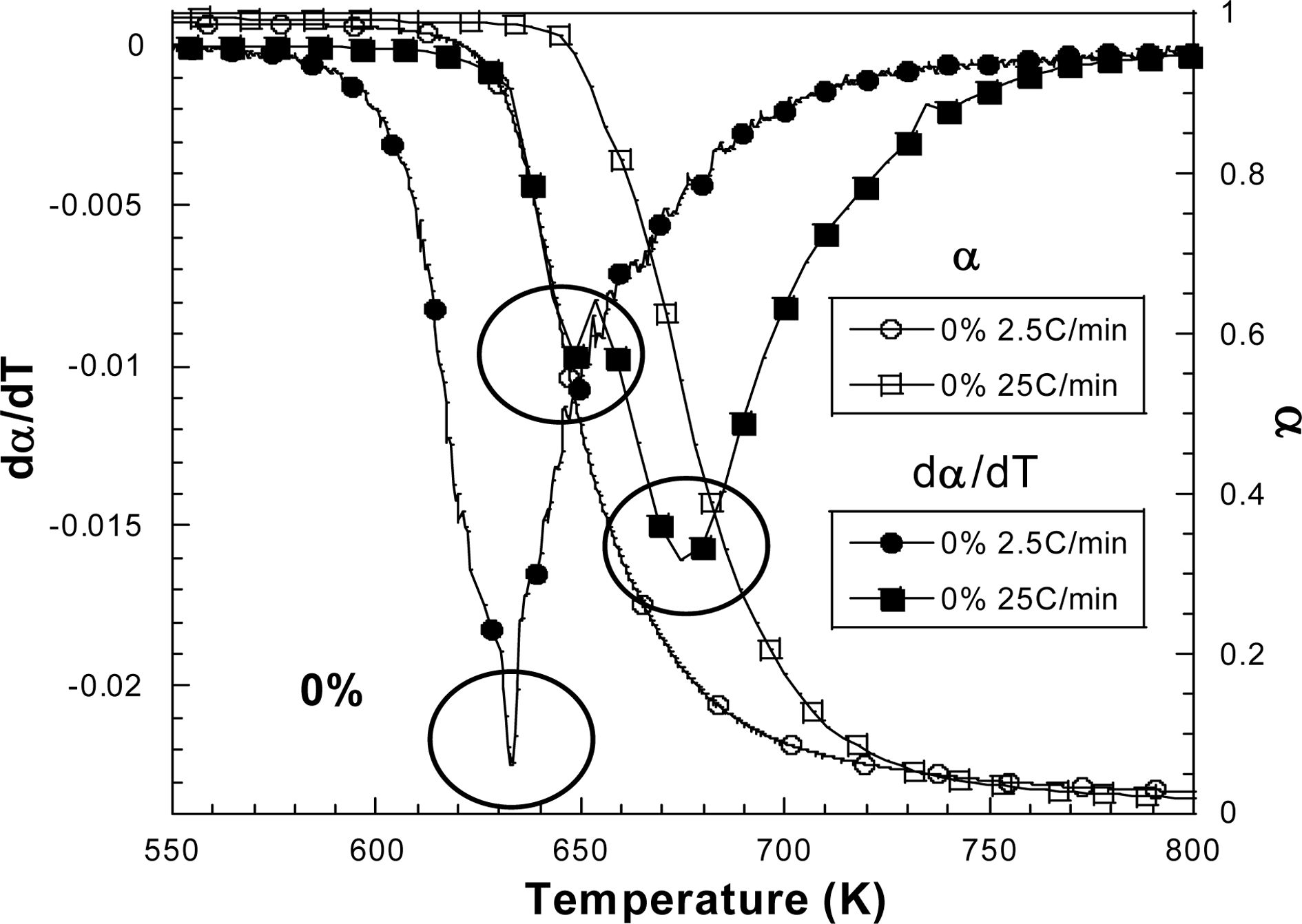
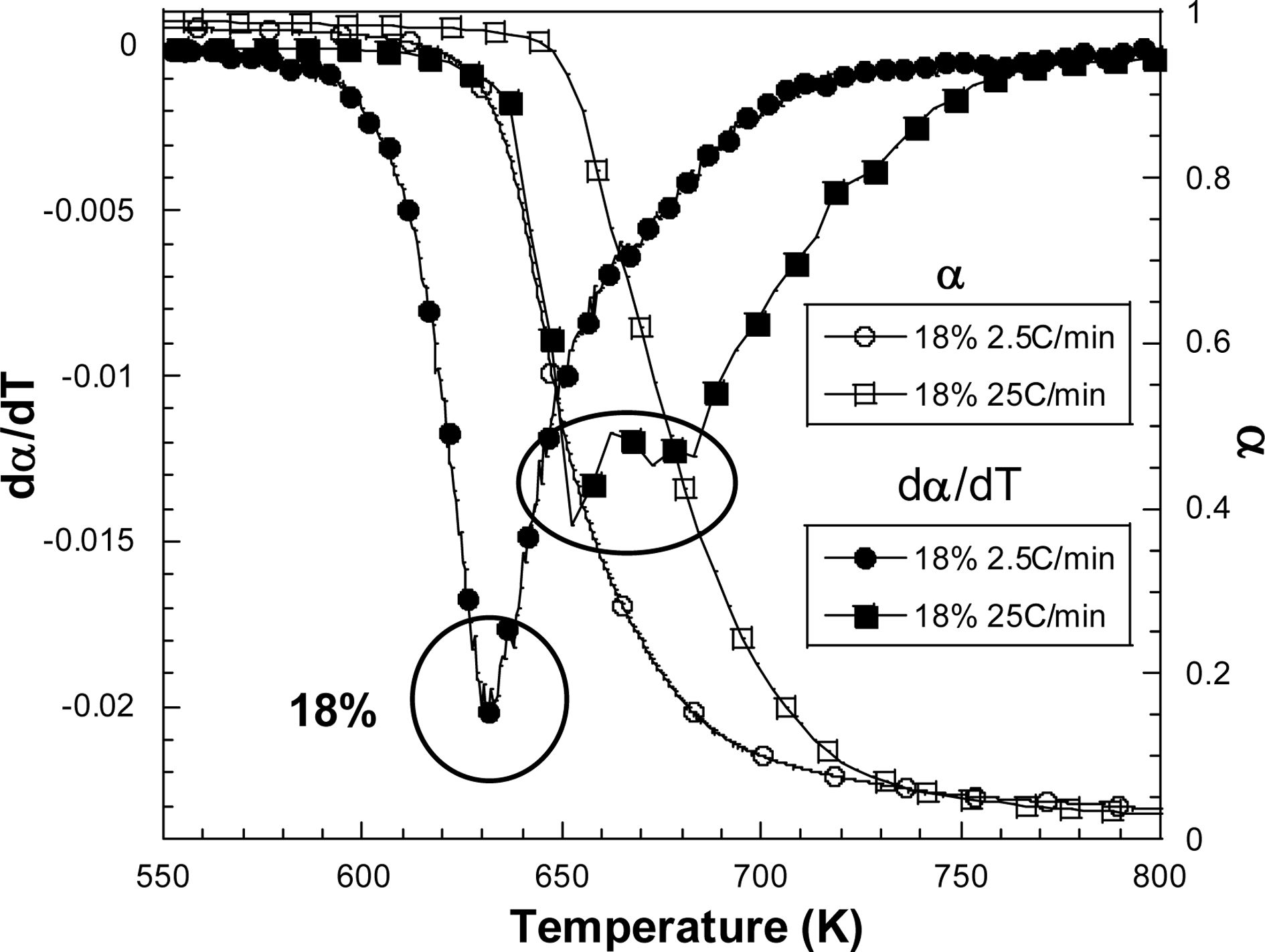
Kissinger 모델은 변화율이 최대가 될 때, 즉 (d[dα/(dt]))/(dt = 0)인 경우 T_p를 결정하고 그에 따라 식 (3)을 변형하여 유도한 모델이다. 이 모델에 대해서는 Blaine 등에 의해 상세히 설명되어 있다[14]. 따라서 재료의 열화가 하나의 T_p를 갖도록 거동하는 것이 중요하다. 그러나 실험 결과 승온률이 높을수록 그리고 실리카 함량이 높을수록 T_p 값이 하나가 아닌 두개, 혹은 정확치 않은 값이 관찰되었다. Fig. 9와 Fig. 10은 실리카가 섞이지 않은 경우와 18% 섞였을 경우, 승온률이 2.5oC/min와 25oC/min일 때와 그에 따른 T_p 값이 각각 원호안에 표시되었다. 보는 바와 같이 0%인 경우 승온률이 높음에 따라 작지만 새로운 T_p 값이 측정되었고, 이러한 현상은 18%인 경우 더욱 두드러져서 25oC/min인 경우 확실한 T_p 값을 결정하기가 어려워 보이고 따라서 활성화 에너지의 값의 오차가 더욱 확대된 것으로 분석된다. 이러한 경향은 나노 입자가 섞임으로 인해 열화 거동에 무시할 수 없는 변화를 주는 것으로 보이며, 이와 같은 거동은 Kissinger 모델을 적용하는데 있어서 처음부터 끝까지 일관된 반응을 보여야 한다는 중요한 가정에 위배되며[14], 따라서 실리카 함량이 높을수록 계산값의 오류가 커지는 것으로 분석된다.  Fig. 11

나노 실리카 입자가 섞인 에폭시 고분자재료에 대한 열화 거동을 분석한 결과 입자의 함량에 따라 활성화 에너지가 변함을 관찰하였다. 활성화 에너지 계산을 위해 네가지 다른 방법이 이용되었고, 그중 Friedman, FWO 방법 그리고 DAEM은 계산된 에너지의 값은 다르지만 나노 실리카를 섞음으로써 전반적으로 활성화 에너지가 증가하였으며, 이는 열화거동이 향상됨을 나타낸다. 특히 열화 초기와 후반부의 활성화 에너지가 증가하며 중반부에서는 큰 차이를 보이지 않았다. 그러나 나노입자 함량이 0%에서 10%로 증가하였을 때 활성화에너지가 크게 증가한 반면 10%에서 18%로의 함량 변화에 따른 활성화에너지 변화는 미미하거나 오히려 감소하는 모습을 보였다. 이러한 결과는 나노입자 함량이 열화 거동 향상에 선형적으로 기여하지 않는 것을 보여주며 최적의 나노입자 함량의 임계값이 존재한다는 점을 시사한다. 또한 적용된 모델에 따라 계산값과 에너지 거동이 달라짐이 확인되었고, 특히 Kissinger 모델은 다른 세가지 모델값과 상이한 결과를 보여주었는데, 이는 Kissinger 모델에서 가장 중요한 파라메터인 T_p 값이 승온률이 커짐에 따라 하나의 온도 이상에서 나타나고, 나노 입자의 함량이 커짐에 따라 T_p 값이 정확하지 않아, Kissinger 모델을 적용하는데 있어서 적절하지 않음을 알 수 있었다. 

이 연구를 지원해준 한국 항공우구연구원과 인하대학교 에 감사를 드립니다.