- Thermal Deformation Analysis of L-shaped Composite During Cure Process by Viscoelastic Model
Dong-Yun Seong*, Wie-Dae Kim*†
Aircraft Structural Design Lab, Department of Aerospace Engineering, Pusan National University
- 점탄성을 고려한 L-형상 복합재료 성형시 열변형 해석
성동윤* · 김위대*†
When curing the composite, the fibers have little
thermal deformation, but the resin changes its properties with time and
temperature, which leads to residual stress in the product. Residual stress is
caused by the difference in the coefficient of thermal expansion of the fibers
and resin during the curing process and the chemical shrinkage of the resin.
This difference causes thermal deformation such as spring-in and warpage.
Thermal deformation of composite structure is important issue on quality of product,
and it should be considered in manufacturing process. In this study, a
subroutine was developed to predict thermal deformation by applying 3-D
viscoelastic model. The finite element analysis was verified by comparing the
results of the plate analysis of the 2-D viscoelastic model. Spring-in of
L-shaped structure was predicted and analyzed by applying the 3-D viscoelastic
model.
탄소 섬유 강화 복합재료 성형 시 섬유는 열변형이 거의 없는 반면에 수지는 시간 및 온도변화에 따라
물성이 변화하며 제품에 잔류응력이 발생한다. 잔류응력의 원인은 경화 과정에서의 섬유와 수지의 열팽창
계수 차이, 수지의 화학 수축이며 이로 인해 스프링 인, 뒤틀림
등의 열 변형이 발생한다. 열 변형은 제품의 품질을 결정하는 주요한 요인으로 복합재료 공정에 있어 반드시
고려되어야 한다. 본 연구는 잔류응력에 의한 열 변형을 예측하기 위해
3-D 점탄성 모델을 적용하여 서브루틴을 제작하고 기존의 2-D 점탄성 모델의 평판 유한
요소 해석 결과와 비교해 유한 요소 해석 기법을 검증하였다. 검증된 기법으로 L-형상 구조를 해석하여 스프링 인 현상을 예측, 분석하였다.
Keywords: 복합재료(Composite materials), 점탄성(Viscoelasticity), CHILE(Cure hardening instantaneously linear elastic), 유한 요소 해석(Finite element analysis)
탄소 섬유 강화 복합재료(Carbon fiber reinforced composite material)는 우수한
비강성과 낮은 밀도, 적층 배열 설계에 따라 원하는 성능의 구조물을 설계할 수 있어 다양한 분야에서 연구하고 있다. 복합재료를 사용하는 제품은
주로 오토클레이브(Autoclave vacuum molding) 공정으로 제작된다. 오토클레이브 공정으로 제품으로 성형할 경우 잔류응력(Residual
stress)으로 인한 제품의 결함이나 열 변형이 발생한다. 열 변형의 원인은 수지의 경화 중 발생하는 화학수축(Chemical
shrinkage), 섬유와 수지의 열팽창계수(Coefficient of thermal expansion) 차이로 인해 복합재료 성형 과정에서 잔류응력이 발생하고 스프링 인(Spring-in), 뒤틀림(Warpage)과 같은 열 변형이 일어난다.
열 변형은 제품의 결함을 발생시키며 이러한 결함을 방지하기 위해 성형 공정에서 잔류응력을 예측하기 위한 다양한 기법들이 개발되고 있다.
성형 공정에서 복합재료의 물성 변화를 예측하는 대표적인 방법으로는 CHILE 모델과 점탄성 모델이 있다. CHILE 모델은 계산 과정에서
온도와 경화도의 변화만을 고려하지만 점탄성 모델은 시간의 변화를 포함하여 계산하기 때문에 복잡한 계산이 요구된다. White와 Kim은
AS4/3501-6 복합재료에 대해 점탄성 모델을 적용하여 잔류응력, 응력완화 거동 등을 연구하였다[1-4]. Jung은 복합재료 평판을 점탄성
모델을 적용해 잔류응력과 열 변형을 예측하였다[5]. Kim은 CYCOM 970 L-형상 복합재료에 대한 스프링 인을 예측하는 유한 요소 해석을
연구하였고, Choi는 M55J/M18 복합재료 구조물에 CHILE 모델을 적용하여 복합재료 성형공정에서 화학 수축이 열 변형에 미치는 영향을
분석하였다[6,7]. 열팽창, 화학수축에 의한 변형뿐만 아니라 성형공정에서 몰드의 열팽창계수, 표면 상태 변화를 고려한 연구도 이루어졌다[8,9].
Zhang 등은 AS4/3501-6 복합재료 구조물에 CHILE 모델을 적용하여 L-형상의 길이, 곡률, 두께를 바꿔가며 강성의 변화를 해석하였다[10].
Hubert 등은 경화도의 변화를 DSC(Differential scanning calorimeter)로 다양한 온도에서 실험하여 경화도 변화를
예측하는 모델을 완성하고 수지의 점성 유동을 포함하는 모델을 추가적으로 해석하였다[11]. Loos와 Springer는 평판 형상에 대해서 경화
사이클, 온도 변화, 수지의 경화, 수지의 점성, 보이드(Void)의 크기 및 공정에서의 보이드 생성, 그리고 잔류응력 등 다양한 요인을 고려한
실험과 해석을 병행하였다[12,13]. L-형상뿐만 아니라 원통 구조 등 다양한 형상의 복합재 구조물의 잔류응력과 그 영향을 해석한 논문도 다수
존재한다[14-17].
본 연구에서는 유한 요소 해석 프로그램인 ABAQUS의 서브루틴을 기반으로 복합재료의 점탄성을 고려한 스프링 인을 예측하였다. 기존의
2-D 점탄성 해석 모델을 3-D 로 확장하여 평판 해석 결과를 통해 해석기법을 검증하고 동일 재료, 동일 형상의 선행 연구[10]를 선정하여
CHILE 모델과 스프링 인의 결과를 비교하여 복잡한 형상에 대해서도 해석 기법이 적용 가능함을 검증하였다.
2.1 경화도
경화도는 수지의 경화 정도를 0~1로 나타낸 값으로 완전 액체 상태를 0, 완전 경화된 상태를 1로 표현한다. 본 연구에서 사용한 수지는
AS4/3501-6으로 경화율은 식 (1)과 같이 표현할 수 있고 시간 변화에 따른 경화도의 변화이며 온도와 경화도의 함수이다[1].
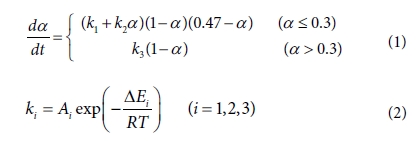
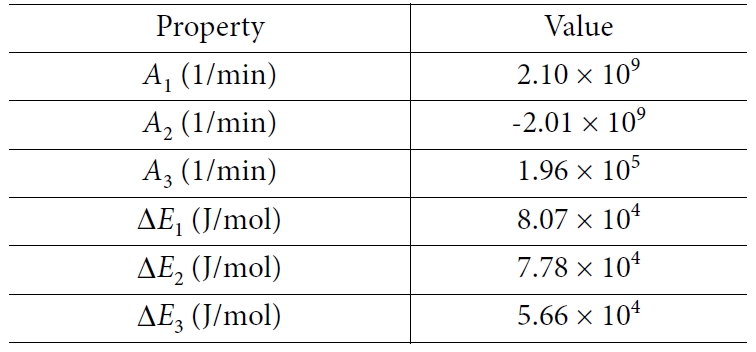
ki (i = 1, 2, 3)는 아레니우스 식으로 수지의
화학반응에서 반응속도상수와 온도의 관계를 나타낸 식 이다. Ai (i = 1, 2, 3)는 빈도계수(Pre-exponential factor)이다. ΔEi (i = 1, 2)는 활성화 에너지(Activation
energy y)이며 R은 일반기체상수(Universal gas
constant), T는 절대온도(Absolute
temperature)이다. 각각의 상수들은 Table 1과 같다[11].
2.2 열팽창
열팽창은 열팽창계수의 함수로 열팽창계수는 일정한 압력 조건에서 물체와 열팽창 사이의 관계이다. CTE1
은 섬유 길이 방향의 열팽창계수, CTE2는 섬유 길이에 수직한 방향의 열팽창계수로 단위 증분 당 물질의 변형은 식 (3)과 같이 나타낼 수 있다.
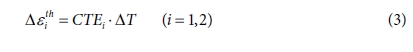
2.3 화학 수축
화학 수축은 수지의 경화 과정에서 원자의 재배열에 의한 부피 변화로 잔류응력, 열변형의 주요 원인 중 하나이다. 본 연구에서는 수지의 화학적 수축 거동을 등방성으로 가정하고 해석을 진행하였다. Vsr는 화학 수축 변형 Δεri는 단위 증분당 수지의 화학 수축으로 식 (4)와 같은 관계를 가진다[10].
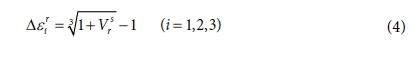
2.4 CHILE 모델
CHILE 모델은 α-mixing rule을 적용한 모델과 유리 전이 온도(glass transition
temperature, Tg)를 고려한 모델이 있다.
본
논문에서는 α-mixing rule을 적용한 모델을 사용했다. 수지의 물성 변화를 경화도를 기준으로 3 단계로 구분한다. 첫 번째 단계는 액체상태,
두 번째 단계는 수지가 경화되는 단계이며 마지막 단계는 수지가 완전 경화되어 화학적 수축이 발생하지 않는 상태이다.
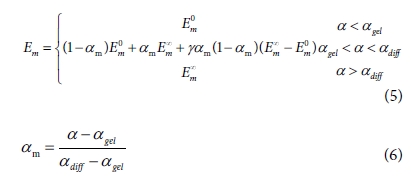
E0m와 E∝m는 수지의 초기 탄성계수, 완전경화 탄성계수이다. g는 수지의 탄성계수와 화학적
경화의 관계이다. αgel , αdiff는 각각 수지의 겔화(gelation)가
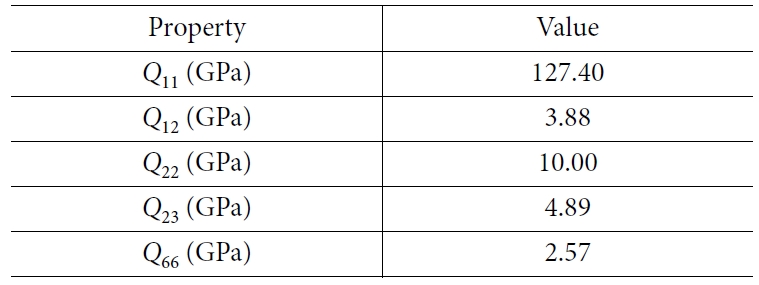
시작될 때의 경화도와 수지가 유리 상태(glassly state)에 도달했을 때의 경화도이다. CHILE 모델의 상수들은 DMA(dynamic
mechanical analyzer) 시험을 통해 구할 수 있으며 Table 2에 정리하였다[10].
2.5 점탄성 모델
복합재료 성형공정에서 수지의 점탄성 거동은 경화도, 온도와 시간을 모두 포함하여 정의되며 식 (7)은 응력, 강성, 변형률의 관계식이다.
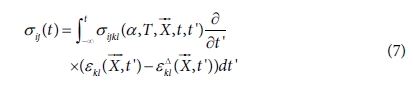
σij는 응력 텐서(Stress tensor), εkl, εΔkl는 각각 진변형율(Total strain), 비 기계적 변형율(Non-mechanical
strain)이다. ![]() 는 위치벡터, t, t'는 각각 현재 시간과 과거
시간을 뜻한다. 복합재료 수지의 응력 완화 거동을 선형화된 점탄성 모델인 맥스웰 모델(Generalized Maxwell model)로 아래 식
(8)과 같이 표현할 수 있다.
는 위치벡터, t, t'는 각각 현재 시간과 과거
시간을 뜻한다. 복합재료 수지의 응력 완화 거동을 선형화된 점탄성 모델인 맥스웰 모델(Generalized Maxwell model)로 아래 식
(8)과 같이 표현할 수 있다.
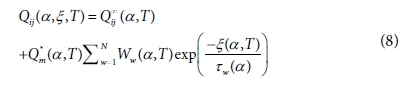
Qij는 복합재의 완화 탄성계수, Q∝ij는 섬유의 완화 탄성계수, Qm은 수지의 완화 탄성계수, Ww는 가중치, ξ는 완화시간, τw는 응력 완화시간이다. 식 (8)에서 Q∝ij, Q∝im, Ww를 경화도, 시간에 독립적이라고 가정하면 식 (9)와 같이 나타낼
수 있다[5].
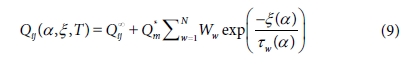
위의 식에서 ξ는 변환 함수(Shift function) αT를 사용해 식 (10)과 같이 표현할 수 있고 완화 시간과 변환 함수는
식 (11)과 같이 표현 가능하다. 변환 함수는 온도에 관한 선형 함수이며 응력 완화시간은 유리 전이 온도 경험식으로 도출할 수 있으며 식은
(12)와 같다. 식 (10)을 경화도 αref = 0.98일 때의 유리 전이
온도로 나누면 화학적 경화 함수를 식 (13)과 같이 표현할 수 있다.
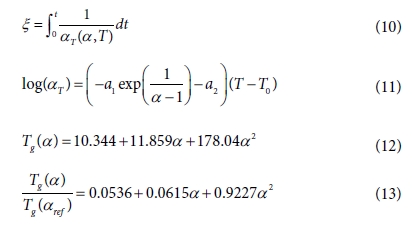
응력 완화시간은 유리 전이 온도를 기초로 한 경험식으로 표현 가능하다[8]. 제품의 두께가 길이, 폭에 비하여 매우 작을 경우 복합재료를
횡 등방성(transversely isotropic)재료로 가정하면 유효 강성 매트릭스인 Qij(t) 는 식 (15)에서 (19)까지의 5개의 독립적인 항으로 구성될 수 있다. 푸아송
비 νij(t)는 식 (20)과 같이 정의할 수 있고 푸아송 비의 비율은 시간에 독립적으로 가정하였고
섬유 길이 방향의 탄성계수 Εij(t)도 시간에 독립적인 항으로 가정했다.
따라서 섬유 길이에 수직한 방향의 탄성계수 Ε2(t), 전단 탄성계수 G12(t)의 변화, 그리고 유효한 푸아송 비인 ν12(t), ν23(t)이 응력 완화 거동의 주요 계수들이다. Table 3은 완전 경화된
AS4/3501-6의 완화 탄성 계수이다[1].
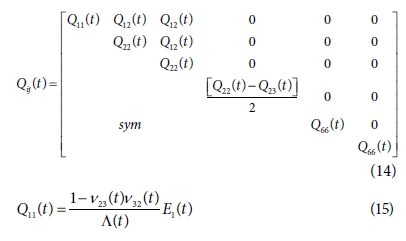
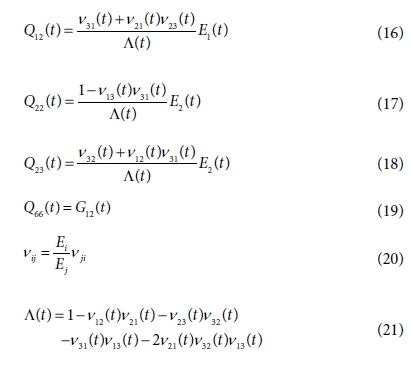
2.6 User
Subroutine
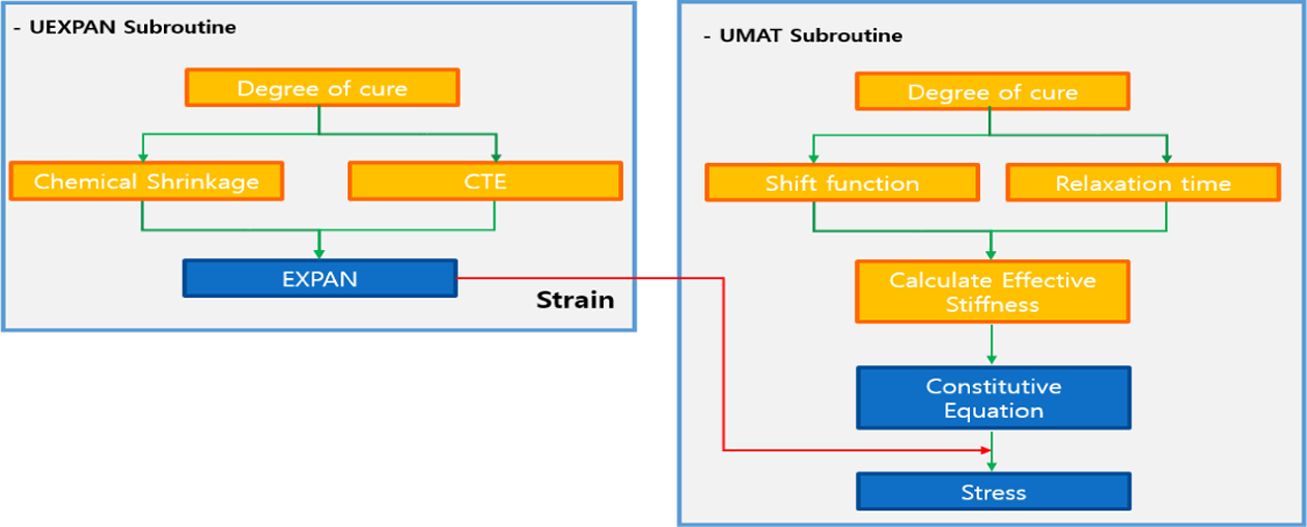
ABAQUS User Subroutine은 Fig. 1과 같이 UEXPAN과 UMAT으로 구성되어 있다. UEXPAN에서 경화도와 열팽창, 화학수축을 고려한 최종 변형을 계산하며 UMAT에서는 변환함수와 가중치, 응력 완화 시간을
고려한 유효강성을 계산하여 복합재료 구조물의 잔류응력을 구할 수 있다.
2-D 점탄성 모델의 경우 식 (22)와 같이 행렬을 구성하였으며
평면응력 상태로 가정했기 때문에 두께 방향의 응력과 변형을 계산할 수 없다. 본 연구에서는 식 (14)와 같이 행렬을 확장하여 두께 방향의 응력과
변형을 계산할 수 있게 구성하였다. 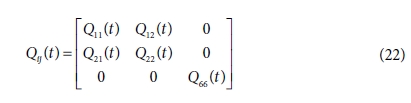
|
Fig. 1 Schematic of User Subroutine for ABAQUS |
3.1 경계조건 및 하중조건
위의 식들을 적용한 3-D 점탄성 모델의 유한 요소 해석 결과를 2-D 점탄성 모델, 실험 결과와 비교하였다. 실험에 사용된 복합재료는
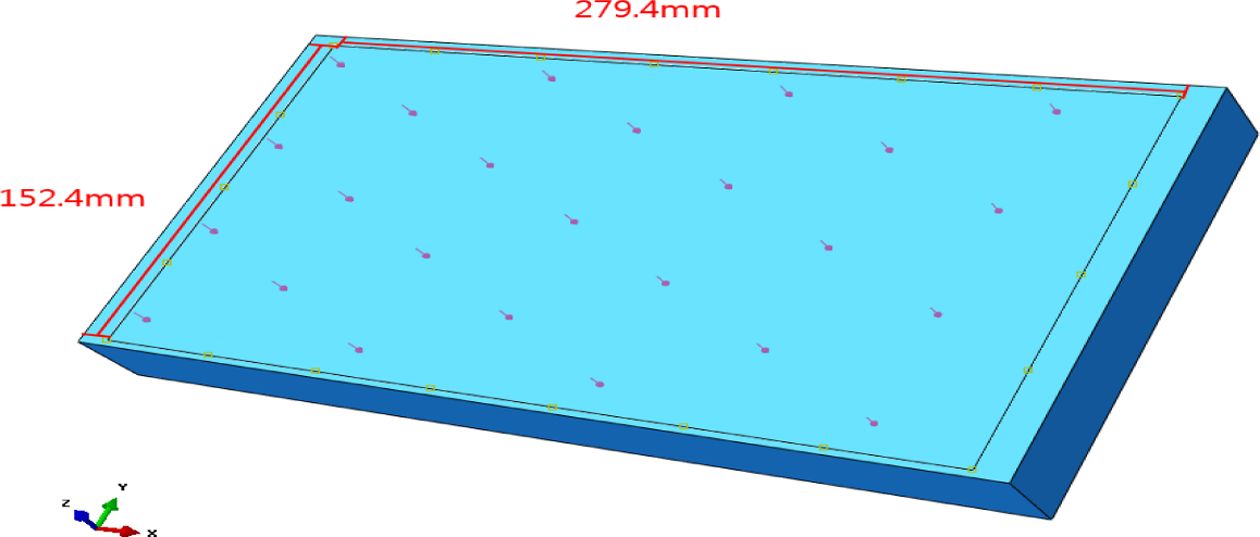
P2352-19로 형상은 Fig. 2와 같으며 두께는 1 ply당 0.21(mm)로 모델을 제작하였다. 복합재료의 적층은 Fig. 1의 x-축을
섬유 길이 방향으로 지정하여 z-축으로 적층하고 평판 아래 몰드를 생성해 고정시키고 접촉조건을 부여하였다.
평판의 윗면에 0.5(MPa)의 압력을 부여하였고 해석에 사용된 경화 사이클은 303.15(K)에서 2.5 (k/min)으로 60분을
가열하여 453.15(K)으로 경화 120분, -2.5(k/min)의 냉각속도로 303.15(K)까지 냉각하는 사이클을 적용하였다.
해석 모델의 정보는 Table 4, 경화 사이클과 경화도의 결과는 Fig. 3에 정리하였다.
3.2 해석결과
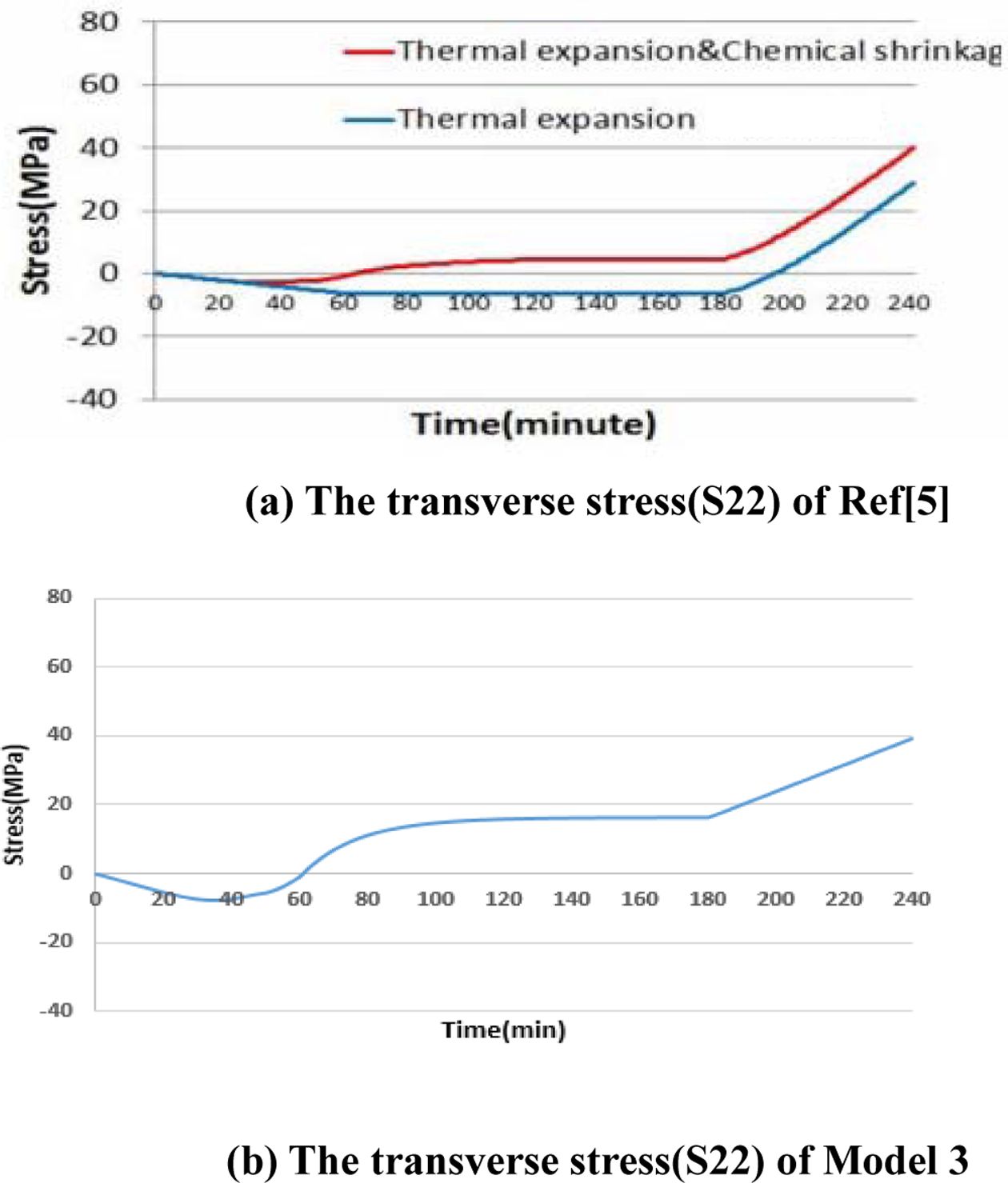
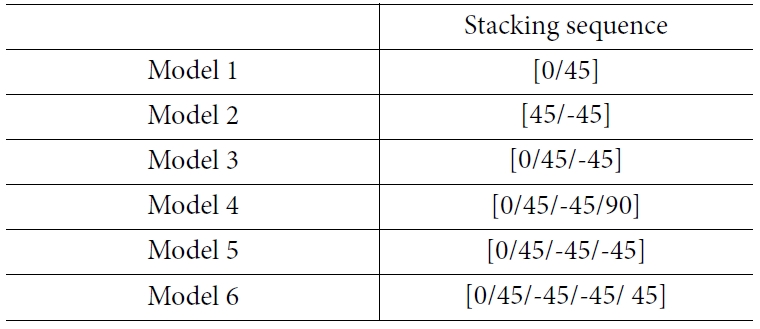
해석 모델은 총 6가지로 각각의 적층 배열은 Table 5와 같다. 해석의 결과를 검증하기 위해 선행 연구[5]와 같은 모델인 [0/45/-45] 적층 모델의 σ22의 분포를 Fig. 5에 비교하였다.
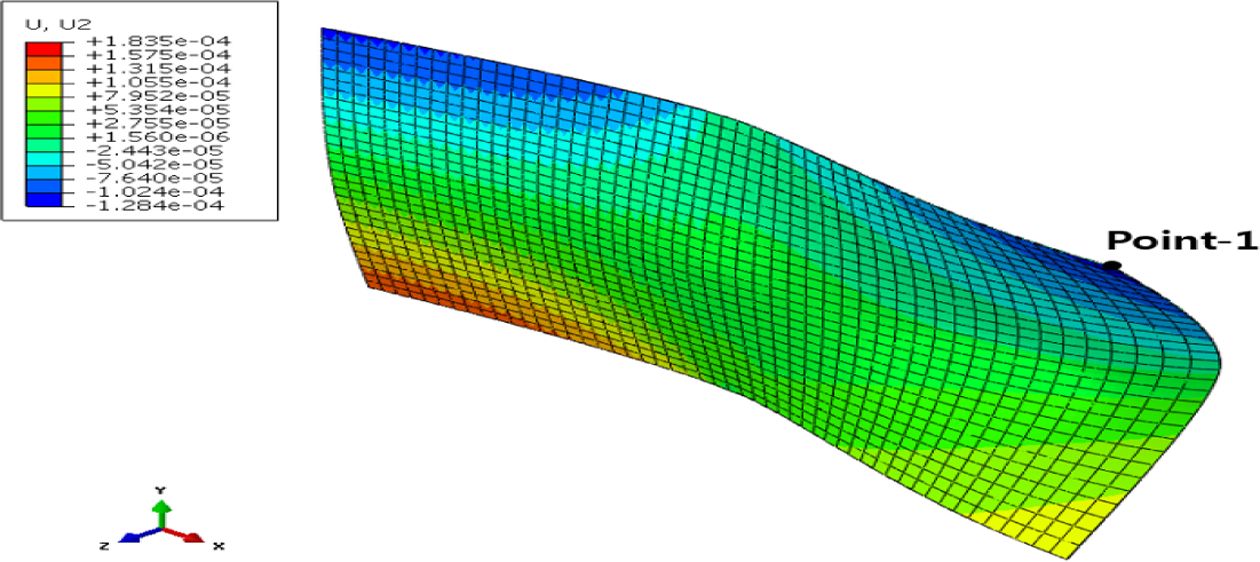
Fig. 4의 point-1에서 응력을 도출하였고 Fig. 5의 (a)는 2-D 점탄성 모델, (b)는 3-D 점탄성 모델의 시간에
따른 응력분포 그래프이다. 2-D 점탄성 모델의 경우 AS4/3501-6의 해석 모델에서 P2352W-19 수지의 물성치를 대입하여 해석하였기
때문에 3-D 점탄성 모델에 비해 낮은 값을 가지지만 경화도, 섬유의 물성 등 다른 모든 값들이 같기 때문에 수치의 차이가 있을 뿐 같은 개형을
그리는 것을 볼 수 있으며 해당 서브루틴이 타당하다고 판단하였다.
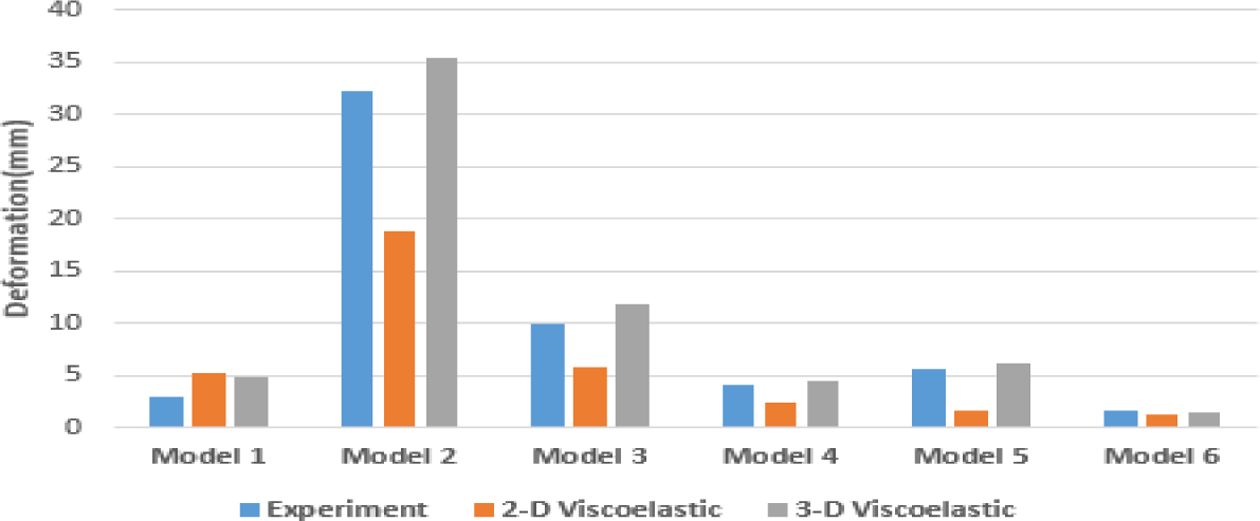
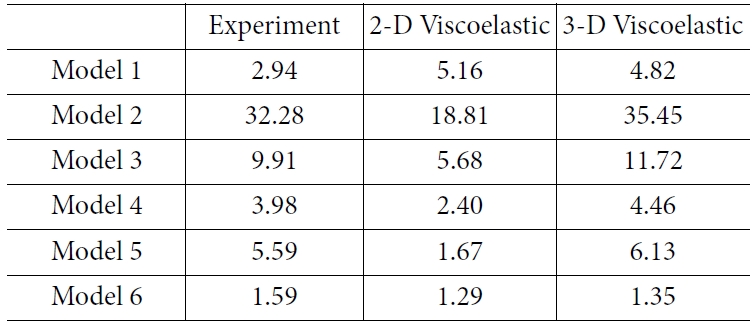
평판의 변형을 비교하기 위하여 두께 방향 변형의 최댓값을 뒤틀림으로 정의하고 해석의 결과를 Table 6, Fig. 6에 정리하였다.
모든 적층 배열에서 3-D 점탄성 모델의 결과가 2-D 점탄성 모델보다 실험 결과와 유사한 결과를 나타내었다. [45/-45] 적층 배열에서 뒤틀림이 가장 크게 발생하였으며, 이는 [0] 적층이 존재하지 않기 때문으로 판단되며 두께가 증가할수록 뒤틀림 거동이
작게 발생하는 것을 알 수 있다.
Fig. 5의 결과를 비교했을 때 잔류응력 및 열 변형을 해석하는데 3-D 점탄성 모델이 2-D 점탄성 모델보다 잔류응력에 의한 열
변형을 정확히 예측할 수 있음을 확인하였다.
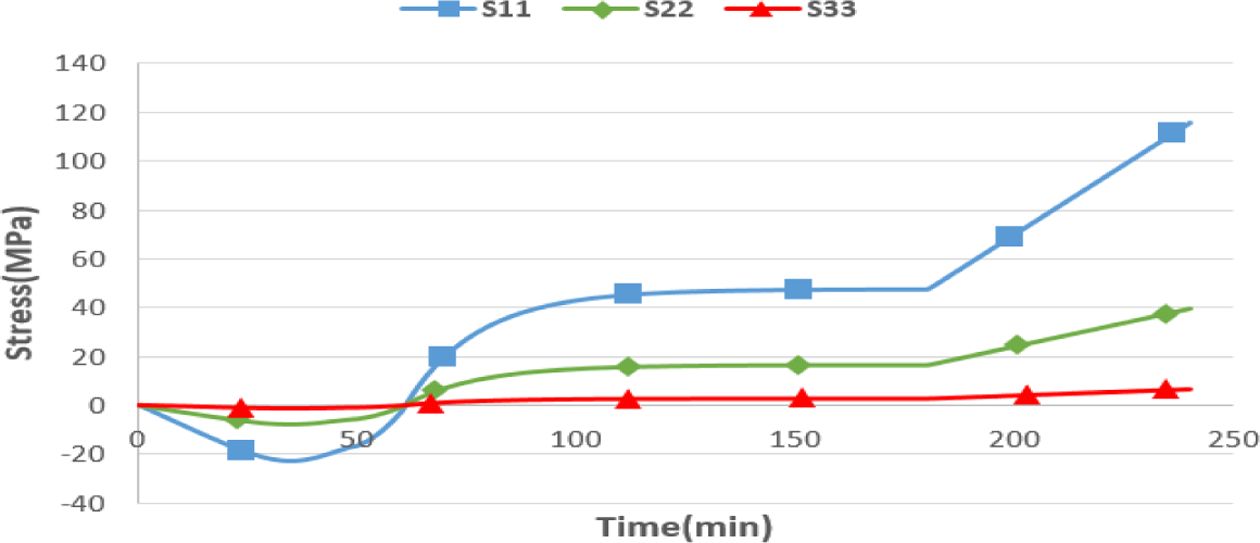
Fig. 7은 [0/45/-45] 적층 배열 Fig. 3의 point-1에서 시간 변화에 따른 응력분포를 나타낸 것이다. 전체적으로 응력이 온도가 증가하는 구간에서 완만하게 증가하고,
온도를 유지시키는 과정에서 응력의 변화가 거의 없는 것을 볼 수 있다. 마지막으로 냉각과정에서 응력이 급격하게 증가하는 것을 알 수 있으며
그래프를 확인하였을 때 잔류응력은 경화 사이클의 냉각과정에서 발생하였다.
|
Fig. 2 Geometry & boundary condition of plate model |

|
Fig. 3 Cure cycle and degree of cure of plate model |
|
Fig. 4 Displacement contour of lay-up [0/45/-45] |
|
Fig. 5 Stress distribution at point-1 of lay-up [0/45/-45] |
|
Fig. 6 Warpage of plate |
|
Fig. 7 Stress distribution of the plate model |
평판 해석을 통해 3-D 점탄성 모델이 2-D 점탄성 모델보다 우수함을 확인할 수 있었다. L-형상 복합재 구조를 선정하여 동일 재료,
동일 형상인 Zhang 등의 선행 연구와 비교하였다[10]. 선행 연구에서 사용한 해석 기법은 CHILE 모델이며 몰드의 효과를 경계조건의 변화를
통해 구현하였다.
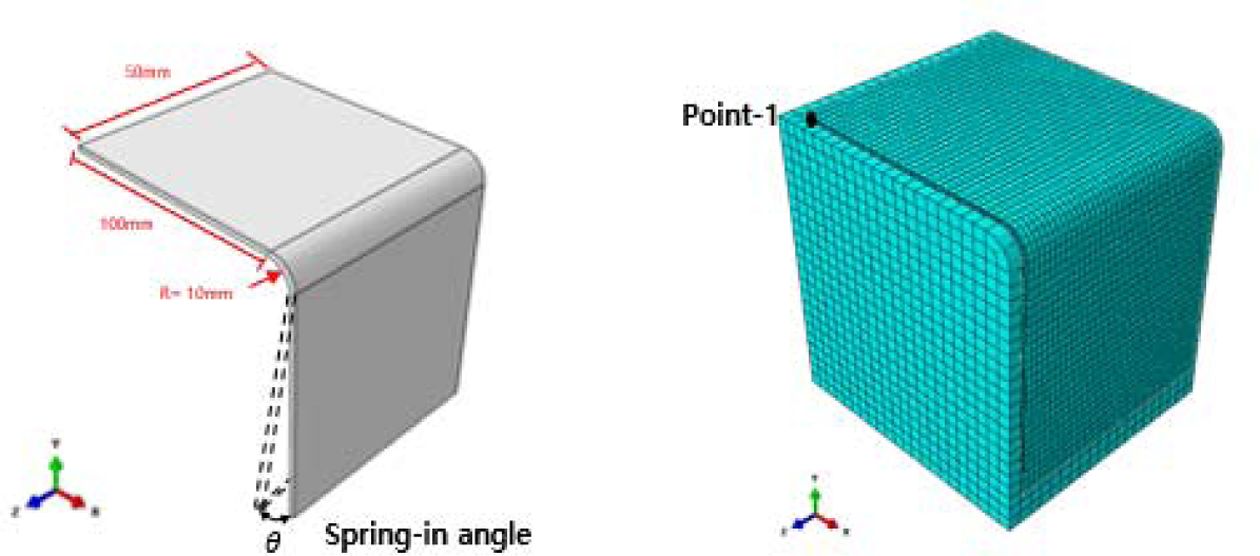
본 연구에서 사용한 해석 기법은 CHILE 모델과 점탄성 모델 두 가지로 해석모델의 형상은 Fig. 8과 같다. 경계조건은 경화 과정에서
몰드를 고정하고 몰드와 L-형상 구조물에 접촉 조건을 부여하고 성형이 끝난 후 몰드를 제거하여 스프링 인 거동을 확인하였다. 하중 조건은
0.7(MPa)의 압력을 복합재의 윗면에 부여하였고 경화 사이클은 상온에서 2.0(K/min)으로 40분을 가열하여 383(K)으로 60분 동안
유지하고
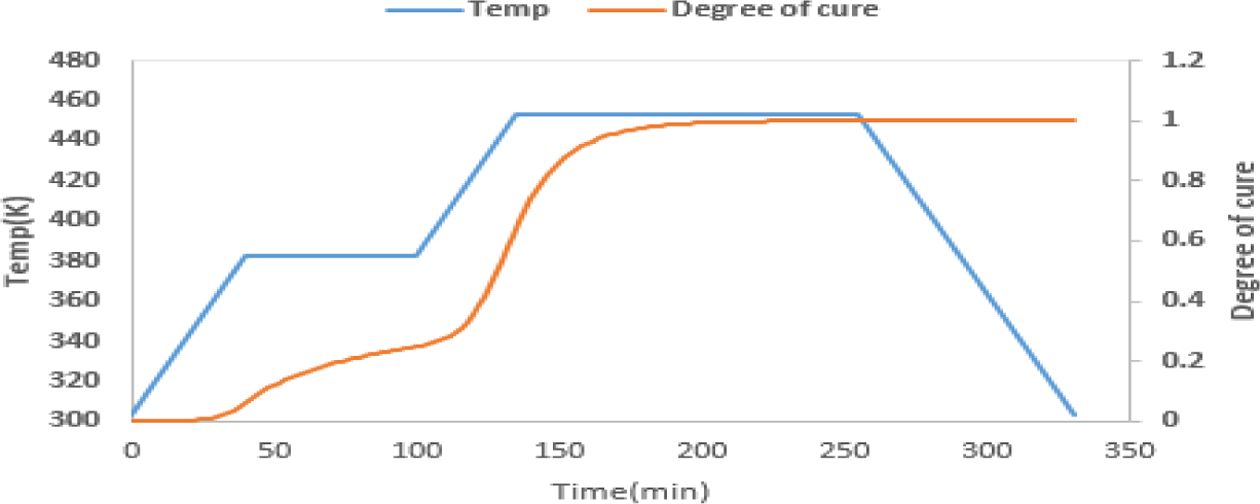
다시 2.0(K/min)으로 453(K)까지 가열시킨 후 120분 동안 유지하였다. 마지막으로 2.0(k/min)으로 상온까지 냉각하였다.
해석 모델의 정보는 Table 7, 경화 사이클과 경화도의 결과는 Fig. 9에 정리하였다.
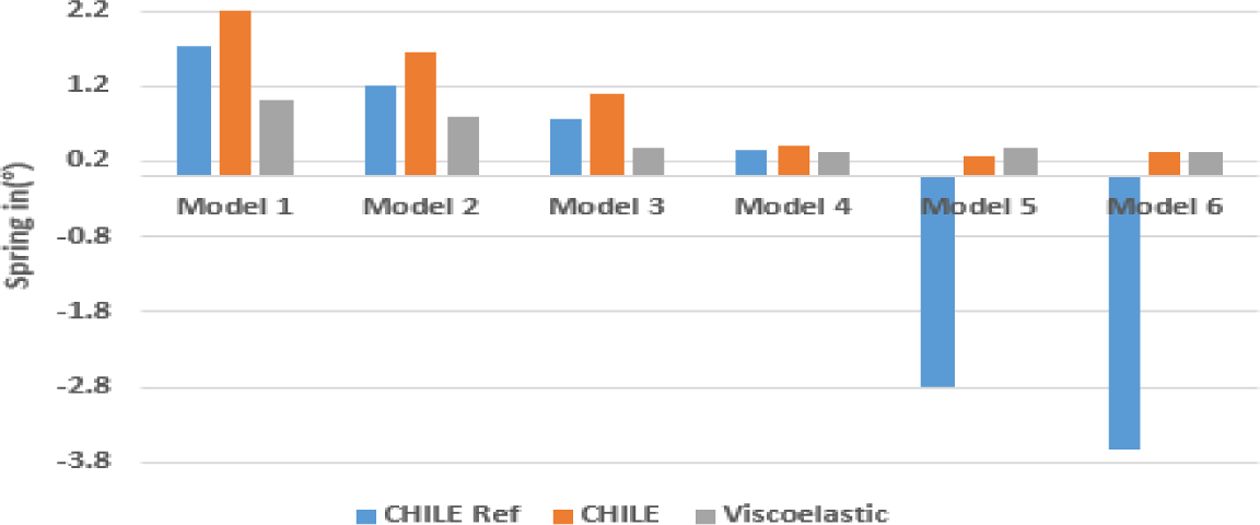
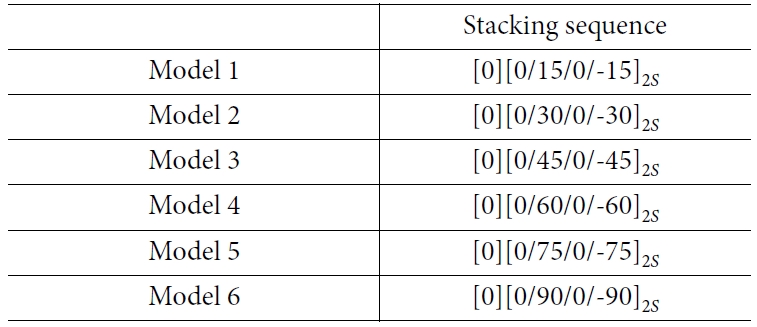
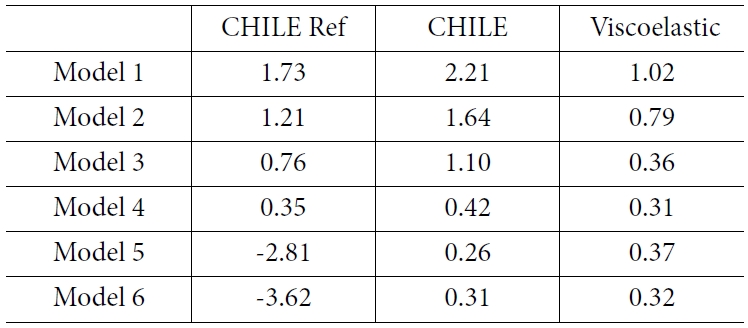
해석에 사용된 적층 배열을 Table 8에 나타내었다. 해석 결과는 Table 9, Fig. 10과 같으며 모든 적층 배열에서
CHILE 모델의 스프링 인이 높게 예측되었다. 특히 1~3번째 모델에서 본 연구의 CHILE 모델 스프링 인이 다른 해석 기법보다 높게 예측되었다.
하지만 선행 연구와 같은 스프링 백 현상은 발생하지 않았고 스프링 백이 발생하기 이전의 모델들의 경우 각 적층 배열에서 스프링 인 발생 경향이
유사한 것을 알 수 있다. 선행 연구의 스프링 백은 경계조건으로 몰드의 효과를 고려했을 때 발생한 오차로 보이며 선행 연구의 CHILE 모델도
직접적으로 몰드의 효과를 고려할 경우 스프링 백 현상이 발생하지 않을 것이다.
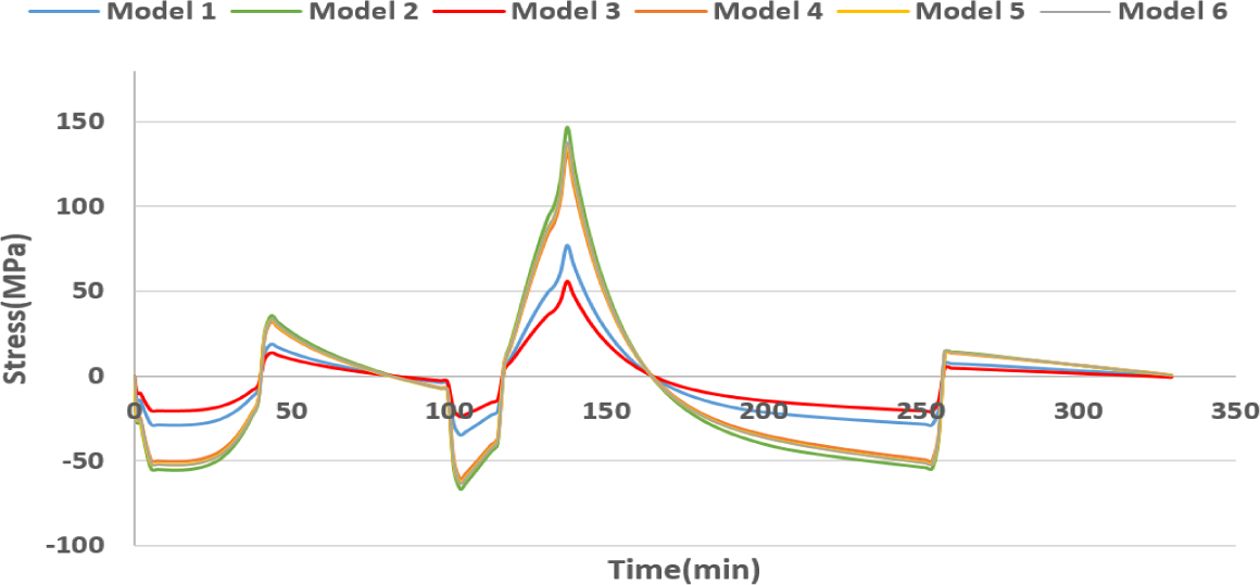
적층 배열에 따른 응력 분포를 분석하기 위해 각 모델들의 σ11, σ12를 Fig. 11, Fig. 12에 나타내었다. Fig. 7의
Point-1에서 응력을 도출하였으며 σ11는 섬유 길이 방향의 응력으로
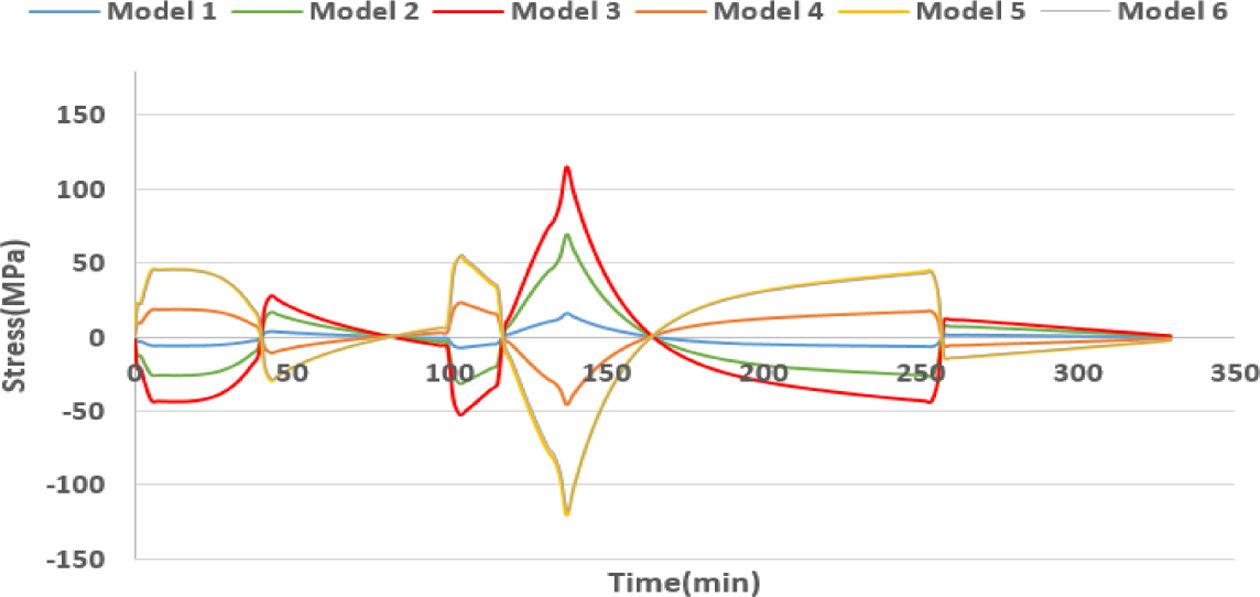
경화 사이클에 따른 응력분포를 확인했을 때 값의 차이가 있지만 응력분포가 같은 것을 알 수 있다. σ22는 두께 방향의 응력으로 모델 1~3과 모델 4~6으로 분류했을 때
응력분포가 반대의 개형을 그리는 것을 볼 수 있다. 경화 사이클의 115분 구간부터 σ22의 인장응력이 발생할 경우
스프링 인이 크게 발생하고 압축응력이 발생할 경우 스프링 인이 작게 발생하는 것을 확인할 수 있고 σ11, σ22 모두 복합재료 성형이 끝나는 구간에서 응력이 수렴하는 것을 볼 수
있다. 경화 사이클에 따른 응력분포를 확인 했을 때 온도가 변화하는 구간에서 응력이 증가하는 것을 알 수 있다.
위의 결과를 통해 3-D 점탄성 모델이 L-형상 구조물에서도 잔류응력과 잔류응력으로 인한 열 변형을 예측할 수 있다는 결론을 얻을 수 있었다.
|
Fig. 8 Geometry and mesh of L-shaped panel |
|
Fig. 9 Cure cycle and degree of cure of L-shaped mode |
|
Fig. 10 Spring in of L-shaped panel |
|
Fig. 11 Stress(S11) distribution of L-shaped panel |
|
Fig. 12 Stress(S22) distribution of L-shaped panel |
본 연구는 오토클레이브 성형에서 발생하는 잔류응력과 잔류응력으로 인해 발생하는 열 변형을 분석하기 위한 유한 요소 해석 기법을
ABAQUS 서브루틴으로 제작하여 검증하였다. 기존의 2-D 점탄성 모델에서 다양한 형상의 열 변형을 분석하기 위해 3-D 점탄성 모델을 제작하고
선행 연구과 비교하여 그 결과를 검증하였다. 또한 검증된 해석 기법을 사용하여 L-형상 구조를 해석하고 선행 연구와 비교하였다.
평판 해석을 통해 3-D 점탄성 모델의 응력이 높게 계산되지만 평판 뒤틀림 실험 결과와 비교하여 열 변형을 보다 정확하게 예측함을 알
수 있었다.
L-형상 구조를 검증하기 위해 선정하여 비교한 선행 연구는 CHILE 모델을 기반으로 해석하였고, 몰드의 효과를 경계조건의 변화로 고려하여
점탄성 모델과 스프링 인 거동이 다소 차이가 있으나 Model 4에서 스프링 인이 가장 적게 발생하였고 스프링 백이 발생하기 이전의 적층 배열들은
스프링 인의 거동이 유사하게 발생하여 해석의 신뢰성을 확인할 수 있었다. 선행 연구 L-형상 구조물의 Model 5, 6에서 발생하는 스프링 백
현상을 분석하기 위해 CHILE 모델로 해석하여 각 모델들의 스프링 인을 확인했으나 스프링 백 현상은 발생하지 않았으며 선행 연구의 다른 형상
조건의 해석 결과를 확인한 결과 위의 경우 이외의 스프링 백 현상이 발생하지 않았다.
또한 시간 변화에 따른 응력 분포를 확인했을 때 Fig. 12와 같이 온도가 상승하는 120분 부근에서 두께 방향으로 압축응력이 발생했을
때 스프링 인이 작게 발생하였다. σ11, σ22 모두 성형 과정에서 온도가 변화하는 구간에서 급격하게 증가하며 온도가 유지되는 구간에서 응력이
서서히 완화되는 것을 볼 수 있고 경화가 끝난 후의 응력이 수렴하는 것으로 봤을 때 3-D 점탄성 모델이 잔류응력과 잔류응력으로 인한 열 변형을
예측하는데 적합하다고 판단하였다.
위의 검증들을 통해 3-D 점탄성 모델을 다양한 구조물에 적용하여 잔류응력 및 열 변형을 예측할 수 있음을 확인하였고 해석을 통해 복합재료
성형 공정의 시간과 비용을 절감할 수 있을 것이다. 현재의 해석기법에서 수지의 유동, 몰드의 형상 및 표면상태 등을 고려하여 해석한다면 잔류응력에
의한 열 변형을 더욱 정확하게 예측할 수 있을 것으로 기대된다.
본 연구는 부산대학교 기본연구지원사업(2년)의 지원으로 수행된 것이며, 지원에 진심으로 감사드립니다.
- 1. White, S.R., and Kim, Y.K., “Process-Induced Residual Stress Analysis of AS4/3501-6 Composite Material,” Mechanics of Compo-site Materials and Structures, Vol. 5, No. 2, 1998, pp. 153-186.
-

- 2. Kim, Y.K., and White, S.R., “Stress Relaxation behavior of 3501-6 Epoxy Resin During Cure”, Polymer Engineering & Science, Vol. 36, No. 23, 1996, pp. 2852-2862.
-

- 3. Kim, Y.K., and White, S.R., “Process-induced Stress Relaxation Analysis of AS4/3501-6 Laminate,” Journal of Reinforced Plastics and Composites, Vol. 16, No. 1, 1997, pp. 2-16.
-

- 4. White, S.R., and Hahn, H.T., “Process Modeling of Composite Materials: Residual Stress Development during Cure. Part II. Ex-perimental Validation,” Journal of Composite Materials, Vol. 26, No. 16, 1992, pp. 2423-2453.
-

- 5. Jung, S.R., Kim, W.D., and Jim, J.H., “Analysis of Thermal Deformation of Carbon-fiber Reinforced Polymer Matrix Composite Considering Viscoelasticity,” Journal of the Korean Society for Composite Materials, Vol. 27, No. 4, 2014, pp. 174-181.
-

- 6. Kim, Y.S., and Kim, W.D., “Prediction of Spring-in Deformation of carbon Fiber Reinforced Composite by Thermal Residual Stress”, Composites Research, Vol. 30, No. 6, 2017, pp. 410-415.
-

- 7. Choi, E.S., and Kim, W.D., “Thermal Deformation of Carbon Fiber Reinforced Composite by Cure Shrinkage,” Composites Re-search, Vol. 31, No. 6, 2018, pp. 404-411.
-

- 8. Oh, J.M., and Kim, W.D., “Prediction of Spring-in of Curved Laminated Composite Structure,” Journal of the Korean Society for Aeronautical & Space Sciences, Vol. 43, No. 1, 2015, pp. 1-7.
-

- 9. Sung, S.H., and Kim, W.D., “Prediction of Deformation of Carbon-fiber Reinforced Polymer Matrix Composite for Tool Materials and Surface Conditions,” Composites Research, Vol. 27, No. 6, 2014, pp. 231-235.
-

- 10. Zhang, G., Wang, J., Ni, A., Hu, H., Ding, A., and Li, S., “Process-induced Deformation of L-shaped Variable-stiffness Composite Structures during Cure”, Composite Structures, Vol. 230, 2019, 111461.
-

- 11. Hubert, P., Johnston, A., Poursartip, A., and Nelson, K., “Cure Kinetics and Viscosity Models for Hexcel 8552 Epoxy Resin,” Inter-national SAMPE Symposium and Exhibition, SAMPE 1999, pp. 2341-2354.
- 12. Lee, W.I., Loos, A.C., and Springer, G.S., “Heat of Reaction, Degree of Cure, and Viscosity of Hercules 3501-6 Resin,” Journal of Composite Materials, Vol. 16, No. 6, 1982, pp. 510-520.
-

- 13. Loos, A.C., and Springer, G.S., “Curing of epoxy matrix composites,” Journal of Composite Materials, Vol. 17, No. 2, 1983, pp. 135-169.
-

- 14. Bogetti, T.A., and Gillespie, J.W. Jr., “Process-induced Stress and Deformation in Thick-section Thermoset Composite Laminates,” Journal of Composite Materials, Vol. 26, No. 5, 1992, pp. 626-660.
-

- 15. Roozbehjavan, P., Tavakol, B., Ahmed, A., Koushyar, H., Das, R., Joven, R., and Minaie, B., “Experimental and Numerical Study of Distortion in Flat, L-shaped, and U-shaped Carbon Fiber-Epoxy Composite Parts,” Journal of Applied Polymer Science, Vol. 131, No. 13, 2014.
-

- 16. Piovan, M.T., and Cortínez, V.H., “Linear Viscoelastic Analysis of Straight and Curved Thin-walled Laminated Composite Beams,” International Journal of Solids and Structures, Vol. 45, No. 11-12, 2008, pp. 3466-3493.
-

- 17. Hwang, H.Y., Kim, Y.K., Rim, C., Kwon, Y.D., and Choi, W., “Thermo-viscoelastic Residual Stress Analysis of Metal Liner-inserted Composite Cylinders,” KSME International Journal, Vol. 17, No. 2, 2003, pp. 171-180.
-

 This Article
This Article
-
2020; 33(4): 220-227
Published on Aug 31, 2020
- 10.7234/composres.2020.33.4.220
- Received on Jun 11, 2020
- Accepted on Aug 19, 2020
 Services
Services
Shared
 Correspondence to
Correspondence to
- Wie-Dae Kim
-
Aircraft Structural Design Lab, Department of Aerospace Engineering, Pusan National University
- E-mail: wdkim@pusan.ac.kr









 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.