In this study, we employ the full atomistic molecular dynamics simulation and finite element homogenization method to predict the thermo-mechanical properties of nanocomposites including carbon nanotube bundle. As the number of carbon nanotubes within the single bundle increases, the effective in-plane Young's modulus and in-plane shear modulus decrease, and in-plane thermal expansion coefficient increases, despite the same volume fraction of carbon nanotubes. To investigate the thickness of interphase zone, we employ the radial density distribution. It is investigated that the interphase thickness is almost independent on the number of carbon nanotubes within the single bundle. It is assumed that the matrix and interphase are isotropic materials. According to the predicted thermo-mechanical properties of interphase zone, the Young's modulus and shear modulus of interphase zone clearly decrease, and the thermal expansion coefficient increases. Based on the thermo-mechanical interphase behavior, we developed the multiscale homogenization model to predict the thermo-mechanical properties of PLA nanocomposites that include the carbon nanotube bundle.

본 연구에서는 탄소나노튜브 다발을 포함하는 나노복합재료의 열-기계적 특성을 정량적으로 예측하기 위하여 분자동역학 전산모사와 유한요소 기반 균질화 기법을 적용하였다. 응집된 탄소나노튜브의 수가 증가함에 따라 동일한 탄소나노튜브의 체적분율에도 불구하고, 면내 영률 및 면내 전단계수는 감소하였고, 면내 열팽창계수는 증가함을 확인할 수 있었다. 계면의 두께를 조사하기 위하여 밀도의 반경 방향 분포(Radial density distribution)을 조사하였으며, 계면의 두께는 탄소나노튜브의 수와는 거의 무관함을 확인할 수 있었다. 기지와 계면은 등방성 재료로 가정하였으며, 예측한 계면의 열-기계적 특성에 따르면, 응집된 탄소나노튜브의 수가 증가함에 따라 계면의 영률 및 전단계수는 감소하였으며, 열팽창계수는 반대로 증가하였다. 이를 토대로, 탄소나노튜브 다발을 포함하는 PLA 나노복합재료의 열-기계적 특성 예측을 위한 멀티스케일 균질화 모델을 개발하였다.

Keywords: 분자동역학 전산모사(Molecular dynamics simulations), 유한요소 균질화(Finite element homogenization), 나노복합재(Nanocomposites), 탄소나노튜브(Carbon nanotube), 폴리유산(Polylactic acid)

탄소나노튜브를 포함하는 고분자 나노복합재료는 기존의 고분자 기지에 비해 높은 강성, 파괴 인성, 열전도율, 전기전도율 등으로 많은 연구자의 주목을 받았다[1-5]. 하지만, 탄소나노튜브 간 강한 인력은 응집 현상을 유발하고 다발형 탄소나노튜브를 형성하게 된다. 탄소나노튜브의 응집 현상은 일반적으로 기계적 성능을 약화하는 것으로 알려져 있다[6-9]. 그러나 아직 다발형 탄소나노튜브의 기계적 성능 약화의 원인에 대해서 분자스케일에서 규명하고자 한 시도는 없었으며, 본 연구에서는 이를 이론적으로 규명하고 이를 토대로 모델을 개발하고자 한다.
본 연구에서는 친환경 고분자 소재이자 3차원 프린터의 대표적인 필라멘트로 사용되고 있는 폴리유산(Polylactic acid, PLA)를 고분자 기지로 하여, 단일벽 탄소나노튜브 다발을 포함하는 고분자 나노복합재료에 대해서 연구를 수행하였다. 나노복합재의 열-기계적 특성을 정량적으로 예측하기 위하여 분자동역학 전산모사와 유한요소 기반 균질화 기법을 적용하였다. 폴리유산에 대한 분자동역학 해석 연구는 이미 수행된 바 있으며, 열탄성 물성 예측에서의 적절함이 확인되었다[10]. 일정한 체적분율에 대해, 응집된 탄소나노튜브의 수를 조절하며 분자동역학 해석을 수행하였으며, 계면의 두께를 조사하기 위하여 반경 방향 밀도 분포(Radial density distribution)를 조사하였다. 예측한 계면의 열-기계적 특성을 토대로, 탄소나노튜브 다발을 포함하는 PLA 나노복합재료의 열-기계적 특성 예측을 위한 멀티스케일 균질화 모델을 개발하였다.

본 연구에서는 상용 소프트웨어인 Materials studio 2019를 이용하여, 분자 모델링과 분자 동역학 전산 모사를 수행하였다. 모든 과정에서 원자간 상호작용력을 모사하기 위하여 PCFF(Polymer-Consistent Force Field)를 사용하였다.

2.1 단위 셀 분자 모델링
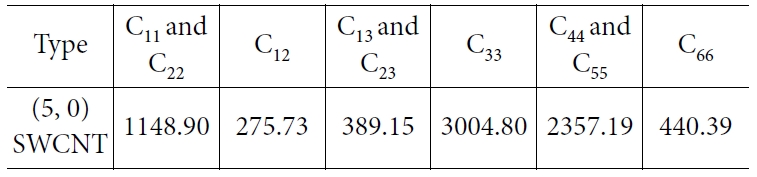
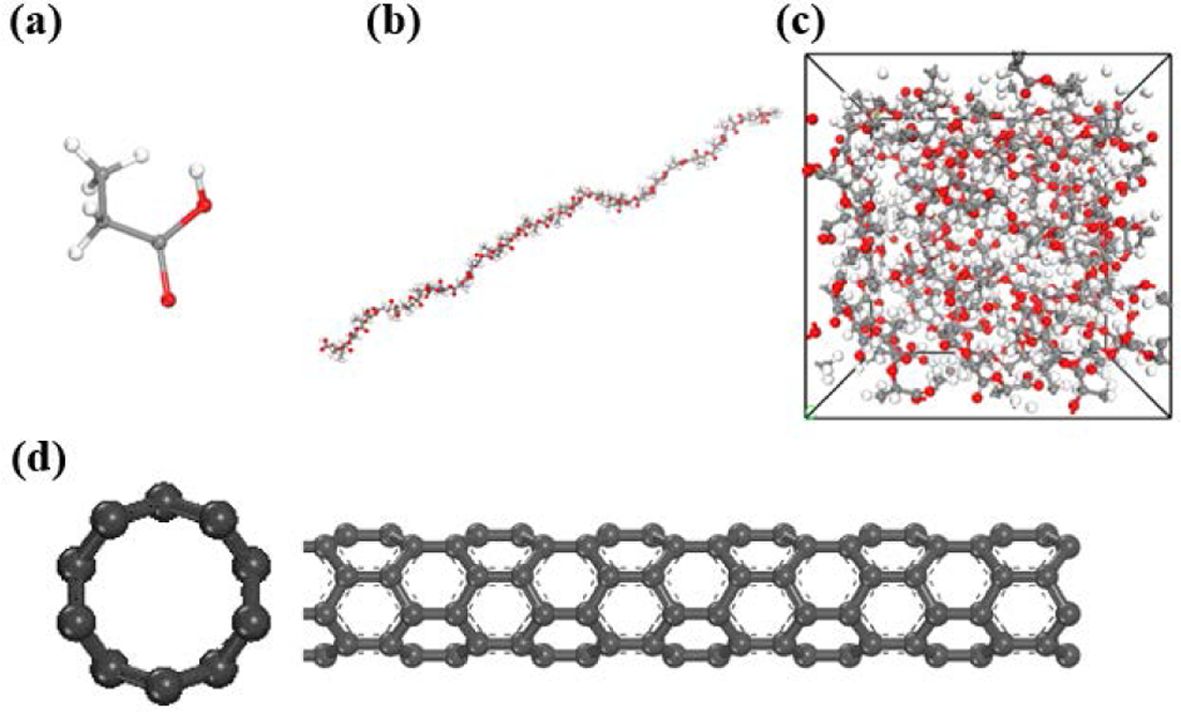
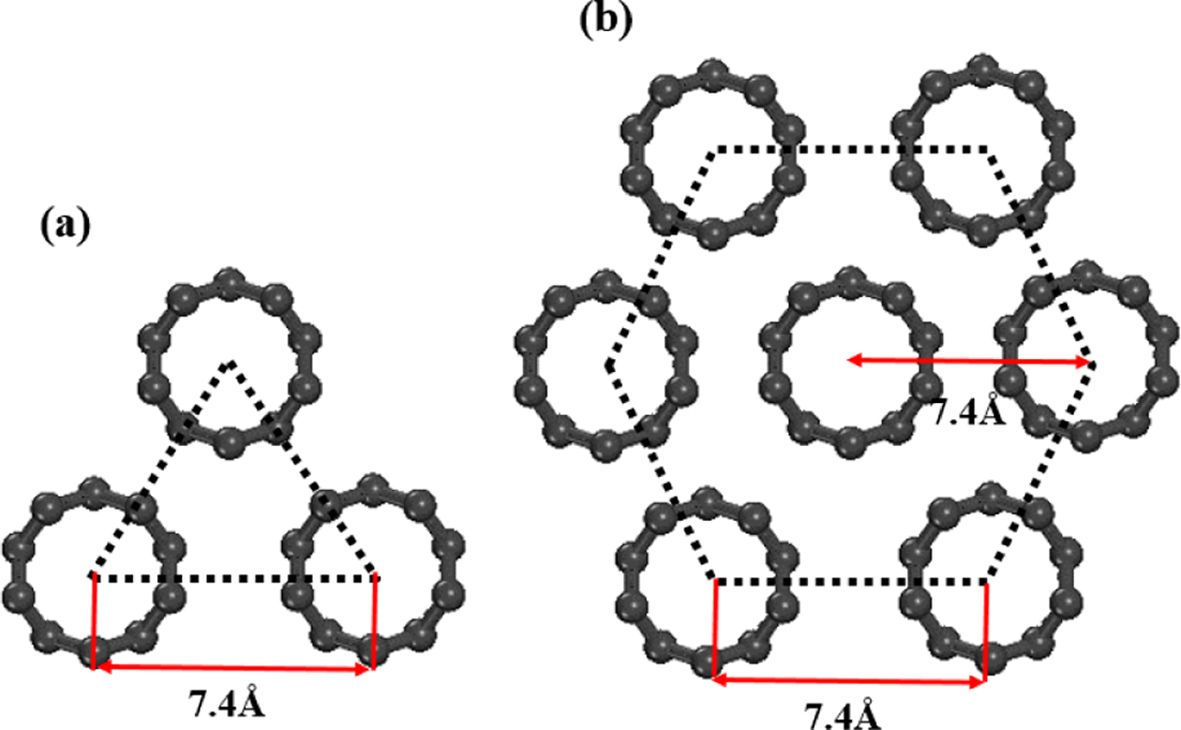
본 연구에서는 50개의 단량체를 중합하여 만든 PLA 사슬과 (5, 0) 단일벽 탄소나노튜브를 포함하는 나노복합재료를 이용하였다. 그림은 Fig. 1에 제시하였다. 동일한 체적분율에 대하여, 탄소나노튜브의 개수를 조절함으로써 탄소나노튜브 다발을 구성하였다. 탄소나노튜브 간 중심거리는 안정화된 거리인 7.4 Å으로 정하였으며(Fig. 2), 복합재료 단위 셀의 체적분율은 5.77%가 되도록 구성하였다. 단위 셀의 구조적 정보는 Table 1에 제시하였으며, z축을 탄소나노튜브의 길이 방향으로 설정하였다. 벌크 물성을 예측하기 위하여, x, y, z축 각 방향에 대해서 주기 경계 조건을 부여하였으며, 탄소나노튜브와 PLA 사이에는 비공유결합(반데르발스 힘과 전자기적 인력)만 작용하는 것으로 가정하였다. 본 연구에서 PLA 탄소 나노복합재의 분자모델 그림은 Fig. 3에서 제시하였다.

2.2 열-기계적 물성 도출을 위한 앙상블 시뮬레이션
나노복합재료의 안정화된 셀을 구성하기 위하여, 초기 셀을 구성한 이후, geometric optimization 기능을 통하여 힘 평형이 만족되는 구조를 도출하였다. 이후 NVT, NPT, NσT 앙상블 시뮬레이션을 각각 500 ps, 1500 ps, 500 ps 수행하여 상온 조건(300 K, 1 atm)에서의 안정화된 셀을 구축하였다. 이후, Parrinello-Rahman fluctuation analysis를 통하여 탄성행렬을 도출하였으며, 이로부터 면내 영률과 면내 전단계수를 도출하였다.
 

 
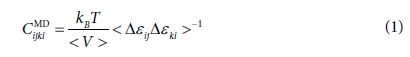
여기서 ε_ij, V 및 T는 각각 단위 셀의 변형률 텐서, 부피 및 온도이고, k_B 는 볼츠만 상수를 의미한다. 여기서 <•> 기호는 물리량의 앙상블 평균을 의미한다.
나노복합재료의 유리 전이 온도와 면내 열팽창 계수(coefficient of thermal expansion)를 도출하기 위하여, 고온 조건(440 K, 1 atm) 조건에서 안정화된 셀을 구성하고 20 K씩 준차적으로 절대온도를 낮추는 시뮬레이션을 진행하였다. 냉각 과정에서 도출된 온도-밀도 관계로부터 기울기의 변화가 일어나는 점으로부터 유리전이온도를 정의하였으며, 상온 주변에서의 기울기 값을 통해서 다음과 같이 면내 열팽창 계수를 도출하였다.
 

 
여기서 A₀ 은 상온에서의 탄소나노튜브에 수직한 방향의 단위셀 면적이다.

2.3 계면의 두께 조사
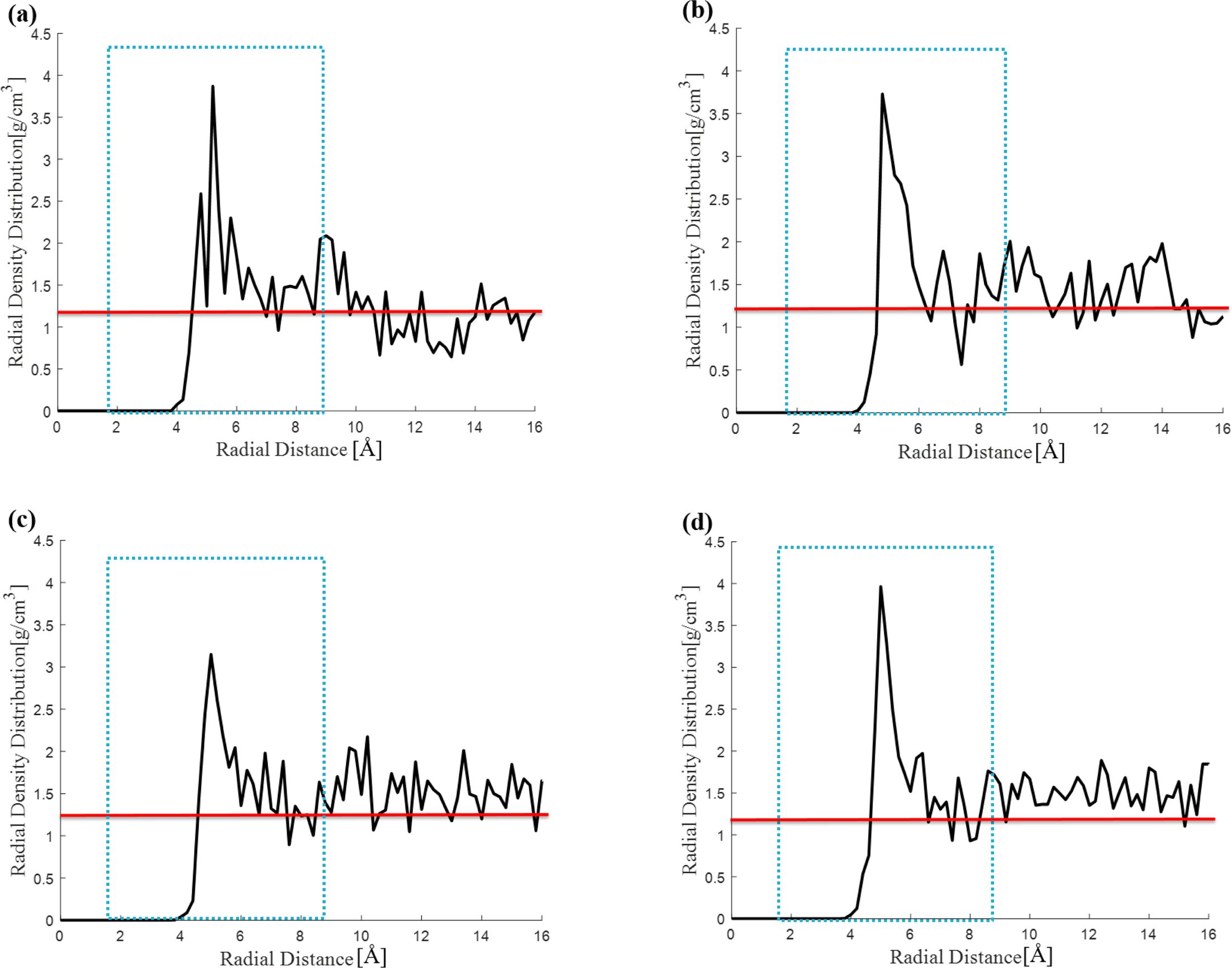
PLA 기지 재료의 나노 튜브의 중심 축을 기준으로 한 반경 방향 밀도 분포(radial density distribution)는 Fig. 4에서 제시하고 있다. 반경 방향 밀도 분포를 통해서 계면의 존재를 확인할 수 있었다. 파란 색 점선으로 이루어진 네모 상자 안쪽의 영역의 경우 반경 방향 밀도가 일반 기지재의 밀도(빨간 실선)에 비해 높음을 알 수 있는데, 이것이 곧 계면의 존재를 의미한다. 탄소나노튜브 다발 내부의 탄소나노튜브의 개수에 무관하게 계면의 존재는 명확하게 보였으며, 대략적으로 계면의 두께가 7 Å 정도임을 확인할 수 있었다.

본 연구에서는 계면의 영률, 전단계수, 열팽창계수를 얻기 위하여, 유한요소 기반 균질화 기법을 접목하였다. 유한요소 기반 균질화 기법을 통해서 나노복합재료의 유효 열-기계적 특성을 예측하였다[11,12].
 

 
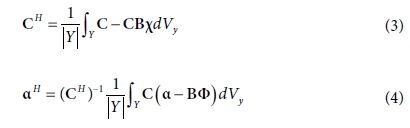
여기서, Y는 단위 셀의 체적을 의미하며, χ와 Φ는 다음 방정식을 통해서 계산할 수 있다.
 

 
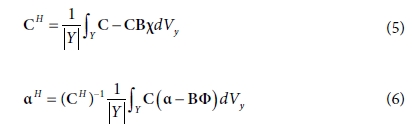
유한요소 모델링을 위하여, ANSYS Workbench 19.2를 이용하였다. 유한요소 모델링 과정에 사용한 탄소나노튜브의 탄성계수는 참고문헌[1]의 값으로부터 회귀분석을 해서 얻었다. 탄성계수의 값은 Table 2에 제시하였다. 열팽창계수는 가로방향은 –3.3 × 10^-6/K로 정하고 길이방향은 2.1 × 10^-6/K로 사용하였다[13]. 사용한 PLA의 영률와 열팽창계수는 분자동역학 시뮬레이션을 통해서 얻은 값을 사용하였다.
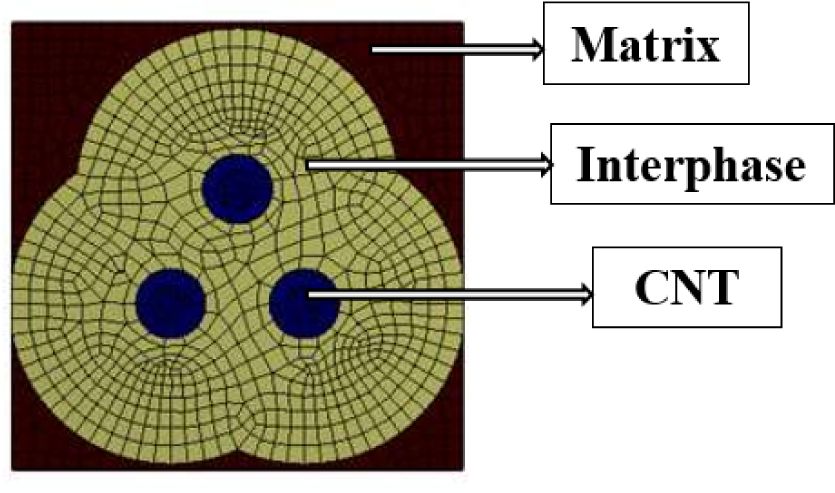
균질화를 통해서 얻은 복합재의 면내 영률, 면내 전단계수, 면내 열팽창계수가 분자동역학의 결과와 동일한 값을 갖도록 하는 계면의 영률, 전단계수, 열팽창계수를 도출하였다. 본 연구에서 응집된 탄소나노 3개 포함된 PLA 탄소 나노복합재료의 유한요소모델 그림은 Fig. 5에 제시하였다.

4.1 순수 PLA의 분자동역학 결과 및 실험과의 검증
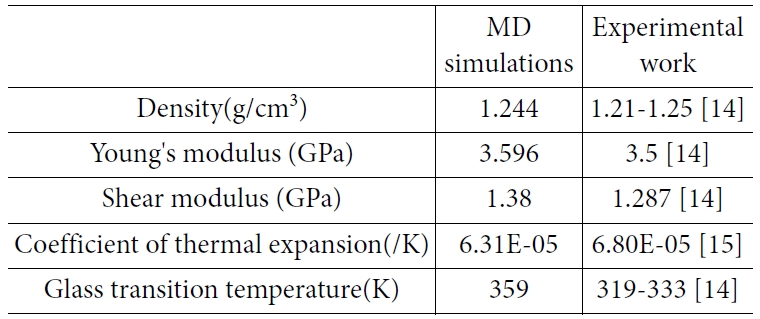
분자동역학 모델링 및 해석을 통해서 예측한 순수 PLA 재료의 밀도, 영률, 전단계수, 열팽창계수, 유리전이온도는 Table 3와 같다. 참고문헌의 실험값과의 비교를 제시하였으며, 높은 정확도를 보였음을 알 수 있었다.

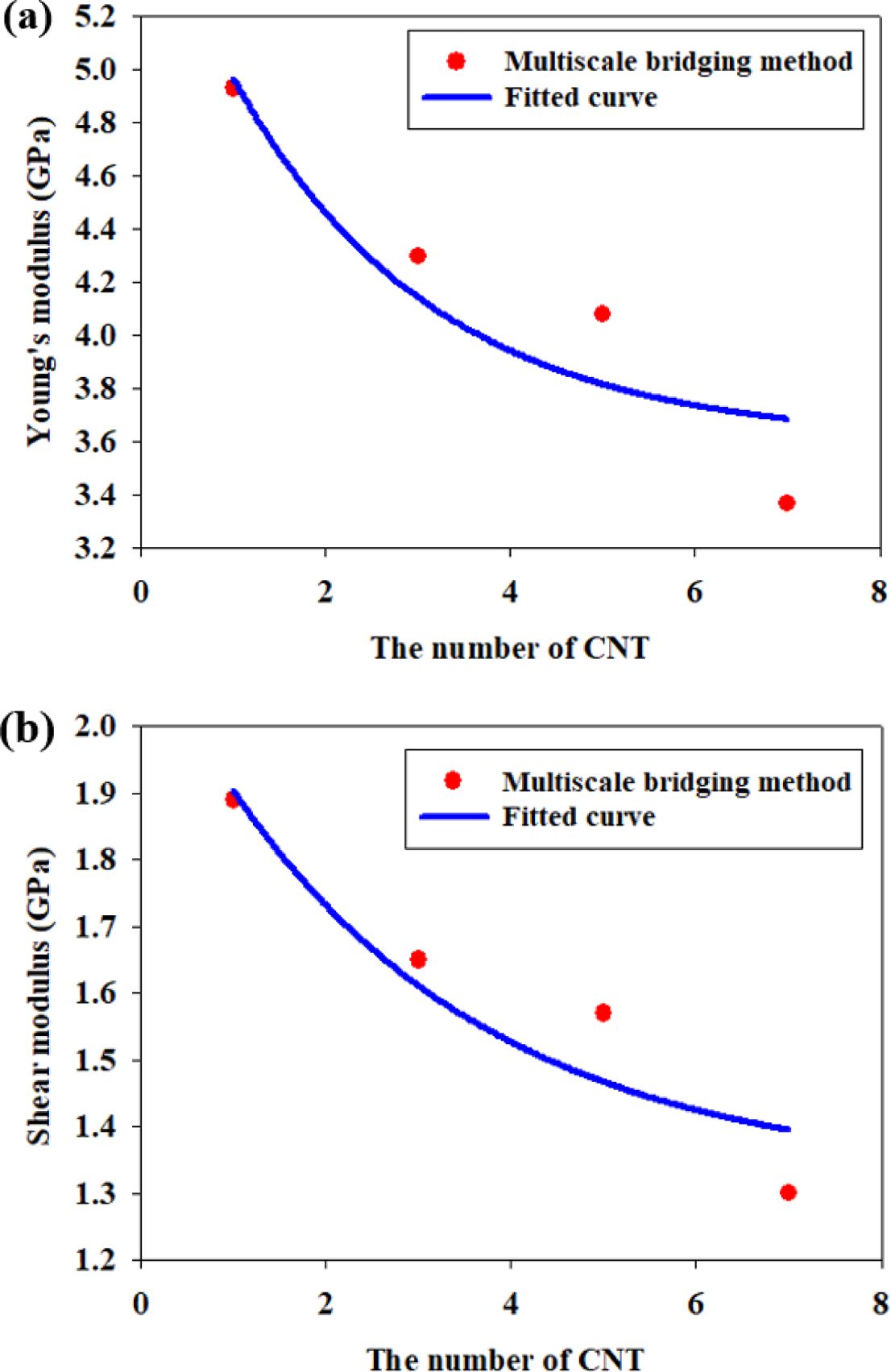
4.2 계면의 영률 및 전단계수의 도출
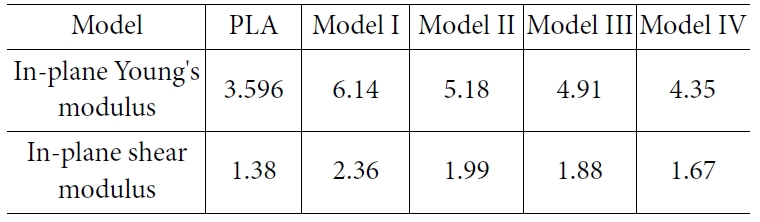
Table 4는 분자동역학 전산모사를 통해 예측한 순수 PLA와 나노복합재료의 면내 영률과 면내 전단계수를 정리한 표이다. 면내 영률과 면내 전단계수는 모두 나노복합재료의 값이 순수한 PLA의 값보다 더 크게 나타났으며, 탄소나노튜브에 의한 강화 효과가 보인다. 탄소나노튜브 다발을 포함하는 나노복합재료의 멀티스케일 모델을 개발하기 위하여, 유한요소 기반 균질화 기법과 같이 제안된 멀티스케일 브리징 방법론을 통하여 계면에서의 영률과 전단계수를 역산하였다. 그 결과는 Fig. 6과 같다. 각 빨간점은 제안된 멀티스케일 브리징 방법론을 통하여 직접 예측한 계면에서의 영률과 전단계수이다. 다발당 탄소나노튜브의 수가 증가함에따라 계면에서의 영률과 전단계수가 점진적으로 감소함을 확인할 수 있었으며, 최소자승법을 통하여 구한 파란선과 같이 exponential decay 함수 형태의 계면모델을 구성하였다.
 

 
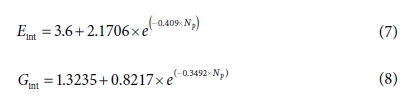
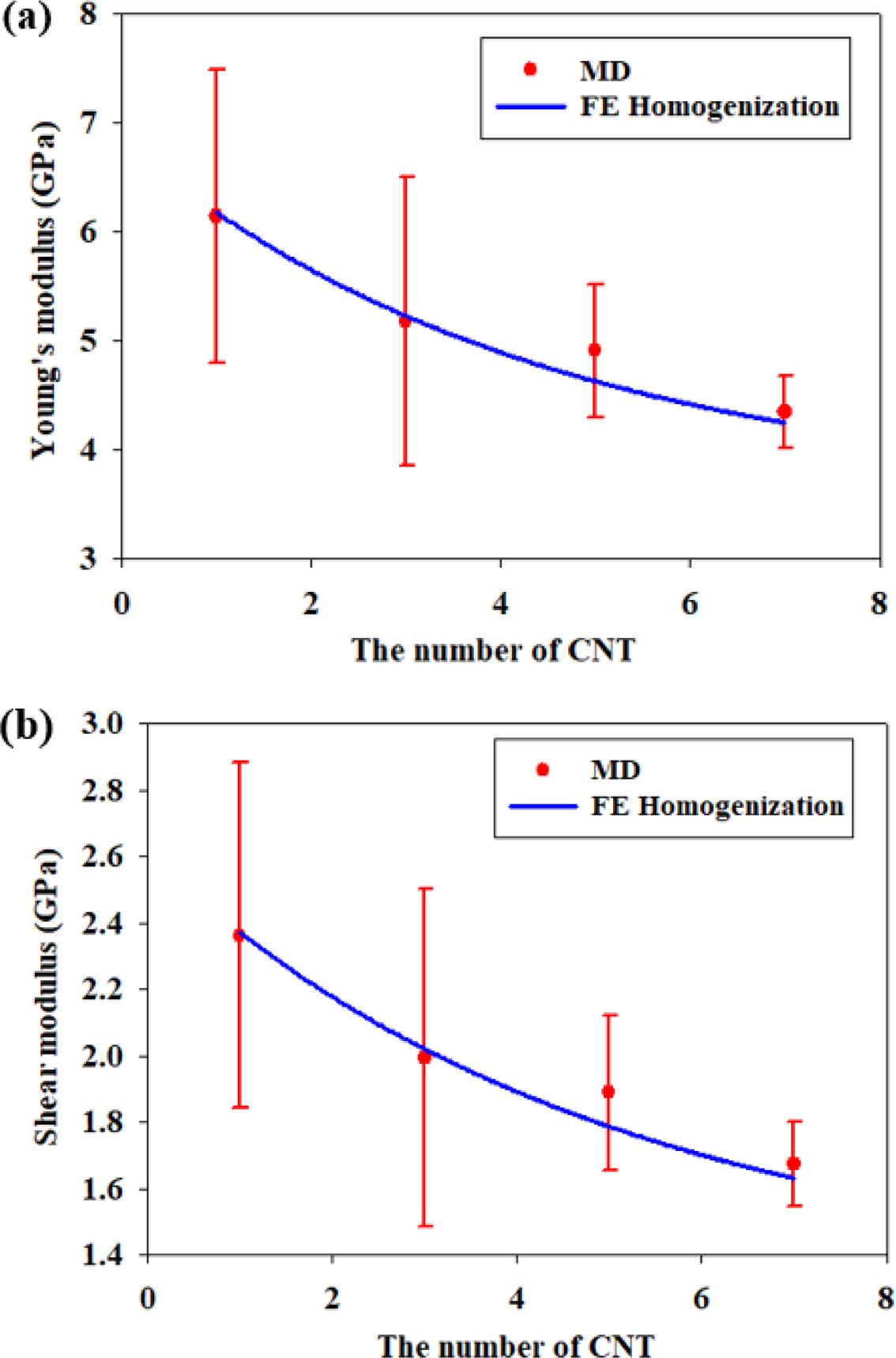
제안된 계면 모델을 반영한 멀티스케일 유한요소 모델의 정확성을 검토하기 위하여, 직접적으로 계산한 분자동역학 해와 비교를 하였다. Fig. 7는 제안된 계면 모델과 멀티스케일 균질화 기법을 기반으로 계산한 나노복합재료의 면내 영률 및 면내 전단계수이다. 실제로 Table 4와 거의 일치함을 확인할 수 있었으며, 제안된 계면 모델에 기반한 멀티스케일 균질화 방법론이 적절함을 확인할 수 있었다.

4.3 열 특성 예측
4.3.1 유리전이 온도
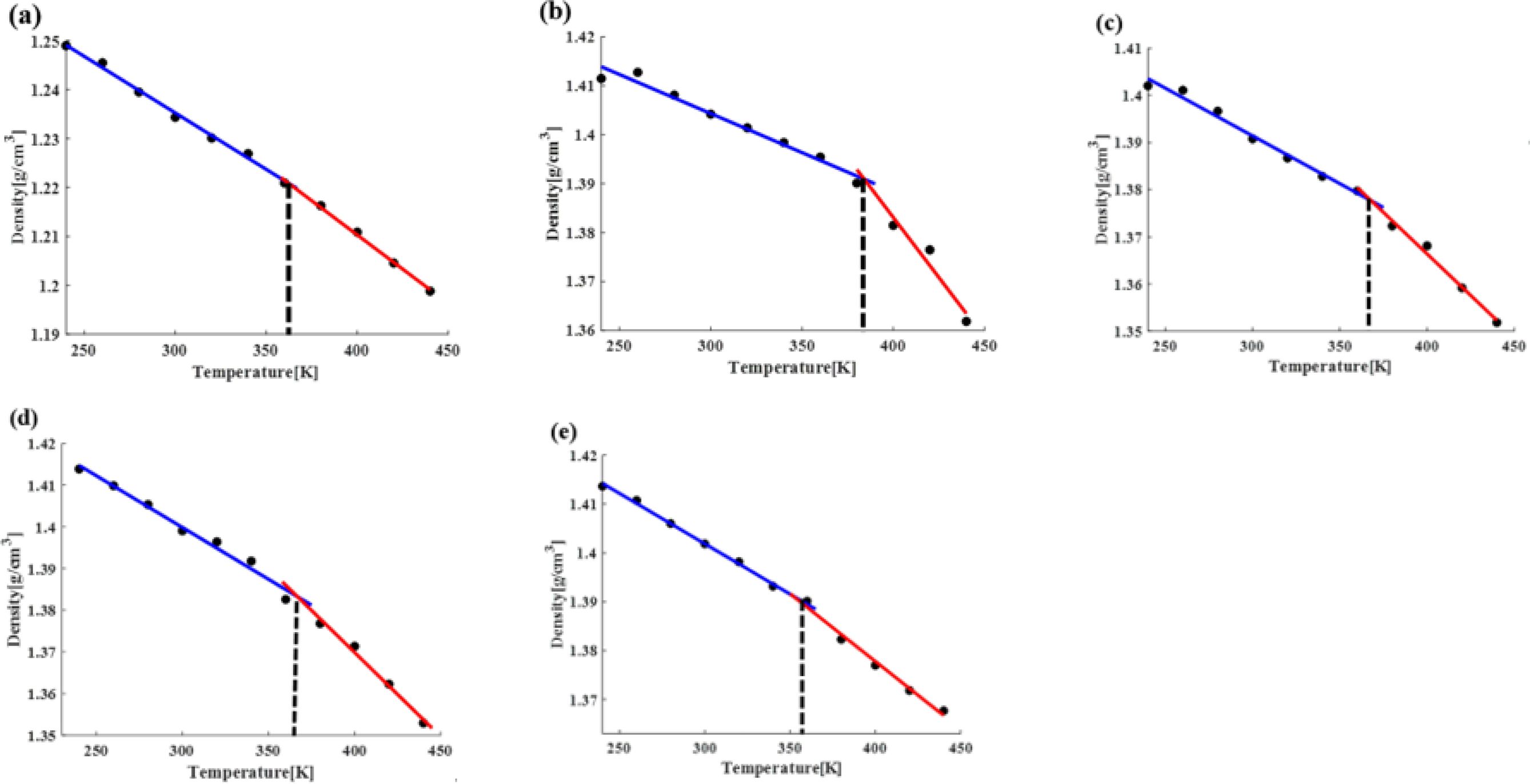
순수한 PLA와 나노복합재료의 온도-밀도 관계를 Fig. 8와 같이 도출할 수 있었다. Fig. 8에서 파란선은 유리상(glassy state)에서의 회귀분석 선도, 빨간선은 고무상(rubbery state)에서의 회귀분석 선도에 해당한다. 함수의 기울기가 변하는 부분을 유리전이온도로 계산하였다. 순수한 PLA와 나노복합재료의 유리전이온도(glass transition temperature)는 Table 5과 같다. 균일하게 분산된 탄소나노튜브를 포함하는 나노복합재료의 경우 높은 유리전이온도를 가졌지만, 다발당 탄소나노튜브의 수가 증가함에 따라 점차 유리전이온도가 작아진다는 것을 확인할 수 있었다. 탄소나노튜브가 균일하게 분산될 경우, 계면의 결정화도가 증가함이 알려져 있으며 그에 따라 계면의 강성이 증가하며, 나노복합재료의 유리전이온도가 증가한다. 하지만, 탄소나노튜브의 분산 특성이 나빠질 경우, 계면의 강성이 약화되며, 나노복합재료의 유리전이온도 또한 급격하게 감소한다는 것을 분자동역학 전산해석 결과를 통해서도 확인할 수 있었다.
 
4.3.2 열팽창 계수
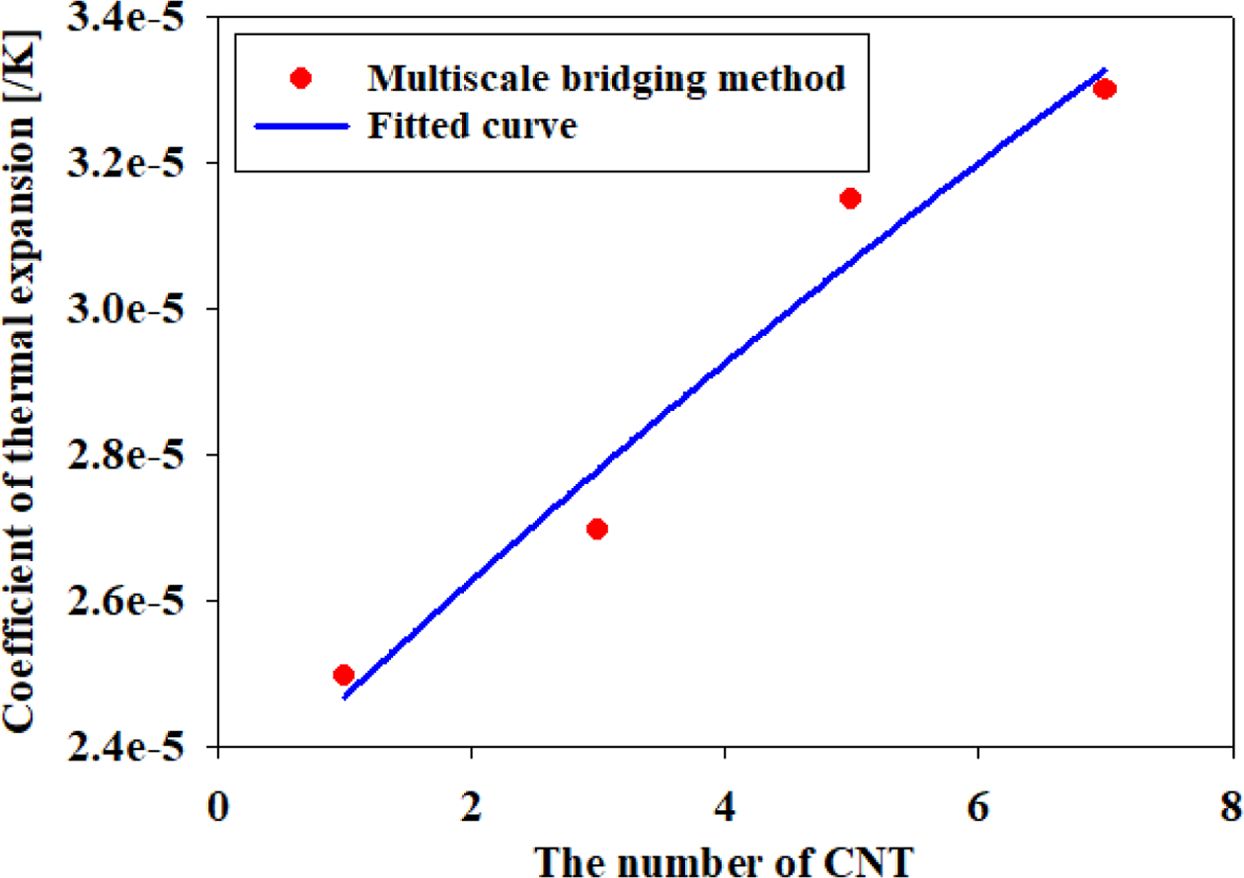
분자동역학 전산모사를 통해서 도출한 순수한 PLA 및 나노복합재료의 면내 열팽창계수의 예측 결과를 Table 6와 같이 정리하였다. 나노복합재료의 열팽창계수가 순수한 PLA에 비해서 낮다는 것을 확인할 수 있었으며, 이는 실험에서의 경향과도 일치한다. 계면에서의 결정화도가 증가함에 따라 열팽창계수가 감소했을 것으로 예상하고, 유한요소 기반 균질화 기법에서 제안된 멀티스케일 브리징 방법론을 통하여 계면에서의 열팽창계수를 역산하였다. 그 결과, Fig. 9과 같이 계면에서의 열팽창계수를 도출하였다. 탄소나노튜브가 균일하게 분산된 경우, 실제로 계면에서의 열팽창계수가 순수한 PLA에 비해 2배 이상 낮음을 확인할 수 있었다. 다발당 탄소나노튜브의 수가 증가함에 따라 계면에서의 열팽창계수가 점차 증가함을 확인할 수 있었는데, 이는 다발당 탄소나노튜브가 증가함에 따라 계면의 결정화도가 낮아지고 이에 따라 열팽창계수가 증가한 것으로 예상한다. 역산된 계면에서의 열팽창계수를 최소자승법을 통해서 지수함수로 만들었으며, 그 결과는 다음과 같다.
 

 
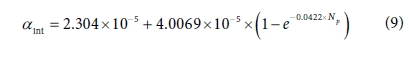
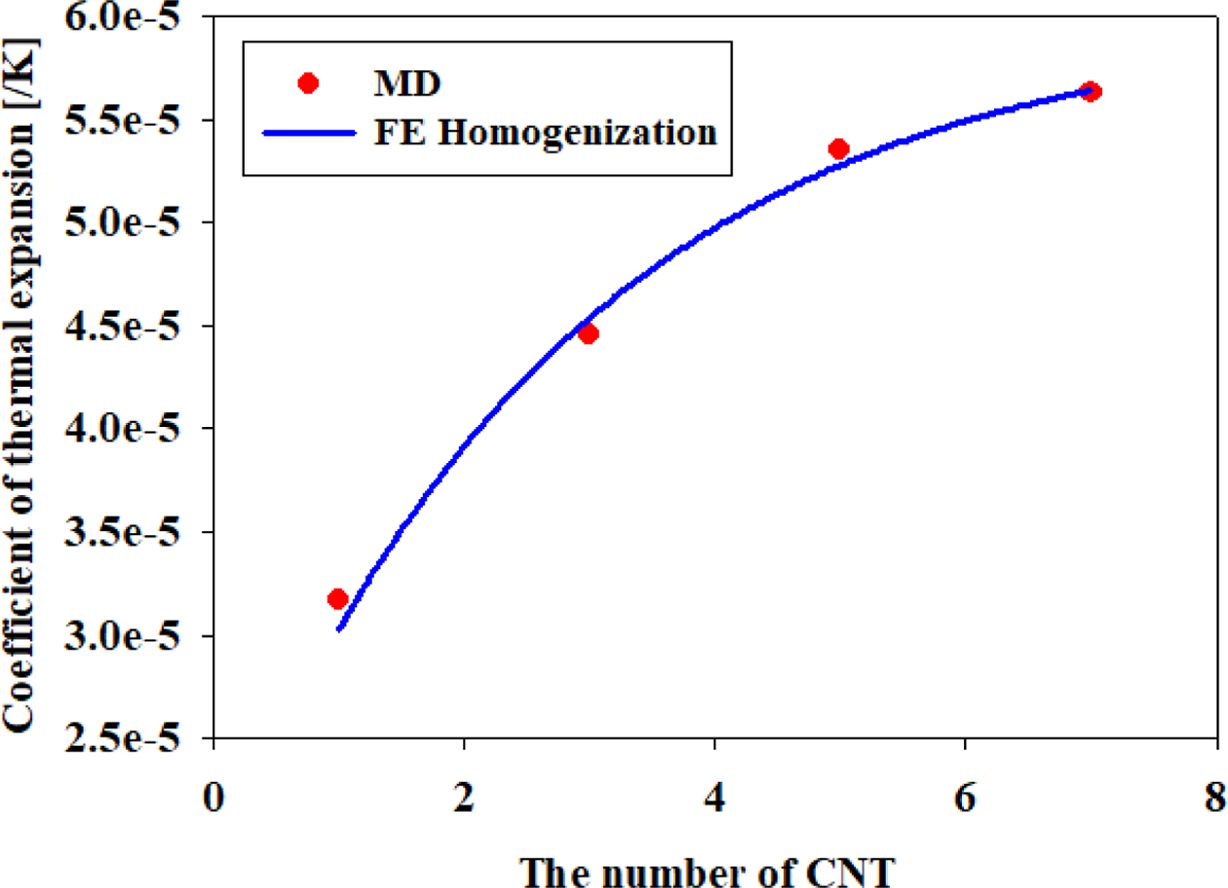
제안된 계면 모델을 반영한 멀티스케일 유한요소 모델의 정확성을 검토하기 위하여, 직접적으로 계산한 분자동역학 해와 비교를 하였다. Table 6과 Fig. 10은 제안된 계면 모델과 멀티스케일 균질화 기법을 기반으로 계산한 나노복합재료의 면내 열팽창계수이다. 분자동역학 전산해석을 통해서 직접 예측한 결과와 거의 일치함을 확인할 수 있었으며, 제안된 계면 모델에 기반한 멀티스케일 균질화 방법론이 적절함을 확인할 수 있었다.

본 연구에서는 PLA와 탄소나노튜브 다발을 포함하는 나노복합재료의 멀티스케일 모델링 기술을 개발하였다. 순수한 PLA와 나노복합재료의 열-기계적 특성을 분자동역학 전산해석을 통해서 예측하였으며, 순수한 PLA의 결과에 대해서 실험값과 비교하였다. 그 결과, 높은 정합성을 보임을 확인할 수 있었다. 더 나아가, 계면에서의 열-기계적 특성을 역산하기 위하여 분자동역학-유한요소 균질화 연계 멀티스케일 브리징 기법을 제안하였으며, 계면에서의 열-기계적 특성을 다발당 탄소나노튜브의 수에 대한 함수로 모사하였다. 제안된 계면 모델을 반영한 유한요소 균질화 모델이 분자동역학 모델을 통해서 예측한 해와 거의 일치함을 확인할 수 있었다.
해석 결과, 다발당 탄소나노튜브의 수가 증가함에 따라, 계면에서의 영률 및 전단계수는 점차 감소함을 확인할 수 있었고, 열팽창계수는 점차 증가함을 확인할 수 있었다. 이는, 탄소나노튜브의 분산이 균일하지 않을 경우, 균일하게 분산된 경우에 비해 열-기계적 특성이 약화될 수 있음을 알려준다.
향후 연구에서는 임의로 분산된 다량의 다발이 포함된 나노복합재료의 유효 물성을 효율적으로 예측하기 위한 멀티스케일 균질화 모델을 개발하고자 한다. 더 나아가, 비선형 기계적 거동(탄소성 거동, 점탄성 거동 등)이나 열전도율의 예측 모델 개발로 확장하고자 한다.

본 연구는 2020년 (재)동일문화장학재단 학술연구조성비 지원에 의해 수행되었음.