The compression and tension test were performed to evaluate the stiffnesses of the conical composite lattice structures and results of test were compared with finite element analysis results. Because of difficulty to perform simple tension and compression test due to conical shape, suitable specimens and jig for test were made. Subelements extracted from the structure were prepared for compression test. Compression test of subelement was performed and compressive strains in fiber direction were measured. Compressive stiffness of the helical rib was verified by finite element analysis results. For stiffness of hoop rib, hoop ring specimens were extracted from the structure. Tension test of hoop ring specimen was performed to apply bending deformation to hoop rib. Stiffness of hoop rib was verified by finite element model considering various fiber volume fraction in thickness direction.

콘형 복합재 격자 구조체의 강성 평가를 위한 두 종류의 시편 단위 압축 및 인장 시험을 수행하였으며 유한요소해석 결과와 비교하였다. 구조체는 높이별로 반경이 변화하는 콘형이므로 단순 압축 및 인장 시험이 어려우므로 시험 수행이 가능한 형태의 시편 및 지그를 제작하여 시험을 수행하였다. 압축 시험이 가능하도록 단위 격자 구조체를 Subelement 형태로 가공하였으며, 압축 시험을 수행하여 측정된 섬유방향 압축 변형률을 유한요소해석 결과와 비교하여 헬리컬 리브의 강성을 확인하였다. 후프 리브의 강성 평가를 위해서는 구조체에서 후프 링 시편을 가공하여 인장 시험을 수행하였다. 후프 링에 인장 하중을 가하여 굽힘 변형이 크게 발생하도록 하였으며, 두께 방향 섬유체적비를 고려한 유한요소해석 결과와 비교하여 후프 리브의 강성을 확인하였다.

Keywords: 콘형 복합재 격자 구조(Conical Composite Lattice Structures), 단위 격자 구조(Unit Lattice Structure), 후프 링(Hoop Ring), 유한요소해석(Finite Element Analysis)

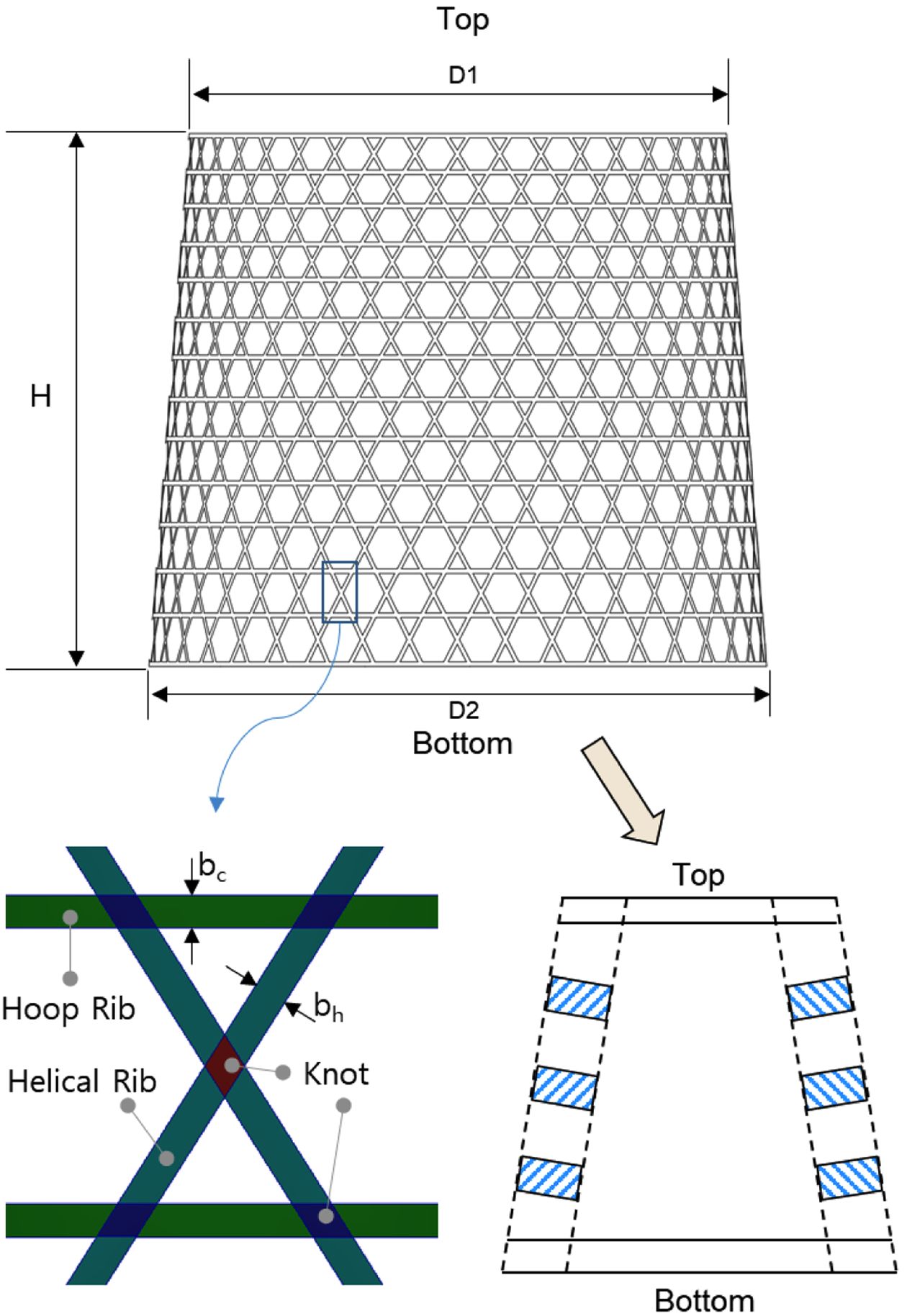
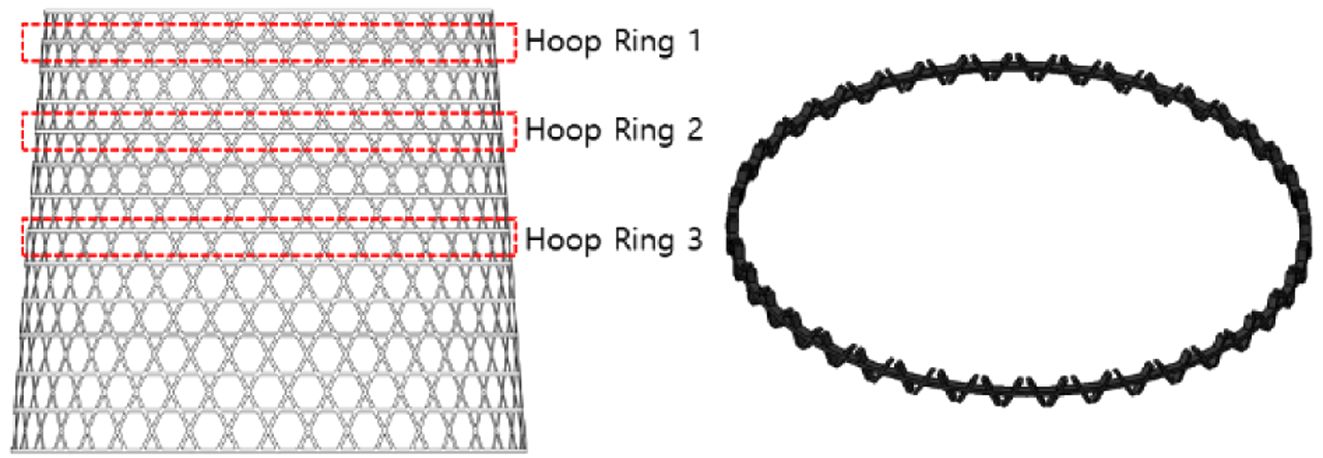
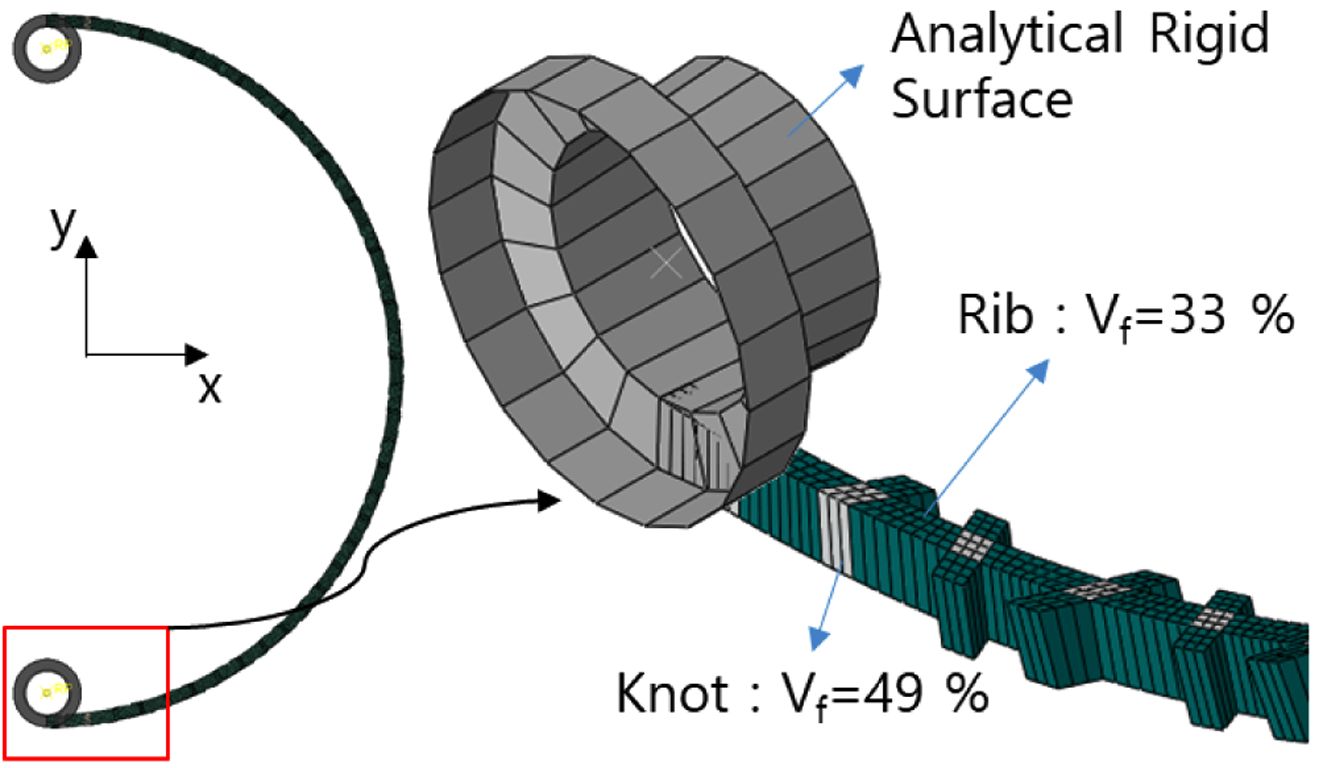
비강성, 비강도가 우수한 탄소섬유 복합재료로 제작된 복합재 격자 구조는 경량화를 주 목적으로 주로 압축 하중을 받는 항공우주 구조물에 많이 사용되고 원통형 및 콘형으로 제작되며 항공기의 동체, 날개, 우주 발사체의 인터스테이지(Inter-Stage)에 적용할 수 있다[1]. 복합재 격자 구조는 필라멘트 와인딩 공법으로 제작되며 Fig. 1과 같이 나선 방향의 헬리컬 리브(Helical Rib)와 원주 방향의 후프 리브(Hoop Rib)로 구성된다. 복합재 격자 구조는 섬유를 연속해서 적층하는 방식으로 인하여 섬유가 교차하는 섬유교차부(Knot)가 존재한다. 구조체의 두께는 일정하게 제작하므로 섬유교차부의 두께는 섬유교차부가 없는 리브의 두께와 동일하지만 적층수는 두 배가 되어 섬유체적비가 일정하지 않다. 섬유체적비에 따라 구조체의 각 요소에서 강성이 다르게 나타날 수 있다. 특히, 콘형 구조는 구조의 높이별로 헬리컬 리브의 각도가 달라지므로 제작 과정에서 섬유가 편중되는 현상이 나타날 수 있다. 운용중 발생하는 변형 및 좌굴 예측을 위해 제작이 완료된 구조의 강성을 평가할 수 있는 방법이 필요하지만 전체 구조의 압축 시험을 반복적으로 수행하기에는 공간, 시간 및 비용의 제약이 크다. 각 리브들은 기하학적으로 원주 방향과 나선 방향으로 곡률을 갖는 형상이며 콘형 구조는 Fig. 1에서 볼 수 있듯이 구조 단면에 기울기가 있어 단순한 인장, 압축 및 휘임 시험에 어려움이 많다. 따라서 간단하고 단순한 단위 시편의 시험을 수행할 수 있는 시험법이 필요하다.
Terashima 등[2]은 원통형 복합재 격자 구조의 각 요소별로 CT 검사를 통하여 섬유체적비를 확인하였다. 각 리브와 단위 시편의 압축 시험을 수행하여 강성 및 강도를 확인하였으며 좌굴 및 변형 해석에 적용하여 시험 결과와 유사한 결과를 도출하였다. Aoki 등[3]은 리브의 단면적 및 재료 구성에 따른 단위 시편의 압축 시험을 수행하여 좌굴 하중 예측에 적용하였다. 전 등[4]은 원통형 복합재 격자 구조 단위시편의 압축 시험 및 후프 리브의 휘임 시험 수행 및 유한요소해석 결과와 비교하여 원통형 구조의 강성을 확인하였다. 강 등[5]은 헬리컬 및 후프 리브의 단면 검사를 수행하여 섬유체적비를 측정하였으며 그에 따른 강성을 확인하였다. 임 등[6]은 콘형 복합재 격자 구조의 유한요소해석을 수행하였으며 압축 시험 결과와 비교하여 구조안정성을 평가하였다. 압축 하중을 받는 콘형 복합재 격자 구조는 좌굴에 취약하므로 좌굴 하중에 대한 제약조건하의 최적설계 연구와 굽힘, 비틀림 및 축방향 변형 예측을 위한 연구가 다수 수행되었다[7-10]. 설계 및 최적화 단계에 앞서 압축 하중이 작용하는 구조의 정확한 변형 및 좌굴 하중 예측을 위한 콘형 복합재 격자 구조의 강성 평가가 선행되어야 한다.
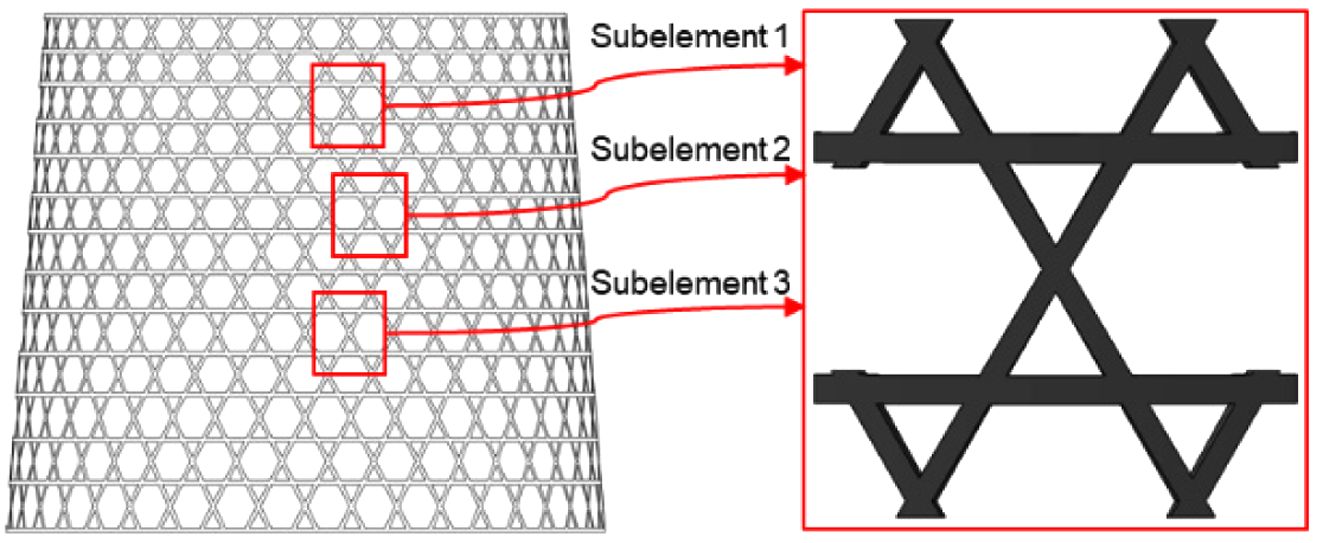
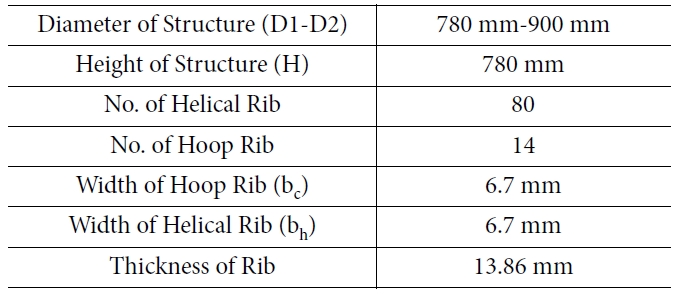
본 논문의 콘형 복합재 격자 구조는 필라멘트 와인딩 공법으로 제작되었으며 상세 치수는 Table 1과 같다. 구조체로부터 두 가지 시편을 가공하여 시험을 수행하였다. 헬리컬 리브의 강성 도출을 위해 압축 시험이 가능하도록 Fig. 2와 같은 단위 격자 구조 Subelement로 가공하여 압축 시험을 수행하였다. 후프 리브는 구조체에서 후프 링 시편을 가공하여 인장 시험을 수행하였다. 각 리브에서 측정된 변형률을 유한요소해석 결과와 비교하여 콘형 복합재 격자 구조의 강성을 확인하였다.

2.1 Subelement의 압축 시험 방법
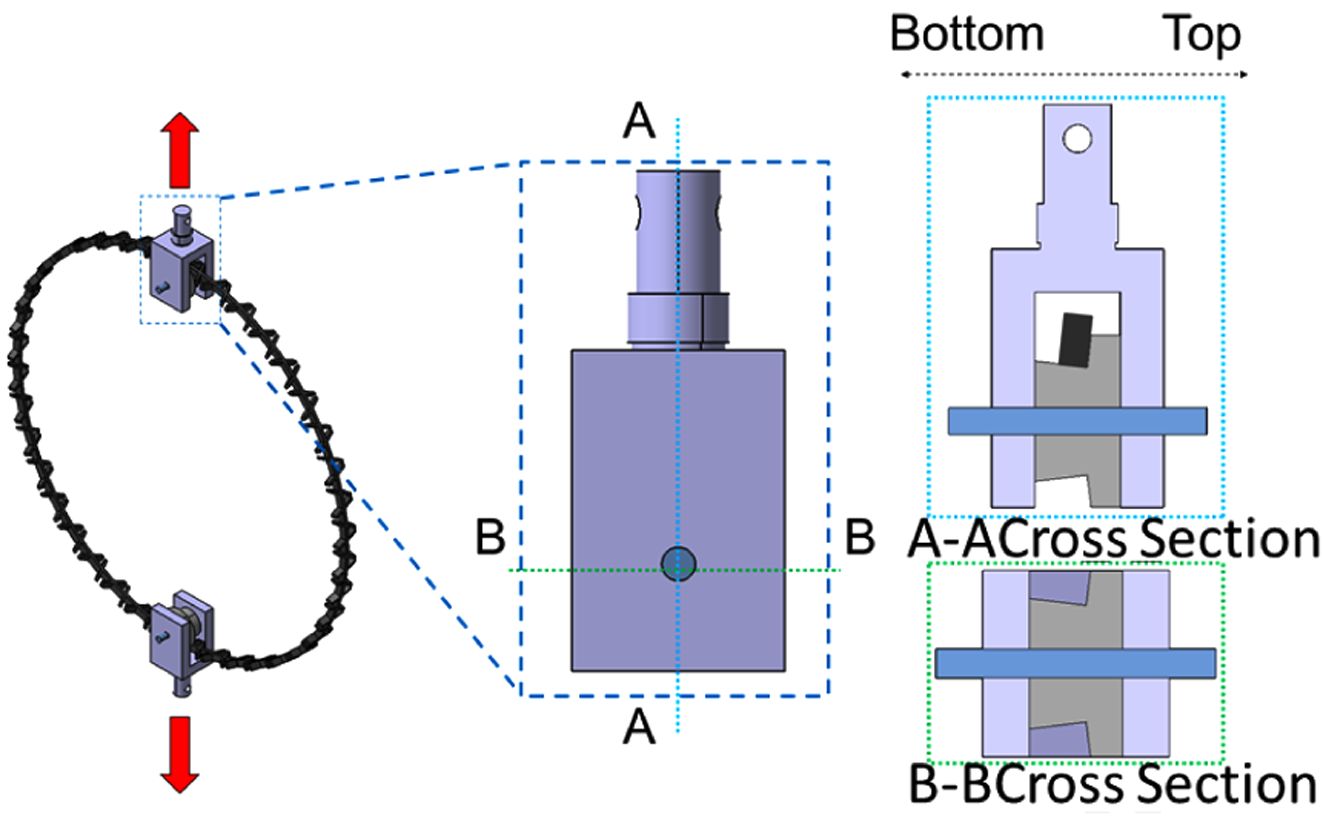
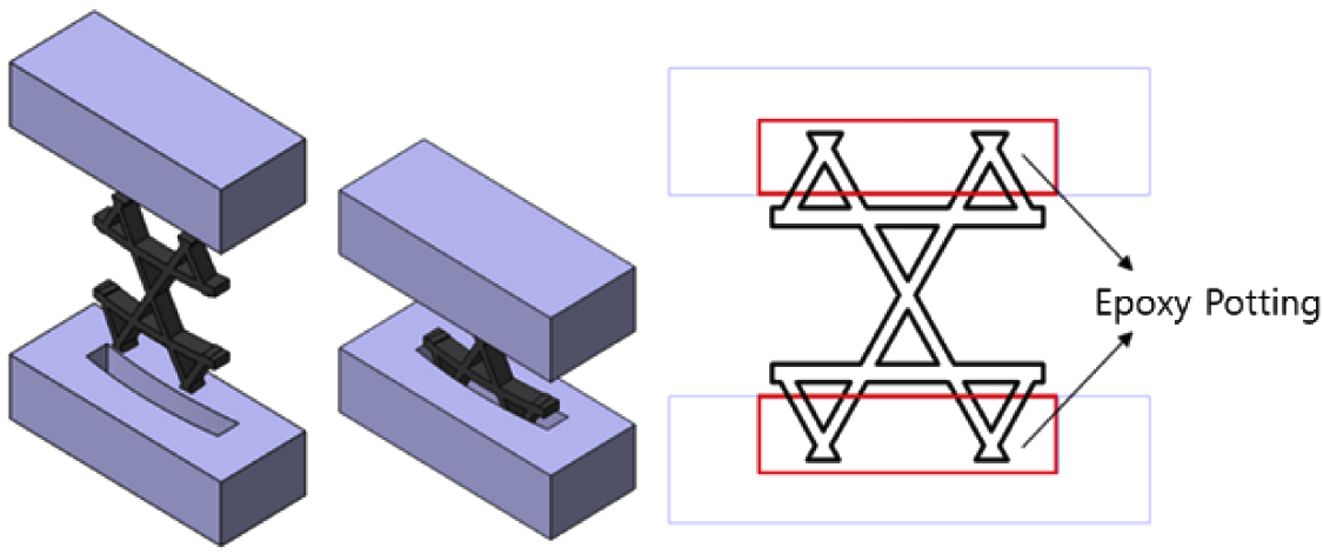
헬리컬 리브의 강성 확보를 위해 Subelement를 가공하여 압축 시험을 수행하였다. 단위 격자에 압축 하중을 가하는 것이 주 목적이며 각 리브에 하중이 균일하고 안정적으로 가해질 수 있도록 Fig. 2와 같이 확장된 형태로 시편을 가공하였다. 원통형 구조는 후프 리브의 외형이 균일하므로 단순한 압축 치구와의 접촉으로 압축 하중을 전달할 수 있다[4]. 콘형 복합재 격자 구조는 높이별로 직경이 변화하며 단면이 기울어진 형태이다. 형상이 일정하지 않으므로 시편을 고정할 수 있는 치구를 만드는 것은 큰 비용과 시간이 소모된다. 따라서 시편 형상에 알맞은 치구를 제작하지 않고 Fig. 3과 같이 시편과 금속 치구를 에폭시로 접착하여 하중을 전달할 수 있도록 시험 치구를 제작하였다. 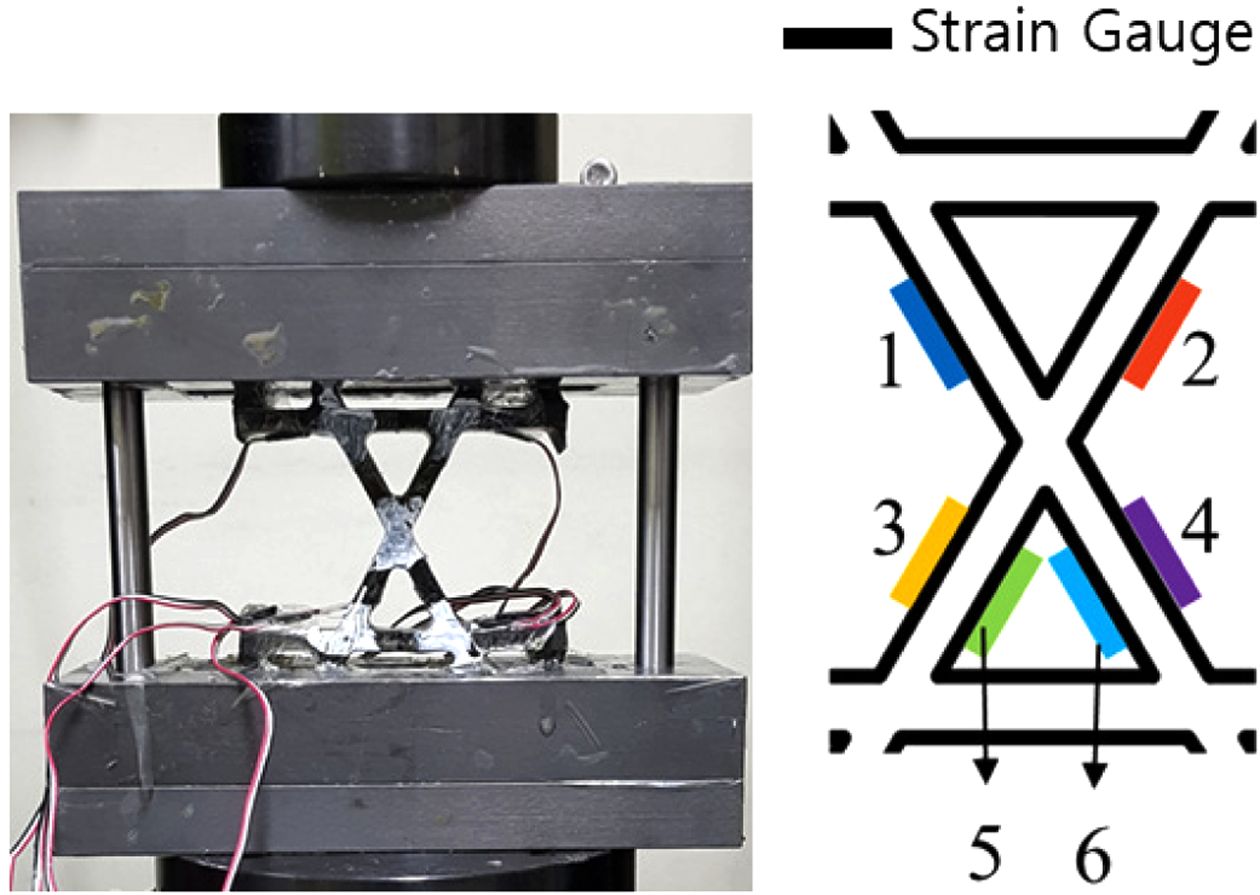유한요소해석 결과 비교를 통한 헬리컬 리브의 강성 평가를 위해 Fig. 4와 같이 리브의 옆면에 스트레인 게이지를 부착하여 섬유방향 변형률을 측정하였다.

2.2 후프 링의 인장 시험 방법
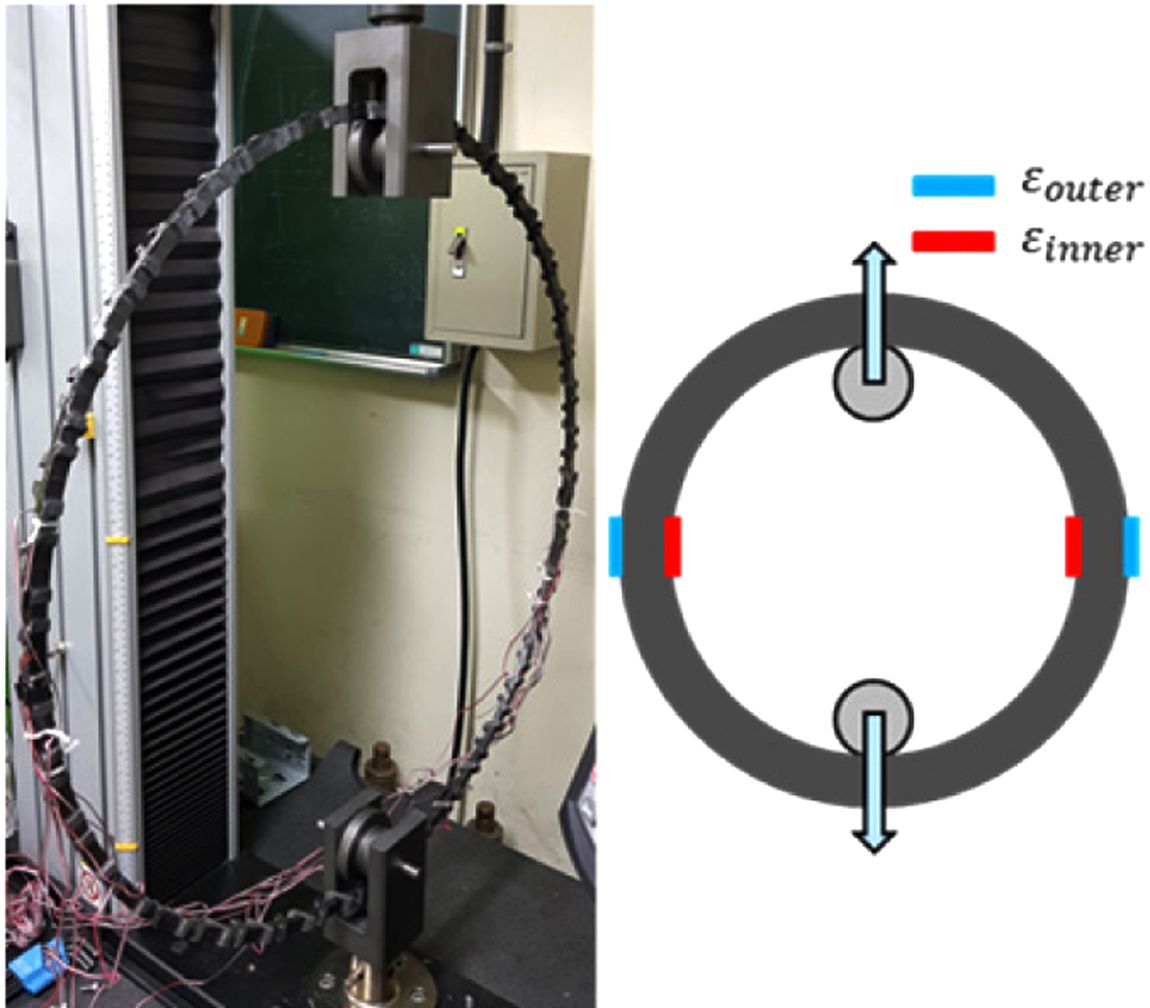
후프 리브의 강성 확보를 위해 콘형 격자 구조체에서 후프 링을 가공하여 인장 시험을 수행하였다. 원통형 격자 구조의 후프 리브는 형상이 균일하므로 단순한 4점 휘임 시험이 가능하다[4]. 그러나 콘형 격자 구조 후프 리브의 단면은 기울어진 형태이므로 4점 휘임 시험 치구에 안정적인 고정이 어렵지만, 기울어진 경사 각도는 균일하므로 경사 각도에 맞는 치구를 제작하여 후프 링의 반복 시험을 수행하였다. Fig. 5와 같이 서로 다른 높이에 위치한 후프 링 시편을 가공하였으며, Fig. 6과 같이 후프 링에 접촉을 통한 인장 시험을 가할 수 있는 금속 치구를 제작하여 인장 시험을 수행하였다. Fig. 7은 후프 링의 인장 시험을 수행하는 사진이며 굽힘 변형이 크게 발생하므로 후프 리브의 내경, 외경면에 스트레인 게이지를 부착하여 섬유방향 변형률을 측정하였다.

3.1 Subelement의 유한요소해석
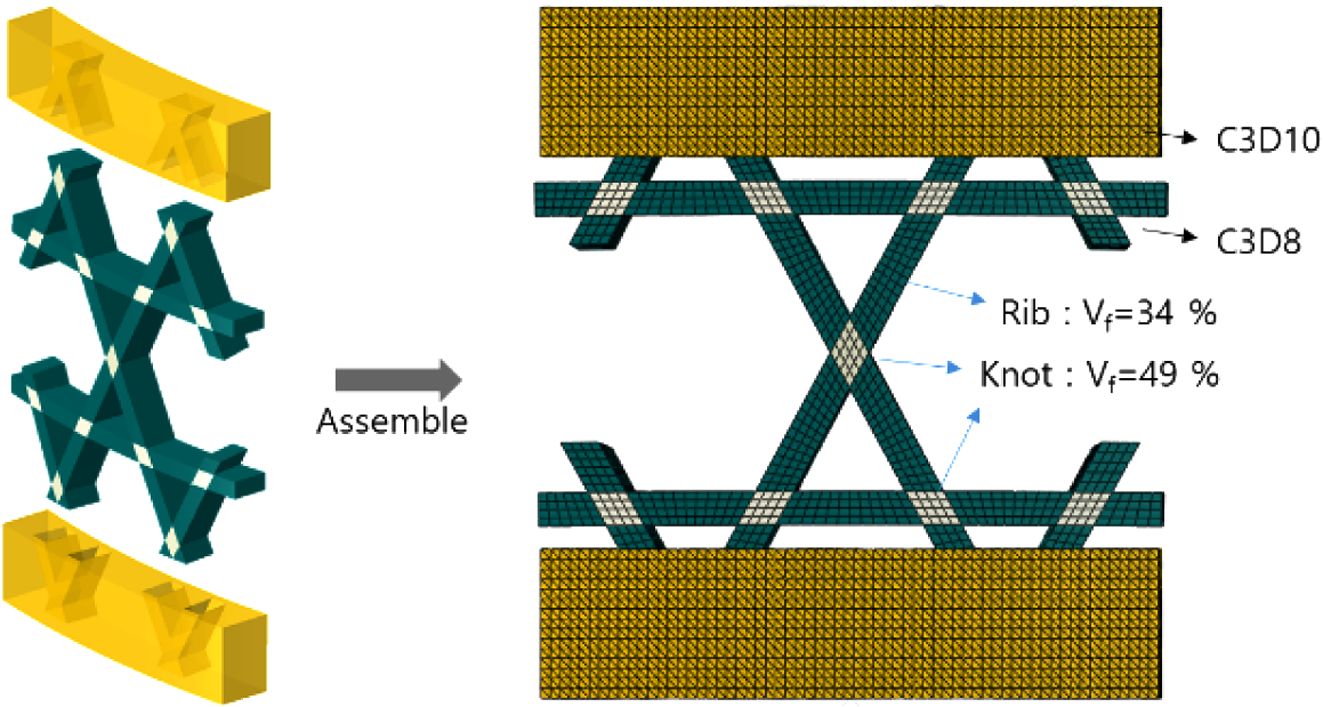
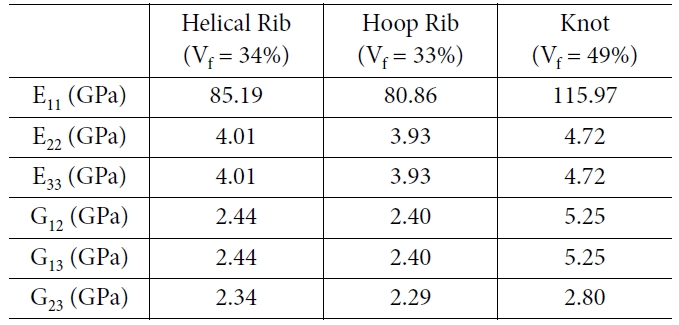
시편 형상 및 측정된 치수를 이용하여 Fig. 8과 같이 Subelement 및 포팅 에폭시를 모델링하였다. Subelement 시편은 ABAQUS의 3차원 6면체 요소인 C3D8로 모델링하였으며 포팅된 에폭시 영역은 3차원 4면체 요소인 C3D10으로 모델링하였다. Subelement와 에폭시 요소는 Tie 조건으로 완전 접착 조건을 적용하였다. 복합재 물성은 제작에 사용된 섬유의 개수 및 측정된 치수를 이용하여 계산된 섬유체적비에 따라 각 리브 및 섬유교차부에 적용하였다. 섬유체적비는 헬리컬 리브와 후프 리브에서 각각 34, 33%, 섬유교차부에서 49%로 측정되었다. 각 영역에 적용된 물성은 Table 2와 같다.

3.2 후프 링의 유한요소해석
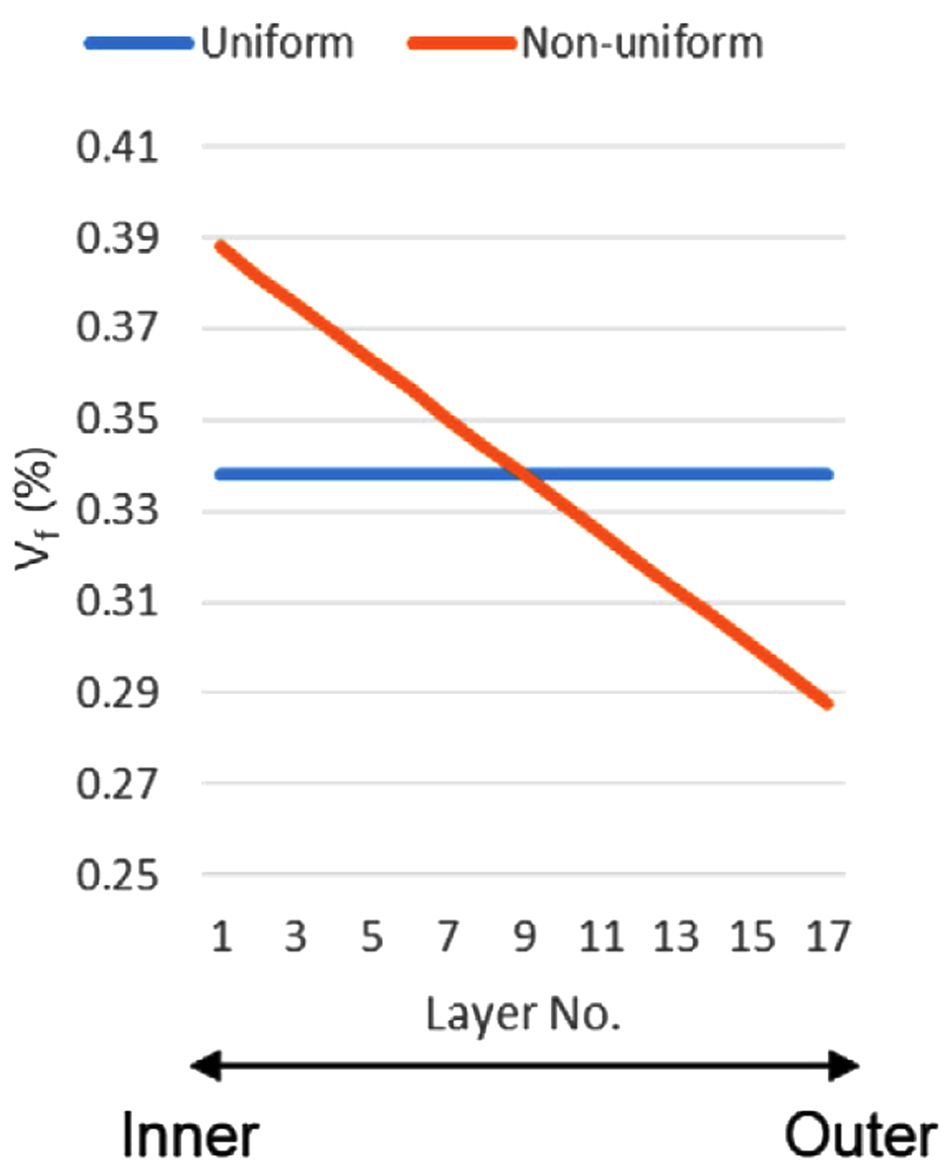
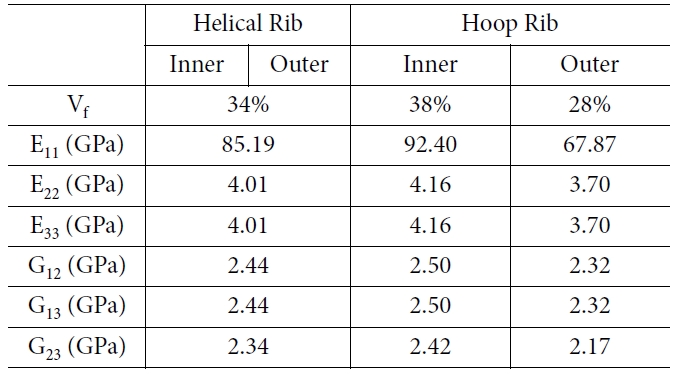
Fig. 9와 같이 후프 링을 모델링하였다. 후프 리브의 섬유체적비는 두께 방향으로 다를 수 있으며 내경측에서 더욱 크게 측정된다[5]. 후프 리브의 섬유체적비는 33%로 측정되었으며 측정된 수치를 기준으로 Fig. 10과 같이 두께 방향의 섬유체적비가 선형적으로 변화한다고 가정
하여 각 층의 물성을 다르게 적용하기 위해 후프 링은 Continuum Shell, SC8R 요소를 사용하였다. 후프 링에 하중을 가하는 금속 치구는 Analytical Rigid Surface로 모델링하였으며 Surface-to-Surface 접촉 조건을 부가하여 하중을 전달하였다. 또한 대변형에 의한 비선형성을 고려한 정적 해석을 수행하였다.

4.1 헬리컬 리브의 강성도 평가
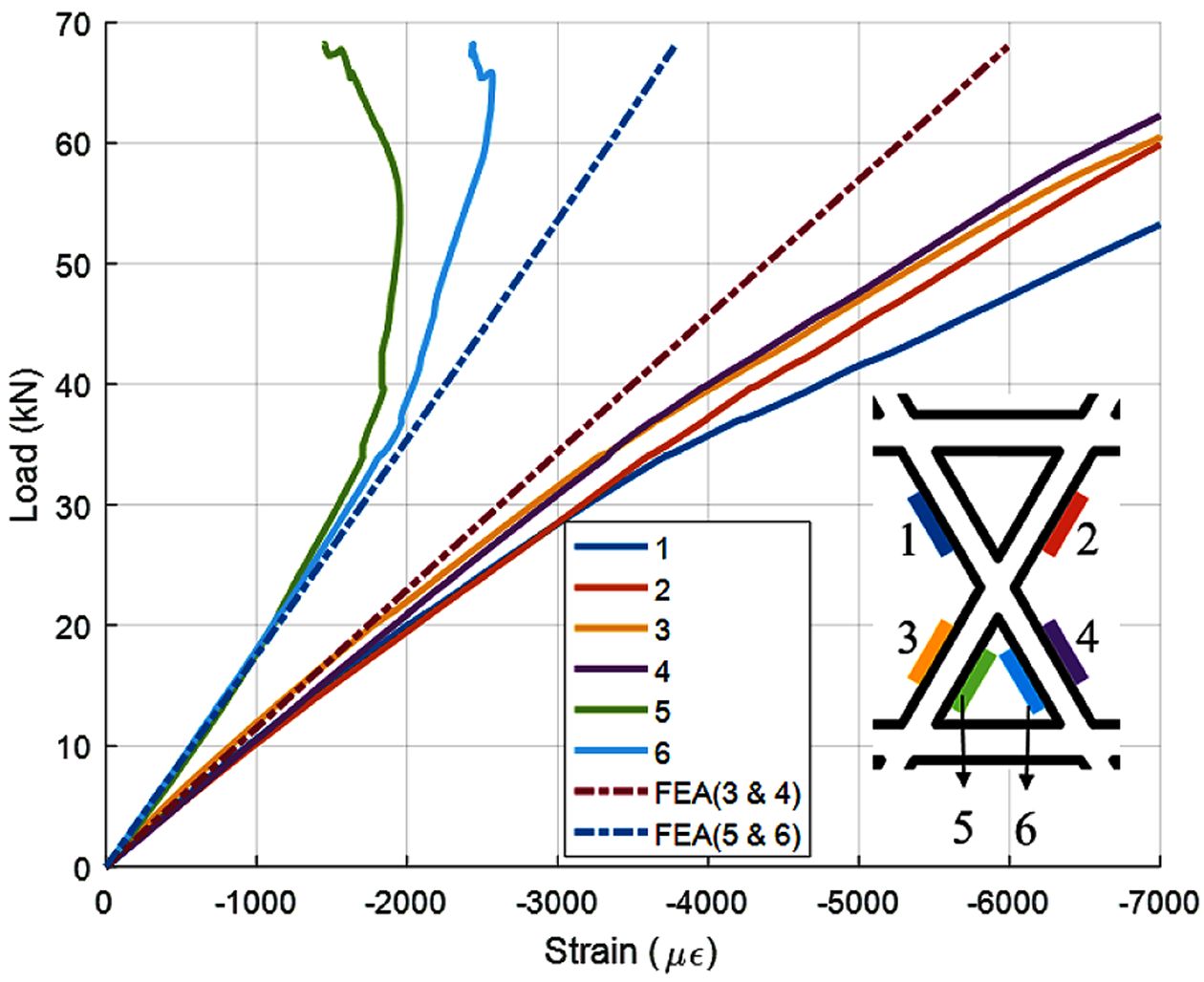
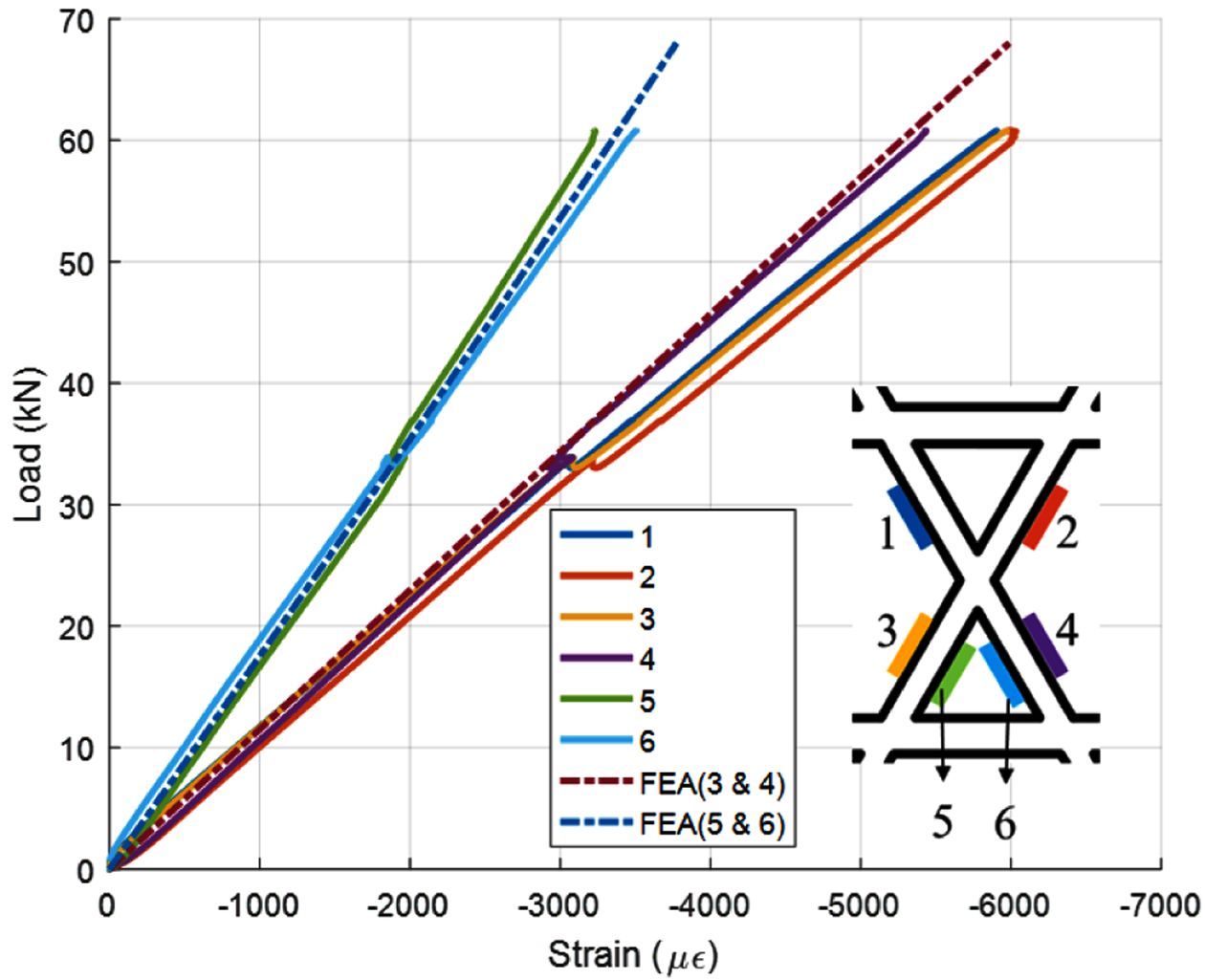
Fig. 11과 같이 3개 시편의 압축 시험을 수행한 결과, 시편 상단의 섬유교차부 부근에서 파손이 발생하였다. Fig. 12~14는 Subelement의 압축 시험에서 측정된 변형률을 유한요소해석 결과와 비교한 그래프이다. 파손이 발생한 시점까지의 해석 결과와 비교하였다. 3개 시편의 압축 시험 결과, 최대 하중에 도달하기 이전에 비슷한 하중에서 변형률의 변곡점이 발생하였다. 시험 종료 후 시편과 치구를 분리하여 시편의 상태를 관찰한 결과, Fig. 15와 같이 시편을 치구에 고정하기 위한 에폭시 부분에서 균열이 발생하였다. 특히, Subelement #1 시편에서 에폭시 균열 및 파손이 크게 발생하여 변곡점이 발생한 이후 변형률은 비선형적으로 측정되었다. 포팅 에폭시 파손 이후 시편의 양쪽에서 하중이 균일하게 전달되지 않아 굽힘 변형이 발생한 것으로 판단된다. 그러나 Subelement #2, #3 시편에서는 변곡점 이후에도 하중이 균일하게 전달되어 하중에 따라 선형적으로 증가하였다. 유한요소해석에서 계산된 변형률은 시험 결과와 잘 일치하였으며, 헬리컬 리브의 강성을 시험 및 해석을 통해 도출하였다. Fig. 13

4.2 후프 리브의 강성도 평가
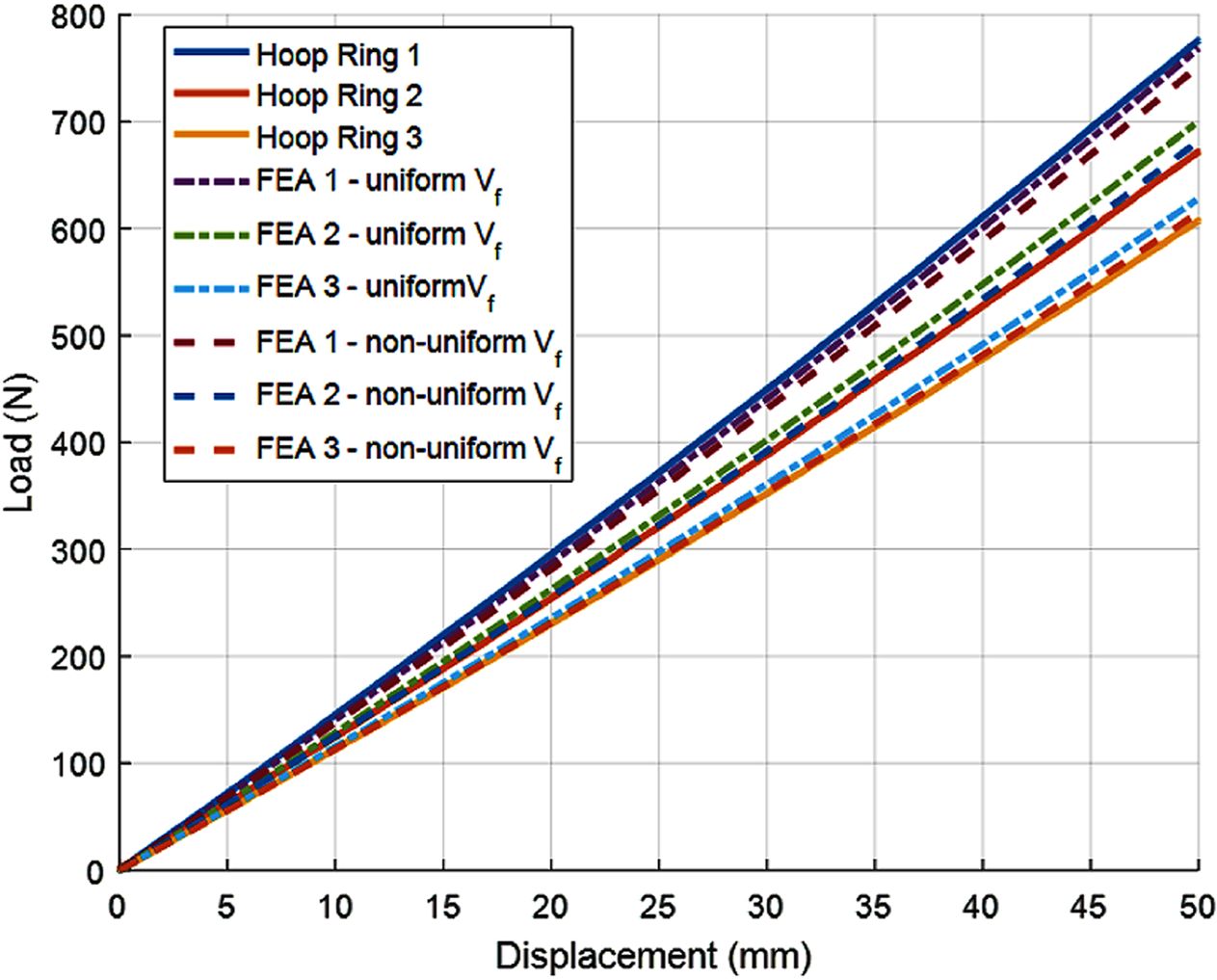
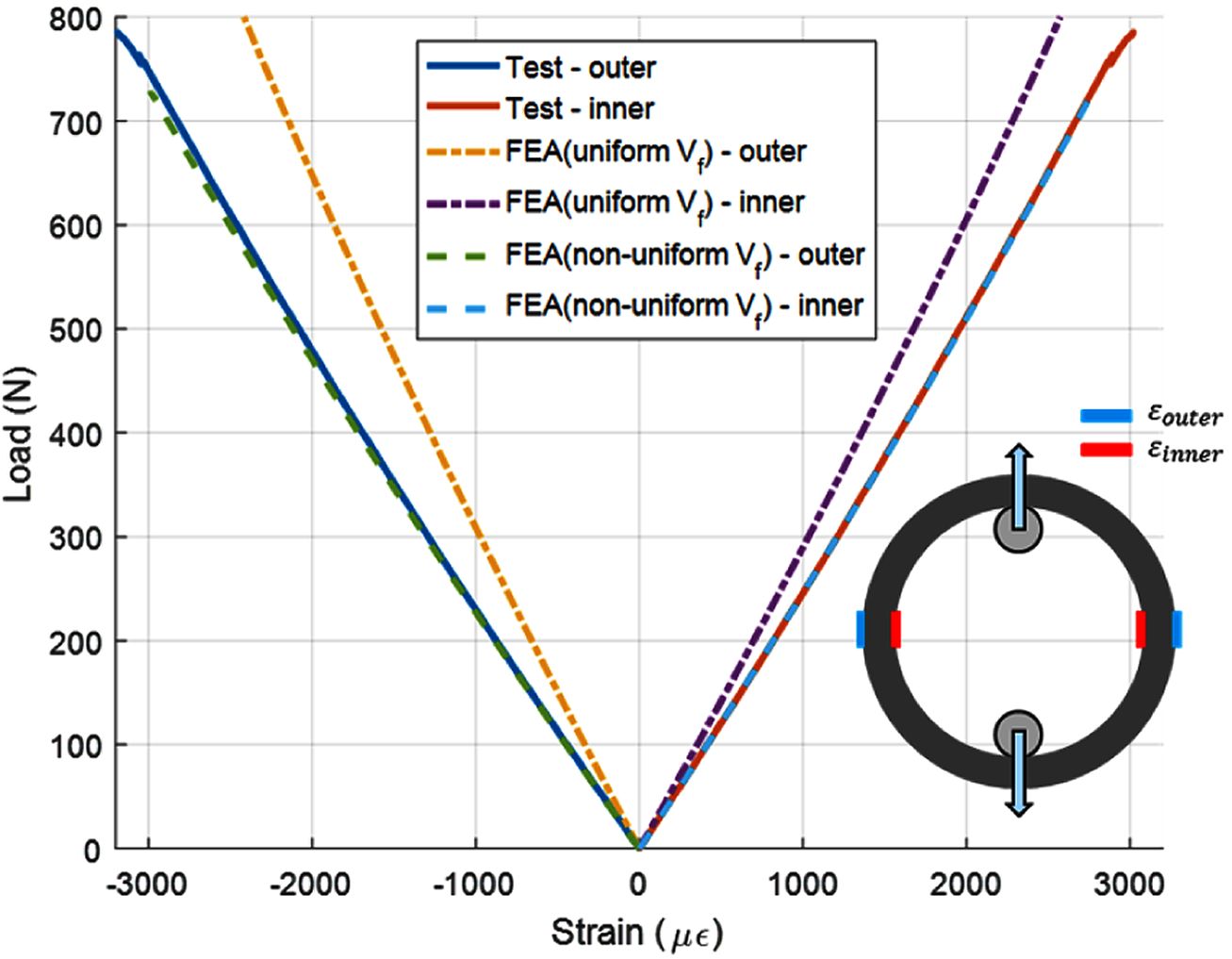
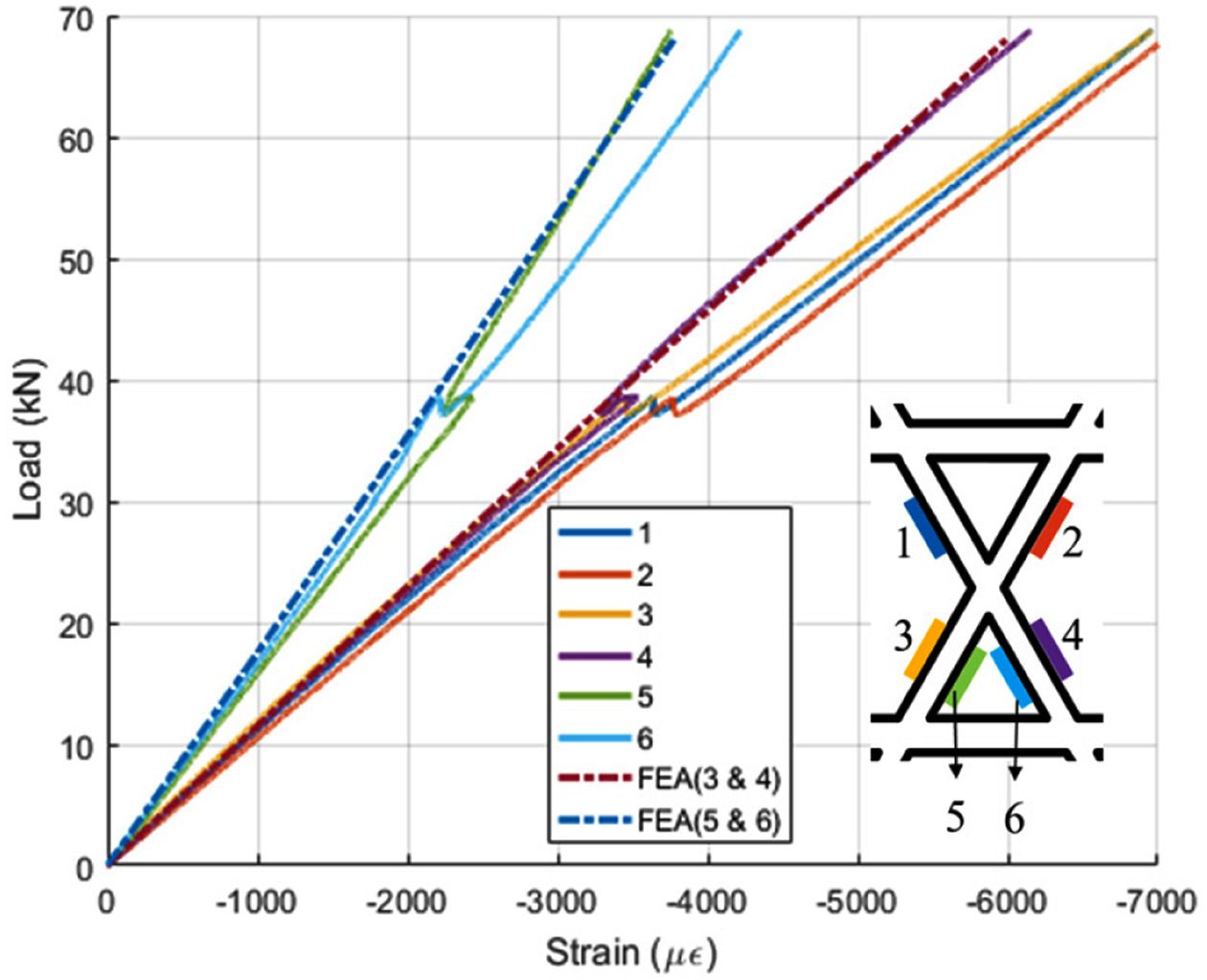
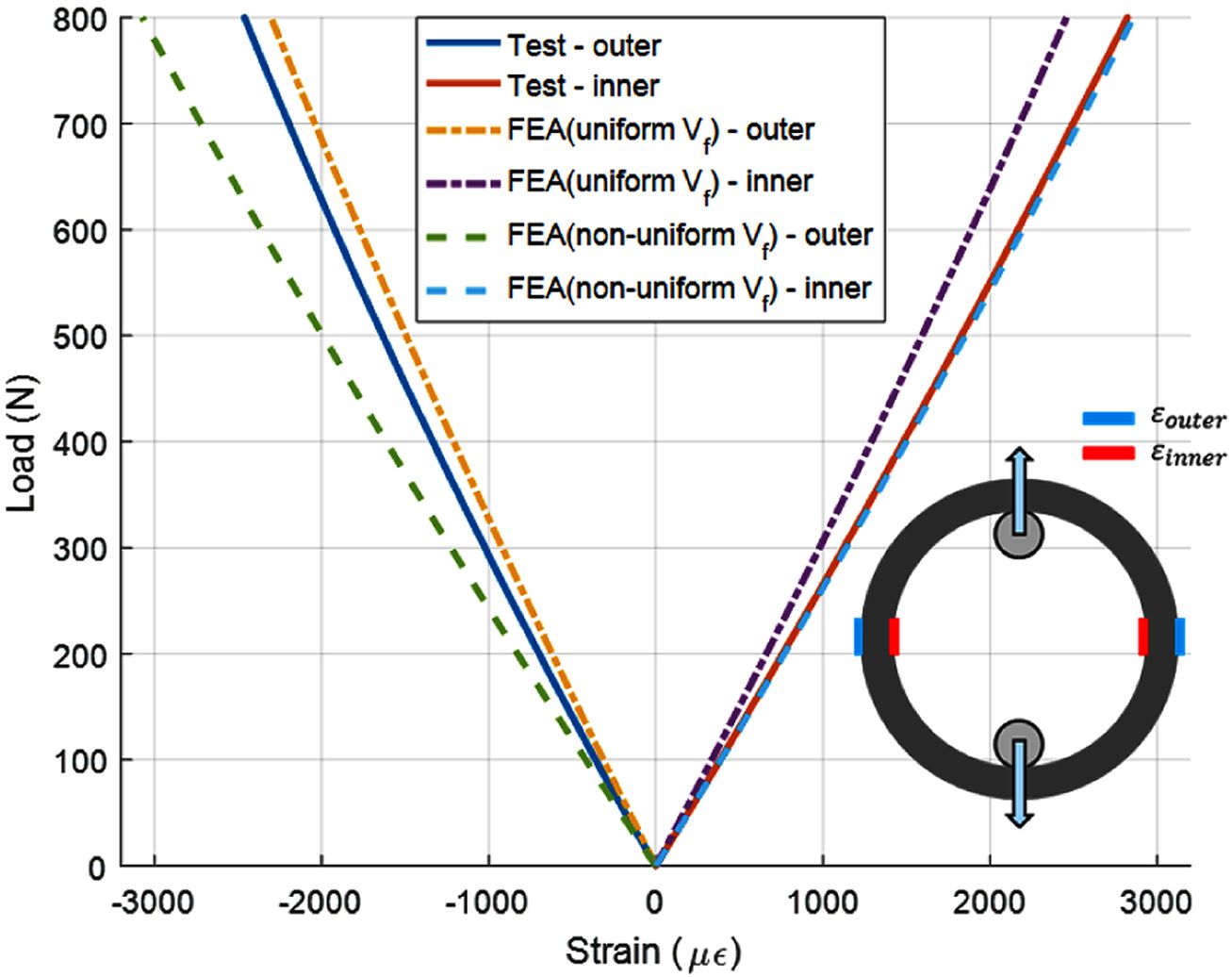
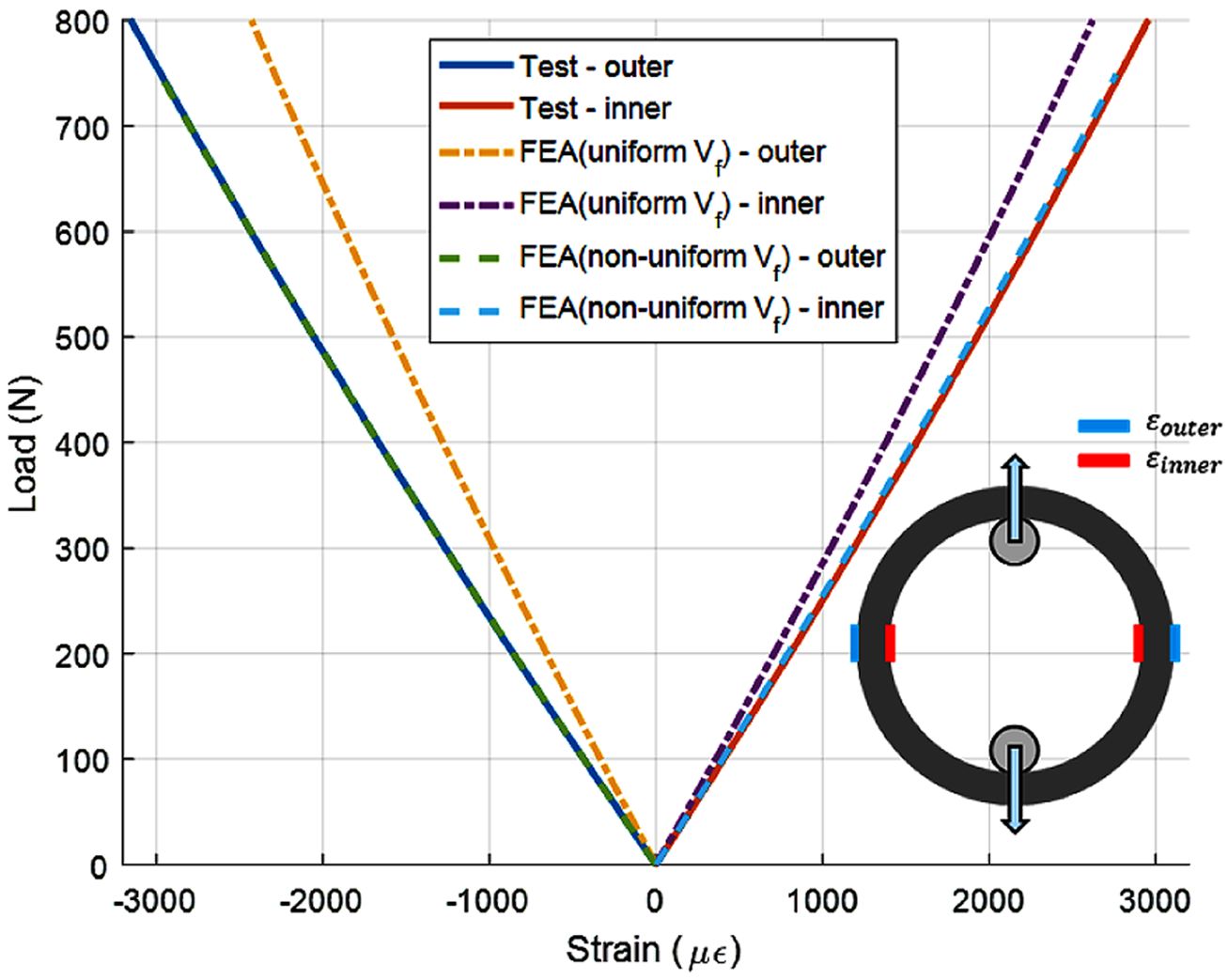
Fig. 16은 후프 링의 인장 시험에서 측정된 하중 및 변위를 유한요소해석 결과와 비교한 그래프이다. 두께방향 섬유체적비가 일정한 모델(uniform V_f)과 섬유체적비가 불균일한 모델(non-uniform V_f)의 해석 결과와 비교하였다. 인장 시험을 수행한 3개의 후프 링의 변위 측정 결과는 섬유체적비가 불균일한 모델의 해석 결과와 잘 일치하였다. Fig. 17~19는 3개의 후프 링 시험 결과와 유한요소해석의 하중-변형률 그래프를 비교한 결과이다. 후프 링의 변형률은 섬유체적비가 불균일한 모델의 변형률 계산 결과는 대부분의 시험 결과와 잘 일치하였다. 후프 링 #1 시편의 변형률은 해석 결과가 더욱 크게 계산되었다. 시험 종료 후 후프 링 #1 시편을 관찰한 결과, 시편과 하중 전달을 위한 치구가 접촉하는 면이 불균일하여 오차가 발생한 것으로 판단된다.
후프 링의 인장 시험에서 측정된 하중, 변위 및 변형률 결과와 섬유체적비 불균일에 따른 유한요소해석 결과를 비교하였으며, 후프 리브의 두께방향 섬유체적비를 불균일한 조건으로 해석한 결과가 시험 결과와 잘 일치하였다. Fig. 18

4.3 콘형 복합재 격자 구조의 강성
콘형 복합재 격자 구조 Subelement의 압축 시험 및 후프 링의 인장 시험 및 유한요소해석 결과를 비교하여 헬리컬 리브 및 후프 리브의 강성을 확보하였다. 헬리컬 리브와 두께 방향으로 섬유체적비가 변화하는 후프 리브의 확보된 강성을 Table 3에 정리하였다.

본 논문에서는 단순 인장, 압축 및 굽힘 시험이 어려운 콘형 복합재 격자 구조의 Subelement 및 후프 링의 시험 및 해석적 연구를 수행하였으며, 구조체의 강성을 도출하였다. Subelement의 압축 시험 및 해석 결과를 비교하여 헬리컬 리브의 강성을 확인하였다. 후프 리브는 후프 링 형태로 구조체로부터 가공하여 인장 시험을 수행하였으며, 해석 결과와 비교하여 강성을 확인하였다.
Subelement의 압축 시험에서 헬리컬 리브 길이방향의 압축 변형률을 측정하였으며 헬리컬 리브의 섬유체적비를 적용한 유한요소해석 결과와 비교하였다. 각각의 헬리컬 리브에 균일하게 압축 하중이 작용하였으며 압축 변형률이 지배적으로 발생하였다. 측정된 변형률은 해석 결과와 잘 일치하였다. 후프 링의 인장 시험에서도 마찬가지로 후프 리브의 길이방향 변형률을 측정하였으며 굽힘 변형이 발생하는 후프 리브의 변형률을 측정하였다. 기하학적 대변형이 크게 발생하였으므로 비선형 정적 해석을 수행하였으며, 계산된 변위 및 변형률은 시험 결과와 잘 일치하였다. 측정 및 계산된 변위는 섬유체적비 불균일이 큰 영향을 미치지 않았으나, 변형률은 섬유체적비를 불균일하게 적용한 모델의 결과가 시험 결과를 잘 모사하였다.
본 연구에서는 콘형 복합재 격자 구조의 기본 요소인 헬리컬, 후프 리브의 강성을 시험과 해석을 통하여 도출하였으며, 도출된 리브의 강성을 활용하여 콘형 복합재 격자 구조의 변형 및 좌굴 해석의 보다 정확한 예측이 가능할 것으로 기대된다.

본 연구는 민군협력진흥원(ICMTC)의 지원을 받아 수행한 연구입니다(15-CM-MA-12).