- Research of Vibration Analysis and Resonance Avoidance Design of Composite Quadcopter
Sang-Ryul Kim*, Wie-Dae Kim*†
* Aircraft Structural Design Laboratory, Pusan National University
*† Aircraft Structural Design Laboratory, Pusan National University
- 복합재 쿼드콥터의 진동 특성 분석과 공진 회피에 대한 연구
김상률* · 김위대*†
In this research, the vibration characteristics of
composite quadcopter are analyzed, and avoidance design and analysis are
performed to avoid resonance. The full platform of a commercial quadcopter with
composite rotor arm is analyzed to see the vibration characteristics using FEM
program. The manufactured stacking sequences of rotor arm is used for analysis,
and the natural frequencies are compared with experimental results and simple
analytic model results. It is also confirmed that the natural frequency of the
particular mode is included within the operation range of the motor. The
resonance avoidance design is carried out by selecting three variables from the
existing model: stacking sequence, rotor-arm pipe length, and pipe thickness.
본 연구에서는 복합재료가 적용된 쿼드콥터의 진동 특성을 분석하고, 공진에
대해 회피 설계 및 해석을 수행하였다. 로터-암의 파이프가
복합재료로 구성된 상용 쿼드콥터의 플랫폼을 모사하고 상용 해석 프로그램을 이용하여 진동 특성 분석을 하였다. 실제
적층 배열을 해석에 적용하고, 참고 문헌과의 비교를 통해 신뢰성을 판단하였다. 그리고 모터의 가동범위 내에 특정 모드의 고유 진동수가 포함되는 것을 확인하였다. 기존 모델에서 적층 배열, 로터-암의
길이, 두께의 총 3가지의 변수를 선정해 공진 회피 설계를
수행하였다. 공진 회피 설계의 3가지 변수에서 각 해석의
결과를 비교한 후, 공진 회피 설계의 효율성 측면에서 방향을 제시하였다.
Keywords: 공진 회피 설계(Resonance avoidance design), 복합재료(Composite materials), 쿼드콥터(Quadcopter), 진동 해석(Vibration analysis)
드론은 과거에 정찰, 감시와 같은 군사용으로만 운용했지만, 최근에는 농업, 레저와 물류 수송과 같은 민수 분야의 수요가 급격히 증가하고
있는 추세이다[1]. 전 세계적으로 중국을 선두로 미국과 프랑스가 드론 시장에서 우위를 다투고 있고[2], 우리나라도 2026년까지 기술경쟁력
세계 5위를 목표로 드론 산업 신장에 박차를 가하고 있다.
드론은 경량화와 요구되는 구조적 성능으로 인하여 복합재료가 자주 쓰이고 있다. 다른 금속을 사용하였을 때보다 가볍고 강성이 크기 때문에
비강도가 중요한 드론에 적합하고, 우수한 성능과 장기체공을 위해 그 중 탄소섬유 복합소재가 많이 쓰인다[3].
쿼드콥터는 기존의 회전익 항공기에 비해 양력을 얻기 쉽고 높은 기동성을 가지며 구조적으로 단순한 장점이 있다. 하지만 호버링 중일 때와
모터 가동 시 긴 세장비(Slenderness ratio)를 가진 로터-암(Rotor-arm)과 그 끝 단에 비교적 큰 질량의 구동모터가 달려있어
항시 가진(Excitation)되는 구조이므로 공진 현상과 같은 동적 불안정성 현상이 발생할 수 있다.
공진은 특정 진동수에서 큰 진폭으로 진동하는 현상을 말한다. 또한 모든 물체는 여러 개의 고유 진동수를 가질 수 있으므로 어떠한 구조물의
진동 특성 분석을 할 때, 여러 개의 고유 진동수를 분석해야 한다. 본 연구에서는 복합재료가 적용된 쿼드콥터의 진동 특성을 분석해, 고유 진동수가
구동 모터의 가동범위에 속해있는지 분석한다.
쿼드콥터의 정확한 안전성 검증을 위해 복합재 쿼드콥터(Composite quadcopter)를 연구 대상으로 선정하였고 Fig. 1에
나타내었다. 드론의 로터-암 부분은 복합재료로 구성되어 있고 그 외는 알루미늄 합금으로 이루어져 있다. 유한요소해석 프로그램을 사용하여 드론의
진동 특성을 분석하고 모터의 운용 회전수 범위와 비교한다[4]. 그리고 Kim 등[5]의 쿼드콥터를 대상으로 한 고유 진동수 해석과 실험의 결과와
비교하여 신뢰성을 획득한다. 더 나아가 Lee 등[6]처럼 공진 회피를 위한 변수를 설정하여 고유 진동수를 변화시켰다. 복합재의 특성에 기반한
적층 배열(Stacking sequence) 변화와 구조물의 형상 변경으로 고유 진동수가 모터의 가동범위에서 최대한 멀어지게 하는 공진 회피 설계를
수행하였다.

|
Fig. 1 Commercial quadcopter |
2.1 Rayleigh’s
method
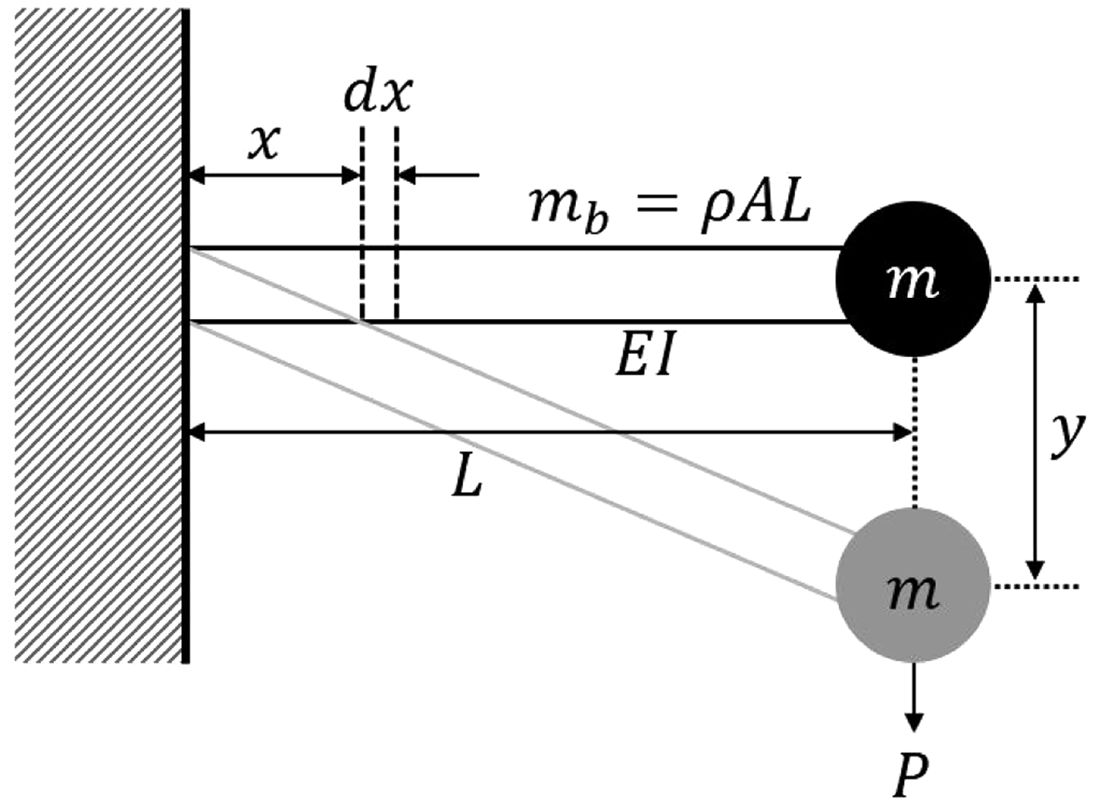
이론적으로 고유 진동수를 해석하기 위해서 Rayleigh’s method를 사용한다[7]. Fig. 2과 같이 로터가 끝 단에 달려있어
하중이 작용하는 외팔보로 가정하여 1차 모드의 진동수를 구할 수 있다. Rayleigh’s method에서는 계에 충분히 작은 변형(Infinitesimal
change)만이 있다고 가정한다. 외팔보 상태에서 위치에너지와 운동에너지의 식을 구하면 식 (1), (2)와 같다. k는 강성이고, E는 탄성 계수(Elastic modulus)이고, I는 이차 관성 모멘트(Moment of inertia)이다. L은 로터-암의 길이, P는 끝 단에서 가해지는 하중이다.
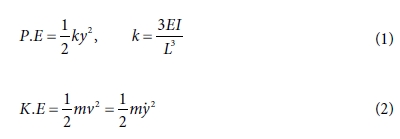
위의 식 (1)에 근거하여 위치에너지의 최댓값을 식 (3)과 같다. 운동에너지의 값을 구하기 위하여 y의 값부터 정의해야 한다. 식 (4)는 x에 따른 y의 크기를 나타낸 것이다. 또한, x에 대한 y를 속도의 항으로 미분하여 식 (5)에 나타내었다. 끝 단에 달려있는 물체를 제외한 외팔보에만
해당하는 운동에너지는 식 (6)과 같고, 끝 단에 달려있는 물체를 포함한 운동에너지는 식 (7)와 같다.
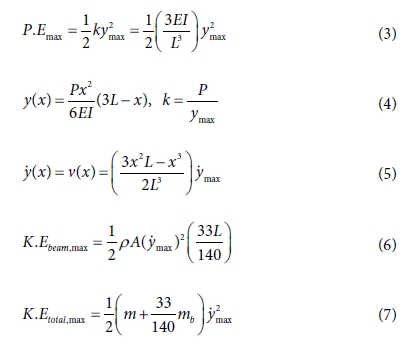
운동에너지를 진동수에 대해 표현하기 위해 식 (8)을 식 (7)에 적용시켜 식 (9)와 같이 나타냈다. wn는 이 계의 고유 진동수이다.

Rayleigh’s method에 근거하였을 때, 운동에너지의 최대치와 위치에너지의 최댓값은 같다. 식 (3)과 (9)를 같다고 하여
정리하면 식 (10)과 같이 표현될 수 있다.
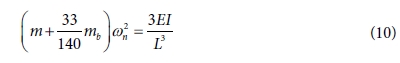
위의 식 (10)을 고유 진동수 wn에 대해서 나타나게 되면
식 (11)과 같다. 밑의 식에서 외팔보 문제의 경우, 고유 진동수는 강성과 이차 관성 모멘트, 길이와 질량에 관한 함수이다.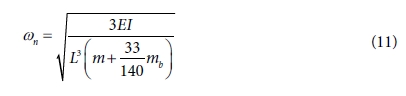
|
Fig. 2 Cantilever beam with tip mass |
3.1 형상 설계
진동 특성을 분석하기 전에, 구조가 간략화된 해석 모델을 설계하기 위해 CAD 프로그램을 통하여 설계하였고, 유한요소해석인
Abaqus를 사용하여 복합재 쿼드콥터의 유한요소모델을 구성하였다. 해석모델은 Fig. 3과 같으며, 기존 기체와 같이 모터와 로터-암을 연결하는
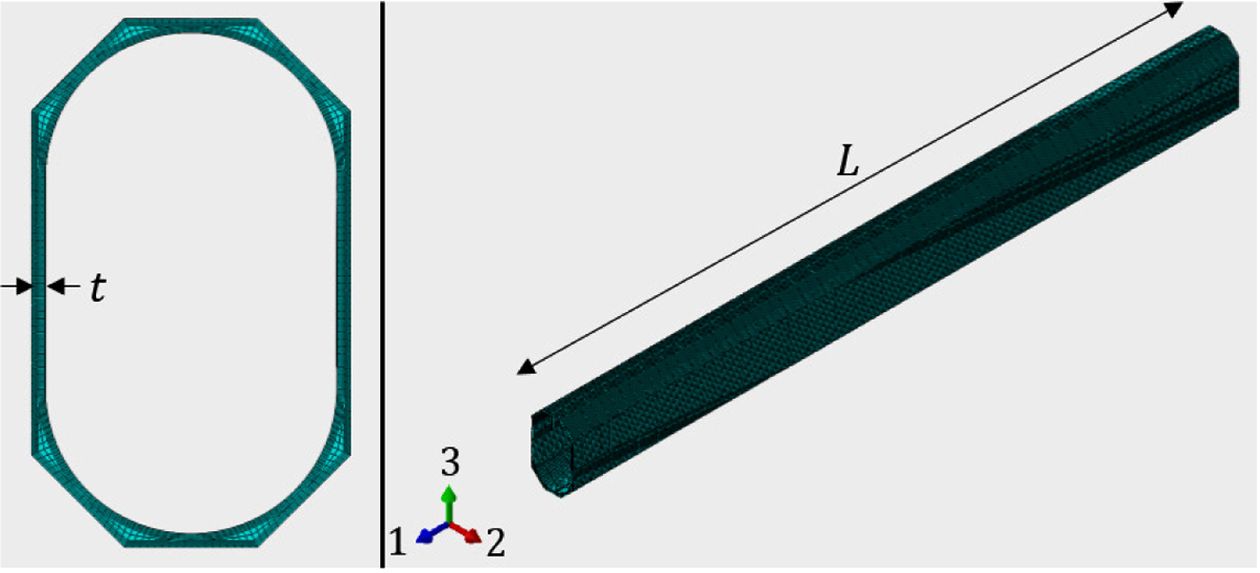
부품들은 기존 기체의 형상과 동일하게 설계하였고, 나사 부분은 생략하였다. 로터-암의 파이프 단면과 복합재 적층을 위한 방향을 Fig. 4에 나타내었다.
두께 t는 1 mm이고 L은 390 mm이다.
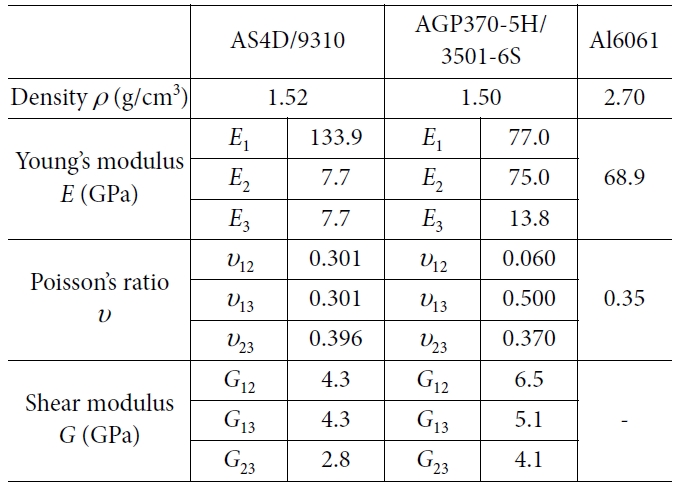
물성치(Material properties)는 Table 1에 나타내었다. 로터-암의 파이프는 AS4D/9310과
AGP370-5H/3501-6S를 적용하였고, 나머지 모터, 결합부 등은 알루미늄 합금을 사용하여 구성하였다.
해석 방법은 Natural frequencies을 사용하였고, 진동 해석에 사용된 Solver는 Lanczos를 사용하였다.
Mesh는 8개의 절점을 가지는 육면체 3D solid 요소를 적용하였으며 해석모델의 총 요소와 절점의 수는 각 619,276개와
706,260개이다. 대부분의 요소들이 로터-암에 위치하고 있는데, 그 이유는 적층 배열로 인해 두께방향으로 요소의 배치가 이루어져
있기 때문이다.
적층 배열은 AS4D/9310 재질을 0o와 90o를 동일하게 하였고 겉에 Woven재질인
AGP370-5H/3501-6S으로 한 층 둘러서 적층하였다. 적용된 적층 배열은 겉에서부터 [W/0/90/90/90/0/0]이다. 실제 적층
배열을 Fig. 5에 나타내었다.
3.2 고유 진동 해석
해석대상이 호버링할 때, 모터의 회전 속도는 약 7,000 RPM이고, 동작구간은
0에서 8,000 RPM이다. 하지만 모터의 회전 주파수는 빠른 시간 안에 7,000 RPM을 넘어서서 비행하기
때문에 0~7,000RPM에서는 공진이 발생하지 않는다고 가정한다.
주파수 범위는 7,000~8,000 RPM이 되고 이를
Hz의 단위로 바꾸게 되면 116.67~133.33 Hz가 된다. 유한요소해석을
사용하여 도출되는 진동수가 가동범위인 116.67~ 133.33 Hz에 포함이 되는지 검토해보았다.
1차에서 4차 모드는 로터 끝 단에서 가장 진폭이 컸고 모터의 가동범위인 116.67~133.33 Hz에 속하지 않았다. 따라서 제어 회로와 센서 등이 포함되는 센터 플레이트에 영향을 미칠 가능성은
낮을 것이라고 판단하였다.
5차 모드에서 z축의 Bending으로 인해 중앙 연결부 부분에서 가장 큰 상대적 진폭이 발생하였다. 또한, 고유 진동수의 5차 모드
해석 값은 119.74 Hz로 해석대상의 가동범위에 들어가는 것을 알 수 있다. 5차 모드 진동수로 장시간 비행을 할
경우 공진으로 인한 증폭된 진동으로 회로 손상과 제어기능 상실이 발생할 가능성이 크다[9].
6차 모드의 경우 Z축 2차 Bending이 발생하는데, 로터 끝 단에서 가장 큰 진폭이 발생하고 있음을 알 수 있다. 또한, 가동범위를 벗어난
162.95 Hz의 고유 진동수의 6차 모드를 가지고 있기 때문에 공진이 발생할 가능성이 낮으며 센터 플레이트에
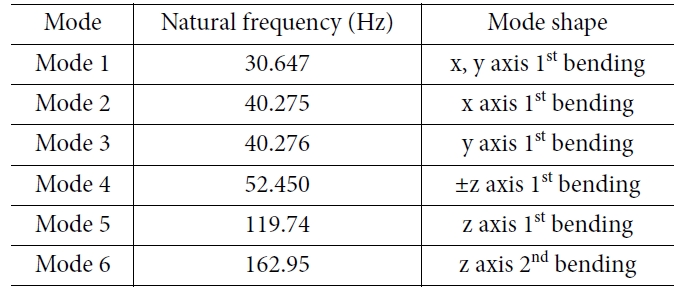
영향을 미칠 가능성이 낮을 것이라고 판단되었고, 각 모드 별 진동수에 대하여 Table 2에 나타내었다. 그리고
5차 모드의 모드 형상을 Fig. 6에 나타내었다.
3.3 결과 분석 및 비교
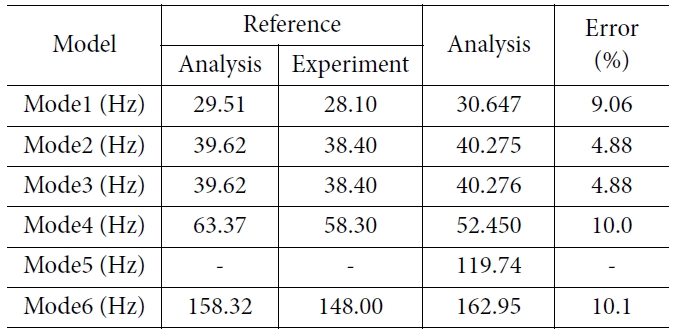
우선, 해석모델의 1차에서 6차 모드까지의 진동수의 해석 결과를 Kim 등[5]의 결과와 비교하여 Table 3에 나타내었다. 결과에서의 가장 큰 차이점은 5차 모드의 유무이다. 5차 모드를 제외한 비교할 수 있는 나머지 모드들은 실험 결과와는
오차율 약 10% 이하로 확인되었으며, 참고 문헌의 해석 결과와는 더 작은 차이를 보이는 것을 알 수 있다.
1차에서 4차 모드는 로터 끝 단에서 가장 진폭이 컸고 모터의 가동 범위에 속하지 않았다. 따라서 제어 회로와 센서 등이 포함되는 센터
플레이트에 영향을 미칠 가능성은 낮을 것이라고 판단하였다. 또한 진동수 30~60 Hz 사이에서 고유 진동수가 분포되어, 실제 운용 시 빠르게 회전수가 증가해 이 영역을 통과하므로
공진이 일어나지 않는다. 4차 모드가 다른 모드에 비해 오차가 발생하는 방향이 다른데, 그 이유는 참고 문헌과
끝 단 질량을 주는 방법이 달랐기 때문이다.
3.2절의 결과에서 5차 모드가 116.67~133.33 Hz 사이에 포함되는 것을
알 수 있는데, 5차 모드가 중앙에서 위아래로 진동하는 모드이므로 위험하다고 판단하였다. 참고 문헌과 다르게 60 Hz에서 140 Hz 영역 사이에 하나의 모드가 더 생기는 것에 대해서 분석하였다.
먼저 참고 문헌의 실험에서 실험의 구성은 플랫폼을 두고 4개의 번지코드를 각 로터-암 중앙에 설치하여 중앙의 연결부에서 진동이 나타났다.
게다가 1축 센서 하나로 실험을 했기 때문에 5차 모드가 나타나지 않을 수 있다고 판단하였다. 또한 참고 문헌의 해석에서는 물성치를 2.1절의
이론에서 전개한 Rayleigh’s method을 이용하여 역으로 강성을 도출하였다. 하지만 도출된 강성은 역으로 계산된 등방성 물성치이다.
이처럼 등방성의 물성치를 사용한다면 응력 해석은 비교적 정확한 결과가 도출된다. 하지만 진동 해석의 경우, 고차 모드로 갈수록 많은
형상 정보가 쓰인다. 위의 Rayleigh’s method는 단순히 외팔보에서 단면의 이차 관성 모멘트만 사용하므로, 고차 모드로 갈수록 등방성의
물성치보다 직교이방성, 혹은 횡등방성의 물성치가 더욱 많은 모드를 표현할 수 있다. 6차 이상의 비틀림과 관계된 고유진동수는 직교이방성, 횡등방성의
물성치가 훨씬 많은 결과를 도출한 것을 확인하였다.
앞의 결과에서 실제로 해석 결과 참고 문헌에는 발견되지 않은 고차 모드가 모터의 가동범위 안에 속하였다. 따라서 복합재 쿼드콥터의 안정성을
확인하는 본 연구의 목표에 맞게 변수를 조절하여 고유 진동수가 가동범위에 포함되는지 확인할 필요성이 있다고 판단하였다.

|
Fig. 3 Model assembly |
|
Fig. 4 Cross section of composite pipe |

|
Fig. 5 Cross-section image of composite pipe |

|
Fig. 6 5th mode shape |
앞에서 고유 진동수의 5차 모드가 모터가동범위에 들어가는 것을 알 수 있다. 그래서 공진의 위험으로부터 멀어지게 하기 위해, 공진 회피
설계를 하기 전에 이론적인 부분에서 고유 진동수는 탄성계수(E)와 이차 관성 모멘트, 무게(m), 길이(L)에 따라서 값이 바뀌는 것을 알 수
있다. 그래서 탄성계수를 바꾸기 위해 적층 배열을 다양화하여 해석하고, 이차 관성 모멘트에 관련된 파이프의 두께(thickness, t), 그리고
로터-암의 길이와 관련된 파이프의 길이를 각각의 변수로 설정하고 각 변수에 대한 해석을 진행하면서 공진 회피 설계를 진행하였다.
4.1 적층 배열 변경
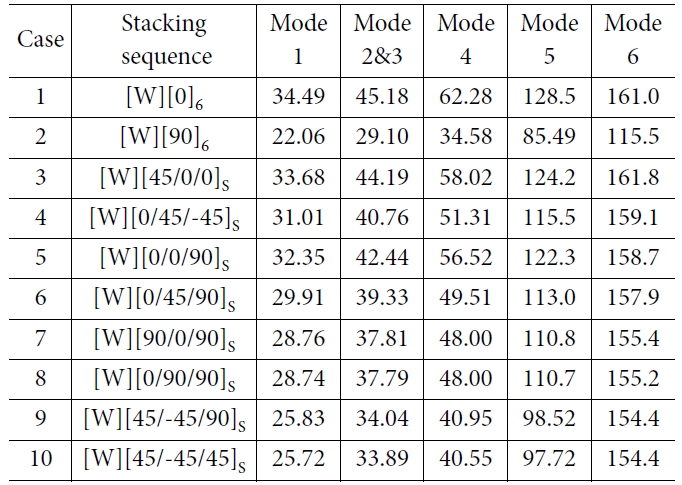
먼저 탄성계수에 직접적인 영향을 주는 복합재료의 적층 배열을 변화시켜 고유 진동수 변화를 관찰하였다. 기존의 적층 배열은
[W/0/90/90/90/0/0]으로 단순히 0o와 90o로만 이루어져 있는 형상이고 이것을 0o와 90o 이외의 45o, -45o와 같은 특수 각을 추가하면서 다양한 조합을 만들었다. 각 적층 배열과 그에 따른 해석
결과를 Table 4에 나타내었고, 모터의 가동범위인 116.67~133.33 Hz에서의 분리여유를 표시하였다.
위의 결과에서 0o의 적층이 많을수록 고유
진동수가 높다. 로터-암을 구성하고 있는 복합재 파이프가 길이 방향이 1방향이므로 0o 적층했을 때가 가장 강성이
높다. 강성이 높아지면 고유 진동수는 높아지게 된다. 그리고 45o와 -45o가 많을수록 몇몇 고차 모드의 고유 진동수가 증가하게 되는데, 45o와 -45o가 있으면 비틀림에 대한 저항이 높아지게 되므로 고차 모드에서의 Torsion 모드가 나타나는 진동수가 높아진다.
결과적으로 가장 고유 진동수가 낮아지는 적층 배열은 [W][90]6이지만 실제 복합재 구조물 제작에서는 층간 박리(Delamination)의
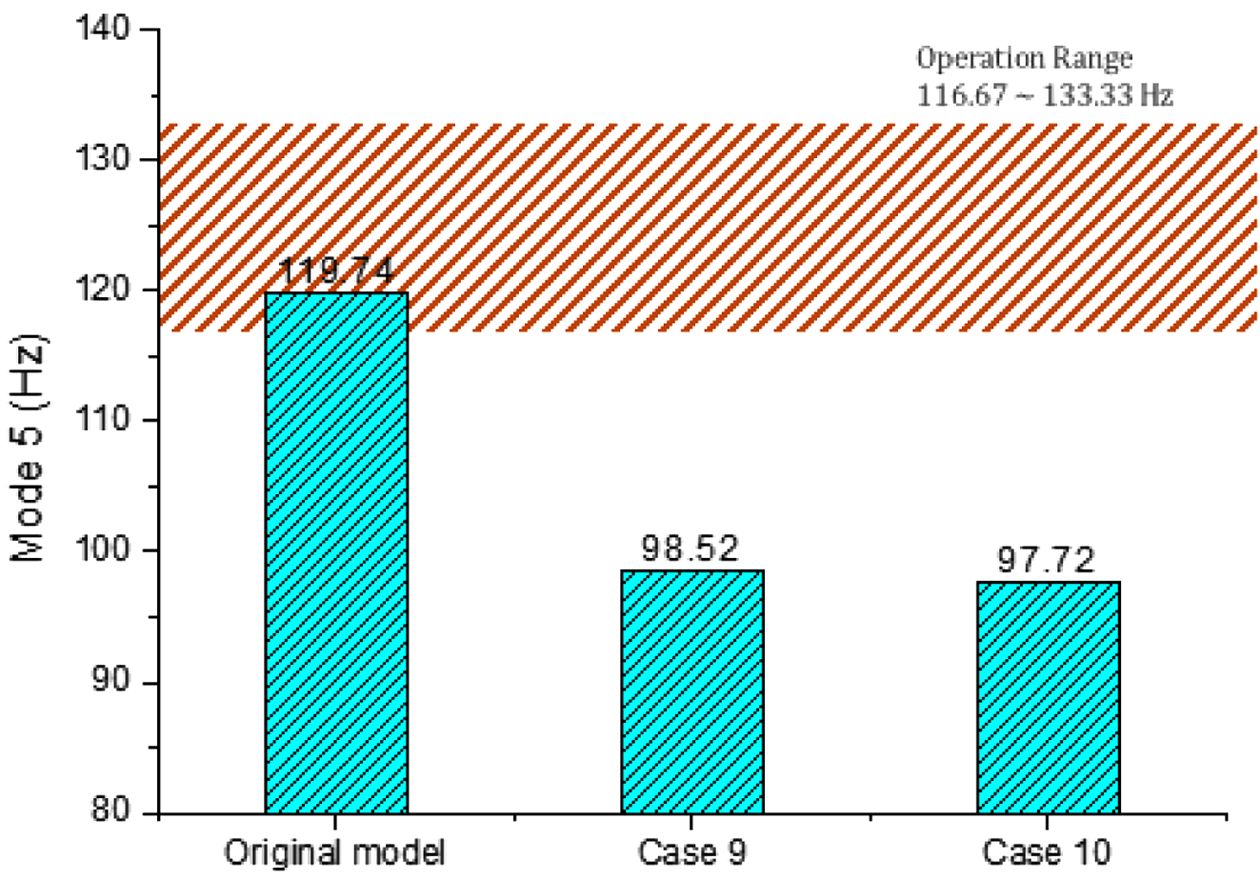
위험성 때문에 단일 적층은 쓰이지 않는다. 고유 진동수가 모터의 가동범위와 10% 정도 분리 여유를 가지는 Case 9인
[W][45/-45/90]S과 Case 10인 [W][45/-45/45]S의 적층 배열이 적절하다. 위의
Case 9과 10에 대한 5차 모드의 진동수를 기존 적층 배열과 비교하여 Fig. 7에 나타내었다.
4.2 로터-암 길이
변화
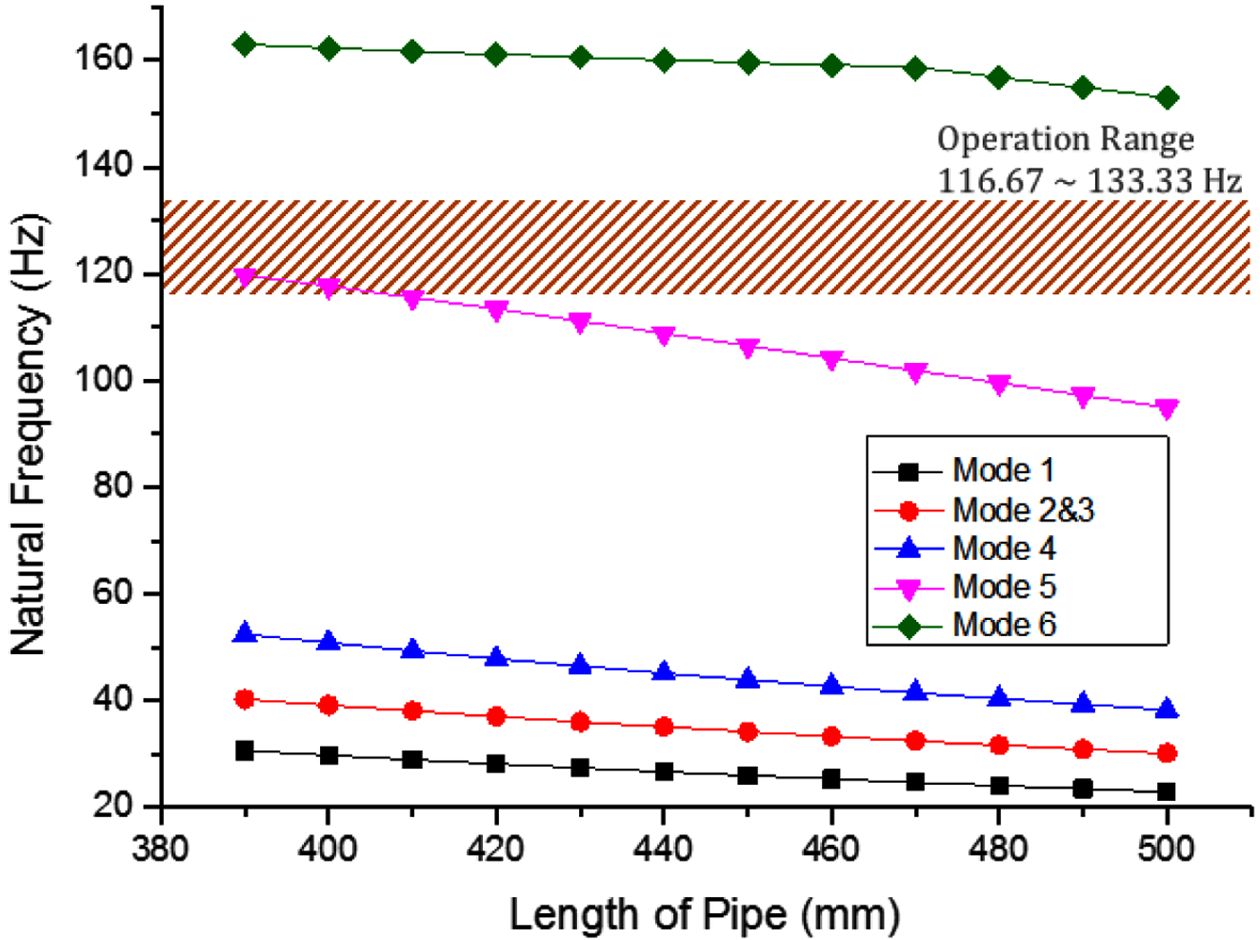
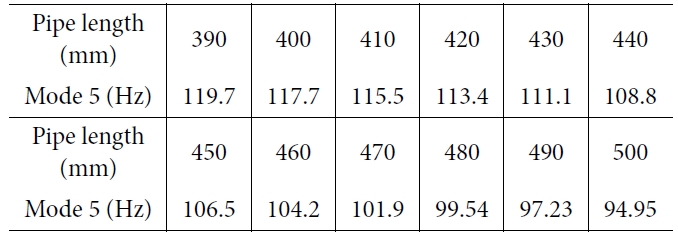
로터-암의 길이와 관련된 복합재 파이프의 길이변화를 통하여 해석 대상의 고유 진동수를 관찰하였다. 기존의 파이프의 길이는 390 mm이고 이것의 길이를
10 mm씩 일정하게 증가시켜 최대 500 mm까지 증가시키면서 고유
진동수 변화를 Fig. 8에 나타내었다. 빗금 친 부분은 모터의 가동범위인 116.67~133.33 Hz를 나타낸다. 그리고 가장 공진과 관련이 있다고 생각되는 5차 모드에 대해서 각각의 길이
변화에 따라 Table 5에 정리를 하였다.
위의 Fig. 8와 Table 5에서 볼 때, 길이가 길어지면 길어질수록 고유 진동수는
감소하는 경향을 보인다. 파이프의 길이가 길어질수록 로터-암의 길이도 길어지면서 고유 진동수가 하락하는 것으로 해석된다. 410 mm의 길이부터 5차 모드의
고유 진동수가 모터의 가동범위를 벗어났다.
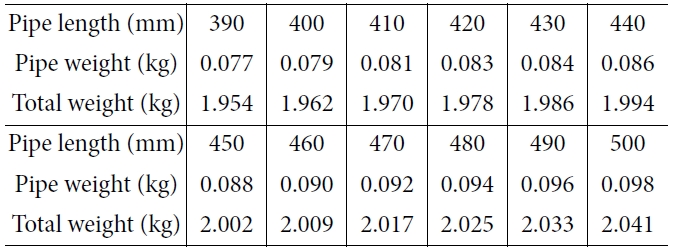
위의 Table 6에서, 길이가 길어지면 파이프의 무게도 같이 증가하는데
전체 플랫폼 무게에 비하면 비중이 낮다. 390 mm의 파이프에서 모터의
가동범위를 벗어나는 410 mm로 바뀐다면 파이프의 무게 증가율은 5.1%이지만 전체 플랫폼의 무게 증가율은 0.8%이다.
그리고 5차 모드의 변화율은 3.5%로 무게보다는 길이 변화가 더 5차 모드에 지배적인 영향을 끼친다.
4.3 로터-암 두께
변화
이차 관성 모멘트를 변화시킬 수 있는 두께 변화를 통하여 진동 특성 분석을 하였다. 두께가 증가하면 이차 관성 모멘트가 커지고, 무게가
무거워진다. 또한 복합재료로 구성된 파이프의 특성상 두께가 변화하면 적층 배열도 늘어날 수 밖에 없는데, 최대한 적층 배열에 의한 고유 진동수
변화를 억제하기 위하여 기존의 [W/0/90/90/90/0/0]에서 적층의 배열을 유지하며 두께를 늘렸다. 파이프의 중심 방향으로 두께는 기존
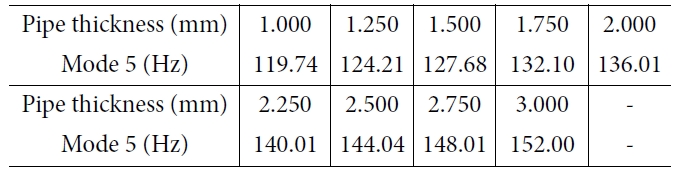
1 mm에서 최대 3.0 mm까지 0.250 mm씩 늘려서 총 8개의
추가 모델을 만들고 각 모델의 5차 모드의 고유 진동수를 Table 7에 나타내었다. 또한
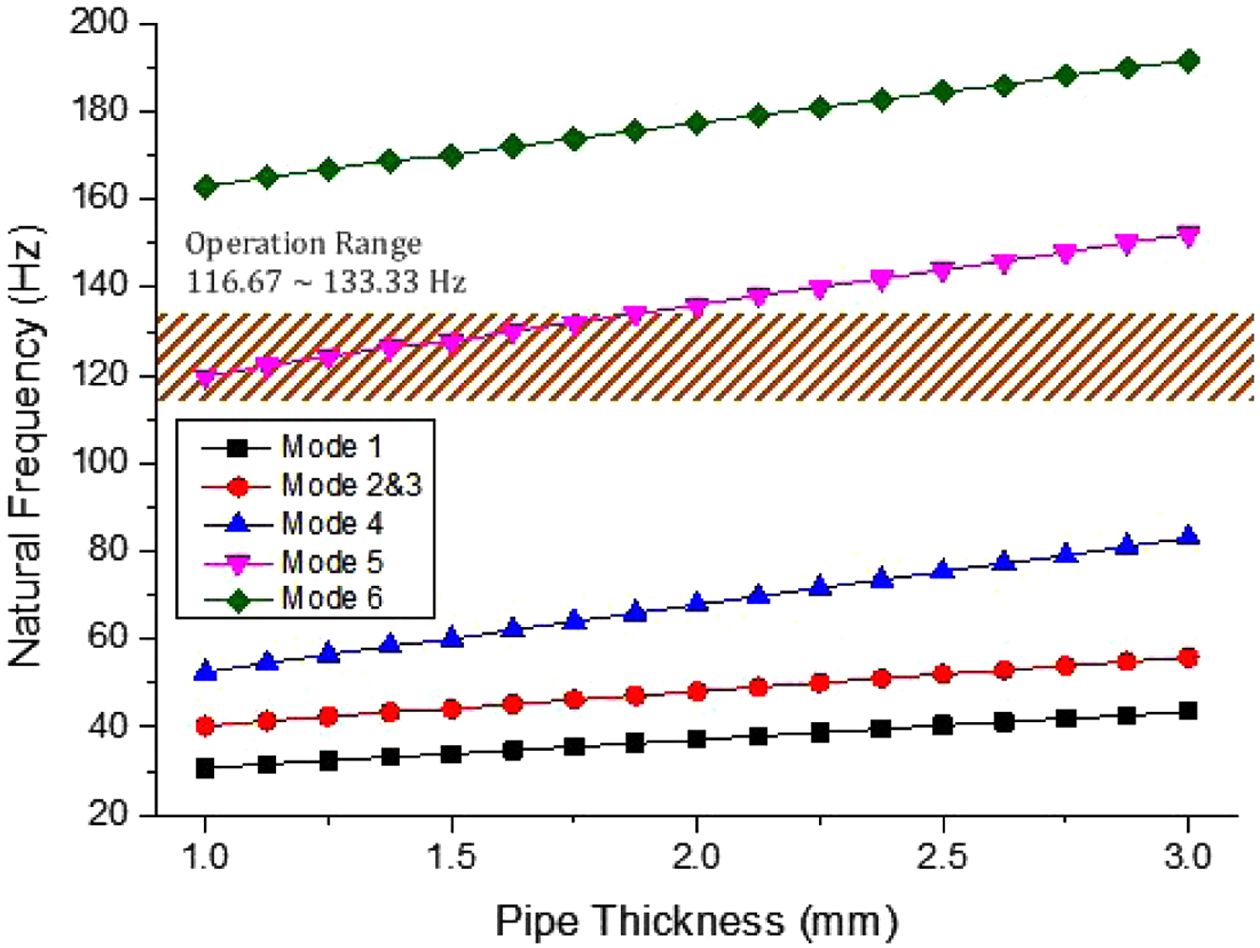
각 모델의 고유 진동수를 Fig. 9에 나타내었다.
위의 Table 7에서 볼 때, 두께가 증가할수록 고유 진동수는 증가하는 경향을 보인다. 4.1과 4.2절에서는 5차 모드의 고유 진동수를
낮추면서 공진 회피를 한 반면에, 두께 변화에 의한 공진 회피 설계에서는 두께가 증가하면 고유 진동수도 증가한다.
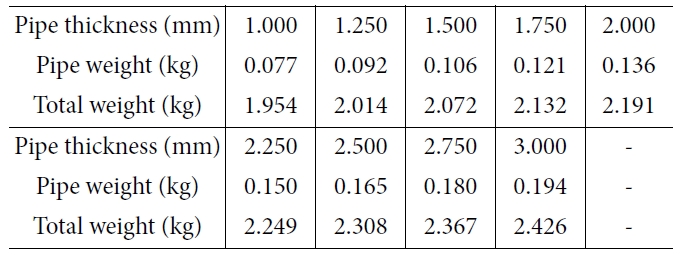
위의 Table 8에 두께 증가에 따른 파이프와 플랫폼의 무게를 나타내었다. 두께가 증가하면 이차 관성 모멘트가 증가하고 무게도 증가한다.
모터의 가동범위를 벗어나는 두께인 2.000 mm에서 1.000 mm와의 고유 진동수는
13.6%의 차이가 있다. 파이프 무게 차이는 77.1%, 전체 무게는 12.1%가 변한다. 마지막으로 단면 이차 모멘트의 차이는 64.3%로
두께에서도 무게보다는 이차 관성 모멘트가 지배적이다.
|
Fig. 7 5th mode frequency according to stacking sequence change |
|
Fig. 8 Natural frequency according to pipe thickness |
|
Fig. 9 Natural frequency according to pipe thickness |
본 연구에서는 복합재료가 적용된 쿼드콥터의 진동 특성을 분석하였다. 분석된 고유 진동수들을 Kim 등[5]의 결과와 비교하여 해석의
신뢰성을 획득하였다. 진동 특성에서 플랫폼의 고유 진동수가 모터의 가동범위 안에 속해있는 5차 모드에 대해 공진의 위험이 있다고 판단하였다.
공진 회피를 위하여 적층 배열의 변경에 따른 강성 변화, 로터-암의 길이, 두께 변경에 따른 이차 관성 모멘트, 3가지 변수를
각각 하나씩만 변수로 두고 나머지 변인을 통제하여, 유한요소해석 프로그램으로 각 변수의 변화에 따른 고유 진동수의 변화를 분석하였다.
(1) 적층 배열 변경에 따른
강성에 대해 공진 회피 설계를 하였다. 층간 박리가 일어날 수 있는 단일 적층을 제외하고 가동범위에서 10% 이상의 분리 여유를 보이는
[W][45/-45/90]S와 [W][45/-45/45]S의 적층 배열이 5차 모드 고유 진동수 각
98.52, 97.72 Hz로 공진 회피가 이뤄진 적층 배열로 판단하였다.
(2) 기존 390 mm의 파이프를 500 mm까지 길이를 증가시키면서
고유 진동수의 변화를 분석하였다. 이 플랫폼에서는 410 mm부터 고유 진동수가
115.54 Hz로 모터의 가동범위를 벗어난 것을 알 수 있다.
(3) 두께를 기존 1.0 mm에서 3.0 mm까지 증가시키면서 고유
진동수 변화를 분석하였다. 앞의 (1), (2)과는 다르게 두께가 증가하면 고유 진동수가 증가하는 경향을 보였다. 두께가 2.000 mm이 될 때, 고유 진동수가
136.01 Hz로 모터의 가동범위를 벗어났다.
위의 같은 공진 회피 설계에서 적층 배열 변경, 로터-암의 길이, 두께를 각각 변화시켰다. 쿼드콥터와 같은 플랫폼을 제작할 때, 위
3개이외에 고려해야 될 부분은 변화에 따른 무게 증가이다. 변화에 따른 무게 증가는 복합재 파이프의 길이와 두께 변화에서 나타나게 된다. 무게
증가는 곧 유상하중(Payload)을 감소시키고, 부피 증가는 생산비용의 증가를 의미한다. 두께 변화를 이용한 공진 회피 설계에서는 전체 무게
변화율이 10%가 넘는다. 그러므로 두께를 증가시키는 방법은 강성이 우수할 수 있으나 효율 측면에서는 좋지 않다고 판단하였다. 하지만 두께를 감소시키는
것은 구조적 안전성을 낮출 수 있다. 그러므로 고유 진동수를 낮추는 방향의 적층 배열과 길이 변화를 이용한다면 플랫폼 자체에서 공진의 위험에도
벗어날 수 있다고 기대된다.
- 1. Jeong, J.H., “Development Status of the Drones and Prospect for the Market,” The Optical Journal, Vol. 158, No. 6, 2015, pp. 40-47.
- 2. Park, J.K., Seo, B.K., and Oh, C., “Development of High-tech Industry and the Evolution of Chinese Industrial Policy: Case of Drone Industry,” The Journal of Modern China Studies, Vol. 19, No. 1, 2017, pp. 175-210.
-

- 3. Paredes, J.A., Acevedo, J., Mogrovejo, H., Vilaita, J., and Furukawa, R., “Quadcopter Design for Medicine Transportation in the Pe-ruvian Amazon Rainforest,” Proceeding of IEEE XXIII International Congress on Electronics, Electrical Engineering and Compu-ting. IEEE, Piura, Peru, Aug. 2016.
-

- 4. Verbeke, J., and Debruyne, S., “Vibration Analysis of a UAV Multirotor Frame,” Proceedings of ISMA 2016 Inernational Confer-ence on Noise and Vibration Engineering, Leuven, Belgium, Sep. 2016.
- 5. Kim, M.S., Kim, J.N., Kim, J., and Kang, B.S., “Study on Analysis of Vibration Characteristics and Modal Test for a Quad-Rotor Drone,” Journal of the Korean Society for Precision Engineering, Vol. 33, No. 9, 2016, pp. 707-714.
-

- 6. Lee, S.C., Son, I.S., and Heo, K.D., “Vibration Analyses and Design of Resonance Avoidance of the Unmanned Helicopter Master,” Journal of the Korean Society for Precision Engineering, Vol. 28, No. 8, 2011, pp. 951-958.
- 7. Thomson, W., Theory of Vibration with Applications, CRC Press, 2018.
- 8. Barbero, E.J., Finite Element Analysis of Composite Materials Using ABAQUS, CRC Press, 2013.
- 9. Hong, D.K., Jeong, J.B., Jung, S.W., Kim, G.B., and Ahn, C.W., “Investigating Natural Frequency Analysis and Measurement of Railway Vehicle to Avoid Resonance,” The Korean Society for Noise and Vibration Engineering, Vol. 22, No. 8, 2012, pp. 713-719.
-

 This Article
This Article
-
2020; 33(3): 133-139
Published on Jun 30, 2020
- 10.7234/composres.2020.33.3.133
- Received on Dec 12, 2019
- Revised on Mar 26, 2020
- Accepted on May 27, 2020
 Services
Services
Shared
 Correspondence to
Correspondence to
- Wie-Dae Kim
-
Aircraft Structural Design Laboratory, Pusan National University
- E-mail: wdkim@pusan.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.