- A Review of Mean-Field Homogenization for Effective Physical Properties of Particle-Reinforced Composites
Sangryun Lee*, Seunghwa Ryu*†
* Department of Mechanical Engineering, KAIST
- 평균장 균질화를 이용한 입자 강화 복합재의 유효 물성치 예측 연구 동향
이상륜* · 유승화*†
In this review paper, we introduce recent research
studied effective physical properties of the reinforced composite using mean-field
homogenization. We address homogenization for effective stiffness and expand it
to effective thermal/electrical conductivity and dielectric constant.
Multiphysics problems like piezoelectricity and thermoelectricity are
considered by simplifying the constitutive equation into the linear equations
like Hooke’s law. We present a generalized
theoretical formula for predicting effective physical properties of composite
and validation by against finite element analysis.
본 리뷰 논문에서는 최근에 연구된 평균장 균질화법을 이용한 다양한 물성치 예측 연구의 동향에 대해
소개한다. 유효 강성 예측에 사용되는 기존의 균질화법을 소개하고 이를 확장하여 유효 열/전기 전도성 및 유전 상수를 예측하는 방법을 소개한다. 압전 및 열전과
같이 2개의 물리현상이 중첩된 다중 물리 현상의 구성방정식은 훅 법칙과 같이 단순한 선형 형태로 변환하여
복합재의 유효 물성치를 예측하는 연구를 소개하고 마지막으로 복합 재료의 유효 물성치를 예측하기 위한 일반화된 식을 제시하고 유한 요소 해석과 비교한
검증/연구를 소개한다.
Keywords: 균질화법(Homogenization), 미시역학(Micromechanics), 유효 물성치(Effective property), 다중 물리(Multiphysics)
보편적으로 모재와 강화재로 구성된 복합재는 고강도, 단열, 절연 등, 단일 물질로는 얻을 수 없는 뛰어난 물성치를 갖기 때문에 다양한
분야에 활용되어 왔다. 예를 들어 가벼운 구조용 탄소섬유 복합재는 자동차 산업과 항공 산업에 활용되어 왔고[1,2], 절연/단열 복합재는 전선/배관 산업에 사용되고 있다[3,4]. 따라서, 효율적인 설계와 활용을 위해서는 복합재의 유효 물성치에 대한 이론 연구가 필수적이다.
유한 요소 해석은 복합재의 기계[5-8], 열[9,10], 전기[11,12], 압전[13-16], 열전[17] 등 유효 물성치를 예측하는데 널리 사용되어왔다. 그러나 통계적으로 의미있는 결과를 얻기 위해서는 많은 강화재가
포함된 큰 시뮬레이션 셀(cell)과 계면에서 많은 미세 격자망(fine mesh)가 사용돼야 대표 체적 요소(representative
volume element)로서 의미를 갖기 때문에 계산 시간이 많이 소요되는 한계가 존재한다[10,18]. 이러한 수치 계산을 사용하여 선형 영역에서 복합재의 유효 물성치를 예측하는 것은 가능하지만 여러 번의
선형화 및 수렴 작업이 필요한 비선형 영역에서 복합재의 물성치를 수치적으로 예측하는 것은 어렵다.
강화재가 비교적 주기적/규칙적으로 배열된 경우, 단위 셀의 하중 전달 메커니즘에 초점을 둔 이론 모델을 사용하여 해석할 수 있으며 전형적인
예는 매우 긴 섬유 강화재[19]와 자연 판상 적층 구조를
가진 복합재이다[20]. 반대로, 무작위로 분산 된 강화재의 경우, 하중 전달
메커니즘을 사용하여 모델링 할 수 없기 때문에 단(short) 섬유 강화재 또는 구형 강화재의 무작위 배열을 포함하는 복합재는 균질화법을 통해
연구해야한다.
이러한 복합재의 기계적 특성은 강화재 및 모재의 평균 변형률을 계산하여 예측 할 수 있다[21]. 특히, 낮은 부피 분율(volume fraction)에서 잘 분산 된 강화재(20% 미만)를 포함하는
복합재의 경우 강화재들 간의 영향은 평균화 작업을 통해 근사된 모재의 변형률을 사용하여 고려할 수 있다. 예를 들어 모재의 변형률이
평균 변형률과 동일하거나[22]
(Mori-Tanaka 방법) 복합재의 평균 변형률과 동일하다고 가정한다(self-consistent 방법)[23]. 평균의 근사값이 유효한 이 영역에서는 단일 비균질(single inhomogeneity)
문제의 해를 사용하여 유효 물성치를 예측 할 수 있으며, 선형 영역에서의 균질화법을 사용하여, 증분 접선 방법(increment
tangent) [24], 증분 할선(increment secant) 방법[25], 변분법(variational approach)[26] 등을 활용한 비선형 물성치 예측에 활용될 수 있다.
본 리뷰 논문은 최근 다양한 물성치를 예측하는데 사용되는 균질화법 연구 동향에 대해 소개하며 다음과 같이 구성된다. 2장에서는 탄성학에서
Eshelby 텐서의 개념과 복합재의 유효 강성 계수 계산에 대해 간략히 요약한다. 3장에서 다양한 물리 현상을 지배하는 정상 상태에서의 지배
방정식들과 Eshelby 텐서 및 균질화 개념의 수학적 유사성에 대해 나타낸다. 4장에서는 다양한 물성치 예측과 유한요소법을 이용한 계산결과를
비교하고 마지막으로 5장에서 결론에 대해 고찰한다.
함유체와 비균질의 변형률을 고려하여 입자/섬유 강화 복합재의 기계적 특성을 추론하기 때문에 이에 대한 이해가 필요하다. 함유체는 고유
변형률(eigenstrain, ε*rs)을 가지면서 모재와 동일한 탄성 강성 텐서(Lpqrs)를
갖는 재료를 지칭하는 반면, 비균질은 다른 강성(L′pqrs)를 갖는 재료를 지칭한다. Eshelby[27]는 무한 모재에 매립 된 타원 함유체 내부의 구속 변형률(constrained strain εcrs)이 균일하다는 것을 증명하였다. 여기서 고유 변형률은 열팽창[28], 초기 변형[29] 또는 상 변형[30]과 관련된, 응력이 없는 상태의 변형률을 의미한다. 이때 구속 변형률은 Eshelby 텐서를
사용하여 구할 수 있다(εcij = Sijrsε∗rs)[27]. 이 장에서는 (1) Eshelby 텐서의 주요 개념, (2) 외부
하중을 받는 타원체 비균질이 유효 단일 함유체 문제로 변환되는 방법 및 (3) 복합재의 유효 강성 예측에 사용되는 균질화법에 대해 소개한다.
2.1 단일 함유체(single
inclusion) 문제
점 y에서 j방향 점 하중이 있을 때 x에서 i방향의 변위를 나타내는
탄성학에서의 Green 함수 Gij(x– y)의 지배 방정식은 아래와 같이 나타낼 수 있다[21].
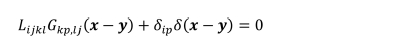
여기에서 Lijkl은 4차 탄성 강성 텐서이며, 반복된 지수는 1부터 3까지의 모든 값에 대한 합을
의미한다. 등방성 재료의 경우 Lijkl은 두 개의 독립적인 탄성 계수로 구성 될 수 있고 이 때 Green 함수는
아래와 같이 닫힌 형태(closed form)로 유도된다[21].
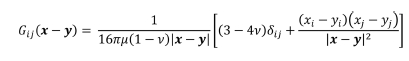
여기서 μ와 ν는 각각 재료의 전단 계수와
푸아송 비이며, |χ-y|는 벡터 χ-y의 크기를 의미한다.
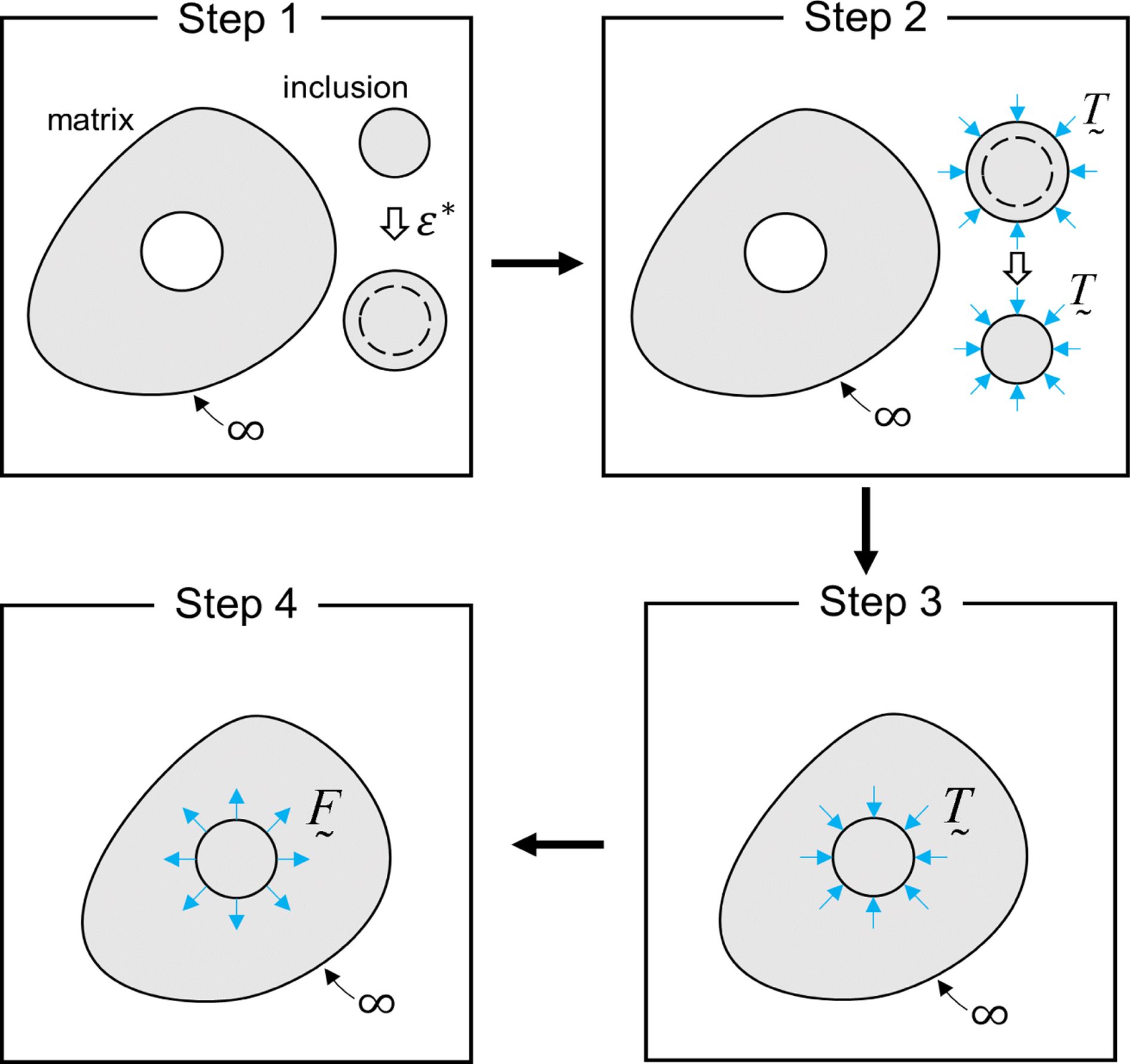
단일 함유체 문제는 4 단계로 나타낼 수 있다(Fig. 1). 외부 변위 또는 하중이 없는 경우 함유체가 고유 변형률 ε*만큼 변형될 수 있다고
가정한다(step 1). 원래의 형상을 유지하기 위해, 하중(T)가 가해지고(step 2) 그 후, 함유체는 무한 모재
내에서 원래의 형상 및 크기를 갖는 구멍에 들어가게 된다(step 3). 적용된 하중(T)을 제거하게 되면 함유체는 모재에
F = -T의
힘을 가하게 되고(step 4) 모재의 구속 효과로 인해 함유체는 고유 변형률 ε*과 다른 구속 변형률 εc만큼
변형하게 된다. 이때 Eshelby 텐서는 아래과 같이 Green함수를 사용하여 표현할 수 있다.
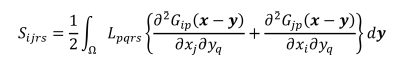
여기서 Ω는 함유체의 부피를 의미한다. ε*와 εc이
대칭 행렬이므로 Eshelby 텐서는 단대칭(minor symmetry)(Sijkl = Sjikl = Sijlk)을 갖지만 주대칭(major
symmetry) (Sijkl ≠ Sklij)은 없다. 등방성 물질에서,
3개의 다른 반축 a1, a2 및 a3을 갖는 타원체 함유체에 대해,
Eshelby 텐서는 타원 적분으로 표현되고[21] 축대칭 강화재에 대해서 닫힌 형태의 해가 존재한다[32]. 구형 함유체의 경우
Eshelby 텐서는 아래와 같이 표현된다.
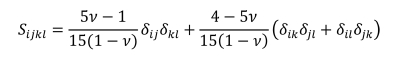
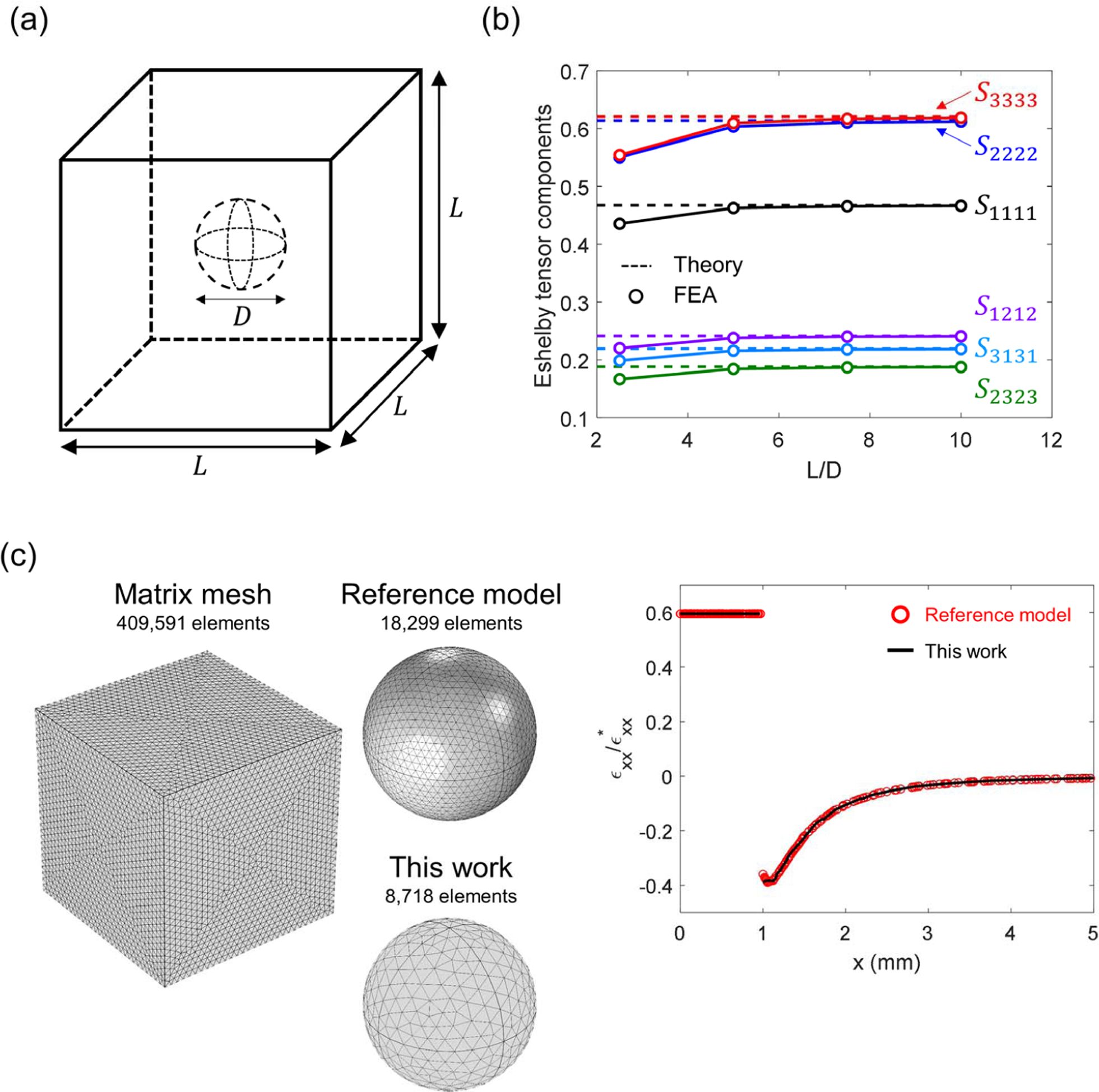
유한요소법을 이용하여 Eshelby 텐서를 예측할 경우, 먼저 무한한 크기의 모재를 모사하기 위해 충분히 큰 모재를 사용해야 한다.
두번째로 계면에서 변형률의 불연속(jump)가 발생하기 때문에, 충분히 작은 요소를 사용해야 한다. 최근에 연구된 결과에 따르면 구형 함유체의
경우, 지름에 비해 10배 큰 정육면체 모재를 사용할 경우 그 결과가 이론 예측 값과 같다는 것이 연구되었으며, 요소 크기에 따른 정확도에 대해서도
연구되었다(Fig. 2)[8,31]. 특정 모재와 강화재
모양에 대해 Eshelby 텐서를 얻은 후에는 부피 분율, 강화재의 방향 분포, 그리고 강화재의 강성등 다양한 경우에 대해 복합재의 유효 물성치를
계산할 수 있기 때문에 FEA로 Eshelby 텐서를 예측하더라도 FEA로 유효 물성치를 예측하는 것에 비해 빠르게 예측할 수 있다.
2.2 단일 비균질 문제
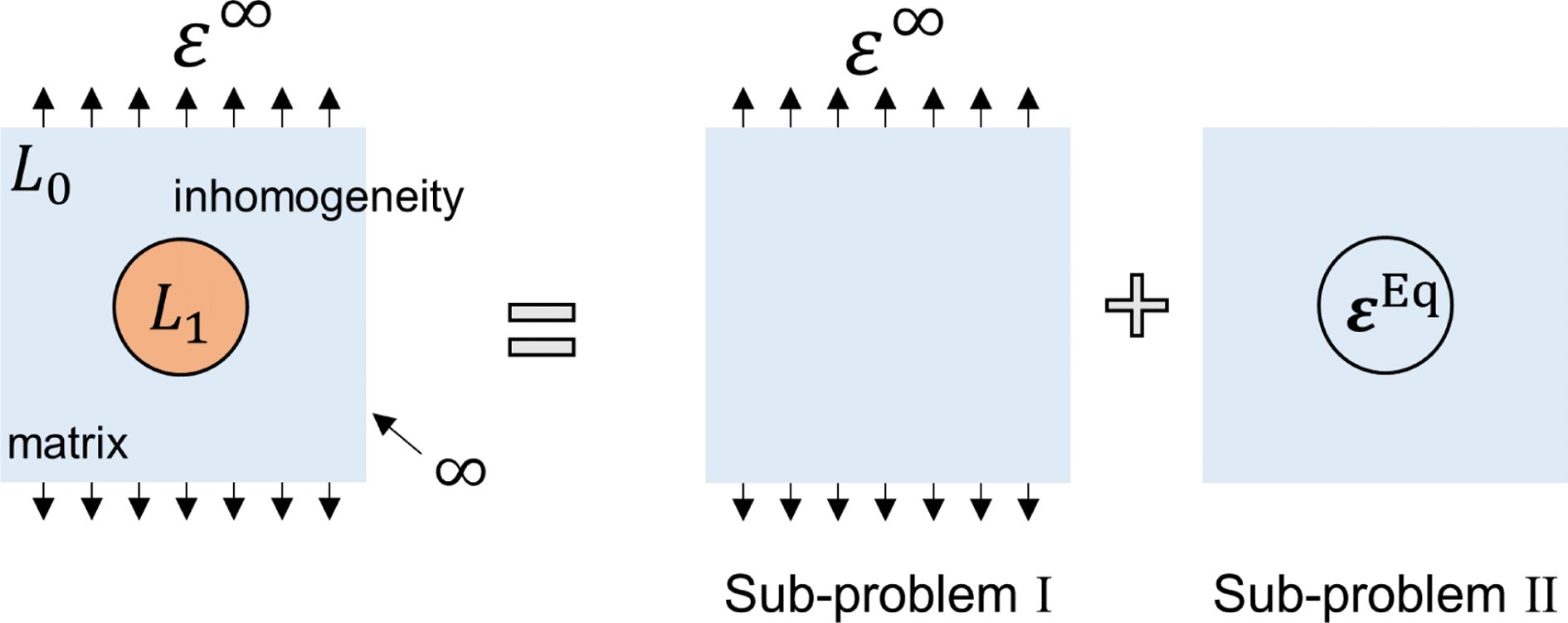
본 장에서는 균일 한 외부 하중 εAkl 을 받는 타원체 단일 비균질 문제를 유효 단일 함유체 문제로 변환하는 방법에 대해
논의한다. 균일한 외부 하중(응력 또는 변형)이 있는 단일 함유체 문제의 경우 전체 변형률은 εtkl = εAkl + εckl가 되고 응력은 σIij = Lijkl(εtkl - ε*,Eqkl)로 나타낼 수 있다. 동일한 하중을 받는 비균질의 전체 변형률 εt′kl = εAkl + εc′kl 및 응력장 σI′ij = L′ijkl + εt′kl이 하중을 받는 함유체의 결과와 동일 할 때 ε*,Eqkl를 등가 고유 변형률(equivalent eigenstrain)라고 정의한다(Fig.
3). 따라서, εAkl + εc′kl = εAkl + εckl 및 L′ijkl (εAkl + εc′kl) = Lijkl(εAkl + εckl - ε*,Eqkl)로부터 등가 고유 변형률을 아래와 같이 구할 수 있다.
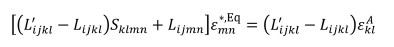
텐서 표현으로 나타내면 아래와 같이 나타낼 수 있으며,
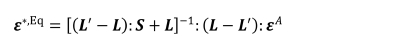
여기서 : 및 [ ]-1은 각각 이중 점곱(double dot product) 및 역 연산자(inverse)를
의미한다.
선행 연구에서는 강성 텐서를 6 × 6 매트릭스 연산으로 변환하는
Mandel 표기법을 채택하여 텐서의 이중 점곱 및 역 텐서 계산을 하였다[8,13,17,31,33]. 대부분의 연구에서는 Voigt 표기법을 사용했지만[14-16,34,35], Mandel 표기법을 사용하여 텐서 계산을 할 경우, 계산 측면에서의 편의성과 수학적 일관성을 유지하지
한다는 것이 최근 연구 되었다[13]. Mandel 표기법에
따르면 응력 벡터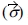 , 변형률 벡터
, 변형률 벡터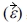 , 강성 행렬(L) 그리고 Eshelby 행렬(S)은 아래와 같이 나타낼 수 있다.
, 강성 행렬(L) 그리고 Eshelby 행렬(S)은 아래와 같이 나타낼 수 있다.
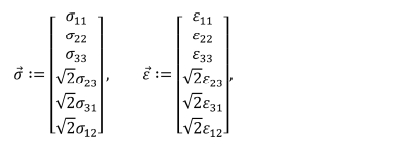
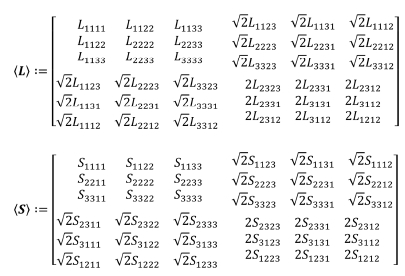
계수 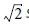 와 2는 행렬-행렬 곱과 역수가
각각 4차 텐서의 이중 점곱과 역으로 일치하도록 한다. 따라서 A, B가 단대칭(Aijkl = Ajikl = Aijlk)을 갖는 4차 텐서이고 <A>, <B>가 Mandel 표기법에
따라 나타낸 6 × 6 행렬이면, 아래와 같이
나타낼 수 있다.
와 2는 행렬-행렬 곱과 역수가
각각 4차 텐서의 이중 점곱과 역으로 일치하도록 한다. 따라서 A, B가 단대칭(Aijkl = Ajikl = Aijlk)을 갖는 4차 텐서이고 <A>, <B>가 Mandel 표기법에
따라 나타낸 6 × 6 행렬이면, 아래와 같이
나타낼 수 있다.
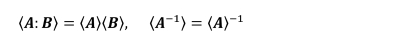
2.3 유효 탄성계수 예측을 위한
균질화법
비균질들 간의 상호 작용을 고려하여 복합재의 유효 강성을 예측하기 위해 본 논문에서는 Mori-Tanaka 방법을 소개한다.
Mori-Tanaka 방법은 비선형 방정식 형태의 해를 갖는 self-consistent 방법과 달리 닫힌 형태의 식이 존재하기 때문에 계산이
간편하여 널리 사용되어 왔다. 각각의 비균질은 모재의 평균 변형률을 갖는 모재에 삽입되는 것을 가정하므로, 이 기술을 균질화법이라고 한다. 비균질들
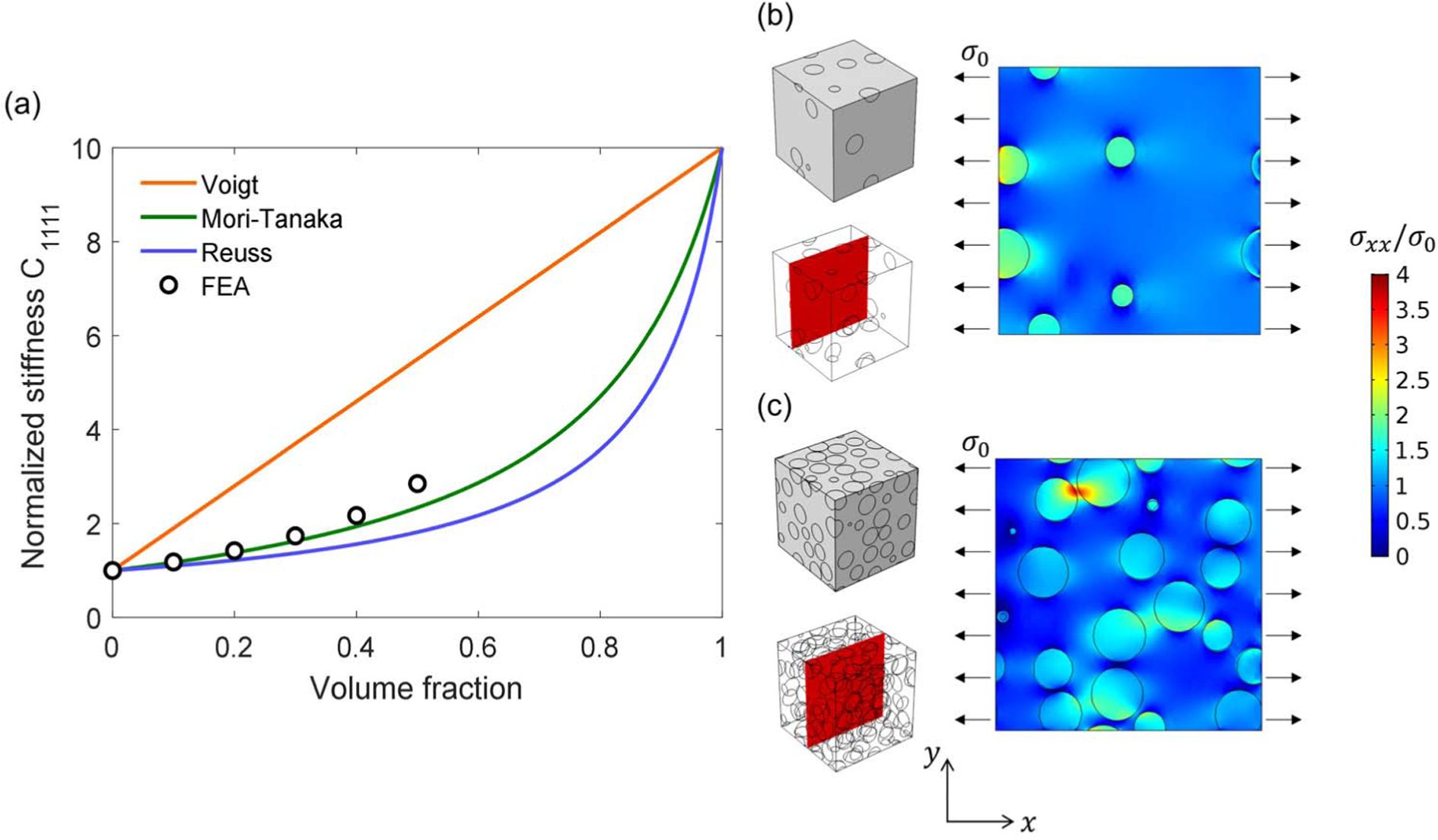
사이의 상호 작용은 부피 분율이 높을수록 커지기 때문에, Mori-Tanaka 방법은 상대적으로 적은 부피 분율 (<20%)에서 신뢰할 수
있는 것으로 알려져 있다[7,8,33](Fig. 4). 계산량
측면에서 살펴본다면, Intel(R) Xeon(R) CPU E5-2687W @ 3.10GHz을 이용하여 유한요소법을 계산할 경우 대략 14분 정도가
소요되고, 균질화법을 이용하여 계산할 경우 0.00015초가 소요된다. 따라서, 균질화법을 사용할 경우 더 효율적으로 유효 물성치를 예측 할 수
있다.
이때, 모재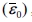 , 비균질
, 비균질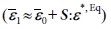 및 복합재의 평균 변형률
및 복합재의 평균 변형률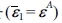 는 아래의 식을 만족한다.
는 아래의 식을 만족한다.
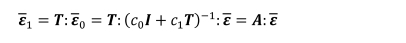
여기서 A = T:(c1I+c1T)–1 (T = [I + S:L0–1:(L1 - L0]–1는 Mori-Tanaka
방법에 사용되는 변형률 집중(strain concentration) 텐서이며, 작은 부피 분율에서 (c1<<1) 단일 불균질 문제에서의
변형률 집중 텐서 T로 수렴한다. 복합재의
유효 강성은 다음과 같이 복합재의 평균 응력과 변형률 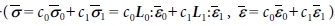 의 연립 계산을 통해 아래와 같이 정리된다.
의 연립 계산을 통해 아래와 같이 정리된다.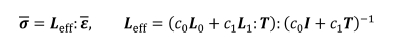
|
Fig. 1 The schematic of single inclusion problem. Image from [31] |
|
Fig. 2 (a) Geometry used for the FEA. (b) Eshelby tensor for L/D. (c) Mesh size-dependent convergence test for single inclusion problem. Image from [31] |
|
Fig. 3 The schematic of single inhomogeneity problem |
|
Fig. 4 (a) Effective stiffness prediction with different models. The stress field within simulation cell for (b) 5% (c) 34% volume fraction. The material properties used for the simulations are E1 = 10E0, ν1 = ν0 = 0.25 |
3.1 수학적 유사성
본 장에서는 수학적 유사성을 사용한 다양한 유효 물성치 예측에 대해 살펴본다. 정상 상태에서의 두 가지 대표 지배 방정식인 전도/유전체
관련 방정식과 결합(couple)된 다중 물리 방정식을 고려한다.
전도/유전체와 같은 물리 현상의 경우, 정상 상태에서 내부 소스(source)가 없을 때 물질의 모든 지점 x에서의 지배 방정식은 아래의 방정식을 사용하여 나타낼
수 있다.
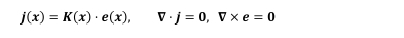
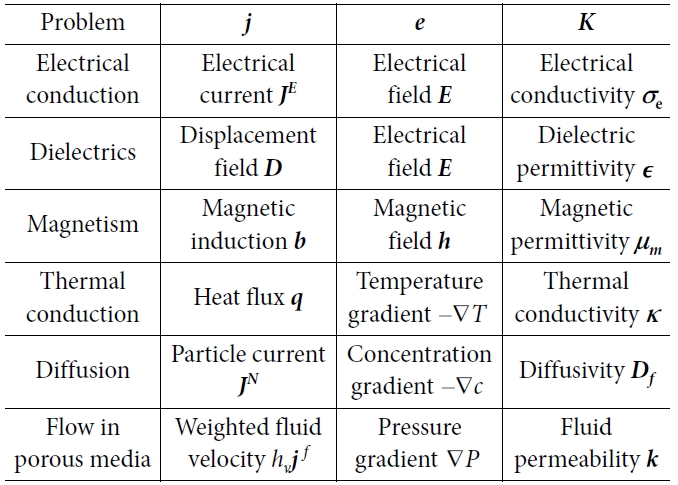
이는 전기 전도, 유전 현상, 자성, 열 전도, 및 확산 현상을 모사하는 수식에서 나타난다. 벡터 j(x), e(x)
및
2차 텐서 K(x)는 Table 1에 주어진 물리적 의미를 갖는다[33]. 정상 상태에서의 지배 방정식은 수식의 형태가 수학적으로 동일하기 때문에 이러한 물리 현상들
중 하나에 대해 얻은 균질화법 결과를 Table 1의 다른 방정식에 직접 적용하여 유효 전기 및 열 전도도, 자기 유전율, 및 유효 확산 성 등을
예측할 수 있다.
두 번째 종류의 방정식의 예로 압전 및 열전에서의 방정식이 있다. 전술 한 전도/유전체 관련 방정식은 이상적인 반면에 실제 격자 왜곡으로
인해 일부 이방성 물질에서 전기 분극(polarization)이 발생할 수 있으며, 그 반대도 마찬가지이다[35]. 또한 전도성 전자는 열을 전달할 수 있어서 열과 전기 현상 사이에 결합을 일으킨다[36]. 전자를 압전이라 하고 후자를 열전이라고 한다.
먼저, 압전의 구성 방정식은 다음과 같다.
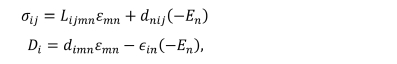
여기서 Di는 전기 변위(electric
displacement), En은 전기장, 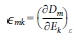 는 일정한 변형률에서의 유전율이며
는 일정한 변형률에서의 유전율이며 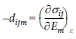
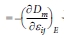 는 일정한 변형률에서의 압전 상수이다. Barnett과 Lothe[37]가 제안 한 표기법을 사용하여 탄성, 열 및 전기 전도의
구성 방정식과 유사하게 압전의 구성방정식을 선형 방정식의 형태로 표현할 수 있다. 이 표기법은 대문자 반복 지수가 1부터 4까지의 합을 의미한다는
점을 제외하고는 기존 텐서 표기법과 동일하다. 이 표기법을 사용하면 변형률과 전기장을 결합하여 다음과 같이 표현할 수 있다.
는 일정한 변형률에서의 압전 상수이다. Barnett과 Lothe[37]가 제안 한 표기법을 사용하여 탄성, 열 및 전기 전도의
구성 방정식과 유사하게 압전의 구성방정식을 선형 방정식의 형태로 표현할 수 있다. 이 표기법은 대문자 반복 지수가 1부터 4까지의 합을 의미한다는
점을 제외하고는 기존 텐서 표기법과 동일하다. 이 표기법을 사용하면 변형률과 전기장을 결합하여 다음과 같이 표현할 수 있다.
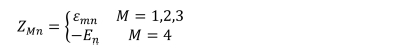
여기서 ZMn은 UM을 xn에 대해 미분하여 얻을 수 있고 UM은 아래와 같이 나타낼 수 있다.

유사한 방식으로 응력과 전기 변위를 하나의 변수 ∑iJ로 정리할 수 있다.

새로 정의한 변수를 사용하면 압전 상수와 구성 방정식은 아래와 같이 1개의 선형 방정식으로 나타낼 수 있다.
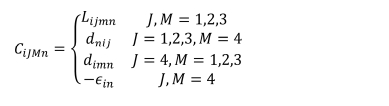

반면에 열전 물질의 구성 방정식은 아래와 같이 행렬 형태로 나타낼 수 있다.
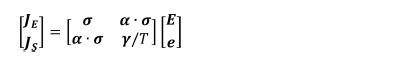
압전 물질 방정식에서 사용했던 표기법을 따라 아래와 같이 나타낼 수 있다.
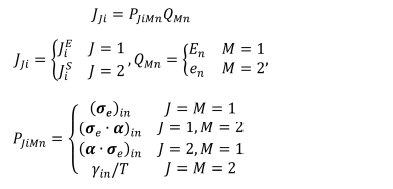
여기서 JE는 전류 밀도, JS (=q/T)는 엔트로피 유속,
q는 열 유속, T는 온도, σe는 전기 전도도,
α는 Seebeck 계수, γ(= κ + Tα ∙ σe ∙ α)는 전기장이 없을 때의
열전도도이고, κ는 전류가 흐르지 않을 때의 열전도도이다. PJiMn은 위치
x에 의존하는 T를 포함하므로 일반적으로 다른 물리 현상에서의 방정식과 수학적으로 유사하지 않다. 최근 연구에서는 고온/저온면에서
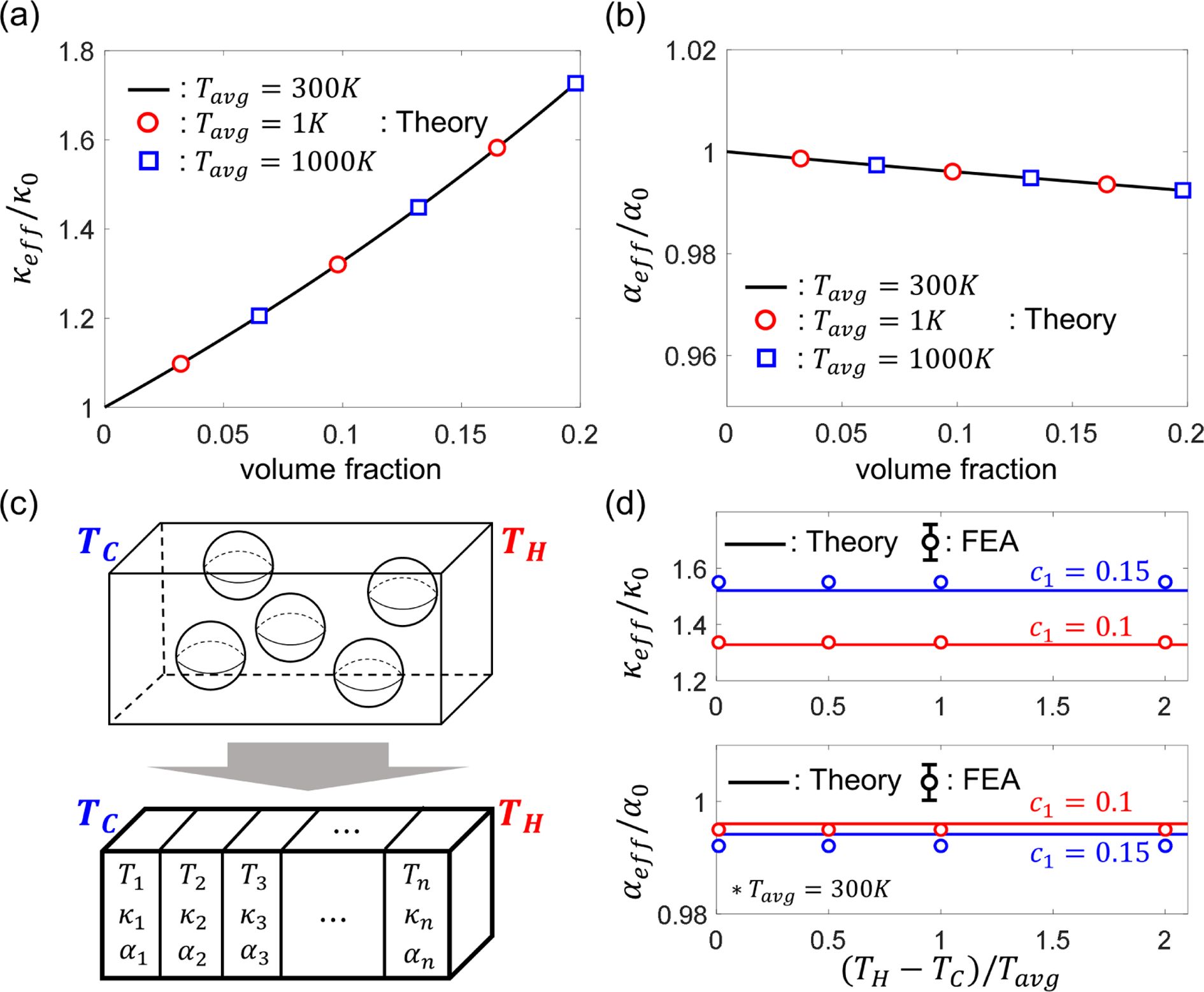
온도 차이가 작은 경우(TH - TL = ΔT ≈ 0), 구성 방정식의 온도
변수 T가 일정한 평균 온도 Tavg (=((TH + TL))/2)라고 가정하였다. 이 가정의 타당성은 유한 요소 분석 결과와 비교하여 광범위한 ΔT 범위에 대해 연구되었다(Fig. 5)[17].
3.2 다양한 물리 현상에서의
Eshelby 텐서
수학적 유사성을 사용하면 다양한 물리 현상에서의 Eshelby 텐서는 탄성학에서의 Eshelby 텐서와 비슷한 형태로 전개가 가능하다.
일반적인 비등방성 물질에서 반축 a1, a2, a3을 갖는 타원체 함유체의
경우 탄성학에서 Eshelby 텐서는 아래와 같이 표현된다[21,31].
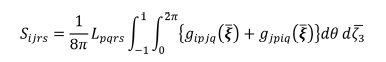
여기서 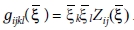 로 나타나고, Z(x) = [(L ∙ x) ∙ x]-1와 x 는 각각 푸리에 공간(Fourier
space)에서의 Green 함수와 벡터를 의미한다. 특히
로 나타나고, Z(x) = [(L ∙ x) ∙ x]-1와 x 는 각각 푸리에 공간(Fourier
space)에서의 Green 함수와 벡터를 의미한다. 특히 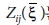 는 2계 균일함수(homogenous function)이기 때문에 xkxlZij(x)는
는 2계 균일함수(homogenous function)이기 때문에 xkxlZij(x)는 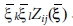 와 같다. 벡터
와 같다. 벡터 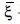 는 적분 변수
는 적분 변수 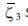 와 θ를 사용하면
와 θ를 사용하면 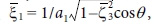 ,
, 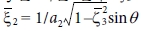
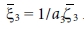 그리고
그리고 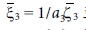 로 나타낼 수 있다.
로 나타낼 수 있다.
비슷한 방법으로 분극과 그로 인한 격자 비틀림으로 발생하는 3개의 자유도를 추가한다면, 압전에서의 Eshelby 텐서는 아래와 같이
나타낼 수 있다[13,34].
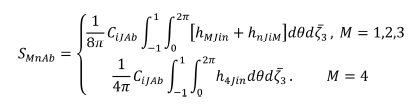
여기서 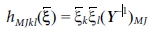 이며
이며 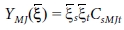 이다. 중앙대칭(centrosymmetric) 결정은 압전상수가 모두 0이기 때문에
등방성 압전 물질의 Eshelby 텐서는 존재하지 않는다.
이다. 중앙대칭(centrosymmetric) 결정은 압전상수가 모두 0이기 때문에
등방성 압전 물질의 Eshelby 텐서는 존재하지 않는다.
전도와 유전 현상에서 2차 물성치 텐서가 K일 때 Eshelby 텐서는 아래와 같이 나타낼 수 있다[9,11].
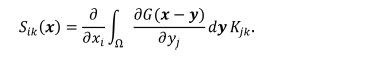
탄성학과 달리, 임의의 대칭 구조를 갖는 물질에 대해서 Green 함수는 아래와 같이 닫힌 형태로 존재한다.
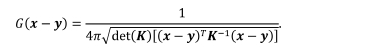
2차 텐서 형태로 나타나는 Eshelby 텐서는 하나의 적분변수 s를 갖도록 아래와 같이 표현 가능하며[9,11]
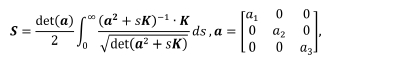
탄성학에서의 Eshelby 텐서와 비슷한 수식으로도 나타낼 수 있다.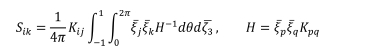
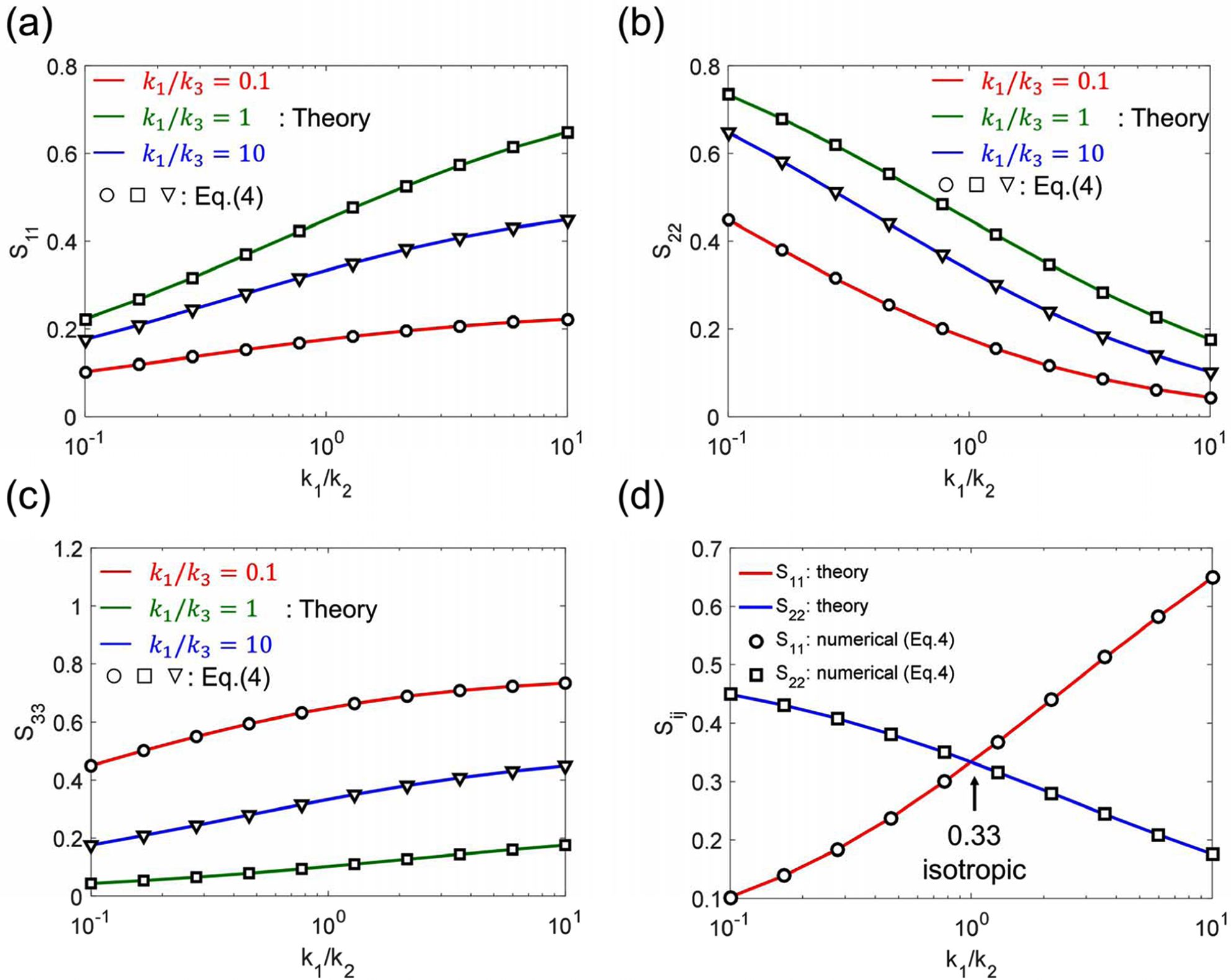
등방성 물질속에 있는 구형 함유체의 Eshelby 텐서는 Sik = 1/3δik로 간단하게 나타낼 수 있다(Fig. 6).
전기 전도와 열전도의 결합으로 이루어진 열전 물질의 Eshelby 텐서는 아래와 같이 나타낼 수 있으며,
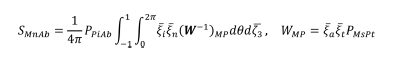
가장 간단한 형태의 Eshelby 텐서는 등방성 물질속 구형 함유체이며 SMnAb = 1/3δMAδnb로 나타낼 수 있다[17]. 본 장에서의 수학적
해석을 통해서 열전도, 전기전도 그리고 유전에서의 Eshelby 텐서가 탄성학과 압전에서의 Eshelby 텐서보다 간단한 것을 알 수 있는데,
이는 열전도, 전기전도 그리고 유전에서의 Green 함수가 다른 두 경우와 달리 간단한 스칼라로 나타나기 때문이다.
|
Fig. 5 Theoretically predicted (a) κeff/κ0 and (b) αeff /α0 with different average temperatures. (c) Configuration for converting the composite into a serial connection of homogenized pieces when a large temperature difference is imposed. (d) κeff/κ0 and αeff /α0 when a large temperature difference is imposed. Image from [17] |
|
Fig. 6 The independent Eshelby tensor components for a spherical inclusion in an orthotropic ((a) S11, (b) S22, (c) S33) and (d) transversely isotropic matrix. Image from [9] |
4.1 수치 해법 및 유한요소법을
통한 검증
본 장에서는 수학적 유사성을 이용하여 예측한 복합재의 다양한 유효 물성치를 소개한다. 입력 변수 q, 출력
변수 p, 그리고 선형 연산자 X로 구성된 물리 현상의 구성방정식은 Mandel 표기법에 따라
높은 차수의 텐서를 행렬로 나타낼 수 있다(p = Xq). 탄성학에서의 Lijmn,
전도/유전에서의 κin, 압전에서의 CiJMn 그리고 열전에서의 PJiMn는
각각 6 × 6, 3 × 3, 9 × 9 그리고 6 × 6 대칭행렬로 변환된다.
일반적으로 Eshelby 텐서는 무차원 변수지만, 압전과 열전의 경우 결합되어 있는 항에서는 각각 N/C와 V/K 단위를 갖는다. 일반적으로 탄성계수와
압전 상수는 정도(order)의 차이가 크기 때문에 수치 계산하는 과정에서 오차가 발생할 수 있으므로 전하를 나타내는 단위는 SI 단위를 사용하지
않고 1nC = 10-9 C를 사용해야 한다[33].
p = Xq 행렬곱으로 나타난는 물리
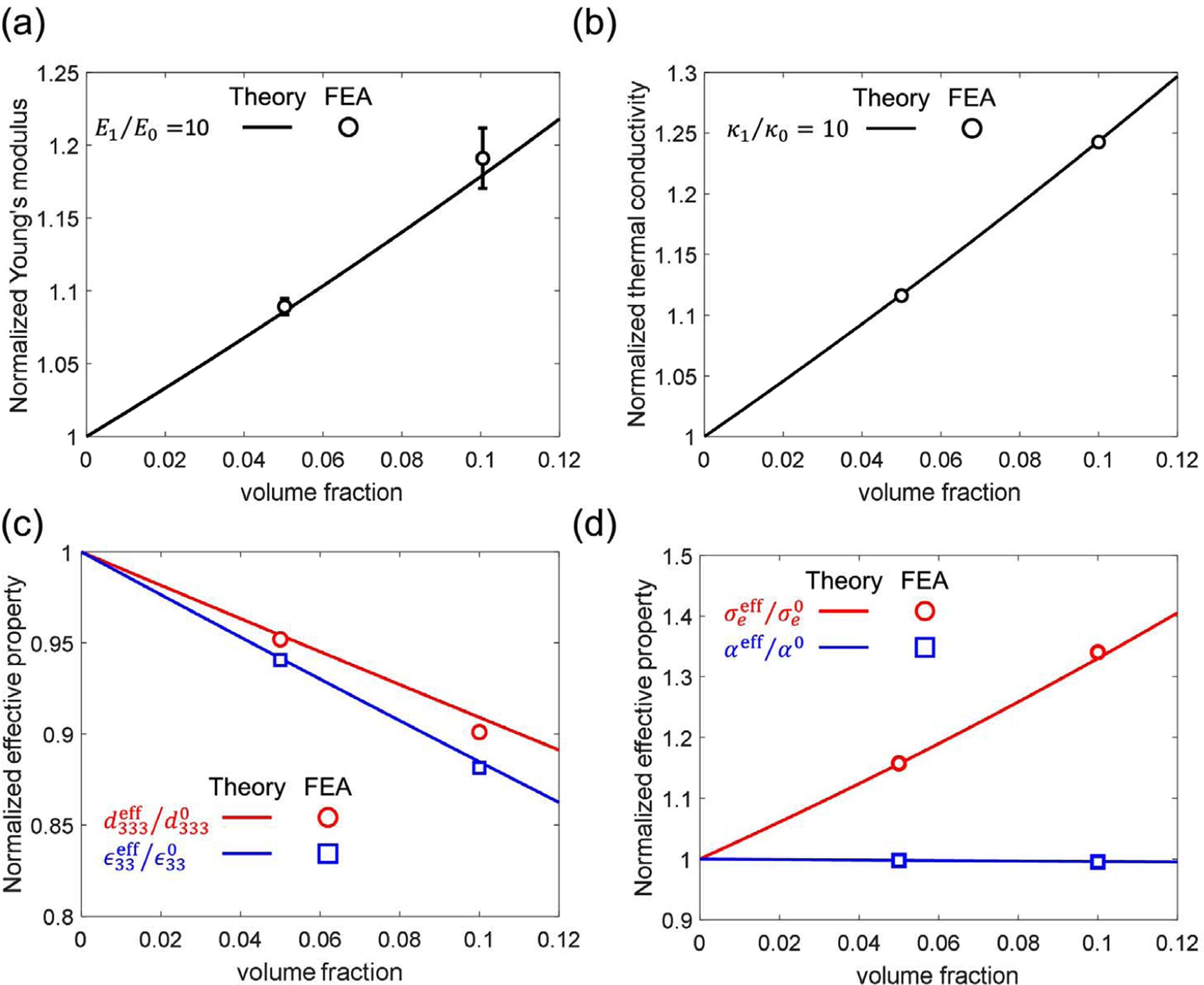
현상의 유효 물성치는 아래와 같이 나타낼 수 있다(Fig. 7).
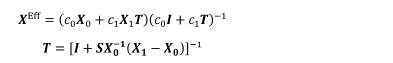
이론의 타당성을 검증하기 위해서 많은 연구에서 유한요소법을 이용하여 입자 강화 복합재의 유효 물성치를 예측하였다[8,9,16,17,38]. 양쪽 경계(면)에 단위 입력 변수(q)를 가하도록 경계조건을 부여하였고 (탄성학: 변위, 전도/유전: 온도/전위,
압전: 변위/전위, 열전: 온도/전위) 계산 결과로부터 얻는 출력 변수(p) (탄성학: 응력, 전도/유전: 열유속/전기 변위, 압전: 응력/전기 변위, 열전: 열 유속/전류
밀도)를 사용하여 물성치를 계산하였다. 물리적으로 타당한 결과를 얻기 위해서 시뮬레이션 셀 내부 입자의 위치를 바꿔가면서 여러개의 다른 셀을 사용하였다(Fig.
8).
그 결과, 수학적 유사성을 바탕으로 균질화법을 사용하여 예측한 유효 물성치가 유한요소법을 사용하여 예측한 계산결과와 잘 맞는 것으로
알려졌다(Fig. 7). 모재와 강화재의 큰 물성차이(10배)와 10% 부피 분율까지 두 결과가 일치하였으며 이론과 시뮬레이션 오차는 부피 분율이
커질수록 증가하는 것을 알 수 있었다. 이러한 이유는 앞서 설명한 균질화법의 가정에 의해 설명이 가능하다(Fig. 4).
|
Fig. 7 (a) Effective Young’s modulus, (b) thermal conductivity, (c) thermoelectric properties and (d) piezoelectric coefficient of particle reinforced composite. Image from [33] |

|
Fig. 8 Representative volume elements used for FEA. Image from [13] |
본 리뷰 논문에서는 균질화법을 이용하여 복합재의 다양한 유효 물성치를 이론적으로 예측한 연구들을 소개하였다. 특히 선행 연구를 통해
서로 다른 물리현상에 존재하는 수학적 유사성에 대해 소개하였다. 선행 연구에서 많이 사용되어 왔던 Voigt 표기법과 다른 Mandel 표기법을
소개하면서 고차원 텐서 계산에 관한 논의를 하였고, 균질화법을 이용한 예측 결과와 이를 검증하기 위한 유한요소법에 대해 서술하였다.
본 논문에서 소개했던 수학적 유사성을 이용한다면, 3장에서 논의했던 물리현상뿐만 아니라 다른 단순한 물리 현상, 혹은 2개의 물리현상이
결합된 다중물리에도 적용이 가능하기 때문에 다양한 물성치를 예측할 수 있다. 유한요소법과 다른 수치해법에 비해 복합재의 유효물성치를 빠르게 예측할
수 있기 때문에 다양한 물성치가 고려돼야 하는 실제 설계에 유용하게 적용 가능하다고 사료된다.
- 1. Obradovic, J., Boria, S., and Belingardi, G., “Lightweight Design and Crash Analysis of Composite Frontal Impact Energy Absorbing Structures,” Composite Structures, Vol. 94, No. 2, 2012, pp. 423-430.
-

- 2. Immarigeon, J-P., Holt, R.T., Koul, A.K., Zhao, L., Wallace, W., and Beddoes, J.C., “Lightweight Materials for Aircraft Applications,” Materials Characterization, Vol. 35, No. 1, 1995, pp. 41-67.
-

- 3. Imai, T., Sawa, F., Nakano, T., Shimizu, T., Kozako, M., and Tanaka, T., “Effects of Nano- and Micro-filler Mixture on Electrical Insulation Properties of Epoxy Based Composites,” IEEE Transactions on Dielectrics and Electrical Insulation, Vol. 13, No. 2, 2006, pp. 319-326.
-

- 4. Zheng, Y., Kim, C., Wang, G., Wei, P., and Jiang, P., “Epoxy/nano-silica Composites: Curing Kinetics, Glass Transition Tempera-tures, Dielectric, and Thermal-mechanical Performances,” Journal of Applied Polymer Science, Vol. 111, No. 2, 2009, pp. 917-927.
-

- 5. Pan, Y., Igora, L., and Pelegri, A.A., “Numerical Generation of a Random Chopped Fiber Composite RVE and Its Elastic Properties,” Composite Science and Technology, Vol. 68, No. 13, 2008, pp. 2792-2798.
-

- 6. Wang, H.W., Zhou, H.W., Peng, R.D., and Mishnaevsky, L., “Nanoreinforced Polymer Composites: 3D FEM Modeling with Effec-tive Interface Concept,” Composite Science and Technology, Vol. 71, No. 7, 2011, pp. 980-988.
-

- 7. Doghri, I., and Ouaar, A., “Homogenization of Two-phase Elasto-plastic Composite Materials and Structures: Study of Tangent Op-erators, Cyclic Plasticity and Numerical Algorithms,” International Journal of Solids and Structures, Vol. 40, No. 7, 2003, pp. 1681-1712.
-

- 8. Lee, S., Kim, Y., Lee, J., and Ryu, S., “Applicability of the Interface Spring Model for Micromechanical Analyses with Interfacial Im-perfections to Predict the Modified Exterior Eshelby Tensor and Effective Modulus,” Mathematics and Mechanics of Solids, Vol. 24, No. 9, 2019, pp. 2944-2960.
-

- 9. Lee, S., Lee, J., Ryu, B., and Ryu, S., “A Micromechanics-based Analytical Solution for the Effective Thermal Conductivity of Com-posites with Orthotropic Matrices and Interfacial Thermal Resistance,” Scientific Reports, Vol. 8, No. 1, 2018, 7266.
-

- 10. Mortazavi, B., Baniassadi, M., Bardon, J., and Ahzi, S., “Modeling of Two-phase Random Composite Materials by Finite Element, Mori-Tanaka and Strong Contrast Methods,” Composite Part B: Engineering, Vol. 45, No. 1, 2013, pp. 1117-1125.
-

- 11. Giordano, S., and Palla, P.L., “Dielectric behavior of anisotropic inhomogeneities: interior and exterior Eshelby tensors,” Journal of Physics A: Mathematical and Theoretical, Vol. 41, No. 41, 2008, 415205.
-

- 12. Bednarcyk, B.A., Aboudi, J., and Arnold, S.M., “Micromechanics of Composite Materials Governed by Vector Constitutive Laws,” International Journal of Solids and Structures, Vol. 110-111, 2017, pp. 137-151.
-

- 13. Lee, S., Jung, J., and Ryu, S., “Micromechanics-based Prediction of the Effective Properties of Piezoelectric Composite Having Inter-facial Imperfections,” Composite Structures, Vol. 240, 2020, 112076.
-

- 14. Odegard, G.M., “Constitutive Modeling of Piezoelectric Polymer Composites,” Acta Materialia, Vol. 52, No. 18, 2004, pp. 5315-5330.
-

- 15. Huang, J.H., and Kuo, W-S., “Micromechanics Determination of the Effective Properties of Piezoelectric Composites Containing Spatially Oriented Short Fibers,” Acta Materialia, Vol. 44, No. 12, 1996, pp. 4889-4898.
-

- 16. Martínez-Ayuso, G., Friswell, M.I., Adhikari, S., Khodaparast, H.H., and Berger, H., “Homogenization of Porous Piezoelectric Mate-rials,” International Journal of Solids and Structures, Vol. 113-114, 2017, pp. 218-229.
-

- 17. Jung, J., Lee, S., Ryu, B., and Ryu, S., “Investigation of Effective Thermoelectric Properties of Composite with Interfacial Resistance Using Micromechanics-based Homogenisation,” International Journal of Heat and Mass Transfer, Vol. 144, 2019, 118620.
-

- 18. Xu, Y., and Yagi, K., “Automatic FEM Model Generation for Evaluating Thermal Conductivity of Composite with Random Materi-als Arrangement,” Computational Materials Science, Vol. 30, No. 3-4, 2004, pp. 242-250.
-

- 19. Lee, D., and Suh, N., Axiomatic Design and Fabrication of Composite Structures Applications in Robots, Machine Tools, and Auto-mobiles, NY Oxford University Press., New York, USA, 2005.
- 20. Kim, Y., Kim, Y., Lee, T-I., Kim, T-S., and Ryu, S., “An Extended Analytic Model for the Elastic Properties of Platelet-staggered Composites and Its Application to 3D Printed Structures,” Composite Structures, Vol. 189, 2018, pp. 27-36.
-

- 21. Mura, T., Micromechanics of Defects in Solids, Kluwer Academic Publishers, Netherlands, 1982.
-

- 22. Benveniste, Y., “A New Approach to the Application of Mori-Tanaka’s Theory in Composite Materials,” Mechanics and Materials, Vol. 6, No. 2, 1987, pp. 147-157.
-

- 23. Hill, R., “A Self-consistent Mechanics of Composite Materials,” Journal of the Mechanics and Physics of Solids, Vol. 13, No. 4, 1965, pp. 213-222.
-

- 24. Castañeda, P.P., and Tiberio, E., “A Second-order Homogenization Method in Finite Elasticity and Applications to Black-filled Elas-tomers,” Journal of the Mechanics and Physics of Solids, Vol. 48, No. 6-7, 2000, pp. 1389-1411.
-

- 25. Wu, L., Noels, L., Adam, L., and Doghri, I., “A Combined Incremental-secant Mean-field Homogenization Scheme with Per-phase Residual Strains for Elasto-plastic Composites,” International Journal of Plasticity, Vol. 51, 2013, pp. 80-102.
-

- 26. Castañeda, P.P., “The Effective Mechanical Properties of Nonlinear Isotropic Composites,” Journal of the Mechanics and Physics of Solids, Vol. 39, No. 1, 1991, pp. 45-71.
-

- 27. Eshelby, J.D., “The Determination of the Elastic Field of an Ellipsoidal Inclusion, and Related Problems,” Proceedings of the Royal Society A, Vol. 241, No. 1226, 1957, pp. 376-396.
-

- 28. Jun, T-S., and Korsunsky, A.M., “Evaluation of Residual Stresses and Strains Using the Eigenstrain Reconstruction Method,” Inter-national Journal of Solids and Structures, Vol. 47, No. 13, 2010, pp. 1678-1686.
-

- 29. Chiu, Y.P., “On the Stress Field due to Initial Strains in a Cuboid Surrounded by an Infinite Elastic Space,” Journal of Applied Me-chanics, Vol. 44, No. 4, 1977, pp. 587-590.
-

- 30. Dvorak, G.J., and Benveniste, Y., “On Transformation Strain and Uniform Fields In Multiphase Elastic Media,” Proceedings of the Royal Society A, Vol. 437, No. 1900, 1992, pp. 291-310.
-

- 31. Lee, S., Lee, J., and Ryu, S., “Modified Eshelby Tensor for an Anisotropic Matrix with Interfacial Damage,” Mathematics and Me-chanics of Solids, Vol. 24, No. 6, 2019, pp. 1749-1762.
-

- 32. Lee, S., and Ryu, S., “Theoretical Study of the Effective Modulus of a Composite Considering the Orientation Distribution of the Fillers and the Interfacial Damage,” European Journal of Mechanics - A Solids, Vol. 72, 2018, pp. 79-87.
-

- 33. Ryu, S., Lee, S., Jung, J., Lee, J., and Kim, Y., “Micromechanics-based Homogenization of the Effective Physical Properties of Com-posites with an Anisotropic Matrix and Interfacial Imperfections,” Frontiers in Materials, Vol. 6, No. 21, 2019, pp. 1-17.
-

- 34. Dunn, M.L., and Taya, M., “Micromechanics Predictions of the Effective Electroelastic Moduli of Piezoelectric Composites,” Inter-national Journal of Solids and Structures, Vol. 30, No. 2, 1993, pp. 161-175.
-

- 35. Fu, H., and Cohen, R.E., “Polarization Rotation Mechanism for Ultrahigh Electromechanical Response in Single-crystal Piezoelec-trics,” Nature, No. 403, No. 6767, 2000, pp. 281-283.
-

- 36. Zhao, L-D., Lo, S-H., Zhang, Y., Sun, H., Tan, G., Uher, C., Wolverton, C., Dravid, V.P., and Kanatzidis, M.G., “Ultralow Thermal Conductivity and High Thermoelectric Figure of Merit in SnSe Crystals,” Nature, No. 508, No. 7496, 2014, pp. 373-377.
-

- 37. Barnett, D.M., and Lothe, J., “Dislocation and Line Charges in Anisotropic Piezoelectric Insulators,” Physics Status Solidi (b), Vol. 67, No. 1, 1975, pp. 105-111.
-

- 38. Duschlbauer, D., Böhm, H.J., and Pettermann, H.E., “Computational Simulation of Composites Reinforced by Planar Random Fi-bers: Homogenization and Localization by Unit Cell and Mean Field Approaches,” Journal of Composite Materials, Vol. 40, No. 24, 2006, pp. 2217-2234.
-

 This Article
This Article
-
2020; 33(2): 81-89
Published on Apr 30, 2020
- 10.7234/composres.2020.33.2.081
- Received on Mar 3, 2020
- Accepted on Apr 9, 2020
 Services
Services
Shared
 Correspondence to
Correspondence to
- Seunghwa Ryu
-
* Department of Mechanical Engineering, KAIST
- E-mail: ryush@kaist.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.