Stress distributions dependent on fiber arrangements are studied using the two-dimensional representative volume element (RVE) model for uni-directionally continuous fiber-reinforced composites subjected to transverse tensile loading. It is easily expected that the stresses around the fibers are concentrated mainly due to the stiffness mismatch between the fiber and matrix materials. In this presentation, it is shown that the stresses are not always increased although the distance between two fibers is shortened. The 2D RVE models, originally having a regular hexagonal fiber array, is utilized to study the effect of the fiber locations on the stress distributions. As the central fiber is relocated, the stress distributions around the fiber are obtained through finite element analysis. It is found that the stresses around the fiber are strongly dependent on the fiber distance as well as the angle between the loading direction and the line connecting two fibers

단방향 연속 섬유 강화 복합소재에 대하여 섬유 배열에 따른 응력 분포 양상을 연구하기 위해 단면 형상을 대표하는 체적 요소를 생성하였다. 대표 체적 요소에 횡방향 하중을 가하였을 때, 섬유와 기지재 강성의 차이로 인해 섬유 둘레에서 응력 집중 현상이 발생하며, 섬유 간 좁은 간격 때문에 집중된 응력이 중첩되며 섬유 주변에서 높은 응력이 구해질 것이라 쉽게 예측할 수 있다. 본 연구에서는 섬유 둘레 응력 증감이 단순히 섬유 간 간격 뿐 아니라 섬유의 상대적 위치가 하중 방향과 이루는 각도에 의해서도 결정됨을 보여준다. 정규 육각 구조를 가지는 대표 체적 요소의 중앙에 위치한 섬유를 다양한 방향으로 이동시키며 횡방향 하중을 가하여, 섬유 주변 응력이 증가하거나감소하는 양상을 유한요소해석 기법을 이용해 측정하였다. 섬유 간 거리가 최소이면서 두 섬유의 중심을 잇는 선분의 방향이 하중 방향과 일치할 때 응력이 최대로 증가하였으며, 섬유 간 거리가 최소라 하더라도 하중 방향에 수직일 때 최대 응력은 오히려 감소한다는 것을 보여준다

Keywords: 미시 구조 해석(Microstructure analysis), 섬유 배열(Fiber arrangement), 응력 분포(Stress distribution), 대표 체적 요소(Representative volume element)

복합소재는, 단일 소재에서 얻을 수 없는 물성이나 성능을 구현하기 위해, 두가지 이상의 이종(異種) 소재를 결합하여 만든 소재를 통칭한다. 근래 자동차, 항공기, 선박 등 여러 산업군에서 구조 경량화용 소재로 주목받고 있는 복합소재는 보통 섬유 강화재(reinforcement)와 기지재(matrix)로 구성되어 있다. 강화재로는 탄소 섬유나 유리 섬유가 많이 사용되며, 복합재의 기계적 성능 요구 조건에 따라 섬유의 종류 및 길이가 결정된다. 기지재로는 열가소성 혹은 열경화성 플라스틱이 사용되며, 성형 방법, 부품의 사용 온도 등에 의해 특정 소재가 선정된다.
섬유 강화 복합소재는 비강성(比强性, specific stiffness) 및 비강도(比强度, specific strength)가 우수하여 자동차나 항공 산업에서 금속 소재를 대체할 수 있는 경량화 소재로 각광받고 있다. 하지만 섬유 강화 복합소재는 금속과 달리 소재 결함이 발생하는 양상이 매우 다양하고 복잡하여 복합재를 이용한 구조의 설계 및 해석에 주의가 요구된다. 특히 마이크로미터 단위의 섬유 강화재로 인하여 복합소재 내부 미시 스케일에서 다양한 결함이 발견된다. 이러한 결함의 종류로는 섬유/기지재 접착면 분리, 기지재 균열, 섬유 파단 등이 있다. 마이크로 스케일에서 발생한 결함은 소재 내부에 작게 존재하여 쉽게 파악하기 힘들지만, 복합재 구조의 기계적 성능, 특히 강성을 약화시키는 주요 원인이 된다[1].
미시 스케일에서 결함이 발생하는 이유는 섬유와 기지재 간에 큰 강성의 차이로 매우 큰 차이의 응력이 섬유와 기지재 영역에서 불연속적으로 형성되기 때문이다. 따라서, 섬유가 불균일하게 분포되어 있는 경우, 섬유가 응집되어 있는 영역은 응력집중 현상이 발생하여 결함이 더 일찍 생성되고 더 빠르게 전파될 가능성이 높다.
섬유 단위에서 불균일한 섬유 분포를 고려하여 복합소재의 기계적 성능을 계산하는 연구는 많이 수행되어 왔다. 하지만 대부분의 연구는 실제 섬유 분포 측정치와 통계적으로 등가한 섬유 배열을 가지는 대표체적요소를 생성하는 방법을 개발하는 데 집중하고 있다[2-9]. Yang 등[2]은 하나의 섬유 주변에 무작위로 섬유를 배치하는 random sequential adsorption (RSA) 알고리듬을 이용하여 세라믹기지복합재(ceramic matrix composite, CMC)의 2차원 횡단면 대표체적요소를 생성하였다. Merlo 등[3]은 RSA 모델을 기반으로 “stirring” 알고리듬을 추가하여 보다 높은 섬유 분율을 가질 수 있게 하였다. Yang 등[4] 역시 RSA를 확장하여 섬유 분율을 높일 수 있는 random sequential expansion (RSE) 알고리듬을 개발하였다. RSA 알고리듬은 연속섬유 복합재의 2차원 횡단면 대표체적요소 뿐 아니라 단섬유가 강화 복합재의 3차원 대표체적요소를 만드는데도 사용되었다[6,7]. Vaughan과 McCarthy[7]는 무작위로 섬유를 추가하는 RSA 기법과 달리 섬유 간 간격이 측정 통계를 따르게 제한하는 nearest neighboring algorithm (NNA)를 개발하였다. 섬유를 추가하는 RSA나 NNA 방법 대신 Ismail 등[8]과 Weng 등[9]은 먼저 균일한 간격으로 섬유를 배열한 수 섬유에 속도를 부여하여 섬유가 이동할 수 있게 하였다. 이 때, 섬유 간 충돌은 Hertz 법칙을 따른다고 가정하여 불균일한 섬유 분포를 가지는 대표체적요소를 만들었다.
불균일한 실제 섬유 분포와 통계적으로 등가한 섬유 배열을 가지는 대표체적요소들은 복합재의 방향별 유효 강성(effective stiffness)을 계산하는데 주로 사용되었다. Choi와 Woo[10]는 3차원 평직 복합재료의 3-방향 섬유다발의 굴곡각에 따른 등가 물성치를 예측하기 위해 섬유 단위 모델을 통해 섬유 다발 물성치를 구하였다. 하지만 섬유의 불균일한 분포는 복합재 강성보다는 응력 집중 및 결함 발생에 더 큰 영향을 끼친다[11-13]. Choi 등[14]은 Hashin 파괴 기준을 직조 복합재 대표체적요소에 적용하여 점진적 파괴 모델을 개발하였으며 실험에서 구한 강도 및 강성과 비교하여 적합성을 확인하였다. Yang과 Shin[15]은 다공성 복합재의 내부 기공을 반영한 대표체적요소 모델을 이용하여 유효 탄성 계수 뿐 아니라, 기공 탄성 계수, 파손 강도를 산출하였다. 이을 통해 재료 내부 기공이 재료의 유효 탄성 계수, 기공 탄성 인자, 파손 강도에 미치는 영향을 확인하였다. 위 논문에서는 단위 격자 모델을 사용하여 섬유 분포가 복합재 물성에 끼치는 영향은 확인하지 않았다. Park 등[16]은 대규모 통계적 체적요소 모델에 연속체손상역학을 적용하여 복합재의 강성 뿐 아니라 강도를 예측하는 연구를 수행하였다. Kim 등[17]은 무작위 섬유 분포를 가지는 단방향 복합재의 대표체적요소를 생성하여 섬유와 기지재 계면이 횡방향 물성에 끼치는 영향을 연구하였다. 이 때 계면에 응집영역요소를 사용하여 섬유/기지재 계면 분리를 모사하였으며, 계면의 물성 및 두께가 복합재 강도에 끼치는 영향을 연구하였다.
하지만 무작위 혹은 불균일한 섬유 분포를 가지는 대형 대표체적요소 모델은 섬유 분포가 응력 분포에 주는 영향을 면밀히 파악하는 데 적용하기에는 어려움이 있다. 섬유 분포 및 위치에 따라 응력이 변화하는 양상을 알기 위해서는 정규 섬유 분포 모델에서 출발하여 섬유의 위치를 변화시키며 응력 변화 양상을 관찰하는 것이 필요할 것이다. 본 연구에서는 섬유 분포 및 위치에 관련된 변수가 응력 분포 변화에 어떻게 영향을 끼치는지 알아보고자 하였다. 먼저 균일한 간격으로 배열된 섬유를 가진 대표체적요소에 횡방향 하중을 가하여 균일한 응력 분포를 구하였다. 그 후 중심 섬유 하나의 위치를 변화시키면서 섬유간 간격 변화, 이동 각도 등 섬유 배열에 관련된 변수들이 응력 분포를 어떻게 변화시키는지 수치적으로 해석해보았다.

2.1 Finite element-based RVE model
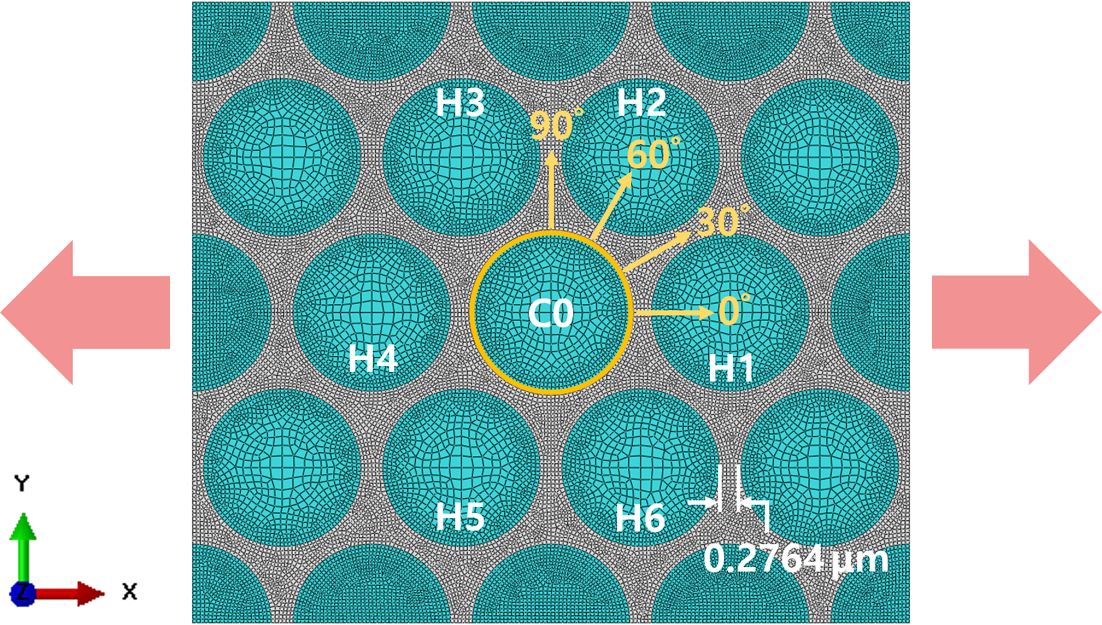
복합재료를 구성하는 섬유와 기지재의 경계에서 섬유 배열에 따라 응력 분포가 변화하는 양상을 관찰하기 위해 Fig. 1과 같은 2차원 대표체적요소(representative volume element, RVE) 모델을 이용하였다. Fig. 1의 RVE 모델은 연속섬유 강화 복합재의 단면을 나타낸다. 섬유 반지름은 1 μm(단위길이)로 모두 동일하게 설정하였고, 70.0%의 섬유분율로 섬유를 균등한 간격으로 배열하였다. 이 때 인접한 섬유 간 거리 d₀는 0.276 μm, 대표체적요소의 크기는 가로 9.106 μm, 세로 7.886 μm로 측정되었다. Fig. 1에 표기되어 있는 바와 같이 중앙에 위치한 섬유는 C0라 지칭하였으며, 정규 육각 구조 (regular hexagonal pack)로 중앙의 섬유를 둘러싸고 있는 주위 섬유들은 H1~H6로 식별하였다.
RVE 모델은 평명변형률(plane strain) 상태에 있다고 가정하였으며, 4절점 쌍선형 사각 요소(4-node bilinear quadrilateral element)를 이용하여 RVE 모델의 요소망 (mesh)을 구성하였다. 총 26000개 이상의 요소가 사용되었으며, Fig. 1과 같이 섬유내부 영역은 성글게, 섬유와 기지재 경계 등 관심 영역은 촘촘하게 요소를 배치하였다.

2.2 Material properties
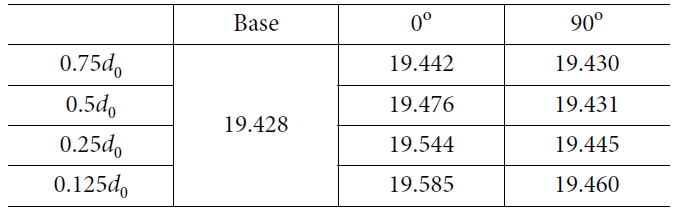
RVE 모델의 섬유와 기지재는 모두 등방성(isotropic) 물질로 가정하였으며, 탄성변형만을 고려하였다. 섬유와 기지재의 물성치는 각각 Soden 등[18]와 Fiedler 등[19]에 보고된 값을 이용하였으며, 계면 강도(interfacial strength)는 Melro 등[20]에서 사용한 값을 해석에 적용하였다. 본 연구에 사용된 물성치는 Table 1에 나타나 있다.

2.3 Numerical analysis approach
실제 복합재 내부의 섬유들은 불균일하게 배열되어 있어, 단면 내 응력 분포가 매우 복잡한 양상을 띠게 된다. 따라서 무작위 배열의 RVE에서는 섬유 간 간격 및 각도 등이 응력 분포에 끼치는 영향을 정량적으로 분석하기가 쉽지 않다. 섬유 위치 변수의 변화에 따라 응력 분포가 달라지는 양상을 연구하기 위해 먼저 Fig. 1과 같이 16개 동일 크기의 섬유가 균등한 간격으로 육각배열을 이룬 base RVE model의 응력 분포를 구하였다. 섬유들이 균등한 간격으로 배열된 base model의 응력 분포 결과를 바탕으로, 중앙에 위치한 섬유를 하중 방향 대비 0^o, 30^o, 60^o, 90^o 방향으로 이동시키면서 섬유와 기지재 경계에서 응력 분포가 변화하는 양상을 유한요소해석을 통해 구하였다.
RVE의 응력 분포를 구하기 위해 RVE 모델이 x-방향으로 0.01의 변형율을 가지게 하는 인장 하중을 가하였다. 이 때, 주기적 경계 조건(periodic boundary condition, PBC)을 사용하여 변위 제어 하중(displacement controlled loading)을 가하였다. RVE 모델링과 수치해석은 상용 유한요소해석 프로그램 ABAQUS 6.14를 사용하였다.

3.1 Stress distribution of the base RVE model
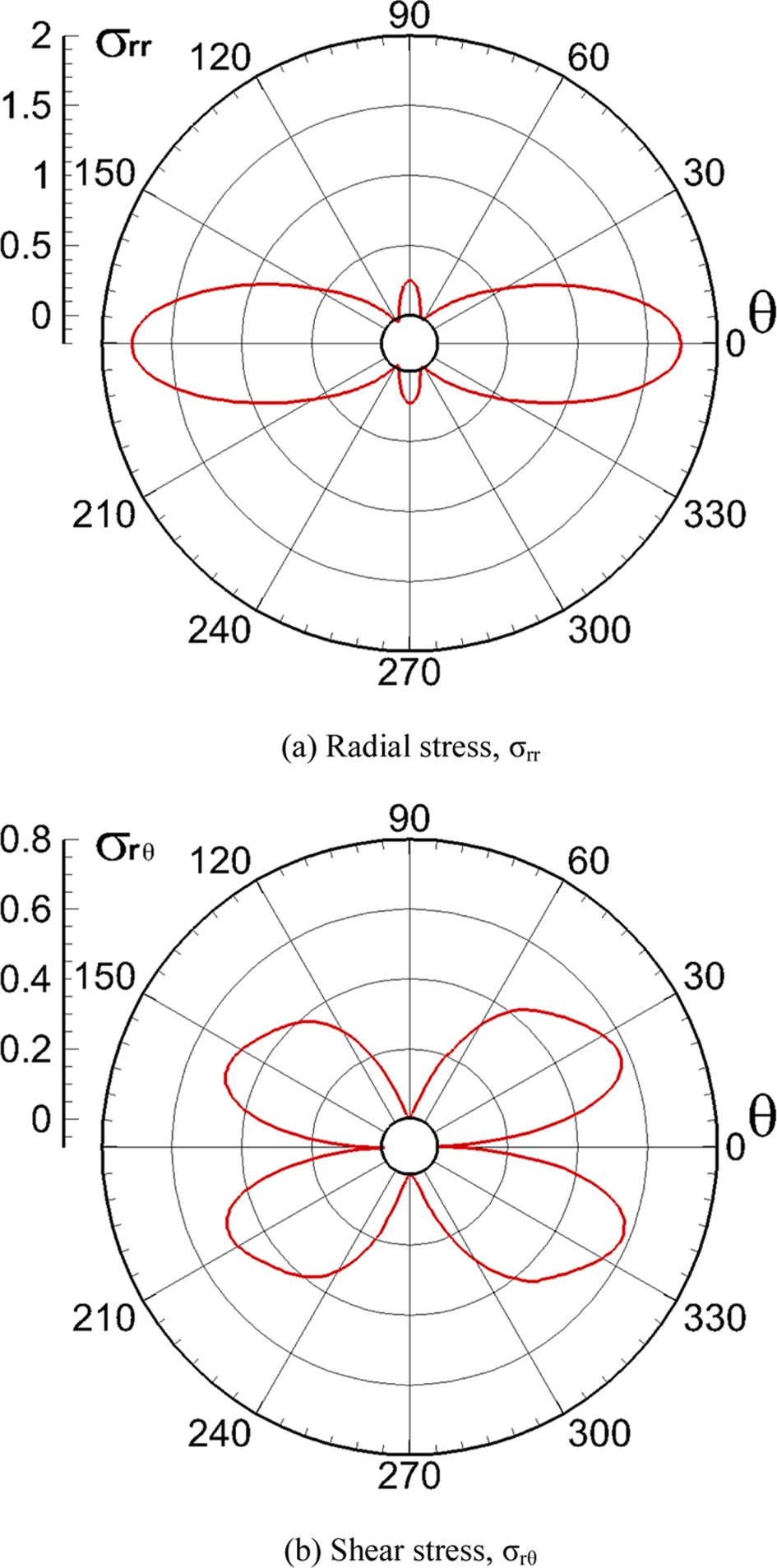
섬유들이 정규 육각 구조(regular hexagonal pack)로 배열되어 있는 base RVE model에 20 MPa에 해당하는 인장하중을 가한 후, 중앙에 위치한 C0 섬유(Fig. 1에 노란색으로 표시된 섬유)의 둘레를 따라 경방향 응력(radial stress, σ_rr)과 전단응력(shear stress, σ_rθ)을 구하여 Fig. 2에 도시하였다. 이 때 각각의 응력은 가력 대비 증감율을 확인하기 위해 20 MPa로 정규화하였다. Fig. 2(a)에서 보이는 바와 같이 경방향 응력은 횡방향 하중 기준으로 0^o와 180^o 위치에서 최대 응력이 나타났으며, 그 값은 가해진 인장 응력보다 1.788배 증가한 35.764 MPa이었다. Fig. 2(b)의 전단응력은 하중 방향 대비 25^o, 155^o, 205^o, 335^o에서 최대가 되었으며, 이 때 응력의 크기는 가해진 인장 응력의 58.0%였다.
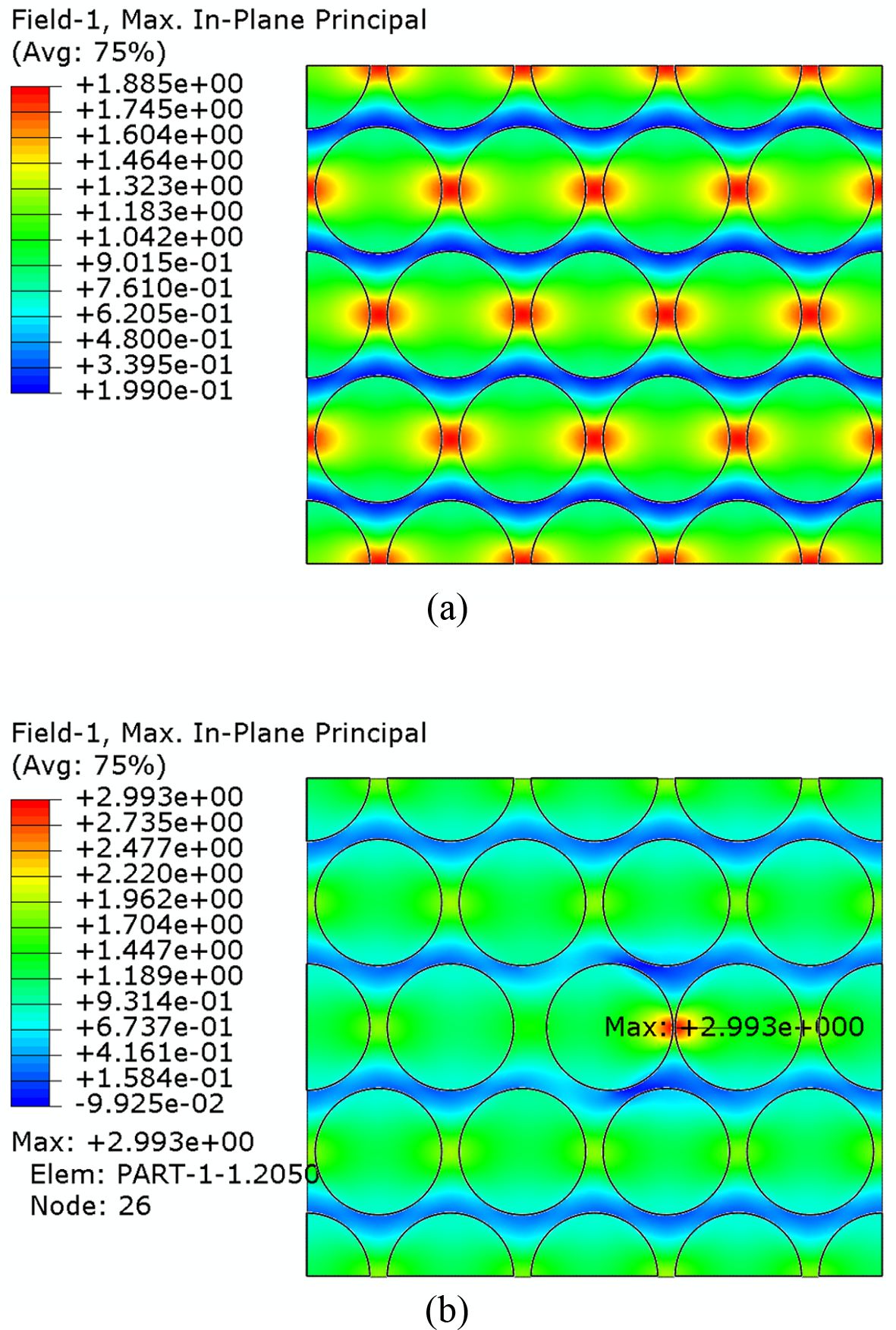
Fig. 3(a)는 전체 RVE영역에서 분포된 주응력(principal stress)을 보여주고 있다. 균등한 섬유 배열로 인해 규칙적인 응력 분포 양상을 나타내고 있음을 알 수 있다. 최대 주응력은 섬유와 섬유 사이 기지재에서 하중 방향 대비 0^o와 360^o 위치에서 발생하며, 가해진 응력보다 1.885배 높은 값을 가진다.
Base RVE model의 유효성을 확인하기 위하여 횡방향 유효 강성을 Halpin-Tail 모델에서 구한 강성값과 비교해보았다. Base RVE model에서 구한 유효 강성은 19.442 GPa, Halpin-Tasi 모델(ξ = 1.6)에서 구한 유효 강성은 19.342 GPa로, 0.5%의 매우 작은 오차를 보인다. 또한 Nguyen 등[21]은 RVE의 균일화된 응력-변형률 응답 특성은 RVE 크기에 영향을 받지 않음을 보여준 바 있다.

3.2 Normal stress 0^o, 30^o, 60^o, 90^o
섬유 배열이 응력 분포 변화에 직접적으로 끼치는 영향을 알아보기 위해 Fig. 1에 표시한 바와 같이 base RVE model 중앙에 위치한 C0 섬유를 0^o, 30^o, 60^o, 90^o 방향으로 이동시킨 후 인장하중을 가해 대표체적요소의 응력 분포를 구하였다. 각 방향에 대해 중앙에 위치한 섬유가 다른 섬유와 접할 때까지 이동한 거리를 d₀라 할 때, 섬유간 최소 거리가 0.75d₀ 0.5d₀, 0.25d₀, 0.125d₀인 경우에 대하여 해석을 수행하였다. 이 때 하중은 Fig. 2 결과와 같이 20 MPa을 동일하게 가하였다. Fig. 3(b)에는 중앙의 섬유가 0^o 방향으로 이동하여 근접 섬유간 거리가 0.125d₀로 최소일 때의 응력 분포를 보여주고 있다.
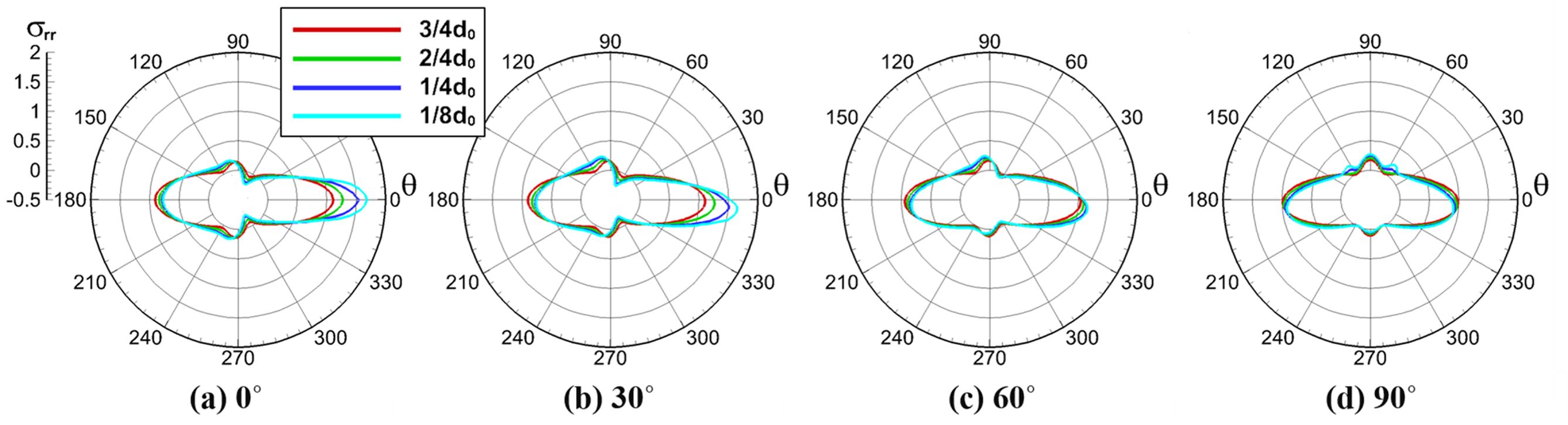
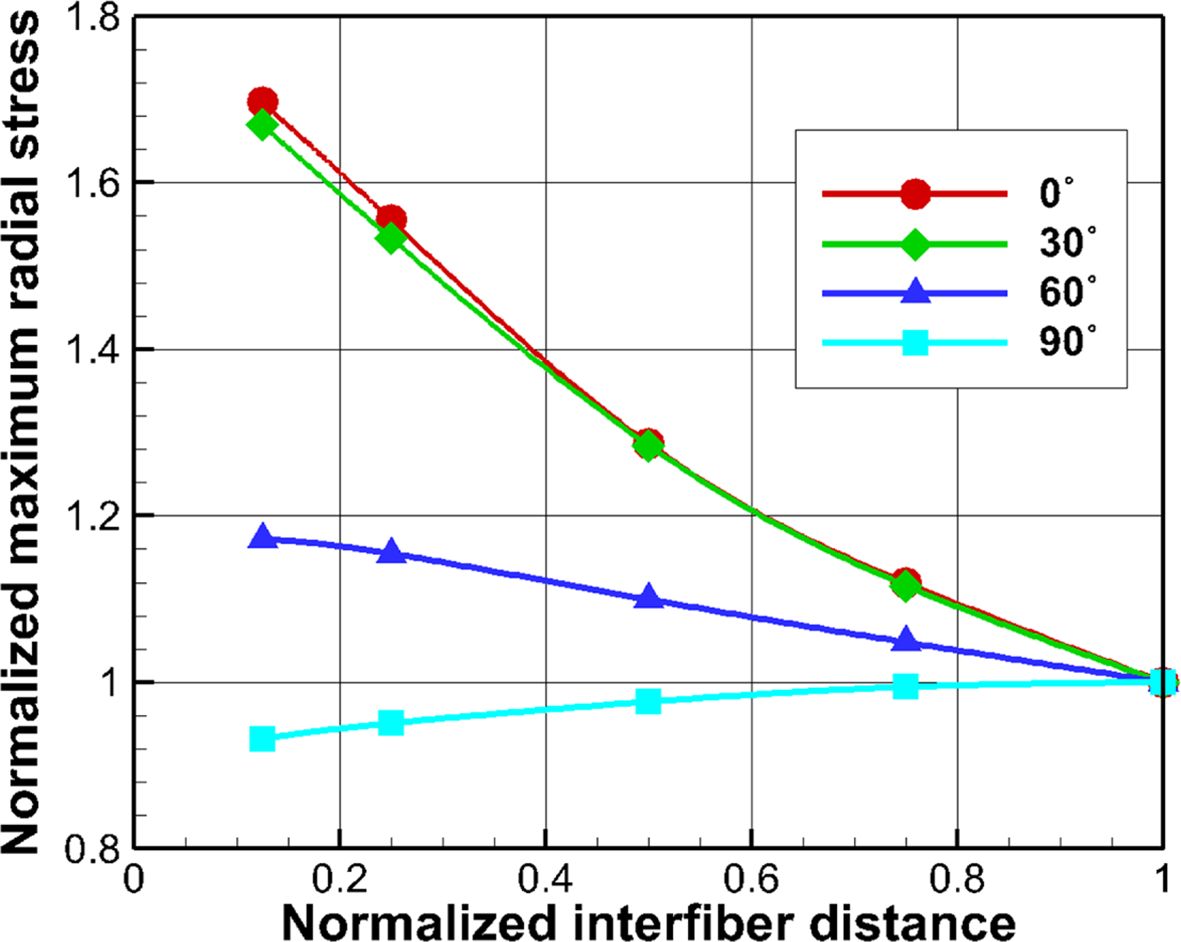
섬유 위치에 따른 응력 분포 양상을 알아보기 위해, 각 위치에 대하여 C0 섬유 둘레 경방향 응력을 구하여 Fig. 4에 나타내었다. 이 때 응력값은 base model 결과 대비 증감율을 확인하기 위하여 base model의 최대 응력값 35.764 MPa로 정규화하였다. Fig. 4(a)에서 보듯이 섬유가 하중 방향으로 이동할 때 경방향 응력 최대값 변화폭이 가장 크다는 것을 알 수 있었다. 섬유와 섬유간 거리가 가장 가까운 0.125d₀인 경우 base RVE model의 최대 응력 대비 1.686배로 증가하였다. 반면 섬유가 하중 방향 대비 수직으로 이동하는 경우 경방향 응력의 최대값은 오히려 소폭 감소한다는 것을 Fig. 4(d)를 통해 알 수 있다. 이 경우 경방향 응력 최대값은 범례 순서대로 358^o, 185^o, 186^o, 188^o의 위치에서 나타났다. 이 각도는 C0 섬유의 중심과 H1 혹은 H4 섬유의 중심을 잇는 선분이 하중 방향과 이루는 각도와 일치한다. 최대 응력은 base model에 비해 0.932배로 감소했고, 오히려 90^o위치에서 1.93배 증가하였음을 Fig. 4(d)를 통해 알 수 있다. 이와 같은 섬유 간격 및 이동 방향에 따른 최대 응력값 변화는 Fig. 5에서 종합하여 볼 수 있다. Fig. 5의 y축 값은 base model의 최대 응력값으로 정규화하였으며, x축은 base model의 섬유간 거리로 정규화하였다.
인장하중을 받는 평판이 중심에 원형의 구멍 혹은 강성이 높은 봉입체(封入體, inclusion)를 가지고 있을 때 원 둘레 주변 응력이 원거리 응력(far-field stress)보다 증가한다는 것은 이론적으로 잘 알려져 있다[22]. 복합재 횡단면에서 섬유는 강성이 높은 봉입체로 볼 수 있어 섬유 주변에서 응력이 증가한다는 것은 이론적으로 알 수 있다. Tabiai 등은 실험적으로 단일 섬유 경계에서 응력이 국소적으로 증가함을 보여주었다[23]. 그들은 하중 방향에 수직으로 단일 섬유가 삽입된 ASTM D638 규격 시편을 제작 후 인장 실험을 수행하여, 이미지 상관법(digital image correlation, DIC)을 통해 섬유 주변의 불균일한 변형률 분포를 보여주었다. 여러 개의 섬유가 존재하는 실제 복합재의 경우 간섭에 의해 섬유 둘레 응력이 더욱 증가하게 된다. 섬유 간 거리가 가까워질 수록 간섭 효과도 커지게 되므로 Fig. 4(a)와 같은 결과를 얻게 된다. Fig. 4의 결과에서 얻을 수 있는 또 하나의 중요한 결론은 섬유 간 거리 뿐 아니라 최소 섬유 거리와 하중 방향이 이루는 각도가 최대 응력값을 결정하는데 매우 큰 영향을 끼친다는 점이다. Fig. 5에서 보듯이, 최소 섬유 거리가 모두 0.125d₀라 하더라도, 최소 거리를 만든 선분이 하중 방향과 정확히 일치할 때 응력이 최대로 증가하며, 수직인 경우 오히려 감소한다.
Table 2에서는 base RVE model에서 계산된 횡방향 유효 강성(effective transverse stiffness)과 C0 섬유를 0^o, 90^o 방향으로 이동시킨 RVE에서 계산된 유효 강성를 비교하였다. Base model의 유효 강성과 최대 오차 0.8% 이내로 중앙의 섬유 위치를 변화시켜도 강성값에 큰 변화를 주지 않는 것을 알 수 있다. 이를 통해 섬유 분포는 RVE의 균일화 탄성 영역보다는 국부적인 응력 분포 및 집중 현상에 훨씬 더 큰 영향을 끼친다는 것을 알 수 있다.
 
3.3 Shear stress 0^o, 30^o, 60^o, 90^o
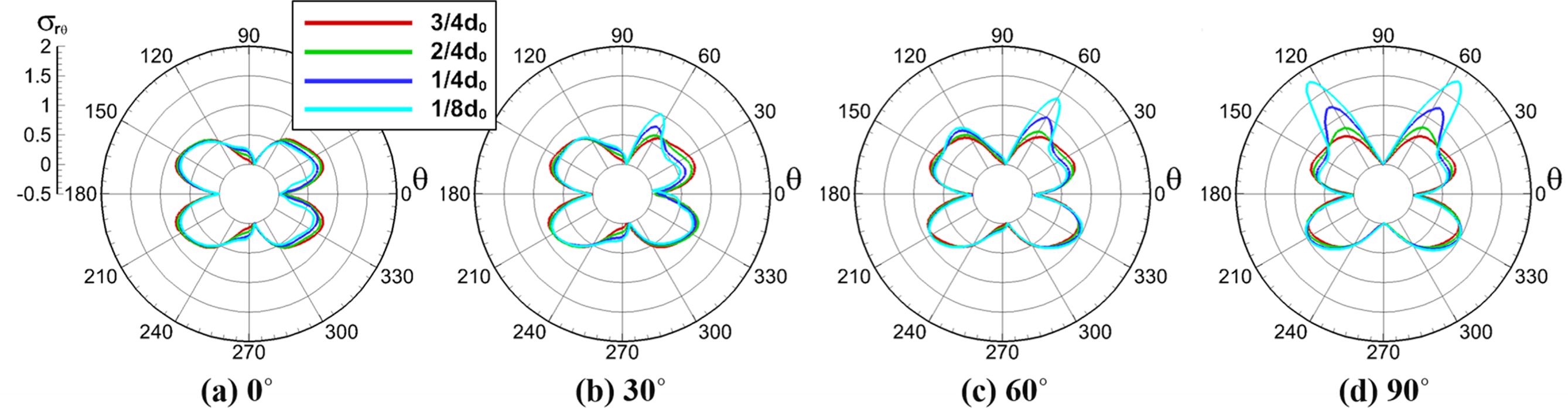
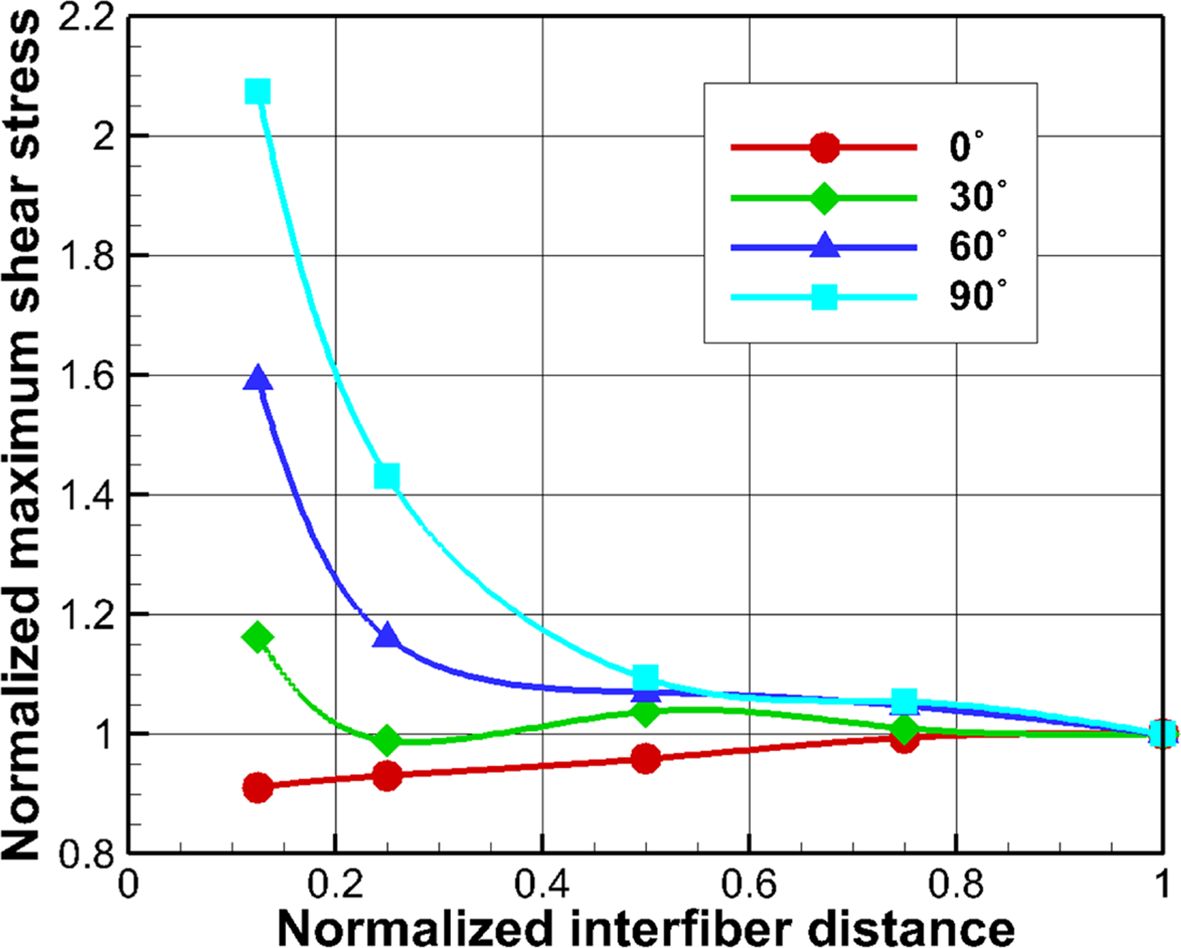
중앙에 위치한 섬유를 0^o, 30^o, 60^o, 90^o 방향으로 이동시키면서 전단방향 응력을 측정하여 그 결과를 Fig. 6에 나타내었다. 이 때, 전단방향 응력은 base model 결과에 대비한 증감율을 알아보기 위해 Fig. 2(b)에서 구한 최대 전단 응력값으로 정규화하였다. Fig. 7에는 섬유 이동 방향과 섬유간 최소 거리에 따른 최대 응력 변화 양상을 보여주고 있다. Fig. 6(a)와 같이 섬유를 하중 방향과 같은 방향으로 움직였을 때, 최대 전단응력은 범례 순서대로 336^o, 154^o, 154^o, 151^o에서 나타났다. 하지만 base model 최대값보다 감소한 경향을 보였으며, 0.125d₀인 경우 0.911배로 감소하였다. 특히 base model에서 최대값을 가졌던 335^o 위치에서는 H1 섬유와 가까워질 수록 전단응력이 감소하여, 0.125d₀인 경우 0.809배로 감소하는 결과를 보였다.
섬유의 이동 방향이 하중 방향 기준 30^o에서 90^o를 향해 갈 때, C0 섬유 둘레 전단응력은 60^o 부근에서 점차 증가함을 Fig. 6(b)와 (c)를 통해 알 수 있다. 이동 방향이 90^o일 때, 0.125d₀ 간격에서 최대값은 base model에 비해 2.07배 증가했고, 55.6^o와 124^o 위치에서 나타났다. 이 각도는 C0 섬유의 중심과 H2, H3 섬유 중심을 이은 선이 하중 방향과 이루는 각각의 각도와 일치한다. 섬유가 0^o, 30^o 방향으로 이동했을 때와는 다르게 60^o, 90^o방향으로 이동할 때 120^o 위치에서 전단응력이 증가하는 것을 Fig. 6(c)와 (d)에서 관찰할 수 있다. 섬유가 정규 육각 구조로 배열되어 있는 base model의 경우 기기재 영역이 전단응력을 균등하게 분포시킬 수 있지만, 하중 방향과 수직인 방향의 섬유 간 거리가 변할 수록 전단응력 간섭 및 증가에 큰 영향을 끼치는 것을 Fig. 6과 Fig. 7의 결과를 통해 알 수 있다.

3.4 Interfacial strength
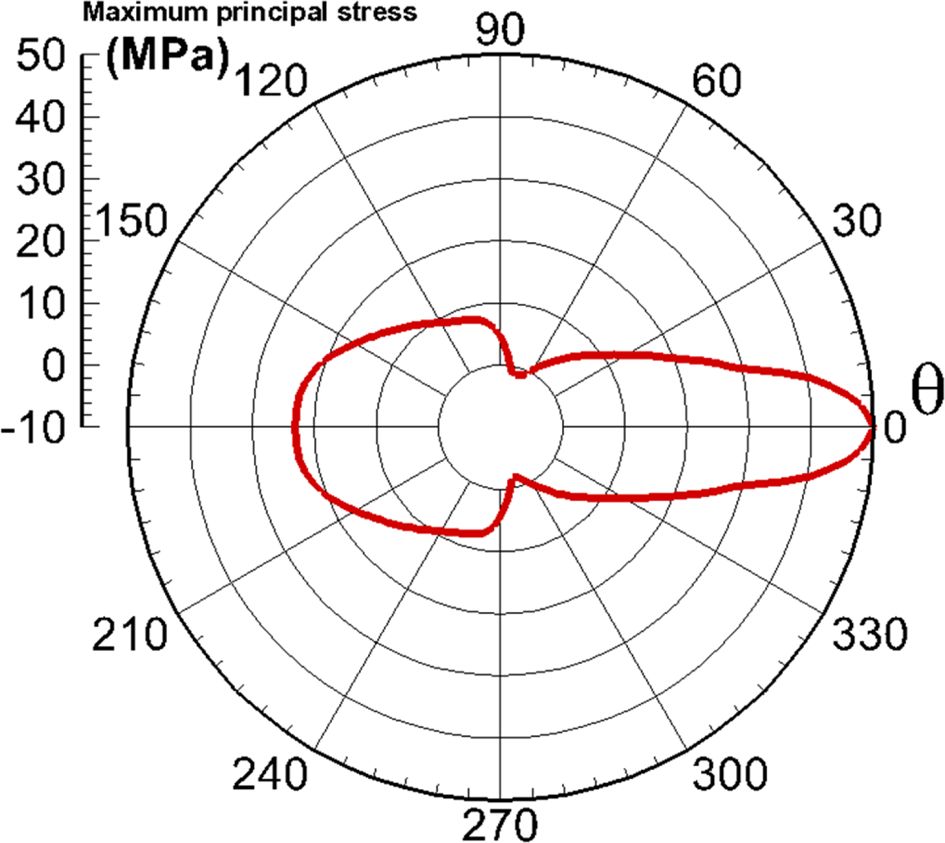
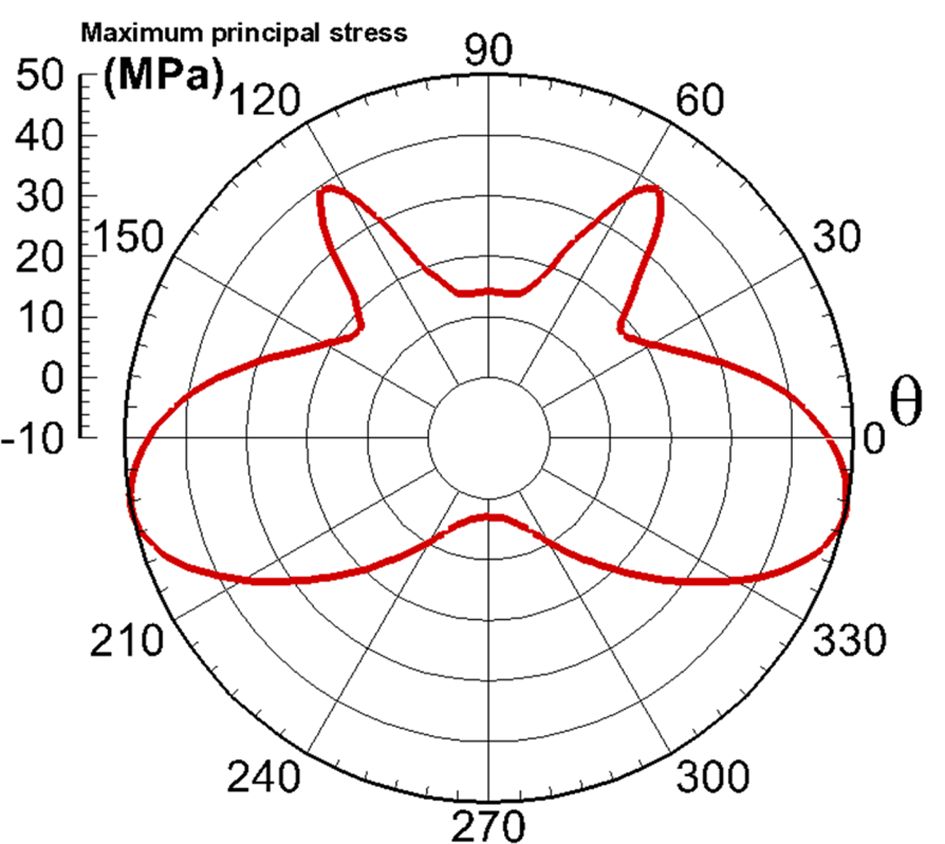
Merlo 등[20]의 연구에 의하면, RVE 모델이 횡방향 하중을 받을 때 섬유와 기지재 경계에서 분리가 제일 먼저 발생한다. 따라서 본 단원에서는 섬유와 기지재 경계에서의 응력 분포 및 최대 응력 지점의 응력을 집중적으로 분석한다. 이를 위해 중앙의 섬유가 0^o 방향과 90^o 방향으로 이동하여 최소 섬유 거리가 0.125d₀인 2개의 모델을 이용하였다. 각 모델에 대해 섬유 둘레 최대 응력이 Table 1의 계면 강도 σ_C (50 MPa)와 같아지는 임계 하중을 구하였다. 섬유간 최소 거리가 0.125d₀가 되게끔 중앙의 섬유를 0^o 방향으로 이동시킨 모델에서 나타난 최대 주응력(maximum principal stress) 분포는 Fig. 8과 같다. 하중방향 대비 0^o 위치에서 최대 주응력값이 구해졌으며, 계면 강도 50 MPa과 같았다. Fig. 6(a)에서 보듯이 0^o 위치에서 전단응력은 0이므로 경방향 응력에 의해 이 지점에서 결함이 생길 것으로 예측된다. 섬유 둘레를 따라 발생한 전단응력은 Table 1의 계면 강도 τ_C를 초과하지 않았다. Fig. 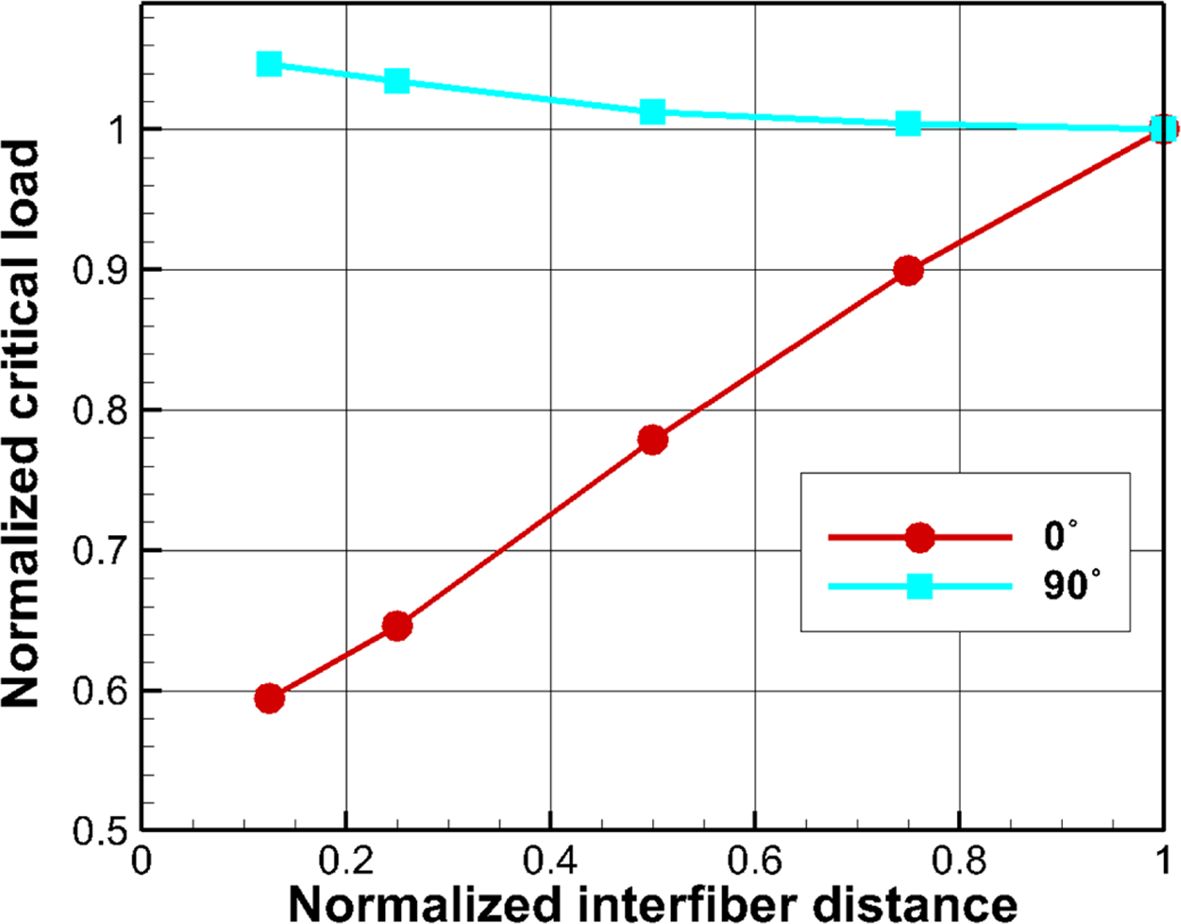9는 이동 방향 90^o, 최소 섬유 거리 0.125d₀인 모델에서 얻은 최대 주응력 분포를 나타내고 있다. Fig. 8의 경우와 마찬가지로 최대 주응력의 크기가 50 MPa이 되도록 인장 하중을 가하였다. 56^o와 124^o 위치에서 전단응력이 크게 집중되긴 하지만 계면 전단 강도 τ_C를 초과하지 않았으며, 0^o 위치에서 집중된 경방향 응력으로 인해 결함이 생길 것으로 예측된다.
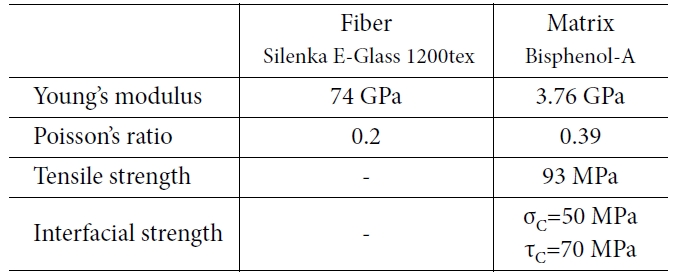
0^o 방향 그리고 90^o 방향으로 중앙의 섬유를 이동시키면서 최소 섬유 거리가 d₀, 0.75d₀, 0.5d₀, 0.25d₀, 0.125d₀일 때, 최대 경방향 응력이 계면 강도와 같아지는 임계 하중을 구하여 Fig. 10에 비교하였다. Fig. 10의 y축 값은 base model의 임계 하중으로 정규화하였으며, x축은 base model의 섬유간 거리로 정규화하였다. Fig. 10의 결과에서 알 수 있듯이 0.125d₀ 간격의 모델은 base model 대비 0.6배의 인장하중으로도 계면 강도 σ_C를 초과할 수 있었다. 반면, 중앙의 섬유를 90^o 방향으로 움직이며 관찰했을 때, 0.125d₀ 모델은 σ_C를 초과하기 위해 base model 대비 1.05배 더 큰 인장하중이 필요했다.

섬유 위치에 따른 응력 변화 양상을 알아보기 위해 단방향 연속 섬유 복합재의 2차원 대표 체적 요소를 이용하여 유한요소해석을 수행하였다. 정규 육각 구조로 배열된 base RVE 모델의 결과를 바탕으로 중앙의 섬유를 다양한 방향으로 이동시키며 섬유 간 근접 거리가 변함에 따라 응력이 변화하는 양상을 수치해석적으로 측정하였다. 주요 결과는 다음과 같이 정리할 수 있다.
● 섬유와 기지재 간 강성의 차이로 인해 섬유 둘레에서 응력 집중 현상이 발생한다. 이 때, 섬유 간 거리가 가까워질 수록 중첩에 의해 해당 영역의 응력이 증가한다.
● 섬유 사이의 중심을 잇는 선분이 하중 방향과 이루는 각도에 따라 응력이 급격히 증가할 수도, 감소할 수도 있다. 섬유 간 최소 거리가 하중 방향과 일치할 때 응력이 최대로 증가하며, 하중 방향에 수직일 때 응력은 오히려 감소한다.
● 따라서, 섬유와 기지재 계면 손상 위치는 섬유 간 거리 및 거리 벡터가 하중 방향과 이루는 각도에 따라 결정된다고 볼 수 있다. 섬유 간 최소 거리가 하중 방향과 일치할 때 적은 하중으로도 계면에 손상이 발생할 수 있으며, 수직일 때 더 큰 하중이 요구된다.
● 반면 섬유의 위치 변화는 유효 강성에는 큰 변화를 주지 않음을 확인하였다. 섬유 분포는 탄성 영역에서는 큰 영향이 없으며 국부적인 응력 증가에 더 관여하게된다. 이를 통해 섬유 분포는 복합재의 탄성값보다는 최대 강도에 더 큰 영향을 준다고 유추할 수 있다.
본 연구 결과는 연속섬유 복합재 횡단면 RVE 모델에 인장하중을 가하여 얻은 것으로, 실제 적층식 복합재의 경우 90^o 층에 해당된다. 횡방향 파손 (transverse fracture)은 낮은 하중에서 일찍 발생하여 전체 복합재 구조의 기계적 성능을 저하시키는 주요 원인이 된다[24,25]. 가력이 낮더라도 응력 집중 현상에 의해 섬유 주변 응력은 높아지기 때문이다. 위에 정리된 결론을 통해 특정 섬유 배열이 하중 방향과 이루는 각도를 알면 최대 응력 증감 예측이 가능함을 알 수 있었다. 섬유가 불균일하게 분포되어 있는 실제 단면 구조에 대해서도 하중 방향, 섬유 간 최소 거리, 하중 방향과 최소 거리 간의 각도에 대한 정보를 얻는다면, 본 연구 결과를 활용하여 최대 응력 지점 및 값을 예측할 수 있어 섬유/기지재 계면 분리 위치와 이 때 임계 하중을 예측할 수 있으리라고 기대한다.

본 연구는 한국연구재단 주관 기본연구 지원 사업 (2017R1D1A1B03033591) 연구과제 및 울산과학기술원 UK Brand 육성사업(1.190009.01)으로 수행되었습니다. 지원에 감사드립니다.