- The Study on the Characteristics of Mode I Crack for Cross-ply Carbon/Epoxy Composite Laminates Based on Stress Fields
Min-Song Kang*, Min-Hyeok Jeon*, In-Gul Kim*†, Kyeong-Sik Woo**
* Department of Aerospace Engineering, Chungnam National University
*† Department of Aerospace Engineering, Chungnam National University
** School of Civil Engineering, Chungbuk National University- 응력장을 이용한 직교적층 탄소섬유/에폭시 복합재 적층판의 모드 I 균열 특성 연구
강민송* · 전민혁* · 김인걸*† · 우경식**
The delamination is a special mode of failure
occurring in composite laminates. Several numerical studies with finite element
analysis have been carried out on the delamination behavior of unidirectional
composite laminates. On the other hand, the fracture for the multi-directional
composite laminates may occur not only along the resin-fiber interface between
plies known as interply or interlaminar fracture but also within a ply known as
interyarn or intralaminar fracture accompanied by matrix cracking and fiber
bridging. In addition, interlaminar and intralaminar cracks appear at irregular
proportions and intralaminar cracks proceeded at arbitrary angle. The
probabilistic analysis method for the prediction of crack growth behavior
within a layer is more advantageous than the deterministic analysis method. In
this paper, we analyze the crack path when the mode I load is applied to the
cross-ply carbon/epoxy composite laminates and collect and analyze the
probability data to be used as the basis of the probabilistic analysis in the
future. Two criteria for the theoretical analysis of the crack growth direction
were proposed by analyzing the stress field at the crack tip of orthotropic
materials. Using the proposed method, the crack growth directions of the
cross-ply carbon/epoxy laminates were analyzed qualitatively and quantitatively
and compared with experimental results.
층간분리는 복합재 적층판에서 발생하는 특수한 파손 모드이다. 유한요소해석기법을
활용하여 균열 성장 방향이 확실히 예측되는 일방향 복합재 적층판의 층간분리 거동과 관련된 많은 수치적 연구가 수행되었다. 반면에 여러 방향으로 적층된 복합재 적층판의 층간분리는 층간 균열 뿐 만 아니라 기지재료 파손 및 섬유 브릿징을
수반하는 층내 균열이 발생한다. 또한 층간 균열과 층내 균열이 불규칙적인 비율로 나타나고 층내 균열도
임의의 각도로 성장한다. 이러한 직교적층 복합재 적층판의 균열 성장 방향에 대한 예측은 확정론적 해석
방법 보다는 확률론적 해석 방법이 유리하다. 본 논문에서는 직교적층 탄소섬유/에폭시 복합재 적층판에 모드 I 하중이 가해질 때 균열 경로를 분석하여 향후 확률론적 해석의 기반 자료로
사용할 수 있는 확률 데이터를 수집하고 분석하였다. 직교이방성 재료의 균열선단에서의 응력장 해석결과를 활용하여
균열 성장 방향을 분석할 수 있는 두 가지 기준을 제안하였다. 제안한 방법을 이용하여 직교적층 탄소섬유/에폭시 복합재 적층판의 균열 성장 방향을 정성적, 정량적으로 분석하고
실험값과 비교분석하였다.
Keywords: 직교적층 복합재 적층판(Cross-ply composite laminates), 모드 I(Mode I), 층간분리(Delamination), 응력장(Stress fields), 층내 균열(Intralaminar crack)
층간분리는 복합재 적층판에서 발생하는 특수한 파손 모드로 제작 공정상의 결함, 외부 하중 및 환경 요인 등에 의해 적층간의 분리가 발생하는
파손 모드이다. 복합재 적층판에서 층간분리가 발생할 경우, 복합재의 강성도 및 강도는
현저히 저하된다. 따라서 설계 단계에서 층간분리가 발생하기 쉬운 적층 복합재 구조물의 층간분리 거동을 분석하여 층간분리 파손으로부터 강건한 구조물을
설계하여야 한다[1].
층간분리와 관련한 주요 설계 변수는 층간 파괴인성(Interlaminar Fracture Toughness)이다. 면내 수직 방향 응력으로
인해 균열이 개방되는 하중 조건인 모드 I 하중 조건에서의 복합재 적층판의 층간분리 저항성을 모드 I 층간 파괴인성(Mode I
Interlaminar Fracture Toughness), 기호로는 GIc로 표현한다[2]. 그리고 면내 전단 응력에 의해 균열이 성장하는 하중 조건인 모드 II 하중 조건에서의 복합재
적층판의 층간분리 저항성을 모드 II 층간 파괴인성(Mode II Interlaminar Fracture Toughness), 기호로는 GIIc로 표현한다[3]. 일반적인 복합재 적층판의 경우 GIc가 GIIc보다 낮은 값을 가지므로[4] GIc가 설계 변수로서 매우 중요하다.
일방향 복합재 적층판의 층간분리의 경우, 균열은 초기 균열이 내재되어 있는 층간에서 일정한 방향으로 성장한다. 일방향 복합재 적층판에서
층간 균열(Interlaminar Crack)이 아닌 두께 방향 층내 균열(Intralaminar Crack)이 성장하기 위해서는 기지재료 파손보다
섬유 파손이 먼저 발생해야 하는데, 일반적인 일방향 탄소섬유/에폭시 복합재에서 그러한 거동은 물리적으로 불가능하다. 이러한 균열 성장 방향이 확실히
예측되는 일방향 복합재 적층판의 층간분리 거동과 관련된 많은 수치적 연구[5-7]가 유한요소해석기법을 활용하여 수행되었다. 그러나 여러 방향 복합재 적층판의 경우
Lamina와 Lamina 사이의 층간 균열 뿐 만 아니라 기지재료 파손 및 섬유 브릿징을 수반하는 층내 균열이 발생할 수 있다. Morais
등[8]의 연구와 선행 연구[1]에서 직교적층 탄소섬유/에폭시 복합재 적층판에 대한 Double-Cantilever
Beam(DCB) 시험을 통해 층간 균열 및 층내 균열이 불규칙하게 발생하는 것을 관찰하였다. 이와 같이 여러 방향 복합재 적층판의 층간분리는
층간 균열과 층내 균열이 불규칙적인 비율로 나타남은 물론 층내 균열이 임의의 각도로 성장하기 때문에 균열 성장 방향을 예측하는 것이 어렵다. 따라서
여러 방향 복합재 적층판의 층간분리 거동을 예측하기 위해서는 확정론적 해석방법보다는 확률론적 해석방법으로 분석하는 것이 유리할 수 있으며, 이를
위해서는 확률 분포와 적절한 분석 기준이 필요하다.
본 논문에서는 직교적층 탄소섬유/에폭시 복합재 적층판에 모드 I 하중이 가해질 때 균열 경로를 분석하여 향후 확률론적 해석의 기반 자료로
사용할 확률 데이터를 수집하고 분석하였다. Chalivendra[9]이 수행한 연구 결과를 활용해 모드 I 하중 조건에서 직교적층 탄소섬유/에폭시 복합재 적층판의
90°층을 직교이방성재료로 가정하고 균열선단 주변의 응력장을 분석하여 균열 성장 방향을 이론적으로 분석할 수 있는 두 가지 분석 기준을 제안하였다.
응력장 분석에는 선행 연구[1]에서 구한 재료의 물성과
층간 파괴인성 정보를 활용하였다. 제안한 방법을 이용하여 직교적층 탄소섬유/에폭시 복합재 적층판의 균열 성장 방향을 정성적 및 정량적으로 분석하고
실험값과 비교분석하였다.
2.1 응력장(Stress
Fields)
균열을 가진 물체에 외력이 작용할 때 균열 선단 부근에서의 응력분포를 균열 선단에 원점을 둔 함수로 표현할 수 있으며, 이를 응력장(Stress
Fields)이라고 한다[10].
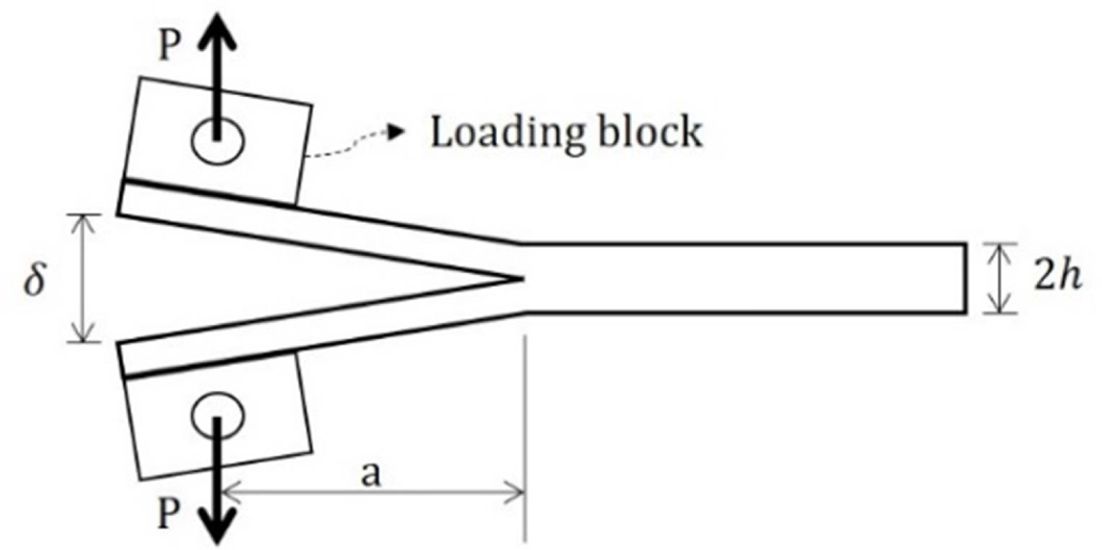
본 연구에서는 Fig. 1의
Double-Cantilever Beam(DCB) 시험 모식도와 같이 직교적층 탄소섬유/에폭시 복합재 적층판에 모드 I 하중이 가해질 때 균열
선단 부근에서의 응력장을 분석하였다.
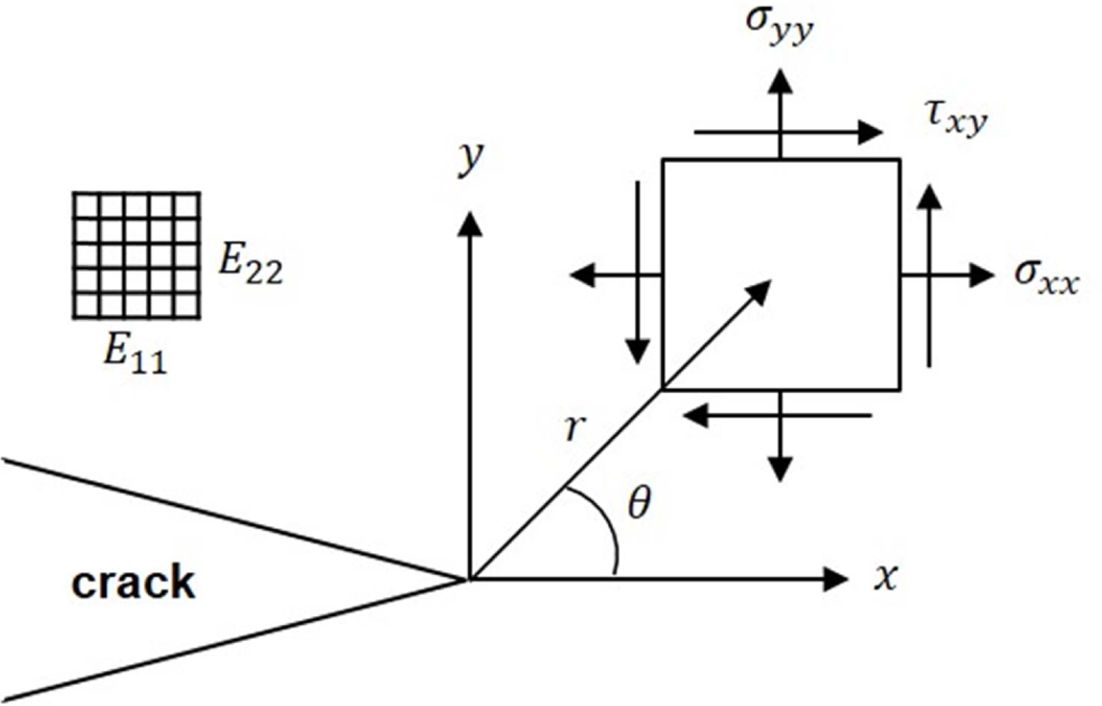
Chalivendra[9]는 Fig. 2와 같이 균열이 존재하는 Inhomogeneous Orthotropic 재료에 모드 I 하중이
가해질 때 균열 선단 부근에서의 응력장을 유도하였다. Inhomogeneous Orthotropic 재료의 물성을 유효 탄성 계수와 유효 포아송비
그리고 강성도비로 정리한 Krenk[11]의 연구와 Hook’s
Law, Airy’s Stress Function을 적용하여 유도한 응력장은 식 (1)-(3)과 같으며 응력장을 구성하고 있는 주요 변수의 구성은 식 (4)-(8)과 같다. 여기서 각도 q의 부호는 반시계 방향을 양의 부호(+)로 하였다. a는 non-homogeneity 파라미터로 5로 가정한다.
식 (1)-(3)에서 볼 수 있듯이 응력장의 크기를 나타내는 주요 변수는 A0이다. A0를 구성하는 GIc는 응력장의 크기를 결정하는
주요 인자로 작용한다.
본 논문에서는 선행 연구[1]에서 활용된
Lamina의 물성과 모드 I 층간 및 층내 파괴인성을 이용하여 응력장을 구하였다. 구해진 응력장을 이용하여 일방향 및 직교적층 DCB 시편의
모드 I 균열 성장 방향을 확인하였다. 
2.2 균열 성장 방향 분석 지표
균열 성장 방향을 분석하기 위하여 두 가지 기준을 제안하였다.
첫 번째 기준은 각도(θ)에 따라 σxx,σyy,τxy 에 의한 주응력을 식 (9)와 같이 계산하여 최대 주응력에 의하여 기지재료의 균열이 발생하는 각도로 균열이 성장할 것이라고
정성적으로 추정하는 ‘최대 주응력 분석방법’이다.
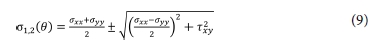
두 번째 기준은 혼합모드 파손기준식(Mixed Mode Failure Criteria)을 이용한 ‘파손지표 분석방법’으로, 먼저 재료의
항복 강도와 본 연구를 통해 구한 파괴인성(임계 변형률 에너지 해방률)을 이용해 기준 응력-변위 선도(Traction-Separation
Curve)를 작성한다. 이때 기준 응력-변위 선도의 넓이는 파괴인성 값이 된다. 다음으로 응력장에서 계산된 응력을 기준 응력-변위 선도에 대입하여
해당 응력에 의해 발생된 변형률 에너지 해방률을 계산한다. 그리고 변형률 에너지 해방률을 혼합모드 파손기준식에 적용하여 파손지표가 1을 초과하는
균열 각도를 정량적으로 분석한다.
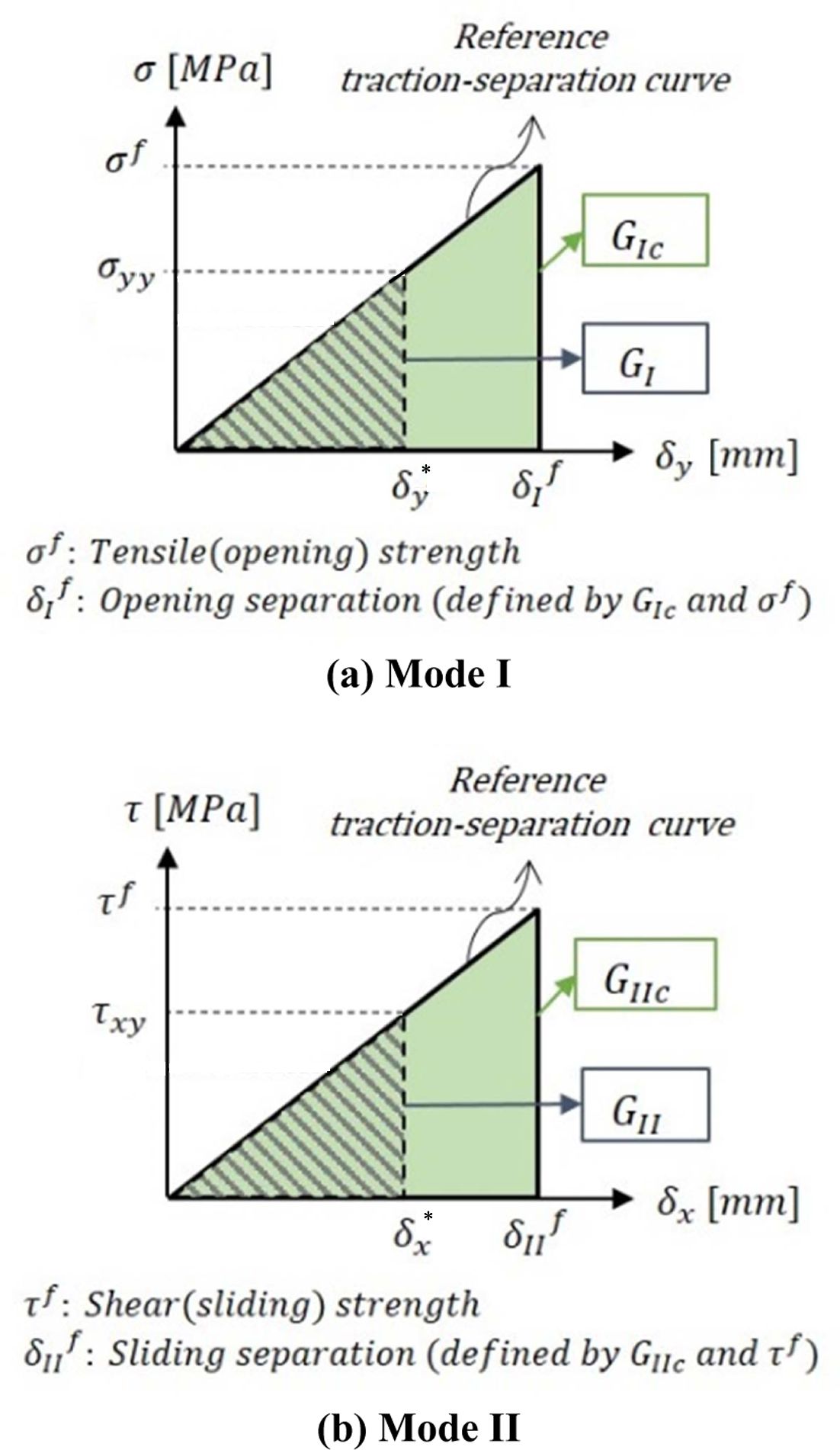
파손지표 분석방법을 위해서는 기준 응력-변위 선도(Reference Traction-Separation Curve)의 형태를 가정해야
한다. 본 연구에 사용된 시편은 경질의 기지재료로 제작되었기 때문에 Wei[12]의 연구를 참고하여 경질의 분리 단면을 분석할 때 적용하는 직각 삼각형 형태의 기준 응력-변위
선도로 가정하였다.
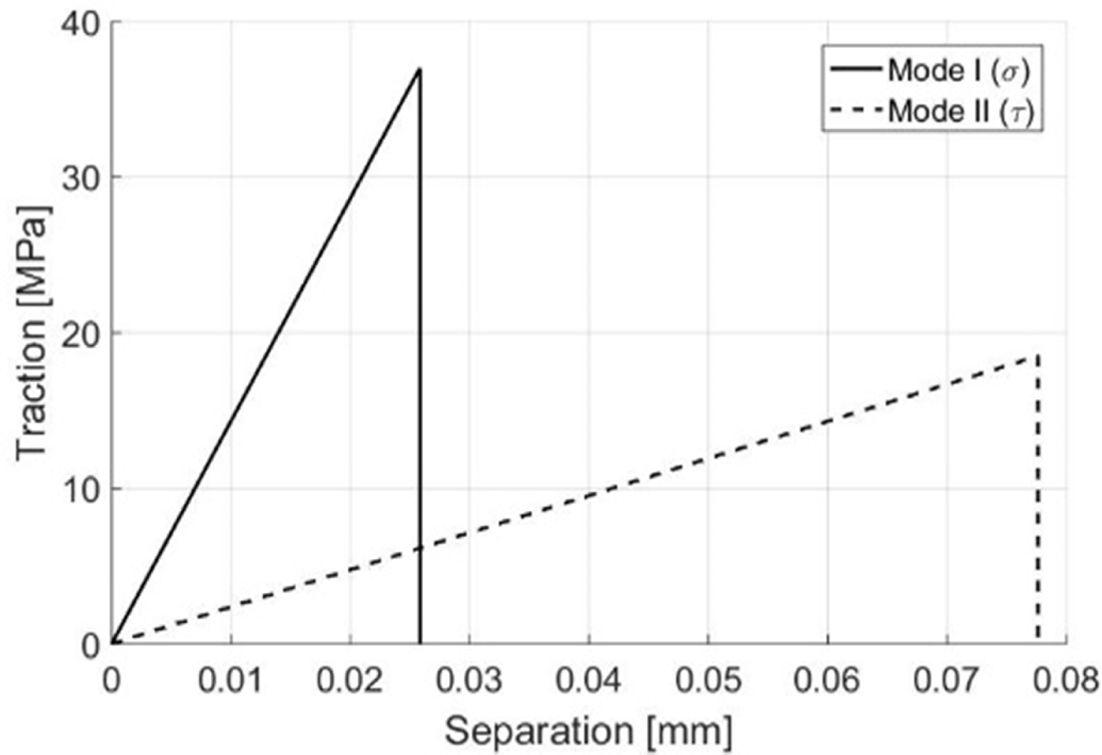
파손지표 분석방법에 사용된 기준 응력-변위 선도와 응력장의 응력에 따라 응력-변위 선도의 넓이로 계산되는 변형률 에너지 해방률은 Fig. 3과 같다. 식 (10)과 같이 재료의 항복 인장 강도(sf)와 모드 I 파괴인성(GIc)을 이용해 모드 I 파손 변위(δI f)를 구하였다. 식 (11)과 같이 재료의 항복 전단 강도(τf)와 모드 II 파괴인성(GIIc)을 이용해 모드 II 파손 변위(δI f)를 구하였다. 재료의 강도와 구해진 파손 변위를 이용해 Fig. 3과 같이 기준 응력-변위 선도를 작성하였다. 그리고 식 (12), (13)과 같이 응력장에서 계산된 응력을 이용해 모드 I 변형률 에너지 해방률(GI)과 모드 II 변형률 에너지 해방률(GII)을 계산하였다. 계산된 변형률 에너지 해방률을 혼합모드 선형 파손기준식 (14)에 적용하여 파손지표가 1을 초과하는 균열 각도를 정량적으로 분석하였다.
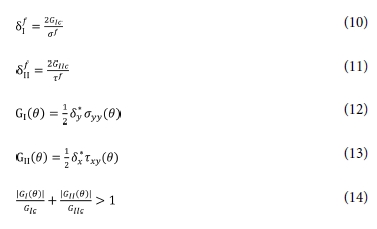
|
Fig. 1 Diagram of DCB Test[1] |
|
Fig. 2 Stress Fields around Crack Tip |
|
Fig. 3 Traction-Separation Curve |
3.1 직교적층 DCB 시편의 균열
형상
선행 연구[1]에서는 Fig. 1과 같이 직교적층 탄소섬유/에폭시 복합재 적층판에 대한 DCB 시험을 수행하였다. 광학장비를
이용해 Fig. 4와 같이 모드 I 하중에
의한 균열 성장 경로를 기록하였다. 시편을 구성하는 Prepreg의 1 ply 당 두께는 0.125 mm로 실제 두께비로 그래픽화할 경우 균열
성장 경로를 구별하기 어렵기 때문에 두께를 8 배로 늘려 Fig. 5와 같이 표현하였다.
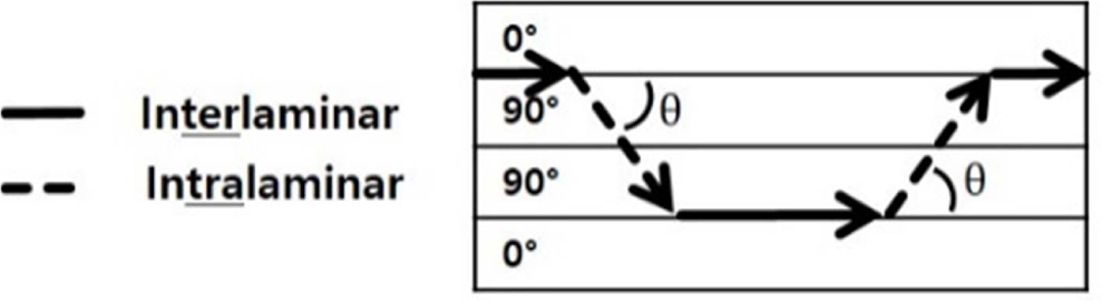
균열 성장 경로를 분석한 결과는 Fig. 6의 모식도와 같다. 직교적층 DCB 시편의 모드 I 하중에 따른 균열은 0° 층과
90° 층 사이에서 발생하는 층간(Interlaminar) 균열과 90° 층내에서 발생하는 층내(Intralaminar) 균열로 나타났다. 선행
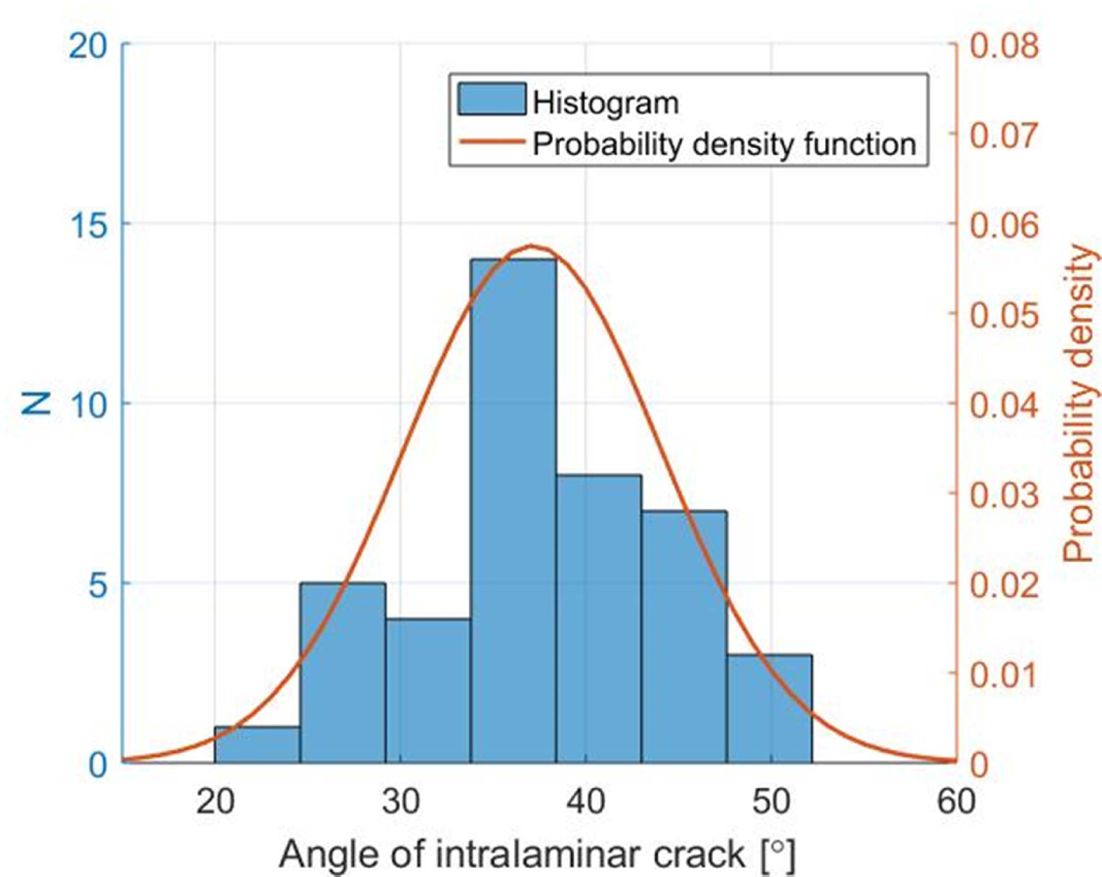
연구의 층내 균열 성장 각도를 측정하여 작성한 층내 균열 각도의 Histogram 및 확률 밀도 함수는 Fig. 7과 같으며 균열 각도의 범위는 5o 간격으로 통계처리하였다.
균열성장 각도 분석 결과를 이용하여 층간 및 층내 균열의 비율을 구하였다. 직교적층 DCB 시험에서 균열 시작점은 55 mm이고 균열
끝점은 97 mm로 균열 시작점에서 끝점까지의 단순 수평 길이는 42 mm이다. 수평 방향으로 성장하는 층간 균열의 길이는 24.4 mm로 나타났고
층내 균열의 수평 길이는 17.6 mm로 나타났다. 전체 수평 균열 길이 42 mm 중 층간 균열이 58.1%를 차지하였고 층내 균열이
41.9%를 차지하였다.
직교적층 DCB 시편의 층내 균열 각도는 23°부터 52°까지 다양한 분포를 보였고 평균은 37°로 계산되었다. 층내 균열은 임의의
각도를 가지고 성장하므로 층내 균열의 수평 길이와 층내 균열의 평균 각도를 이용하여 층내 균열의 실제 길이를 추정하였다.
층내 균열의 평균 각도를 이용하여 구한 실제 층간 균열의 성장 길이는 22 mm로 층간 및 층내 균열의 실제 성장 길이는 46.5
mm로 계산되었다. 전체 균열 길이 46.5 mm 중 층간 균열이 52.6%를 차지하였고 층내 균열이 47.4%를 차지하였다. 직교적층 DCB
시편의 균열 길이 및 비율은 Table 1과 같다.
3.2 응력장 계산 결과
Chalivendra[9]와 선행 연구[1] 결과를 이용하여 직교적층 DCB 시편의 균열 선단 근처에서의 응력장을
분석하였다. 응력장 계산은 선행 연구[1]에서 구한 물성을 사용하였으며,
추가적으로 필요한 물성은 연구의 시편과 유사한 물성을 가진 탄소섬유/에폭시 복합재의 물성[13]을 적용하였다. 모드 II 파괴인성(GIIc)은 ASTM D7905[3] 규격에 따라 직교적층 복합재 적층판에 대한 End-Notched
Flexure(ENF) 시험을 통하여 구하였다.
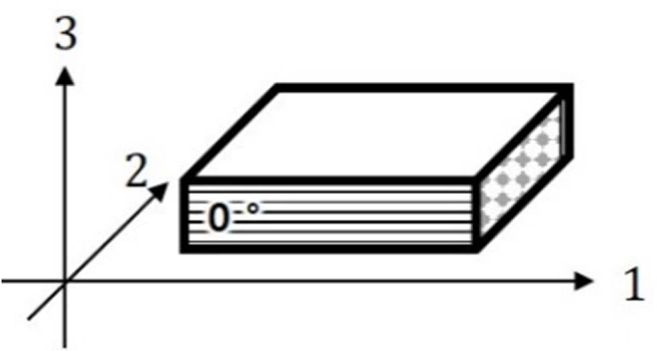
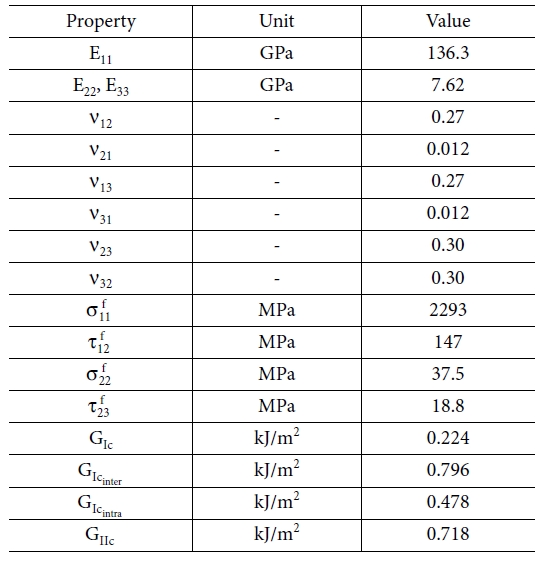
직교적층 DCB 시편의 물성 좌표계는 Fig. 8과 같으며, 시편의 물성은 Table 2와 같다. Table 2에서 E, n, sf, tf는 각각 일방향
Lamina의 탄성계수, 포아송 비, 항복 인장강도, 항복 전단강도이며 방향은 하첨자로 표기하였다. 그리고 GIc는 0o 층간의 모드 I 층간 파괴인성, GIcinter는 0o 층과 90o 층간의 모드 I 층간 파괴인성, GIcintra는 90o 층내에서의 모드 I 층내 파괴인성, GIIc는 0o 층과 90o 층간의 모드 II 층간
파괴인성이다.
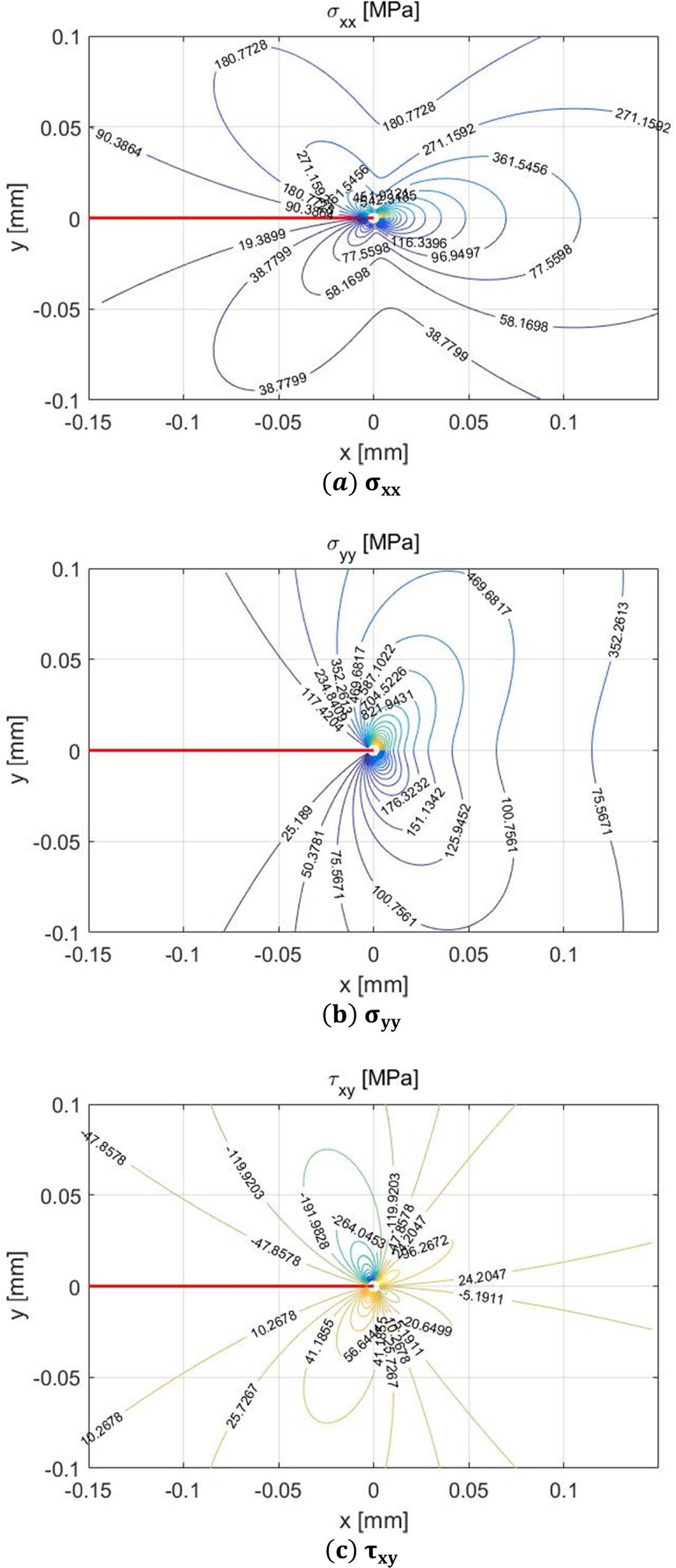
직교적층 DCB 시편의 물성을 이용해 구한 응력장은 Fig. 9와 같다. 균열 선단은 (0, 0) 지점이며, (-0.15, 0) 점에서 (0, 0) 점을 잇는
선은 균열을 표시한 것이다.
균열 선을 기준으로 +y층(0~0.1 mm)은 0° 층이며, -y층 (-0.1~0 mm)은 90° 층이다. 0° 층의 GIc는 0.224 kJ/m2, 0° 층과 90° 층간의 GIcinter는 0.796 kJ/m2, 90° 층내의 GIcintra는 0.478 kJ/m2이다. 응력장에서 응력의 크기는 파괴인성을 주요 변수로하는 A0(식 (1)-(3))와 비례한다. 0° 층의 A0는 2.76 MPa 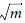 이며 90° 층의 A0는 0.92 MPa
이며 90° 층의 A0는 0.92 MPa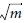 로 계산됨에 따라 0° 층에서 응력의 절대값이 더욱 크게 나타난 것을 확인하였다.
로 계산됨에 따라 0° 층에서 응력의 절대값이 더욱 크게 나타난 것을 확인하였다.
3.3 균열 성장 방향 분석 결과
구해진 응력장을 이용하여 직교적층 DCB 시편의 모드 I 균열 성장 방향을 분석하였다.
응력장은 Fig. 2와 식 (1)-(3)에서 볼 수 있듯이 균열 선단으로부터 떨어진 거리 r과 x축으로부터의 각도 q의 함수이다. 이론적으로 균열 선단에서는 응력이 발산하기때문에 본 연구에서는 균열 성장 방향을
확인하기 위해 r을 프리프레그 두께의 1/10인 0.013 mm 지점부터
응력장을 계산하였다. 그리고 이론적으로 크게 계산된 응력을 이용해 재료의 강도와 비교하거나 변형률 에너지 해방률을 계산하여 분석하기 보다는 실질적으로
유효한 응력을 이용하여 분석하였다. 90°층에서 최대 응력 파손기준을 적용하였을 때 파손지표가 1.5 정도되는 응력값이 발생할 수 있도록 전체적인
응력장의 크기를 6.2배 정도 낮추어 주응력과 변형율 에너지 해방율을 계산하였다.
0°층을 관통하여 균열이 성장하는 것은 물리적으로 불가능한 거동이므로 90°층내의 균열 성장(-180° < q < 0°)을 분석하였다.
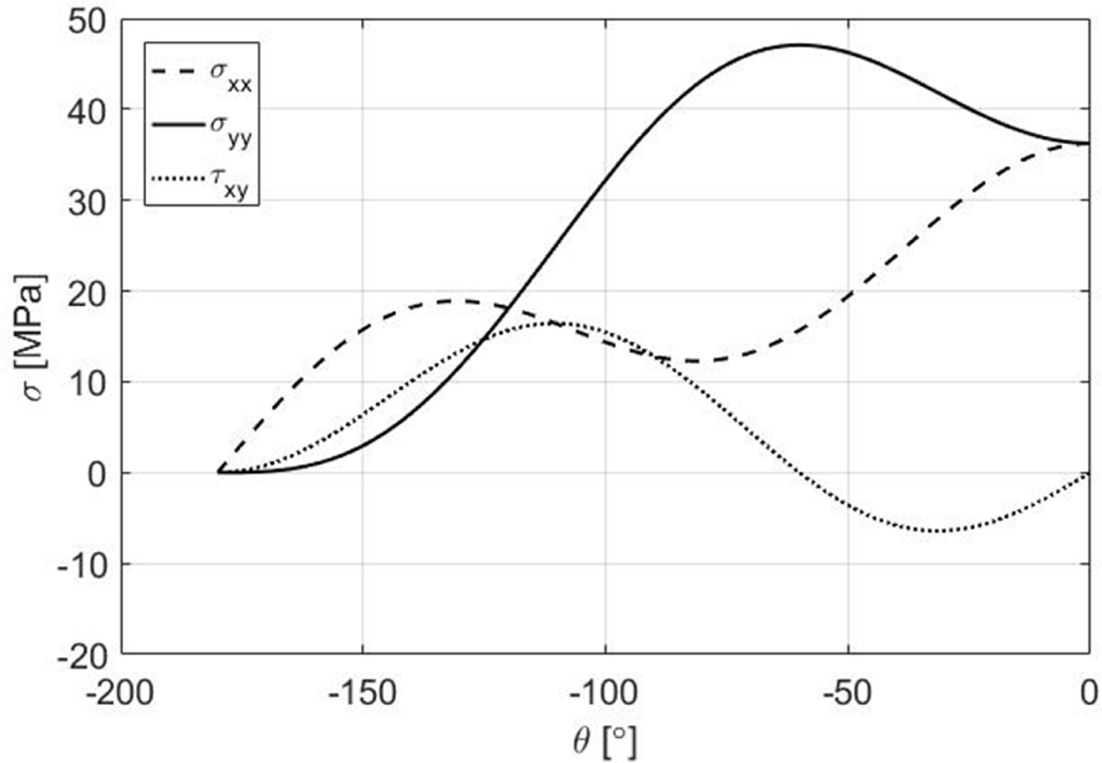
각도 q에 따른 응력은 Fig. 10과 같다. sxx는 0°에서 최대로 발생하였고
syy는 -60°, txy는 -111°에서 최대로
발생하였다.
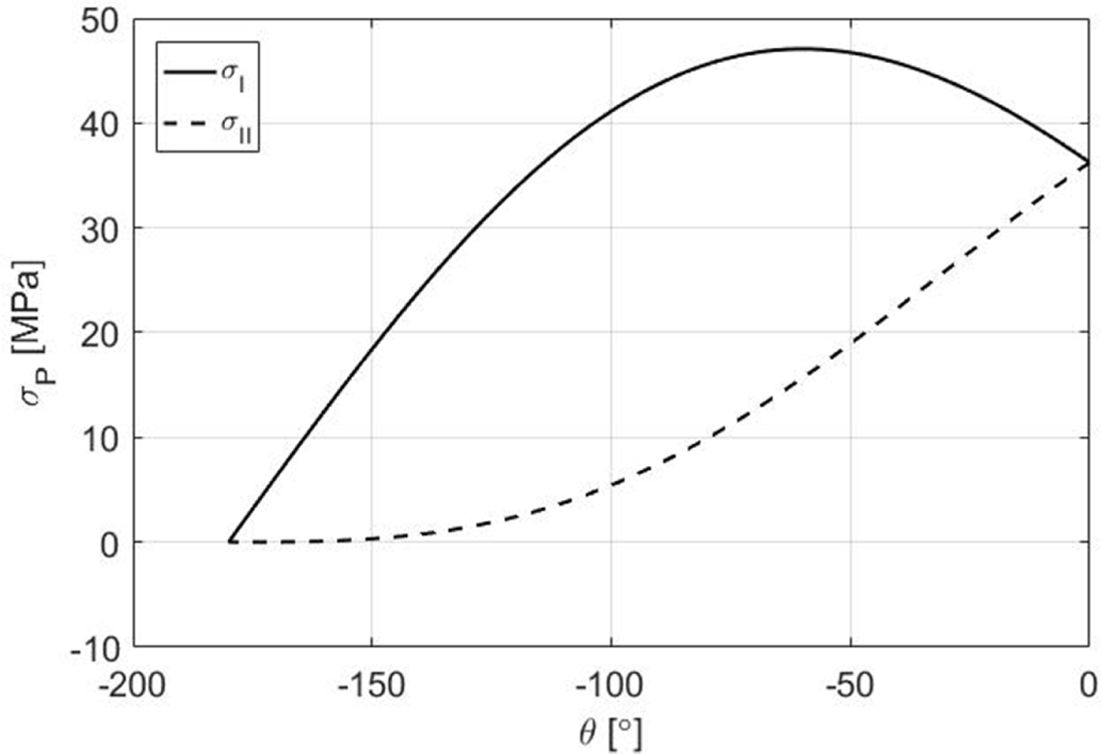
‘최대 주응력 분석방법’을 통해 90° 층내의 균열 성장 방향을 정성적으로 분석하기 위하여 각도 q에 따라 계산된 주응력은 Fig. 11과 같다. Fig. 11에서와 같이 syy가 최대로 나타난 -60°에서 최대 주응력이 발생함을 확인하였다.
그러나 균열선단에서의 응력분포는 폭이 넓은 DCB 시편의 경우 평면변형율 조건으로 가정할 수 있고 이럴 경우, 균열선단에서는 소성 영역이 형성되어
최대 응력의 크기는 항복강도의 3배 정도이내 이므로 기지재료 파손 등의 균열이 발생하지 않음을 알 수 있다.
다음으로 ‘파손지표 분석방법’을 통해 직교적층 DCB 시편의 90° 층내 균열 성장 방향을 분석하였다. 파손지표 분석을 위한 직교적층
DCB 시편의 기준 응력-변위 선도는 Fig. 12와 같다.
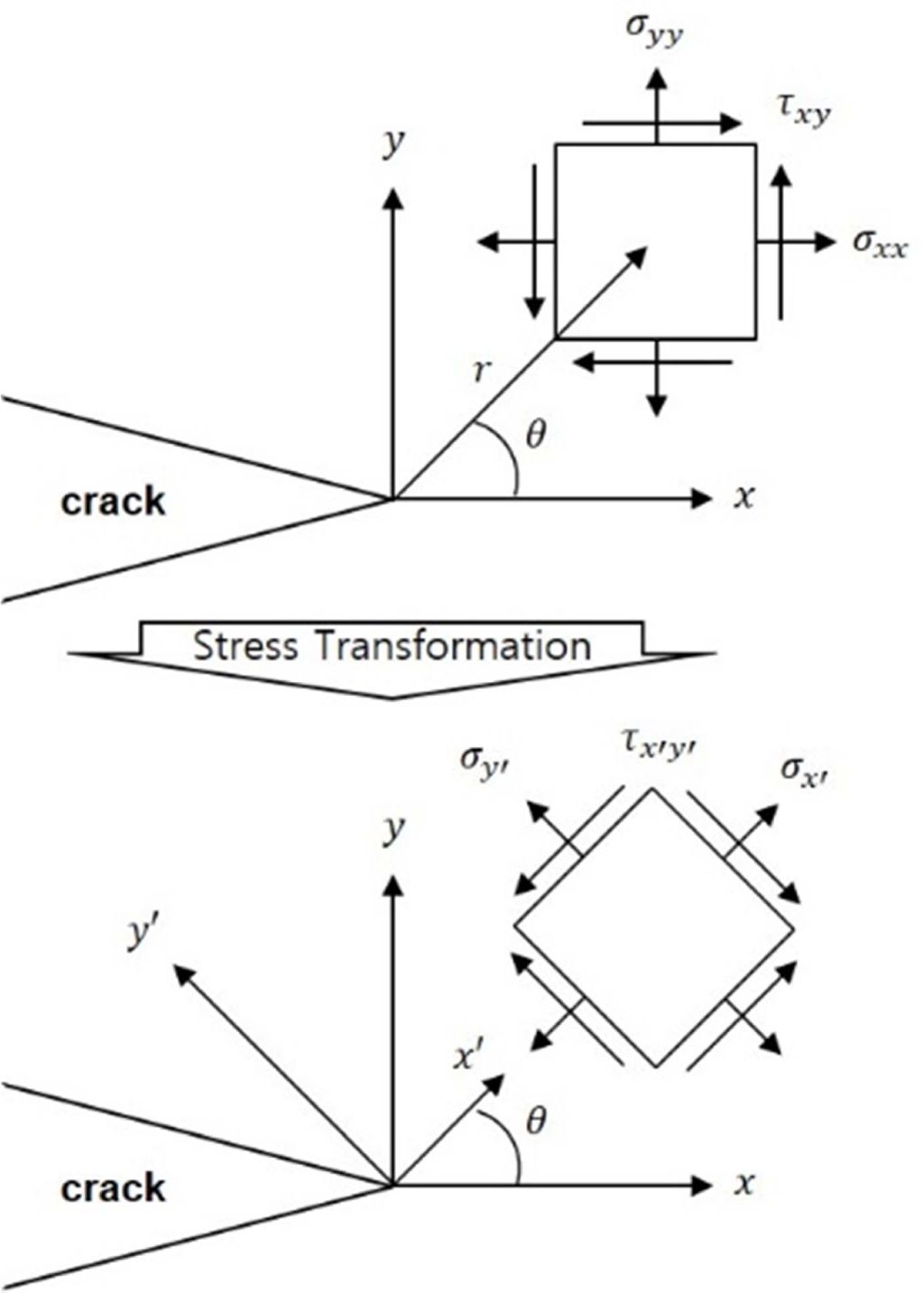
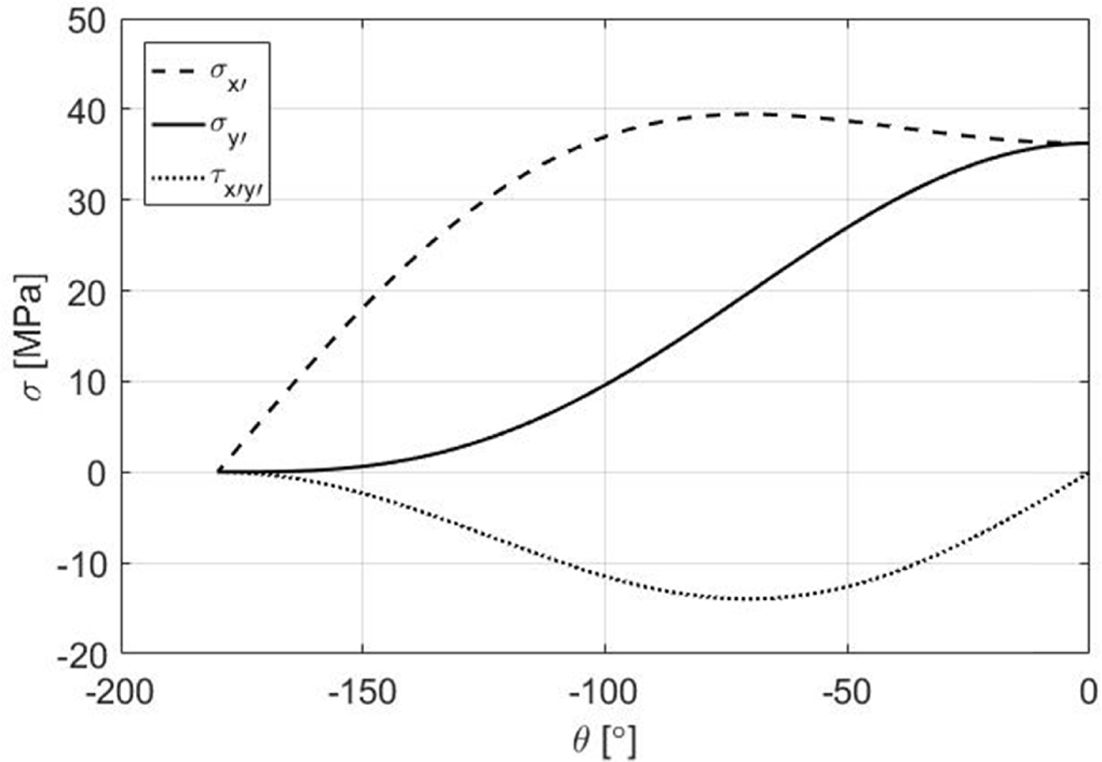
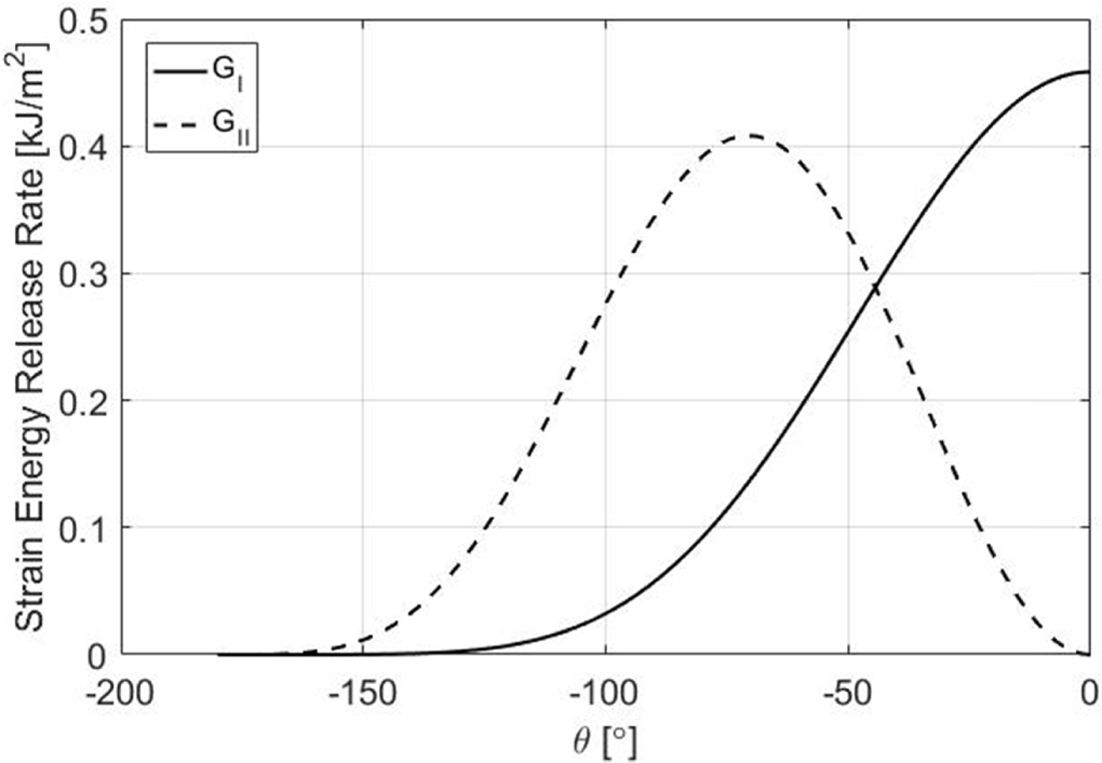
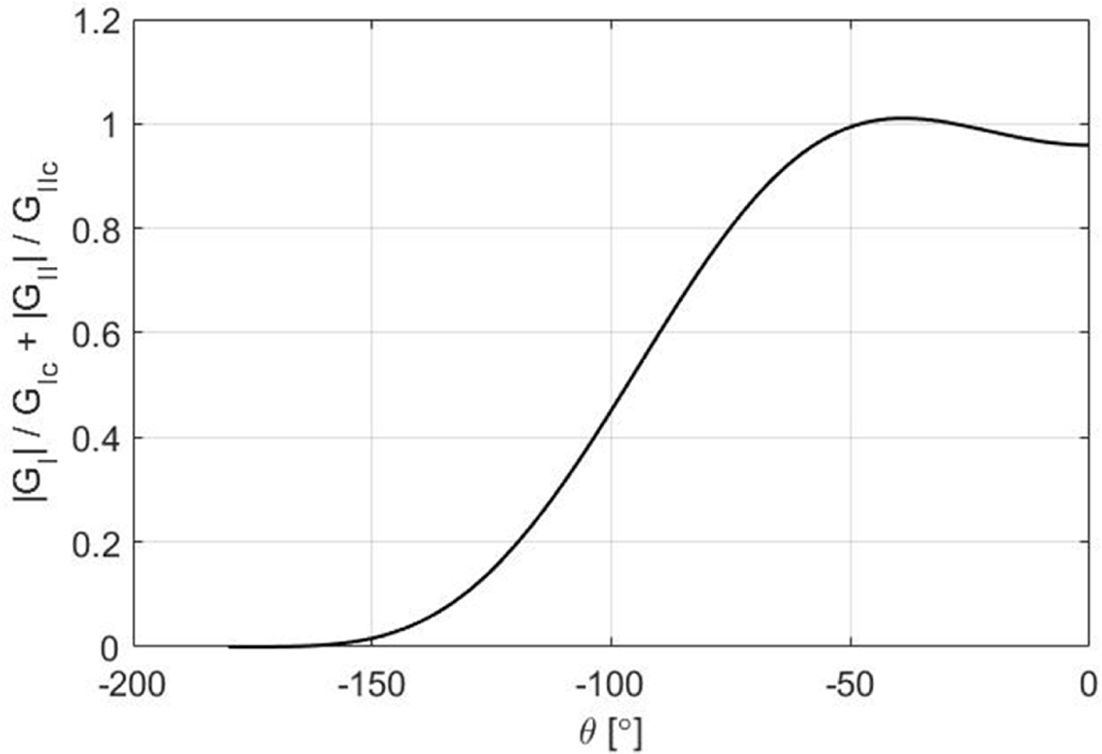
파손지표 분석방법은 각도에 따라 모드 I과 모드 II로 성장하는 균열을 분석하는 것이므로 파손지표를 분석하기 위하여 Fig. 13과 같이 Fig. 10의 응력을 q에 따라 변환해야 한다. 변환된 응력은 Fig. 14과 같다. 응력-변위 선도를 통해 계산된 모드 I 및 모드 II 변형률 에너지 해방률은 Fig. 15와 같으며, 식 (14)로 계산된 파손지표는 Fig. 16과 같다.
직교적층 DCB 시편의 경우 면내 수직방향 응력인 sy'는 θ가 0°일 때 가장 크게 계산되었다. 따라서 sy'로 계산되는 GI도 θ가 0°일 때 가장 크게
계산되었다. 그리고 면내 전단방향 응력인 τx'y'는 θ가 -70.9°일 때 가장 크게 계산되었다. 따라서 τx'y'로
계산되는 GII도 θ가 -70.9°일 때 가장 크게 계산되었다.
최대 σy'대비 최대 τx'y'의 비율은 약 38% 정도로 계산되었으나 최대 GI 대비 최대 GII의 비율이 약 89%로 계산되었다. 따라서 직교적층 DCB
시편의 경우 모드 I 하중이 가해지더라도 면내 전단방향 응력에 의한 모드 II가 균열 성장에 크게 기여하는 것을 확인하였다. 결과적으로 파손지표
분석방법을 통해 직교적층 DCB 시편에 모드 I 하중이 가해질 경우 모드 I과 모드 II의 영향으로 인해 균열이 -40° 방향으로 성장하는 것을
확인하였다.
직교적층 DCB 시편의 90° 층내에서의 GIIc/GIc
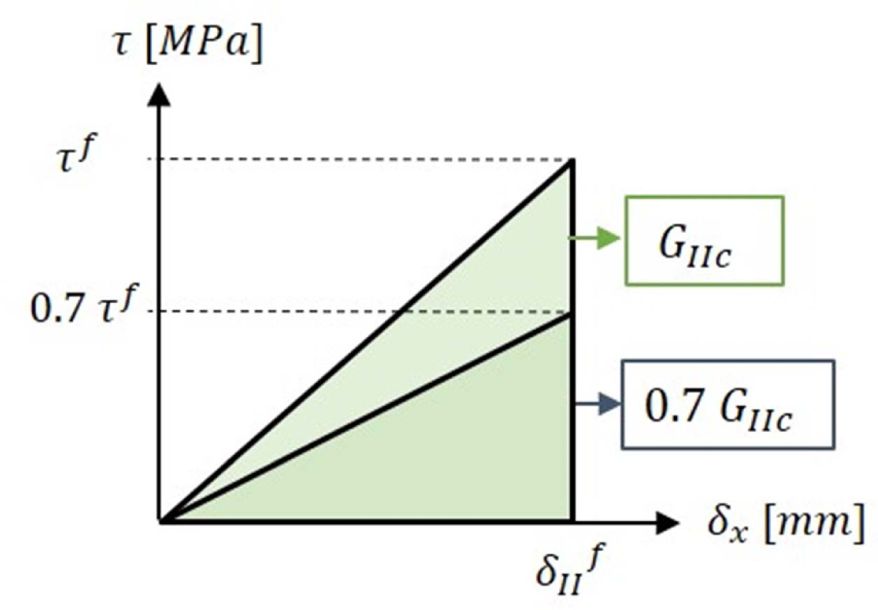
비율이 달라질 경우, 균열 성장의 방향이 변화하는지 여부를 파손지표 분석방법으로 확인하였다. GIIc의 증감비율에 따라 Fig. 17과 같이 τf는 동일한 비율로 증감하나 δIIf는 동일하다고
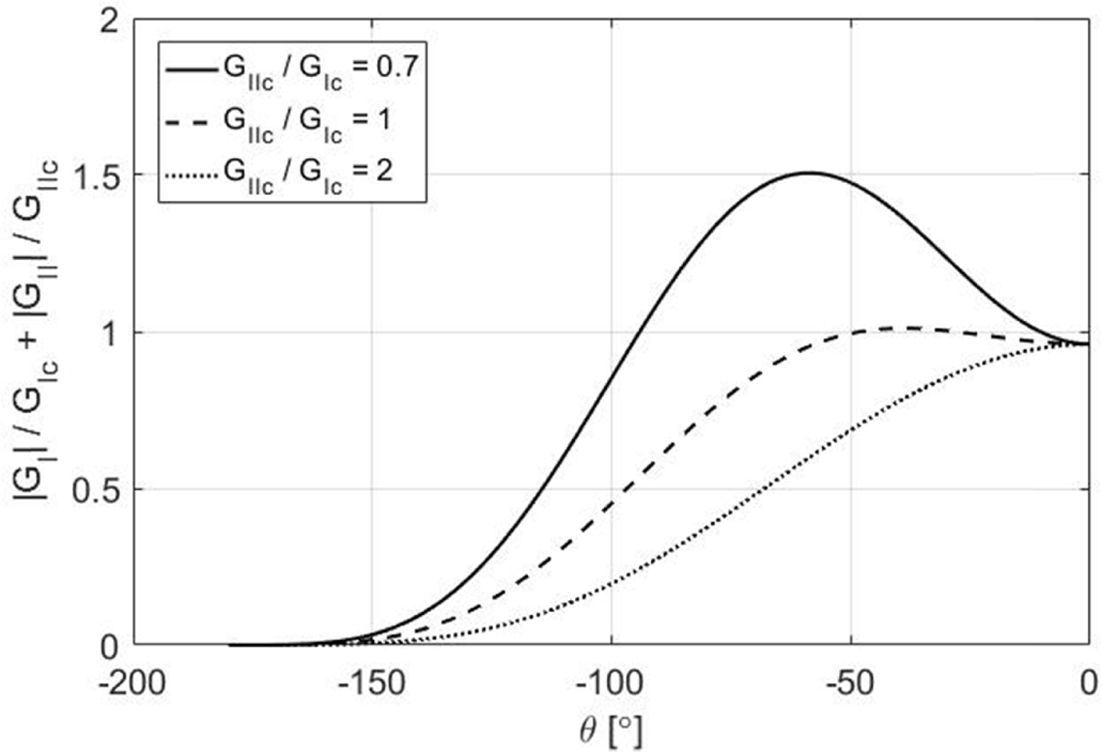
가정하고, GIIc/GIc 비율이 각각 0.7, 1, 2인 경우로 나누어 분석한 결과는 Fig. 18과 같다.
직교적층 DCB 시편의 경우 GIIc/GIc 비율이 변할 경우 모드 I 하중에 의한 균열 성장
방향이 변하는 것을 확인하였다. 이는 직교적층 DCB 시편의 경우 90° 층내에서는 면내 전단방향 응력에 의한 모드 II가 균열 성장에 크게 기여하기
때문이다. GIIc/GIc 비율이 감소할수록, 즉 GIIc가 감소할수록 τx'y'가
가장 크게 계산되는 –70.9° 방향으로 최대
파손지표가 이동하는 것을 볼 수 있으며, 파손지표 역시 증가하는 것을 볼 수 있다.
최대 주응력 및 파손지표 분석방법을 통하여 직교적층 DCB 시편의 90° 층내 균열 성장 방향을 확인하였다. 최대 주응력 분석방법으로
계산된 층내 기지재료 균열파손으로 인한 균열성장가능 각도는 60° 이지만 균열 선단에서의 소성영역 생성으로 최대 주응력 파손조건에서도 기지재료의
균열파손(Matrix Cracking)은 발생하지 않을 것으로 예상된다. 그러나 균열선단 주변에서의 동일한 응력장 분석결과를 혼합모드 파손기준식에
대입하여 파손지표 분석방법으로 계산된 층내 균열 각도는 40°로 실제 DCB 시험에서 측정한 균열성장 각도의 평균값 37°와 유사하게 계산되었다.

|
Fig. 4 Mode I Crack Propagation Shape for Cross-ply DCB Specimen[1] |

|
Fig. 5 Diagram of Crack Propagation Shape for Cross-ply DCB Specimen[1] |
|
Fig. 6 Definition of Interlaminar and Intralaminar Crack |
|
Fig. 7 Distribution for Angle of Intralaminar Crack |
|
Fig. 8 Material Coordinate |
|
Fig. 9 Stress Fields |
|
Fig. 10 Stresses-Angle(θ) for CP DCB Specimen |
|
Fig. 11 Principal Stresses-Angle(θ) for CP DCB Specimen |
|
Fig. 12 Reference Traction-Separation Curve |
|
Fig. 13 Stress Transformation at Specified Angle (θ) |
|
Fig. 14 Transformed Stresses at Specified Angle (θ) |
|
Fig. 15 Strain Energy Release Rate-Angle (θ) |
|
Fig. 16 Mixed Mode Failure Index-Angle(θ) for CP DCB Specimen |
|
Fig. 17 Change of Traction-Separation Curve according to Different GIIc Value |
|
Fig. 18 Mixed Mode Failure Index according to GIIc/GIc Ratio |
|
Table 1 Characteristics of Cracks |
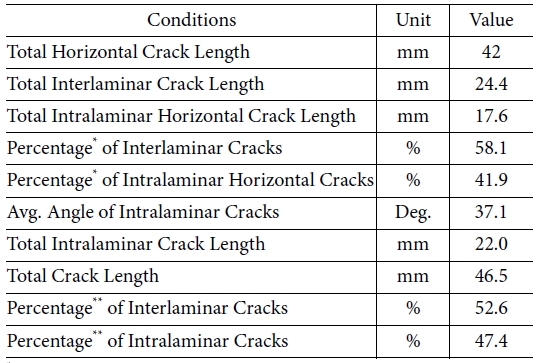
*Based on the total horizontal crack length |
|
Table 2 Material Properties of Unidirectional Lamina (UD Carbon (T700 Grade)/Epoxy, AP125NS.AX, T&S Advanced Material Co.) |
본 논문에서는 모드 I 파괴인성과 응력장을 이용하여 직교적층 탄소섬유/에폭시 복합재적층판의 균열 성장의 방향을 정성적, 정량적으로 분석하였다.
균열 성장에는 균열 선단에 작용하는 모든 수직 응력과 전단 응력이 영향을 준다고 가정하고 최대 주응력 분석방법과 최대 파손지표 분석방법을 제안하였고
응력장 분석 결과를 대입하였다.
두 가지 분석방법 중 최대 주응력 분석방법에 의한 기지재료 균열 파손에 의한 균열성장보다는 최대 파손지표 분석방법을 적용하였을 때 실제
직교적층 DCB 시험에서 관찰된 층내 평균 균열성장 각도인 37°에 근접한 40° 방향으로 균열이 성장하는 것으로 분석되었다. 모드 I 파괴인성과
모드 II 파괴인성의 비율에 따라 균열의 성장 각도가 변경되는 것을 확인하였다. 이를 통하여 모드 I 하중이 가해지더라도 직교적층 DCB 시편의
90° 층내에서의 균열 성장에는 면내 전단방향 응력이 크게 기여하는 것을 확인하였고, 모드 I과 모드 II 파괴인성의 비율이 직교적층 복합재 적층판의
균열 성장 각도에 영향을 미침을 확인하였다.
향후 직교적층 복합재 적층판의 0°/90° 층간의 층간 파괴에서 90° 층의 층내 파괴로 천이되는 조건과
균열 성장 각도에 대한 직교적층판의 모드 I 균열 성장 예측 및 확률론적 해석에 대한 연구를 수행할
예정이다.
본 연구는 충남대학교 학술연구비의 지원으로 수행되었으며 이에 감사드립니다.
- 1. Kang, M.S., Jeon, M.H., Kim, I.G., and Woo, K.S., “The Characteristics for Mode I Interlaminar and Intralaminar Fractures of Cross-ply Carbon/epoxy Composite Laminates Based on Energy Release Rate,” Composites Research, Vol. 32, No. 1, 2019, pp. 6-12.
-

- 2. ASTM D5528-13, Standard Test Method for Mode I Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites, ASTM International, West Conshohocken, PA, 2013.
-

- 3. ASTM D7905 / D7905M-14, Standard Test Method for Determination of the Mode II Interlaminar Fracture Toughness of Unidirectional Fiber-Reinforced Polymer Matrix Composites, ASTM International, West Conshohocken, PA, 2014.
- 4. Reeder, J.R., and Rews, J.H., “Mixed-mode Bending Method for Delamination Testing,” AIAA Journal, Vol. 28, No. 7, 1990, pp. 1270-1276.
-

- 5. Borg, R., Nilsson, L., and Simonsson, K., “Simulating DCB, ENF and MMB Experiments Using Shell Elements and a Cohesive Zone Model,” Composites Science and Technology, Vol. 64, No. 2, 2004, pp. 269-278.
-

- 6. Harper, P.W., and Hallett, S.R., “Cohesive Zone Length in Numerical Simulations of Composite Delamination,” Engineering Fracture Mechanics, Vol. 75, No. 16, 2008, pp. 4774-4792.
-

- 7. Camanho, P.P., Davila, C.G., and De Moura, M., “Numerical Simulation of Mixed-mode Progressive Delamination in Composite Materials,” Journal of Composite Materials, Vol. 37, No. 16, 2003, pp. 1415-1438.
-

- 8. De Morais, A., De Moura, M., Marques, A., and De Castro, P., “Mode-I Interlaminar Fracture of Carbon/epoxy Cross-ply Composites,” Composites Science and Technology, Vol. 62, No. 5, 2002, pp. 679-686.
-

- 9. Chalivendra, V.B., “Mode-I Crack-tip Stress Fields for Inhomogeneous Orthotropic Medium,” Mechanics of Materials, Vol. 40, No. 4-5, 2008, pp. 293-301.
-

- 10. Anderson, T.L., Fracture Mechanics: Fundamentals and Applications, CRC Press, 2017.
-

- 11. Krenk, S., “On the Elastic Constants of Plane Orthotropic Elasticity,” Journal of Composite Materials, Vol. 13, No. 2, 1979, pp. 108-116.
-

- 12. Wei, Y., “A Stochastic Description on the Traction-separation Law of an Interface with Non-covalent Bonding,” Journal of the Mechanics and Physics of Solids, Vol. 70, 2014, pp. 227-241.
-

- 13. De Moura, M., Campilho, R.D., Amaro, A., and Reis, P., “Interlaminar and Intralaminar Fracture Characterization of Composites under Mode I Loading,” Composite Structures, Vol. 92, No. 1, 2010, pp. 144-149.
-

 This Article
This Article
-
2019; 32(6): 327-334
Published on Dec 31, 2019
- 10.7234/composres.2019.32.6.327
- Received on Mar 22, 2019
- Revised on Nov 25, 2019
- Accepted on Dec 23, 2019
 Services
Services
Shared
 Correspondence to
Correspondence to
- In-Gul Kim
-
Department of Aerospace Engineering, Chungnam National University
- E-mail: igkim@cnu.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.