As the use of composite materials of woven structure has expanded to various fields such as automobile and aviation industry, there has been a need for reliability problems and prediction of mechanical properties of woven composites. In this study, finite element analysis for predicting the mechanical properties of composite materials with different weaving structures was conducted to verify similarity with experimental static properties and an effective modeling method was developed. To reflect the characteristics of the weave structure, the meso-scale representative volume element (RVE) was used in modeling. Three-dimensional modeling was carried out by separating the yarn and the pure matrix. Hashin’s failure criterion was used to determine whether the element was failed, and the simulation model used a progressive failure model which was suitable for the composite material. Finally, the accordance of the modeling and simulation technique was verified by successfully predicting the mechanical properties of the composite material according to the weave structure.

직조 구조의 복합재의 쓰임이 자동차, 항공 산업 등 여러 분야로 확장됨에 따라, 직조 복합재의 신뢰성 문제 및 물성예측에 대한 필요성이 대두되었다. 본 연구에서는 직조 구조가 다른 복합재료의 물성 예측을 위한 유한요소해석을 수행하여 실험으로 얻은 정적 물성과의 유사성을 검증하였고, 효과적인 모델링 방법을 개발하였다. 직조 구조의 특성을 반영하기 위하여 모델링은 메소 스케일의 대표 체적 요소(RVE)를 이용하였다. 섬유 다발과 순수 기지를 분리하여 3차원 모델링을 진행하였다. 하신 파괴 기준(Hashin’s failure criteria)을 적용하여 요소의 파괴 유무를 판단하였고, 해석 모델은 복합재에 적합한 점진적 파괴 모델을 사용하였다. 최종적으로, 직조 구조에 따른 복합재의 물성을 성공적으로 예측하여 본 모델링 및 해석 기법에 대한 적합성을 검증하였다.

Keywords: 직조복합재(Woven composite), 대표 체적 요소(RVE), 점진적 파괴 모델(Progressive failure model), 굴곡 각도(Crimp angle)

높은 비강도, 비강성 등의 우수한 기계적 성질으로 인하여, 섬유강화 복합재료는 자동차, 항공, 기계 산업 등 다양한 분야에서 점차 쓰임새가 확장되고 있다. 그 중에서도, 일반적으로 사용되는 단방향 섬유강화 복합재료는 섬유 방향의 면내 물성이 매우 뛰어난 특성을 가지고 있다. 하지만, 섬유 수직 방향의 경우에는 기지의 물성에 지배적이기 때문에 상대적으로 낮은 물성을 보인다. 반면, 이러한 문제점을 보완한 직조 복합재료의 경우에는 방향에 따른 구조적 안정성이 뛰어나며, 단방향 복합재료에 비하여 우수한 면외 방향 기계적 특성을 지니고 있다. 또한, 성형성이 뛰어나기 때문에 활용도가 높은 재료로 평가받고 있다. 이러한 이유들 때문에 직조 복합재의 활용도는 점차 증가하고 있다[1,2]. 따라서, 직조 복합재의 신뢰성을 향상시키기 위하여 물성 예측에 대한 연구가 활발히 진행되고 있다.
선행연구로 점진적 파괴 모델을 사용하여 직조 복합재의 물성을 예측한 연구들이 수행된 바 있다. 초기 탄성 강성 및 손상 정도를 성공적으로 예측한 연구가 존재하며 거시 스케일의 직조 복합재 구조에 대한 물성을 예측하는 연구가 다양하게 진행되었다[3]. 또한, 재료 내부의 국부적인 변화를 파악하기 위하여 미시적인 접근 방법을 사용하여 복합재의 구성 요소의 다양한 물성으로부터 등가 유효 물성치(effective material property)와 파손 강도(failure strength)를 예측하는 연구가 진행되어 왔다[4]. 하지만, 이는 규칙적인 배열을 가지는 단방향(UD) 복합재료에 적합한 모델링 방법으로, 복잡한 기하학적 형상을 가지는 직조 복합재료에 적용하기에는 제한적이다. 한편, 직조 복합재료는 섬유 부피 분율, 직조 구조에 따라 물성이 상이한 특성을 가지고 있다. 이러한 직조 복합재의 특성을 적용할 수 있는 모델과 물성 예측 방법에 대한 연구는 부족한 실정이다.
본 연구에서는 직조 복합재의 구조적 특성을 고려할 수 있는 모델으로서 메소 스케일의 대표 체적 요소(Representative Volume Element, RVE)를 설정하였다. 섬유다발과 순수 기지를 분리하여 직조 구조의 특성을 반영할 수 있게 모델을 설정하였으며, 각각의 파괴 모델을 구분하여 적용하였다. 섬유 다발의 경우, 단방향 복합재로 가정하여 이에 적합한 하신 파괴 기준(Hashin’s failure criteria)을 적용하였고, 점진적 파괴 모델을 적용하여 파괴가 일어난 이후 물성이 점차 감소되게 하였다. 최종적으로, 직조 구조에 따른 복합재의 물성을 성공적으로 예측하여 본 모델링 및 해석 기법에 대한 적합성을 검증하였다.

2.1 모델 구성
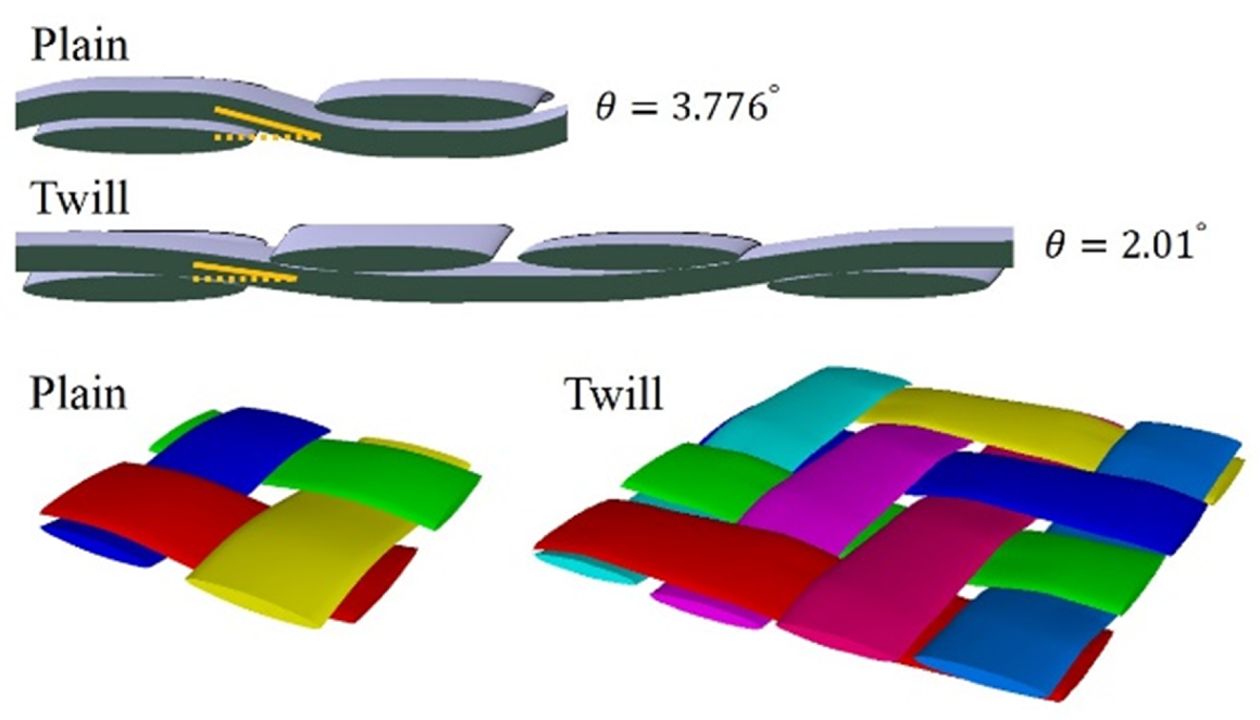
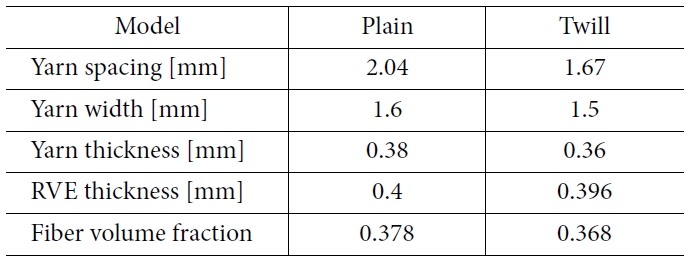
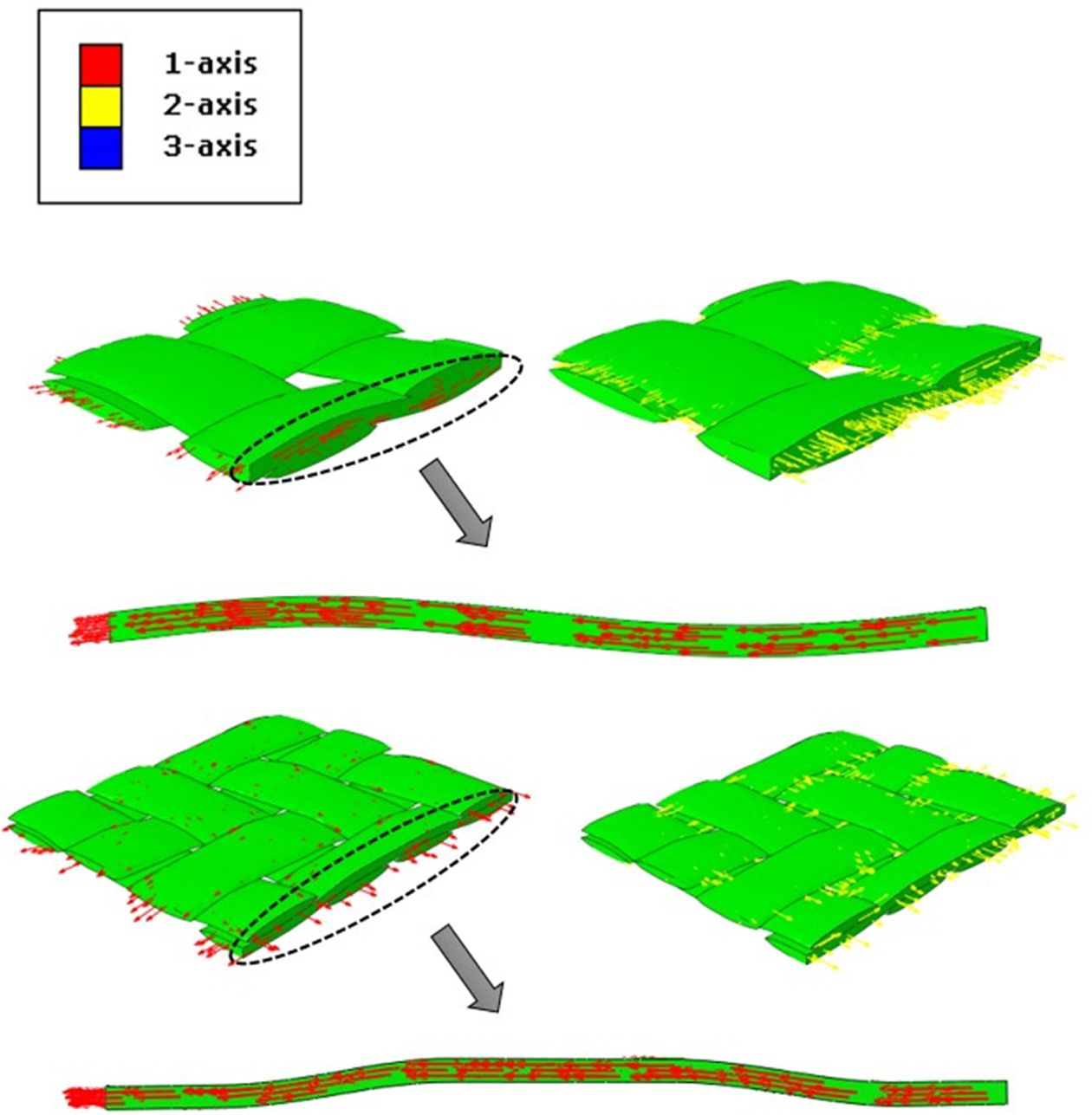
본 연구에서는 복합재의 직조 구조에 따른 차이를 보기 위하여 섬유 부피 분율이 유사한 평직(Plain), 능직(Twill) 모델을 생성하였다. 직조 구조에 따른 영향을 모델에 반영하기 위하여 본 연구에서는 메소 스케일의 대표 체적 요소를 설정하였다. 직조 구조 모델은 오픈 소스 소프트웨어인 TexGen을 이용하여 형성하였다. Fig. 1에서 볼 수 있듯이 평직, 능직 대표 체적 요소 모델을 형성하였다. 섬유 다발 단면의 폭과 높이는 실제 CF/Epoxy 복합재의 단면을 관찰하여 측정한 값으로 설정하였으며, Table 1에 그 치수를 나타내었다. Fig. 1에서 볼 수 있듯이, 직조 구조가 달라지게 되면 굴곡 각도가 달라지게 된다. 평직 모델과 능직 모델의 굴곡 각도를 계산해 보면, 평직은 약 3.776^o, 능직은 약 2.01^o로, 평직의 굴곡 각도가 능직보다 큰 것을 확인할 수 있다. 이 때, Fig. 2에서 볼 수 있듯이, 굴곡에 따라 변화하는 섬유방향(Fiber orientation)을 모델에 반영하여 굴곡 각도에 대한 영향을 고려할 수 있게 하였다.
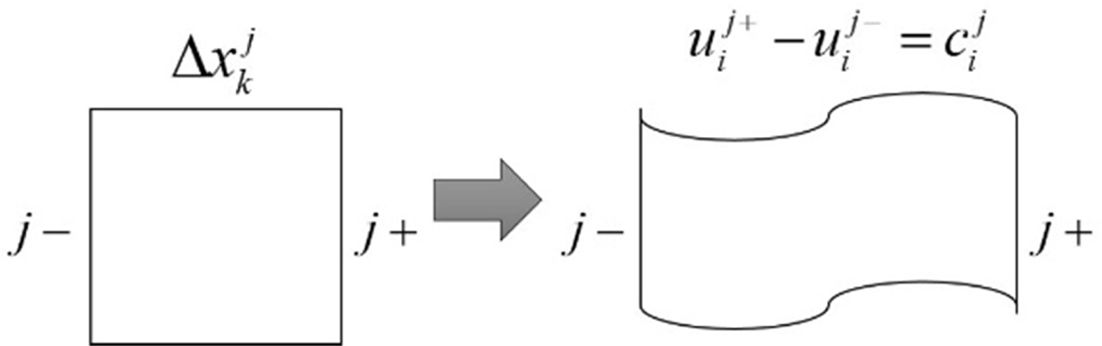
또한 대표 체적 요소의 구조적인 특성을 고려하여 적절한 구속조건을 적용해야 유효한 등가 유효 물성치를 계산할 수 있다. 선행 연구로서, 대표 체적 요소에 주기적 구속 조건(Periodic boundary condition)을 적용하면 보다 정확한 해석이 가능하다는 것이 Li에 의해 제시되었다[5]. 따라서 본 연구에서도 대표 체적 요소의 마주보는 면을 변형률로 서 각각 구속하는 주기적 구속 조건을 적용하였다(Fig. 3). 각 면에 위치한 노드(node)의 변위를 아래와 같은 방정식을 통하여 구속하였다.



여기서 는 각각 i = x, y, z 방향의 변위를, j+, j- 는 한 쌍의 대응되는 면의 노드의 위치를 의미하며, 는 거시적인 변형률을 의미한다.

2.2 점진적 파괴 모델
본 연구에서는, 섬유 다발을 단방향 복합재로 가정하고 이에 점차적으로 물성이 감소하는 점진적 파괴 모델을 적용하였다. 섬유 다발은 횡 방향 등방성인(transversely isotropic) 물성을 적용하였다. 섬유 다발의 파괴 기준은 여러 상용 유한요소해석 프로그램에서 널리 사용되고 정확성이 입증된 하신 파괴 기준을 변형률 기반의 식으로 이용하였다. 그 식은 다음과 같이 나타내어진다.
섬유 인장 파괴 모드(ε₁₁ > 0)



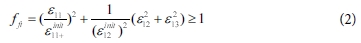
섬유 압축 파괴 모드(ε₁₁ < 0)



기지 인장/전단 파괴 모드(ε₂₂+ε₃₃ > 0)



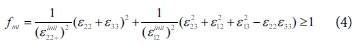
기지 압축 파괴 모드(ε₂₂+ε₃₃ < 0)



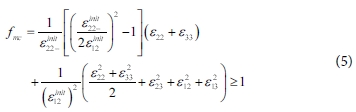
 여기서 f_ft, f_fc, f_mt, f_mc는 하신 파괴 초기값을 파괴 모드에 따라 나타낸 것이고, ε_ij는 방향에 따른 변형률을 나타낸 것이다. 는 전체 복합재의 인장, 압축, 전단 파괴 변형률을 의미한다.
인장/압축, 기지 방향의 인장/압축의 경우로 나누어 총 4가지의 파괴 모드를 바탕으로 점진적 파괴 모델을 구성하였다. 앞서 언급하였듯이, 섬유 다발을 횡 방향 등방성인 복합재로 가정하여 물성을 정의하였고, 파괴 전 컴플라이언스 행렬(S_UD)을 통하여 강성 행렬(DC_UD)을 구할 수 있다.

 

식 (2-5)에서 하신 파괴 초기값이 1 이상일 경우, 요소에 파괴가 일어남에 따라 강성을 점차 감소시키게 된다. 감소 정도는 다음과 같이 파괴 모드에 따른 감소 상태 변수(Degradation state variable, w_ft, w_fc, w_mt, w_mc)로 계산되어 적용된다[6].



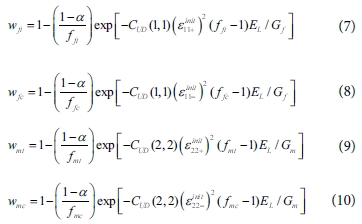
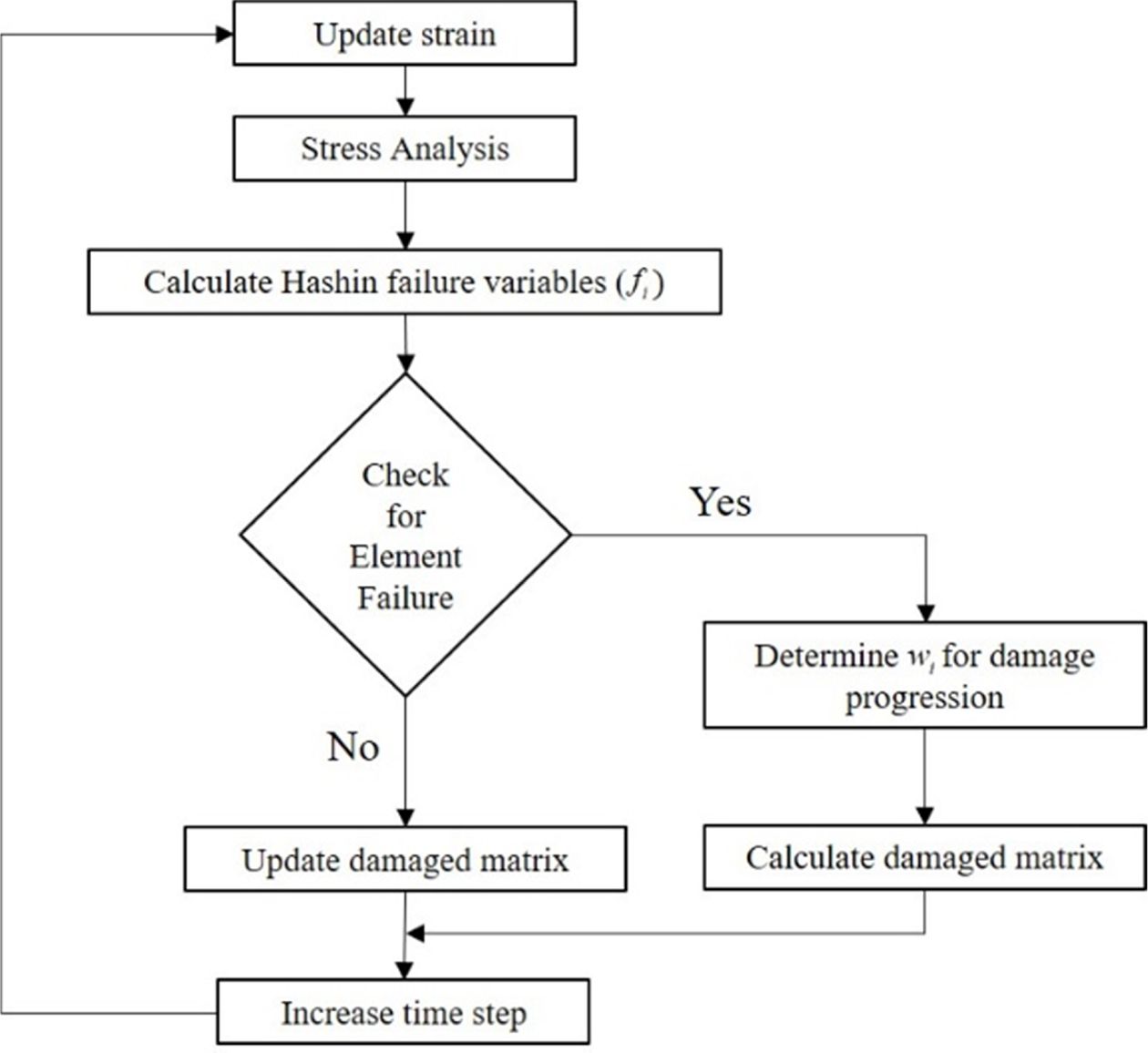
  여기서 G_f, G_m은 섬유와 기지의 파괴 에너지이며, a는 손상 요소, E_L은 요소 특성 길이(element characteristic length)이다. 손상 요소의 값은 섬유의 인장 파괴 같은 경우 급격하게 물성이 감소하기 때문에 0.8 이상이 적절하다. 각각의 감소 상태 변수는 0에서부터 시작되어 하신 파괴 초기값이 1을 초과할 때부터 점차 증가하여 1까지 증가하게 된다. 계산된 감소 상태 변수는 손상된 강성 행렬(C_D)에 적용된다. 점진적 파괴 모델의 순서도는 Fig. 4에 나타내었다.
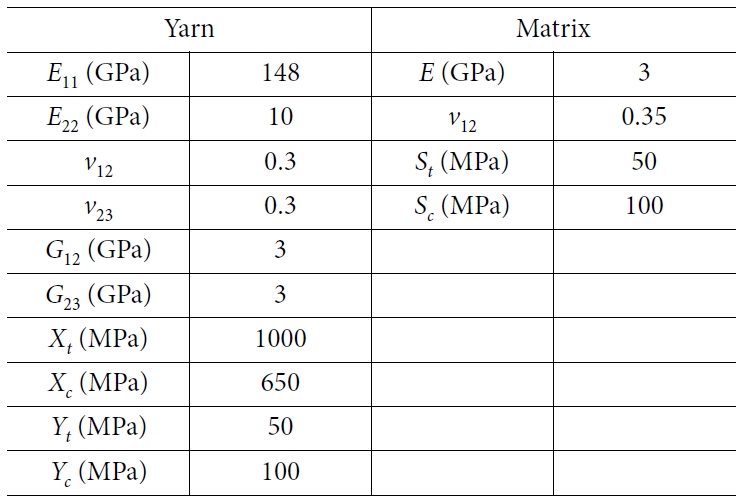
본 점진적 파괴 모델은 상용 유한 요소 해석 소프트웨어인 ABAQUS의 user material subroutine으로 구현되었다. 물성의 경우 문헌값[7,8]을 사용하였고, 이는 Table 2에 나타내었다. 순수 matrix에 적용되는 물성의 경우, 에폭시는 선형 탄성 재료로 가정하였다.
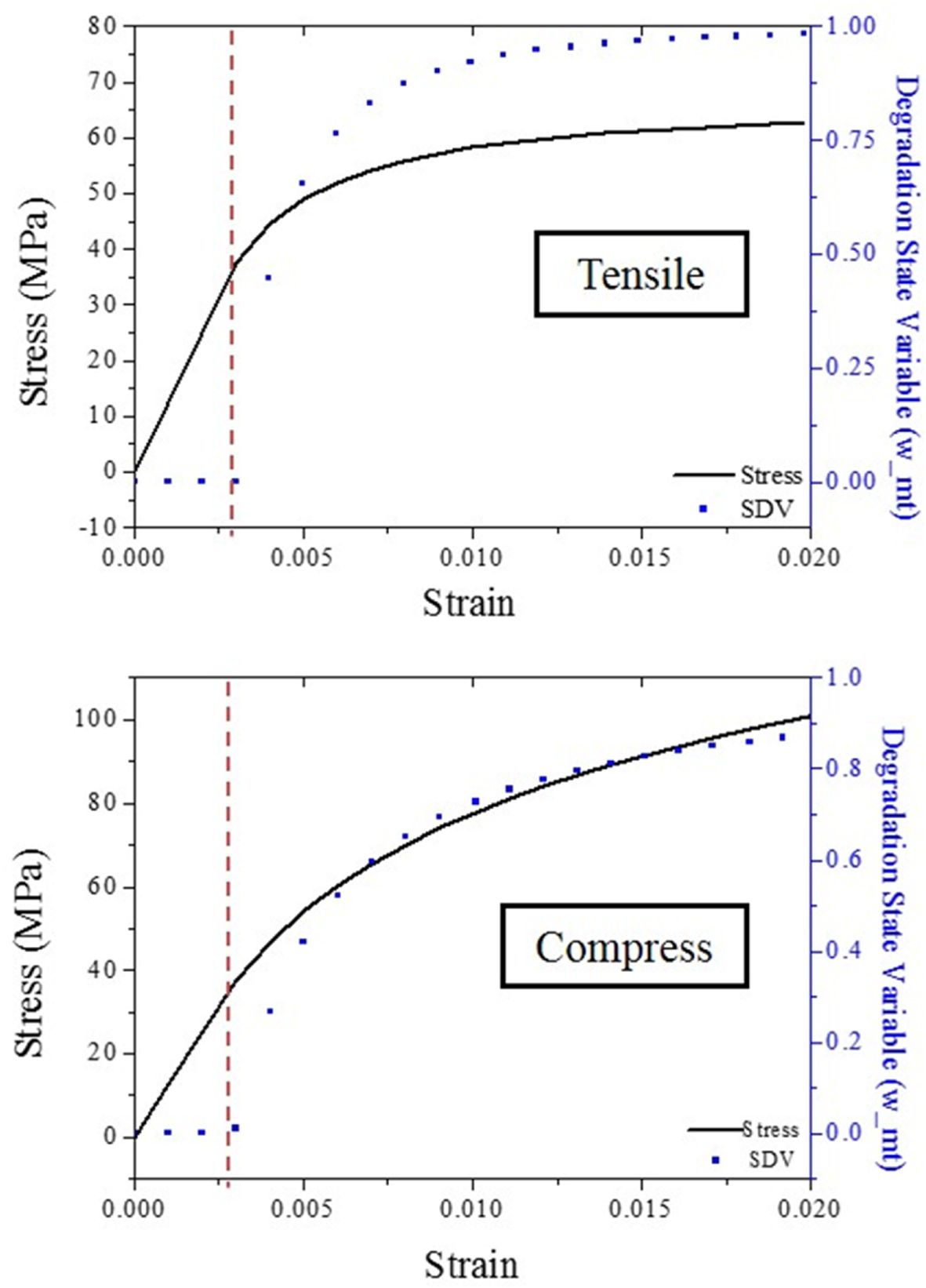
이와 같은 점진적 파괴 모델이 잘 구현되었는지 확인 하기 위하여 단일 요소 해석을 진행하였다. Fig. 5에서 요소에 파괴가 일어나는 시점을 빨간 점선으로 나타내었다. 요소에 파괴가 일어나기 전, 응력은 선형적으로 증가하며 감소 상태 변수는 0인 것을 확인할 수 있다. 반면, 요소에 파괴가 일어난 후에는 감소 상태 변수의 값이 점차적으로 증가하며 응력은 비선형적으로 증가하는 것을 확인 할 수 있다. 이는 감소 상태 변수가 증가하면서 요소의 물성이 감소하기 때문이다. 결과적으로, 점진적 파괴 모델이 잘 구현된 것을 확인할 수 있다.

직조 복합재의 구조적 특성을 고려한 점진적 해석 기법을 검증하기 위하여 평직, 능직 복합재의 인장, 압축, 전단 시험을 수행하였다. 시험은 만능 인장 시험기를 이용하여 2mm/min의 속도로 수행하였다. 인장, 압축, 전단 물성 시험의 경우 각각 ASTM D 3039, D 6641, D 5379 기준에 따라 실험을 수행하였다. 그 중, 전단 시험의 경우 V-notch 시험 방법을 통하여 수행하였다.
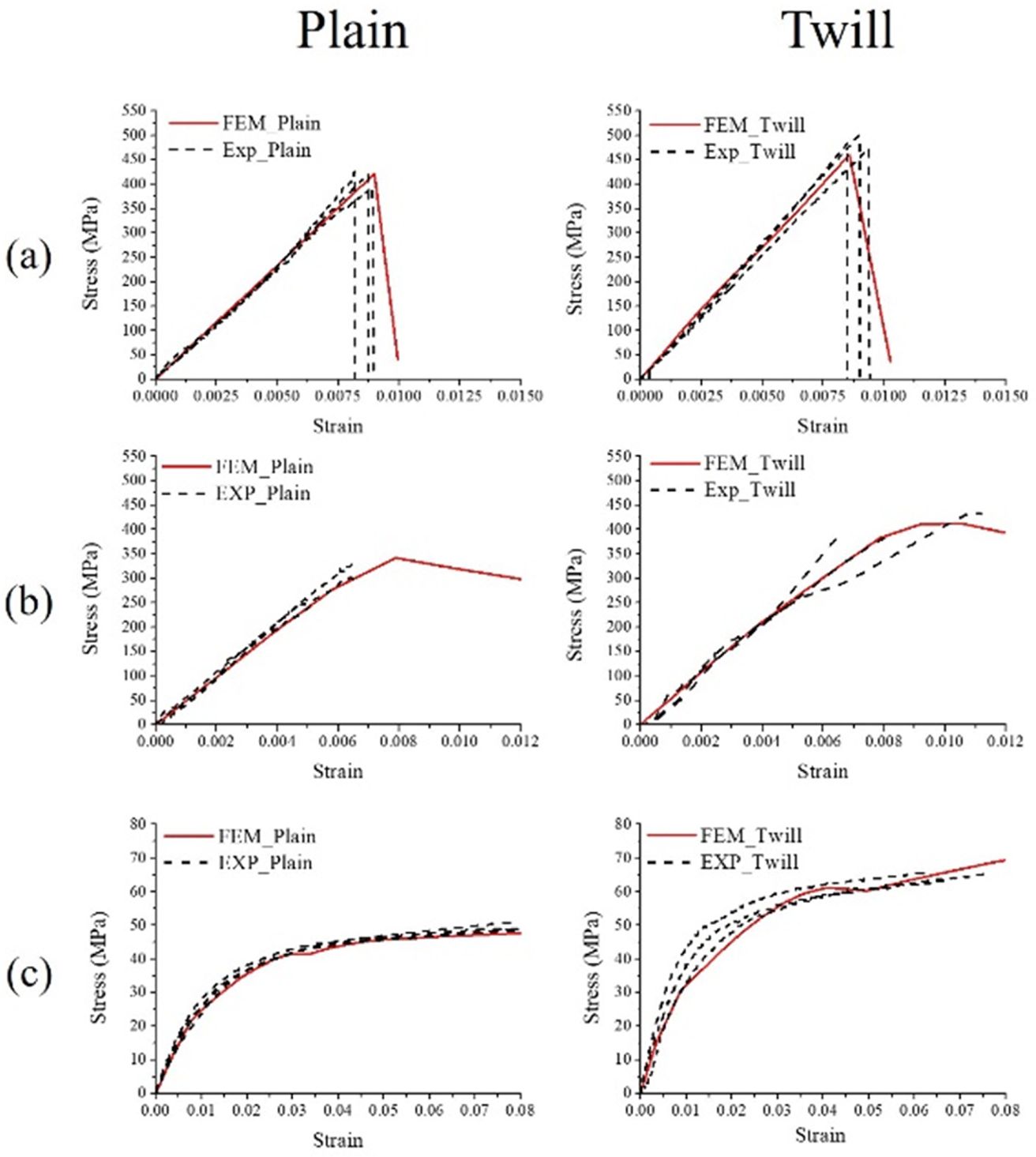
인장, 압축, 전단 시험 결과를 해석 결과와 비교하여 Fig. 6에 각각 나타내었다. 그림에서 볼 수 있듯이, 해석 결과와 시험 결과가 유사하게 나온 것을 확인할 수 있다. 인장과 압축의 경우, 시편에 파괴가 일어나면서 응력이 감소하는 것을 확인할 수 있고, 전단의 경우, 응력이 점차적으로 증가하는 것을 확인할 수 있다.
평직과 능직의 시험 결과를 비교하면, 굴곡 각도가 더 큰 평직의 강성, 강도가 능직보다 더 작게 나타난 것을 확인 할 수 있다. 평직과 능직 모델의 섬유 부피 분율이 유사한 것을 고려하면, 이 두 모델의 차이는 굴곡에 대한 차이임을 알 수 있다. 이는 굴곡이 클수록 재료에 변형이 일어났을 때 재료의 변형률이나 하중을 버티는 강도가 작아지는 것을 나타낸다. 최종적으로, 본 연구에서 직조구조에 따른 굴곡의 영향을 고려하여 성공적으로 복합재의 물성을 예측하였다.

본 연구에서는 직조구조에 따른 복합재의 물성을 예측하였다. 직조 구조의 영향을 모델에 고려하기 위하여 메소 스케일의 대표 체적 요소를 이용하였다. 섬유 다발과 순수 기지를 분리하여 3차원 모델링을 진행하였고, 점진적 파괴 모델을 섬유 다발에 적용하여 복합재료의 파괴를 구현하였다. 평직과 능직 복합재료의 물성이 다르게 나타남으로서 직조 구조의 영향을 고려해야 보다 정확한 물성 예측이 가능함을 확인하였다. 본 연구에서는 직조 구조에 따라 변화하는 섬유의 방향을 적용하여 직조 구조에 대한 영향을 고려 할 수 있었다. 결과적으로, 물성 시험 결과와 해석 결과가 유사한 것을 확인하였다. 본 연구에서 고려한 모델링 방법을 이용하면 보다 정확한 직조 복합재료의 물성 예측이 가능할 것으로 사료된다.

This research was supported by a development project of design techniques of fiber-reinforced thermoset composite materials for automobile parts between Hanyang University and LG Hausys R&D center. This work was supported by the Industrial Strategic technology development program (10076562, Development of fiber reinforced thermoplastic nano-composite via fiber bundle spreading for high quality resin impregnation process and its application to the underbody shield component for protecting battery pack of an electric-vehicle) funded By the Ministry of Trade, industry & Energy(MI, Korea).