- Experimental and Numerical Study on the Structural Stiffness of Composite Rotor Blade
Hyeon-Kyu Jeon*, Min-Hyeok Jeon*, Min-Song Kang*, In-Gul Kim*†, Jae-Sang Park*, Jin-Young Seok*
* Department of Aerospace Engineering, Chungnam National University
*† Department of Aerospace Engineering, Chungnam National University- 복합재 로터 블레이드의 구조 강성도에 대한 실험적/수치적 연구
전현규* · 전민혁* · 강민송* · 김인걸*† · 박재상* · 석진영*
The basic mechanical properties of helicopter rotor blade are important parameters for the analysis of helicopter performance. However, it is difficult to estimate these properties because the most of rotor blades consist of various materials such as composite materials and metals, etc. In this paper, the bending/torsional stiffness for composite rotor blade of unmanned helicopter were evaluated through experimental and analytical studies. In finite element analysis, the bending/torsional stiffness were evaluated through the relationship of load-displacement and element stiffness matrix. The evaluated stiffness from the measured strains and displacements in bending and torsional test agreed well with the derived results of FEA.
헬리콥터의 주 로터 블레이드는 헬리콥터의 양력과 추력을 발생시키는 구조물로, 헬리콥터의 성능을 좌우하는 중요한 구조 구성품이다. 헬리콥터의 기계적 특성값은 헬리콥터 성능해석 단계에 활용되는 중요한 매개변수이나 대부분의 로터 블레이드는 복합재 등과 같은 여러가지 재료의 조합으로 제작되므로 기계적 특성값을 추정하는 것은 쉽지 않다. 본 논문에서는 유한요소해석과 실험적 방법을 통하여 무인 헬기 복합재 로터 블레이드의 단면별 휘임 및 비틀림 강성도를 취득하였다. 유한요소해석을 통해 요소 강성 행렬과 하중-변위 관계식을 이용하여 단면별 강성도를 계산하였으며, 스트레인 게이지를 이용한 휘임 및 비틀림 시험에서 구한 변형률 값을 이용하여 단면별 강성도를 계산하였다. 유한요소해석으로 계산한 단면별 강성도와 시험 결과를 이용하여 계산한 단면별 강성도가 잘 일치함을 확인하였다.
Keywords: 복합재 로터 블레이드(Composite Rotor Blade), 단면 강성도(Cross Sectional Stiffness), 휘임 시험(Bending Test), 비틀림 시험(Torsional Test), 강성 행렬(Stiffness Matrix)
헬리콥터의 로터 블레이드(Rotor Blade)는 헬리콥터의 양력, 추력 및 조종력을 발생시키는 역할을 하는 헬리콥터의 핵심 구조물로써 헬리콥터의 성능에 중요한 영향을 준다. 그러나 복잡한 공기역학적 환경에서 운용되어 공기역학적-구조적 연계에 의한 안정성, 피로, 진동 등과 같은 문제를 일으킬 수 있으므로 헬리콥터의 개발 시, 로터 블레이드의 구조적, 공기역학적 특성을 고려한 설계가 이루어져야 한다[1].
특히, 로터 블레이드를 탄성체로 가정하여 헬리콥터의 성능을 해석할 경우, 로터 블레이드의 구조적 연성, 전단 응력과 워핑 등에 의한 영향을 고려해야 한다[2]. 그러므로 해석의 입력 값으로 질량 분포와 같은 기본 물리량뿐만 아니라, 휘임 및 비틀림 강성도 등의 기계적인 특성값이 필요하고 이러한 기계적 특성값의 정확도에 따라서 해석 결과의 신뢰성이 좌우되므로, 보다 정확한 기계적 특성값을 확보하는 것이 중요하다. 그러나 현대의 일반적인 로터 블레이드는 복합재와 금속 등의 다양한 재료로 제작되고, 특히 복합재의 보강 섬유 및 기지 재료의 종류, 적층 각도에 따라 휘임 및 비틀림 강성도가 달라지므로 이를 예측하는 것은 쉽지 않다. 또한 로터 블레이드 시위(chord) 방향으로의 휘임 강성도의 경우, 하중에 대한 변위가 매우 작아 오차를 유발할 수 있기 때문에[3] 시험, 해석을 통한 추정이 필요하다.
Enei[4]는 영상촬영으로 취득한 변위 정보를 통해 단면 특성을 계산할 수 있는 시험 방법을 소개하고 이를 활용하여 복합재 로터 블레이드의 기계적 특성값을 취득하였다. Hoffmann[5]은 로터 블레이드의 비회전 동특성 해석을 위해 영상촬영을 통해 취득한 변위와 비틀림각으로 로터 블레이드의 전단 중심과 단면별 강성도를 계산하였다. You[6]는 터빈 블레이드의 최적구조설계를 위하여 유한요소해석을 이용해 상자형 복합재 외팔보의 단면별 강성도를 계산하였다.
본 논문에서는 복합재로 제작된 무인 헬기 로터 블레이드의 단면별 전단 중심과 강성도를 취득하기 위하여 두께(Flap) 방향 휘임 시험 및 비틀림 시험을 수행하였다. 로터 블레이드를 유한요소 모델링하여 해석을 수행하였으며 계산된 변위와 하중 관계인 강성 행렬을 이용하여 로터 블레이드 보에 대한 등가 강성도를 계산하였다.
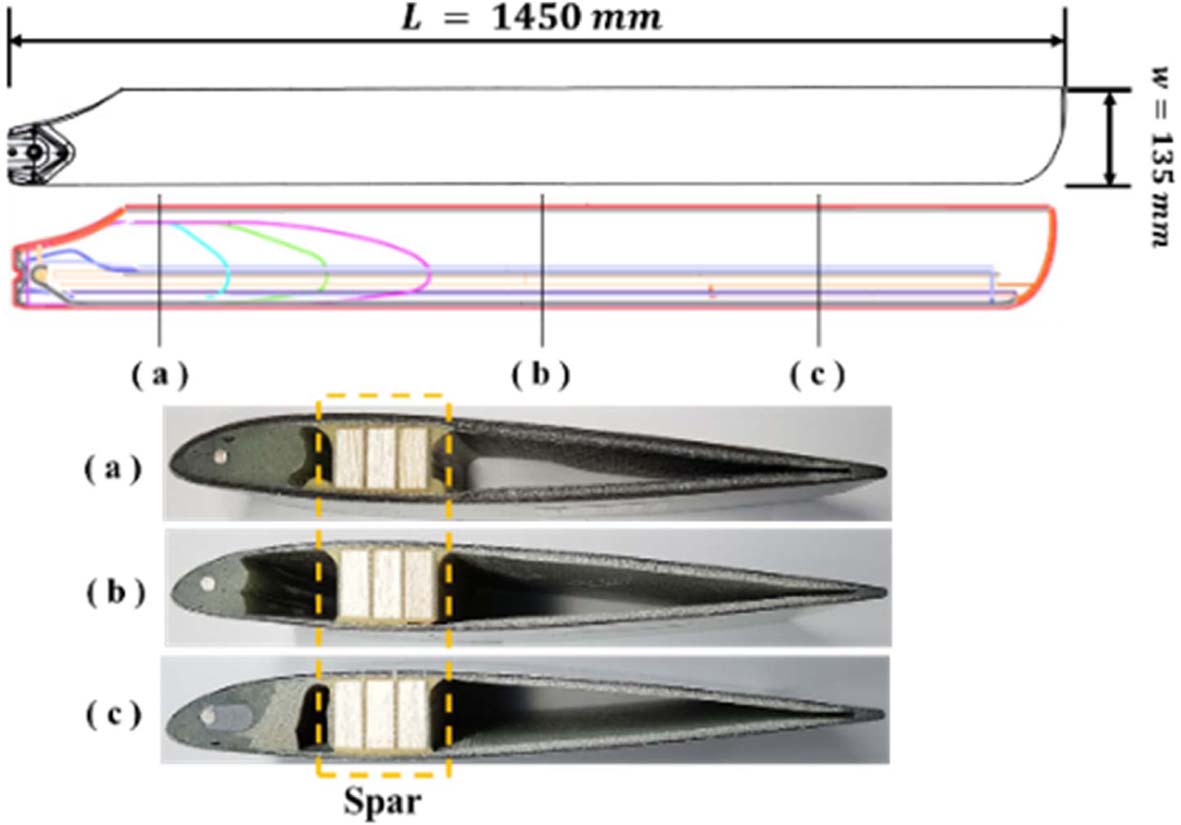
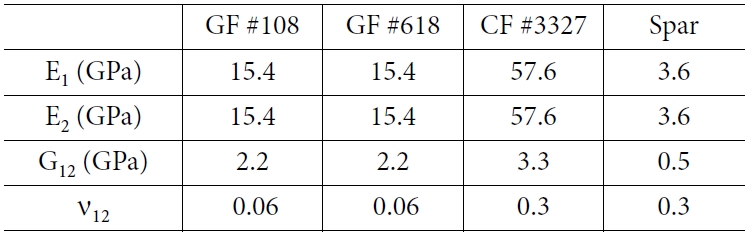
본 논문의 연구 대상은 소형 무인 헬기의 로터 블레이드이다. 로터 블레이드의 단면 형상은 Fig. 1과 같다. 로터 블레이드의 스킨(Skin)은 평직 유리 섬유 복합재(GF #108, GF #618)와 평직 탄소 섬유 복합재(CF #3327)를 로터 블레이드의 부분 별로 두께와 적층 방향을 달리 적용하여 제작되었으며, 스파(Spar)는 발사 목재와 유리섬유 직물로 제작되었다. 익근(Root)부터 끝단(Tip)까지 초기 비틀림 각이 있는 것으로 설계되어 있다. 로터 블레이드에 적용된 재료의 물성은 Table 1과 같다.
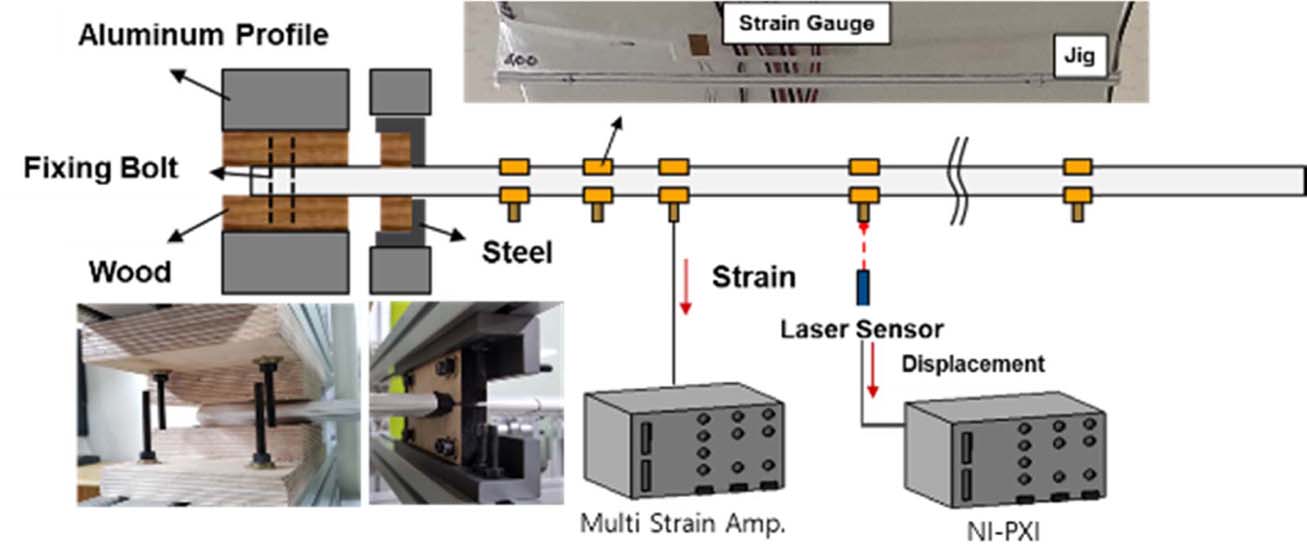
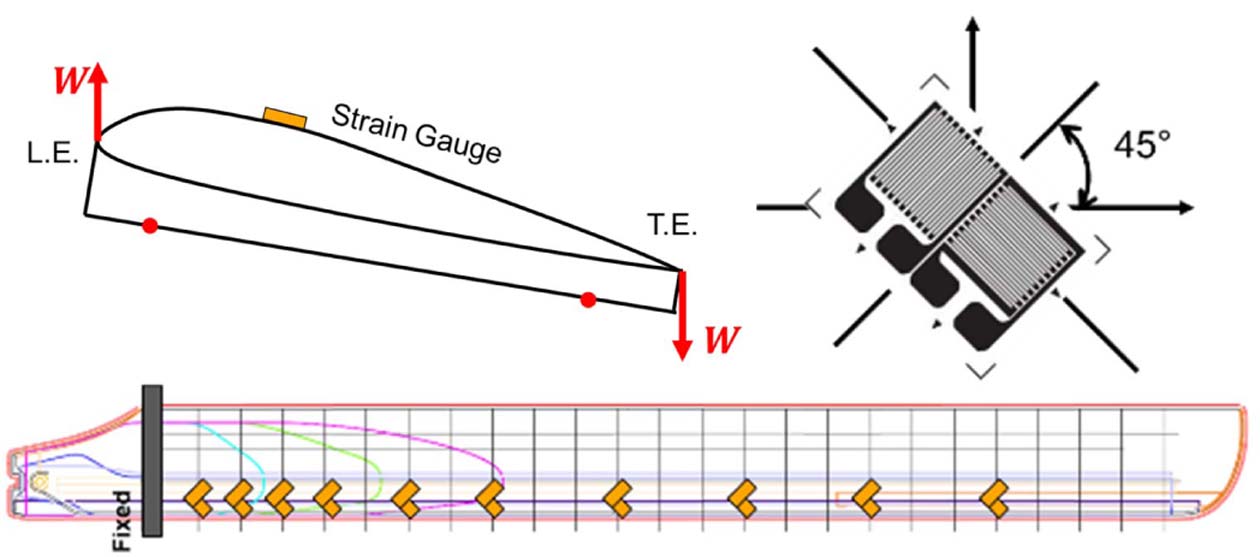
로터 블레이드의 단면별 강성도를 취득하기 위한 휘임 및 비틀림 시험을 수행하였다. 휘임 및 비틀림 시험을 위한 장치도는 Fig. 2와 같다. 고정(Fixed)조건을 구현하기 위하여 체결부와 로터 블레이드의 익근 부분을 합판과 체결 볼트를 이용하여 고정하였다. 로터 블레이드의 지점 별로 스트레인 게이지를 부착하고 다중 스트레인 앰프(MGC. PLUS)를 이용하여 변형률 데이터를 취득하였다. 하중에 의해 발생한 변위를 레이저 센서(Sensor Partners; L-LAS-LT-30-SL-P)로 측정하기 위하여 로터 블레이드의 밑면에 아크릴 지그(Jig)를 부착하였고, 측정된 변위 데이터는 NI-PXI 장비를 통해 취득하였다.
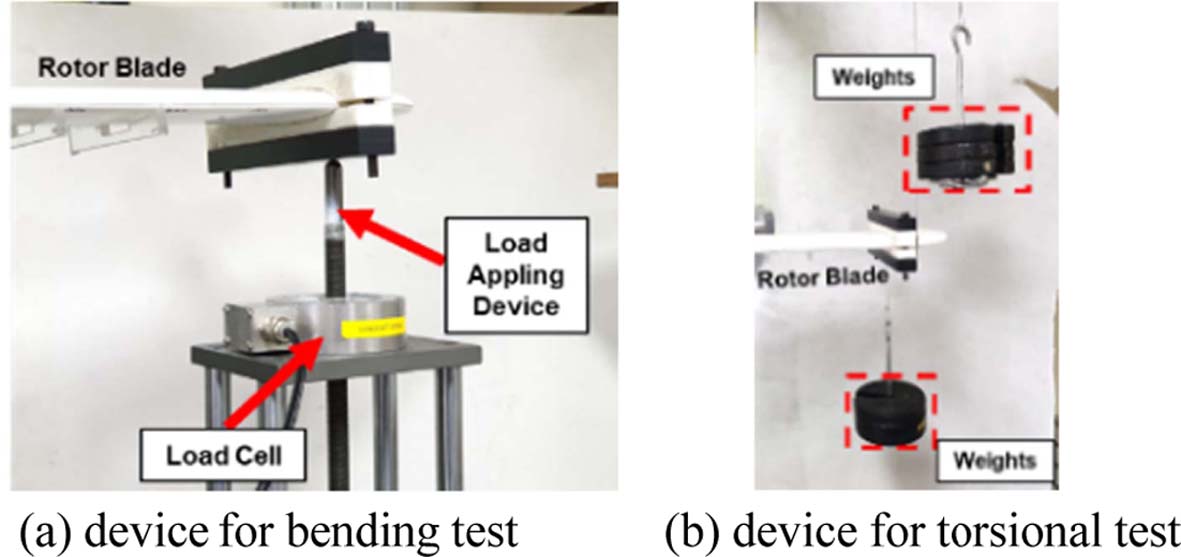
로터 블레이드의 휘임 및 비틀림 시험을 위한 하중 부가 장치는 Fig. 3과 같다. 휘임 시험을 위한 하중 부가 장치는 로터 블레이드의 두께 방향의 휘임 변위를 만들어 낼 수 있는 봉을 로드셀에 부착하여 봉에 작용하는 로터 블레이드의 변형에 의한 반력을 측정할 수 있도록 제작하였다. 비틀림 시험은 로터 블레이드 끝단의 앞전(Leading edge)과 뒷전(Trailing edge)에 무게 추와 도르레를 이용하여 비틀림 하중을 부가하였다.
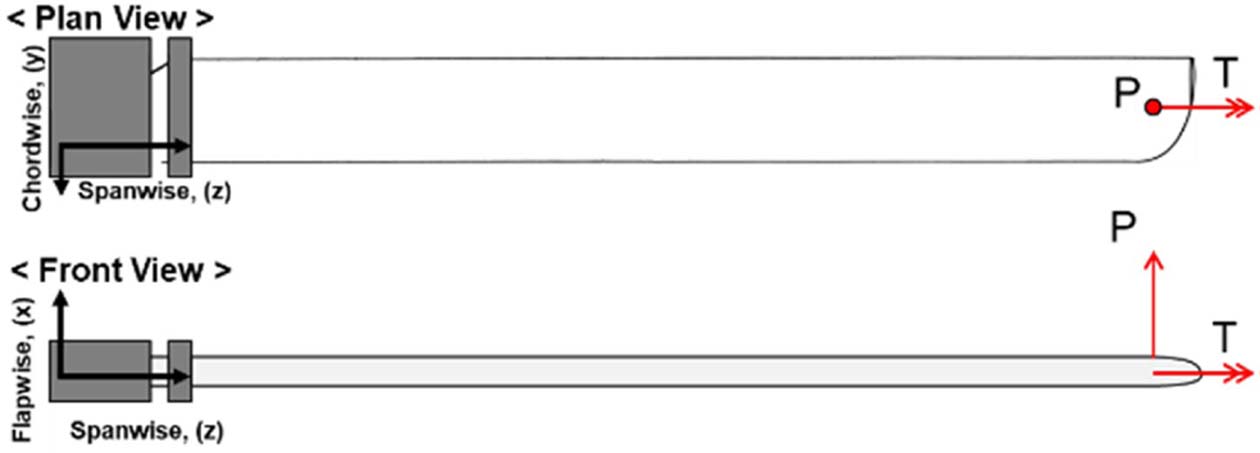
로터 블레이드의 단면별 휘임 및 비틀림 강성도를 취득하기 위한 시험 모식도는 Fig. 4와 같다. 휘임 및 비틀림 시험 수행 전, 하중에 의한 휘임-비틀림 등의 변형의 연계를 최소화하기 위하여 로터 블레이드의 단면별 전단 중심을 추정하였다. 휘임 시험은 추정된 시위 방향 전단 중심의 평균 위치에 집중 하중의 형태로 수직하중(P)을 부가하였으며, 끝단 하중과 변형률, 변위의 관계를 이용하여 휘임 강성도(EI)를 계산하였다. 비틀림 시험은 로터 블레이드의 끝단에 비틀림 하중(T)을 부가하고 비틀림 하중과 전단 변형률의 관계를 이용하여 비틀림 강성도(GJ)를 계산하였다.
|
Fig. 1 Rotor blade specimen |
|
Fig. 2 Schematic representation of test apparatus |
|
Fig. 3 Load applying devices |
|
Fig. 4 Schematic representation for bending/torsional test |
시험 및 해석에서 휘임 변형과 비틀림 변형의 연계를 최소화하기 위하여 각 단면별 전단 중심을 추정하는 것이 선행되어야 한다.
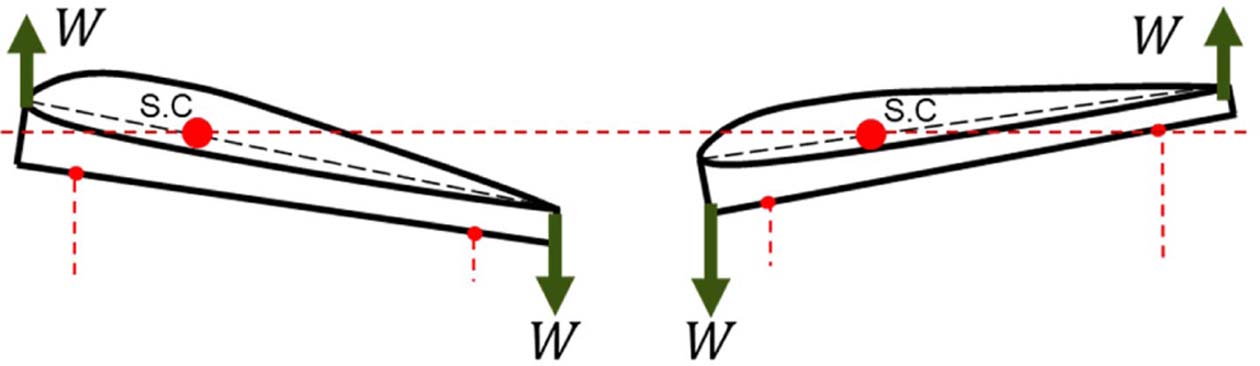
전단 중심(Shear Center)은 단면 내에서 휘임 변형과비틀림 변형이 독립적으로 발생하는 지점이므로, 비틀림 하중에 대한 단면의 변형은 전단 중심을 기준으로 발생한다. 본 논문에서는 Fig. 5와 같이 서로 다른 비틀림 하중에 대해 변형이 발생했을 때 단면 내에서 생기는 교차 지점을 전단 중심으로 추정하였다.
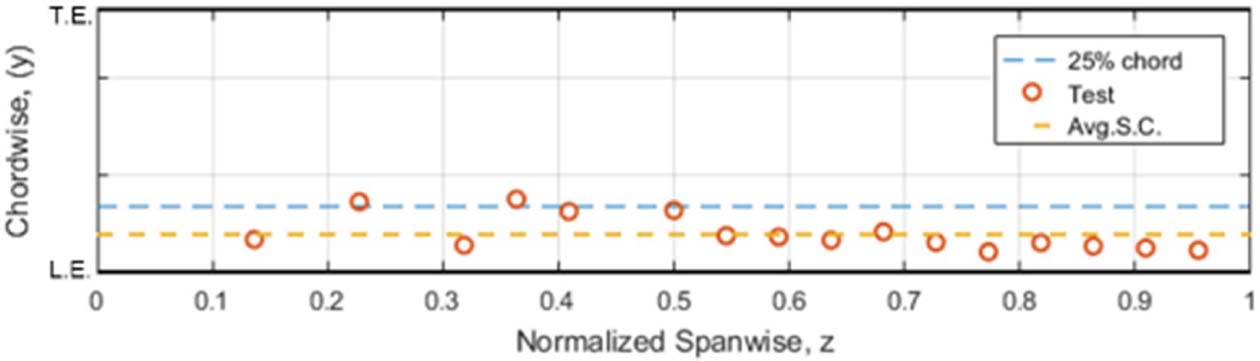
전단 중심의 추정을 위해 로터 블레이드 끝단에 두 가지 종류(pitch-up/down)의 비틀림 하중을 가하였고, 레이저 센서로 측정한 수직 변위값을 이용해 로터 블레이드의 비틀림을 측정하였다. 단면별 전단 중심 추정의 결과는 Fig. 6과 같다.
|
Fig. 5 Schematic representation of twisted cross section under different load case |
|
Fig. 6 Estimated and average position of shear center |
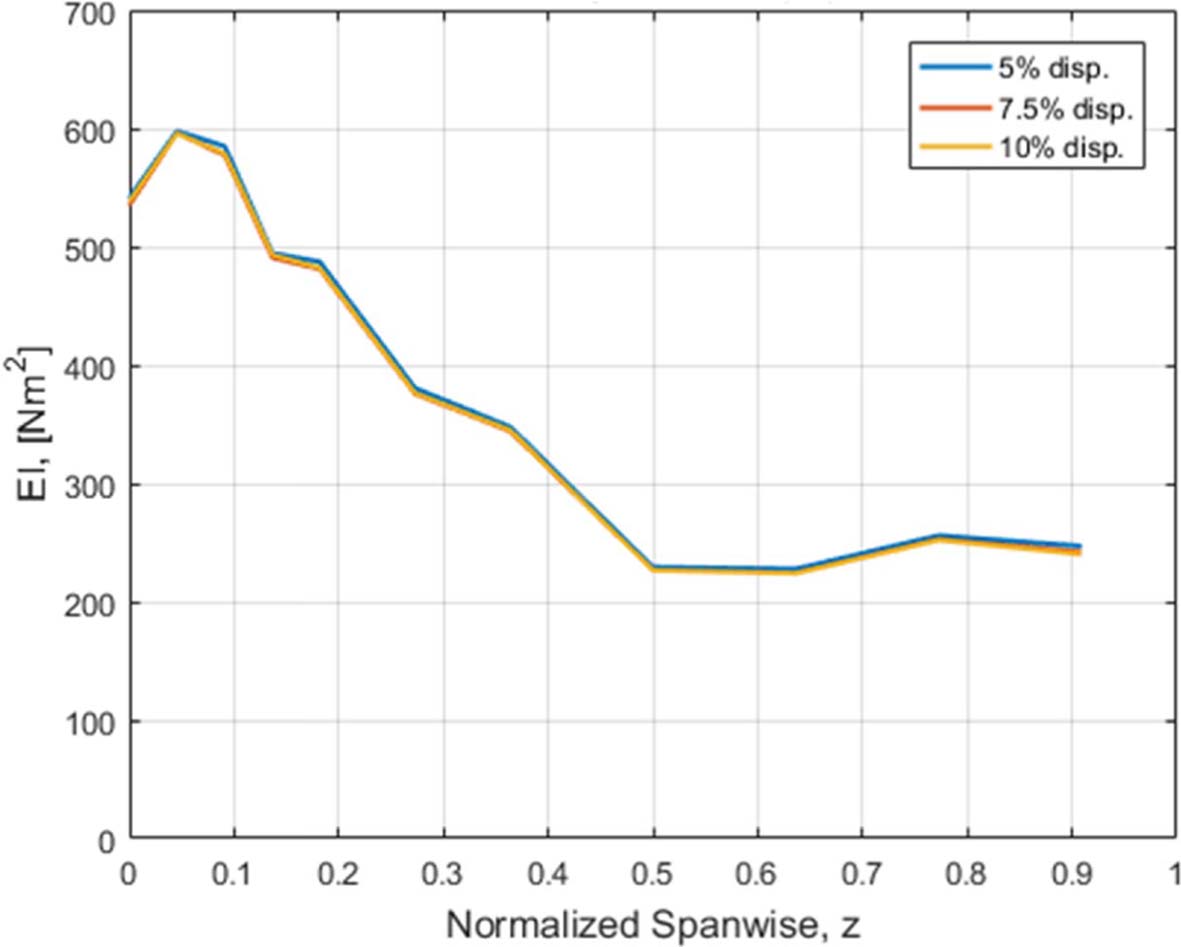
로터 블레이드의 휘임 강성도(EI)를 휘임 시험을 통해 취득하였다. 휘임 강성도 측정을 위해 스트레인 게이지를 Fig. 7과 같이 11개 지점의 로터 블레이드 윗면과 아랫면에 부착하였으며, 휘임 하중에 대한 지점별 앞전과 뒷전의 변위를 레이저 센서를 이용하여 측정하였다. 휘임 하중은 앞서 추정한 로터 블레이드의 시위 방향으로의 평균적인 전단 중심 위치에 집중하중을 부가하여 시험 조건에 따라 Fig. 8과 같이 로터 블레이드 전체 길이의 5%, 7.5%, 10%의 변위가 발생하도록 하였다.

|
Fig. 7 Strain gauges installation and displacement measurement points for bending test |

|
Fig. 8 Deflection of rotor blade under bending loads |
비틀림 강성도(GJ)를 취득하기 위한 비틀림 시험은 Fig. 9와 같이 로터 블레이드 끝단의 앞전과 뒷전에 짝힘 형태의 pitch-up 비틀림 하중을 부가하였으며[3], 지점별로 ±45°로 부착된 2축 스트레인 게이지를 이용하여 비틀림 하중에 대한 전단 변형률을 측정하였다.
|
Fig. 9 Strain gauges installation for torsional test |
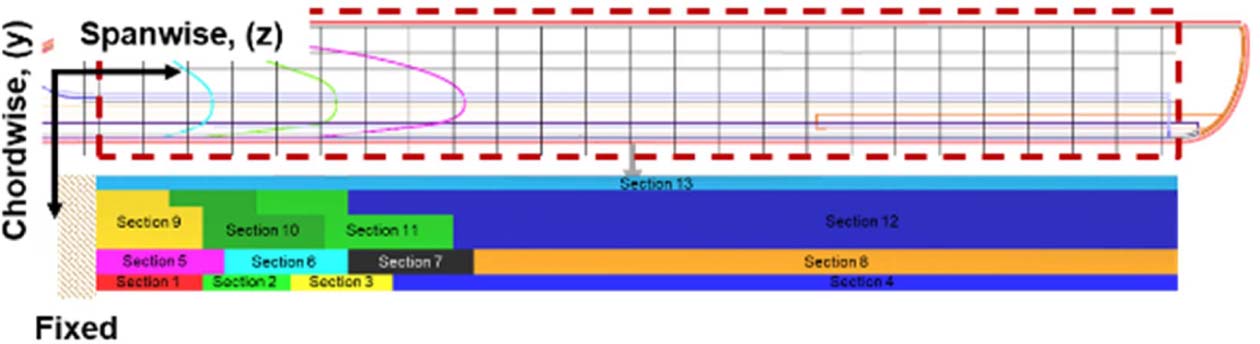
로터 블레이드의 단면별 전단 중심 및 강성도 계산을 위해 상용 유한요소해석 프로그램인 MSC. NASTRAN/ PATRAN을 이용하여 수행하였다. 휘임 및 비틀림 시험이 재료 및 기하학적 비선형이 발생하지 않은 탄성 영역 내에서 수행 되었으므로 시험 결과와의 비교를 위해 선형 정적 해석(SOL 101)을 수행하였다. 유한요소모델은 제작된 로터 블레이드의 단면 검사를 통하여 확인된 단면 형상을 참고하여 스킨은 2-D Shell (CQUAD4) 요소를, 스파 및 접착제 등은 3-D Solid (CHEX8)요소를 이용하여 모델링하였다. 유한요소모델의 스킨에 적용된 물성은 Fig. 10과 같이 로터 블레이드에 적용된 복합재 적층을 고려하여 나뉘어진 몇 개의 구역에 CFRP 및 GFRP의 물성을 입력하였으며, 스파는 유리섬유 직물 복합재와 발사 목재로 적층된 등가의 3-D Orthotropic 물성을, 접착제는 일반적인 Epoxy의 물성을 입력하였다. 경계조건은 익근 부분을 고정 조건으로 구속하였다.
|
Fig. 10 Finite element model for rotor blade |
로터 블레이드 단면 내 전단 중심은 Fig. 11과 같이 기하학적 방법으로 추정할 수 있다[7]. 단면 내 임의의 지점(p)의 좌표는 전단 중심에 대한 상대 거리를 이용한 좌표()로 나타낼 수 있고, 임의의 하중에 의해 변형된 좌표()는 전단 중심의 변위() 및 임의 지점(p)의 변위() 그리고 비틀림각(Φ)으로 식 (1)과 같이 나타낼 수 있다.

단면 내 전단 중심의 위치는 각각의 하중 조건에 의해 유도된 식 (1)의 지점(p)의 변위와 비틀림 각의 연립방정식을 통해 계산할 수 있다.
유한요소해석의 결과로 추정한 로터 블레이드의 전단 중심의 결과는 Fig. 12와 같다. 시위 방향의 전단 중심 위치는 25% 보다 앞인 20% 에 위치하며 두께 방향의 전단 중심 위치는 로터 블레이드의 중심선(mid-line)으로부터 위쪽으로 두께의 11% 떨어진 지점에 위치하는 것으로 계산되었다.
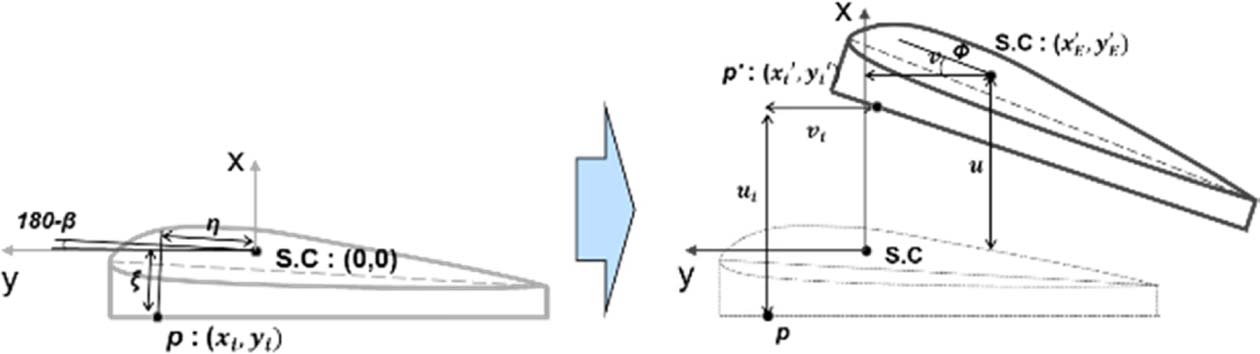
|
Fig. 11 Schematic representation for estimating shear center |
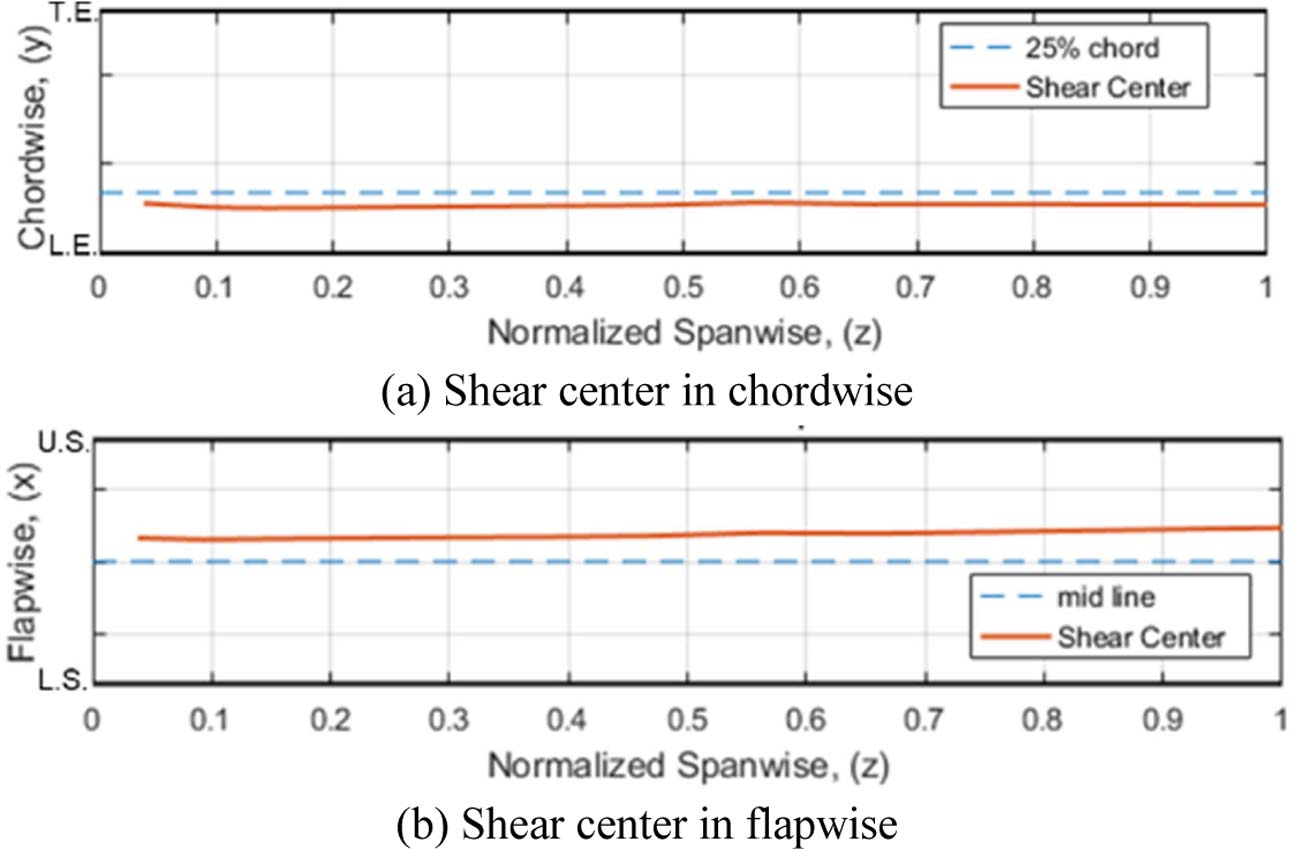
|
Fig. 12 The position of shear center in (a) chordwise, (b) flapwise |
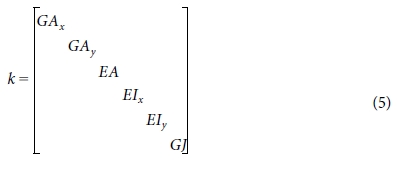
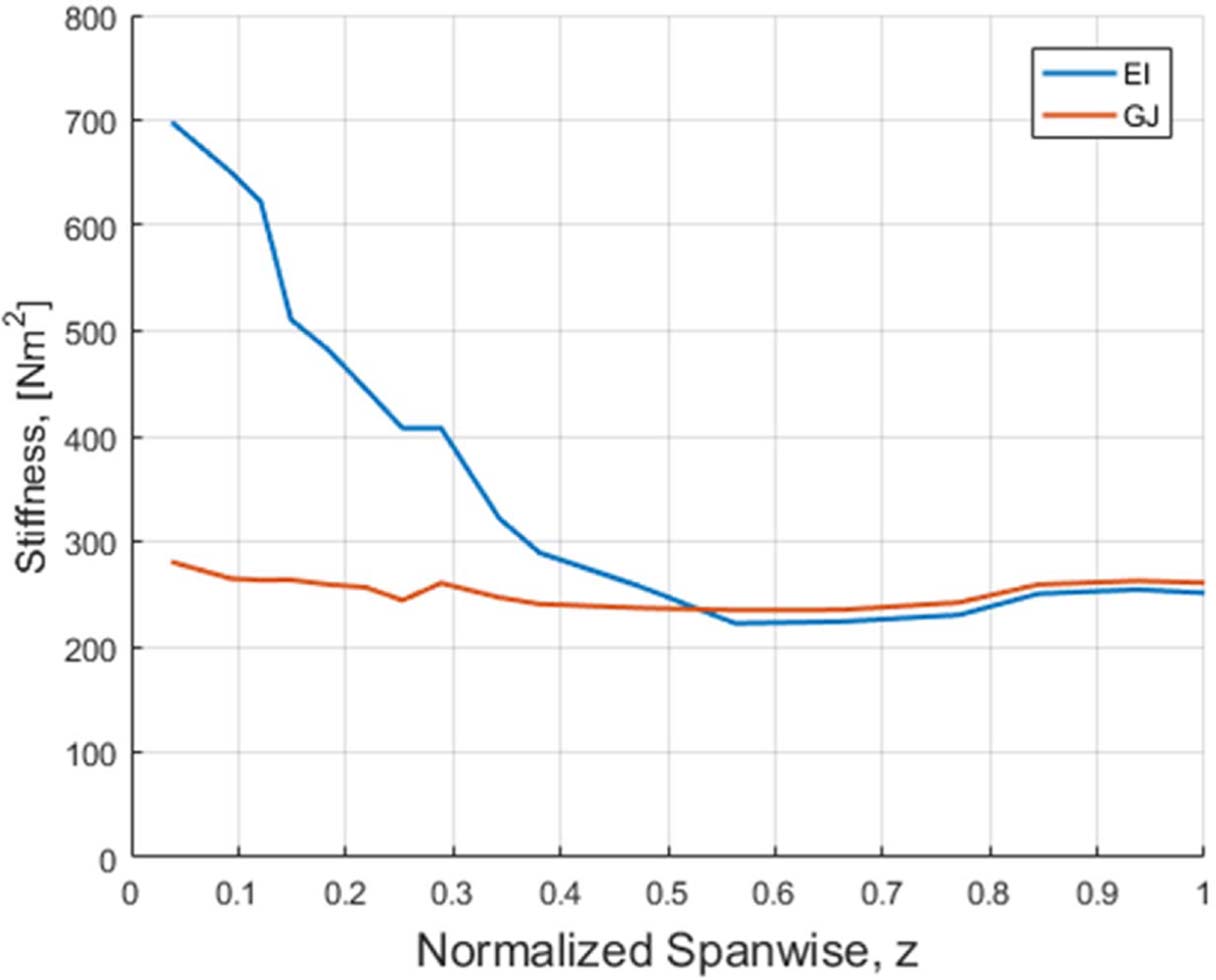
유한요소해석의 결과값은 각 절점의 변위 정보를 제공해주므로 이를 이용하여 단면의 강성도를 계산할 수 있다. Fig. 13과 같이 보의 끝단에 작용하는 6개의 하중 조건()에 대한 하중-변위 관계식 (2)와 내력-요소의 상대변위 관계식 (3)의 조합을 통해 식 (4)를 도출할 수 있다. 식 (4)는 Lyapunov 방정식의 형태이며, 단면 강성 행렬 k에 관한 해를 계산하면 식 (5)와 같이 각 단면에서의 강성도를 계산할 수 있다[6]. 단면 강성 행렬을 이용해 계산한 로터 블레이드의 휘임 및 비틀림 강성도는 Fig. 14와 같다.



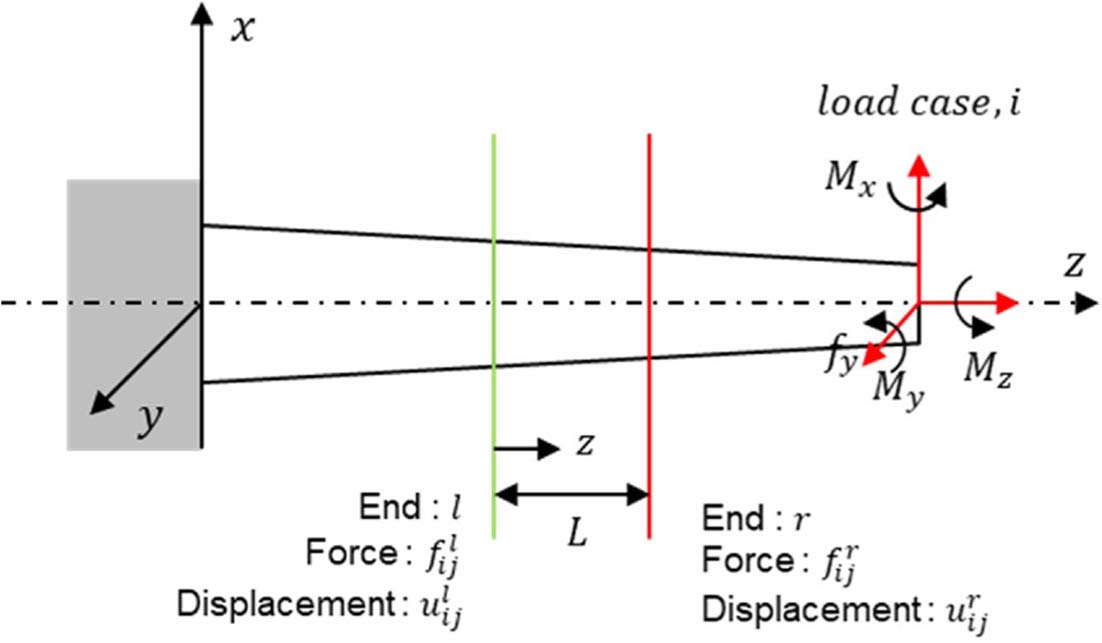
|
Fig. 13 Equivalent beam model of rotor blade |
|
Fig. 14 Evaluated bending stiffness (EI) and torsional stiffness (GJ) |
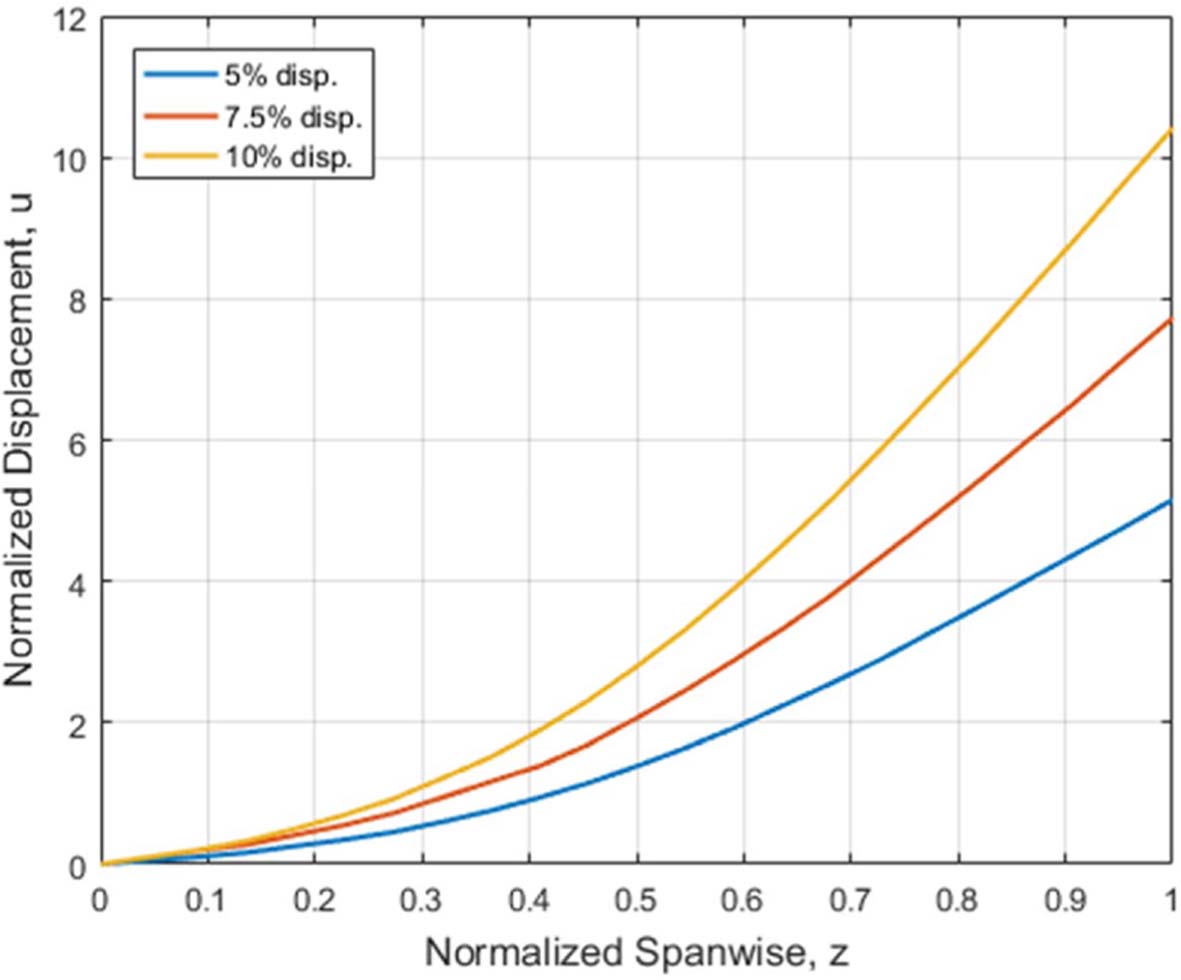
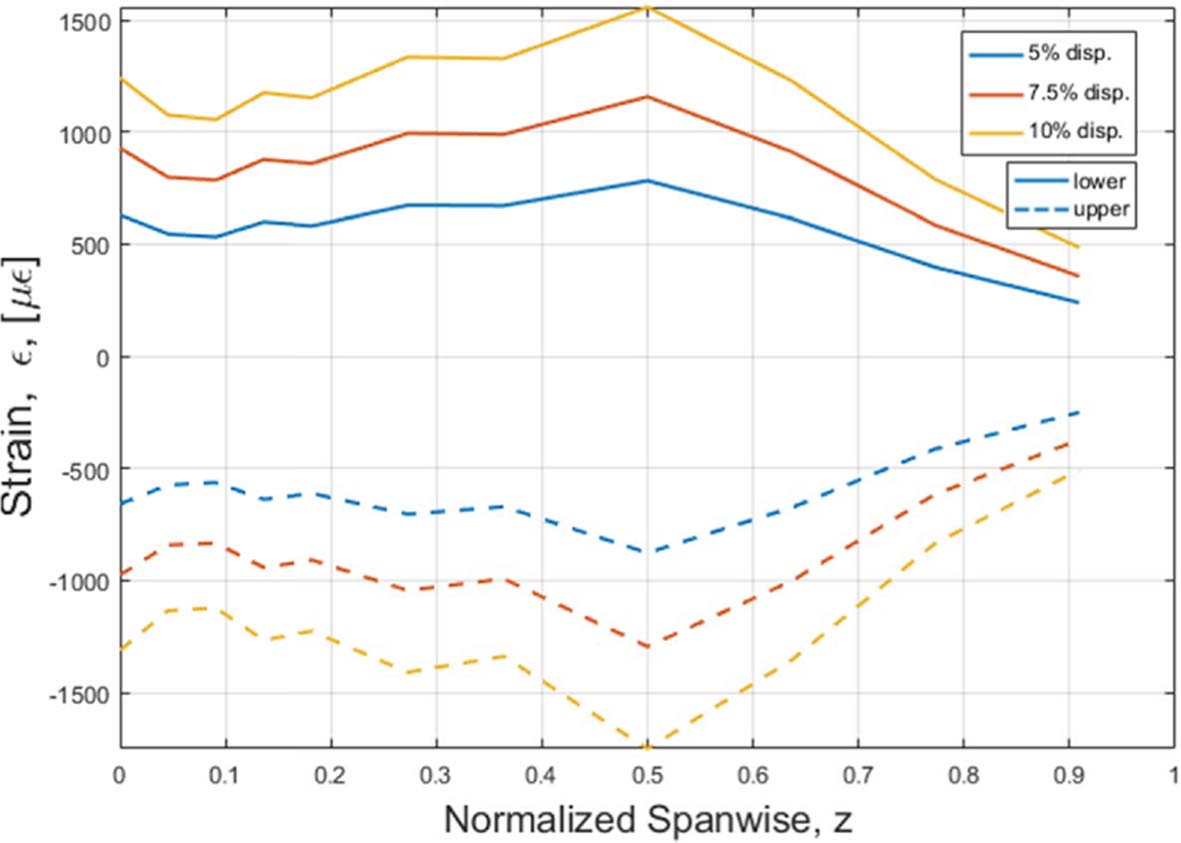
로터 블레이드 변위에 대한 하중은 로터 블레이드 길이 대비 5%, 7.5%, 10% 끝단 변위 조건에 대해 차례대로 33.52 N, 50.33 N, 66.22 N을 가하였으며, 지점별로 측정된 변위는 Fig. 15, 변형률은 Fig. 16과 같다.
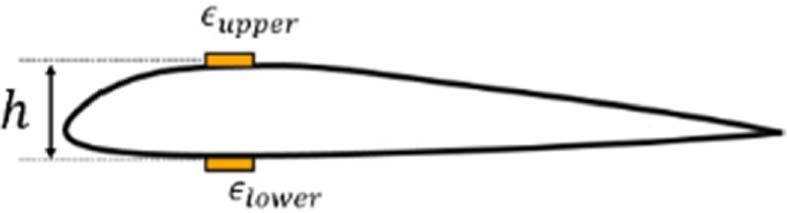
휘임 강성도(EI)는 오일러 보 이론을 통해 부가된 모멘트(M)와 Fig. 17의 스트레인 게이지 사이의 거리(h) 및 측정된 변형률(ε)로부터 식 (6)과 같이 계산된다.

식 (6)을 통해 계산된 휘임 강성도(EI)의 결과는 Fig. 18과 같이 모든 하중 조건에 대해서 동일하게 계산되었다.
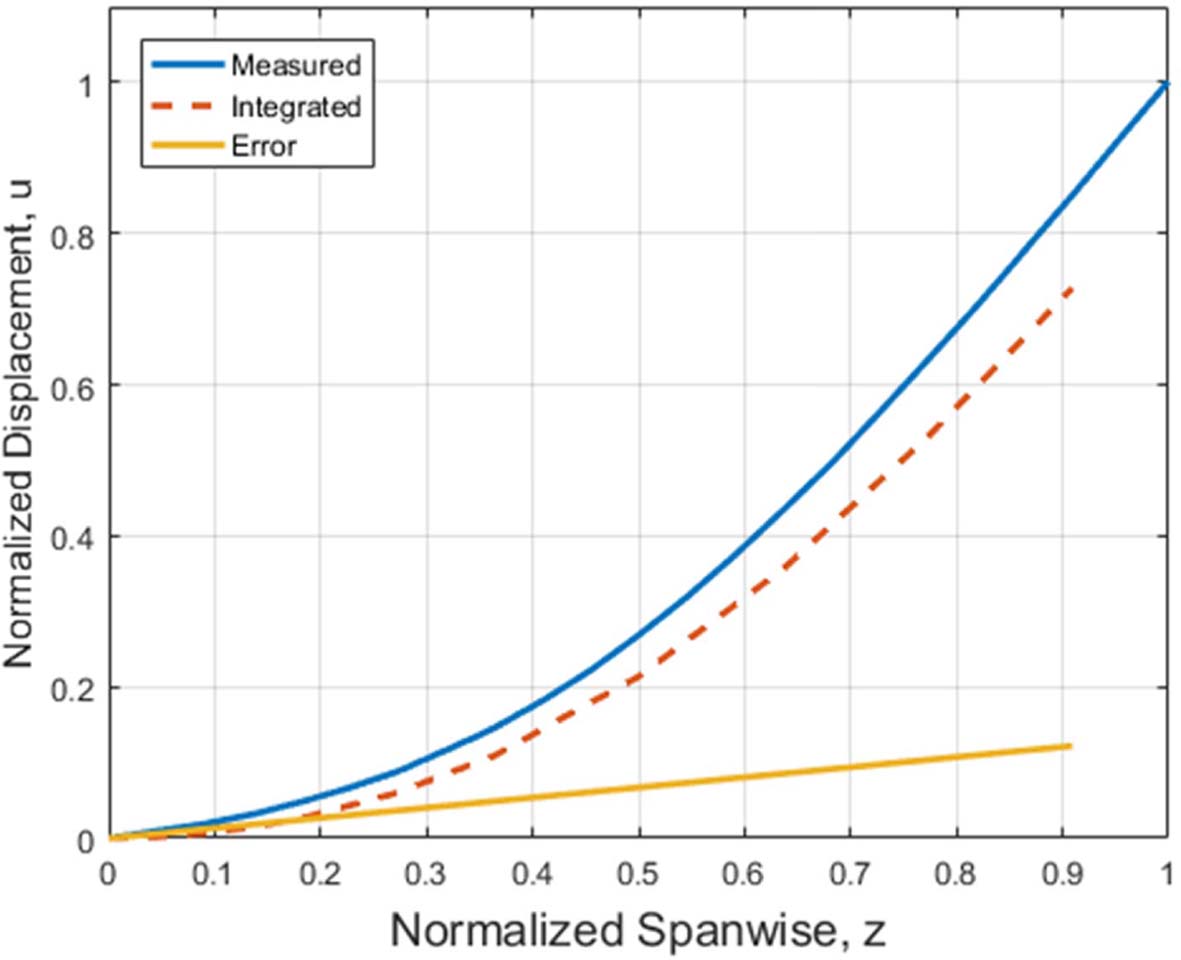
계산 된 휘임 강성도의 타당성을 알아보기 위해 이중 적분을 통하여 휘임 하중에 대한 변위를 계산하였다[8]. 사다리꼴 적분법을 이용해 두 번 적분 된 식 (7)의 결과는 Fig. 19와 같으며, 이를 측정된 변위와 비교하였다.

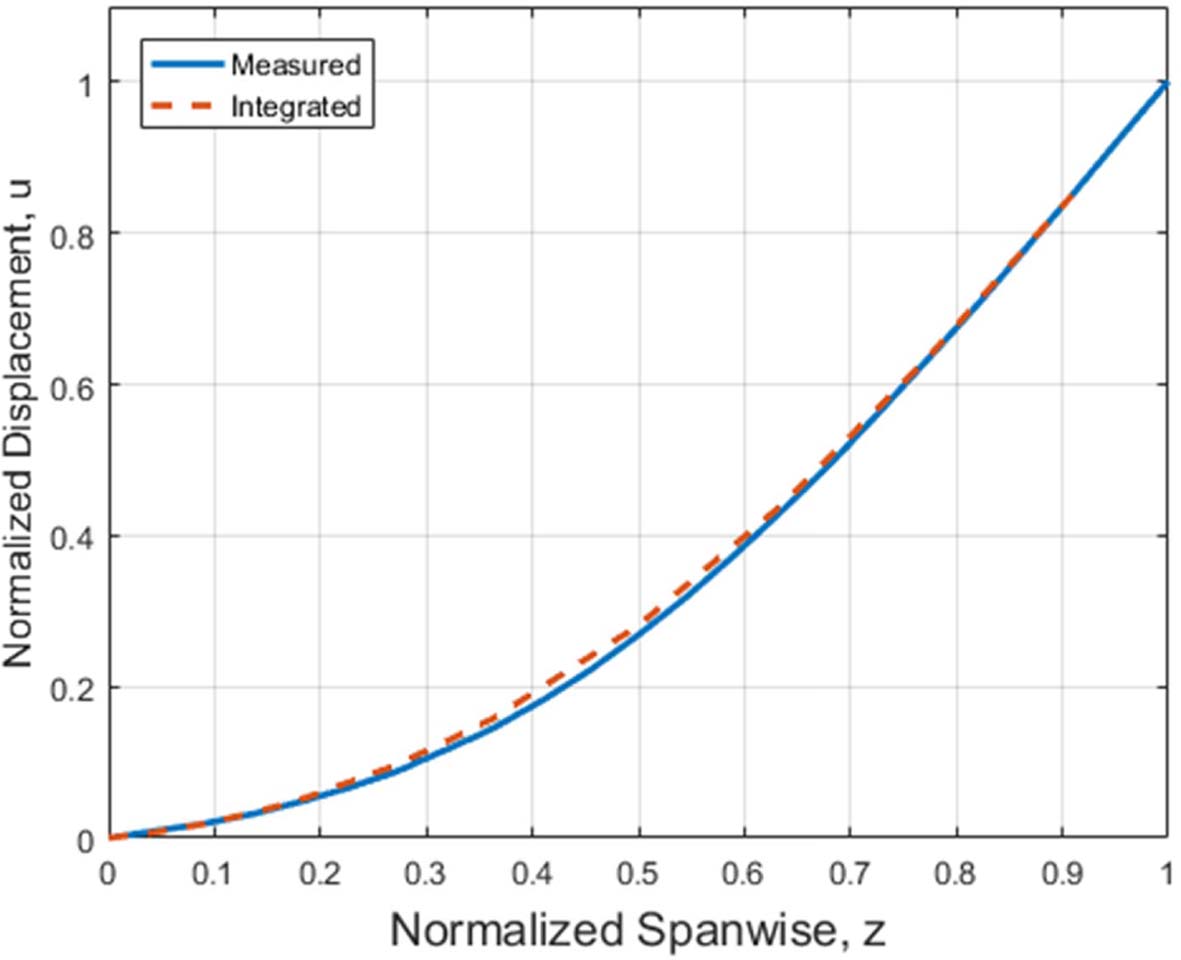
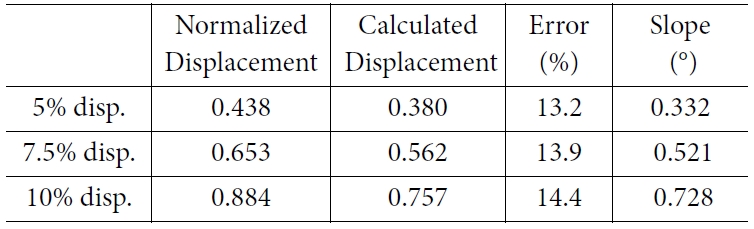
계산된 변위는 모든 하중 조건에서 측정된 변위와 지점별로 Table 2와 같이 일정한 비율을 가지며 선형적으로 증가하는 오차가 있는 것으로 나타났다. 이러한 오차는 시험 치구에 의해 로터 블레이드가 완전 고정 구속 조건을 만족하지 못하고 일부 회전에 의해 발생한 것으로 판단된다. 치구의 일부 회전에 의해 발생한 초기 기울기는 적분 상수가 되므로 이를 기울기에 의한 변위를 더함으로써 보정할 수 있다. 보정된 변위는 가장 큰 하중조건에서 Fig. 20과 같으며, 이는 측정된 변위와 매우 잘 일치하는 것으로 나타났다.
|
Fig. 15 Measured displacements under bending loads |
|
Fig. 16 Measured strains under bending loads |
|
Fig. 17 Thickness of rotor blade and measured strains |
|
Fig. 18 Test results of bending stiffness (EI) |
|
Fig. 19 Comparison of deflection from test with calculated displacement from double-integration and its error (10% disp. Case) |
|
Fig. 20 Comparison of deflection from test with corrected displacement (10% disp. Case) |
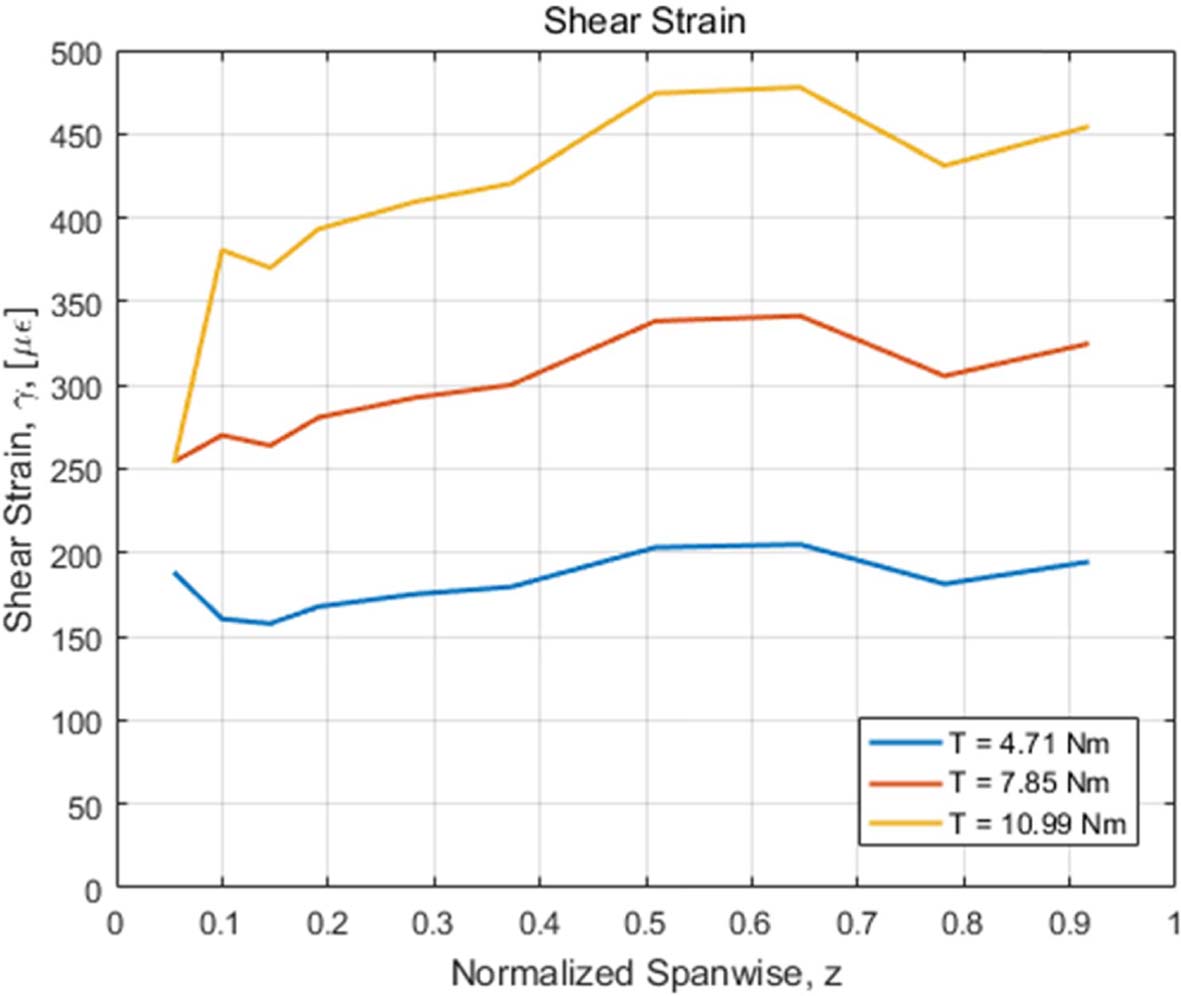
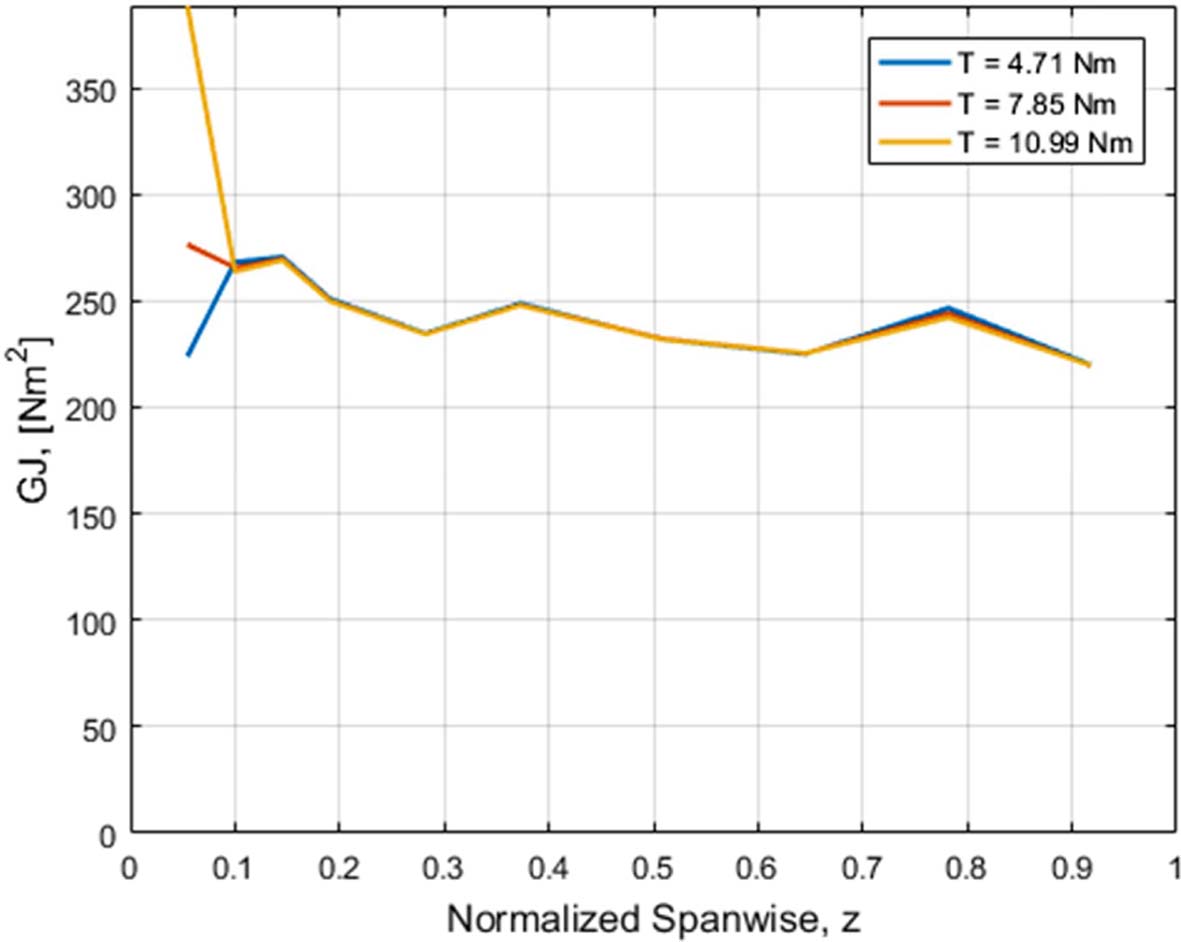
비틀림 하중에 의해 측정된 지점별 전단 변형률은 Fig. 21과 같다. 비틀림 강성도(GJ)는 부가된 하중인 토크(T), 전단 변형률(g), Fig. 22의 단면의 전단 중심에서부터 변형률 측정 지점까지의 수직 접선 거리(r)에 의해 식 (8)과 같이 구할 수 있다. 계산된 비틀림 강성도의 결과는 Fig. 23과 같이 모든 하중 조건에서 익근 부근을 제외하고 전체적으로 일치하는 것을 확인하였다.

|
Fig. 21 Measured shear strains under torsional loads |

|
Fig. 22 Test results of torsional stiffness (GJ) |
|
Fig. 23 Tangential distance to shear center in cross section |
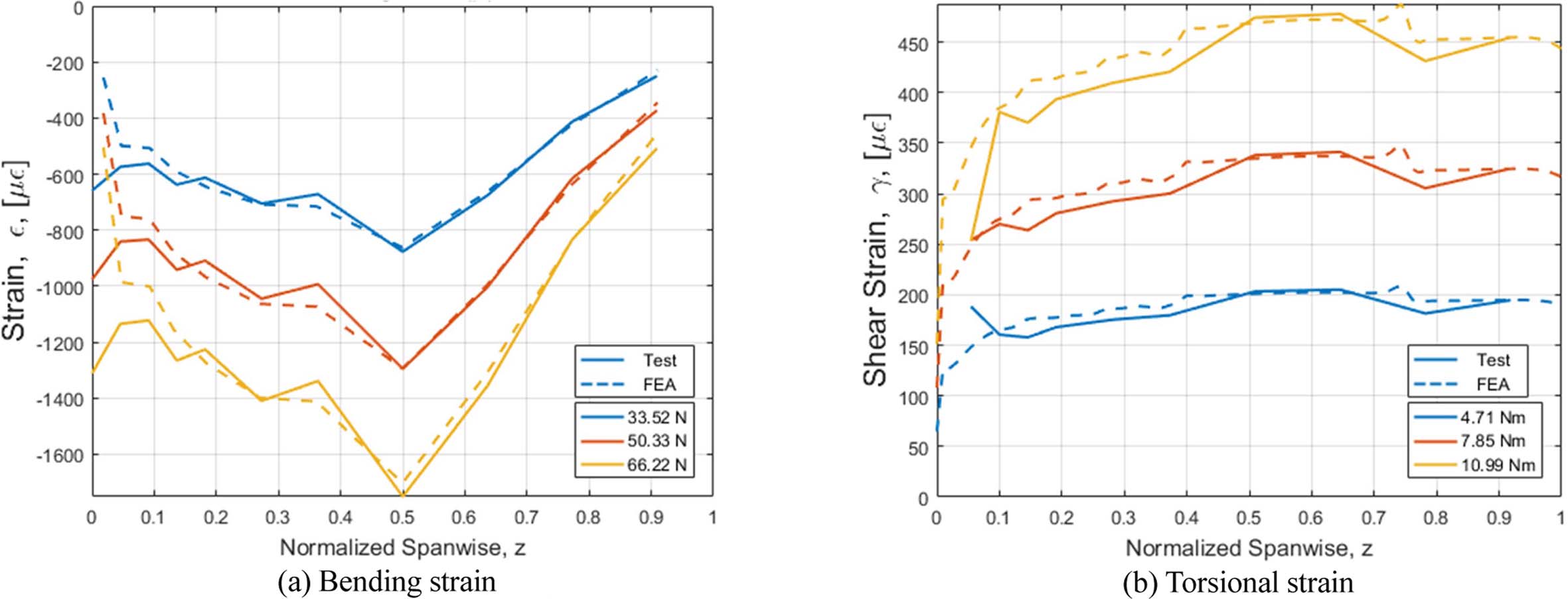
유한요소해석의 변형률 결과는 Fig. 24와 같이 치구의 완전 고정 경계 조건 구현의 어려움으로 익근 부근을 제외한 영역에서는 시험 결과값과 매우 유사한 것을 확인하였다.
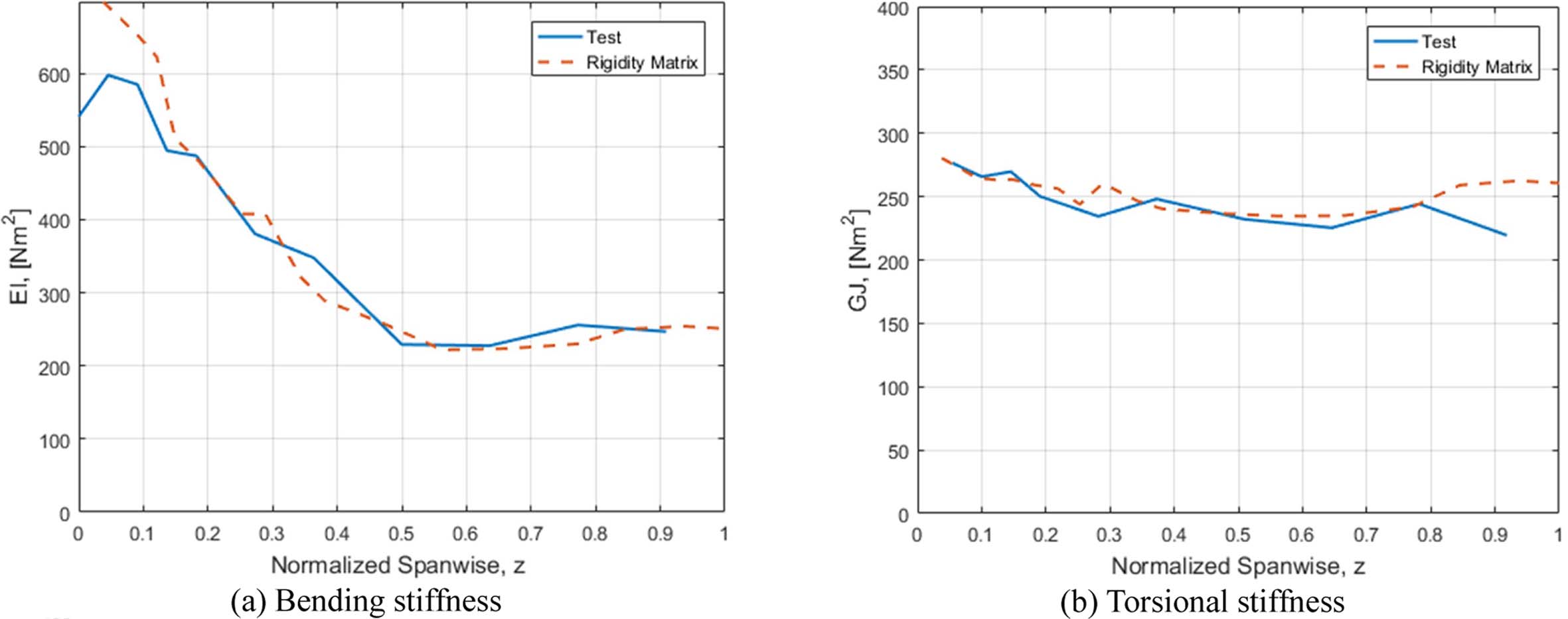
단면 강성 행렬을 통해 계산한 휘임 및 비틀림 강성도와 시험을 통해 취득한 휘임 및 비틀림 강성도의 비교는 Fig. 25와 같다. 휘임 및 비틀림 강성도 모두 해석적 결과와 실험적 결과가 잘 일치함을 확인하였다.
|
Fig. 24 Strain comparison of strain from test with FEA |
|
Fig. 25 Comparison of bending and torsional stiffness |
본 논문에서는 실험적/수치적 방법을 통해 복합재 로터 블레이드의 단면별 전단 중심과 휘임 및 비틀림 강성도를 취득하였다. 로터 블레이드의 휘임 변형과 비틀림 변형의 연계를 최소화하기 위해 단면별 전단 중심을 추정한 후 휘임 및 비틀림 시험을 수행하여 단면별 휘임 및 비틀림 강성도를 취득하였다. 유한요소해석을 통해 기하학적 방법으로 단면별 전단 중심을 추정하였고 단면 강성 행렬을 이용해 단면의 휘임 및 비틀림 강성도를 계산하였다.
유한요소해석을 통하여 계산한 휘임 강성도(EIy) 및 비틀림 강성도(GJ) 값의 정확도는 휘임 및 비틀림 시험을 통하여 타당성을 검증하였다. 이러한 검증 결과를 근거로 실험적으로 구하기 힘든 시위 방향 휘임 강성도(EIx), 전단 강성도(GAy)와 두께 방향 전단 강성도(GAx) 그리고 블레이드 길이 방향의 인장 강성도(EA) 값은 유한요소해석법으로 구한 단면 강성 행렬 값을 활용할 수 있으리라 생각된다.
본 연구를 통해 복합재 로터 블레이드의 전단 중심과 단면별 강성도를 취득할 수 있었고, 이러한 결과는 탄성체 로터 블레이드를 고려한 헬리콥터 성능해석에 이용될 수 있을 뿐만 아니라 향후 복합재 로터 블레이드의 신규 개발 시에도 활용될 수 있을 것으로 기대된다.
본 연구는 민군협력진흥원(ICMTC)의 재원으로 무인 헬리콥터의 Rotor Blade 구조 시험의 지원을 받아 수행한 연구과제입니다.
- 1. Yun, C.Y., and Kim, D.K., “The Measurement Test of Stiffness and Natural Frequencies for Bearingless Rotor System of Helicopter,” Journal of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 12, 2015, pp. 881-887.
-

- 2. Lim, I.G., Choi, J.H., Lee, I., and Han, J.H., “Aeroelastic Stability Analysis of Bearingless Rotors with Composite Flexbeam in Hover,” Journal of the Korean Society for Composite Materials, Vol. 17, No. 3, 2004, pp. 29-37.
- 3. Berring, P., Branner, K., Berggreen, C., and Knudsen, H.W., “Torsional Performance of wind turbine blades - Part 1: Experimental Investigation,” Proceeding of the 16th International Conference on Composite Materials, Kyoto, Japan, July 2007, pp. 3-7.
- 4. Enei, C., Bernardini, G., Serafini, J., Mattioni, l., Ficuciello, C., and Vezzari, V., “Photogrammetric Detection Technique for Rotor Blades Structural Characterization,” Journal of Physics : Conference Series, Vol. 658, No. 1, 2015, p. 012003.
-

- 5. Hoffmann, F., Keimer, R., and Riemenschneider, J., “Structural Modeling and Validation of an Active Twist Model Rotor Blade,” CEAS Aeronautical Journal, Vol. 7, No. 1, 2016, pp. 43-55.
-

- 6. You, G.S., An Optimal Structural Design of Composite Box Structure Using Equivalent Cross-section Characteristics, Master Thesis, Chungnam National University, Republic of Korea, 2011.
- 7. Houbolt, J.C., and George, W.B., “Differential Equations of Motion for Combined Flapwise Bending, Chordwise Bending, and Torsion of Twisted Nonuniform Rotor Blade,” NACA Technical Note 3905, NACA Report, 1957.
- 8. Larsen, G.C., and Kretz, A., “Experimental Determination of Structural Properties by Non-Destructive Methods,” Proceeding of the European Wind Energy Association Conference and Exhibition, Thessaloniki, Greece, Oct. 1994, pp. 42-46.
 This Article
This Article
-
2019; 32(4): 191-198
Published on Aug 31, 2019
- 10.7234/composres.2019.32.4.191
- Received on May 9, 2019
- Revised on Jul 31, 2019
- Accepted on Aug 26, 2019
 Services
Services
Shared
 Correspondence to
Correspondence to
- In-Gul Kim
-
Department of Aerospace Engineering, Chungnam National University
- E-mail: igkim@cnu.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.