This work investigates the elastic buckling characteristics of laminated composite trapezoidal corrugated plates with simply supported edges using the analytical method. In the analysis, three types of in-plane loading conditions: uniaxial, biaxial and shear loads are considered. Because it is very difficult to determine the mechanical behavior of 3-dimensional corrugated structures analytically, the equivalent homogenization model is adapted to investigate the overall mechanical behavior of corrugated plates. The corrugated element is homogenized as an orthotropic material. The previous formulae for bending rigidities of corrugated plate are adapted in this paper. The comparisons of the proposed analytical results with those of FEA based on the shell element are made to verify the proposed analytical method. In the comparison study both the critical buckling loads and the buckling mode shapes are presented. Some numerical results are presented to check the effect of the geometric properties.

본 연구에서는 단순지지 경계조건을 갖는 적층 복합재료 사다리꼴 주름판에 대한 탄성 좌굴특성을 이론적 방법을 이용하여 분석하였다. 좌굴 해석에서는 한 방향 하중, 두 방향 하중 및 전단하중 등 3가지 유형의 내평면 하중조건이 고려되었다. 3차원 주름 구조물을 해석적으로 기계적 거동을 표현하는 것이 매우 어렵기 때문에 본 해석에서는 주름판의 전반적인 좌굴 거동을 분석하기 위해 등가균질모델을 적용하였다. 이를 위해 단위 주름을 직교이방성재료로 등가시켰으며, 이전 연구에서 유도한 주름판에 대한 등가 굽힘강성계수식을 본 해석에 적용하였다. 제안된 이론해석 결과의 타당성을 검증하기 위해 셸요소를 바탕으로 한 3차원 유한요소해석을 수행하였으며, 두 방법을 이용해 얻은 임계 좌굴하중 및 좌굴형상을 비교하였다. 주름판의 기하형상에 따른 영향을 분석하기 위해 다양한 수치 예가 제시되었다.

Keywords: 적층 복합재료(Laminated Composite), 주름판(Corrugated Plate), 균질 모델(Homogenization Model), 등가강성(Effective Stiffness)

두께가 얇은 판은 구조 요소로써 많은 분야에 널리 사용되고 있다. 그러나 이들 얇은 구조물은 좌굴 및 굽힘 등에 매우 취약하기 때문에 경우에 따라 구조물의 강성을 증가시켜야 한다. 재료 변경 없이 강성을 증가시키는 방법 중에 하나는 판에 주름을 주는 것이다. 이와 같이 강성을 높인 주름 구조요소는 해양 구조물, 비행기, 선박 및 철도차량의 바닥, 수직 칸막이 등과 같이 길이가 길고 질량 대비 큰 굽힘강성이 요구되는 구조물에 사용된다. 3차원 기하형상을 갖는 주름판의 기계 거동을 해석적으로 파악하기가 매우 어렵기 때문에 일반적으로 실험 및 3차원 유한요소해석을 이용한다. 그러나 3차원 유한요소해석의 경우 모델링이나 해석에 많은 작업량과 시간이 소요되기 때문에 주름 구조물의 국부적인 거동이 아닌 전반적인 거동에 관심이 있는 경우에는 적당하지 않다. 이와 같은 이유로 주름 구조물의 전반적인 거동을 파악하기 위해 주름판을 2차원 직교 이방성판으로 등가시켜 해석에 적용하고 있다. 또한 복합재료는 기존의 금속재료에 비해 비강도, 비강성이 매우 우수하기 때문에 이들 구조물의 보다 높은 효율을 얻기 위해 금속재료를 대신하여 복합재료가 주름판 제작에 사용되고 있다 [1-8]. 그러나 복합재료 주름판에 대한 연구는 주로 등가강성 유도에 주안점을 두고 있으며, 등가모델을 이용하여 기계적 거동을 분석한 연구는 매우 제한적이다[4,5,7]. Boorle[4]은 주름 코어를 갖는 복합재료 샌드위치판에 대한 굽힘 및 진동해석을 수행하였으며, Shaw 등[5]은 모핑 날개의 압축 좌굴 능력을 향상시키기 위해 날개의 표피로 사용되는 복합재료 주름요소의 주름형상에 대해 최적설계를 수행하였다. 또한 Park 등[7]은 적층 복합재료 주름판에 대해 진동 특성을 이론적으로 분석하였다. 한편 주름판이 전단벽이나 교량 거더의 웨브 등에 사용될 경우 주름판은 주로 내평면 압축하중 및 전단하중을 받으며, 이들 하중으로 인해 좌굴이 발생될 수 있다. Farzampour 등[9]은 유한요소법을 이용하여 개구부가 있는 주름판에 대해 극한전단강도를 예측하였다. Dou 등[10]은 사인파형 등방성 주름판에 대해 전단좌굴해석을 이론적으로 수행하였다. Jiaoa 등[11]은 직교이방성 복합재료 주름 웹을 갖는 I형보에 대해 횡비틀림좌굴을 이론 및 실험을 통해 연구하였다. Cao 등[12]은 실험과 수치해석을 통해 주기 하중을 받는 주름 전단벽에 대해 비탄성 좌굴 부하능력과 파손 모드를 검토하였다. 이들 전단벽에 대한 해석은 모두 등방성 또는 직교이방성 재료에 대한 것이다.
이상에서와 같이 적층 복합재료 주름판의 좌굴해석에 대한 연구는 거의 찾아 볼 수 없다. 따라서 본 연구에서는 이전 연구[6,7]에서 유도한 적층 복합재료 주름판의 등가 강성계수를 활용하여 단순지지 경계조건을 갖는 적층 복합재료 주름판에 대한 내평면 하중에 의한 좌굴 특성을 분석하였다. 이를 위해 복합재료 평판을 주름판으로 제작함으로써 나타나는 임계 좌굴하중 및 좌굴형상의 변화를 평판의 거동과 비교하였다. 이론해석의 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하여 그 결과를 비교/검토하였다. 또한 다양한 형상의 주름에 대한 거동도 분석하였으며, 주름판의 기형상을 결정하는 여러 변수에 대한 영향도 검토하였다.

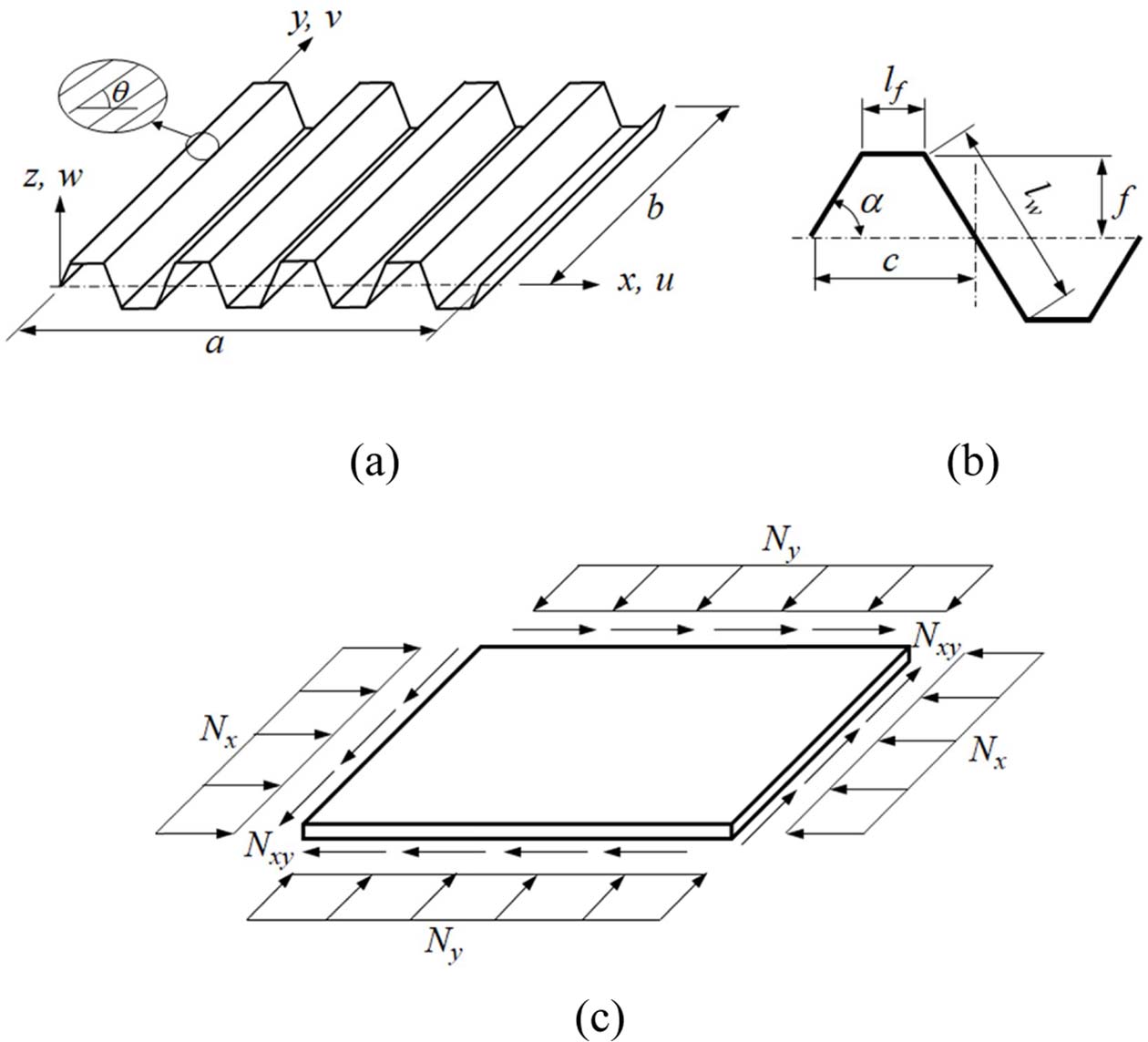
사다리꼴 주름형상을 갖는 주름판, 단위 주름형상 및 내평면 하중 조건을 Fig. 1에 나타냈다. 고려된 내평면 하중은 주름판의 중립면에 대해 x 및 y 방향 내평면 압축 하중 N_x, N_y 또는 내평면 전단하중 N_xy를 받는다. 이를 직교이방성판으로 등가시킨 모델에 표시하면 면 Fig. 1(c)와 같다. 판의 x, y 방향 길이를 a, b로, 단위 주름의 절반에 대한 축 방향 길이(주름 주기), 이에 대한 주름 길이, 주름 높이 및 주름각을 각각 c, l, f 및 α로 표현하였으며 주름판의 두께는 t이다. 적층 복합재료에서 적층각 θ는 x축에 대한 각으로 나타냈다.
주름판을 직교이방성판으로 등가시킬 때 등가 직교이방성판에 대한 변형에너지는 다음과 같이 된다.

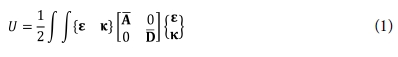
여기서 ε과 k는 직교이방성판에 대한 내평면 변형률과 곡률로 다음과 같다.

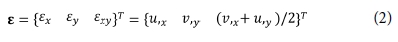
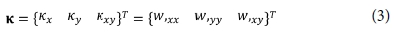
식에서 u, v 및 w는 사각판의 중립면에 대한 각 방향 변위이며, (,)는 하첨자에 대한 미분을 나타낸다. 식 (1)에서 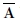및 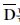는 직교 이방성판의 등가 신장 및 굽힘 강성계수로 다음과 같다.

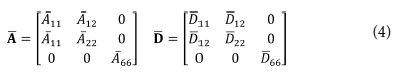
본 연구에서는 Fig. 1(b)와 같은 사다리꼴 형상의 주름을 고려하였다. 주름각이 90°이면 직사각형 주름이 되고, 그 이상이 되면 요각 사다리꼴 주름이, 주름각을 최소로 하면 삼각형 주름이 된다. 이들 주름에 대한 등가강성계수는 이전 연구의 결과[6,7]를 사용하였으며, 정리하면 다음과 같다.

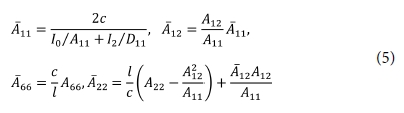
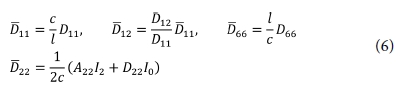
여기서 A_ij,D_ij(i, j = 1,2,6)는 적층 복합재료의 신장 및 굽힘 강성계수이며, 매개변수 I₀ 및 I₂는 다음과 같다.

Fig. 1(c)의 내평면 압축 하중 N_x, N_y 또는 내평면 전단하중 N_xy에 의한 판의 변형에너지는 다음과 같이 된다.

따라서 내평면 하중에 의해 판에 저장되는 총 에너지는 다음과 같이 정리할 수 있다.

본 연구에서는 단순지지 경계조건을 고려하였다. 고려한 경계조건을 만족하는 판의 중립면에 대한 변위식을 다음과 같이 표현할 수 있다.

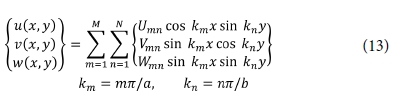
식에서 U_mn, V_mn 및 W_mn는 좌굴 형상에서의 진폭을 나타내며, m 및 n은 좌굴 형상을 나타내는 각 방향 반파수이다.
가정된 변위식 (13)를 총 변형에너지식 (12)에 대입한 후 Rayleigh-Ritz 정리에 적용하면 다음과 같은 좌굴해석을 위한 고유치 문제를 얻을 수 있다.

여기서 [K], [L]는 3 M N × 3 M N 크기의 행렬이고, {d}는 3 M N 크기의 계수행렬로 좌굴 형상을 결정한다. λ는 좌굴하중을 나타내는 행렬이다. 이와 같이 유도된 이론해석 과정에서의 좌굴하중 및 좌굴형상을 구하기 위해 Mathematica를 이용하여 프로그램을 작성하였다.

수치결과를 분석하기 위해 AS4/3501-6 carbon/epoxy 복합재료가 고려되었다[2,7]. 이 복합재료의 물성은 E₁ = 148 GPa, E₂ = 10.5 GPa, G₁₂ = 5.61 GPa, G₂₃ = 3.17 GPa, ν₁₂ = 0.3, ν₂₃ = 0.59 및 ρ = 1590 kg/m³이다. 판의 기본적인 기하형상은 a = 500 mm, b/a = 1, t = 1 mm 및 적층방법은 [±45°/0°/90°]S이다. 특별한 언급이 없는 한 이 모델이 수치 예에서 사용된다. 좌굴하중은 다음과 같이 무차원화하여 수치결과를 제시하였다.

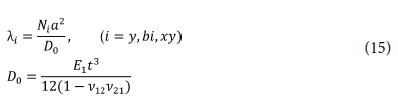
매개변수에서의 첨자는 하중방향을 나타내며, bi는 N_x 및 N_y를 동시에 받는 양방향 압축하중을 의미한다. 제안된 해석방법의 타당성을 검증하기 위해 압축하중을 받는 경우와 전단하중을 받는 경우에 대해 ANSYS를 이용하여 3차원 유한요소해석을 수행하여 그 결과를 Fig. 2 및 3에 제시하였다. 유한요소해석에서 적층 복합재료 주름판을 모델링하기 위해 SHELL181 요소가 이용되었다. 이 때 주름판의 주름수는 20, 주름 높이 f = 3t 및 주름각 a = 45°이다.
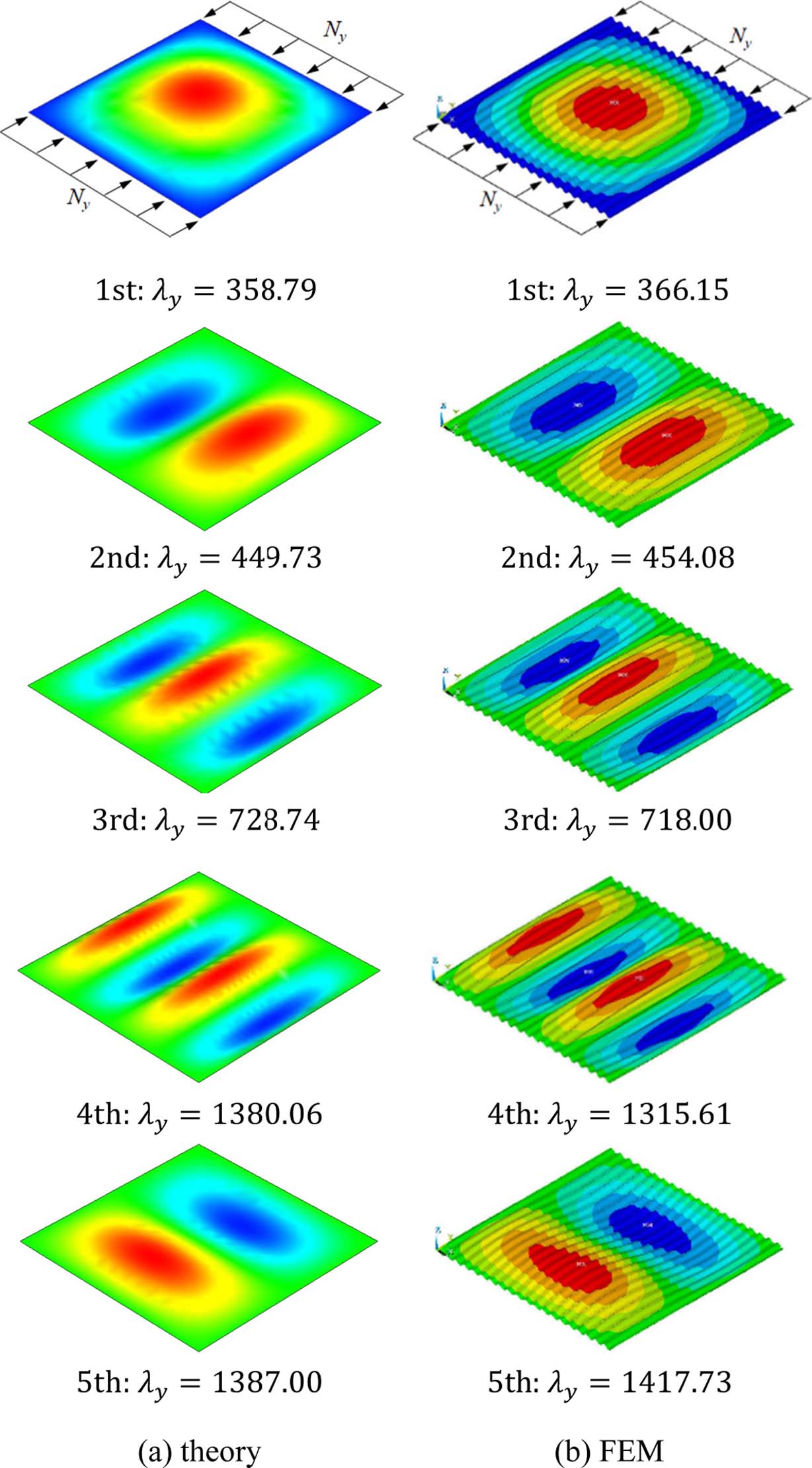
먼저 압축하중 Ny를 받는 복합재료 주름판에 대해 이론해석 및 유한요소해석으로부터 얻은 최저 5차까지의 좌굴하중 및 좌굴형상을 Fig. 2에 제시하였다. 그림에 제시된 것처럼 두 결과간의 좌굴하중 차이는 최대 약 4.94%(4차)로 잘 일치하며, 좌굴형상의 경우에도 매우 잘 일치한다.
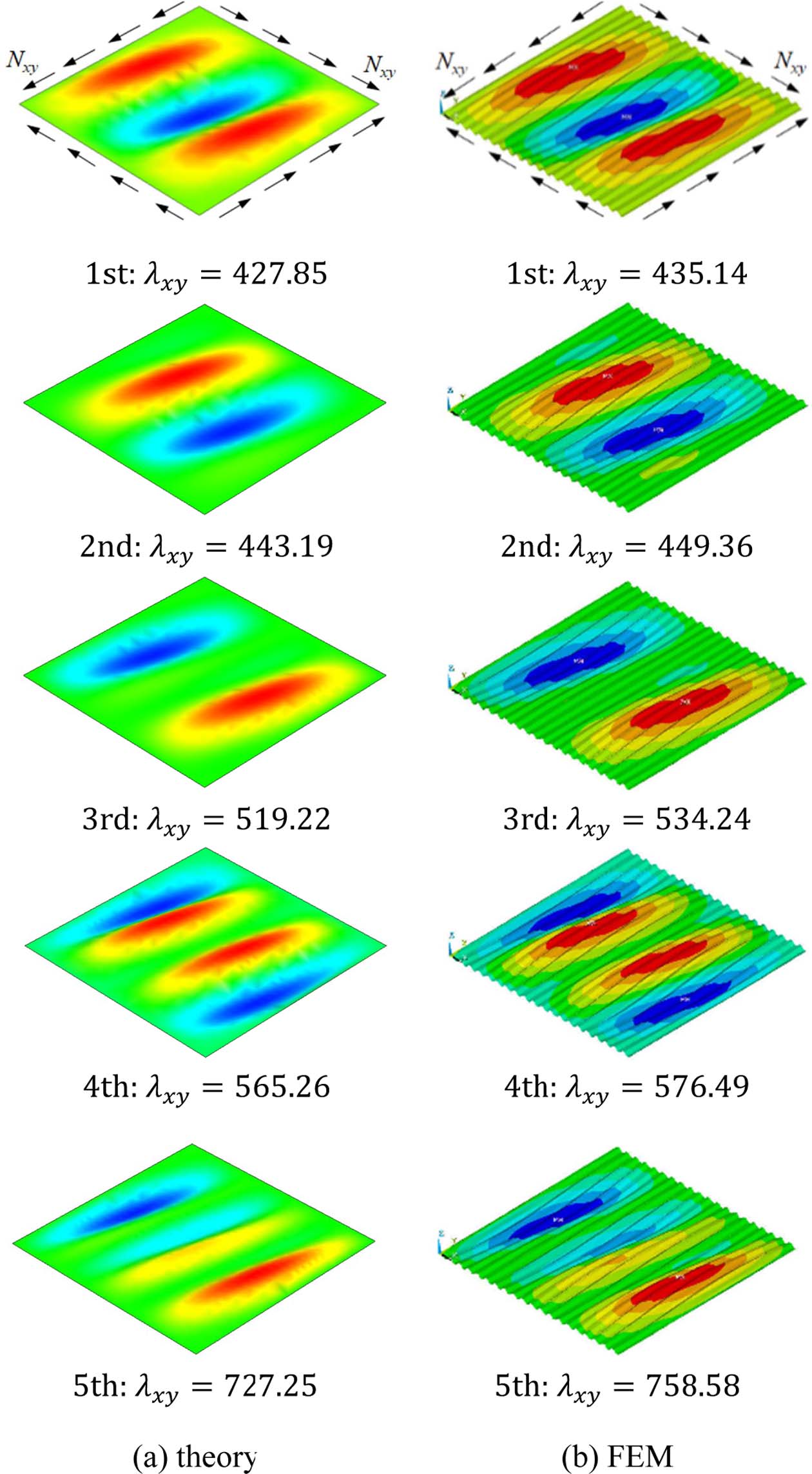
한편 내평면 전단하중에 대해 복합재료 주름판에 대한 이론 및 유한요소해석으로부터 얻은 좌굴하중과 좌굴형상을 Fig. 3에 제시하였다. 그림에 제시된 것처럼 좌굴하중은 최대 4.2%(5차)의 차이를 보이고 있으며, 등가모델 및 유한요소해석으로부터 얻은 좌굴형상도 매우 잘 일치하는 것을 볼 수 있다.
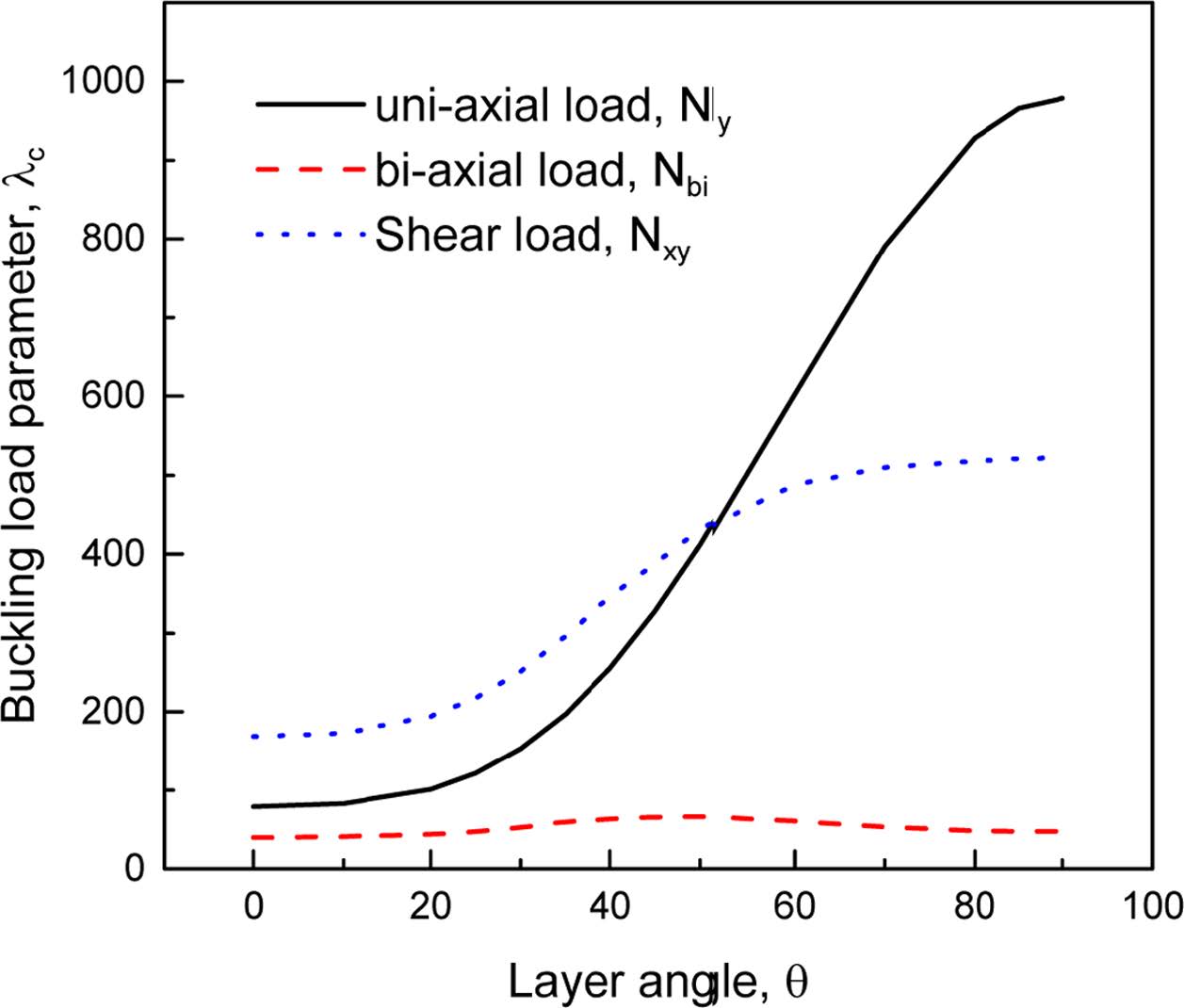
[(±θ)₂]_S로 적층된 복합재료 주름판에 대해 적층각 θ가 좌굴하중에 미치는 영향을 알아 보기 위해 Fig. 4를 제시하였다. 이때 고려된 주름판은 앞의 예제 Fig. 2 및 Fig. 3에서 사용한 것으로 주름각 만을 a = 60°로 변경하였다. 양방향 압축인 경우 좌굴이 상대적으로 약한 주름 방향으로 일어나기 때문에 좌굴하중이 다른 하중과 달리 매우 작은 값을 갖으며, 좌굴하중이 적층각에 따라 증가하다 감소하는 거동을 한다. 내평면 전단하중을 받는 경우에는 적층각에 따라 좌굴하중이 초기에는 거의 변화가 없다가 서서히 증가를 하다가 거의 일정한 값으로 접근을 한다. y 방향 압축하중 Ny를 받는 경우에도 내평면 하중에 대한 거동과 유사하나 적층각에 따라 좌굴하중이 증가하는 정도가 가파르다. 이와 같이 적층각이 좌굴하중에 미치는 영향이 다른 하중에 비해 크게 나타나는 것은 Fig. 5에 제시된 것처럼 다른 하중에 의한 좌굴형상이 적층각에 따라 x 방향 모드가 변경되지만 한 방향 압축을 받는 경우에는 적층각에 관계없이 항상 좌굴형상이 (1, 1)로 변하지 않기 때문이다.
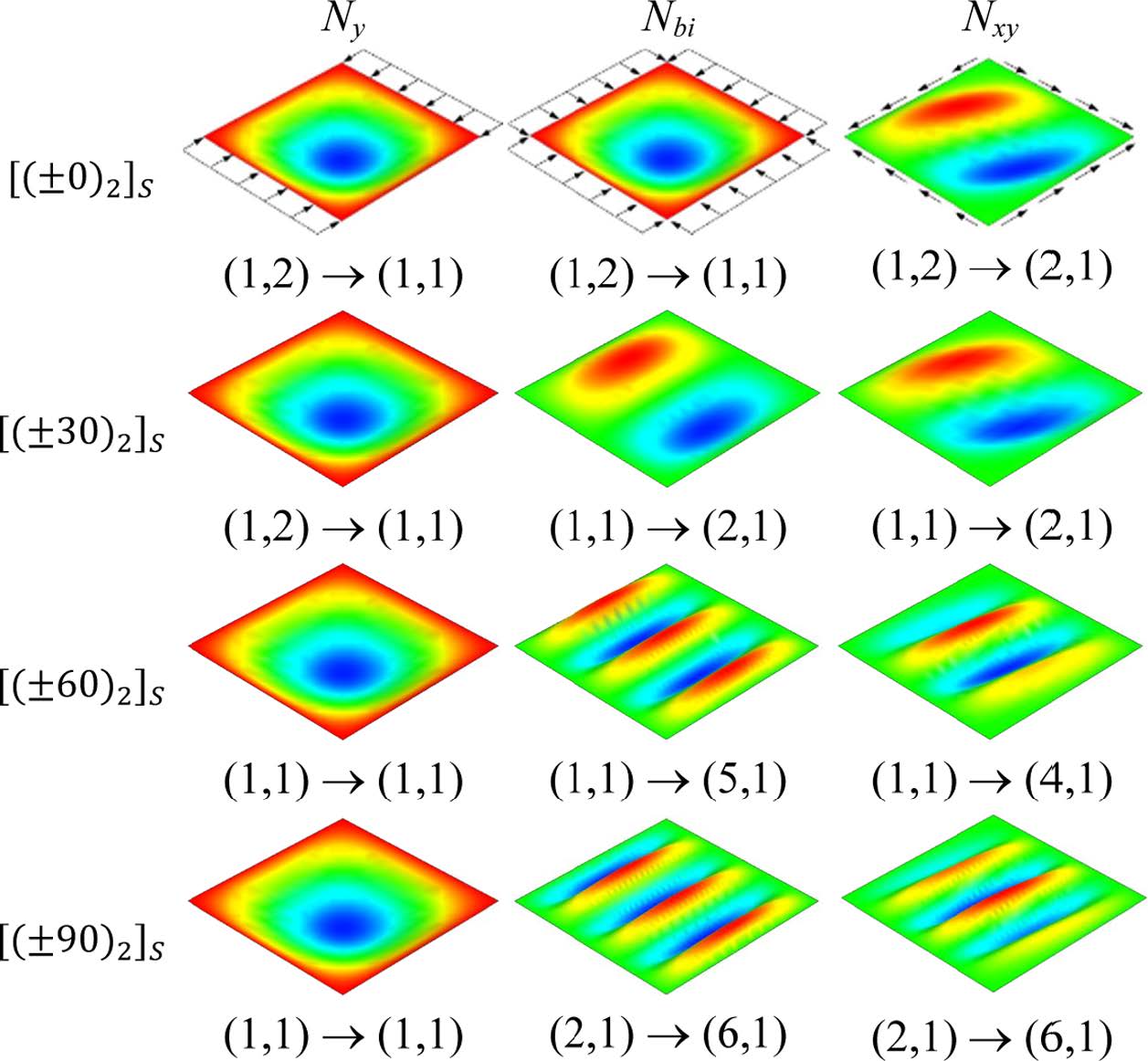
Fig. 5는 Fig. 4의 주름판에 대해 적층각에 따른 좌굴형상을 나타낸 것이다. 좌굴형상을 나타낸 그림에서 (1, 2) → (1, 1) 등은 평판에 대한 좌굴형상 (1, 2)가 같은 적층각에 대한 주름판에 대해 좌굴형상이 (1, 1)로 변경되는 것을 나타낸다. 그림에서처럼 y 방향 압축하중에 대해 적층각에 따라 평판은 좌굴형상이 변화하지만 주름판의 경우에는 적층각에 관계없이 항상 (1, 1)의 좌굴형상을 보이고 있다. 양방향 압축이나 내평면 전단하중의 경우에는 적층각에 따라 평판의 경우에는 (1, 1), (1, 2) 또는 (2,1) 모드에서 좌굴이 형성되지만 주름판의 경우에는 좌굴형상이 크게 변하는 것을 볼 수 있다. 이와 같은 변화는 적층각의 영향뿐만 아니라 주름의 영향이 동시에 반영되기 때문에 나타나는 현상이다.
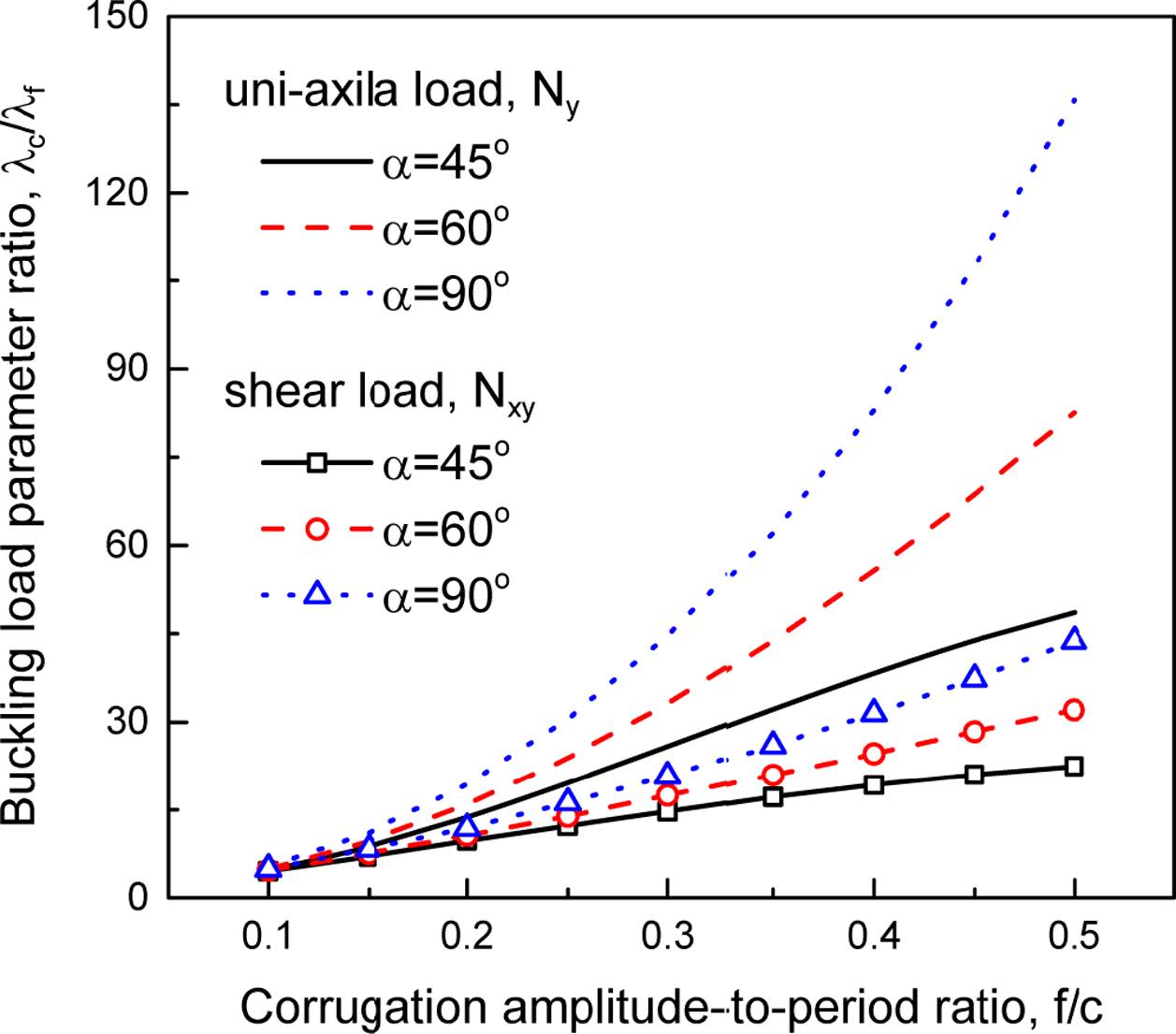
Fig. 6에서는 복합재료 주름판에 대해 주름높이 대 주기의 비(f/c)가 한 방향 압축 및 내평면 전단 좌굴하중에 미치는 영향을 분석하였다. 그림에서 주름판의 좌굴하중(λ_c)에 대한 평판의 좌굴하중(λ_f)의 비를 f/c에 따라 제시하였다. f/c (즉, f)가 증가함에 따라 좌굴하중이 증가하는 것을 볼 수 있다. 특히 압축 좌굴하중의 경우 전단 좌굴하중 보다 급격히 증가를 한다. 이와 같은 현상이 나타나는 이유는 다음과 같다. f/c비의 증가에 따라 y 방향 굽힘강성이 증가하여 f/c에 관계없이 좌굴형상이 항상 (1, 1)에서 나타나며 좌굴하중이 크게 증가를 한다. 그러나 내평면 전단하중에 의한 좌굴형상의 경우에는 f/c가 증가함에 따라 (2, 1) 모드를 시작으로 x 방향으로의 모드 수가 증가하여 최대 m = 6까지 변화되기 때문에 좌굴하중의 증가가 압축좌굴보다 덜하다. 또한 주름각이 클수록 좌굴하중이 증가하는 것을 알 수 있다. 이때 f/c가 클수록 주름각의 영향이 커져 좌굴하중도 보다 크게 증가를 한다.
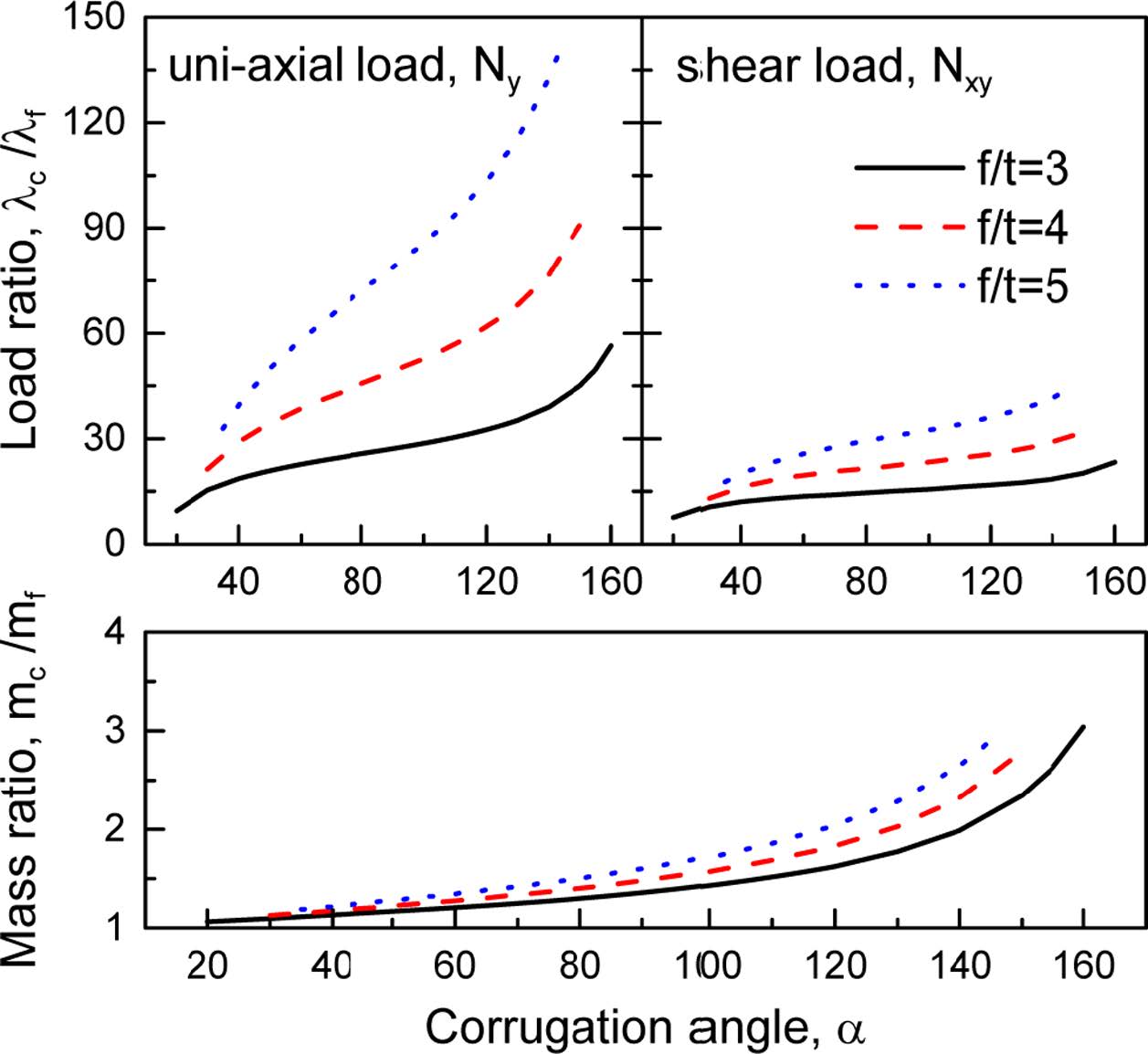
주름각이 내평면 좌굴하중에 미치는 영향을 보다 자세히 알아보기 위해 Fig. 7을 제시하였다. 이때 주름수는 15개이다. 그림에서 좌굴하중비(λ_c/λ_f) 및 질량비(m_c/m_f)를 주름각에 따라 제시하였다. 그림에 나타난 것처럼 주름각의 증가와 함께 질량 및 좌굴하중은 증가를 한다. 특히 f/t가 클수록(즉, 주름높이가 클수록) 보다 민감하게 좌굴하중이 증가를 한다. 또한 f/t가 클수록 전단 좌굴하중보다 압축 좌굴하중에 주름각의 영향은 크다는 것을 볼 수 있다. 예로써 f/t = 5인 경우 질량은 3배정도 증가하지만 전단좌굴하중은 약 45배, y-방향 압축좌굴하중은 150배 증가를 한다. 이처럼 주름판을 제작함으로써 큰 질량 증가없이 좌굴하중을 매우 크게 증가시킬 수 있음을 볼 수 있다.
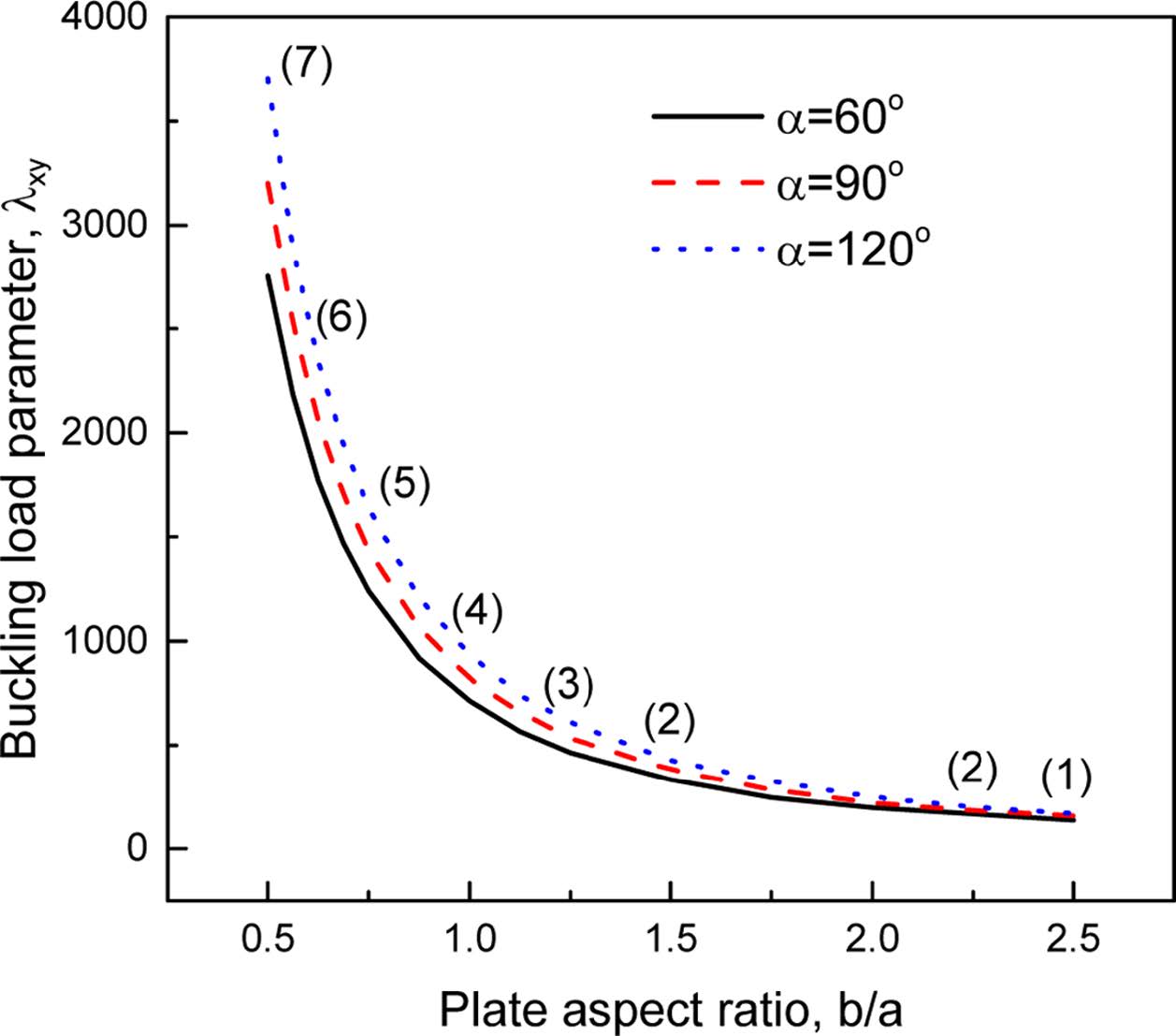
주름판의 형상비인 길이 대 폭의 비(b/a)가 내평면 전단좌굴하중에 미치는 영향을 Fig. 8에 제시하였다. 그림에 나타난 것처럼 모든 주름각에 대해 형상비의 증가에 따라 좌굴하중 매개변수가 감소하는 것을 볼 수 있다. 그림에서 괄호 안의 숫자는 x방향의 좌굴형상에서의 반파수를 나타낸 것으로 형상비 b/a가 커짐에 따라 감소하는 것을 볼 수 있다. 이 때 y 방향의 반파수는 모두 1이다.

단순지지 경계조건을 갖는 적층 복합재료 사다리꼴 주름판에 대해 일정 두께를 갖는 직교이방성판으로 등가시켜 좌굴특성을 얻기 위해 이론해석을 수행하였다. 또한 추가로 3차원 유한요소해석을 수행하였으며 그 결과를 이론해석 결과와 비교/검토하였다. 이를 통해 제안된 이론해석방법이 좌굴하중 및 좌굴형상을 적절히 예측할 수 있음을 보였으며, 몇몇 수치 예를 통해 다음과 같은 결론을 얻었다.
[(±θ)₂]_S로 적층된 복합재료 주름판의 경우 양방향 압축좌굴하중은 적층각 θ = 45°, 주름 횡 방향 압축 및 내평면 전단 좌굴하중은 θ = 90°에서 최대가 된다. 단위 주름의 주름 높이가 증가함에 따라 좌굴하중이 증가를 하며 압축하중에 대해 그 영향이 가장 크게 나타난다. 또한 좌굴형상이 내평면 전단하중에 대해 주름 높이에 따라 크게 변한다. 주름각이 커질수록 좌굴하중은 증가를 하며, 주름 높이가 클수록 보다 민감하게 증가를 한다. 또한 주름 높이가 클수록 전단 좌굴하중보다 압축 좌굴하중에 주름각이 미치는 영향이 크다는 것을 알 수 있었다. 주름판의 길이 대 폭의 비가 증가함에 따라 좌굴하중 매개변수는 감소를 하며, 형상비가 작을수록 매개변수에 큰 영향을 미친다.