- Prediction of Material Properties of Carbon Fiber Prepreg in the Laminated Composite Using Reverse Analysis with Dynamic Characteristics
Mun-Young Hwang*, Lae-Hyong Kang**†
* Department of Mechatronics Engineering, and LANL-CBNU Engineering Institute-Korea, Chonbuk National University, Jeonju 54896, Korea
**† Department of Mechatronics Engineering, Department of Flexible and Printable Electronics, and LANL-CBNU Engineering Institute-Korea, Chonbuk National University, Jeonju 54896, Korea- 동적 특성이 고려된 역해석를 이용한 적층 복합재료 내부의 탄소섬유 프리프레그의 물성 예측
황문영* · 강래형**†
If what the mechanical properties according to a layer have was found out by analyzing the already fabricated composite, it could be possible to develop the composite of the better performance than the existing products. In this study, we tried to calculate the mechanical properties of the inner prepreg lamina by applying the reverse design technique to the composite structure made by laminating prepregs. When the physical quantities obtained by the simple tensile test are used alone and the physical quantities obtained by the tensile test and the mode analysis are used at the same time, the results of this study show that the accuracy of the latter is higher Finally, the maximum error of E1 predicted was 0.09% and the maximum error of predicted E2 was 7%.
이미 제작된 복합재료 제품을 분석하여 층별로 어떤 기계적 물성을 가지는지 알아낼 수 있다면, 기존 제품에 비해 더 좋은 성능을 내는 복합재료 개발을 수행할 수 있게 된다. 본 연구에서는 프리프레그를 적층하여 제작된 복합재료 구조물에 대해 역설계 기법을 적용하여 내부 프리프레그 층의 물성을 계산하고자 하였다. 단순히 인장시험으로 얻어지는 물리량을 이용한 경우와 인장시험 및 모드 해석을 통해 얻어지는 물리량을 이용한 경우를 비교한 결과 후자의 정확도가 더 높음을 알 수 있었다. 최종적으로 예측된 E1의 최대 오차는 0.09%였고 예측된 E2의 최대 오차는 7%였다.
Keywords: 적층복합재(Laminated composite), 유한요소분석(Finite element analysis), 역공학(Reverse-engineering), 예측(Prediction)
연료의 효율을 높이고 배기가스의 배출을 줄이기 위해서, 구조 경량화 연구가 지속적으로 이뤄지고 있다. 섬유강화복합재료의 경우 다른 금속재료와 비교하여 비강도, 비강성이 높기 때문에, 경량화 설계의 중요한 해결책으로 각광받고 있다. 많은 연구자들이 섬유강화복합재료를 이용한 부품 개발 및 해당 부품의 해석 방법 개발에 대한 노력을 수행하고 있는데, 일예로 Mahmood 등[1]은 단일 방향 E-유리 섬유를 적용한 판 스프링을 설계하여, 80%의 경량화 효과를 분석했다. Choi 등[2]은 부품구조에 대한 유한요소 모델의 타당성을 연구했고, 실험을 통해 얻은 결과와 비교했다.
처음부터 복합재료를 설계하여 목적에 맞도록 설계하는 기법도 중요하지만, 복합재료 후발 주자인 기업들에게는 선진 복합재료 구조물을 벤치마킹하여 분석한 후 새로운 제품 개발에 적용하는 과정을 거치게 된다. 전체 구조물의 거동을 알고 있는 상태에서 내부 층별 물성을 알아내는 기법을 역설계 기법이라고 한다. 하지만, 이방성 재료들로 구성된 복합재료 구조에 대해서는 기존의 역설계 방법을 적용하는 것이 다소 어렵다. 그 이유는 각 층별 재료 강성, 층 두께, 적층 각도, 순서 등이 다양하게 포함되기 때문이다. 정확하게 적층 복합재료에서 사용된 재료를 역설계적인 방법으로 분석하기 위해서는 반복하중시험, 단면 정보 분석, 섬유 부피 비율 분석 등 반복적인 실험적 분석이 필요하다. 그러나 설계 과정에서 구성요소의 변화가 발생할 경우, 기존 실험 결과 이외에 새로운 실험 결과를 필요로 하기 때문에 많은 시간과 비용이 소모될 수 있다.
한편, 오직 실험적 접근법만을 이용한 역설계법은 이상적이지 않다. 그럼에도 아직까지 역설계 기법에 관한 기존 연구[3-7]에서 보듯 3D 스캐닝으로 얻어진 CAD 모델을 정확하게 구축하는 방법에 대한 연구가 주로 수행되고 있는 실정이다. 재료 선정을 위한 역설계에 관한 연구[8]도 일부 있으나 등방성 재료에만 적용이 가능하다는 단점이 있다.
따라서, 복합재료에 대한 역설계 기법이 고전 적층판 이론(Classical laminated plate theory, CLPT)[9] 기반으로 개발되었다[10-12]. 그러나 이러한 수식적인 방법은 혼합법칙(Rule of mixture) 기반의 수학적인 역계산이 수행되며, 섬유 방향에서의 물성 예측은 정확도가 높지만, 매트릭스 방향에서의 물성 예측은 정확도가 떨어지는 단점이 있다.
본 연구는 매트릭스 방향에 대한 예측 정확도가 떨어지는 단점을 보완하기 위해 동적 특성 기반의 모달 해석 시뮬레이션 방법을 활용하였다. 동적 특성 기반의 해석을 고려함으로써 섬유 방향뿐 만 아니라 매트릭스 방향의 물성을 고려하여 역계산이 수행되도록 경계조건을 선정하였다. 즉, 기존의 역설계의 단점을 극복하고, 내부 섬유의 적층 방향을 고려할 수 있는 방법론을 제시하였다. 상용 해석 프로그램인 ANSYS Composite PrepPost(ANSYS ACP)을 활용하여 시편 단위 인장시험을 다양한 경계조건에서 반복 해석하여 사용된 재료의 물성을 예측하였다. 제시된 방법론은 유한요소 시뮬레이션 활용하여 직관적으로 예측 결과를 확인할 수 있다. 예측된 물성의 신뢰도는 수행된 시뮬레이션의 결과를 역추적하여 검증했다.
적층 복합재는 다양한 각도의 lamina 층이 다중의 층으로 구성된 구조를 의미한다. 본 논문에서는 혼란을 방지하기 위하여 lamina 층은 섬유 및 매트릭스가 이루는 한 층을 의미하는 용어로 사용하였다. 적층 복합재의 강성은 적층하는 lamina 층의 종류, 두께 및 각도에 의해 결정될 수 있다. 이러한 적층 복합재의 일반적인 설계 과정의 첫 번째 단계는 CLPT와 표본 시편의 실험에 의해 얻어진 층의 특성을 사용하여 최종 적층 복합제의 강성을 계산하는 것이다. 두 번째 단계는 적층 복합 재료의 계산된 강성을 구조 해석에 직접적으로 적용하는 것이다. 그러나, 이미 제조가 완료된 복합재의 역설계 과정에서는 이러한 일반적인 방법으로 설계를 수행하는 것이 어렵다. 사용된 lamina 층의 물성 계산이 제작이 완료된 복합재로부터 추출된 재료의 시험이나 참조 데이터로부터 수행해야만 하기 때문에. 추출된 시편의 내부의 lamina 층의 각도와 두께 등을 고려할 수 있는 해석 방법이 필요하다. 본 연구에서는 CAE 해석을 이용하여 재료 내부의 각도와 두께를 고려할 수 있는 해석 방법을 제시하였다. 제시된 해석기법에는 다음과 같은 가정이 존재한다. 첫 번째 가정은 변형이 발생하지 않은 요소 내부에서 두께 방향을 따라 그려진 요소의 직선은 회전할 수 있지만, 요소가 변형되었을 때, 곡선이 아닌 직선을 유지한다. 만약 변형이 발생하지 않은 요소간의 계면이 존재한다면, 그러한 면에 수직인 각도는 Fig. 1(c)에 나타낸 x-y 평면과 y-z 평면에서 측정된 것 같이 Φx, Φy으로 표시된다. 둘째, 요소가 변형되어도, 요소의 자체의 두께 변화는 무시될 수 있다. 요소의 3차원 구성 방정석은 요소에 가해지는 응력과 변형에 연관이 있고, 동시에 lamina 층의 구성 방정식은 lamina 층 계면의 변형 및 곡률과 연관된다. lamina 층의 구성 방정식은 3차원 구성 방정식에서의 응력 행렬을 통해 계산될 수 있다.
재료의 모든 요소에서의 3차원 성분의 탄성 영역 강성은 Eq. (1)으로부터 각 요소의 두께 방향 성분에 따른 단순한 적분 형태로부터 얻어지는 응력 행렬에 의해 결정될 수 있다(Fig. 1 참조)[13].
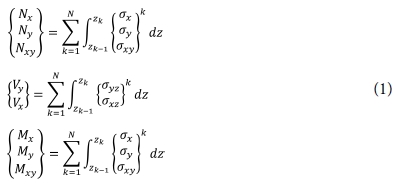
N은 lamina 층의 수, zk-1 및 zk는 적층 구조에서 각각 k 번째 층의 바닥 좌표와 상부 표면의 좌표이다. 각각의 lamina 층 요소의 로컬 좌표를 3D 구성 방정식의 평면 응력 형태로 바꾸고 적분하면 아래와 같은 매트릭스 구성 방정식을 얻는다.
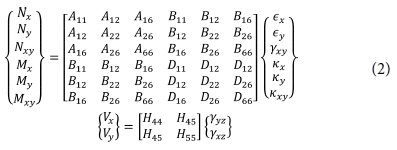
여기에서
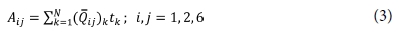
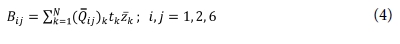
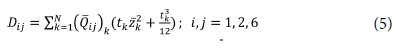
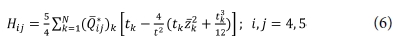
(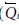 ij)k는 k 번째 lamina 층에 관한 강성 매트릭스의 상수이다. tk는 k 번째의 lamina 층 두께이고,
ij)k는 k 번째 lamina 층에 관한 강성 매트릭스의 상수이다. tk는 k 번째의 lamina 층 두께이고, 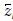 k는 k 번째 lamina 층의 계면의 좌표이다. Aij는 적층 복합재의 평면 강성을 나타내고, Dij는 굽힘 강성을 나타낸다. Bij는 휨-인장 연계를 나타내며, Hij는 층내 전단 강성을 나타낸다. 모든 상수들은 위에 언급된 Eq. (3)-(6)에 계산될 수 있다. 모든 요소에 대한 복잡한 계산과 많은 계산량은 상용 소프트웨어를 이용하면 쉽게 계산할 수 있다. 본 연구에서는 이러한 계산을 위해 ANCSY ACP를 이용했다. 위에서 얻어진 계수 정보를 활용하여, 다음의 구성요소를 이용하면 적층 복합재의 특성을 계산할 수 있다.
k는 k 번째 lamina 층의 계면의 좌표이다. Aij는 적층 복합재의 평면 강성을 나타내고, Dij는 굽힘 강성을 나타낸다. Bij는 휨-인장 연계를 나타내며, Hij는 층내 전단 강성을 나타낸다. 모든 상수들은 위에 언급된 Eq. (3)-(6)에 계산될 수 있다. 모든 요소에 대한 복잡한 계산과 많은 계산량은 상용 소프트웨어를 이용하면 쉽게 계산할 수 있다. 본 연구에서는 이러한 계산을 위해 ANCSY ACP를 이용했다. 위에서 얻어진 계수 정보를 활용하여, 다음의 구성요소를 이용하면 적층 복합재의 특성을 계산할 수 있다.
- A, B, D 및 H 구성행렬
- 구성된 섬유층의 물성과 지정된 적층 순서
계산된 구성 행렬 A, B, D, H는 적층 복합재의 구성 정의에 이용된다. 요소에서 일반화된 하중과 모멘트는 오직 요소에서의 변형과 요소의 곡률에만 적용시킬 수 있다. 위에서 언급된 구성 매트릭스 요소와 일련의 계산 과정을 거쳐 적층 복합재의 물성을 계산하는 것이 가능하다.
적층 복합재에 사용된 재료 물성의 역설계는 제작된 적층 복합재에 사용된 lamina 층에 대하여 모든 응력과 변형률을 계산해야 한다. 그 다음, 적층 순서를 고려하여 계산을 수행해야 한다. 해당 계산을 수행하기 위해서는 사용되는 종류의 모든 lamina 층의 탄성영역 강성뿐 만 아니라 lamina 층의 두께와 적층 방향이 반드시 주어져야 한다. 그러나 본 연구에서는 적층 복합재의 시험 정보을 기반으로 적층 복합재의 인장 시험 해석을 통해 적층 복합재 내부의 lamina 층의 특성을 역계산하였다. 수행된 해석에 관한 자세한 알고리즘은 다음 장에서 설명한다.
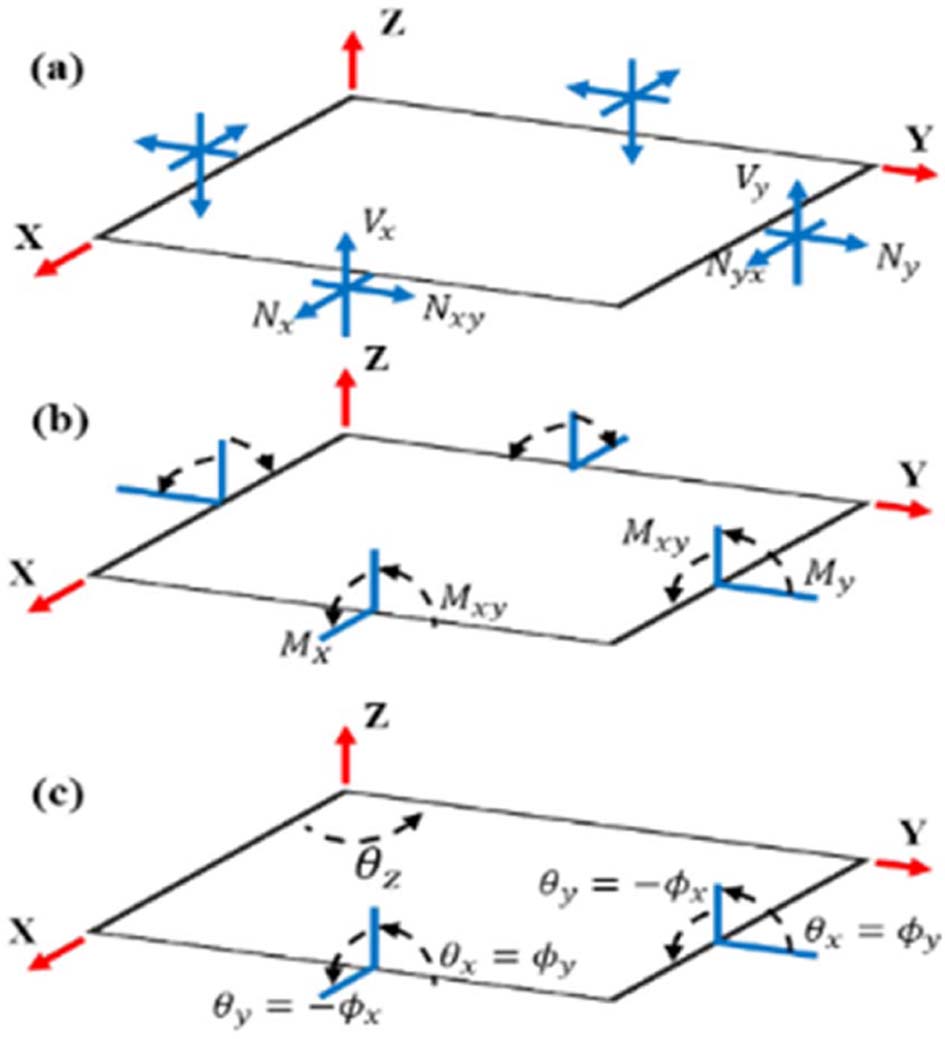
|
Fig. 1 Stress resultants on an element: (a) force per unit length; (b) foments per unit length; and (c) definition of rotation Φ compared to the angle Θ |
적층 복합재에서 사용된 lamina 층 강성을 예측하기 위한 해석 절차는 Fig. 2와 같이 다섯 단계로 세분화 된다. 첫 번째, 강성을 예측하고자 하는 구조물로부터 채취된 시편으로부터 내부의 lamina 층의 순서, 각도, 두께의 정보를 파악한다. 역설계에서 시편의 분석은 예측 오차를 줄일 수 있는 중요한 기술이다. 적층 정보를 정확하게 분석하기 위한 방법들은 수지를 연소시키고 lamina 층의 섬유의 정보를 파악하는 번 아웃(burn out) 테스트와 광학 현미경 등을 활용하여 채취 시편의 단면을 분석하는 광학적 방법이 존재한다[14,15]. 그러나 본 연구에서는 이러한 적층 정보를 정확하게 파악할 수 있다는 가정에서 CAE의 해석적 방법만을 활용하여 적층 복합재 내부에 사용된 lamina 층의 물성을 예측하는 기법에 중점을 두고 기술했다.
둘째, 인장 시험 해석 결과, 모달 시험 해석 결과와 시편 분석의 정보를 이용하여 채취된 시편의 적층 복합재의 강성 EX, EY (직교 좌표계에서의 적층 복합재의 탄성 계수; 아래 첨자는 직교 좌표계에서의 방향을 나타냄.)을 예측한다.
셋째, 반복 수행되는 인장시험, 모달 시험 해석결과와 유전자 알고리즘 기반의 직접 최적화 방법을 사용하여 내부의 lamina층 한 장의 강성 E1, E2(직교 좌표계에서의 섬유층 시트 한 장의 탄성 계수; 아래첨자는 직교 좌표계서의 방향을 나타냄; 1: X-방향, 2: Y-방향)을 예측한다.
넷째, 예측된 lamina 층의 강성 E1, E2을 기반으로 계산된 적층 복합재의 강성 EX, EY와 인장 시험 해석을 통해 계산된 적층 복합재의 강성 EX, EY(또는 채취된 복합재료 시편의 인장 시험 결과를 통해 계산된 강성 EX, EY)을 비교하여 lamina 층 강성의 예측 결과를 검증하고 다음 단계의 진행 여부를 결정한다.
최종적으로, lamina 층 강성 E1, E2을 활용하여 사용 목적에 맞는 복합재료의 적층 정보 최적화 해석을 수행한다. 각각의 하위 단계에 대한 자세한 설명은 다음 하위 절에서 설명했다. 이러한 최적화 과정은 구조물이 사용되는 환경과 형상에 따라 경계 조건이 다양하므로 사용되는 경계조건에 따라 별도로 수행되어야만 한다.
즉 본 연구에서는 취득된 시편으로부터 lamina 층의 물성을 역추적하는 방법에 집중하여 기술하였다.
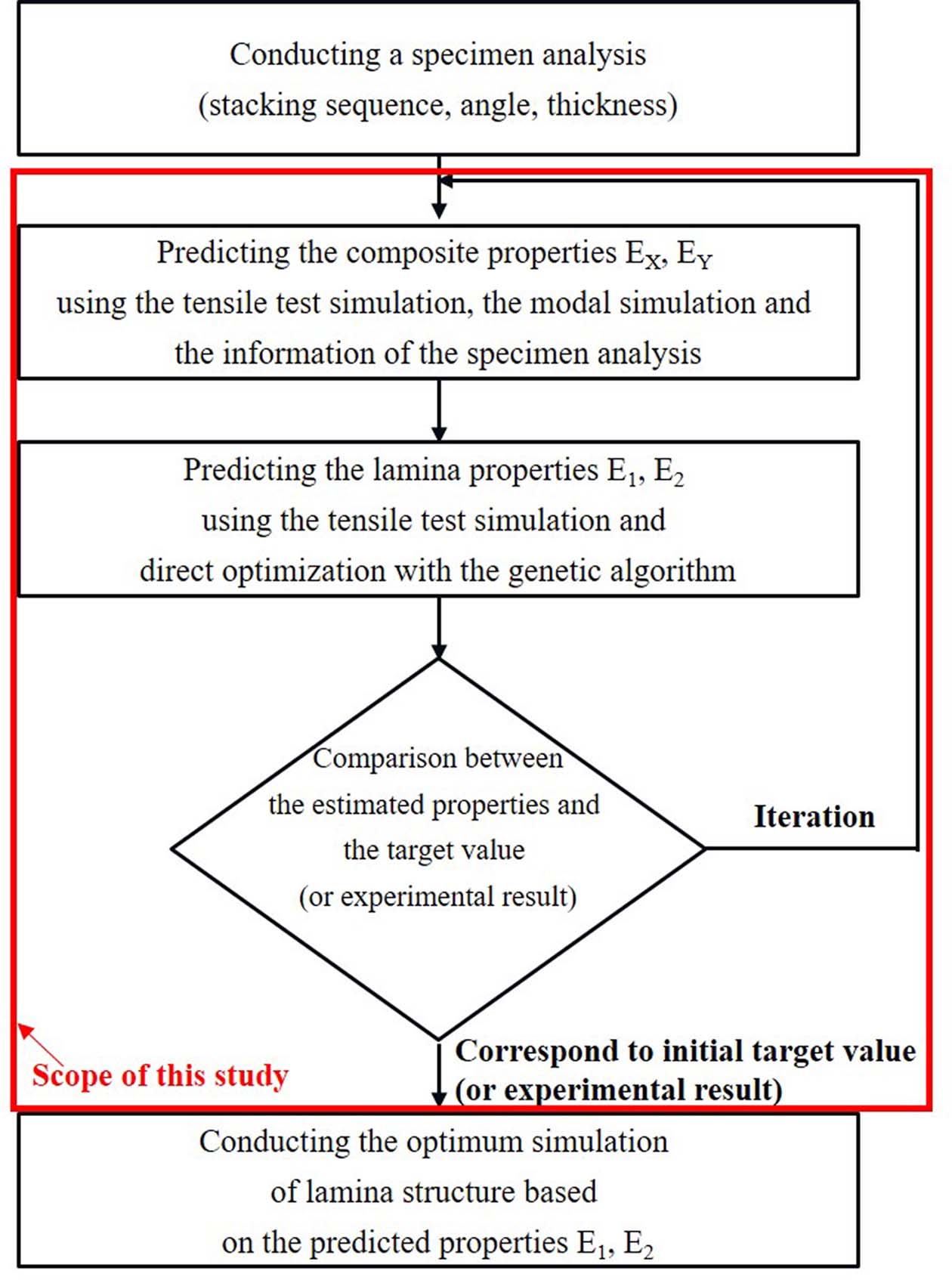
|
Fig. 2 Principle of the prediction of the lamina properties in this research |
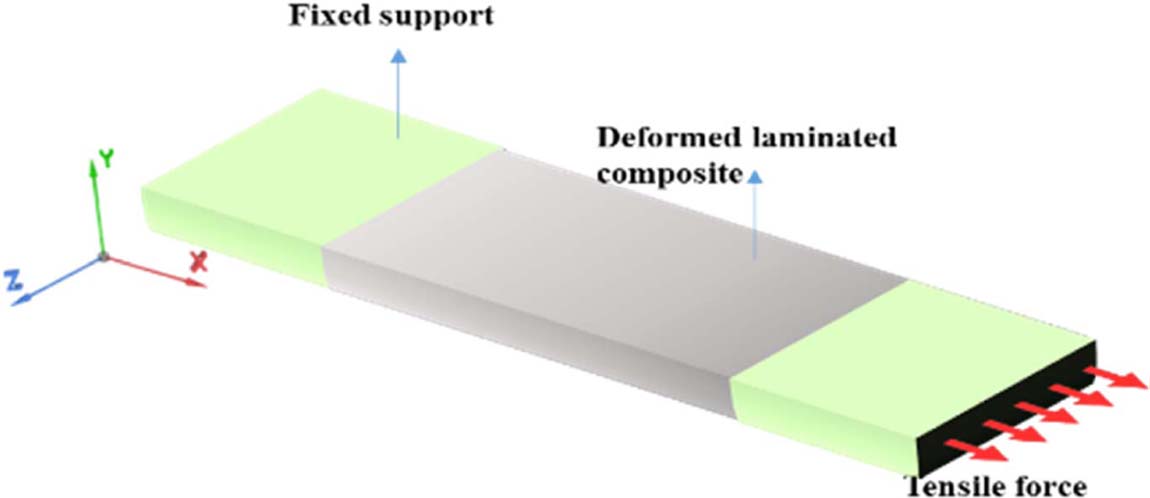
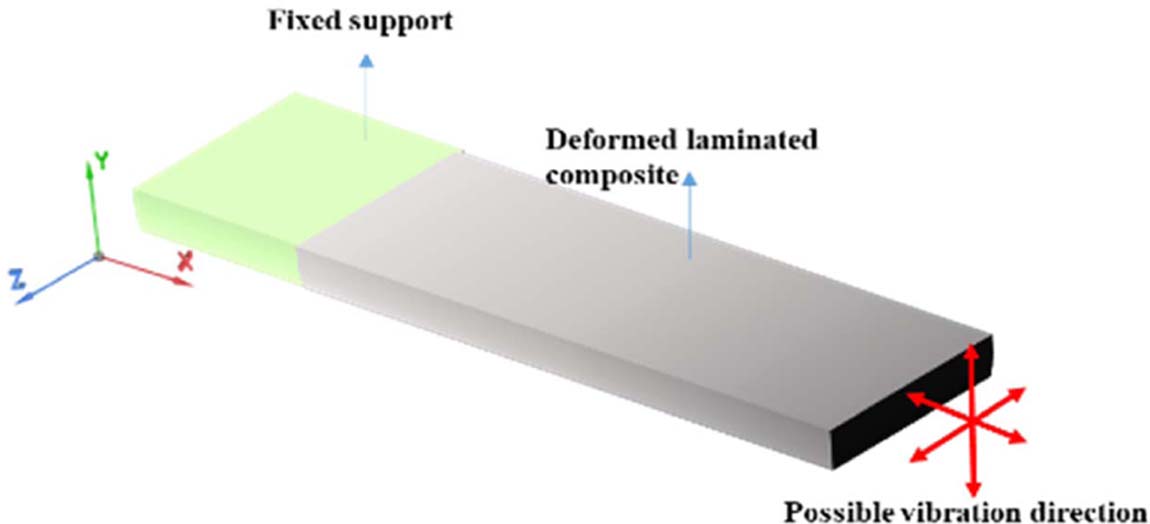
적층 복합재의 인장 시험, 모달 시험의 해석은 상용 유한요소 해석 툴인 ANSYS을 활용했다. 적층 복합재 구조의 3차원 모델링을 위하여 요소는 각 지점에서 X, Y, Z 방향의 3 자유도를 갖는 8개의 노드로 구성된 SOLID 185 요소를 선택했다. 인장 해석을 위한 하중에 대한 경계조건은 실제 인장 시험의 조건과 동일하게 복합재 시편의 한쪽 고정 면에 대하여 Fig. 3과 같이, 좌표의 X-방향으로 2 mm/min의 속도 (복합 재료의 인장 시험의 규격인 ASTM D3039[16]의 시험 조건을 고려함)로 변형이 발생하도록 설정했다. 또한 모달 해석을 위한 경계조건은 Fig. 4와 같이 실제 주파수 응답 특성(FRF) 분석 조건과 동일하도록 시편의 한쪽 일부를 고정하고, 내부 섬유의 비등방성 물성을 고려할 수 있도록 모든 방향에서 진동이 가능하도록 설정했다. 해석 시간의 절약과 절차의 단순화를 위해 선형 해석만을 고려하였고, 재료의 파손은 고려하지 않았다. 변형량에 따른 하중을 확인 후, 사용되는 재료의 최대 인장 강도 등에 따른 파손 여부, 시간에 따른 점진적인 인장에 따른 단계적인 인장 하중 결과 확인을 위한 각각의 해석 결과가 모두 기록된다. 모달 해석는 복합재 시편의 섬유 방향에 따른 다양한 모드 형상을 관찰하기 위하여 6차 주파수 형상까지 해석했다. 시편의 모델은 Fig. 5와 같이 복합재 내부 lamina 층의 순서, 각도, 두께를 고려하여 모델링 한다. 이러한 적층 정보를 고려한 모델 작성은 ANSYS ACP를 활용하여 수행한다. 첫 번째 단계의 해석을 수행하기 위해필요한 재료의 물성은 일반적인 재료 특성 혹은 채취된 시편의 유사 재료의 물성을 입력한다. 경계조건과 입력되는 물성에 관한 정보는 4절에서 설명했다. 경계 조건에 따라 해석 후에, 선형 영역에서 적층 복합재의 변형-응력 곡선을 얻을 수 있다. 얻어진 곡선의 기울기를 통해 적층 복합재의 강성 EX, EY을 예측하고, 비교할 수 있다. 수행된 모달 해석의 결과는 수지 방향에 따른 예측 정확도를 증가시키기 위하여 굽힘, 비틀림, 리드-래그(Lead-lag)의 형상을 보이는 첫 번째 응답 주파수를 확인한다.
|
Fig. 3 Schematic of tensile test simulation for prediction of lamina properties of laminated composite |
|
Fig. 4 Schematic of modal test simulation for prediction of lamina properties of laminated composite |
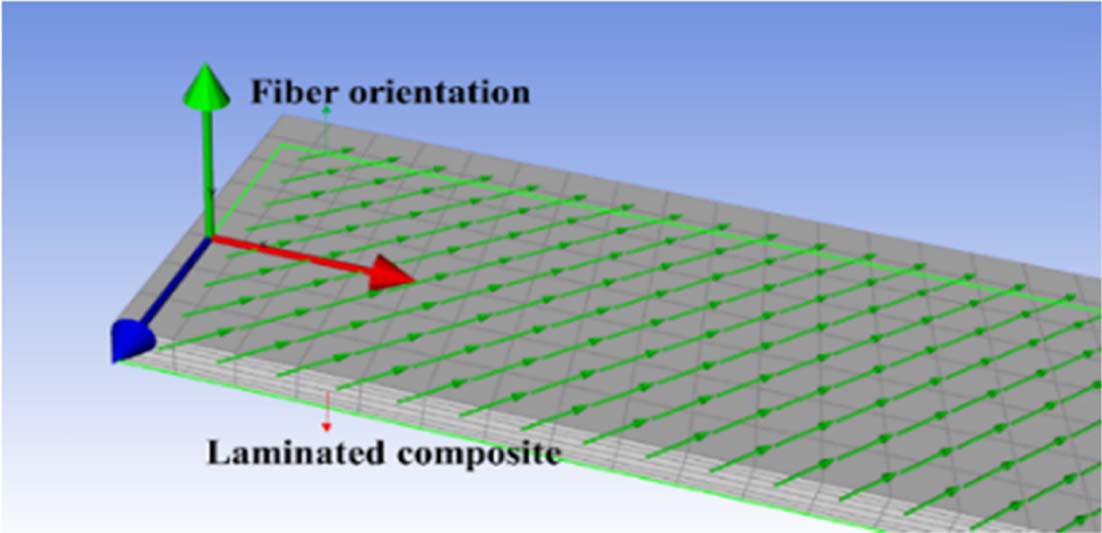
|
Fig. 5 Geometry model of the laminated composite by ANSYS prepost as considering the stacking sequence, angle, thickness of a lamina sheet |
Lamina 층 강성 E1, E2는 인장 시험 해석과 모달 시험 해석을 기반으로 ANSYS의 직접 최적화 툴(Direct optimization tool)을 활용하여 예측된다. 역계산의 시간을 줄이기 위한 예측되는 lamina 층 강성 E1, E2의 경계 범위는 3.1절에서 언급된 적층 복합재의 강성 EX, EY의 해석을 수행하기 위해 임의로 입력한 물성을 기준으로 범위가 선정된다. 예측을 위한 역계산은 직접 최적화 툴의 다목적 유전자 알고리즘(multi-objective genetic algorithm, MOGA)에 의해 수행한다. MOGA 기법은 다중의 목푯값을 계산하는 것이 가능하며, 계산 결과를 통해 최적의 목푯값을 찾는 알고리즘이다. 물성 예측 알고리즘을 안정적으로 수행하고 적절한 해석 시간을 고려하기 위하여, 본 연구에서 선정된 MOGA의 기법의 시작 단계 샘플 수는 20개이며, 반복 횟수 당 증가 샘플 수는 10개이다. 최대 알고리즘 반복 횟수는 20번이다. 알고리즘 반복 수행은 예측된 lamina 층 강성 E1, E2을 활용하여 수행된 인장 시험 해석을 통해 계산된 적층 복합재의 응력과 변형률이 설정한 목표 응력과 변형률이 동일한 값을 획득했거나, 물성을 예측하고자 하는 구조물로부터 추출된 적층 복합재 채취 시편의 인장 시험에서의 응력과 변형률 값과 같아질 때까지 수행한다. 반복되는 인장 시험 해석에서의 경계조건은 첫 번째 해석과 동일한 경계조건으로 자동으로 선정된다. 예측된 lamina 층 강성 E1, E2의 조합들 중에서 목표 응력과 변형률이 동일한 인장 시험 해석 결과를 나타내는 조합이 선정된다. 예측된 lamina 층 강성 E1, E2의 검증은 예측된 적층 복합재의 강성 EX, EY와 실험 측정된 적층 복합재의 강성 EX, EY 혹은 처음 입력되어 계산된 적층 복합재의 강성 EX, EY의 오차율을 통해 수행한다.
연구에서 제시된 적층 복합재 내부의 lamina 층의 강성을 예측하는 역설계 시뮬레이션 알고리즘을 검증하기 위해, 복합재 내부 lamina 층 물성을 임의의 lamina 층 물성 데이터로 입력하여 제시된 시뮬레이션 절차를 수행했다. 예측 정확도는 수행된 시뮬레이션에서의 lamina 층 강성을 활용하여 계산된 적층 복합재의 강성에 의해 확인되었다.
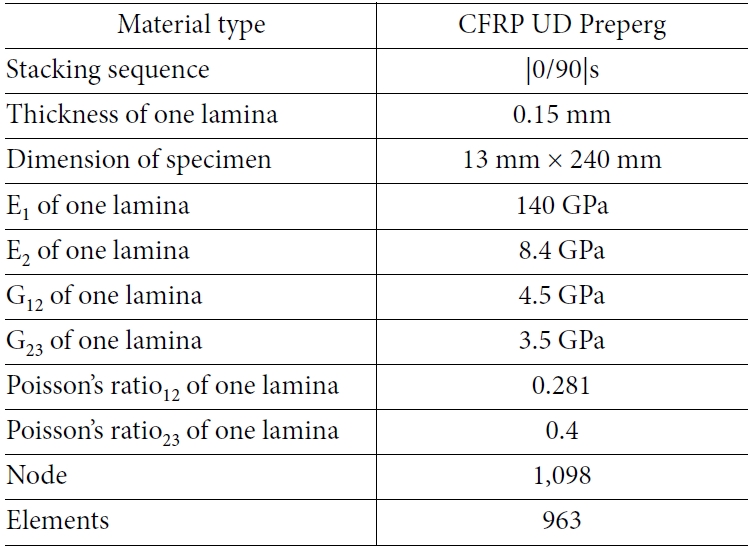
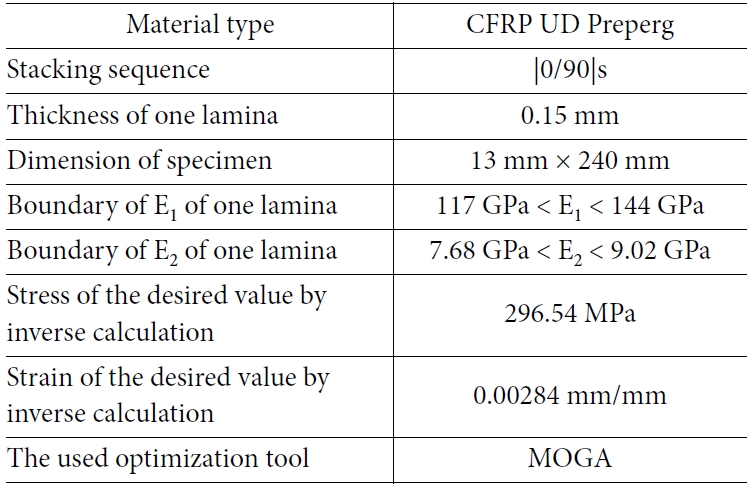
검증을 위한 해석 과정에서는 4개의 CFRP 프리프레그 섬유 시트가 적층된 구조를 가정했다. 시뮬레이션과정을 통해 CFRP의 적층 복합재로부터 CFRP lamina의 물성을 역계산하는 것이 가능한지를 검증하였다. 3장에서 언급된 해석 절차에 따라 인장 시험 해석과 모달 시험 해석을 수행하기 위해 Table 1과 같이 임의의 적층 정보 및 방향성을 고려한 물성을 정의하였다. ANSYS에서 제공되는 일반적인 탄소복합재 프리프래그의 물성을 사용하였으며, 본 연구에서 수행된 해석에서는 탄성영역의 물성만을 고려하기 때문에 Solid 모델의 해석이지만 Table 1에 명시된 이외의 항복과 관련된 물성들은 본 연구의 해석에서는 사용되지 않는다. Fig. 6와 같이 표준 시험 시편을 규격에 따라 적층 복합재 시험 시편을 ANSYS ACP을 이용하여 모델링하고, 표준시험환경과 동일하도록 경계조건을 설정하였다. 모달 해석의 경우, 고정단은 인장시험 해석과 동일하게 적용한 후, 구조물이 모든 방향에서 진동할 수 있도록 어떠한 구속 조건도 설정하지 않았다. 또한, 적층 복합재 시편의 3D 모델은 복합재 내부의 섬유 배향을 고려하여 모델링 되었다. 변형률-응력 곡선(S-S 곡선)은 시편에 대하여 인장 방향으로 0.3 mm 변형이 적용될 때, 계산된 응력과 변형률을 이용하여 작성했다. 연산 시간을 감소시키기 위해 본 연구에서는 탄성 영역의 물성 만을 고려했기 때문에, 총 해석 시간을 1초로 설정하고, 2 mm/min의 인장 속도일 때, 1초 동안에 전체 구조물의 변형은 0.3 mm가 되므로 위와 같은 해석 조건을 선택했다. 이후, Fig. 7과 같이 계산된 S-S 곡선을 활용하여 기울기로부터 적층 복합재 탄성 영역 강도 EX와 EY을 계산하였다.
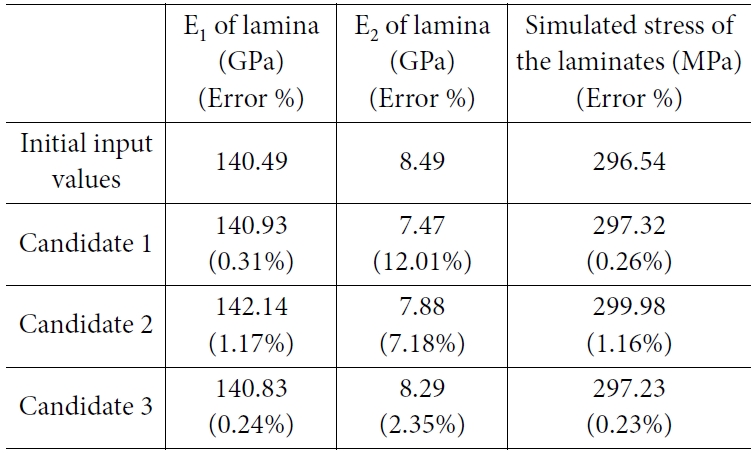
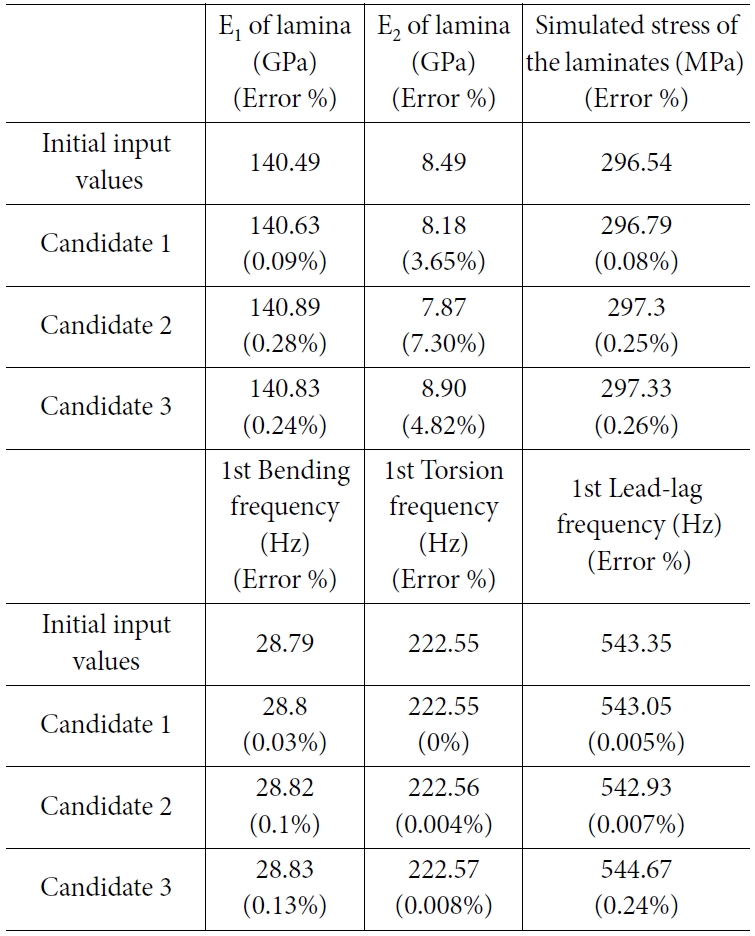
3.2절에서 설명한 것과 같이, 다음 단계에서는 lamina 층 강성 E1과 E2를 예측하기 위한 해석 경계 조건을 Table 2에 나타냈다. 역계산을 위한 응력과 변형량은 적층 복합재 강성 EX와 EY를 예측하기 위해 앞서 수행된 인장 시험 해석과 모달 시험 해석의 결과를 토대로 목푯값을 역계산하도록 설정되었다. 반복 시뮬레이션 루프를 수행하여, 예측 결과에서의 복합재의 응력과 변형률이 목푯값에 근접하도록 유전자 알고리즘 기반으로 lamina 층 강성 E1, E2의 조합을 찾았다. 예측된 E1, E2의 조합과 초기 입력의 물성 (일반적으로 실험 결과와 동일하도록 조절할 수 있는 값)과의 오차를 반복 루프에서 사용된 경계 조건에 따라 Tables 3, 4에 나타냈다.
Table 3에서의 최적화된 후보 3을 통해 계산된 복합재의 응력 오차는 0.23 %, Table 4에서의 최적화된 후보 1을 통해 계산된 응력 오차는 0.08%이므로 반복 루프를 통한 해석 프로세스의 정확도를 증명했다. Table 3에서의 E1의 오차 범위는 0.24-1.17%이며, E2의 오차 범위는 2.35-12.01%이다. 또한, 후보 1의 E2 오차(12.01%)가 후보 2의 E2 오차(7.18%)보다 크더라도 후보 1에서 계산된 응력 오차(0.26%)는 후보 2에서 계산된 응력 오차(1.16%)보다 작다. 이러한 이유는 적층 복합재에서 섬유 방향의 강성은 매우 높은 반면, 매트릭스 방향의 강성은 매우 낮기 때문이다. 이러한 사실을 고려할 때, 예측되는 응력의 결과에 E1은 많은 영향을 미치는 요소이고, 모델링 되는 형상에서 오직 UD 유형의 프리프레그만 고려하였기 때문에 예측 결과에서 E2의 상대적인 큰 오차는 계산 결과에 큰 영향을 미치지 않는다. 따라서 본 연구에서는 정확한 역설계를 수행하고, 예측되는 E2의 물성의 오차를 감소시키기 위해 모달 시험 해석을 통해 동적 특성을 고려하였다. 모달 시험 해석에서 굽힘, 비틀림, Lead-lag의 형상을 보이는 첫 번째 주파수가 반복 루프의 조건으로 고려된 결과인 Table 4에서의 E1의 오차 범위는 0.09- 0.24%이며, E2의 오차 범위는 3.65-7.30%이다. Fig. 8과 같이 예측되는 오차의 범위가 감소하였다. 굽힘이나 리드-래그와 같이 적층 복합재에서의 섬유 방향의 물성에 많은 영향을 받는 시험조건이 고려되었기 때문에, 정확도가 증가했다.
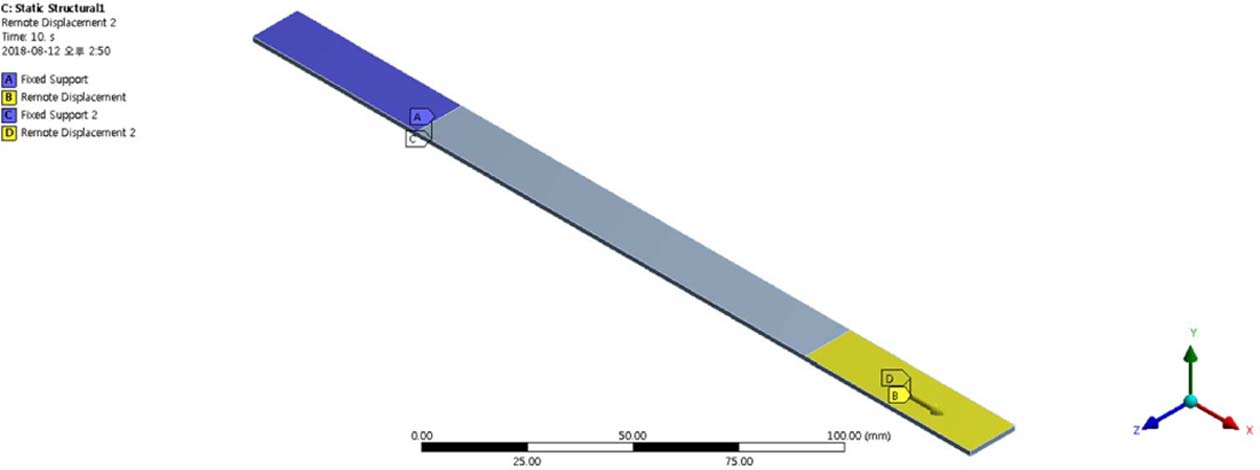
|
Fig. 6 Boundary condition in simulation of tensile test and modal test for calculation of EX and EY |
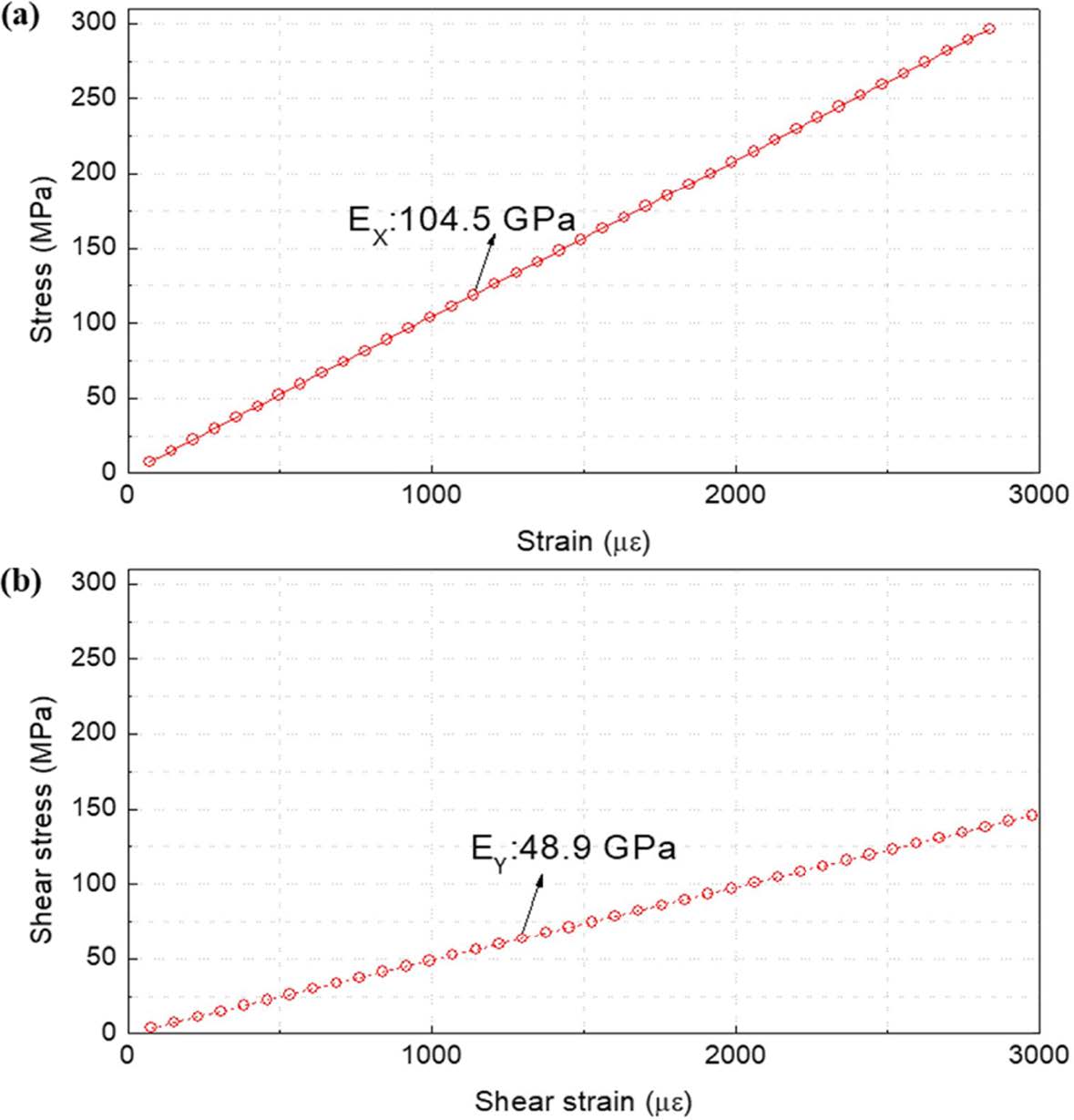
|
Fig. 7 EX and EY of the laminated composite predicted from the slope of the S-S curve that obtained by the tensile test simulation |
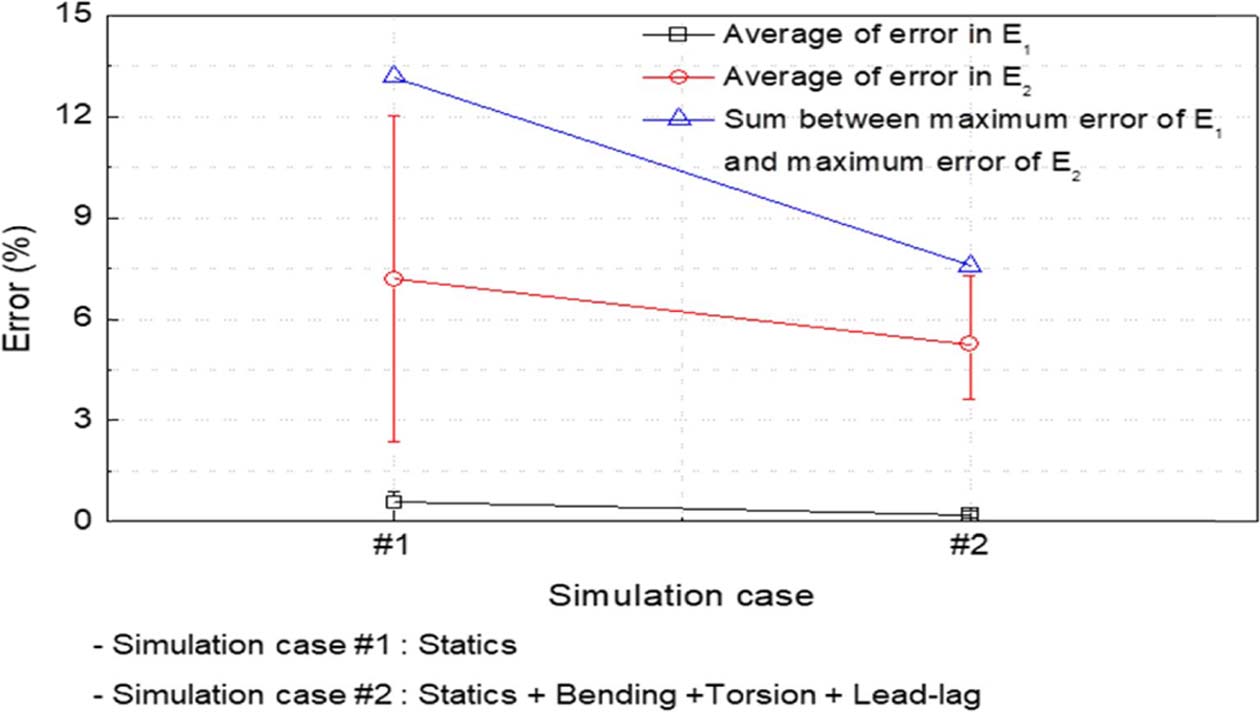
|
Fig. 8 Comparison of estimated E1, E2 according to the simulation condition |
|
Table 1 Boundary condition input in the simulation of tensile test and modal test for calculation of EX and EY |
|
Table 3 Estimated E1, E2 by the simulation in the condition of static (tensile condition) |
|
Table 4 Estimated E1, E2 by the simulation in the condition of statics (tensile) and dynamics (bending + torsion + lead-lag) |
본 논문에서는 적층 복합재료 내부 섬유층의 강성을 예측하는 방법과 관련한 역설계 방법을 제시하였다. 제안된 예측 방법의 핵심은 실제 복합재 구조의 시편을 통해 적층 정보를 기반으로 수행된 실험적 결과 또는 레퍼런스 데이터를 활용하여, 사용된 섬유층의 물성을 예측할 수 있다는 점이다. 강성을 예측하기 위해 적층 정보를 고려한 복합 재의 형상을 ANSYS PrePost를 통해 모델링 했다. 인장 시험 해석과 모달 시험 해석을 사용하여 적층 복합재의 강성 EX, EY를 계산했다. Lamina 층의 강성 E1과 E2는 MOGA를 사용한 반복 계산 알고리즘을 사용하여 예측했다. 검증을 위해 반복 계산 과정의 검증을 수행했다. 동적 특성이 고려된 조건을 고려하여 예측 알고리즘을 수행할 경우 오차율이 감소하는 것을 확인했다. 인장 시험 해석의 경계조건만을 고려한 경우 예측된 적층 복합재의 응력 오차는 0.23%이며, 인장 시험과 모달 분석을 동시에 고려한 경우 예측된 적층 복합재의 응력 오차는 0.08%이므로 반복 루프를 통한 해석 프로세스의 정확도를 증명했다. 또한, 전자의 조건에서는 E1의 오차 범위는 0.24-1.17%이며, E2의 오차 범위는 2.35- 12.01%인 반면, 후자의 조건에서는 E1의 오차 범위는 0.09-0.24%이며, E2의 오차 범위는 3.65-7.30%이다. 예측되는 결과 오차 범위가 감소하였다. 굽힘이나 리드-래그와 같이 적층 복합재에서의 섬유 방향의 물성에 많은 영향을 받는 시험조건이 고려되었기 때문에, 정확도가 증가했다. 제안된 역설계법이 적층 복합재로부터 물성을 역으로 예측할 수 있음을 확인했다. 이러한 해석법은 복합 재료 설계 분야에서 효과적으로 사용될 수 있다고 판단된다.
2018년도 산업통상자원부 및 한국산업기술평가관리원(KEIT) 연구비 지원(과제번호: 20003125)에 의한 연구임.
- 1. Mahmood, M.S., and Davood, R., “Analysis and Optimization of a Composite Leaf Spring,” Composite structures, Vol. 60, No. 3, 2003, pp. 317-325.
-

- 2. Choi, B.H., Lee, J.B., and Choi, B.K., “A Study on the Hysteresis Characteristics and Finite Element Analysis of FRP Leaf Spring,” Journal of Advance Engineering Technology, Vol. 2, No. 2, 2009, pp. 291-298.
- 3. Kim, C.-S., and Park, S.-Y., “Diesel Engine Intake Port Analysis Using Reverse-engineering Technique,” Transactions of the Korean Society of Automotive Engineers, Vol. 23, No. 5, 2009, pp. 502-507.
-

- 4. Roos, T.H., Quin, R.L., De Beer, F.C., and Nshimirimana, R.M., “Neutron Tomography as a Reverse Engineering Method Applied to the IS-60 Rover Gas Turbine,” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, Vol. 651, No. 1, 2011, pp. 329-335.
-

- 5. Dúbravčík, M., and Kender, Š., “Application of Reverse Engineering Techniques in Mechanics System Services,” Procedia Engineering, Vol. 48, 2012, pp. 96-104.
-

- 6. Gameros, A., De Chiffre, L., Siller, H., Hiller, J., and Genta, G., “A Reverse Engineering Methodology for Nickel Alloy Turbine Blades with Internal Features,” CIRP Journal of Manufacturing Science and Technology, Vol. 9, 2015, pp. 116-124.
-

- 7. Oh, S., Chang, B., and Ro, Y., “A Study on the Appropriateness of Virtual Machine for Reverse Engineering,” Transactions of the Korean Society of Automotive Engineers, Vol. 22, No. 6, 2014, pp. 31-38.
-

- 8. Kim, Y.-W., Kim, J.-H., and Jeong, K.-S., “Crash FE Analysis of Front Side Assembly for Reverse Engineering,” Transactions of the Korean Society of Automotive Engineers, Vol. 15, No. 1, 2007, pp. 89-98.
- 9. Gibson, R.F., Principles of Composite Material Mechanics, CRC press, Ohio State Uni., USA, 2011.
-

- 10. Moon, J.B., Kim, J.H., Jang, H.K., and Park, J.S., “A Study on Calculation of Composites Lamina Material Properties through Reverse Engineering of Light Weight Composite Carbody,” Transactions of KSAE, Vol. 25, No. 1, 2017, pp. 1-10.
-

- 11. Lee, Y.-K., Lim, D.-J., Yoon, H.-S., Kim, M.-H., and Kim, C.-H., “Behavior for 2 Ply Rubber/Cord Laminates,” Composites Research, Vol. 16, No. 4, 2003, pp. 1-9.
- 12. Hwang, Y.-T., Lim, J.-Y., Nam, B.-G., and Kim, H.-S., “Analytical Prediction and Validation of Elastic Behavior of Carbon-Fiber-Reinforced Woven Composites,” Composites Research, Vol. 31, No. 5, 2018, pp. 276-281.
-

- 13. Voyiadjis, G.Z., and Kattan, P.I., Mechanics of Composite Materials with MATLAB, Springer Science & Business Media, Louisiana State Uni., USA, 2005.
-

- 14. Zebdi, O., Boukhili, R., and Trochu, F., “An Inverse Approach Based on Laminate Theory to Calculate the Mechanical Properties of Braided Composites,” Journal of Reinforced Plastics and Composites, Vol. 28, No. 23, 2009, pp. 2911-2930.
-

- 15. Sztefek, P., and Olsson, R., “Nonlinear Compressive Stiffness in Impacted Composite Laminates Determined by an Inverse Method,” Composites Part A: Applied Science and Manufacturing, Vol. 40, No. 3, 2009, pp. 260-272.
-

- 16. Standard, A. S. T. M., "Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials," American Society of Testing and Materials D3039/D M 3039, 2008.
 This Article
This Article
-
2019; 32(4): 177-184
Published on Aug 31, 2019
- 10.7234/composres.2019.32.4.177
- Received on Mar 25, 2019
- Revised on Aug 12, 2019
- Accepted on Aug 26, 2019
 Services
Services
- Abstract
1. 서 론
2. lamina 층의 특성을 예측하기 위한 모델링 접근법
3. lamina 층 강성 예측 절차
4. lamina 층 물성 예측 결과
5. 결 론
- 후기
- References
- Full Text PDF
Shared
 Correspondence to
Correspondence to
- Lae-Hyong Kang
-
Department of Mechatronics Engineering, Department of Flexible and Printable Electronics, and LANL-CBNU Engineering Institute-Korea, Chonbuk National University, Jeonju 54896, Korea
- E-mail: reon.kang@jbnu.ac.kr






 Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.
Copyright ⓒ The Korean Society for Composite Materials. All rights reserved.